MEMS陀螺仪的随机误差是影响其输出信噪比的主要因素,降低随机误差对输出精度的影响成为惯性导航研究的重要方向之一。自Allan方差分析法[1]被提出后,通过对时域上采集的陀螺仪信号进行频域稳定性分析,能详细辨识出陀螺仪的各误差项。国外众多学者围绕误差的特性开展相关研究,Dierendonc等[2]采用差分方程法建立随机误差模型,基于梯度下降法计算并获取模型参数,但该方法没有考虑到随机过程的滑动平均部分;Oravetz等[3]用差分器处理非平稳部分,并利用ARMA模型分析数据的平稳特性;Shcheglov等[4]提出一种温度补偿方法,有效提高了陀螺仪的精度。我国对MEMS陀螺仪误差的研究也取得了很大进展,20世纪70年代国内围绕陀螺仪随机漂移建模开展系统研究,其中陈建勤等[5]率先建立了ARMA模型。随后国内科研单位及相关院校逐渐开始陀螺仪随机漂移的理论研究[6-9],基于陀螺仪漂移特性建立数学模型,并通过这些模型进行补偿。吴小文等[10]提出一种基于阈值决策的UKF滤波方法,通过采用无迹卡尔曼滤波对随机噪声进行滤波处理,减小了陀螺仪误差。
本文结合国内外相关技术,针对MEMS陀螺仪建模方法对同型号不同个体存在可适用性的问题提出基于卡尔曼滤波的MEMS陀螺仪随机误差补偿方法,并建立实验方案验证其普适性,结果表明,该方法具有可行性与可靠性。
1 MEMS陀螺仪随机误差辨识由于惯性器件具有振荡特征,对MEMS陀螺仪误差进行处理前,需利用Allan方差法对其随机误差参数进行分析[11-13]。
设t0为陀螺仪随机数据采样时间,N为采样点总和,构成序列wi(i=1, 2, 3, …, N),记每2个连续采样点间的时间间隔为Δt。将获得的N个采样点分为K组,每组采样点记为n=N/K(n≤(N-1)/2),每组所用时间T=nΔt定义为相关时间,得到第k组和第k+1组中陀螺仪输出的平均值为:
| $\begin{array}{l} {\overline w _k}(T) = \frac{1}{n}\sum\limits_{i = 1}^n {{w_{(k - 1)n + i}}} , k = 1, 2, 3, \cdots , K\\ {\overline w _{k + 1}}(T) = \frac{1}{M}\sum\limits_{i = 1}^n {{w_{kn + i}}} , k = 1, 2, 3, \cdots , K \end{array}$ | (1) |
得到Allan方差的表达式为:
| $\begin{array}{c} {\delta ^2}_i(t) = \frac{1}{2} < {[{\overline w _{k + 1}}(T) - {\overline w _k}(T)]^2} > = \\ \frac{1}{{2(K - 1)}}\sum\limits_{k = 1}^{K - 1} {{{[{{\overline w }_{k + 1}}(T) - {{\overline w }_k}(T)]}^2}} \end{array}$ | (2) |
式中,δi(t)为Allan标准差,<>为求平均值。
Allan方差在样本区间进行误差估计的过程中,由于受采样数的限制会产生计算误差,其误差估计公式为:
| $ E{\rm{ = }}\frac{1}{{\sqrt {2(\frac{N}{n} - 1)} }} $ | (3) |
式中,N为总采样数,n为每组样本的采样个数。由式(3)可知,当分组个数增加时,Allan方差的估计误差会减小,即组数越多误差估计的精度越高。
在采集MEMS陀螺仪数据时,采样频率的设置十分重要,频率过高会产生高频噪声,过低则会导致一部分有用信号的缺失[14],影响结果的精度。本文将MEMS陀螺仪的采样频率设置为100 Hz。
假设MEMS陀螺仪对各噪声源独立统计,根据Allan方差与各误差项功率谱密度的关系,即总的Allan方差为各误差项方差之和,可得到由5项误差平方和组成的Allan方差表达式:
| $\begin{array}{l} \delta _{{\rm{total}}}^{\rm{2}} = \delta _Q^2\left( T \right) + \delta _B^2\left( T \right) + \delta _R^2\left( T \right) + \delta _N^2\left( T \right) + \\ \delta _K^2\left( T \right){\rm{ = }}\frac{{3{Q^2}}}{{{T^2}}} + \frac{{2\ln 2}}{{\rm{ \mathsf{ π} }}}{B^2}{\rm{ + }}\frac{{{R^2}{T^2}}}{2} + \frac{{{N^2}}}{T} + \frac{{{K^2}T}}{3} \end{array}$ | (4) |
式中,T为Allan方差分组后每组的相关时间。各误差项都可表示为正比于相关时间T的-2~+2次幂的形式,因此Allan方差模型可表示为:
| ${\delta ^2}_{{\rm total}}(T) = {\delta ^2}{\mathop{\rm total}\nolimits} (T) \approx \sum\limits_{k = - 2}^{k = 2} {{A_k}^2{T^k}} $ | (5) |
将式(5)中的多项式系数采用MATLAB最小二乘拟合,可得如下函数关系:
| $\begin{array}{l} Q = {A_{ - 2}}{\rm{/}}\sqrt 3 \\ N = {A_{ - 1}}\\ B = 1.505{A_0}\\ K = \sqrt 3 {A_1}\\ R = \sqrt 2 {A_2} \end{array}$ | (6) |
式中,Q为陀螺仪量化噪声,N为角度随机游走,B为零偏不稳定性,K为速率随机游走,R为速率斜坡系数。
2 时间序列ARMA建模MEMS陀螺仪的输出数据符合ARMA建模特征,其自相关函数与偏相关函数均具有拖尾性。由于MEMS陀螺仪建模的阶数一般不超过3阶,且通常情况下自回归阶数p较滑动阶数q更大,故可以建立ARMA(i, 1)(i=1, 2, 3)模型,模型的阶数则可以通过AIC准则、BIC准则2种方法确定,其具体计算公式为:
| ${\mathop{\rm AIC}\nolimits} (p, q) = \ln ({\delta ^2}(p, q)) + 2(p + q)/N$ | (7) |
| ${\mathop{\rm BIC}\nolimits} (p, q) = \ln ({\delta ^2}(p, q)) + (p + q) \times \ln (N)/N$ | (8) |
式中,δ2为激励白噪声方差,N为样本总数。把AIC准则和BIC准则最小时p和q的取值称为ARMA模型的定阶。
ARMA模型的表达式为:
| $ \begin{array}{c} {x_t} = {\mathit{\Phi }_1}{x_{t - 1}} + {\mathit{\Phi }_2}{x_{t - 2}} + {\mathit{\Phi }_3}{x_{t - 3}} + \cdots \\ {\mathit{\Phi }_p}{x_{p - 1}} - {\theta _1}{\partial _{t - 1}} - {\theta _2}{\partial _{t - 2}} - \cdots {\theta _n}{\partial _{t - q}} + {\partial _t} \end{array} $ | (9) |
采用自回归逼近方法进行参数估计,计算出Φ1, Φ2, Φ3, …, Φp和θ1, θ2, θ3, …, θq及δa2的值,并建立数据的自回归模型AR。取自回归阶数上界为P0=[N],计算出AR模型的阶数估计
| $\begin{array}{l} {{\hat \partial }_t} = {x_t} - \sum\limits_{j = 1}^{\hat p} {{{\mathit{\hat \Phi }}_j}} {x_{t - j}}, \\ t = \hat p + 1, \hat p + 2, \hat p + 3, \cdots , \hat p + N \end{array}$ | (10) |
近似得到ARMA模型:
| $\begin{array}{l} {x_t} = \sum\limits_{j = 1}^p {{\mathit{\Phi }_j}{x_{t - j}}} + {{\hat \partial }_t} + \sum\limits_{k = 1}^q {{\theta _k}{{\hat \partial }_{t - k}}} , \\ t = L + 1, L + 2, \cdots , N \end{array}$ | (11) |
式中,
| $Q(\mathit{\Phi }, \theta ) = \sum\limits_{t = L + 1}^N {{{({x_t} - \sum\limits_{j = 1}^p {{\mathit{\Phi }_j}{x_{t - j}}} - \sum\limits_{k = 1}^q {{\theta _k}{{\hat \partial }_{t - k}}} )}^2}} $ | (12) |
得到δa2的最小二乘估计式为:
| ${\hat \delta ^2}_a{\rm{ = }}\frac{1}{{N - L}}Q({\mathit{\Phi }_1}, {\mathit{\Phi }_2}, {\mathit{\Phi }_3}, \cdots , {\mathit{\Phi }_p}, {\theta _1}, {\theta _2}, {\theta _3}, \cdots , {\theta _q})$ | (13) |
将式(12)改写,得到Φ和θ的最小二乘估计式为:
| $ Q(\mathit{\Phi }, \theta ) = {\left| {\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{\bar X}}\mathit{\Phi } - \bar \partial \theta } \right|^2} = {\left| {\mathit{\boldsymbol{X}} - (\mathit{\boldsymbol{\bar X}}, \bar \partial )z} \right|^2} $ | (14) |
其中,X=[xL+1 xL+2 … xL+3T],
| $ \mathit{\boldsymbol{\bar X}} = \left[ {\begin{array}{*{20}{c}} {{x_L}}&{{x_{L - 1}}}& \cdots &{{x_{L - p + 1}}}\\ {{x_{L + 1}}}&{{x_L}}& \cdots &{{x_{L - p + 2}}}\\ \vdots & \vdots & \vdots & \vdots \\ {{x_{N - 1}}}&{{x_{N - 1}}}& \cdots &{{x_{N - 1}}} \end{array}} \right], \\\bar \partial {\rm{ = }}\left| {\begin{array}{*{20}{c}} {{{\hat \partial }_L}}&{{{\hat \partial }_{L - 1}}}& \cdots &{{{\hat \partial }_{L - q + 1}}}\\ {{{\hat \partial }_{L + 1}}}&{{{\hat \partial }_L}}& \cdots &{{{\hat \partial }_{L - q + 2}}}\\ \vdots & \vdots & \vdots & \vdots \\ {{{\hat \partial }_N}}&{{{\hat \partial }_{N - 2}}}& \cdots &{{{\hat \partial }_{N - q}}} \end{array}} \right|, \mathit{\boldsymbol{\beta }} = \left[ {\begin{array}{*{20}{c}} \mathit{\Phi }\\ \theta \end{array}} \right]。$ |
由此可得:
| ${(\mathit{\boldsymbol{\bar X}}, \bar \partial )^{\rm{T}}}[\mathit{\boldsymbol{X}} - (\mathit{\boldsymbol{\bar X}}, \bar \partial )\mathit{\boldsymbol{\beta }}] = 0$ | (15) |
当
| $ \begin{array}{c} \left[\begin{array}{l}\mathit{\Phi } \\ {\theta}\end{array}\right]=\left[[\overline{\boldsymbol{X}}, \bar{\partial}]^{\mathrm{T}}[\overline{\boldsymbol{X}}, \overline{{\partial}}]\right]^{-1}[\overline{\boldsymbol{X}}, \overline{{\partial}}]^{\mathrm{T}} \boldsymbol{X}=\\ \left[\begin{array}{cc}{\overline{\boldsymbol{X}}^{\mathrm{T}} \overline{\boldsymbol{X}}} & {\overline{\boldsymbol{X}}^{\mathrm{T}} \bar{\partial}} \\ {\bar{\partial}^{\mathrm{T}} \overline{\boldsymbol{X}}} & {\bar{\partial}^{\mathrm{T}} \bar{\partial}}\end{array}\right]^{-1}\left[\begin{array}{l}{\overline{\boldsymbol{X}}^{\mathrm{T}} \boldsymbol{X}} \\ {\overline{{\partial}}^{\mathrm{T}} \boldsymbol{X}}\end{array}\right] \end{array} $ | (16) |
对预处理后的陀螺仪随机漂移数据建立ARMA模型,通过自回归逼近的方法获得模型参数,并利用式(7)和式(8)求得AIC准则和BIC准则的值,结果见表 1。
|
|
表 1 各ARMA模型参数对比 Tab. 1 Comparison of each ARMA model parameters |
根据AIC准则和BIC准则值越小、模型适用性越强的原则,对比表 1中3种模型的AIC准则和BIC准则值可看出,ARMA(2, 1)模型值最小,故本文选取ARMA(2, 1)模型作为MEMS陀螺仪随机漂移的时间序列模型,得到:
| $ \hat x(t) = - 0.181{\rm{ }}0\hat x(t - 1) + 0.129{\rm{ }}9\hat x(t - 2) - 0.467{\rm{ }}8\hat \partial (t) + \varepsilon (t) $ | (17) |
将卡尔曼滤波应用到MEMS陀螺仪随机误差补偿中,首先应明确观测量和状态转移矩阵。由于原始信号为静态采样,可将随机误差作为系统输入,又由随机信号ARMA(2, 1)模型,可通过将n个随机信号Xn设为状态量将ARMA模型参数应用到卡尔曼滤波状态方程中。
ARMA(2, 1)模型为:
| $ {x_k} = {\mathit{\Phi }_1}{x_{k - 1}} + {\mathit{\Phi }_2}{x_{k - 2}} - {\theta _1}{\partial _{k - 1}} + {\partial _k} $ | (18) |
式中,xk为ARMA模型的输出,∂k为白噪声(均值为0,方差为δa2)。假设系统状态矩阵为Xk=[xk, xk-1]T,过程噪声为Vk=[∂k, 0]T,确定状态方程系数:
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\Phi }_1}}&{{\mathit{\Phi }_2}}\\ 1&0 \end{array}} \right]{\rm{ , }}\mathit{\boldsymbol{B}}{\rm{ = }}\left[ {\begin{array}{*{20}{c}} 1&{{\theta _1}}\\ 0&0 \end{array}} \right] $ | (19) |
设Wk为模型误差估计,Yk为系统输出,则:
| $ \boldsymbol{X}_{k}=\hat{\boldsymbol{X}}_{k}+\boldsymbol{W}_{k}, \boldsymbol{Y}_{k}=\boldsymbol{C} \boldsymbol{X}_{k}+\boldsymbol{W}_{k} $ | (20) |
其中,C=[1 0]。通过系统方程可获得卡尔曼递推公式,再将实测漂移数据作为滤波器输入,则:
| $ \begin{array}{l} {{\mathit{\boldsymbol{\hat X}}}_{k, k - 1}} = \mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{\hat X}}}_{k - 1, k - 1}}\\ {{\mathit{\boldsymbol{\hat X}}}_{k, k}} = {{\mathit{\boldsymbol{\hat X}}}_{k - 1, k - 1}} + {\mathit{\boldsymbol{K}}_k}\mathit{\boldsymbol{[}}{\mathit{\boldsymbol{Y}}_k} - {\mathit{\boldsymbol{C}}_k}{{\mathit{\boldsymbol{\hat X}}}_{k, k - 1}}\mathit{\boldsymbol{]}}\\ {\mathit{\boldsymbol{K}}_k} = {\mathit{\boldsymbol{P}}_{k, k - 1}}{\mathit{\boldsymbol{C}}^\mathit{\boldsymbol{T}}}{\mathit{\boldsymbol{[C}}{\mathit{\boldsymbol{P}}_{k, k - 1}} + {\mathit{\boldsymbol{R}}_k}\mathit{\boldsymbol{]}}^{\mathit{\boldsymbol{ - 1}}}}\\ {\mathit{\boldsymbol{P}}_{k, k - 1}} = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{P}}_{k, k - 1}}{\mathit{\boldsymbol{A}}^\mathit{\boldsymbol{T}}} + \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{Q}}_{k - 1}}{\mathit{\boldsymbol{B}}^\mathit{\boldsymbol{T}}}\\ {\mathit{\boldsymbol{P}}_{k, k}} = [\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_k}\mathit{\boldsymbol{C}}]{\mathit{\boldsymbol{P}}_{k, k - 1}}\\ {{\mathit{\boldsymbol{\hat Y}}}_k} = \mathit{\boldsymbol{C}}{{\mathit{\boldsymbol{\hat X}}}_{k, k}} \end{array} $ | (21) |
式中,
为验证本文提出的MEMS陀螺仪随机误差补偿方法的普适性,将实验室现有的6套同型号MEMS陀螺仪惯性测量单元安装于三轴惯性测试转台(图 1)。设备预热10 min后,同步采集6套系统30 min的陀螺仪输出数据并存储,以X轴陀螺仪为例对提取的陀螺仪数据进行分析。

|
图 1 测试环境 Fig. 1 The test environment |
根据建立的时间序列ARMA(2, 1)模型,将预处理后的每组MEMS陀螺仪随机漂移数据作为卡尔曼滤波输入值,分别进行3次卡尔曼滤波处理。图 2为6组惯性测量单元中同一轴向MEMS陀螺仪每组输出数据经3次卡尔曼滤波后的曲线及Allan方差分析后各误差项系数的变化。

|
图 2 卡尔曼滤波前后陀螺仪输出曲线与Allan方差处理后对比结果 Fig. 2 Comparison of gyro output curve and Allen variance analysis before and after Kalman filtering |
由图 2对比分析可知,时间序列ARMA模型经卡尔曼滤波后,6个MEMS陀螺仪输出信息的幅值都呈明显减少趋势,且随着卡尔曼滤波次数的增加,MEMS陀螺仪的输出幅度越来越小,Allan标准差对数曲线随滤波次数的增加呈明显下移变化。为进一步验证该方法的有效性,计算6组陀螺仪的输出均值、标准差及参数并对比,结果见表 2~6。
|
|
表 2 滤波前后均值对比结果(单位(°)/h) Tab. 2 Comparison of mean values before and after filtering |
|
|
表 3 卡尔曼滤波前后的标准差(单位(°)/h) Tab. 3 Standard deviation before and after Kalman filtering |
|
|
表 4 卡尔曼滤波前后的量化噪声(单位μrad) Tab. 4 Quantization noise before and after Kalman filtering |
|
|
表 5 卡尔曼滤波前后的角度随机游走(单位(°)/h1/2) Tab. 5 Angle random walk before and after Kalman filtering |
|
|
表 6 卡尔曼滤波前后的零偏不稳定性(单位(°)/h) Tab. 6 Zero-bias instability before and after Kalman filtering |
由表 2~6可知,6组MEMS陀螺仪数据经3次卡尔曼滤波处理后,均值和标准差明显减小,对应的误差项系数也都明显降低。1次卡尔曼滤波后所有陀螺仪的随机误差降低近50%,且随着滤波次数的增加,随机误差降低程度更高,证实基于时间序列ARMA模型的卡尔曼滤波建模方法对降低陀螺仪的随机误差具有有效性和普适性,能很好地提高MEMS陀螺仪的精度。
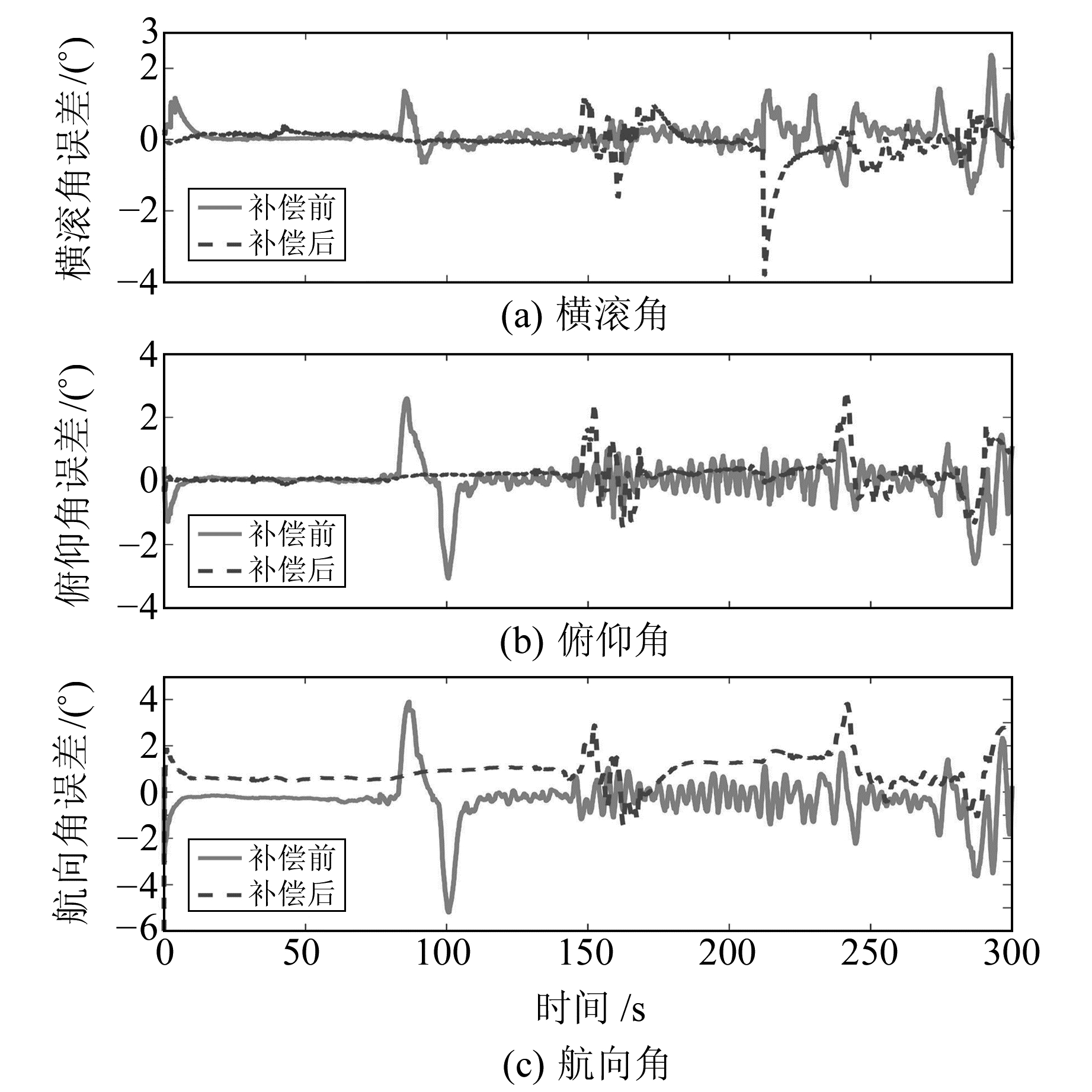
为进一步验证本文滤波方法对系统导航精度的影响,随机选取一组IMU处理前后的数据开展导航解算,获取的三维姿态对比结果见图 3和表 7。
|
图 3 陀螺仪误差补偿前后姿态角误差对比曲线 Fig. 3 Comparison curve of attitude angle error before and after gyro error compensation |
|
|
表 7 陀螺仪误差补偿前后姿态角误差的均值和均方差 Tab. 7 Mean and mean square error of attitude angle before and after gyro error compensation |
通过对比可以看出,对陀螺仪输出滤波后解算得到的载体三维姿态误差的均值和标准差均优于未滤波前获取的结果,特别是航向角的效果更为明显,误差均值由1.450 4降为0.849 3,标准差也由2.210 8降为0.654 4。该结果进一步验证卡尔曼滤波方法对提高陀螺仪的输出信噪比具有可行性。
5 结语本文提出采用卡尔曼滤波方法对同型号不同MEMS陀螺仪个体的随机误差进行估计补偿,并验证该随机误差补偿方法的普适性。通过建立时间序列ARMA模型,并对随机误差进行3次卡尔曼滤波处理,利用Allan方差对比分析滤波前后的误差辨识结果,基于实验室现有的6只同型号MEMS陀螺仪惯性测量单元和三轴惯性测试转台建立实验环境。结果表明,滤波后的各误差项系数有明显的降低,且误差衰减程度随滤波次数的增加而增大。该结果在6组测试设备中呈现一致性,证明了本文方法具有普适性。为进一步验证该方法对提高惯导系统导航精度的可行性,开展滤波前后姿态求取对比实验,滤波后求取的载体姿态误差的均值和标准差均优于未处理的姿态误差结果,证明本文方法具有可行性。
| [1] |
Percival D B. A Wavelet Perspective on the Allan Variance[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2016, 63(4): 538-554 DOI:10.1109/TUFFC.2015.2495012
(  0) 0) |
| [2] |
Dierendonc V A J, Brown R G. Modeling Nonstationary Random Processes with an Application to Gyro Drift Rate[J]. IEEE Transactions on Aerospace and Electronic Systems, 1969, 5(3): 423-428
(  0) 0) |
| [3] |
Oravetz A S, Sandberg H J. Stationary and Nonstationary Characteristics of Gyro Drift Rate[J]. AIAA Journal, 1970, 8(10): 1766-1772 DOI:10.2514/3.5988
(  0) 0) |
| [4] |
Shcheglov K, Evans C, Gutierrez R, et al. Temperature Dependent Characteristics of the JPL Silicon MEMS Gyroscope[C]. IEEE Aerospace Conference, Montana, 2000
(  0) 0) |
| [5] |
陈建勤, 席裕庚, 张钟俊. 一种简单的确定ARMA模型结构的方法[J]. 上海交通大学学报, 1996, 30(4): 25-29 (Chen Jianqin, Xi Yugeng, Zhang Zhongjun. A Simple Method for Srructure Determination of ARMA Model[J]. Journal of Shanghai Jiaotong University, 1996, 30(4): 25-29)
(  0) 0) |
| [6] |
张玉莲, 储海荣, 张宏巍, 等. MEMS陀螺随机误差特性研究及补偿[J]. 中国光学, 2016, 9(4): 501-510 (Zhang Yulian, Chu Hairong, Zhang Hongwei, et al. Characterists and Compensation Method of MEMS Gyroscope Random Error[J]. Chinese Optics, 2016, 9(4): 501-510)
(  0) 0) |
| [7] |
王新龙, 李娜. MEMS陀螺随机误差的建模与分析[J]. 北京航空航天大学学报, 2012, 38(2): 170-174 (Wang Xinlong, Li Na. Error Modeling and Analysis for Random Drift of MEMS Gyroscopes[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(2): 170-174)
(  0) 0) |
| [8] |
孙伟, 文剑, 张远, 等. MEMS陀螺仪随机误差的辨识与降噪方法研究[J]. 电子测量与仪器学报, 2017, 31(1): 15-20 (Sun Wei, Wen Jian, Zhang Yuan, et al. Research on Random Error Identification and Denoising Method of MEMS Gyroscope[J]. Journal of Electronic Measurement and Instrumentation, 2017, 31(1): 15-20)
(  0) 0) |
| [9] |
张谦, 王玮, 王蕾, 等. 基于动态Allan方差的光纤陀螺仪随机误差分析及算法改进[J]. 光学学报, 2015, 35(4): 57-63 (Zhang Qian, Wang Wei, Wang Lei, et al. Research on Random Errors of Fiber Optic Gyro Based on Dynamic Allan Variance and Algorithm Improvement[J]. Acta Optica Sinica, 2015, 35(4): 57-63)
(  0) 0) |
| [10] |
吴小文, 李擎. UKF在MEMS陀螺随机噪声补偿的应用[J]. 火力与指挥控制, 2013, 38(6): 8-10 (Wu Xiaowen, Li Qing. Research on Application of UKF to Compensation of MEMS Gyro Random Noise[J]. Fire Control and Command Control, 2013, 38(6): 8-10 DOI:10.3969/j.issn.1002-0640.2013.06.003)
(  0) 0) |
| [11] |
Quinvhia A G, Ferrer C, Falco G, et al. Analysis and Modelling of MEMS Inertial Measurement Unit[C]. 2012 International Conference on Localization and GNSS, Starnberg, 2012
(  0) 0) |
| [12] |
徐韩, 曾超, 黄清华. 基于卡尔曼滤波算法的MEMS陀螺仪误差补偿研究[J]. 传感技术学报, 2016, 29(7): 962-965 (Xu Han, Zeng Chao, Huang Qinghua. Drift Compensation of MEMS Gyro with Kalman Filtering Algorithm[J]. Chinese Journal of Sensors and Actuators, 2016, 29(7): 962-965 DOI:10.3969/j.issn.1004-1699.2016.07.002)
(  0) 0) |
| [13] |
Sun W, Ding W, Yan H F, et al. Zero Velocity Interval Detection Based on Continuous Hidden Markov Model in Micro Inertial Pedestrian Navigation[J]. Measurement Science and Technology, 2018, 29(6): 1-7
(  0) 0) |
| [14] |
杜少林, 陈书钊, 陈鹏光, 等. 基于Allan方差的MEMS陀螺仪噪声分析[J]. 仪表技术与传感器, 2018(5): 20-22 (Du Shaolin, Chen Shuzhao, Chen Pengguang, et al. Analysis of MEMS Gyroscope Noise Based on Allan Variance[J]. Instrument Technique and Sensor, 2018(5): 20-22 DOI:10.3969/j.issn.1002-1841.2018.05.005)
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39


