2. 高速铁路运营安全空间信息技术国家地方联合工程实验室,成都市二环路北一段111号,610031
不同三维空间直角坐标系统之间的转换是测绘学科中十分重要的环节,而对于大旋转角的坐标转换已有许多研究成果,如七参数模型[1-2]、十三参数模型[3]、四元数模型[4]、罗德里格矩阵模型[5]等。在对转换参数进行求解时,大多采用高斯-牛顿迭代法[1-4],但该方法对初值的选取有很强的依赖性,若初值选取不合理会导致求解结果完全失真[6]。在进行三维坐标转换时,由于选取的公共点经常是非均匀分布且都在局部区域,转换模型的法方程矩阵条件数较大,超过105数量级,即法方程矩阵存在严重的病态性。病态问题的存在使法方程的解很不稳定,岭估计法[7]被认为是求解病态方程的有效方法之一,但该方法改变了方程的等量关系,使估计结果有偏。王新洲等[8-9]提出的谱修正迭代法既保留了法方程解算过程中数值的稳定性,又不改变方程的等量关系,计算结果无偏,但该方法需迭代求解,收敛慢、效率低。
本文基于单位实四元数的大旋转角坐标转换模型,提出一种基于岭参数和泛函矩阵的改进谱修正迭代算法,该算法利用单位实四元数构造旋转矩阵,建立坐标转换模型,并采用谱修正迭代法求解转换参数。考虑到模型法方程矩阵的病态性和谱修正迭代法收敛慢、效率低的特点,引入岭参数和泛函矩阵对谱修正迭代法进行改进,在有效降低由法方程矩阵病态问题造成的影响的同时,也使计算过程中的迭代次数达到优化,提高计算效率。
1 单位实四元数与三维坐标转换根据三维坐标变换的几何意义可得其数学模型为:
| $ \left[ {\begin{array}{*{20}{c}} {{{X'}_i}}\\ {{{Y'}_i}}\\ {{{Z'}_i}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{X_0}}\\ {{Y_0}}\\ {{Z_0}} \end{array}} \right] + (1 + \mu )\mathit{\boldsymbol{R}}\left[ {\begin{array}{*{20}{c}} {{X_i}}\\ {{Y_i}}\\ {{Z_i}} \end{array}} \right] $ | (1) |
式中,(X′i, Y′i, Z′i)和(Xi, Yi, Zi)(i=1, 2, …, n)分别为目标坐标系与原坐标系中的坐标值;(X0, Y0, Z0)为坐标原点平移参数;(1+μ)为两个坐标系的尺度参数;R为旋转矩阵。对于七参数模型,R为3个旋转矩阵RX(α)、RY(β)、RZ(γ)的乘积,即
| $ \begin{array}{c} \mathit{\boldsymbol{R}} = {\mathit{\boldsymbol{R}}_X}(\alpha ){\mathit{\boldsymbol{R}}_Y}(\beta ){\mathit{\boldsymbol{R}}_Z}(\gamma ) = \\ \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&{\cos \alpha }&{\sin \alpha }\\ 0&{ - \sin \alpha }&{\cos \alpha } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\cos \beta }&0&{ - \sin \beta }\\ 0&1&0\\ {\sin \beta }&0&{\cos \beta } \end{array}} \right]\\ \left[ {\begin{array}{*{20}{c}} {\cos \gamma }&{\sin \gamma }&0\\ { - \sin \gamma }&{\cos \gamma }&0\\ 0&0&1 \end{array}} \right] \end{array} $ | (2) |
四元数的概念最早由Hamilton提出,目的是在空间矢量的研究中找到类似解决平面问题时使用的复数方法[10]。在测绘领域,四元数主要应用于摄影测量解算、数字图像处理、大地坐标变换和三维坐标转换等方面。假设三维旋转变换对应的单位实四元数为Q=q0+q1i+q2j+q3k,可得由实四元数Q的分量表示的旋转矩阵R [11]:
| $ \mathit{\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} {q_0^2 + q_1^2 - q_2^2 - q_3^2}&{2({q_1}{q_2} - {q_0}{q_3})}&{2({q_1}{q_3} + {q_0}{q_2})}\\ {2({q_1}{q_2} + {q_0}{q_3})}&{q_0^2 - q_1^2 + q_2^2 - q_3^2}&{2({q_2}{q_3} - {q_0}{q_1})}\\ {2({q_1}{q_3} - {q_0}{q_2})}&{2({q_2}{q_3} + {q_0}{q_1})}&{q_0^2 - q_1^2 - q_2^2 + q_3^2} \end{array}} \right] $ | (3) |
旋转矩阵R中的4个参数中只有3个是独立的,因为旋转矩阵对应的实四元数是单位实四元数,故有:
| $ q_{0}^{2}+q_{1}^{2}+q_{2}^{2}+q_{3}^{2}=1 $ | (4) |
将式(3)代入式(1)中,在所有未知参数的近似值处进行泰勒级数展开并保留至一次项,表示成误差方程的形式可得:
| $ {\mathit{\boldsymbol{V}}_i} = {\mathit{\boldsymbol{A}}_i}\mathit{\boldsymbol{\hat x}} - {\mathit{\boldsymbol{L}}_i}, i = 1, 2, \cdots , n $ | (5) |
根据式(4)可列出线性化的限制条件方程:
| $ \mathit{\boldsymbol{B\hat x}} + \mathit{\boldsymbol{W}} = 0 $ | (6) |
式(5)和式(6)的具体形式可参考文献[4]。
令N=ATPA,权阵P一般设为单位阵,利用拉格朗日乘数法按附有限制条件的间接平差解算式(5)和式(6),得到法方程:
| $ \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{N}}&{{\mathit{\boldsymbol{B}}^T}}\\ \mathit{\boldsymbol{B}}&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat x}}}\\ \mathit{\boldsymbol{K}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}^T}\mathit{\boldsymbol{PL}}}\\ { - \mathit{\boldsymbol{W}}} \end{array}} \right] $ | (7) |
式中,K为对应限制条件方程的联系数向量。
2 病态问题的岭估计求解设有观测方程:
| $ \mathit{\boldsymbol{L}} = \mathit{\boldsymbol{AX}} + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }} $ | (8) |
式中,L为n×1观测向量,A为n×m系数矩阵,X为m×1未知参数向量,Δ为n×1观测误差向量,P为权阵。式(8)的最小二乘估计为:
| $ {\mathit{\boldsymbol{\hat x}}_{LS}} = {({\mathit{\boldsymbol{A}}^T}\mathit{\boldsymbol{PA}})^{ - 1}}({\mathit{\boldsymbol{A}}^T}\mathit{\boldsymbol{PL}}) $ | (9) |
当法矩阵条件数较大,即法矩阵呈病态时,即使观测向量的误差很小也会使解的相对误差很大,所得结果失真严重[12]。
根据Tikhonov正则化原理[13],式(8)的岭估计解为:
| $ \mathit{\boldsymbol{\hat x}} = {({\mathit{\boldsymbol{A}}^T}\mathit{\boldsymbol{PA}} + \alpha \mathit{\boldsymbol{I}})^{ - 1}}({\mathit{\boldsymbol{A}}^T}\mathit{\boldsymbol{PL}}) $ | (10) |
式中,α为岭参数,一般为较小的正数,I为单位阵。
与最小二乘法相比,式(10)通过加入稳定泛函的方式使法方程矩阵ATPA的主对角线元素增加了一个α项,法方程矩阵的条件数变小,方程的病态性减弱,法方程求逆变得正常,因而能得到可靠的估值。但由于引入了一个αI项,使方程的等量关系发生了变化,导致得到的解是有偏估计。
3 基于岭参数的谱修正迭代法 3.1 谱修正迭代法岭估计法等有偏估计方法会破坏方程的等量关系,且解是有偏估计,而谱修正迭代法具有保持方程等量关系且解是无偏估计的优点。其迭代公式为:
| $ {\mathit{\boldsymbol{\hat X}}^{(n)}} = {({\mathit{\boldsymbol{A}}^T}\mathit{\boldsymbol{PA}} + \mathit{\boldsymbol{I}})^{ - 1}}({\mathit{\boldsymbol{A}}^T}\mathit{\boldsymbol{PL}} + {\mathit{\boldsymbol{\hat X}}^{(n - 1)}}) $ | (11) |
当法方程严重病态时,会导致谱修正迭代法出现收敛速度慢、迭代效率低的现象,为此需要对谱修正迭代法进行改进,以提高收敛效率和迭代精度。
3.2 改进谱修正迭代法对于谱修正迭代法的改进,徐文等[14]采用的迭代公式为:
| $ {\mathit{\boldsymbol{\hat X}}^{(n)}} = {({\mathit{\boldsymbol{A}}^T}\mathit{\boldsymbol{PA}} + (\alpha + 1)\mathit{\boldsymbol{I}})^{ - 1}}({\mathit{\boldsymbol{A}}^T}\mathit{\boldsymbol{PL}} + {\mathit{\boldsymbol{\hat X}}^{(n - 1)}}) $ | (12) |
该公式只是在系数矩阵中加入岭参数,并不是严格意义上的谱修正迭代。而刘斌等[15]采用的迭代公式为:
| $ {\mathit{\boldsymbol{\hat X}}^{(n)}} = {({\mathit{\boldsymbol{A}}^T}\mathit{\boldsymbol{PA}} + \mathit{\boldsymbol{K}})^{ - 1}}({\mathit{\boldsymbol{A}}^T}\mathit{\boldsymbol{PL}} + \mathit{\boldsymbol{K}}{\mathit{\boldsymbol{\hat X}}^{(n - 1)}}) $ | (13) |
其中,K为对角矩阵。虽然对角矩阵的加入可有效降低系数矩阵病态性带来的不利影响,但该对角矩阵的取值未知。
综合Tikhonov正则化和谱修正迭代法的思想,本文给出一种新的迭代公式:
| $ {\mathit{\boldsymbol{\hat X}}^{(n)}} = {({\mathit{\boldsymbol{A}}^T}\mathit{\boldsymbol{PA}} + \alpha \mathit{\boldsymbol{T}})^{ - 1}}({\mathit{\boldsymbol{A}}^T}\mathit{\boldsymbol{PL}} + \alpha \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{\hat X}}^{(n - 1)}}) $ | (14) |
式中,α为岭参数(或称正则化参数),T为泛函矩阵(或称正则化矩阵)。
由正则化原理可知,引入岭参数α和泛函矩阵T时,不仅降低了方程病态性带来的不利影响,使方程求解能达到稳定,而且方程在迭代求解时解的估计值接近真值的程度较谱修正迭代法高。这在一定程度上弥补了谱修正迭代法收敛慢、效率低的缺点,加快了谱修正迭代法的收敛速度,减少了迭代次数,提高了计算效率。
改进谱修正迭代的关键在于确定合适的岭参数和泛函矩阵,对于岭参数的确定常用的方法有岭迹法、广义交叉核实法(GCV法)、L曲线法及经验公式法,本文采用公认较优的计算方法——L曲线法[16]。泛函矩阵T的取值为:若已知未知参数先验的方差协方差精度信息,则T的取值为未知参数方差协方差阵的逆阵;若未知,则T的值可取为对角阵、单位阵或其他接近参数方差协方差阵逆阵的矩阵,一般情况下取单位阵。岭参数和泛函矩阵的不合理选取可能会导致迭代收敛慢、效率低。
3.3 三维坐标转换模型求解对于法方程,令
| $ \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{N}}&{{\mathit{\boldsymbol{B}}^T}}\\ \mathit{\boldsymbol{B}}&0 \end{array}} \right] = \mathit{\boldsymbol{M}}, \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat x}}}\\ \mathit{\boldsymbol{K}} \end{array}} \right] = \mathit{\boldsymbol{Y}}, \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}^T}\mathit{\boldsymbol{PL}}}\\ { - \mathit{\boldsymbol{W}}} \end{array}} \right] = \mathit{\boldsymbol{U}} $ | (15) |
则式(7)可写为:
| $ \mathit{\boldsymbol{MY}} = \mathit{\boldsymbol{U}} $ | (16) |
在式(16)两边同时加上αTY,得:
| $ (\boldsymbol{M}+\alpha \boldsymbol{T}) \boldsymbol{Y}=\boldsymbol{U}+\alpha \boldsymbol{T} \boldsymbol{Y} $ | (17) |
因为方程两边都含有未知参数Y,所以需要迭代求解,迭代公式为:
| $ \hat{\boldsymbol{Y}}^{(k)}=(\boldsymbol{M}+\alpha \boldsymbol{T})^{-1}\left(\boldsymbol{U}+\alpha \boldsymbol{T} \hat{\boldsymbol{Y}}^{(k-1)}\right) $ | (18) |
模型求解的详细流程为:1)选取模型参数的迭代初值
本算例模拟8个点在两个坐标系(原坐标系和目标坐标系)下的坐标值,结果见表 1。为与实际情况一致,8个公共点随机选取,非均匀分布(该非均匀分布导致法矩阵的条件数为2.42×106,即法方程矩阵严重病态),且已知这两个坐标系中7个转换参数的真值,其中3个旋转参数分别为α=30°、β=45°、γ=60°,尺度参数为μ=0.2,3个平移参数分别为X0=100、Y0=500、Z0=1 000。因本文的方法采用基于单位四元数的构造旋转矩阵,故只能比较共有参数,分别为3个平移参数、1个尺度参数和旋转矩阵R,这些参数的真值见表 2。
|
|
表 1 公共点坐标数据 Tab. 1 Common point coordinate data |
|
|
表 2 模型转换参数(真值) Tab. 2 Model conversion parameters(true value) |
1) 对未知参数的初始值采用以下3种不同的取值方案。
方案1:X0=0,Y0=0,Z0=0,k=1,q0=0.01,q1=0.01,q2=0.01,q3=0.01。
方案2:
方案3:平移参数初值选取为两个坐标系的重心之差,单位四元数的选取采用文献[4]中的计算方法。
2) 采用本文提出的算法和文献[4]算法(算法二),使表 1中的公共点全部参与解算,得到的结果见表 3。
|
|
表 3 转换参数的计算结果 Tab. 3 The results of transformation parameter after iterative calculation |
3) 初值取为1)中3种方案时,本文算法和文献[4]算法(算法二)的机器耗时分别如表 4(单位s)所示,结果均利用MATLAB编程计算得到。
|
|
表 4 不同方案两种算法机器耗时 Tab. 4 Two algorithm machines take time in different scenarios |
对比表 2和3可以看出,当初值取为方案1和方案2时,本文算法能够有效地收敛到真值,其中平移参数与真值的误差数量级为10-7,尺度参数和旋转矩阵R的各元素与真值的误差数量级为10-8,且迭代次数较少。但对于文献[4]算法,无法有效地收敛到真值,得到的转换参数与真值误差较大,其主要原因是高斯-牛顿迭代法只是一种局部收敛法,当初值选取不合理时会导致算法无法收敛到真值。当初值取为方案3时,两种算法均可有效地收敛到真值,且迭代次数较少。笔者在模拟了更多公共点和选取其他初值方案进行实验后发现,本文算法均可有效收敛到真值,但文献[4]算法则无法有效地收敛到真值,限于篇幅,其他初值方案未给出。通过表 4可知,本文算法在不同取值方案时机器耗时较短,可知本文算法的复杂度不高。综上所述,本文提出的算法具有收敛速度快、不依赖转换参数初值、全局收敛等特点。
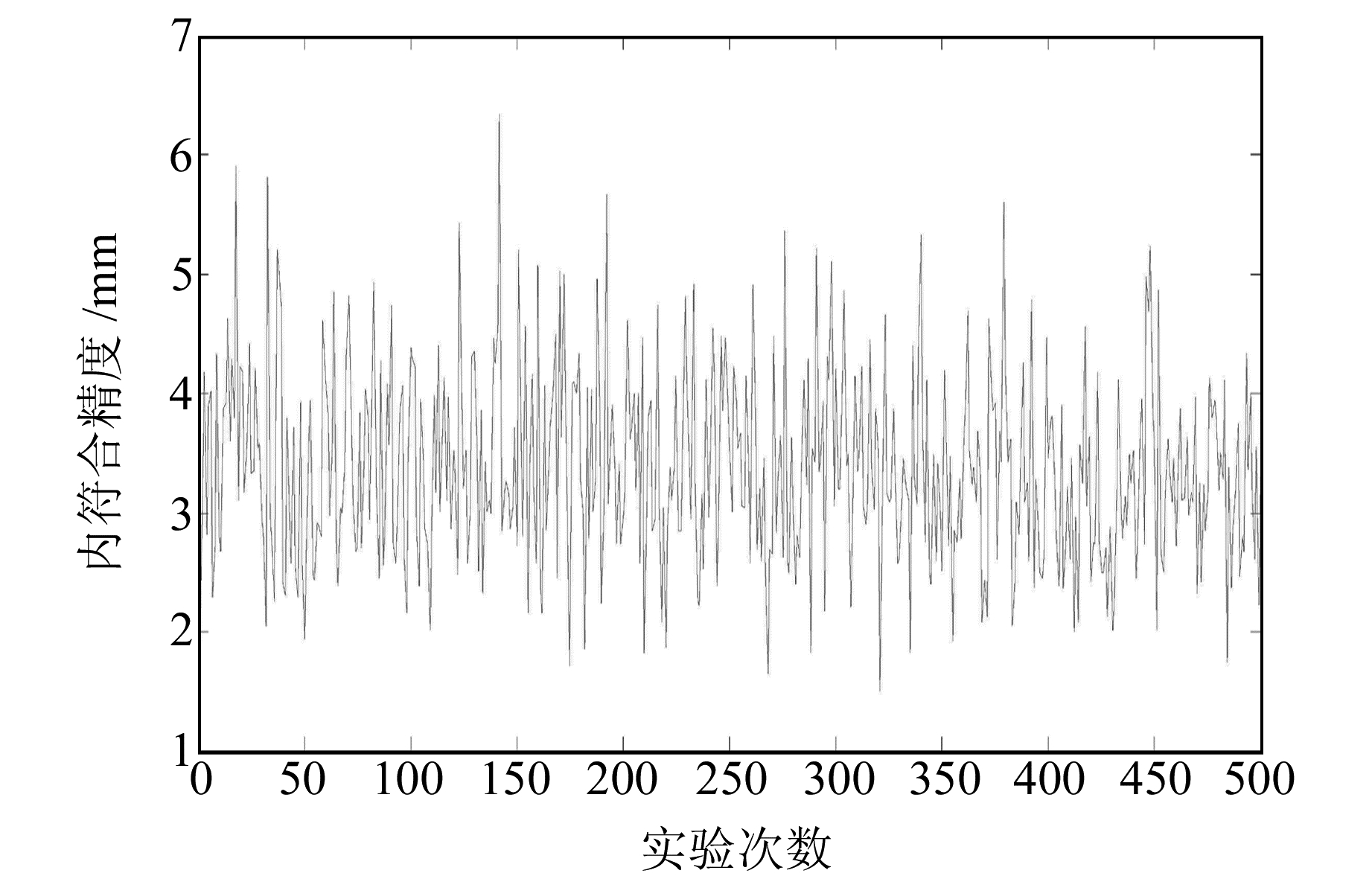
4.2 算例2在实际应用中,坐标数据会出现误差,因此为模拟实际情况,对目标坐标系下的坐标加上标准差σ=5 mm的高斯白噪声扰动,得到一组含有误差的坐标值,假设为新坐标系下的坐标。将原坐标系和新坐标系下的前4个公共点参与计算,后4个点作为检验数据,利用本文算法进行坐标转换并评定坐标转换的内、外符合精度。为保证实验的可靠性,对模拟实验重复500次计算,本文算法各次模拟实验计算的内、外符合精度分别见图 1和2。
|
图 1 内符合精度 Fig. 1 Inner precision |
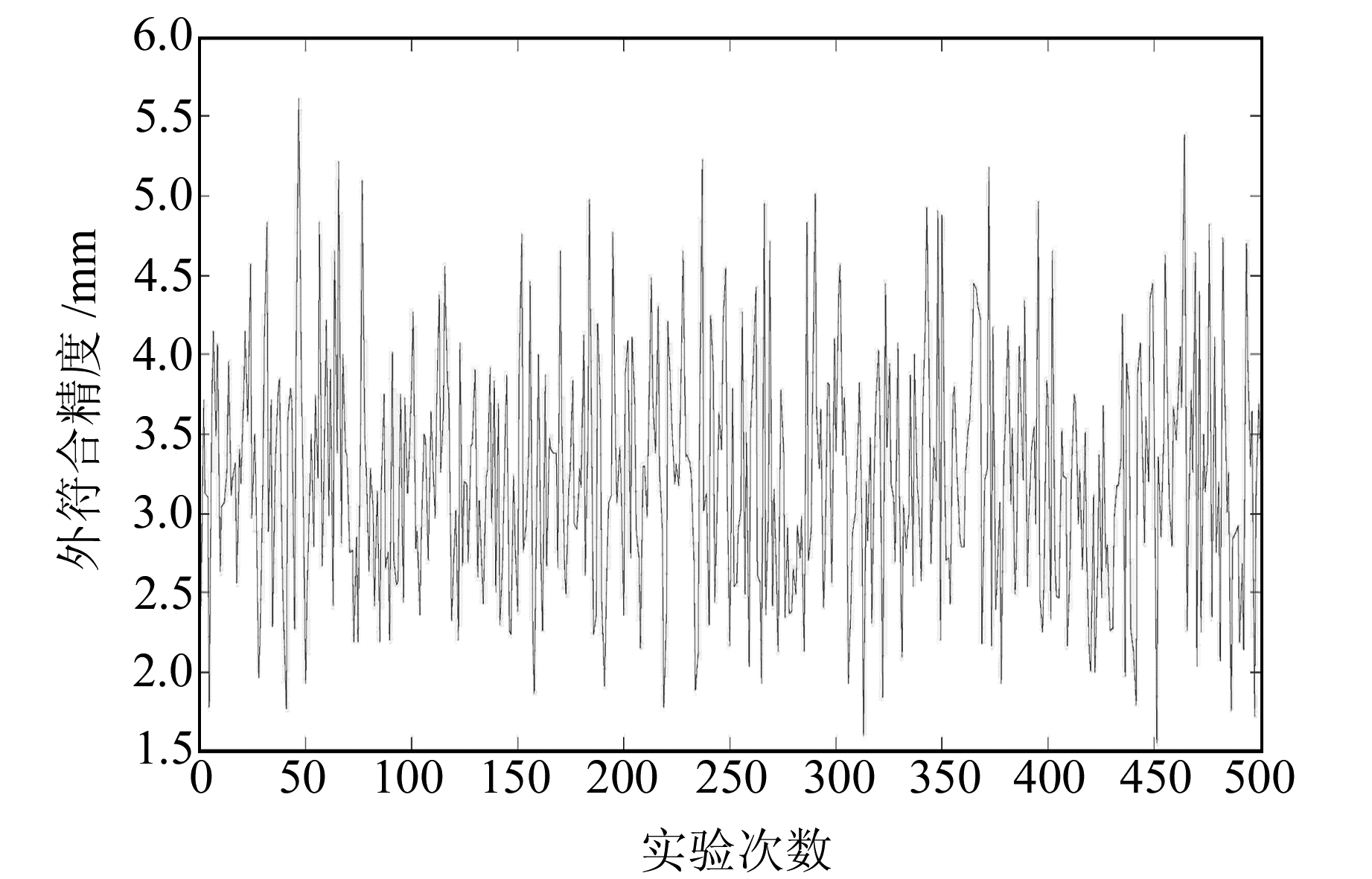
|
图 2 外符合精度 Fig. 2 External precision |
由图 1和2可知,各次模拟实验计算得到的坐标转换内符合精度和外符合精度均呈现出随机的特性。对各次模拟实验的内符合精度和外符合精度求RMS得:σ内=3.2 mm,σ外=3.4 mm,其结果均小于标准差σ=5 mm。因此,本文算法的平差模型正确,平差结果可靠。
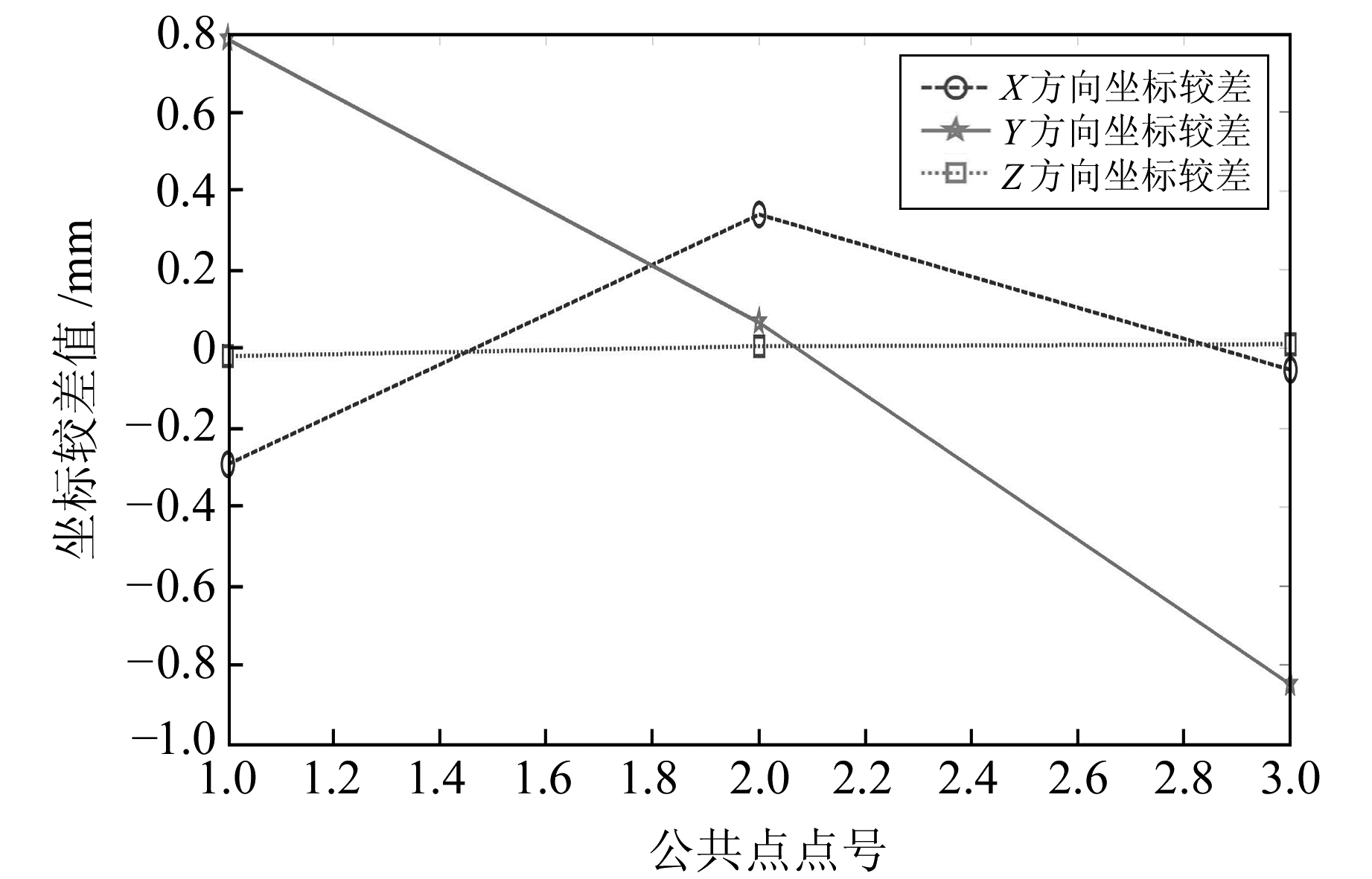
4.3 算例3为与已有的数据进行比较,本算例采用文献[1]中上海某地铁的地下工程自动导向系统进行盾构精密定位采集得到的原始数据。利用本文模型将3个公共点进行三维坐标转换,将计算得到的转换参数代入式(1),分别得到3个公共点的转换坐标,再将转换坐标与已知坐标对比可得坐标较差(图 3)。
|
图 3 坐标较差 Fig. 3 Coordinate difference |
坐标较差偏差的最大值为ΔY3=-0.85 mm,坐标较差绝对值的均值为ω0=0.3 mm。由此可知,本文算法可有效地进行三维坐标转换,满足工程需求。
5 结语1) 本文将三维旋转变换矩阵用四元数进行表示,构造了基于单位实四元数的三维坐标变换模型,并引入岭参数和泛函矩阵,得到改进的谱修正迭代算法。相对于用方向余弦、欧拉角和罗德里格矩阵构造的三维旋转变换矩阵,实四元数几何意义更加直观,且采用单位实四元数构造旋转矩阵无需进行复杂的三角函数求导,易于线性化,系数矩阵更为简洁。
2) 在进行三维坐标转换时,由于选取的公共点都是非均匀分布且都在局部区域,转换模型法方程矩阵的条件数较大,即法方程矩阵存在严重的病态性。考虑到模型法方程矩阵的病态性,引入岭参数和泛函矩阵改进谱修正迭代法求解转换参数,可有效降低法方程病态问题带来的不利影响,使方程求解达到稳定,同时方程迭代求解时解的估计值接近真值的程度较谱修正迭代法高。
3) 通过模拟数据和实测数据对算法进行验证,并与其他算法进行比较表明,本文算法具有收敛速度快、不依赖转换参数初值、全局收敛、解是无偏的、便于程序实现等特点。
| [1] |
潘国荣, 汪大超, 周跃寅. 两种大转角空间坐标转换模型研究[J]. 山东科技大学学报:自然科学版, 2015, 34(1): 61-67 (Pan Guorong, Wang Dachao, Zhou Yueyin. Two Spatial Coordinate Transformation Model of Large Angle[J]. Journal of Shandong University of Science and Technology:Natural Science, 2015, 34(1): 61-67)
(  0) 0) |
| [2] |
姚宜斌, 黄承猛, 李程春, 等. 一种适用于大角度的三维坐标转换参数求解算法[J]. 武汉大学学报:信息科学版, 2012, 37(3): 253-256 (Yao Yibin, Huang Chengmeng, Li Chengchun, et al. A New Algorithm for Solution of Transformation Parameters of Big Rotation Angle's 3D Coordinate[J]. Geomatics and Information Science of Wuhan University, 2012, 37(3): 253-256)
(  0) 0) |
| [3] |
陈义, 沈云中, 刘大杰. 适用于大旋转角的三维基准转换的一种简便模型[J]. 武汉大学学报:信息科学版, 2004, 29(12): 1101-1104 (Chen Yi, Shen Yunzhong, Liu Dajie. A Simplified Model of Three Dimensional-Datum Transformation Adapted to Big Rotation Angle[J]. Geomatics and Information Science of Wuhan University, 2004, 29(12): 1101-1104)
(  0) 0) |
| [4] |
吕志鹏, 伍吉仓, 公羽. 利用四元数改进大旋转角坐标变换模型[J]. 武汉大学学报:信息科学版, 2016, 41(4): 547-553 (Lü Zhipeng, Wu Jicang, Gong Yu. Improvement of a Three-Dimensional Coordinate Transformation Model Adapted to Big Rotation Angle Based on Quaternion[J]. Geomatics and Information Science of Wuhan University, 2016, 41(4): 547-553)
(  0) 0) |
| [5] |
姚吉利, 韩保民, 杨元喜. 罗德里格矩阵在三维坐标转换严密解算中的应用[J]. 武汉大学学报:信息科学版, 2006, 31(12): 1094-1096 (Yao Jili, Han Baomin, Yang Yuanxi. Applications of Lodrigues Matrix in 3D Coordinate Transformation[J]. Geomatics and Information Science of Wuhan University, 2006, 31(12): 1094-1096)
(  0) 0) |
| [6] |
王新洲. 非线性模型参数估计理论与应用[M]. 武汉: 武汉大学出版社, 2002 (Wang Xinzhou. Theory and Application of Parameter Estimation of Nonlinear Model[M]. Wuhan: Wuhan University Press, 2002)
(  0) 0) |
| [7] |
Hoerl A E, Kennard R W. Ridge Regression: Biased Estimation for Non-Orthogonal Problem[J]. Technometrics, 1970, 12(1): 55-67 DOI:10.1080/00401706.1970.10488634
(  0) 0) |
| [8] |
王新洲, 刘丁酉, 黄海兰. 谱修正迭代结果的协因素矩阵[J]. 武汉大学学报:信息科学版, 2003, 28(4): 429-431 (Wang Xinzhou, Liu Dingyou, Huang Hailan. The Co-Factor Matrix of the Iteration Method by Correcting Characteristic Value[J]. Geomatics and Information Science of Wuhan University, 2003, 28(4): 429-431)
(  0) 0) |
| [9] |
王新洲, 刘丁酉, 张前勇, 等. 谱修正迭代法及其在测量数据处理中的应用[J]. 黑龙江工程学院学报, 2001, 15(2): 3-6 (Wang Xinzhou, Liu Dingyou, Zhang Qianyong, et al. The Iteration by Correcting Characteristic Value and Its Application in Surveying Data Processing[J]. Journal of Heilongjiang Institute of Technology, 2001, 15(2): 3-6 DOI:10.3969/j.issn.1671-4679.2001.02.001)
(  0) 0) |
| [10] |
Hamilton S W R. On Quaternions; or on a New System of Imaginaries in Algebra[J]. Philosophical Magazine, 2009, 29(191): 425-439
(  0) 0) |
| [11] |
李亚萍, 黄崇超. 实四元数与三维旋转[J]. 武汉水利电力大学学报, 1995, 28(6): 607-612 (Li Yaping, Huang Chongchao. Using Real Quaternions to Represent Rotation in Three Dimensions[J]. Journal of Wuhan University of Hydraulic and Electric Engineering, 1995, 28(6): 607-612)
(  0) 0) |
| [12] |
李德仁, 袁修孝. 误差处理与可靠性理论[M]. 武汉: 武汉大学出版社, 2002 (Li Deren, Yuan Xiuxiao. Error Processing and Reliability Theory[M]. Wuhan: Wuhan University Press, 2002)
(  0) 0) |
| [13] |
王振杰.大地测量中不适定问题的正则化解法研究[D].武汉: 中国科学院测量与地球物理研究所, 2002 (Wang Zhenjie. Research on the Regularization Solutions of Ill-Posed Problems in Geodesy[D].Wuhan: Institute of Geodesy and Geophysics, CAS, 2002) http://cdmd.cnki.com.cn/article/cdmd-80057-2004041260.htm
(  0) 0) |
| [14] |
徐文, 陈义. 迭代法在病态问题中的应用[J]. 工程勘察, 2016(8): 71-73 (Xu Wen, Chen Yi. Application of Iterative Method in Ill-Posed Problems[J]. Geotechnical Investigation and Surveying, 2016(8): 71-73)
(  0) 0) |
| [15] |
刘斌, 龚健雅, 江万寿, 等. 基于岭参数的谱修正迭代法及其在有理多项式参数求解中的应用[J]. 武汉大学学报:信息科学版, 2012, 37(4): 399-402 (Liu Bin, Gong Jianya, Jiang Wanshou, et al. Improvement of the Iteration by Correcting Characteristic Value Based on Ridge Estimation and Its Application in RPC Calculating[J]. Geomatics and Information Science of Wuhan University, 2012, 37(4): 399-402)
(  0) 0) |
| [16] |
王振杰, 欧吉坤. 用L-曲线法确定岭估计中的岭参数[J]. 武汉大学学报:信息科学版, 2004, 29(3): 235-238 (Wang Zhenjie, Ou Jikun. Determining the Ridge Parameter in a Ridge Estimation Using L-Curve Method[J]. Geomatics and Information Science of Wuhan University, 2004, 29(3): 235-238)
(  0) 0) |
2. State-Province Joint Engineering Laboratory of Spatial Information Technology for High-Speed Railway Safety, 111 First Section of North-Erhuan Road, Chengdu 610031, China
 2019, Vol. 39
2019, Vol. 39


