2. 中国科学院大学,北京市玉泉路19号甲, 100049
随着中国北斗卫星导航系统(BDS)和欧盟Galileo系统卫星的发射,卫星星座逐渐完善,过去单一的GPS定位模式已逐步发展为多系统融合的GNSS定位模式,并广泛应用于地球科学研究和社会生产活动中[1-2]。2012年,随着中国主导发起的全球连续监测评估系统(iGMAS)的建立,iGMAS开始提供GPS、GLONASS、BDS和Galileo四系统的轨道和钟差等参数的综合产品,是目前国际上第一个提供此服务的系统,对GNSS多系统融合的研究和应用提供了很大的便利。iGMAS数据产品的精度和可靠性直接关系到高精度用户导航定位及授时的精度,现阶段是以IGS提供的最终产品为参照基准对其进行精度评定[3]。目前基于精密单点定位(PPP)技术评定iGMAS产品精度的研究大多分析精密产品对GPS PPP定位精度和收敛时间的影响,对iGMAS产品在多系统PPP和BDS、GLONASS、Galileo单系统PPP求解天顶对流层延迟(ZTD)及求解测站钟差的问题研究较少。本文利用iGMAS产品以GPS、BDS、GLONASS和Galileo单系统及四系统融合PPP为基础,主要从定位精度、收敛时间、ZTD和测站钟差求解精度等4个方面分析PPP静态解和动态解的性能,并使用GBM产品进行相同的实验解算,将其结果进行对比,特别分析钟差采样间隔对iGMAS产品精度和性能的影响,对iGMAS综合产品(ISC)的精度和服务的可靠性进行论述,为iGMAS产品的进一步改进给出建议。
1 多系统PPP定位模型和数据处理方法 1.1 多系统PPP观测方程本文采用PPP常规解算模型进行多系统PPP的解算。常规模型(UD模型)是应用最广的数学模型,采用双频伪距和载波相位观测值的无电离层组合作为PPP的函数模型,能消除一阶电离层延迟和内部频偏的影响[4],其表达式为:
| $ \begin{aligned} P_{\mathrm{IF}} &=\frac{f_{1}^{2} P_{1}-f_{2}^{2} P_{2}}{f_{1}^{2}-f_{2}^{2}}=\\ \rho_{\mathrm{r}}^{\mathrm{s}}+& c \delta t_{\mathrm{r}}-c \delta t^{\mathrm{s}}+T_{\mathrm{r}}^{\mathrm{s}}+\varepsilon_{P} \end{aligned} $ | (1) |
| $ \begin{array}{l} {\mathit{\Phi} _{{\rm{IF}}}} = \frac{{f_1^2{\varphi _1} - f_2^2{\varphi _2}}}{{f_1^2 - f_2^2}} = \\ \rho _{\rm{r}}^{\rm{s}} + c\delta {t_{\rm{r}}} - c\delta {t^{\rm{s}}} + T_{\rm{r}}^{\rm{s}} + {\lambda _{{\rm{r}}, {\rm{IF}}}}N_{{\rm{r}}, {\rm{IF}}}^{\rm{s}} + {\varepsilon _\mathit{\Phi} } \end{array} $ | (2) |
式中,
| $ \left\{ \begin{array}{l} P_{\rm{r}}^{\rm{G}} = \rho _{\rm{r}}^{\rm{s}} + c\delta {t_{\rm{r}}} - c\delta {t^{\rm{s}}} + T_{\rm{r}}^{\rm{s}} + {\varepsilon _{P_{\rm{r}}^{\rm{G}}}}\\ \mathit{\Phi} _{\rm{r}}^{\rm{G}} = \rho _{\rm{r}}^{\rm{s}} + c\delta {t_{\rm{r}}} - c\delta {t^{\rm{s}}} + T_{\rm{r}}^{\rm{s}} + \\ {\lambda _{{\rm{r}}, {\rm{IF}}}}N_{{\rm{r}}, {\rm{IF}}}^{\rm{s}} + {\varepsilon _{\mathit{\Phi} _{\rm{r}}^{\rm{G}}}}\\ P_{\rm{r}}^{\rm{C}} = \rho _{\rm{r}}^{\rm{s}} + c\delta {t_{\rm{r}}} - c\delta {t^{\rm{s}}} + c{\rm{ISB}}_{\rm{r}}^{\rm{C}} + \\ T_{\rm{r}}^{\rm{s}} + {\varepsilon _{P_{\rm{r}}^{\rm{G}}}}\\ \mathit{\Phi} _{\rm{r}}^{\rm{c}} = \rho _{\rm{r}}^{\rm{s}} + c\delta {t_{\rm{r}}} - c\delta {t^{\rm{s}}} + c{\rm{ISB}}_{\rm{r}}^{\rm{C}} + \\ T_{\rm{r}}^{\rm{s}} + {\lambda _{{\rm{r}}, {\rm{IF}}}}N_{{\rm{r}}, {\rm{IF}}}^{\rm{s}} + {\varepsilon _{\mathit{\Phi} _{\rm{r}}^{\rm{C}}}}\\ P_{{\rm{r}}k}^{{{\rm{R}}_k}} = \rho _{\rm{r}}^{\rm{s}} + c\delta {t_{\rm{r}}} - c\delta {t^{\rm{s}}} + c{\rm{ISB}}_{\rm{r}}^{{{\rm{R}}_k}} + \\ T_{\rm{r}}^{\rm{s}} + {\varepsilon _{P_{\rm{r}}^{{{\rm{R}}_k}}}}\\ \mathit{\Phi} _{{\rm{r}}k}^{{{\rm{R}}_k}} = \rho _{\rm{r}}^{\rm{s}} + c\delta {t_{\rm{r}}} - c\delta {t^{\rm{s}}} + c{\rm{ISB}}_{\rm{r}}^{{{\rm{R}}_k}} + \\ T_{\rm{r}}^{\rm{s}} + {\lambda _{{\rm{r}}, {\rm{IF}}}}N_{{\rm{r}}, {\rm{IF}}}^{\rm{s}} + {\varepsilon _{\mathit{\Phi} _{\rm{r}}^{{{\rm{R}}_k}}}}\\ P_{\rm{r}}^{\rm{E}} = \rho _{\rm{r}}^{\rm{s}} + c\delta {t_{\rm{r}}} - c\delta {t^{\rm{s}}} + c{\rm{ISB}}_{\rm{r}}^{\rm{E}} + \\ T_{\rm{r}}^{\rm{s}} + {\varepsilon _{P_{\rm{r}}^{\rm{E}}}}\\ \mathit{\Phi} _{\rm{r}}^{\rm{E}} = \rho _{\rm{r}}^{\rm{s}} + c\delta {t_{\rm{r}}} - c\delta {t^{\rm{s}}} + c{\rm{ISB}}_{\rm{r}}^{\rm{E}} + \\ T_{\rm{r}}^{\rm{s}} + {\lambda _{{\rm{r}}, {\rm{IF}}}}N_{{\rm{r}}, {\rm{IF}}}^{\rm{s}} + {\varepsilon _{\mathit{\Phi} _{\rm{r}}^{\rm{E}}}} \end{array} \right. $ | (3) |
式中,G、C、R、E分别代表GPS、BDS、GLONASS和Galileo卫星,ISBrC和ISBrE分别为BDS和Galileo卫星相对于GPS的系统间偏差,Rk中k为GLONASS卫星的频率号,ISBrRk为GLONASS卫星相对于GPS的系统间偏差。由于GLOANSS系统采用频分多址(FDMA)的信号解构,GLONASS的系统间偏差ISBrRk与测站r和卫星s相关。
1.2 数据处理策略本文观测模型采用UD模型。在该模型中,待估参数包括接收机位置、天顶对流层延迟、接收机钟差、系统间偏差和模糊度,其中对接收机的三维位置参数(x, y, z)分别进行静态和仿动态处理,对模糊度、静态坐标、系统偏差参数作为常量进行估计,对接收机钟差、动态坐标当作白噪声进行处理,解算方法采用Kalman滤波[2]。精密轨道、精密钟差等精密产品采用德国波茨坦地学研究中心(GFZ)和iGMAS提供的最终产品,卫星端和接收机端天线相位中心偏差(PCO)和天线相位中心变化(PCV)使用IGS提供的ANTEX文件进行改正。具体的数据处理策略见表 1。
|
|
表 1 多系统GNSS PPP数据处理方法 Tab. 1 Multi-GNSS PPP processing strategy |
为减少低高度角的GNSS卫星观测值中含有的大气延迟和多路径效应对PPP解算精度的影响,本文采用高度角随机模型。该模型是利用卫星高度角为变量的函数模型对观测值的方差进行估计,最常用的为正弦函数模型[5]:
| $ \sigma^{2}=\frac{\sigma_{0}^{2}}{\sin ^{2} \theta} $ | (4) |
式中,θ为卫星高度角。在传统单GNSS随机模型的基础上,综合考虑不同系统现有的精度进行合理的先验方差设置:
| $ \begin{array}{l} \begin{array}{*{20}{l}} {\sigma _{{P^{\rm{G}}}/{\mathit{\Phi} ^{\rm{G}}}, {\mathop{\rm IF}\nolimits} , 0}^2 = {h^{\rm{G}}}\left[ {{{\left( {\frac{{f_{1, {\rm{G}}}^2}}{{f_{1, {\rm{G}}}^2 - f_{2, {\rm{G}}}^2}}} \right)}^2}\sigma _{P_1^{\rm{G}}/\mathit{\Phi} _1^{\rm{G}}}^2 + {{\left( {\frac{{f_{2, {\rm{G}}}^2}}{{f_{1, {\rm{G}}}^2 - f_{2, {\rm{G}}}^2}}} \right)}^2}\sigma _{P_1^{\rm{G}}/\mathit{\Phi} _1^{\rm{G}}}^2} \right], {h^{\rm{G}}} = 1}\\ {\sigma _{{P^{\rm{C}}}/{\mathit{\Phi} ^{\rm{C}}}, {\mathop{\rm IF}\nolimits} , 0}^2 = {h^{\rm{C}}}\left[ {{{\left( {\frac{{f_{1, {\rm{C}}}^2}}{{f_{1, {\rm{C}}}^2 - f_{2, {\rm{C}}}^2}}} \right)}^2}\sigma _{P_{\rm{1}}^{\rm{C}}/\mathit{\Phi} _1^{\rm{C}}}^2 + {{\left( {\frac{{f_{2, {\rm{C}}}^2}}{{f_{1, {\rm{C}}}^2 - f_{2, {\rm{C}}}^2}}} \right)}^2}\sigma _{P_{\rm{1}}^{\rm{C}}/\mathit{\Phi} _1^{\rm{C}}}^2} \right], {h^{\rm{C}}} = \left\{ {\begin{array}{*{20}{l}} {{{100}_{{\rm{GEO}}}}}\\ {{1_{{\rm{IGSO/MEO}}}}} \end{array}} \right.} \end{array}\\ \begin{array}{*{20}{l}} {\sigma _{{P^{\rm{R}}}/{\mathit{\Phi} ^{\rm{R}}}, {\mathop{\rm IF}\nolimits} , 0}^2 = {h^{\rm{R}}}\left[ {{{\left( {\frac{{f_{1, {\rm{R}}}^2}}{{f_{1, {\rm{R}}}^2 - f_{2, {\rm{R}}}^2}}} \right)}^2}\sigma _{P_1^{\rm{R}}/\mathit{\Phi} _1^{\rm{R}}}^2 + {{\left( {\frac{{f_{2, {\rm{R}}}^2}}{{f_{1, {\rm{R}}}^2 - f_{2, {\rm{R}}}^2}}} \right)}^2}\sigma _{P_{\rm{1}}^{\rm{R}}/\mathit{\Phi} _1^{\rm{R}}}^2} \right], {h^{\rm{R}}} = 1}\\ {\sigma _{{P^{\rm{E}}}/{\mathit{\Phi} ^{\rm{E}}}, {\mathop{\rm IF}\nolimits} , 0}^2 = {h^{\rm{E}}}\left[ {{{\left( {\frac{{f_{1, {\rm{E}}}^2}}{{f_{1, {\rm{E}}}^2 - f_{2, {\rm{E}}}^2}}} \right)}^2}\sigma _{P_1^{\rm{E}}/\mathit{\Phi} _1^{\rm{E}}}^2 + {{\left( {\frac{{f_{2, {\rm{E}}}^2}}{{f_{1, {\rm{E}}}^2 - f_{2, {\rm{E}}}^2}}} \right)}^2}\sigma _{P_{\rm{1}}^{\rm{E}}/\mathit{\Phi} _1^{\rm{E}}}^2} \right], {h^{\rm{E}}} = 1} \end{array} \end{array} $ | (5) |
式中,相位观测值的先验方差设置为0.004 m,伪距观测值的先验方差设置为0.6 m[5]。由于北斗的GEO卫星轨道精度和钟差精度低于IGSO和MEO卫星,因此设置h系数对GEO卫星的观测值噪声进行适当放大,以保证PPP解算的准确度和可靠性。
2 实验分析 2.1 数据选取及实验方案选取2018-01-01~01-15全球15个MGEX测站数据,选定的测站均可接收GPS、BDS、CLONASS和Galileo系统的观测数据,数据采样间隔为30 s,测站分布情况见图 1。
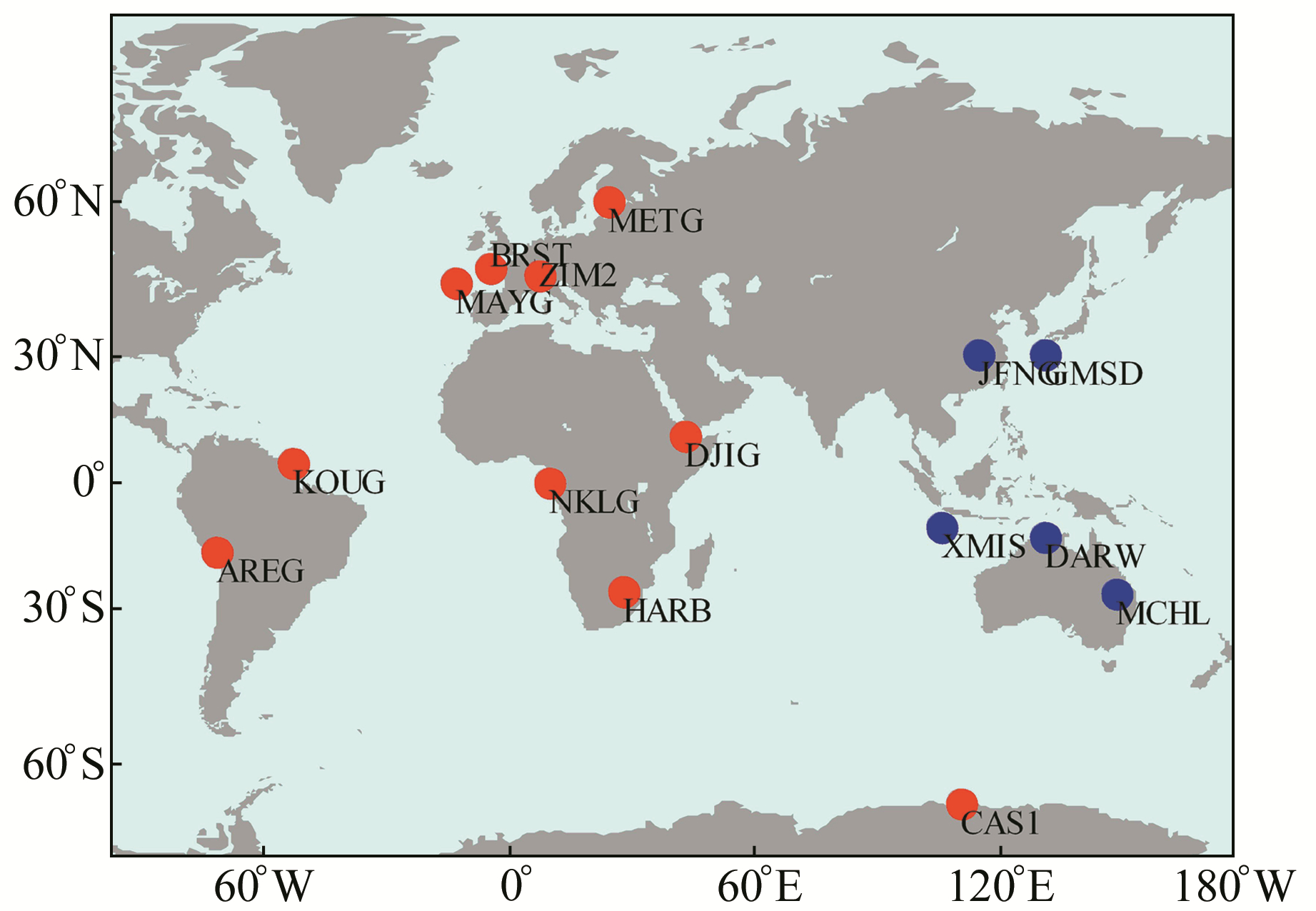
|
图 1 所选取数据的MGEX测站分布 Fig. 1 Geographical distribution of the selected MGEX stations |
iGMAS综合产品的轨道和钟差是由iGMAS产品综合与服务中心提供的ISC产品,其轨道产品采样间隔为15 min,钟差产品采样间隔为5 min,产品为北斗时间系统(BDT)。IGS产品是德国GFZ提供的GBM产品,其轨道产品采样间隔为5 min,钟差产品的采样间隔为30 s,产品为GPS时间系统(GPST)。为分析现阶段iGMAS产品的钟差采样间隔对PPP精度的影响,并客观评定iGMAS产品的精度和服务性能的可靠性,本次实验将GBM产品按照ISC产品的钟差采样间隔进行重采样,生成新的GBM-300 s产品。实验所用产品详细说明见表 2。
|
|
表 2 多系统轨道钟差产品说明 Tab. 2 Description of multi-GNSS satellite orbit and clock offset |
本文以ISC产品、GBM产品和GBM-300 s产品对15个MGEX测站15 d的数据进行单系统(GPS、Galileo、GLONASS和BDS)PPP解算和多系统(GPS+BDS+GLONASS+Galileo)PPP解算,由于BDS主要服务区域为亚太地区,BDS的PPP主要采用图 1中5个蓝色MGEX测站15 d的观测数据进行解算。在上述5种PPP解算模式下,评估ISC产品和GBM产品的PPP定位精度、收敛时间、ZTD解算精度及测站钟差求解精度。
2.2 静态实验分析为分析PPP静态定位精度,基于GBM产品PPP解算所用的测站起始坐标为IGS发布的SNX文件的周解坐标,其坐标框架为IGS14,基于ISC产品PPP解算所用的测站起始坐标为ISC发布的SNX文件的周解坐标,其坐标框架为IGb08。本文中滤波收敛定义为E、N、U各向定位偏差均优于0.1 m。为确保结果的可靠性,同时检查了首次收敛时刻后续20个历元的位置偏差,只有当连续20个历元的偏差都在限值以内时才认为滤波在当前历元收敛[6]。
统计15个测站15 d的PPP定位精度、收敛时间、ZTD和测站钟差求解精度,并进行ISC产品、GBM产品和GBM-300 s产品的评估测试。图 2为GPS、BDS、GLONASS、Galileo单系统PPP及四系统融合PPP等5种解算模式下N、E和U方向坐标分量的均方根(RMS)统计结果。从BDS的PPP可以看出,无论是使用ISC产品、GBM-300 s产品或GBM产品,都与其他4种定位模式的精度在U方向有一定差距,其原因可能是BDS的GEO卫星在现阶段BDS单系统PPP中占有较高的比重。无论是GFZ的BDS GEO卫星定轨精度还是ISC综合13个分析中心得到的BDS GEO卫星轨道精度,都比MEO/IGSO卫星轨道的精度要低[7-8],受BDS GEO卫星特殊星座的影响,使用ISC产品或GBM产品进行BDS PPP解算的精度要相对低于其他解算模式。
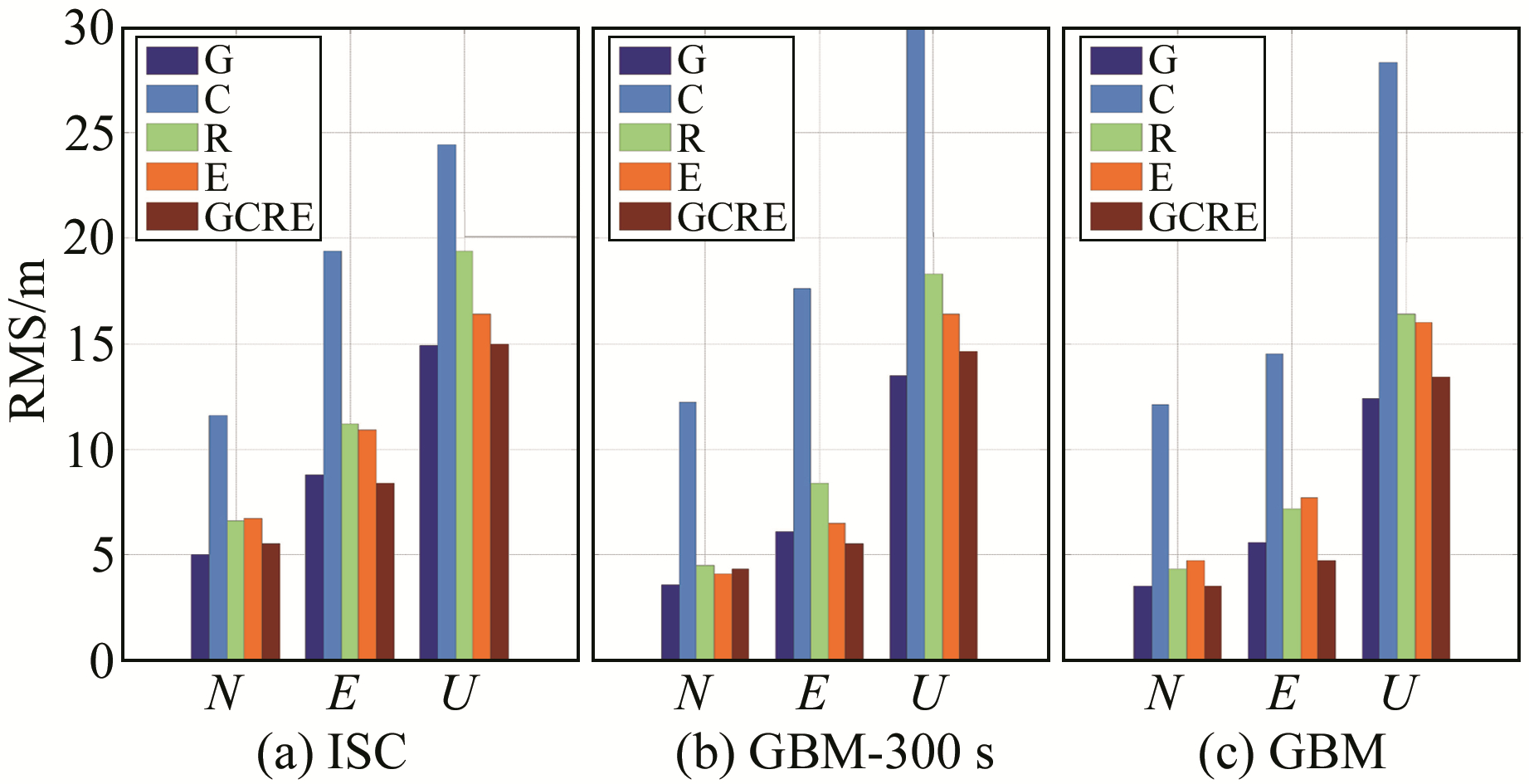
|
图 2 基于ISC产品和GBM产品静态多种PPP的定位精度对比 Fig. 2 Comparison of static multi-PPP positioning accuracy between ISC and GBM products |
在GPS、GLONASS、Galileo单系统PPP及四系统融合PPP中,基于ISC产品的PPP定位精度低于GBM产品2~5 mm,低于GBM-300 s产品2~3 mm。由式(1)和式(2)可知,在滤波解算的过程中,卫星钟差偏差大部分会被接收机钟差所吸收,因此对定位精度的影响较小,但在内插轨道时卫星钟差偏差通过影响从接受时间tr归算到发生时间te的时间间隔来影响内插轨道的精度,进而影响PPP的定位精度。卫星钟差偏差是由内插卫星钟差产品所带来的误差,卫星钟差的变化是一种高频抖动,在较短的时间间隔内(30 s)卫星钟差的变化比较平缓,因此使用9阶拉格朗日插值可获得较高的精度;但在较长的时间间隔内(300 s),使用9阶拉格朗日插值会带来较大的卫星钟差偏差,造成一定的定位精度损失[9]。
为显示PPP静态定位的收敛速度,图 3给出5种解算模式下PPP收敛时间的统计结果。由图可知,在GPS、GLONASS、Galileo单系统PPP及四系统融合PPP中,基于ISC产品的PPP收敛速度要比GBM产品慢5~20 min,但同GBM-300 s产品相比收敛速度基本一致,在BDS单系统PPP中的收敛速度还要优于GBM产品24 min。这是因为在静态PPP实验中高采样率的钟差产品能够加快PPP的收敛速度[10],但对定位结果却没有明显的改善。现阶段的iGMAS产品受钟差采样间隔较大的影响,收敛速度较慢,但在同等采样间隔的条件下,无论是定位精度还是收敛速度都同GBM产品无明显差异。
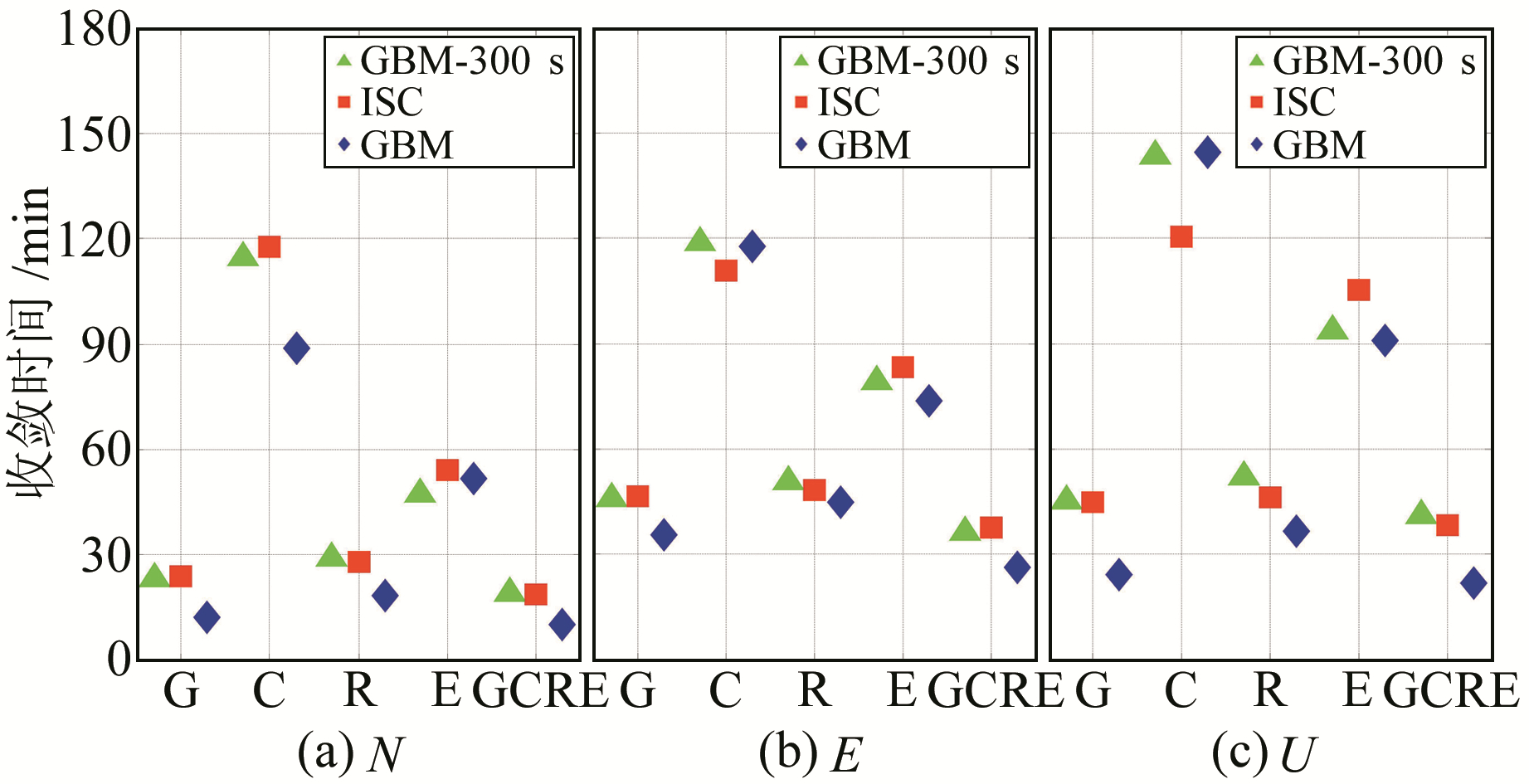
|
图 3 基于ISC产品和GBM产品静态多种PPP的收敛时间的对比 Fig. 3 Comparison of static multi-PPP convergence time between ISC and GBM products |
为分析PPP的ZTD求解精度,本文使用IGS发布的精度为1.5~5 mm的ZPD文件中的ZTD作为真值计算ZTD的残差[11],图 4为5种解算模式下ZTD残差的RMS统计结果。由图 4(a)可知,在BDS定位模式下基于ISC产品的ZTD求解精度优于GBM产品1~2 mm;在GPS、Galileo、GLONASS单系统PPP及四系统融合PPP中,基于ISC产品得到的ZTD的精度与基于GBM-300 s产品得到的ZTD的精度基本一致,但低于GBM产品求得的ZTD的精度2~3 mm。这是因为ZTD和U方向的定位精度有强相关性,U方向定位精度的优劣也反映了ZTD解算精度的高低,因此图 2中3种产品在U方向定位精度的变化趋势与ZTD精度的变化趋势一致。另外,ISC产品在BDS单系统PPP方面的性能优于GBM产品,而在GPS、GLONASS、Galileo单系统PPP及四系统融合PPP方面弱于GBM产品。

|
图 4 基于ISC产品和GBM产品多种PPP的ZTD求解精度对比 Fig. 4 Comparison of multi-PPP ZTD accuracy between ISC and GBM products |
通过PPP浮点解得到的测站钟差包含卫星端和接收机端的硬件延迟等系统误差,为分析iGMAS产品在测站钟差求解精度方面的稳定性和可靠性,本文采用求解相对钟差精度的方法。IGS提供的事后卫星钟差精度为0.1 ns[12],以IGS最终产品进行GPS单系统PPP解算,并将解算得到的测站钟差作为参考值计算上述5种解算模式下接收机钟差的标准偏差(STD),以此作为评判接收机钟差求解精度的指标。由图 5(a)可知,BDS单系统PPP的接收机钟差的标准差比其他系统PPP的结果精度低0.15~0.2 ns;GPS单系统和四系统融合PPP的接收机钟差的标准偏差在0.1ns左右;基于ISC产品解算出的测站钟差精度低于GBM产品0.01~0.04 ns,但优于GBM-300 s产品0.01~0.04 ns。
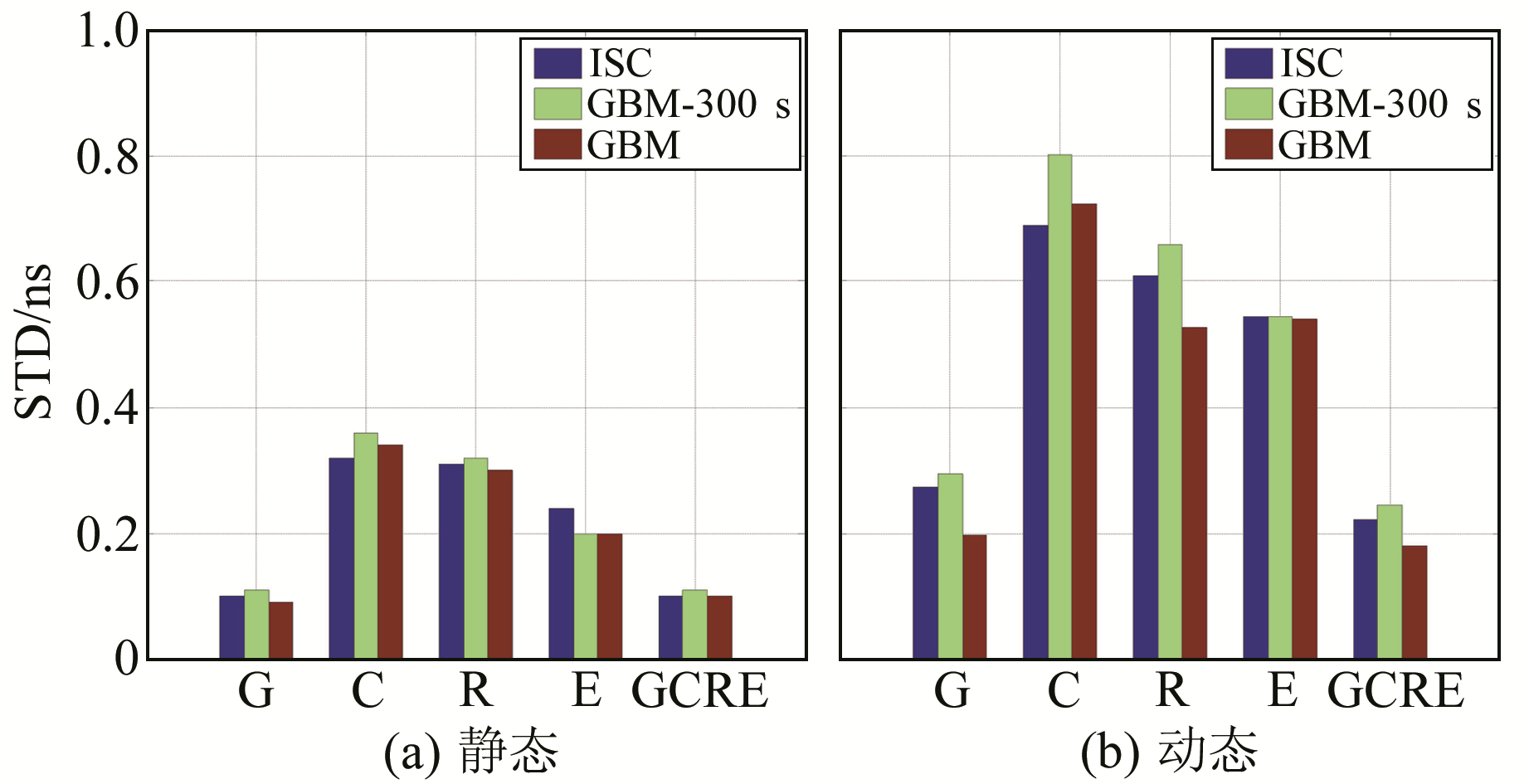
|
图 5 基于ISC产品和GBM产品多种PPP测站钟差求解精度对比 Fig. 5 Comparison of multi-PPP the accuracy of receiver clock offset between ISC and GBM products |
现阶段BDS单系统PPP求解的钟差性能较差是因为BDS GEO卫星的定轨精度较差,在固定轨道生成钟差产品的过程中,轨道精度较低导致钟差产品精度下降。BDS GEO卫星钟差的RMS大概在0.8 ns[3],该误差大部分被接收机钟差吸收,导致钟差解的精度降低;另外由于生成钟差产品的参考基准不同,在将ISC产品(BDT)采用9阶拉格朗日插值[13]内插到GPST时,插值造成的偏差也会被接收机钟差吸收,导致钟差解的精度下降。重采样后的GBM-300 s产品之所以较原始的GBM产品产生偏差,是因为将原始的30 s钟差采样间隔放大到300 s后,卫星钟差中的一部分高频信号被舍弃,采用9阶拉格朗日插值时会带来较大的卫星钟差偏差,该偏差被接收机钟差吸收进而反映到最终统计结果中,造成GBM-300 s产品求解的测站钟差精度下降,同时也是造成ISC产品解算出的测站钟差精度弱于GBM产品的重要原因之一。
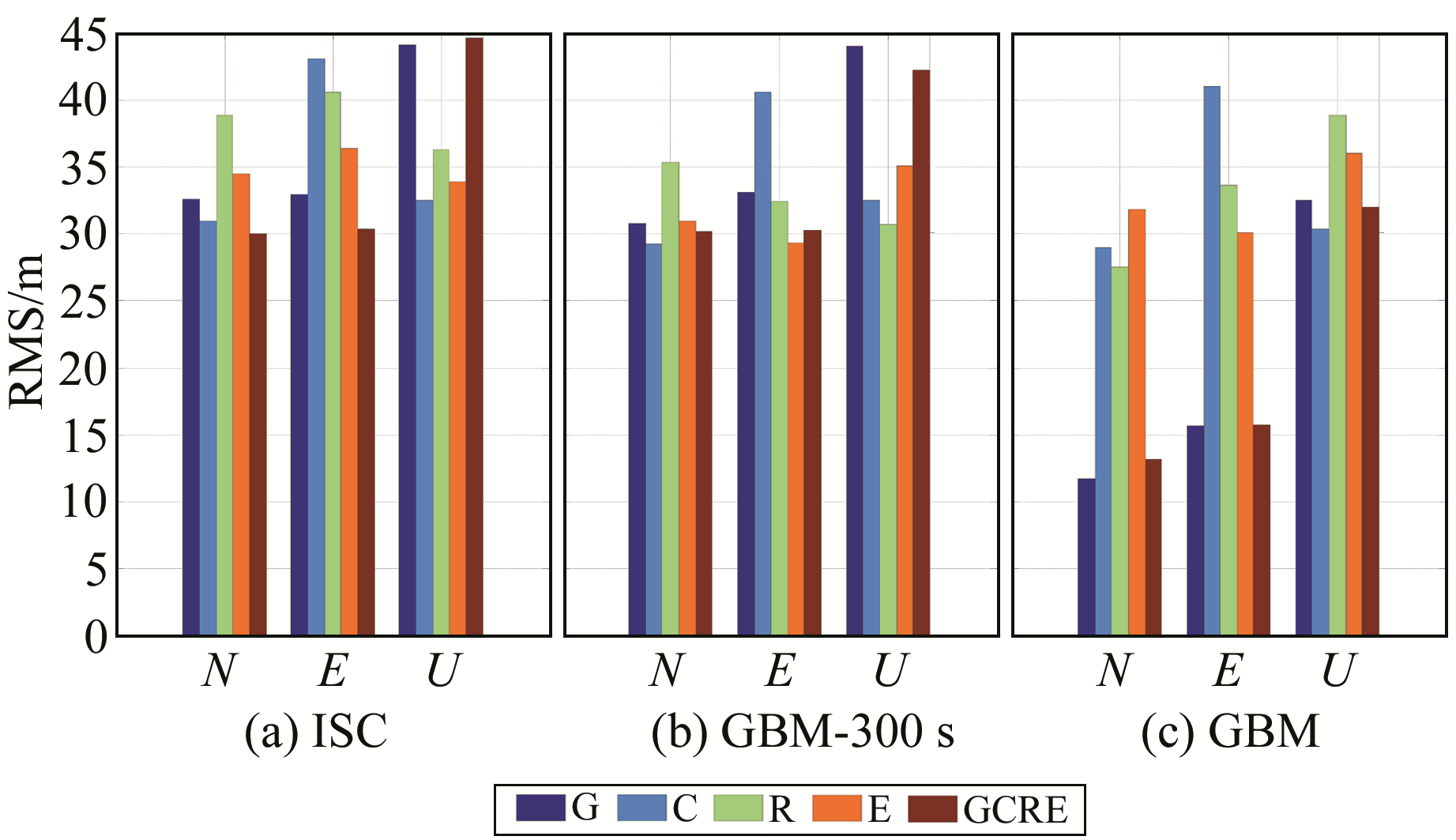
2.3 动态实验分析动态实验同样采用§1.1介绍的数据处理策略和实验数据进行处理,对各个测站进行仿动态PPP并对结果进行统计,图 6和7为基于不同产品的动态PPP定位精度和收敛时间的统计结果。在动态测试中可以看出,钟差采样间隔对动态定位结果的影响很大,ISC产品在BDS和Galileo单系统动态PPP定位方面,由于BDS和Galileo系统卫星在轨数较GPS和GLONASS系统有一定的差别,而该差别也在动态定位中被放大,因此无论是定位精度或是收敛时间均与GPS系统有一定的差距。ISC产品在GPS单系统和四系统融合定位模式下的定位性能明显弱于GBM产品10~20 mm,但与GBM-300 s产品的定位精度相当。对比图 4(a)和4(b)可以看出,无论是静态定位还是动态定位,ISC产品和GBM产品在求解ZTD时的性能和可靠性基本一致,不存在明显的差距。在动态定位的测站钟差求解精度方面(图 5(b)),5种定位模式下动态定位的测站钟差求解精度均低于静态测试结果约0.1 ~0.5 ns。这可能是由于在静态仿动态处理模式下,测站位置参数被模型化为白噪声,不能像静态处理模式那样用明确的运动学模型约束位置参数,部分未模型化误差和一些偏差被接收机钟差吸收, 最终导致PPP的钟差解有较大偏差和波动。
|
图 6 基于ISC产品和GBM产品动态多种PPP的定位精度对比 Fig. 6 Comparison of kinematic multi-PPP positioning accuracy between ISC and GBM products |
|
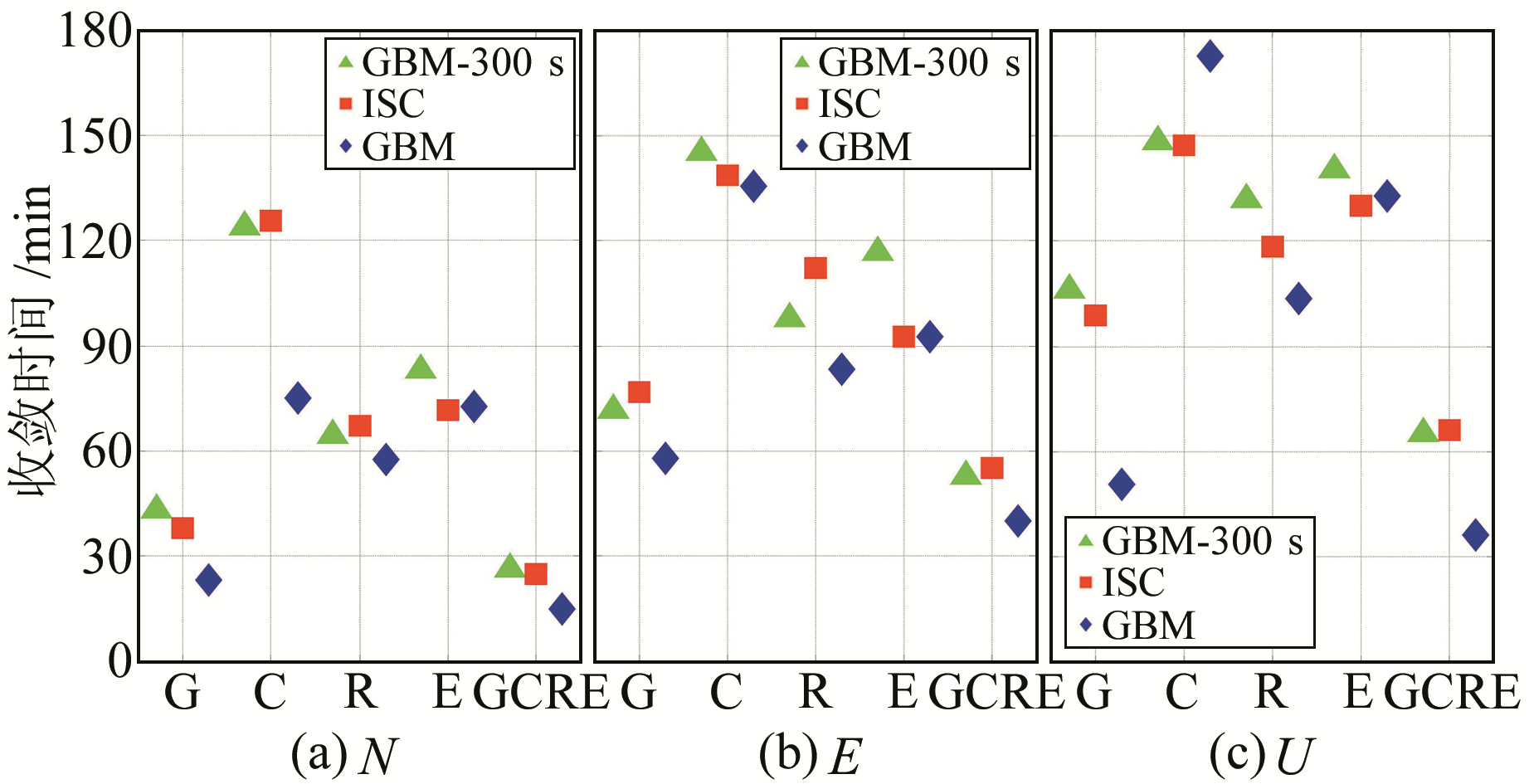
图 7 基于ISC产品和GBM产品动态多种PPP的收敛时间的对比 Fig. 7 Comparison of kinematic multi-PPP convergence time between ISC and GBM products |
本文基于MGEX测站进行大量的实测数据分析,从PPP的定位精度、收敛速度、ZTD求解精度和测站钟差求解精度4个方面对比ISC产品和GBM产品的精度差异,得出以下结论:
1) ISC产品在BDS单系统定位方面比GBM产品的效果好,ISC产品在3D方向的定位精度和收敛速度优于GBM产品0.89 mm和24 min,优于GBM-300 s产品4.72 mm和23 min。
2) 无论是静态定位还是动态定位,ISC产品和GBM产品在ZTD的求解精度和测站钟差的求解精度方面相互差异在1.5 mm和0.05 ns以内,两者的性能和可靠性基本一致,不存在明显的差距。
3) ISC产品的定位精度和收敛速度与相同采样间隔的GBM-300 s产品基本一致,但ISC产品的静态定位精度和收敛速度低于GBM产品2~3 mm和5~20 min,动态定位精度和收敛速度低于GBM产品5~20 mm和10~30 min。ISC产品卫星钟差的采样间隔较大是影响其产品精度的一个重要因素,建议iGMAS进一步提升钟差产品的性能。
4) 受GEO卫星轨道产品精度较低和BDS二代可视卫星数目较少的影响,现阶段BDS单系统PPP相比其他系统解算精度较差。无论是ISC产品或是GBM产品,在BDS单系统PPP模式解算出的定位精度较其他定位模式差5~10 mm,收敛时间较其他定位模式慢30~40 min。
5) BDS单系统PPP由于受到GEO卫星定轨精度较低的影响,测站钟差的精度较差,钟差标准差大约在0.32 ns左右;GPS单系统和四系统融合PPP的接收机钟差标准偏差大概在0.1 ns左右。动态测站钟差的求解精度受部分未模型化的误差被接收机钟差吸收的影响,低于静态测试精度约0.1~0.5 ns。
综上所述,iGMAS产品在定位精度和服务可靠性方面与GBM产品基本相同,iGMAS产品可以较好地应用于高精度的导航定位授时。
致谢: 感谢iGMAS产品综合与服务中心提供多系统精密轨道和钟差产品,感谢IGS提供多系统精密轨道和钟差产品及IGSMGEX提供多系统观测数据。
| [1] |
张小红, 李星星, 李盼. GNSS精密单点定位技术及应用进展[J]. 测绘学报, 2017, 46(10): 1 399-1 407 (Zhang Xiaohong, Li Xingxing, Li Pan. Review of GNSS PPP and Its Application[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1 399-1 407)
(  0) 0) |
| [2] |
任晓东, 张柯柯, 李星星, 等. Beidou、Galileo、GLONASS、GPS多系统融合精密单点[J]. 测绘学报, 2015, 44(12): 1 307-1 313 (Ren Xiaodong, Zhang Keke, Li Xingxing, et al. Precise Point Positioning with Multi-Constellation Satellite Systems: Beidou, Galileo, GLONASS, GPS[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(12): 1 307-1 313)
(  0) 0) |
| [3] |
陈康慷, 徐天河, 杨玉国, 等. iGMAS GNSS钟差产品综合与评估[J]. 测绘学报, 2016, 45(增2): 46-53 (Chen Kangkang, Xu Tianhe, Yang Yuguo, et al. Combination and Assessment of GNSS Clock Products from iGMAS Analysis Centers[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(S2): 46-53)
(  0) 0) |
| [4] |
李博峰, 葛海波, 沈云中. 无电离层组合、UofC和非组合精密单点定位观测模型比较[J]. 测绘学报, 2015, 44(7): 734-740 (Li Bofeng, Ge Haibo, Shen Yunzhong. Comparison of Ionosphere-Free, UofC and Uncombined PPP Observation Models[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(7): 734-740)
(  0) 0) |
| [5] |
Cai C S, Gao Y, Pan L, et al. Precise Point Positioning with Quad-Constellations: GPS, Beidou, GLONASS and Galileo[J]. Advances in Space Research, 2015, 56(1): 133-143 DOI:10.1016/j.asr.2015.04.001
(  0) 0) |
| [6] |
张小红, 左翔, 李盼, 等. BDS/GPS精密单点定位收敛时间与定位精度的比较[J]. 测绘学报, 2015, 44(3): 250-256 (Zhang Xiaohong, Zuo Xiang, Li Pan, et al. Convergence Time and Positioning Accuracy Comparison between BDS and GPS Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(3): 250-256)
(  0) 0) |
| [7] |
刘伟平, 郝金明, 李建文, 等. 多GNSS融合的北斗卫星精密定轨[J]. 测绘学报, 2014, 43(11): 1 132-1 138 (Liu Weiping, Hao Jinming, Li Jianwen, et al. Multi-GNSS Joint Precise Orbit Determination of Beidou Navigation Satellite System[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(11): 1 132-1 138)
(  0) 0) |
| [8] |
Xie X, Geng T, Zhao Q L, et al. Performance of BDS-3: Measurement Quality Analysis, Precise Orbit and Clock Determination[J]. Sensors, 2017, 17(6): 1 233 DOI:10.3390/s17061233
(  0) 0) |
| [9] |
季善标, 朱文耀, 熊永清. 精密GPS卫星钟差的改正和应用[J]. 空间科学学报, 2001, 21(1): 42-48 (Ji Shanbiao, Zhu Wenyao, Xiong Yongqing. Calculate and Application of the GPS Satellite Clock Offset[J]. Chinese Journal of Space Science, 2001, 21(1): 42-48 DOI:10.3969/j.issn.0254-6124.2001.01.006)
(  0) 0) |
| [10] |
张小红, 郭斐, 李星星. IGS卫星钟差产品采样间隔对PPP精度的影响[J]. 武汉大学学报:信息科学版, 2010, 35(2): 152-155 (Zhang Xiaohong, Guo Fei, Li Xingxing. Impact of Sample Rate of IGS Satellite Clock on Precise Point Positioning[J]. Geomatics and Information Science of Wuhan University, 2010, 35(2): 152-155)
(  0) 0) |
| [11] |
Byun S H, Bar-Sever Y E. A New Type of Troposphere Zenith Path Delay Product of the International GNSS Service[J]. Journal of Geodesy, 2009, 83(3-4): 1-7 DOI:10.1007/s00190-008-0288-8
(  0) 0) |
| [12] |
张小红, 蔡诗响, 李星星, 等. 利用GPS精密单点定位进行时间传递精度分析[J]. 武汉大学学报:信息科学版, 2010, 35(3): 274-278 (Zhang Xiaohong, Cai Shixiang, Li Xingxing, et al. Accuracy Analysis of Time and Frequency Transfer Based on Precise Point Positioning[J]. Geomatics and Information Science of Wuhan University, 2010, 35(3): 274-278)
(  0) 0) |
| [13] |
洪樱, 欧吉坤, 彭碧波. GPS卫星精密星历和钟差3种内插方法的比较[J]. 武汉大学学报:信息科学版, 2006, 31(6): 516-518 (Hong Ying, Ou Jikun, Peng Bibo. Three Interpolation Methods for Precise Ephemeris and Clock Offset of GPS Satellite[J]. Geomatics and Information Science of Wuhan University, 2006, 31(6): 516-518)
(  0) 0) |
2. University of Chinese Academy of Sciences, A19 Yuquan Road, Beijing 100049, China
 2019, Vol. 39
2019, Vol. 39


