2. 中国测绘科学研究院,北京市莲花池西路28号,100830;
3. 沈阳市勘察测绘研究院,沈阳市南三好街1号,110004
地球是一个动态变化的系统,大气、土壤水、地表水和海洋非潮汐负荷等环境变化都会引起地球表面物质质量的重新分布。根据质量守恒定律,物质的总质量不变,但质量重新分布会使地球表面发生形变,这种形变响应是一个复杂的地球物理学过程,与环境负荷类型、地球内部结构等多种因素有关[1-2]。随着空间对地观测技术的发展,超导重力仪观测精度已达0.1 μGal,VLBI、SLR和GNSS基线观测精度达到1~10 mm(10-8~10-9 m)量级,这些技术已广泛应用于大地测量学、地球物理学和地球动力学研究[3-4]。全国和省市区域CORS系统长期持续、高精度的监测数据,可应用于地球动力学、板块运动及地质环境稳定性监测等研究,在关注CORS位置长期线性变化的同时,也应注意到环境负荷引起的非线性周期性变化,尤其是环境变化对短期流动站观测数据的影响。
有研究显示,大气负荷变化是环境变化中影响最大的因素,其对GNSS位置时间序列垂直方向影响的年变化量最大可达±25 mm,对水平方向影响较小,约为垂直方向的1/10~1/3[4]。田云锋[5]通过对比分析GPS坐标时间序列加入大气质量负荷改正前后的变化表明,对于区域框架,加入大气负荷改正能带来一定的改进,减小水平分量的白噪声和垂向分量的闪烁噪声,使垂向周年运动振幅降低等。王敏等[6]研究大气、积雪和土壤水等环境负荷对GPS测站位置产生的非构造形变影响表明,对垂向影响显著,但通过地球物理模型改正可使测站垂向位置的RMS降低,修正部分影响。王伟等[7]采用移去恢复法研究大气负荷对区域地壳形变的影响显示,垂直形变在空间分布上中长波占优,三峡地区的年变化幅度大于20 mm,水平形变影响较小。上述研究均表明,对GNSS位置时间序列进行大气负荷影响修正可提高GNSS坐标时间序列的质量,增强对时间序列中信号的解释能力。本文利用全球大气模型数据和CORS时间序列,采用球谐系数法计算大气负荷变化对CORS位置时间序列的影响,通过分析CORS位置时间序列移除大气影响前后RMS值的变化,评估大气负荷修正的重要性,并计算测站位置处大气负荷变化对地壳垂直形变影响的导纳值。
1 理论与方法大气负荷变化对地壳形变的影响分为直接影响(大气对地球表面及内部点产生直接吸引而产生形变)和间接影响(大气作为表面负荷作用于地球,导致地球的弹性形变和内部质量重新分布,产生附加位影响)[8-9]。计算地表质量变化对固体地球形变影响的方法主要有负荷格林函数积分法[10]。另外,许多学者根据Farrell[11]的负荷形变理论推导出利用球谐系数计算负荷变化对地球表面形变影响的公式,称为球谐系数法[12]。从数学本质上讲,这两者是相同的[13]。
地球表面环境负荷变化导致的物质质量变化可用等效水高变化表示,地面点(R, θ, λ)处面密度变化Δq(或等效水高变化hw)的规格化球谐展开公式为:
| $ \begin{array}{l} \Delta q = {\rho _w}{h_w} = R{\rho _w}\sum\limits_{n = 1}^N {\sum\limits_{m = 0}^n {\left[ {\Delta C_{nm}^y\cos m\lambda + } \right.} } \\ \left. {\Delta S_{mn}^q\sin m\lambda } \right]{{\bar P}_{mn}}(\cos \theta ) \end{array} $ | (1) |
式中,R为地球平均半径,ρw≈103 kg·m-3为水的密度,ρe≈5.5×103 kg·m-3为地球密度,N为阶数,ΔCnmq、ΔSnmq为n阶m次规格化球谐系数,
令
| $ \begin{array}{l} {\mathit{\Phi} ^d} = \kappa \frac{{GM}}{R}\sum\limits_{n = 2}^N {\frac{1}{{2n + 1}}} \sum\limits_{m = 0}^n {\left( {\Delta C_m^q\cos m\lambda + } \right.} \\ \left. {\Delta S_{mn}^q\sin m\lambda } \right){{\bar P}_{mn}}(\cos \theta ) \end{array} $ | (2) |
负荷位间接影响为:
| $ \begin{array}{l} {\mathit{\Phi} ^i} = \kappa \frac{{GM}}{R}\frac{1}{{2n + 1}}\sum\limits_{m = 0}^n {\left( {\Delta C_m^q\cos m\lambda + } \right.} \\ \left. {\Delta S_{mn}^q\sin m\lambda } \right){{\bar P}_{mn}}(\cos \theta ) \end{array} $ | (3) |
总负荷位为:
| $ {\mathit{\Phi} ^r} = {\mathit{\Phi} ^d} + {\mathit{\Phi} ^i} = \sum\limits_{n = 2}^N {\left( {1 + k_n^\prime } \right)} {\mathit{\Phi} ^n} $ | (4) |
地面水平形变计算公式为:
| $ \begin{array}{l} e = \kappa \frac{{GM}}{{\gamma R\sin \theta }}\sum\limits_{n = 2}^N {\frac{{l_n^\prime }}{{2n + 1}}} \sum\limits_{m = 0}^n m \left( {\Delta C_{nm}^q\sin m\lambda - } \right.\\ \left. {\Delta S_{mn}^q\cos m\lambda } \right){{\bar P}_{mn}}(\cos \theta ) \end{array} $ | (5) |
| $ \begin{array}{l} n = \kappa \frac{{GM}}{{\gamma R}}\sum\limits_{n = 2}^N {\frac{{l_n^\prime }}{{2n + 1}}} \sum\limits_{m = 0}^n {\left( {\Delta C_{nm}^q\cos m\lambda + } \right.} \\ \left. {\Delta S_{mn}^q\sin m\lambda } \right)\frac{\partial }{{\partial \theta }}{{\bar P}_{mn}}(\cos \theta ) \end{array} $ | (6) |
大地高(垂直方向)形变影响计算公式为:
| $ \begin{array}{l} r = \kappa \frac{{GM}}{{\gamma R}}\sum\limits_{n = 2}^N {\frac{{h_n^\prime }}{{2n + 1}}} \sum\limits_{m = 0}^n {\left( {\Delta C_m^q\cos m\lambda + } \right.} \\ \left. {\Delta S_{mn}^q\sin m\lambda } \right){{\bar P}_{mn}}(\cos \theta ) \end{array} $ | (7) |
上述公式中,h′ n为n阶径向负荷数,l′ n、k′ n为n阶位负荷(勒夫)数,M为地球总质量,γ为地面平均重力。
2 数据处理与形变分析 2.1 数据来源及处理大气变化数据采用欧洲中期天气预报中心(ECMWF)发布的全球大气再分析产品,数据空间分辨率为0.25°×0.25°,观测时间为每日4个时刻(00 :00、06 :00、12 :00、18 :00),根据需要由每日4个时刻观测值获得每日平均气压值[15]。结合研究时间跨度,将2011年年平均气压值作为基准值,由每日气压值扣除基准值得到每日气压变化量(相对于2011年年平均气压值),再根据气压原理(1 hPa=10.197 2 mm)将气压变化量转换为等效水高变化量。
采用的CORS位于我国新疆地区,涵盖该区域内国家“陆态网”、自治区省级CORS网及部分市级CORS网站点,观测时间最大跨度为2011~2017年。因数据来源不同、存储系统升级、测站搬站等情况,存在有荷重复时段数据、信息与数据内容不一致等问题,需对数据进行标准化处理,包括剔除冗余数据、测站重命名等。利用GAMIT/GLOBK软件进行数据解算,采用的数据处理策略是先选取我国及周边的15个IGS得到全球松弛解,再利用GAMIT基线解算软件得到区域站点松弛解,最后利用GLOBK平差软件平差,并根据Helmert转换参数获得各测站在ITRF2014框架下的单日解坐标时间序列。
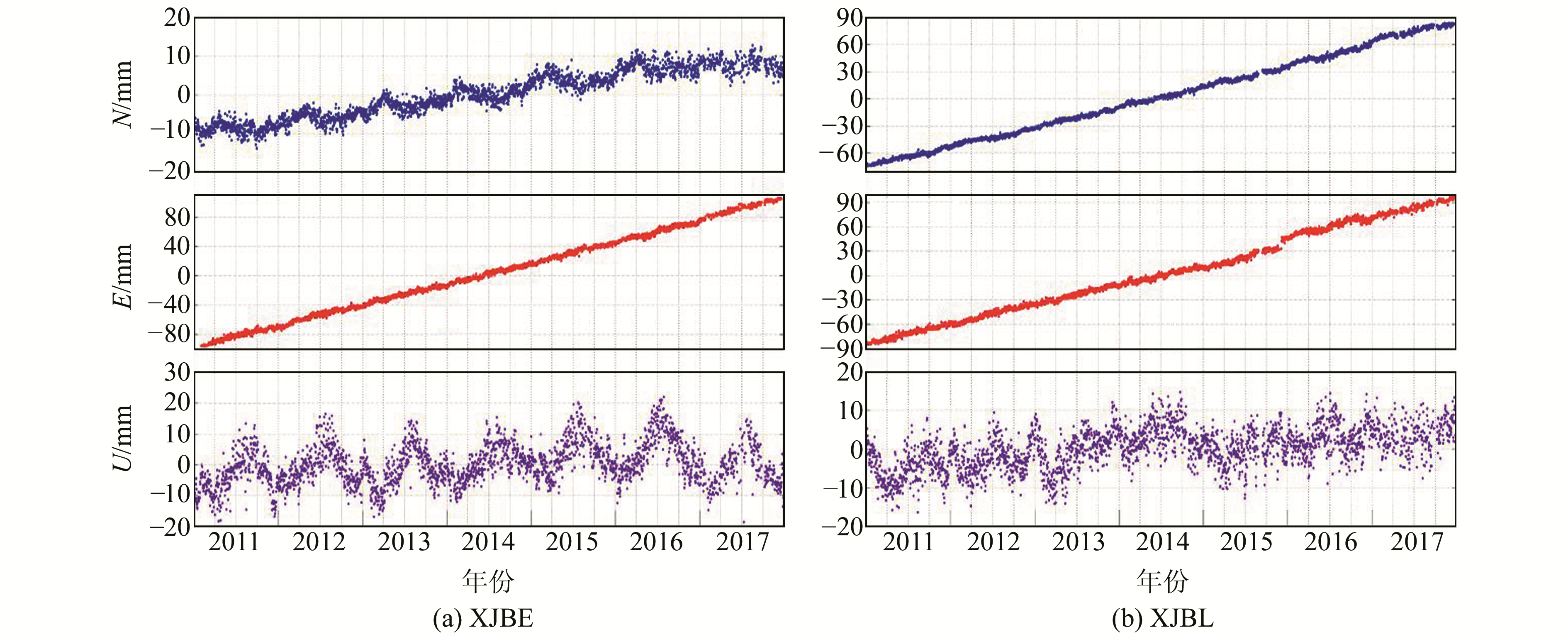
对CORS单日解的时间序列进行粗差与剔除处理,对陡变站点进行逐一分析处理。因篇幅所限,本文只给出具有区域代表性的XJBE站和XJBL站时间序列图(图 1)。为突出时间序列中的非构造形变,采用回归拟合法滤去其线性成分,在发生陡变的站点采取适当分段滤去线性化,并采用3倍标准差原则进行粗差剔除和扣平均值处理,部分测站结果见图 2。
|
图 1 XJBE和XJBL测站时间序列 Fig. 1 Time series of XJBE and XJBL stations |

|
图 2 XJDS和XJFY测站滤去线性项后时间序列 Fig. 2 Time series of filtered XJDS and XJFY stations |
利用式(1)将每日大气负荷变化等效水高进行球谐系数展开,得到720阶球谐系数。根据公式,由球谐系数和CORS坐标计算得到每日大气负荷变化对CORS位置处的单日平均地壳形变位移的影响,结果均表现为U方向最大,E、N方向较小,与已有的研究成果一致[6-7]。大气负荷变化对测站位置地壳垂直方向的影响具有明显的年周期性,影响变化在-15.9~13.2 mm之间,与气压变化成反比,最大值一般出现在年中6~7月,最小值出现在12月至次年1月;水平方向影响较小,约0~2.7 mm(统计E方向与N方向矢量和模的大小),年周期变化不明显。显然大气负荷对垂直方向的影响是不容忽视的,大气负荷变化对XJSS测站位移影响变化序列见图 3。

|
图 3 大气负荷形变对测站位置影响时间序列 Fig. 3 Time series of influence of atmospheric load deformation on stations |
经过滤去线性项和粗差剔除等预处理的单日解CORS位置的时间序列变化,认为其主要是由环境负荷引起的。由图 3可以看出,环境因素对E、N方向影响较小,季节性变化不明显;而对U方向影响较大,且具有明显的年周期和季节性变化,不能忽略该影响,或仅将其当作噪音来处理。同时,大气负荷变化是环境变化中影响较大的因素,研究计算大气负荷影响有助于移除和分离CORS时间序列中的非构造形变影响。
移除CORS时间序列中对应的每日大气负荷形变影响,并统计分析移除前后CORS各方向时间序列的均方根值(RMS),也称作效值变化,以表征数据的一致性,其计算公式为[6]:
| $ {X_{{\rm{RMS}}}} = \sqrt {\frac{{\sum\limits_{i = 1}^N {X_i^2} }}{N}} = \sqrt {\frac{{X_1^2 + X_2^2 + \cdots + X_{\rm{N}}^2}}{N}} $ | (8) |
测站时间序列RMS的统计结果见表 1(单位mm)。由表可知,测站水平的E、N方向RMS均值较小,约为2.5 mm,说明水平方向受到大气负荷变化的影响较小;各测站U方向的RMS差异较大,有的测站高达30 mm,可能受较大未知的不稳定环境因素的影响,通常情况下这类测站进行大气负荷影响改正的效果不明显。分析大气负荷影响修正后的RMS值变化表明,大气负荷在水平方向的改正较小,平均值还有轻微增加,没有明显的改善效果;但在垂直方向大部分测站RMS值减小,减小最多的为SHKE站,减小2.02 mm,变化幅度为25%,整体平均减小0.41 mm,平均变化幅度约为6%,少部分站点RMS值增大,说明大气负荷影响修正在垂向具有明显的效果。同时测站垂直形变还受其他环境因素的影响,如陆地水负荷变化、海潮改正残差、海洋非潮汐负荷及气温变化导致的标墩热胀冷缩等。
|
|
表 1 CORS位置时间序列RMS变化 Tab. 1 RMS change of CORS station location time series |
研究表明,大气负荷变化对地壳垂直形变的影响主要来源于当地气压变化,大气负荷变化对地壳垂向的影响量与气压变化量之间存在线性关系,计算该相关系数可快速计算大气负荷对垂直方向的影响,该系数称为大气负荷变化对地壳垂直形变影响的导纳值。李英冰[2]和Vandam等[16]采用回归方法求得该相关系数,并利用球谐系数计算的垂直形变量时间序列Ui与大气气压变化量ΔPi(采用距离平方反比方法,由全球大气模型数据内插测站位置气压变化得到)建立如下线性关系式:
| $ U_{i}=K \cdot \Delta P_{i} $ | (9) |
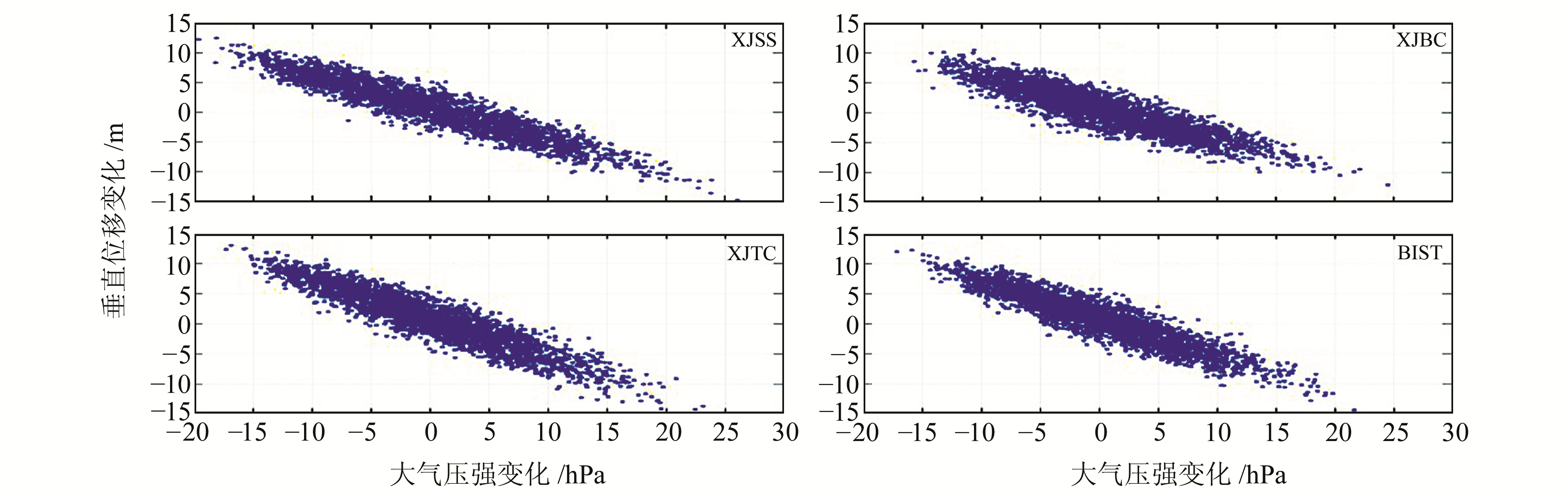
采用最小二乘方法对测站2011~2017年共2 557个观测值进行拟合回归分析,得到各测站的系数K即为大气负荷变化对测站垂直形变影响的导纳值。图 4给出XJSS、XJBC、XJTC、BIST测站大气压强与垂直形变的关系。
|
图 4 测站大气压强变化与垂向形变影响的关系 Fig. 4 Relationship between atmospheric pressure change and vertical deformation of station |
大气负荷变化对垂直形变影响的导纳值见表 2(单位mm/hPa),由表可知,CORS位置处的导纳值为-0.75~-0.43 mm/hPa,平均值为-0.597 mm/hPa,导纳值变化与当地地球表面环境因素的变化有关。由于气压变化与高程变化密切相关,在海拔较高或海拔变化剧烈的区域,大气负荷变化与其垂直形变影响的线性相关性不强,计算的导纳值不可信,表 2中所列测站拟合相关系数R2均大于0.7。
|
|
表 2 大气负荷变化对地壳垂直形变影响导纳值 Tab. 2 Admittance value of atmospheric load change on crustal vertical deformation |
大气负荷变化是环境变化对地球表面形变(特别是地壳垂直形变)影响的主要因素,本文利用ECMWF提供的全球大气模型和解算后的CORS位置时间序列,基于负荷形变理论,采用球谐系数分析方法计算每日大气负荷变化(相对于2011年年平均气压值)对研究区CORS水平和垂直方向的影响。结果显示,垂直形变影响变化量为-15.9~13.2 mm,与气压变化量成反比,水平形变影响较小,为0~2.7 mm。对CORS时间序列进行大气负荷影响移除修正,统计修正前后时间序列的RMS值变化表明,大气负荷修正对水平方向无明显改善,对垂直方向修正效应明显,最大修正效应达到25%,平均改善幅度达6%。结合气压变化序列和大气负荷影响量,计算研究区测站大气负荷变化对地壳垂直形变影响的导纳值,结果显示,其导纳值为0.43~0.78 mm/hPa。本文的研究方法和结果对修正环境负荷对CORS的影响具有一定的参考价值。
| [1] |
张诗玉, 钟敏. 地表流体变化对我国地壳垂直形变的影响[J]. 武汉大学学报:信息科学版, 2007, 32(5): 458-461 (Zhang Shiyu, Zhong Min. Vertical Crustal Displacements in China Due to Surface Fluid Changes[J]. Geomatics and Information Science of Wuhan University, 2007, 32(5): 458-461)
(  0) 0) |
| [2] |
李英冰.固体地球的环境变化响应[D].武汉: 武汉大学, 2003 (Li Yingbing. Solid Earth Response to Environmental Variation[D]. Wuhan : Wuhan University, 2003) http://cdmd.cnki.com.cn/Article/CDMD-10486-2006031873.htm
(  0) 0) |
| [3] |
张诗玉, 钟敏, 唐诗华, 等. 我国GPS基准站地壳垂直形变的大气负荷效应[J]. 武汉大学学报:信息科学版, 2006, 31(12): 1 090-1 093 (Zhang Shiyu, Zhong Min, Tang Shihua, et al. Vertical Crustal Displacements Due to Atmospheric Loading Effects at GPS Fiducial Stations in China[J]. Geomatics and Information Science of Wuhan University, 2006, 31(12): 1 090-1 093)
(  0) 0) |
| [4] |
罗少聪.大气负荷效应问题研究[D].武汉: 中国科学院测量与地球物理研究所, 2003 (Luo Shaocong. Study on the Loading Effects of the Atmospheric Pressure[D]. Wuhan: Institute of Geodesy and Geophysics, CAS, 2003) http://cdmd.cnki.com.cn/Article/CDMD-80057-2004041262.htm
(  0) 0) |
| [5] |
田云锋. 大气质量负荷对GPS基准站的影响[J]. 大地测量与地球动力学, 2010, 30(5): 64-67 (Tian Yunfeng. Effects of Atmospheric Mass Loading on GPS Fiducial Stations[J]. Journal of Geodesy and Geodynamics, 2010, 30(5): 64-67)
(  0) 0) |
| [6] |
王敏, 沈正康, 董大南. 非构造形变对GPS连续站位置时间序列的影响和修正[J]. 地球物理学报, 2005, 48(5): 1 045-1 052 (Wang Min, Shen Zhengkang, Dong Danan. Effects of Non-Tectonic Crustal Deformation on Continuous GPS Position Time Series and Correction to Them[J]. Chinese Journal of Geophysics, 2005, 48(5): 1 045-1 052)
(  0) 0) |
| [7] |
王伟, 党亚民, 章传银, 等. 基于CORS站网监测三峡地区陆地水负荷对地壳形变和重力变化的影响[J]. 地球物理学报, 2017, 60(3): 962-971 (Wang Wei, Dang Yamin, Zhang Chuanyin, et al. Monitoring of Crustal Deformation and Gravity Variation from Terrestrial Water Loading in the Three Gorges Region by the CORS Network[J]. Chinese Journal of Geophysics, 2017, 60(3): 962-971)
(  0) 0) |
| [8] |
党亚民, 章传银, 陈俊勇, 等. 现代大地测量基准[M]. 北京: 测绘出版社, 2015 (Dang Yamin, Zhang Chuanyin, Chen Junyong, et al. Modern Geodetic Datum[M]. Beijing: Surveying and Mapping Press, 2015)
(  0) 0) |
| [9] |
章传银, 王伟, 甘卫军, 等. 利用CORS站网监测三峡地区环境负荷引起的地壳形变与重力场时空变化[J]. 武汉大学学报:信息科学版, 2018, 43(9): 1 287-1 294 (Zhang Chuanyin, Wang Wei, Gan Weijun, et al. Monitoring Temporal and Spatial Changes of Crustal Deformation and Gravity Field Caused by Environmental Load in the Three Gorges Reservoir Region Based on CORS Network[J]. Geomatics and Information Science of Wuhan University, 2018, 43(9): 1 287-1 294)
(  0) 0) |
| [10] |
Longman I M. A Green's Function for Determining the Deformation of the Earth under Surface Mass Loads[J]. Journal of Geophysical Research, 1962, 68(2): 485-496
(  0) 0) |
| [11] |
Farrell W. Deformation of the Earth by Surface Loads[J]. Reviews of Geophysics and Space Physics, 1972, 10(3): 761-797 DOI:10.1029/RG010i003p00761
(  0) 0) |
| [12] |
Spratt R S. Modeling the Effect of Atmospheric Pressure Variations on Gravity[J]. Geophysical Journal of the Royal Astronomical Society, 2010, 71(1): 173-186
(  0) 0) |
| [13] |
沈迎春, 闫昊明, 彭鹏, 等. 质量负荷引起地表形变的格林函数和球谐函数方法对比研究[J]. 武汉大学学报:信息科学版, 2017, 42(7): 1 008-1 014 (Shen Yingchun, Yan Haoming, Peng Peng, et al. Comparative Study of Green's Function and Spherical Harmonic Function Methods on Surface Deformation Caused by Mass Loading[J]. Geomatics and Information Science of Wuhan University, 2017, 42(7): 1 008-1 014)
(  0) 0) |
| [14] |
周旭华, 吴斌. 大气、陆地水储量和海水质量分布变化与地球低阶引力场球谐系数的关系[J]. 天文学报, 2002, 43(3): 327-332 (Zhou Xuhua, Wu Bin. Changes of Atmosphere, Continental Water and Oceanic Mass Distribution in Relation with Low Degree Harmonic Coefficients in the Earth's Gravitational Field[J]. Acta Astronomica, 2002, 43(3): 327-332 DOI:10.3321/j.issn:0001-5245.2002.03.011)
(  0) 0) |
| [15] |
Ray R D, Ponte R M. Barometric Tides from ECMWF Operational Analyses[J]. Annales Geophysicae, 2003, 21(8): 1 897-1 910 DOI:10.5194/angeo-21-1897-2003
(  0) 0) |
| [16] |
Vandam T M, Blewitt G, Heflin M B. Atmospheric Pressure Loading Effects on Global Positioning System Coordinate Determinations[J]. Journal of Geophysical Research: Solid Earth, 1994, 99(B12): 23 939-23 950 DOI:10.1029/94JB02122
(  0) 0) |
2. Chinese Academy of Surveying and Mapping, 28 West-Lianhuachi Road, Beijing 100830, China;
3. Shenyang Research Institute of Surveying and Mapping, 1 South-Sanhao Street, Shenyang 110004, China
 2019, Vol. 39
2019, Vol. 39

