2. 山东科技大学矿山灾害预防控制省部共建国家重点实验室,青岛市前湾港路579号,266590
由于IGS站点具有全球覆盖性,根据其GNSS观测数据反演的全球电离层模型GIM得到广泛应用[1],基于该数据建立的短期TEC预报模型也在不断研究中。但一方面,GIM的最终产品要延迟11 d发布,短期预测的时效性会下降[2];另一方面,IGS站点在中国分布较少,且GIM在中国区域的精度和分辨率都受限[3]。因此,利用中国地区的GNSS实时数据流,对建立实时的高精度区域电离层模型(RIM)并进行预报分析具有重要意义。
基于电离层实测模型的预测方法主要分为线性和非线性两种。在线性预测模型中,ARMA模型因数据处理量少、建模简单等得到广泛应用,但利用ARMA对TEC直接预报[4],或预报球谐函数参数进而拟合全球TEC数据[5],其精度仍需提高。在全球范围内绝大多数网格点预报残差会超过1 TECu,甚至在赤道地区达到5 TECu[6],且随着预报时间的延长,预报精度会明显降低,部分精度较差的区域相对精度甚至会在7 d内下降近30%[7]。而在非线性预测模型中,一些算法如神经网络算法、EMD算法精度较高,但参数选取、网络优化等操作比较复杂[8]。
本文提出利用SSA进行电离层TEC预测的新方法,可较好地从含有噪声的有限尺度时间序列中提取趋势和周期等信息。采用2017年CMONOC的双频GPS观测数据,利用球谐函数解算出中国大陆的区域电离层模型RIM,针对TEC数据非线性、非平稳的特点,基于SSA提取数据的主要信息对TEC的振荡周期进行预测,并对预报结果进行精度评定。
1 方法介绍 1.1 SSA预测模型SSA可以分析时间序列的周期振荡行为,将时间序列周期分解与时间尺度密切关联,从而较好地从含噪声的有限尺度时间序列中提取主要信息[9]。
提取给定的RIM网格点TEC数据作为原始序列,假设序列长度为N,建立起相应的TEC时间序列{x},构建时滞矩阵:
| $ \boldsymbol{X}=\left[\begin{array}{cccc}{x_{1}} & {x_{2}} & {\cdots} & {x_{N-M+1}} \\ {x_{2}} & {x_{3}} & {\cdots} & {x_{N-M+2}} \\ {\cdots} & {\cdots} & {\cdots} & {\cdots} \\ {x_{M}} & {x_{M+1}} & {\cdots} & {x_{N}}\end{array}\right] $ | (1) |
式中,N为时间序列长度,M为嵌套维数(即时间窗口)(1≤M≤
| $ \boldsymbol{T}_{x}=\left[\begin{array}{cccc}{S_{(0)}} & {S_{(1)}} & {\cdots} & {S_{(M-1)}} \\ {S_{(1)}} & {S_{(0)}} & {\cdots} & {S_{(M-2)}} \\ {\cdots} & {\cdots} & {\cdots} & {\cdots} \\ {S_{(M-1)}} & {S_{(M-2)}} & {\cdots} & {S_{(0)}}\end{array}\right] $ | (2) |
式中,Tx为对称阵,对角线S(0)为时间序列{x}的方差,S(j)(0≤j≤M-1)为时间序列{x}迟后为j的自协方差。求得Tx特征值为λk,特征向量为Ek(k=1, 2, 3, …, M),
| $ a_i^k = \sum\limits_{j = 1}^M {{x_{i + j}}} \mathit{\boldsymbol{E}}_j^k, 0 \le i \le N - M $ | (3) |
由特征向量和时间系数可以构建{x}的重构向量(RC),则RCk为:
| $ x_i^k = \left\{ {\begin{array}{*{20}{c}} {\frac{1}{M}\sum\limits_{j = 1}^M {a_{i - j}^k} \mathit{\boldsymbol{E}}_j^k, }\\ \begin{array}{l} M \le i \le N - M + 1\\ \begin{array}{*{20}{c}} {\frac{1}{i}\sum\limits_{j = 1}^M {a_{i - j}^k} \mathit{\boldsymbol{E}}_j^k, }\\ \begin{array}{l} 1 \le i \le M - 1\\ \frac{1}{{N - i + 1}}\sum\limits_{j = i - N + M}^M {a_{i - j}^k} \mathit{\boldsymbol{E}}_j^k, \\ N - M + 2 \le i \le N \end{array} \end{array} \end{array} \end{array}} \right. $ | (4) |
将RCk的特征值λk按照大小排列λ1≥λ2≥…≥λM≥0,通常情况下利用前面的低阶模式即可满足分析需要。以不同信号之间的分离程度作为选取RC个数的准则,其相关性可以用w-correlation公式判断[10],合并对应的RC就可以充分反映TEC原序列的整体特征。首先确定权重因子wi:
| $ w_{i}=\left\{\begin{array}{l}{i, 1 \leqslant i <M^{*}} \\ {M^{*}, M^{*} \leqslant i \leqslant K^{*}} \\ {N-i+1, K^{*} \leqslant i \leqslant N}\end{array}\right. $ | (5) |
式中,
| $ \rho_{i, j}^{w}=\frac{\left(\boldsymbol{Y}^{(i)}, \boldsymbol{Y}^{(j)}\right)}{\left\|\boldsymbol{Y}^{i}\right\|_{w}\left\|\boldsymbol{Y}^{j}\right\|_{w}}, 1 \leqslant i, j \leqslant N $ | (6) |
式中,
本文有关预测期的数据被认为是缺失数据,而SSA可以用来预测TEC数据的主成分。根据w-correlation选择合适的阶次,即RC的个数K确定之后,在原始数据后面添加缺省数据,重复迭代过程直到收敛。更多详细的描述可以参阅文献[11]。
1.2 ARMA预测模型ARMA模型是目前应用最为广泛、最基本的时序模型,ARMA(p, q)[12]模型可表示为:
| $ \begin{aligned} \boldsymbol{X}_{t} &=a_{1} \boldsymbol{X}_{t-1}+\cdots+a_{p} \boldsymbol{X}_{t-p}+\\ \varepsilon_{t} &+b_{1} \varepsilon_{t-1}+\cdots+b_{q} \varepsilon_{t-q} \end{aligned} $ | (7) |
式中,{Xt}为时间序列,εt服从N(0, δ2),a1, …, ap为自回归系数,b1, …, bq为移动平均系数,(p, q)为模型阶数,(p, q)≥0且为整数。本文同时利用SSA和ARMA对TEC进行预测,并对比分析两者的预测精度。
2 数据来源CMONOC是一个以GNSS系统为主的国家级地球科学综合监测网络,其连续运行基准站达260个,在全国范围内分布较均匀,为反演高精度的电离层模型提供了很好的数据基础,可以有效弥补GIM在中国大陆区域上空精度较低、实效性较差的缺点[13]。本文利用CMONOC网260个测站的GPS双频观测数据,基于球谐函数拟合区域电离层。考虑到解算精度和速度,将解算阶次设置为5阶,参考系为日固-地磁坐标系[14],最后生成以2 h为时间间隔,跨度为70°~140°E、15°~55°N,空间分辨率为1°×1°的RIM。
提取RIM和GIM在中国上空的RMS数据,图 1为2017-01-01 UTC 04 :00 (Dst < 30 nT)及03-27 UTC 16 :00(Dst>70 nT)2种不同地磁活动状况下RIM和GIM的RMS空间分布。可以看出,GIM的RMS受地磁活动影响较大,在地磁活动平静期RMS最大为1.4 TECu;由于受磁暴影响,03-27的RMS平均值超过3 TECu,尤其在海洋地区和西部内陆地区模型的精度较差。而RIM的RMS受地磁活动影响较小,2个时段的RMS平均值分别为0.3 TECu和0.4 TECu,RMS分布差异不大。目前IGS提供的最终电离层产品要延迟11 d左右发布[2],采用GIM建立的TEC预测模型精度和时效性较差。因此,本文以CMONOC反演的高精度RIM为原始序列,并利用SSA建立TEC预测模型。

|
图 1 两种电离层模型RMS分布 Fig. 1 The distribution of RMS based on two ionospheric models |
原始序列长度、迭代阶数和窗口长度都会对SSA的预测结果造成较大的影响。本文提取RIM中心格网点(105°E, 35°N)的TEC数据,首先确定上述3个构建SSA预测模型的要素,完成TEC数据7 d的短期预测;然后分析不同预测时段内预报值精度,并判断地磁活动对预测效果的影响;最后将SSA预测模型应用于RIM所有格网点,对中国大陆区域上空的TEC进行预测。
首先判断TEC序列长度对预测的影响效果,分别采用10 d、20 d、27 d、30 d、40 d和50 d的数据长度,提取中心网格点2017年年积日41~50、31~50、24~50、21~50、11~50和1~50的TEC数据,将窗口长度设置为1/3,利用SSA分解后迭代前7阶的RC进行7 d的预测,并与RIM的TEC作为真实值进行对比得到预测相对精度,采用相对精度指标Prel进行评估[8],两种方法的预测结果见图 2。

|
图 2 不同序列长度预测的相对精度对比 Fig. 2 Comparison of relative accuracy of different sequence length prediction |
从图 2可以看出,在一定长度的原始序列范围内,随着序列长度的增加,预测精度逐渐升高,但在序列长度为27 d时达到最大,预测相对精度接近于95%,之后预测精度呈现下降趋势。考虑到电离层本身具有27 d的短周期变化[15],所以选择序列长度为27 d比较合适。
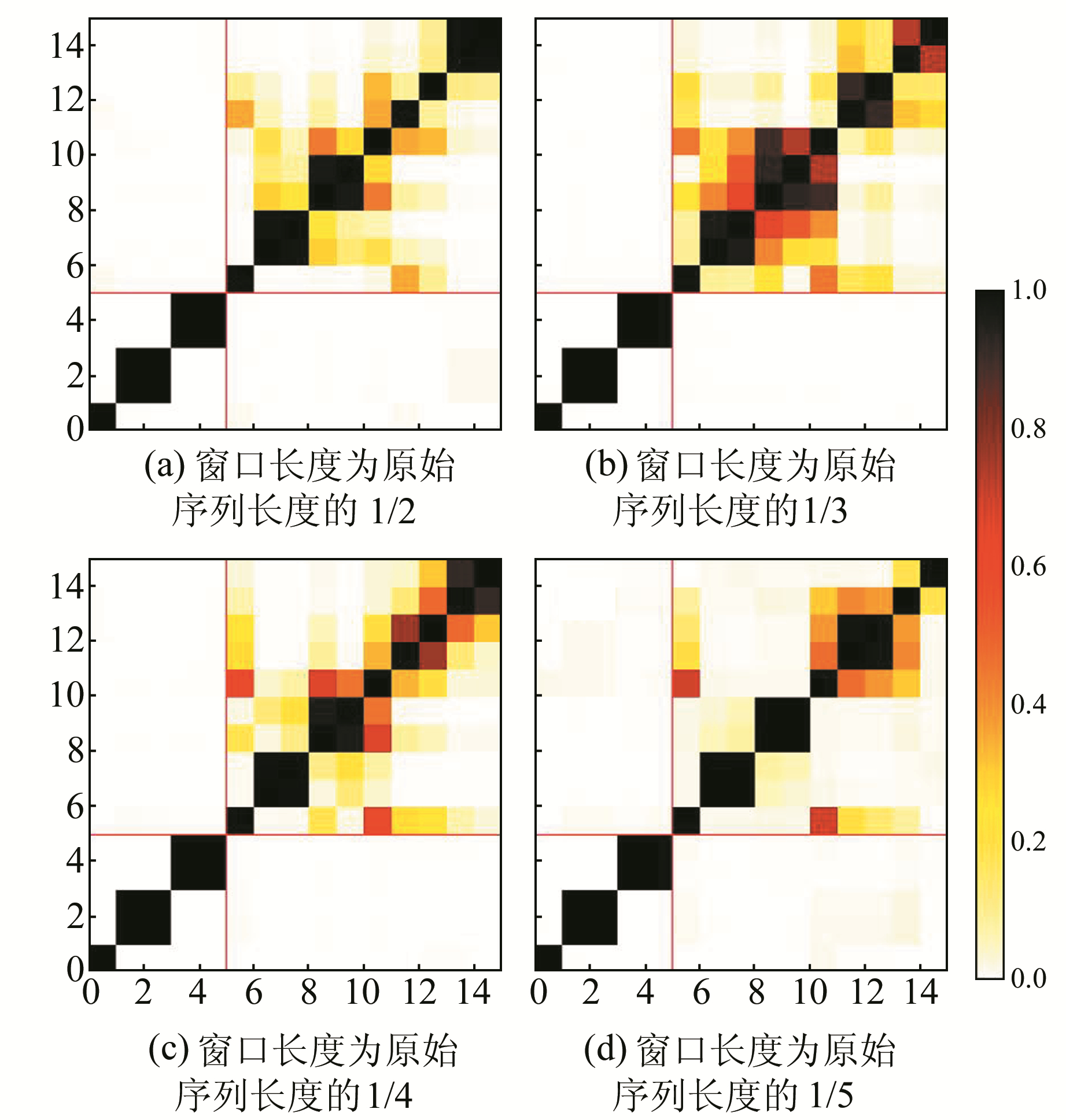
进一步确定RC的迭代阶数和窗口长度。利用年积日24~50的TEC数据,分别将窗口长度设置为原始序列的1/2、1/3、1/4和1/5,并利用SSA分解,计算前15阶RC的w-correlation相关系数,结果见图 3。可以看出,前5项RC之间可以很好地分离,而后面的RC相互之间的w-correlation值较小,很有可能代表了噪声,这在窗口长度为序列的1/3时得到的RC的w-correlation相关系数变化中尤为明显。一般来说,RC1通常代表趋势项,RC2和RC3的相关性较强,代表的是1 d的周期项,而RC5和RC6则反映了0.5 d的周期项,同时前5个RC的累计贡献率可以达到98%以上,包含了原始序列的绝大多数信息。因此,在建立SSA预测模型时,选择27 d的原始序列长度,同时将窗口长度设置为序列的1/3,迭代分解其前5项得到预测值。
|
图 3 不同窗口长度的前15阶RC w-correlation值 Fig. 3 The first 15 order RC w-correlation values of different window length |
为验证SSA预测模型的可靠性和精度,本文同时建立ARMA(p, q)预测模型。考虑到模型的精度和稳定性,将p和q的上下限设置为20,阶数的确定采用AIC准则[16]。
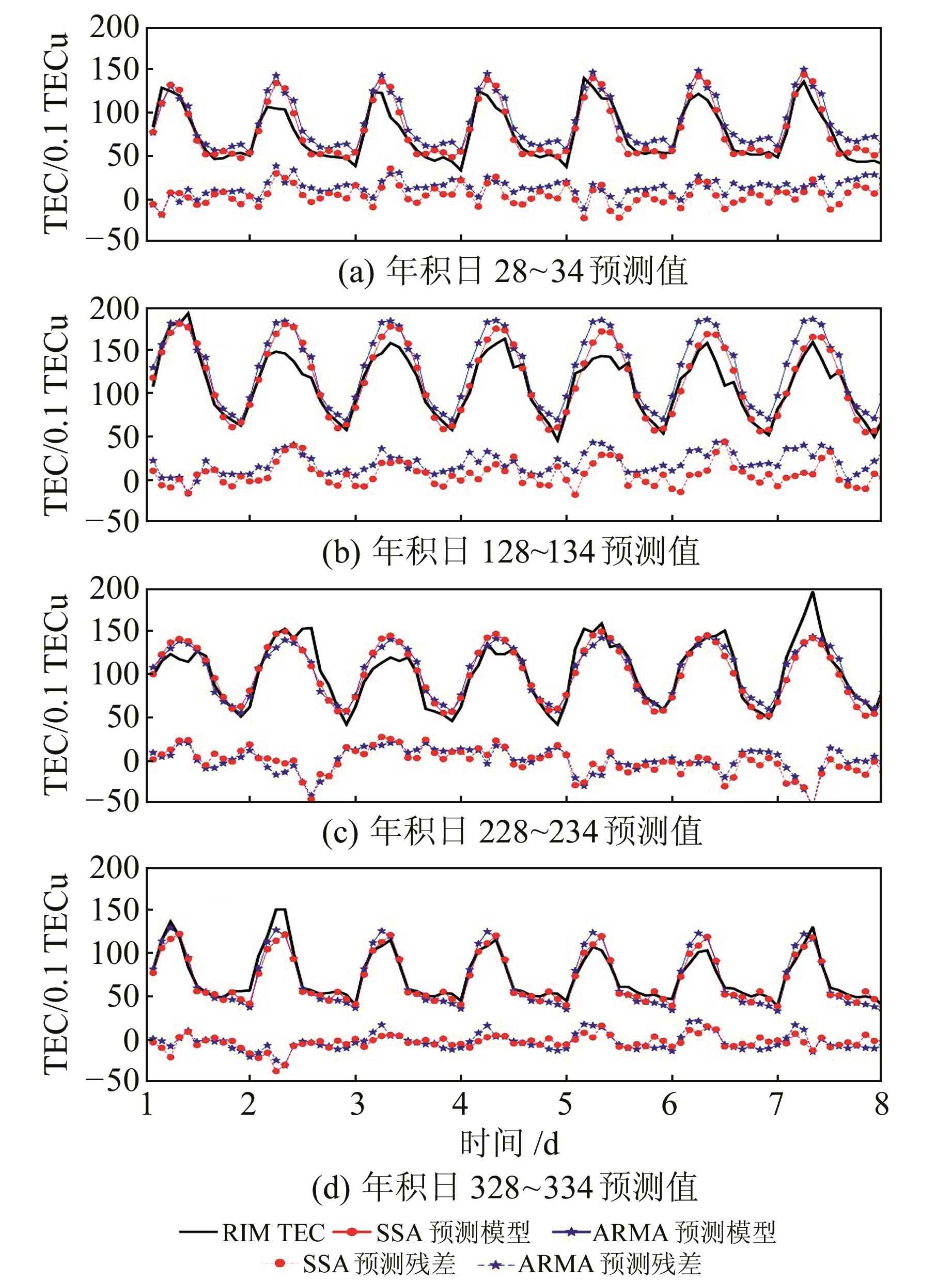
3.1 中心网格点TEC预测提取RIM中心网格点(35°N,115°E)4个时段的TEC数据,时段1~4分别为2017年年积日1~27、101~127、201~227、301~327,基于SSA和ARMA预测模型分别对其进行7 d的数据预测(图 4)。从图中可以看出,基于SSA预测模型预测的TEC精度更高,这是因为该模型可以从TEC序列的趋势项和振荡周期性出发,对于TEC的整体变化趋势和日变化规律具有更好的预测效果。与此相反,ARMA预测模型预测的每天的数据波形相近,TEC的波峰和波谷变化不明显,导致TEC整体的预测效果较差。
|
图 4 TEC预测结果 Fig. 4 Predicted results of TEC |
两种预测模型的残差统计结果见表 1,由CMONOC反演的RIM TEC的RMS最大一般不超过2 TECu。从表中可以看出,SSA预测模型预测结果的差值绝大多数不超过2 TECu,约占88%,其中小于1 TECu的约占69%。而ARMA预测模型预测结果的差值分布不均,其中差值小于1 TECu的和小于2 TECu的预测结果占比分别接近44%和80%,整体精度明显不如SSA预测模型。
|
|
表 1 两种预测模型的预测值残差统计 Tab. 1 The statistic of predicted residual value by different models |
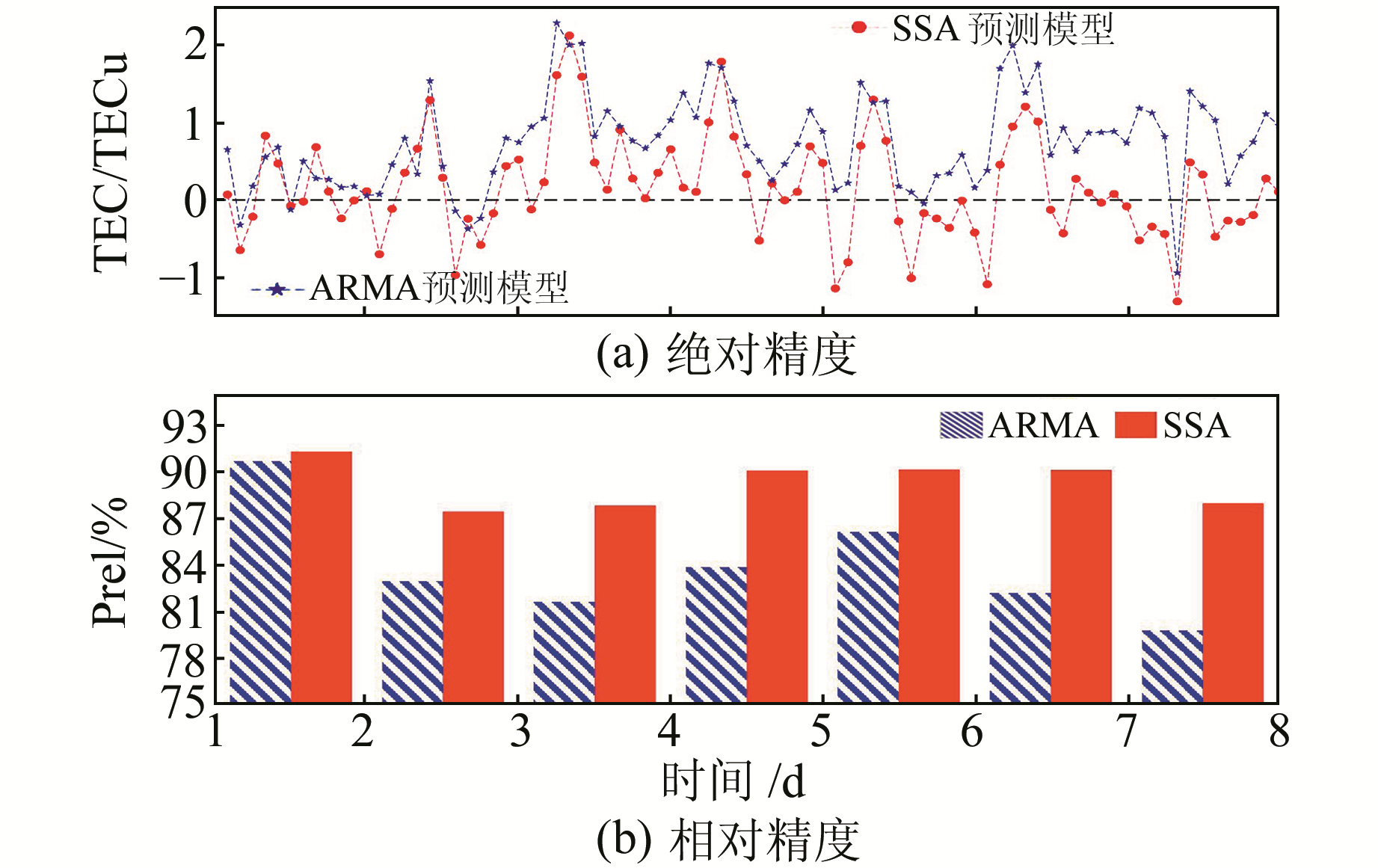
图 5为两种TEC预测模型在随后7 d内的TEC预报值与RIM TEC真实值的对比。可以看出,SSA模型的预测精度在短期的预报时间段内相比于ARMA模型有较大的提高。图 5(a)显示前两天内两种方法预测的TEC差值一般不超过1 TECu,预测精度相当;从第3天开始,基于SSA模型预测的TEC的误差出现了一定的波动,最大达到2.0 TECu,但整体在0 TECu附近,没有超过RIM的最大RMS。相对于SSA模型,ARMA模型的预测精度从第3天起下降较大,最大误差达到2.4 TECu,虽然第4~5天误差稍有减小,但是最后两天误差上升到1 TECu左右,TEC的预测精度随着预报天数的延长有明显下降。图 5(b)为两种模型预测结果相对精度的变化趋势,SSA预测模型的相对精度保持平稳,稳定在90%左右;而ARAM预测模型的相对精度随预报天数的增长下降幅度较大,除第1天相对精度超过了90%,后面几天都出现大幅度下降,第7天甚至下降到78%。
|
图 5 不同模型预测7 d的精度 Fig. 5 7-day accuracy of different models |
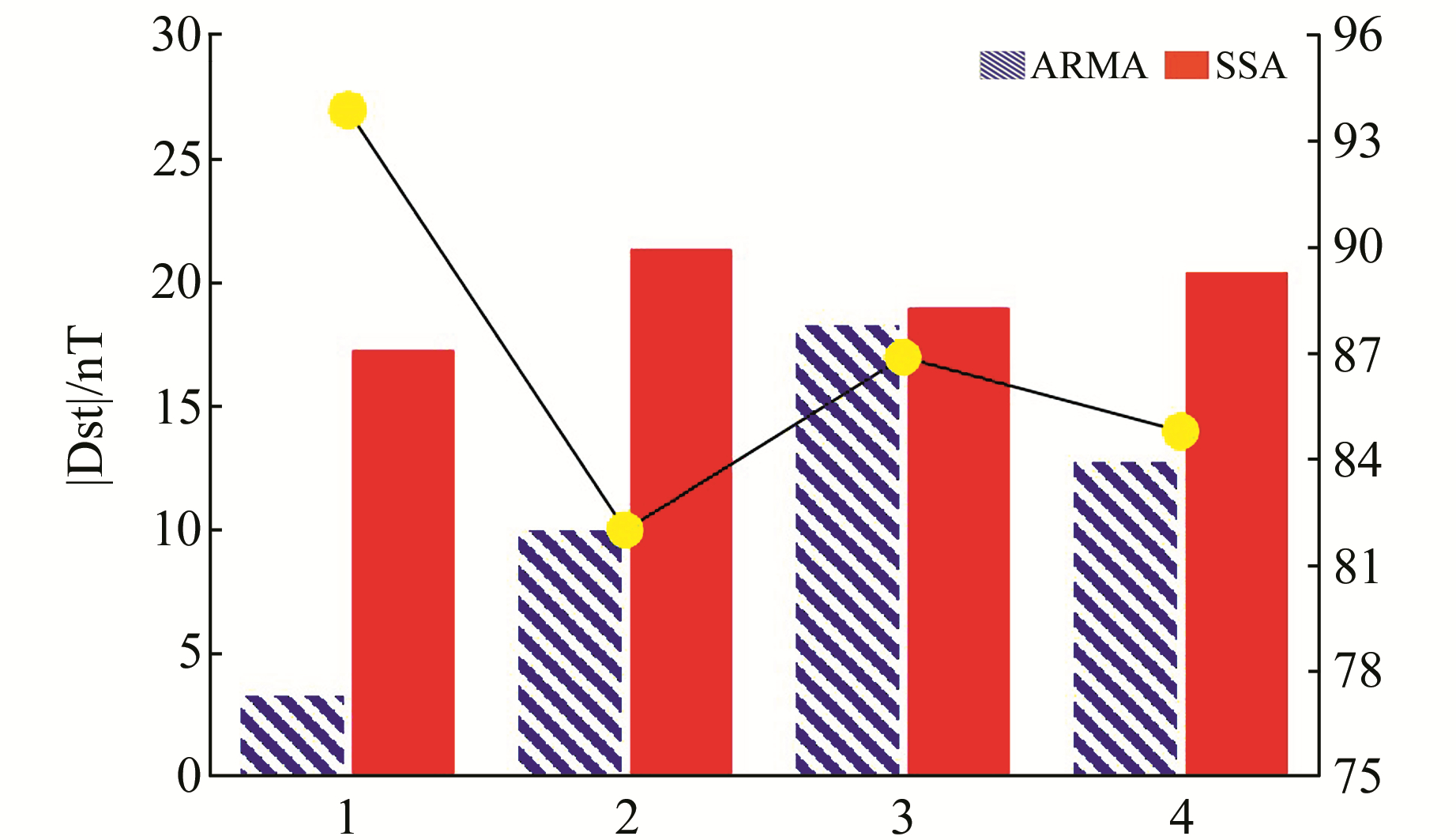
Dst指数表示中低纬度区的地磁活动状况,可以较好地反映中国地区的地磁活动[17]。本文通过统计4个时段的ARMA模型和SSA模型的平均预测相对精度和平均|Dst|信息,观察地磁活动对预测结果的影响。从图 6和表 2可以看出,地磁活动和模型预测结果有一定的相关性,根据两种预测模型所有预测结果的相关精度和对应时刻的Dst指数绝对值计算其相关系数,判断地磁活动对预测结果的影响,SSA模型的TEC预测结果和Dst的相关系数为-0.69,ARMA模型的TEC预测结果和Dst的相关系数为-0.89。可以看出,SSA模型在地磁场平静期的预测精度更高,抗干扰能力也似乎更强。本文仅作初步探索,未来会对磁暴时段的电离层预测展开更多分析。
|
图 6 不同时段的平均|Dst|和两种方法的相对误差 Fig. 6 Average |Dst| and relative errors of the two methods at different time periods |
|
|
表 2 Dst和模型相对精度分时段统计 Tab. 2 The statistic of Dst and the relative accuracy with each period |
为进一步对比分析两种预测模型的预测效果,提取RIM所有2 911个网格点的TEC数据,利用两种方法分别对每个网格点的TEC进行预报。
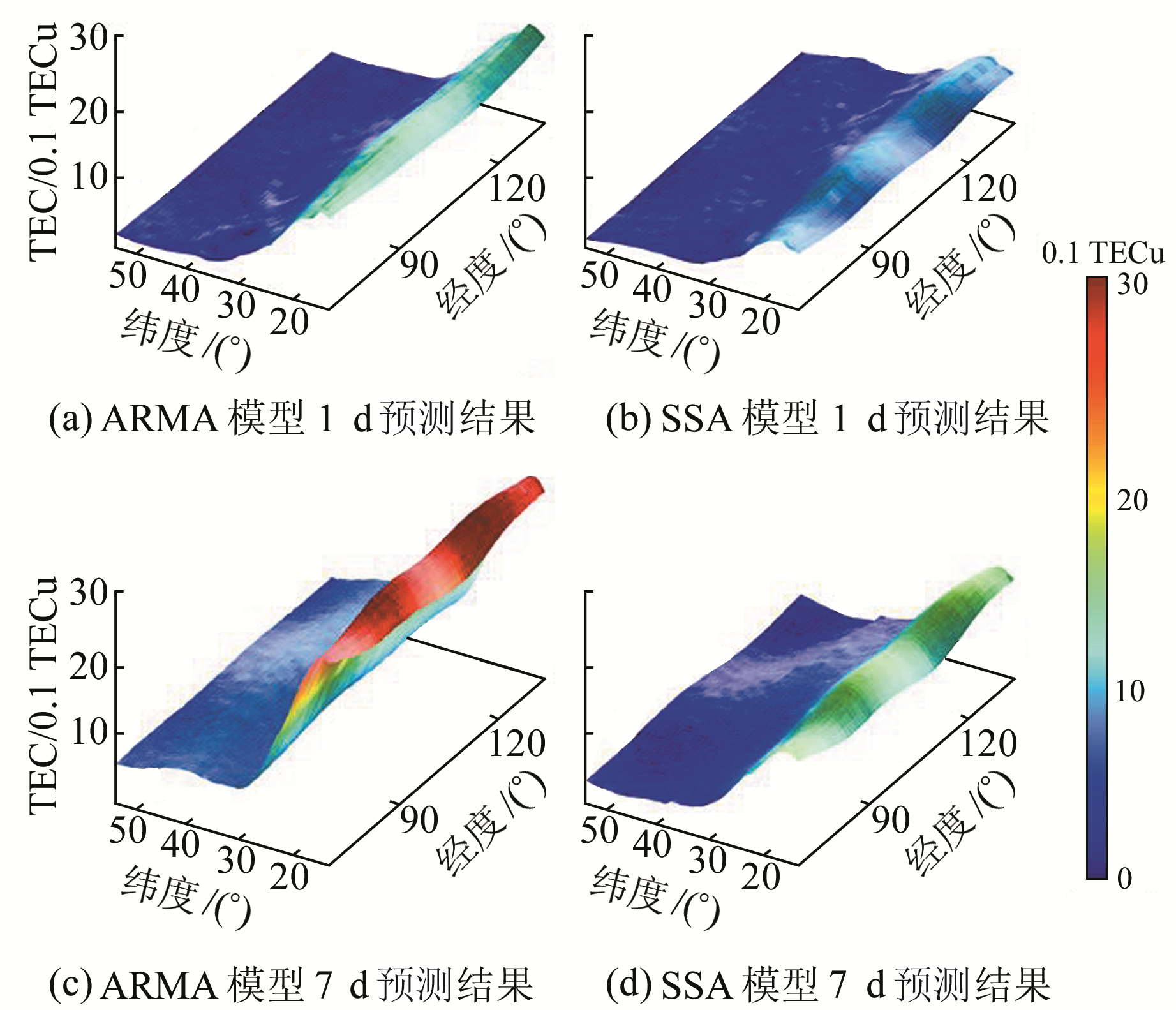
图 7为两种预测模型1 d和7 d预测值的RMSE分布情况。从图中可以看出,第1天两种预测模型的RMSE在中高纬度地区基本不超过0.6 TECu,但ARMA预测模型在低纬度地区预测效果较差,RMSE最大达到1.3 TECu;第7天两种模型的RMSE都有所上升,预测效果逐渐下降,其中SSA模型和ARMA模型的RMSE最大分别达到1.5 TECu和3.2 TECu。总体来看,SSA模型具有更好的预测效果,但无论哪种模型,其预测数据的RMSE在经度方向上变化较小,在低纬度地区RMSE明显偏大,这与低纬度地区电子含量较高且变化明显有关。
|
图 7 RMSE中国大陆及周边区域分布 Fig. 7 RMSE distribution in mainland China and surrounding regions |
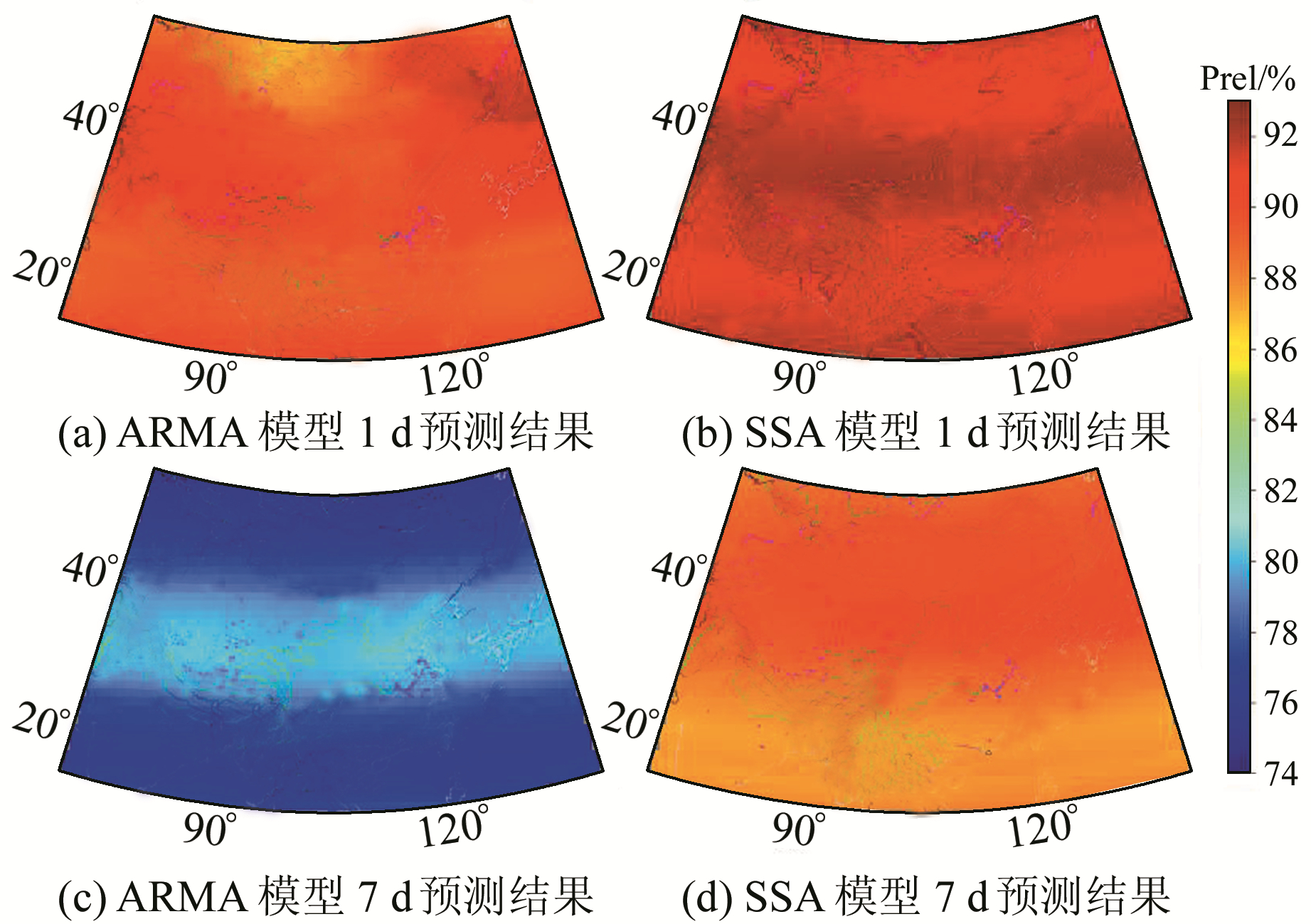
图 8为两种预测模型1 d和7 d预测值的相对精度分布情况。从图中可以看出,第1天,所有网格点基于SSA预测模型的TEC预测相对精度基本都超过90%,预测精度相差不大,不同网格点预测效果也少有差异,仅呈现出一定的纬度差异性;第7天,利用SSA模型预测的中国大陆区域的TEC相对精度下降到87%左右,比第1天的预测精度稍有下降,而ARMA模型的预测效果变化显著,整体的TEC预测相对精度下降到75%左右。TEC预测相对精度的空间分层现象更加明显,呈现出“高低纬度小、中纬度大”的特点,CMONOC的GPS站点在高低纬度地区分布较少,反演的TEC精度较差,可能对传统预测方法造成一定的干扰。总体而言,随着预测时间的延长,ARMA预测模型的预测效果明显下降,同时其也容易受到原始数据精度的影响;而SSA预测模型较好,网格点的最大TEC预测相对精度可以提高10%以上,有效提高了中国大陆及其周边区域的电离层预测精度。
|
图 8 Prel中国大陆及周边区域分布 Fig. 8 Prel distribution in mainland China and surrounding regions |
电离层具有很强的时空变化特征,本文基于RIM建立SSA预测模型,同时和ARMA预测模型进行对比,得到以下结论:
1) 总体来看,SSA模型的预测精度在短期(7 d)内相比于ARMA模型有明显的提高,利用SSA模型不仅可以较好地预测TEC整体变化趋势,同时也可以较好地体现TEC日变化特征。
2) 以本文的4个分析时段为基础,在地磁平静时期,|Dst|和SSA模型的TEC预测值的相关性为-0.69,低于|Dst|和ARMA模型预测值的相关性-0.89。后续工作将对地磁扰动时期进行统计,判断SSA模型在不同地磁条件下的预测精度。
3) 对比两种模型预报结果的RMSE在中国大陆及周边地区的分布情况,发现两者均存在低纬度地区精度低、中高纬度地区精度高的情况,可能与TEC的空间分布有关;同时预测相对精度的空间分布显示出中纬度地区预测精度高、高低纬度地区预测精度较低的特点,这可能与RIM的精度有关。但无论哪种精度指标,SSA模型的预测精度均优于ARMA模型。
| [1] |
Mannucci A J, Wilson B D, Yuan D N, et al. Global Mapping Technique for GPS-Derived Ionospheric Total Electron Content Measurements[J]. Radio Science, 1998, 33(3): 565-582 DOI:10.1029/97RS02707
(  0) 0) |
| [2] |
李强, 宁百齐, 赵必强, 等. 基于陆态网络GPS数据的电离层空间天气监测与研究[J]. 地球物理学报, 2012, 55(7): 2 193-2 202 (Li Qiang, Ning Baiqi, Zhao Biqiang, et al. Applications of the CMONOC Based GNSS Date in Monitoring and Investigation of Ionospheric Space Weather[J]. Chinese Journal of Geophysics, 2012, 55(7): 2 193-2 202)
(  0) 0) |
| [3] |
Li W, Guo J Y, Yue J P, et al. Contrastive Research of Ionospheric Precursor Anomalies between Calbuco Volcanic Eruption on April 23 and Nepal Earthquake on April 25, 2015[J]. Advances in Space Research, 2016, 57(10): 2 141-2 153 DOI:10.1016/j.asr.2016.02.014
(  0) 0) |
| [4] |
Krankowski A, Kosek W, Baran L W, et al. Wavelet Analysis and Forecasting of VTEC Obtained with GPS Observations over European Latitudes[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2005, 67(12): 1 147-1 156 DOI:10.1016/j.jastp.2005.03.004
(  0) 0) |
| [5] |
武文俊, 李志刚, 杨旭海, 等. 利用时间序列模型预报电离层TEC[J]. 时间频率学报, 2008, 31(2): 141-146 (Wu Wenjun, Li Zhigang, Yang Xuhai, et al. Predicting Ionospheric TEC with Time Series Model[J]. Journal of Time and Frequency, 2008, 31(2): 141-146 DOI:10.3969/j.issn.1674-0637.2008.02.012)
(  0) 0) |
| [6] |
鲍亚东, 刘长建, 柴洪洲. 小波分解改进电离层VTEC时间序列预报模型[J]. 大地测量与地球动力学, 2015, 35(5): 784-787 (Bao Yadong, Liu Changjian, Chai Hongzhou. Time Series Prediction Model of Ionospheric VTEC Improved by Wavelet Decomposition[J]. Journal of Geodesy and Geodynamics, 2015, 35(5): 784-787)
(  0) 0) |
| [7] |
李磊.基于GNSS的电离层总电子含量的预测与应用研究[D].大连: 大连海事大学, 2015 (Li Lei. Research on Forecasting and Application of the Ionospheric Total Electron Content Based on GNSS[D]. Dalian: Dalian Maritime University, 2015) http://cdmd.cnki.com.cn/Article/CDMD-10151-1015640050.htm
(  0) 0) |
| [8] |
翁利斌, 方涵先, 缪子青, 等. 利用人工神经网络提前1 h预报电离层TEC[J]. 空间科学学报, 2012, 32(2): 204-208 (Weng Libin, Fang Hanxian, Miao Ziqing, et al. Forecasting of Ionospheric TEC One Hour in Advance by Artificial Neural Network[J]. Chinese Journal of Space Science, 2012, 32(2): 204-208)
(  0) 0) |
| [9] |
Keppenne C L, Ghil M. Adaptive Filtering and Prediction of the Southern Oscillation Index[J]. Journal of Geophysical Research: Atmospheres, 1992, 97(D18): 20
(  0) 0) |
| [10] |
Hassani H. Singular Spectrum Analysis: Methodology and Comparison[J]. Journal of Data Science, 2007, 5(2): 239-257
(  0) 0) |
| [11] |
Shen Y, Guo J Y, Liu X, et al. Long-Term Prediction of Polar Motion Using a Combined SSA and ARMA Model[J]. Journal of Geodesy, 2018, 92(3): 333-343 DOI:10.1007/s00190-017-1065-3
(  0) 0) |
| [12] |
王燕. 应用时间序列[M]. 北京: 中国人民大学出版社, 2008 (Wang Yan. Application Time Series[M]. Beijing: China Renmin University Press, 2008)
(  0) 0) |
| [13] |
周巍, 鲍亚东.基于CMONOC的中国区域电离层分布特征研究[C].第9届中国卫星导航学术年会, 哈尔滨, 2018 (Zhou Wei, Bao Yadong. Research on the Distribution of Ionosphere in China Based on CMONOC[C]. The 9th China Satellite Navigation Conference, Harbin, 2018)
(  0) 0) |
| [14] |
柳景斌, 王泽民, 章红平. 几种地基GPS区域电离层TEC建模方法的比较及其一致性研究[J]. 武汉大学学报:信息科学版, 2008, 33(5): 479-483 (Liu Jingbin, Wang Zemin, Zhang Hongping, et al. Comparison and Consistency Research of Regional Ionospheric TEC Models Based on GPS Measurements[J]. Geomatics and Information Science of Wuhan University, 2008, 33(5): 479-483)
(  0) 0) |
| [15] |
Pancheva D, Lastovika J.Solar or Meteorological Control of Lower Ionospheric Fluctuations(2-15 and 27 days) in Middle Latitudes[Z]. 1986
(  0) 0) |
| [16] |
张硕.电离层TEC实时估计与预测方法研究[D].郑州: 信息工程大学, 2017 (Zhang Shuo. Research on Real-Time Estimation and Prediction Methods of the Ionosphere TEC[D]. Zhengzhou: Information Engineering University, 2017) http://cdmd.cnki.com.cn/Article/CDMD-90005-1018702661.htm
(  0) 0) |
| [17] |
马一方, 姜卫平, 席瑞杰. 利用全球电离层地图分析芦山地震电离层异常变化[J]. 武汉大学学报:信息科学版, 2015, 40(9): 1 274-1 278 (Ma Yifang, Jiang Weiping, Xi Ruijie. Analysis of Seimo-Ionospheric Anomalies in Vertical Total Electron Content of GIM for Lushan Earthquake[J]. Geomatics and Information Science of Wuhan University, 2015, 40(9): 1 274-1 278)
(  0) 0) |
2. State Key Laboratory of Mining Disaster Prevention and Control Cofounded by Shandong Province and Ministry of Science and Technology, Shandong University of Science and Technology, 579 Qianwangang Road, Qingdao 266590, China
 2019, Vol. 39
2019, Vol. 39


