近年来,雾霾对人们的生活和健康产生了深刻的影响,如何有效预测大气PM2.5浓度的变化及提前预警雾霾天气的发生成为新的研究热点[1]。影响大气PM2.5浓度的因素主要有两类[2-3]:1)从PM2.5的化学成因出发,能够直接导致或促进PM2.5浓度变化的环境空气质量因素,如氮氧化物(NOx)、CO、SO2等;2)在污染物排放稳定的情况下,通过大气气候变化机制影响PM2.5时空分布的近地面气象因素,如气温、气压、水汽等。
在传统的基于气象因素的雾霾预测研究中,气象参数主要由地面气象站观测得到,但其时空分辨率低,且难以获取大气可降水量(PWV),在雾霾预测中未考虑大气水汽这一重要影响因子。随着全球卫星导航系统(GNSS)的建设与发展,卫星观测站可获取最高时间分辨率为30 s的气温(T)、气压(P)、相对湿度(HR)及大气可降水量(PWV),利用其得到的气象参数进行雾霾预测具有很大的优势。
常见的雾霾预测模型包括时间序列分析(TSA)[4]、隐马尔可夫模型(HMM)[5]、人工神经网络(ANN)[6]等。其中,ANN是一种模仿动物神经网络行为特征来进行分布式并行信息处理的数学模型,该模型对推理规则模糊、处理信息复杂的非线性目标函数的拟合表现出独特的优越性[7]。神经网络预测模型大致可分为两类:基于时间序列分析(TSA)的网络模型和基于回归分析(RA)的网络模型[8-9]。单一的网络模型存在泛化能力低、适应性差等问题[10],PM2.5序列由于其随机性、突变性等特点,考虑将两类网络预测模型进行融合,在顾及PM2.5序列内在变化规律的同时加入外在气象因子的影响,以改善预测精度。
本文结合北京市GNSS气象数据(T、P、PWV)及PM2.5数据,采用误差后向传播的多层前向神经网络模型[11],即BP神经网络(back propagation neural networks,BPNN),建立一种融合时序网络和回归网络的雾霾预测模型,对大气PM2.5浓度进行预测。通过对引入GNSS气象参数前后模型预测效果的对比分析,验证GNSS气象参数应用于雾霾预测的可行性,拓宽卫星导航技术在气象领域的应用。
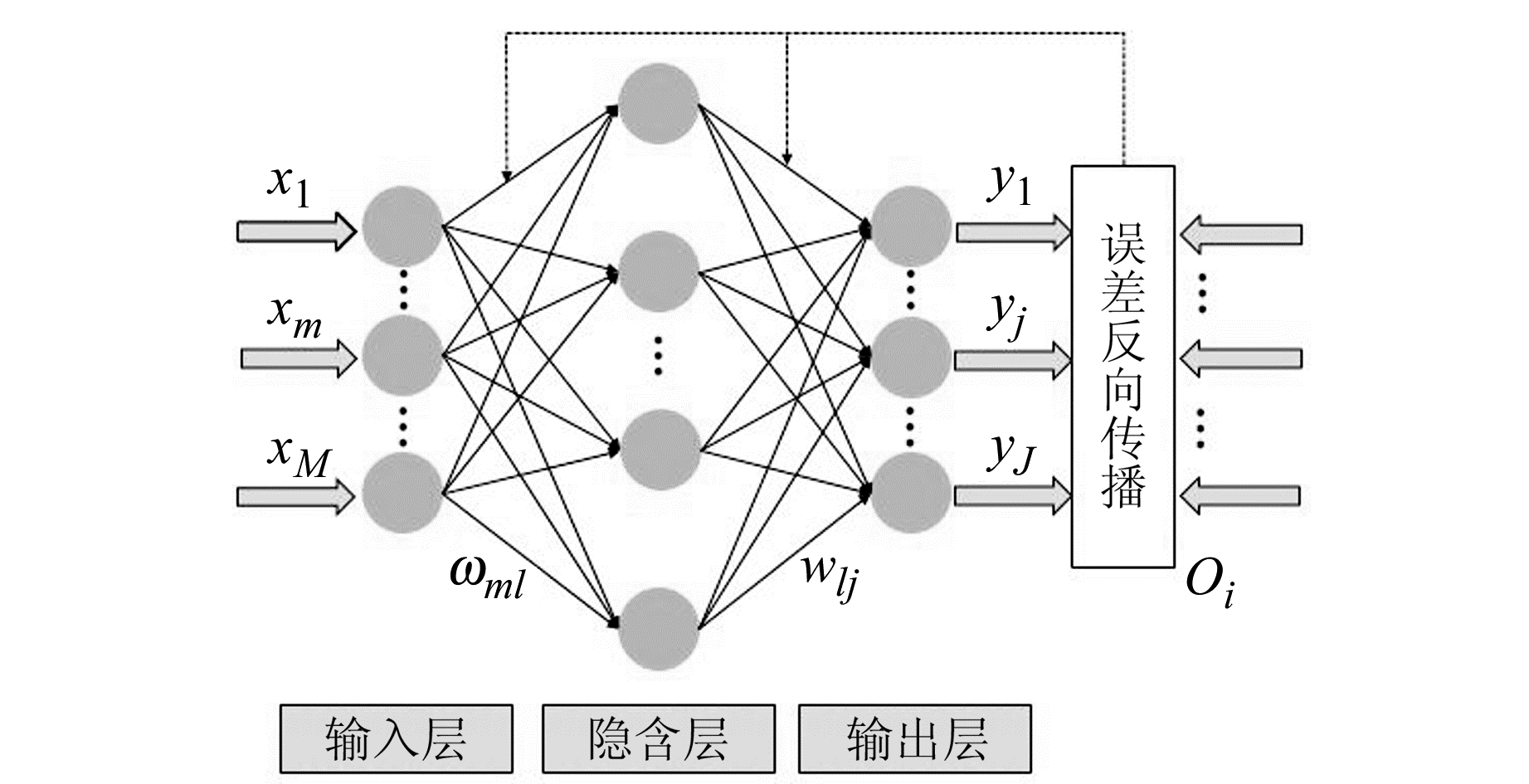
1 雾霾预测模型 1.1 BP神经网络BP神经网络(BPNN)是一种按误差反向传播算法训练的多层前馈网络模型,多用于函数逼近、预测分析等[12],其网络结构通常包含3个层次:输入层、隐含层及输出层。图 1为3层结构的BP神经网络模型结构。
|
图 1 3层BP神经网络结构 Fig. 1 The structure of three-layer BPNN |
BP神经网络每层由一个或多个神经元(网络节点)构成,神经元输入与输出之间的关系为:
| $ {I_j} = \sum\limits_{j = 1}^n {{w_{kj}}} {x_j} - {\theta _k}, {y_k} = f\left( {{I_j}} \right) $ | (1) |
式中,xj(j=0, 1, …, n)为外部第j个神经元对神经元k的输入信号,wkj、θk为神经元j到k的连接权值和阈值,yk为神经元k的输出量,f(Ij)为激励函数[7]。BP神经网络算法的基本思想是根据网络输出结果与实际期望值的误差大小由训练算法反向逐层迭代修正网络权值和阈值,使误差沿负梯度方向下降,直至最小。常见的训练算法有批梯度下降法、动量批梯度下降法、自适应学习率的梯度下降法[13]等。
1.2 雾霾预测模型影响大气PM2.5浓度的因素较多且呈现出复杂的非线性变化规律,而BP神经网络具有高度的非线性特性和较强的泛化能力,可有效拟合两者之间复杂的映射关系,进而对大气PM2.5浓度进行预测。目前,基于BP神经网络的雾霾预测模型主要有两类:基于PM2.5序列的时序网络模型和基于PM2.5影响因子的回归网络模型。前者依据PM2.5序列变化具有连续性的特点,将历史PM2.5序列作为训练样本预测当前PM2.5值,充分考虑了序列间的内在变化规律,预测精度较高,但该模型需要获得连续、完备的PM2.5序列,缺失值和突变值容易对网络训练造成影响;后者引入与PM2.5相关性较强的多个影响因子,通过网络训练不断拟合两者之间的映射关系来推算预测值,外部观测值的引入可提高模型的外符合精度,但该模型对影响因子的依赖性较大,影响因子与PM2.5相关性的强弱及不同影响因子的组合均会对模型预测结果造成影响。本文综合两种模型的优点,在时序网络的基础上加入外在影响因子作为输入变量,同时考虑PM2.5序列内部变化规律及外部影响因子的影响,构建一种融合时序网络和回归网络的雾霾预测模型。
融合模型采用3层结构的BP神经网络,输入层含GNSS气象参数及PM2.5两类变量,输出层为PM2.5预测值。输入层中,由于GNSS可提供的气象参数包含气温(T)、气压(P)、相对湿度(HR)及大气可降水量(PWV)4类,需要统计各气象参数与PM2.5的相关性及互相关性,以筛选出有效的输入变量,统计结果见表 1。
|
|
表 1 各气象参数互相关性及与PM2.5的相关性统计结果 Tab. 1 Correlation between meteorological parameters and correlation with PM2.5 |
由表 1可知,4类气象参数与PM2.5均呈现出显著相关性(|r|基本在0.6以上,p均小于0.01),其中T、P为负相关,HR、PWV为正相关,但PWV与HR之间相关性较高,且PWV与PM2.5的相关性较HR要高。因此,最终确定将T、P、PWV 3类气象参数及PM2.5序列作为输入变量,同时考虑到PWV反演过程有延迟,设置PM2.5预测时效为3 h,融合网络模型结构见图 2。

|
图 2 融合时序网络和回归网络的雾霾预测模型 Fig. 2 The haze prediction model combines time series network and regression network |
本文以北京市作为研究区,数据选取BJFS站的气象参数(T、P、PWV)及雾霾浓度指标(PM2.5)。其中,气象参数由IGS提供的BJFS站气象文件提取得到(PWV经进一步水汽反演[14]得到),PM2.5数据采用北京市环境保护监测中心(http://www.bjmemc.com.cn/)发布的房山良乡监测站数据。由于一年中雾霾天气基本集中在冬春季节,为提高模型对雾霾预测的针对性,训练样本采样时间范围为2016年春季(1~3月)和冬季(10~12月),采样率为1 h,得到183 d共4 392组训练样本数据。
为分析和比较引入GNSS气象参数前后模型预测雾霾的效果,对未考虑GNSS气象参数的时序网络模型(TSA-ANN)和引入GNSS气象参数的融合雾霾预测模型([TSA+RA]-ANN)在相同条件(设置相同的训练函数、激励函数及样本组数)下进行训练。为避免网络权值随机初始化引起的网络差异,防止训练陷入局部最优,每种模型进行5次训练,结果见表 2。
|
|
表 2 两种网络模型5次训练的迭代次数及训练误差 Tab. 2 Iterations and training error of two network models in five training sessions |
为全面比较和分析两种模型的预测性能,本文按城市空气质量划分等级[15],在2017年春、冬季分别选取了3类具有代表性的雾霾天气作为预测样本:空气质量优良(PM2.5avg∈[0, 75)μg/m3)、中轻度污染(PM2.5avg∈[0, 75)μg/m3)。取训练误差最小值对应的网络模型作为最终预测模型,即第4次的[TSA+RA]-ANN模型和第1次的TSA-ANN模型,比较各模型不同空气质量条件和不同季节的预测效果,结果见表 3。
|
|
表 3 预测样本的分类及统计信息 Tab. 3 The classification and statistics of forecast sample |
图 3为3种城市空气质量分类下[TSA+RA]-ANN模型和TSA-ANN模型预测结果的对比,左侧为模型预测值与实测值的变化对比,右侧为对应类别的误差绝对值变化对比。

|
图 3 3种分类情况下预测值与实测值的变化对比结果及对应的误差绝对值 Fig. 3 The comparison between predicted value and measured value in three classification cases and the corresponding absolute value of the error |
从图 3可以看出,[TSA+RA]-ANN模型和TSA-ANN模型对2017年春、冬季对应的3种空气质量条件下的PM2.5均能作出较为准确的预测,预测值与实测值的变化趋势基本一致。对两种模型的误差绝对值按如下方式进行统计:1)按城市空气质量分类统计,误差绝对值均值在空气质量优良时分别为12.1 μg/m3、15.5 μg/m3,中轻度污染时分别为15.1 μg/m3、20.5 μg/m3,重度严重污染时分别为20.5 μg/m3、27.4 μg/m3,结果表明,两种模型在空气质量优良天气的PM2.5预测效果优于中轻度污染天气,在重度严重污染天气时较差,且[TSA+RA]-ANN模型整体优于TSA-ANN模型;2)按季节分类统计,误差绝对值均值在春季时分别为17.5 μg/m3、22.9 μg/m3,冬季时分别为13.6 μg/m3、19.4 μg/m3,结果表明,两种模型在冬季的PM2.5预测效果较春季要好,且[TSA+RA]-ANN模型优于TSA-ANN模型。
此外,由图 3中两种模型的误差绝对值对比可以看出,TSA-ANN模型的误差绝对值在个别时段较高。分析该时段可知,其对应的PM2.5实测值均发生了较大的突变现象,说明仅采用PM2.5历史序列进行预测的TSA-ANN模型对邻近值的变化不敏感,在PM2.5发生突变时难以准确地预测PM2.5的变化。而[TSA+RA]-ANN模型由于考虑气象参数这一外部影响因子,在PM2.5发生突变时仍能较好地预测PM2.5的变化,较TSA-ANN模型具有更好的连续性,与实测值的符合度更高。
2.3 [TSA+RA]-ANN模型精度评价由分析可知,[TSA+RA]-ANN融合模型具有较高的预测精度,对不同的PM2.5环境均表现出较高的适应性。为全面评价该模型的预测精度,采用3类评价指标[16-18],即均方根误差(RMSE)、平均绝对误差(MAD)及决定系数(R2),分别评价模型预测值与实测值的差异水平、绝对误差及模型拟合优度。具体计算公式为:
| $ {\rm{RMSE}} = \sqrt {\frac{1}{N}\sum\limits_{t = 1}^N {{{\left( {{O_t} - {P_t}} \right)}^2}} } $ | (2) |
| $ {\rm{MAD}} = \frac{1}{N}\sum\limits_{t = 1}^N {\left| {{O_t} - {P_t}} \right|} $ | (3) |
| $ {R^2} = {\left( {\frac{1}{{N - 1}}\sum\limits_{t = 1}^N {\left( {\frac{{{O_t} - \bar O}}{{{S_O}}}} \right)} \left( {\frac{{{P_t} - \bar P}}{{{S_P}}}} \right)} \right)^2} $ | (4) |
式中,N为预测样本组数,Ot、Pt分别为PM2.5的实测值与预测值,
计算得到模型预测样本的RMSE、MAD、R2分别为16.473 μg/m3、15.552 μg/m3、0.997 8,表明模型的预测值能较为准确地反映实测值的变化,且两者之间具有良好的一致性,模型对预测值与实测值的拟合度较高。该结果与当前同类研究[19-21]中雾霾预测所能达到的精度接近。
3 结语本文利用卫星导航技术在获取气象参数方面的优势,结合北京市GNSS气象参数和PM2.5数据,构建了一种融合时序网络和回归网络的雾霾预测模型。通过对比分析TSA-ANN模型与引入GNSS气象参数的[TSA+RA]-ANN模型在不同PM2.5环境下的预测结果,认为:1)[TSA+RA]-ANN模型无论是在空气质量优良、中轻度污染、重度严重污染还是冬春季,其预测效果均优于TSA-ANN模型,且预测精度高,时效性可达3 h;2)[TSA+RA]-ANN模型还能有效弥补TSA-ANN模型在PM2.5发生突变时预测误差大的缺陷,适应性强。总而言之,相比单一的网络模型,融合模型具有更高的泛化能力和适应性。
随着全球卫星导航系统的快速发展,大规模的地面卫星观测站点如全球IGS跟踪站、区域连续运行参考站(CORS)将全面建成,数据采集的准确率和实时性也将得到提升。因此,结合卫星观测站在布设及数据获取等方面的优势,本文提出的融合GNSS气象参数的BP神经网络雾霾预测模型为实现大范围内快速、实时、准确的雾霾预测奠定了良好的基础。
| [1] |
Lei Y H. Hazards of Haze and Countermeasures[J]. Applied Mechanics and Materials, 2014, 507: 817-820 DOI:10.4028/www.scientific.net/AMM.507.817
(  0) 0) |
| [2] |
Zhang Q, Quan J N, Tie X X, et al. Effects of Meteorology and Secondary Particle Formation on Visibility during Heavy Haze Events in Beijing, China[J]. Science of the Total Environment, 2015, 502: 578-584 DOI:10.1016/j.scitotenv.2014.09.079
(  0) 0) |
| [3] |
Aldape F, Flores M J, Flores A J, et al. Elemental Composition and Source Identification of PM2.5 Particles Collected in Downtown Mexico City[J]. International Journal of PIXE, 2005, 15(3-4): 263-270
(  0) 0) |
| [4] |
Yang X P, Zhang Z X, Zhang Z Q, et al. A Long-Term Prediction Model of Beijing Haze Episodes Using Time Series Analysis[J]. Computational Intelligence and Neuroscience, 2016
(  0) 0) |
| [5] |
Dong M, Yang D, Kuang Y, et al. PM2.5 Concentration Prediction Using Hidden Semi-Markov Model-Based Times Series Data Mining[J]. Expert Systems with Applications, 2009, 36(5): 9 046-9 055 DOI:10.1016/j.eswa.2008.12.017
(  0) 0) |
| [6] |
Pérez P, Trier A, Reyes J. Prediction of PM2.5, Concentrations Several Hours in Advance Using Neural Networks in Santiago, Chile[J]. Atmospheric Environment, 2000, 34(8): 1 189-1 196 DOI:10.1016/S1352-2310(99)00316-7
(  0) 0) |
| [7] |
Wu Y C, Feng J W. Development and Application of Artificial Neural Network[J]. Wireless Personal Communications, 2018, 102(2): 1 645-1 656 DOI:10.1007/s11277-017-5224-x
(  0) 0) |
| [8] |
Specht D F. A General Regression Neural Network[J]. IEEE Transactions on Neural Networks, 1991, 2(6): 568-576 DOI:10.1109/72.97934
(  0) 0) |
| [9] |
Wen X H, Chen K Z. Time Series Neural Network Forecasting Methods[J]. Journal of Electronics, 1996, 12(1): 1-8
(  0) 0) |
| [10] |
Gemello R, Albesano D, Mana F. Multi-Source Neural Networks for Speech Recognition[C]. International Joint Conference on Neural Networks, Washington DC, 1999
(  0) 0) |
| [11] |
Rumerlhar D E, Hinton G E, Williams R J. Learning Representation by Back-Propagating Errors[J]. Cognitive Modeling, 1986, 5(3): 533-536
(  0) 0) |
| [12] |
Goh A T C. Back-Propagation Neural Networks for Modeling Complex Systems[J]. Artificial Intelligence in Engineering, 1995, 9(3): 143-151
(  0) 0) |
| [13] |
Jin W, Li Z J, Wei L S, et al. The Improvements of BP Neural Network Learning Algorithm[C]. 5th International Conference on Signal Processing Proceedings, 16th World Computer Congress, Beijing, 2000
(  0) 0) |
| [14] |
Xu J J, Liu B, Yuan J G, et al. Inversion of Precipitable Water Vapor in Hongkong[C]. International Workshop on Earth Observation and Remote Sensing Applications, Beijing, 2008
(  0) 0) |
| [15] |
HJ 633-2012, 环境空气质量指数(AQI)技术规定(试行)[S].北京: 中国环境科学出版社, 2016 (HJ 633-2012, Environmental Air Quality Index (AQI) Technical Regulations (Trial)[S]. Beijing: China Environmental Science Press, 2016)
(  0) 0) |
| [16] |
Willmott C J, Ackleson S G, Davis R E, et al. Statistics for the Evaluation and Comparison of Models[J]. Journal of Geophysical Research: Oceans, 1985, 90(C5): 8 995-9 005 DOI:10.1029/JC090iC05p08995
(  0) 0) |
| [17] |
Gunhan T, Demir V, Hancioglu E, et al. Mathematical Modeling of Drying of Bay Leaves[J]. Energy Conversion and Management, 2005, 46(11-12): 1 667-1 679 DOI:10.1016/j.enconman.2004.10.001
(  0) 0) |
| [18] |
Nastos P T, Paliatsos A G, Koukouletsos K V, et al. Artificial Neural Networks Modeling for Forecasting the Maximum Daily Total Precipitation at Athens, Greece[J]. Atmospheric Research, 2014, 144: 141-150 DOI:10.1016/j.atmosres.2013.11.013
(  0) 0) |
| [19] |
Ni X L, Cao C X, Zhou Y K, et al. Spatio-Temporal Pattern Estimation of PM2.5 in Beijing-Tianjin-Hebei Region Based on MODIS AOD and Meteorological Data Using the Back Propagation Neural Network[J]. Atmosphere, 2018, 9(3): 105 DOI:10.3390/atmos9030105
(  0) 0) |
| [20] |
Zhao X R, Shi H Q, Yu H, et al. Inversion of Nighttime PM2.5 Mass Concentration in Beijing Based on the VⅡRS Day-Night Band[J]. Atmosphere, 2016, 7(10): 136 DOI:10.3390/atmos7100136
(  0) 0) |
| [21] |
Feng X, Li Q, Zhu Y J, et al. Artificial Neural Networks Forecasting of PM2.5Pollution Using Air Mass Trajectory Based Geographic Model and Wavelet Transformation[J]. Atmospheric Environment, 2015, 107: 118-128 DOI:10.1016/j.atmosenv.2015.02.030
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39


