2. 上海市地震局,上海市兰溪路87号,200062
潮汐是主要由日月起潮力引起的地球整体周期性形变现象。潮汐会在地球上产生约103 Pa的周期性应力变化,比地震应力降小得多,但其积累速率比构造应力积累速率大,所以当断层的应力状态接近于岩石破裂的临界值时,潮汐应力可能会触发地震[1-2]。Tsuruoka等[3]通过对日本地区浅源逆断层地震的研究认为,潮汐正应力加速了断层的滑动;Klein等[4]和Heaton等[5]的研究显示,地震与潮汐存在正相关。这些研究都证明潮汐可能触发地震。
考虑到地球潮汐由固体潮和海潮2个部分组成,在海洋边缘附近,海潮相比固体潮有相当大的相位差,海洋下的潮汐应力可能比陆地上的潮汐应力高出1个数量级[6],忽略海潮会得出不精确的结果[7]。Tanaka等[8]考虑海洋负荷的影响,利用海洋潮汐模型NAO.99b研究了日本地区地震活动及构造应力场与潮汐现象之间的关系,该研究采用Schuster统计方法,用p值判定地震活动是否与潮汐相关。Ader等[9]进一步利用Schuster谱分析方法,避免丛集性地震活动对p值的计算产生影响[2]。
日本是地震活动受潮汐影响最显著的地区之一,也是潮汐相关性研究的热点区域。本文选取日本及邻区作为研究区,采用Schuster统计方法,利用p值对日本的地震活动进行潮汐相关性分析。利用Schuster谱对满足p<5%的地区进行分析,并研究影响该地区地震活动的潮汐的主要周期,进而探讨日本地区地震活动与潮汐的相关性。
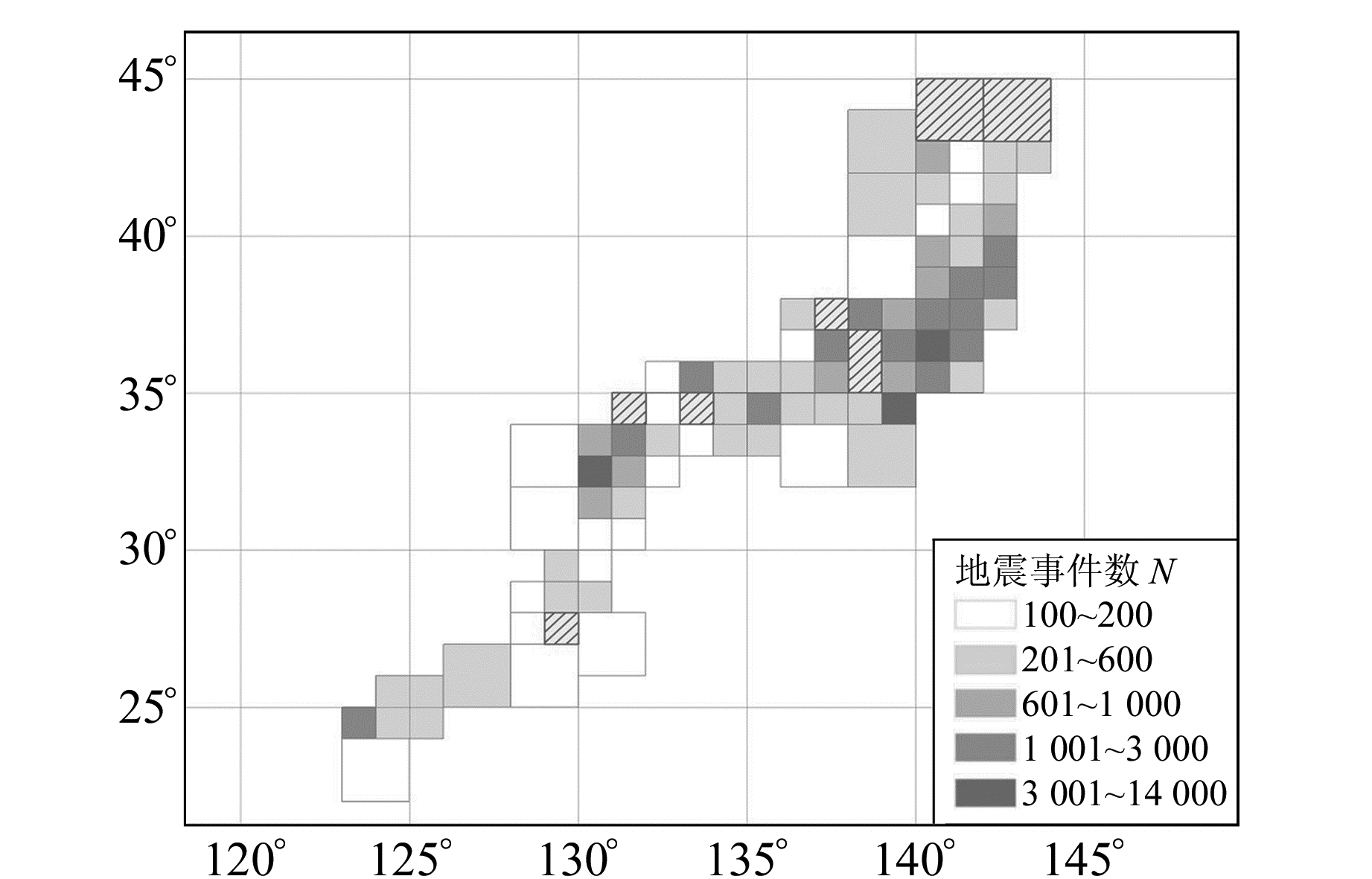
1 研究区域及数据本文选取日本JMA(http://www.jma.go.jp/jma/index.html)1990-01~2018-04地震目录中72 790个地震事件,并依据Tanaka等[8]的子区域划分法,将整个日本及邻区划分为1°×1°的次级子区域,每个子区域至少包含100个地震事件。考虑到有些子区域的地震数量不足100个,将这些子区域的范围扩大至2°×2°,如果扩大后该区域的地震数量仍不足,就舍弃该区域,不进行统计分析。具体划分结果见图 1,其中子区域共有75个,用小方块表示,颜色越深则地震数量越多,阴影部分为地震数目不足100个的区域。
|
图 1 日本及邻区的子区域划分 Fig. 1 Subregional of Japan and adjacent region |
由于日本四面环海,必须考虑海潮对计算结果的影响。Matsumoto等[10]提出的GOTIC2包含了全球模型和局域模型的海陆数据库及海潮模型NAO.99b,相较于旧版本的GOTIC[11],改进了日本地区的海潮模型,提高了计算精度。
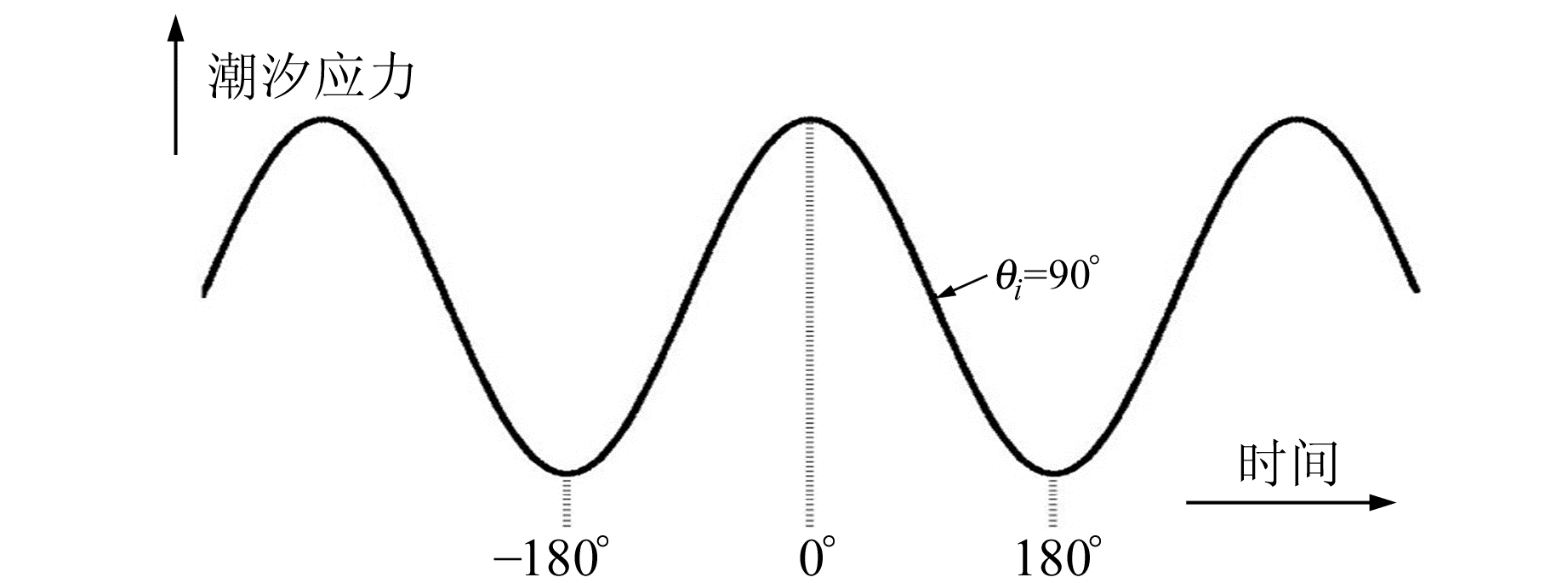
根据Tanaka等[7]的方法,利用初始参考地球模型[12]计算包括固体潮和海潮在内的潮汐与地震的相关性。首先分配每次地震发生时的相位角,根据潮汐应力的变化时程进行赋值[13],如图 2所示,通过线性划分-180°~0°或0°~180°来分配相位角,其值介于-180°~180°之间;再以0°为基准,通过地震发生时间与0°对应的时间差及根据时间等分出每分钟对应度数的乘积,即可分配每次地震的相位角。为测试地震的发生是否集中在某一特定的角度附近,采用Schuster检验[3]进行统计,将每个地震当作1个单位向量,其方向由相对应的相位角来表示,向量的矢量和由D来描述:
| $ \mathit{\boldsymbol{D}}{\mathit{\boldsymbol{}}^2} = {\left( {\sum\limits_{i = 1}^N {{\rm{cos}}{\theta _i}} } \right)^2} + {\left( {\sum\limits_{{\rm{ }}i = 1}^N {{\rm{sin}}{\theta _i}} } \right)^2} $ | (1) |
|
图 2 潮汐相位角的定义 Fig. 2 Definition of tidal phase angle |
式中,θi为第i次地震的相位角,N为包含地震频度的数据集。如果θi在时间上是随机分布的,那么矢量和的长度等于或大于D的概率为:
| $ p = {\rm{exp}}\left( { - \frac{{\mathit{\boldsymbol{D}}{\mathit{\boldsymbol{}}^2}}}{N}} \right){\rm{ }} $ | (2) |
式中,p值介于0~1之间,且p值越小,拒绝零假设的置信度越高,一般设置p < 5%为判断地震是否受潮汐触发的阈值[7]。
用GOTIC2[10]计算由固体潮和海洋潮汐引起的体应变,然后按照上述方法分配每个地震事件所对应的潮汐相位角,最后对这些潮汐相位角进行统计,分析其是否集中在某特定角度附近。
为检测地震是否受潮汐周期性成分的控制,在Schuster检验的基础上,使用Schuster谱进行进一步分析研究。Schuster谱提供了一种能够检测地震目录中任何未知周期性的方法,并分析地震活动率是否存在周期变化[9],例如该地区的地震活动是否受潮汐中短周期潮(如0.5 d潮、1 d潮)和长周期潮或其他未知周期的控制。Schuster谱原理上就是进行n次Schuster检验,而Schuster检验可以理解为以某一周期(如潮汐的短周期潮)进行堆叠,然后分配相位角,算出p值。要对p < 5%的地区进行Schuster谱分析,首先要确定每次Schuster检验的周期,建立一个全面的Schuster谱,然后根据所建立的Schuster谱计算出置信水平,来检验这些地区是否存在周期性。根据适当的周期采样:
| $ \Delta {T_i} = \frac{{\varepsilon T_i^2}}{{t}}{\rm{ }} $ | (3) |
式中,ΔTi为进行每次堆叠的周期增量,每次堆叠后进行1次Schuster检验,求出1个p值,如以周期Ti进行第i次堆叠,则第i+1次的堆叠会以周期Ti+1=Ti+ΔTi进行;t为所要测试的周期长度,即地震目录的长度;ε值决定了周期的采样是否合理。如果ε值过大,根据式(3),ΔTi会增大,则进行堆叠的周期Ti+1=Ti+ΔTi也会增大,导致在堆叠的过程中会漏掉过多的地震事件;若ε值太小,则会造成周期的过采样,即ΔTi太小,延长了不必要的计算时间,所以ε存在一个最优值ε0,使得Ti+1=Ti+ΔTi能最大限度地减少漏掉的地震个数,同时又不会延长不必要的计算时间。根据Ader等[9]的计算,通过推导出的ε的不同值随机生成目录的Schuster谱,重复地赋予ε不同的初始值,建立概率密度函数ε0,最后给出的ε0≈1。利用ε0值可以估计期望阈值,其意义是如果Schuster谱的p值在该阈值之上,则说明该p值可以表明地震活动率存在周期性。包含n个独立Schuster检验的Schuster谱中p值的最小期望值为:
| $ \left\langle {{\delta _m}} \right\rangle = \frac{1}{n} \approx {\varepsilon _0}{T_{{\rm{min}}}}/t \approx {T_{{\rm{min}}}}/t $ | (4) |
值得注意的是,Schuster检验中p值只要小于5%就可以说明地震活动与潮汐存在相关性,其阈值是固定值。而式(4)中,Schuster谱的期望阈值〈δm〉与每次Schuster检验选定的周期有关,周期在Tmin和Tmax之间选定,即期望阈值〈δm〉是变化的。进行Schuster谱分析时,计算得到的p值要小于〈δm〉才能说明地震活动率存在周期性,一般95%置信水平就可以作为判断标准,定量地说,如果相应的p值低于0.05×〈δm〉=0.05×T/t,则可以表示在95%置信水平以上检测到周期性。
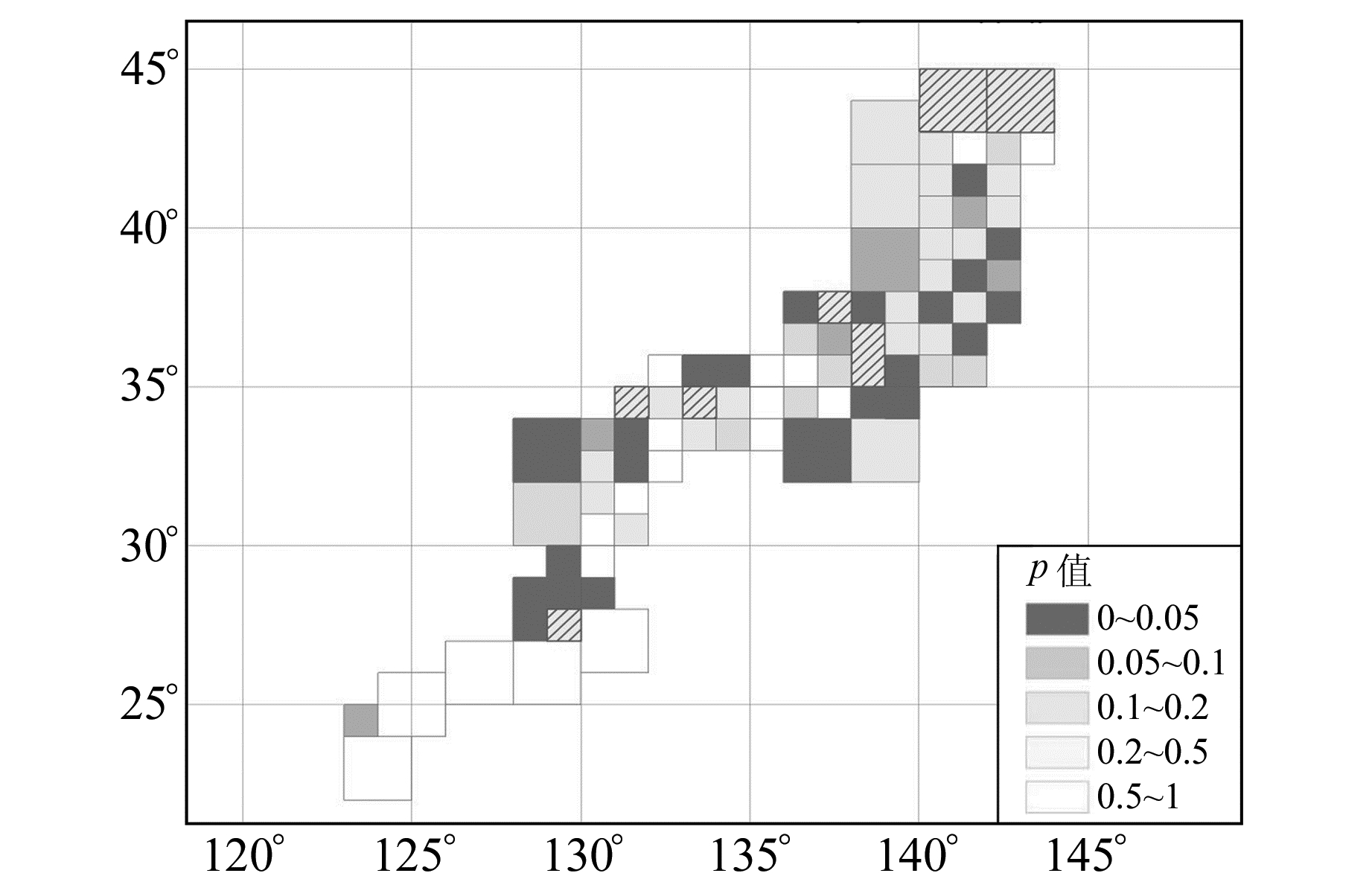
3 计算结果本文选用1990-01~2018-04期间的地震,采用Schuster方法分别计算每个子区域的p值,得到日本及邻区的p值空间分布情况,结果见图 3,图中颜色越深表示p值越小。将本文计算结果与Tanaka等[8]的计算结果进行对比,结果见表 1。在本文计算的75个子区域中,有22个子区域p < 5%,即本文检测到更多地区的地震活动与潮汐具有相关性。
|
图 3 日本及邻区的Schuster检验p值分布 Fig. 3 Schuster test p-value distribution of Japan and adjacent region |
|
|
表 1 Tanaka等[8]与本文结果的对比 Tab. 1 Differences between the work of this study and Tanaka's |
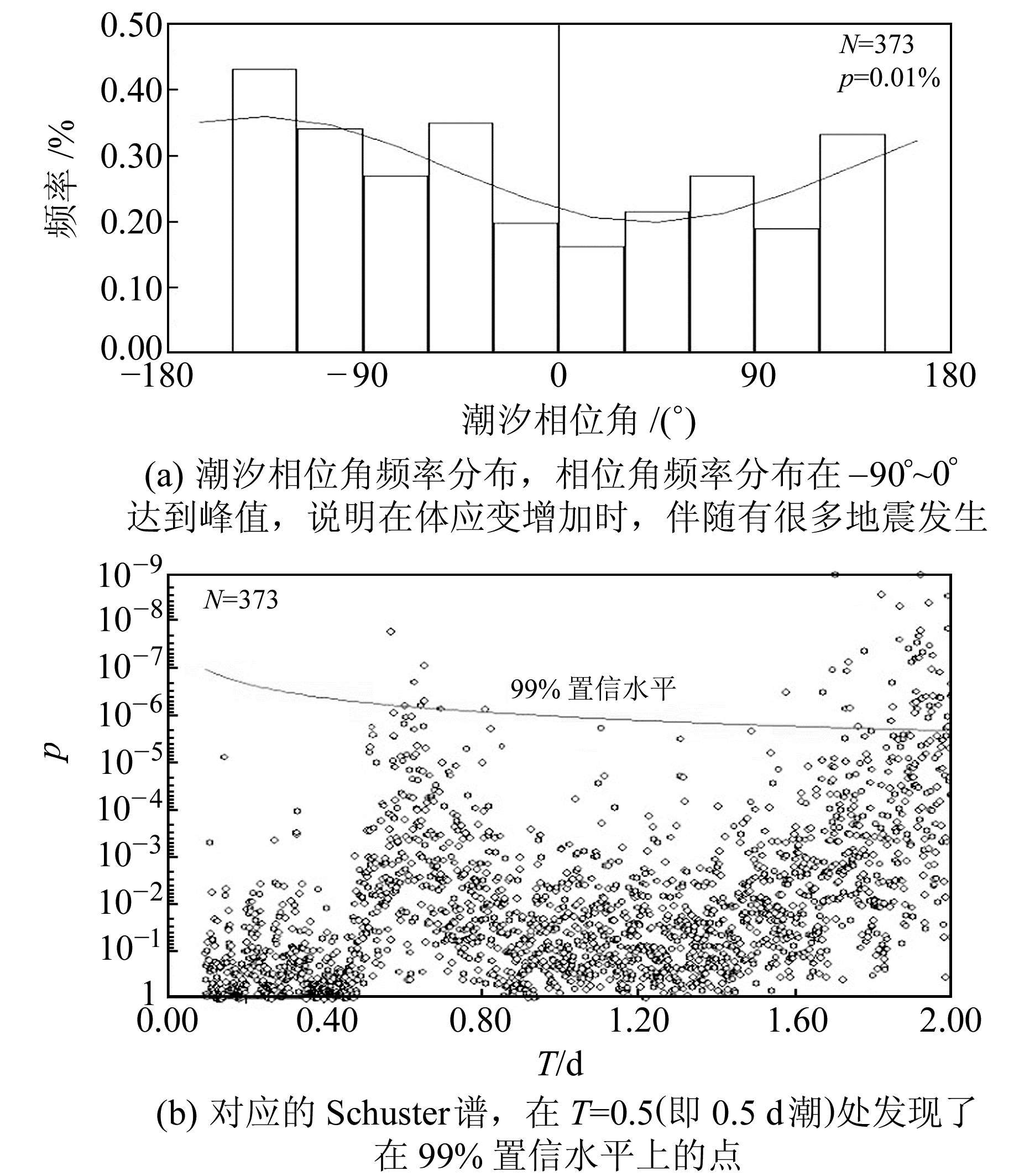
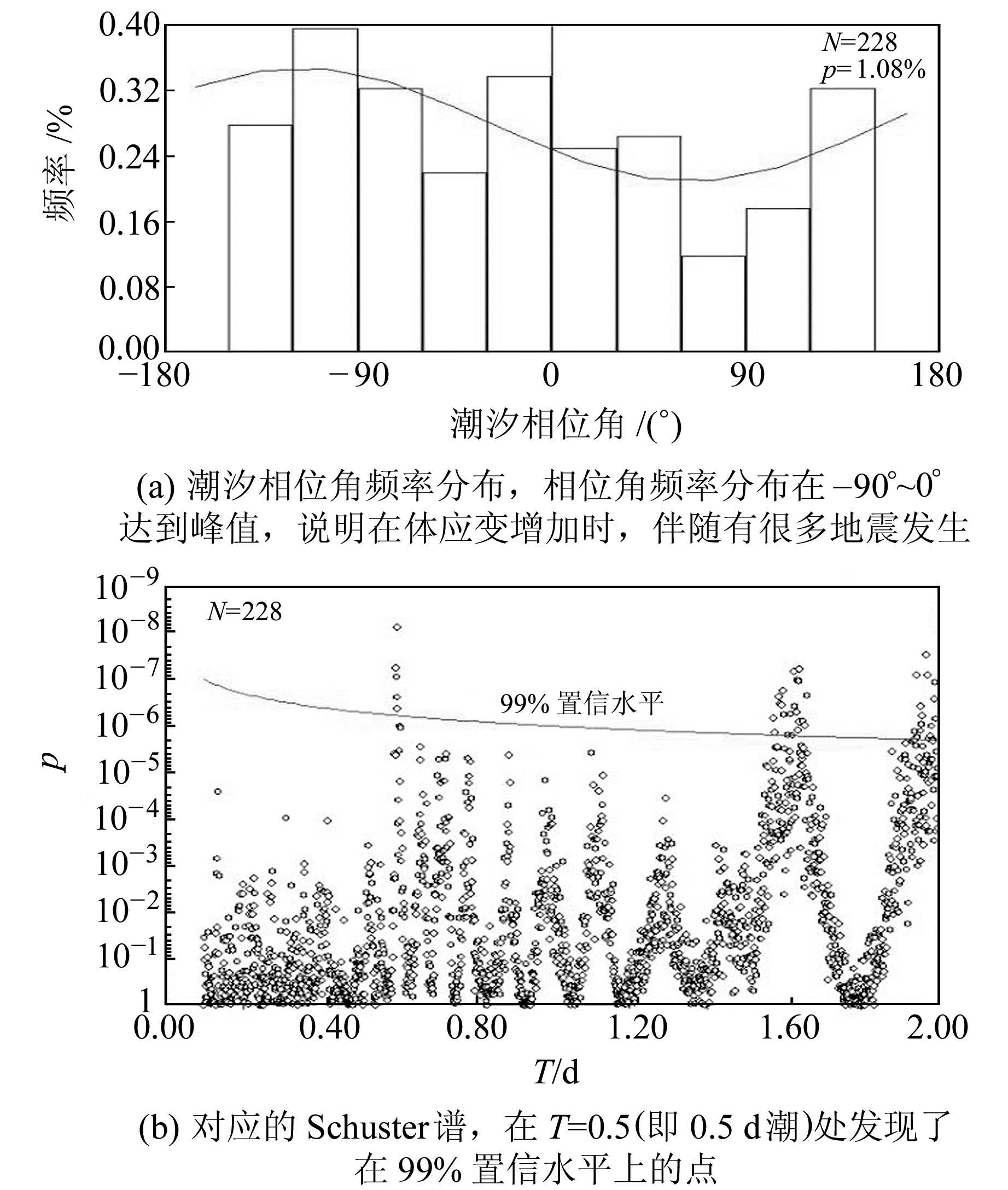
在此基础上,利用Schuster谱对这些地区进行进一步研究,确认地震活动与潮汐周期的相关性。图 4(a)和4(b)分别显示了日本奄美岛地区(130°E~131°E,28°N~29°N)潮汐相位角的频率分布及对应的Schuster谱,图 5(a)和5(b)显示了日本大阪湾地区(134°~135°E,35°~36°N)潮汐相位角的频率分布和对应的Schuster谱。图 4(a)和5(a)中的曲线表示潮汐相位角的分布特征,图 4(b)和5(b)中的曲线表示99%的置信水平。根据式(4)计算出期望阈值〈δ〉,每个〈δ〉乘以0.01,进行n次Schuster检验得到n个〈δ〉×0.01结果,构成表示99%置信水平的曲线。这2个地区的p值小于潮汐触发地震的临界值5%,分别为0.01%和1.08%,说明该地区的地震活动在某一潮汐相位附近较其他相位比较有优势,不是随机发生。由图 4(b)和5(b)可知,在T=0.5处检测到明显的周期性,均达到99%的显著置信水平,但在T=1.6~2.0处也达到99%的置信水平,说明这2个地区的地震活动中有些受0.5 d潮的调制作用[14],有些则受该地区其他因素的影响。
|
图 4 日本奄美岛地区Schuster检验及Schuster谱的测试结果 Fig. 4 Results of Scuster test and Schuster spectral in Amami island, Japan |
|
图 5 日本大阪湾地区的Schuster及Schuster谱检验结果 Fig. 5 Results of Scuster test and Schuster spectral in Osaka bay, Japan |
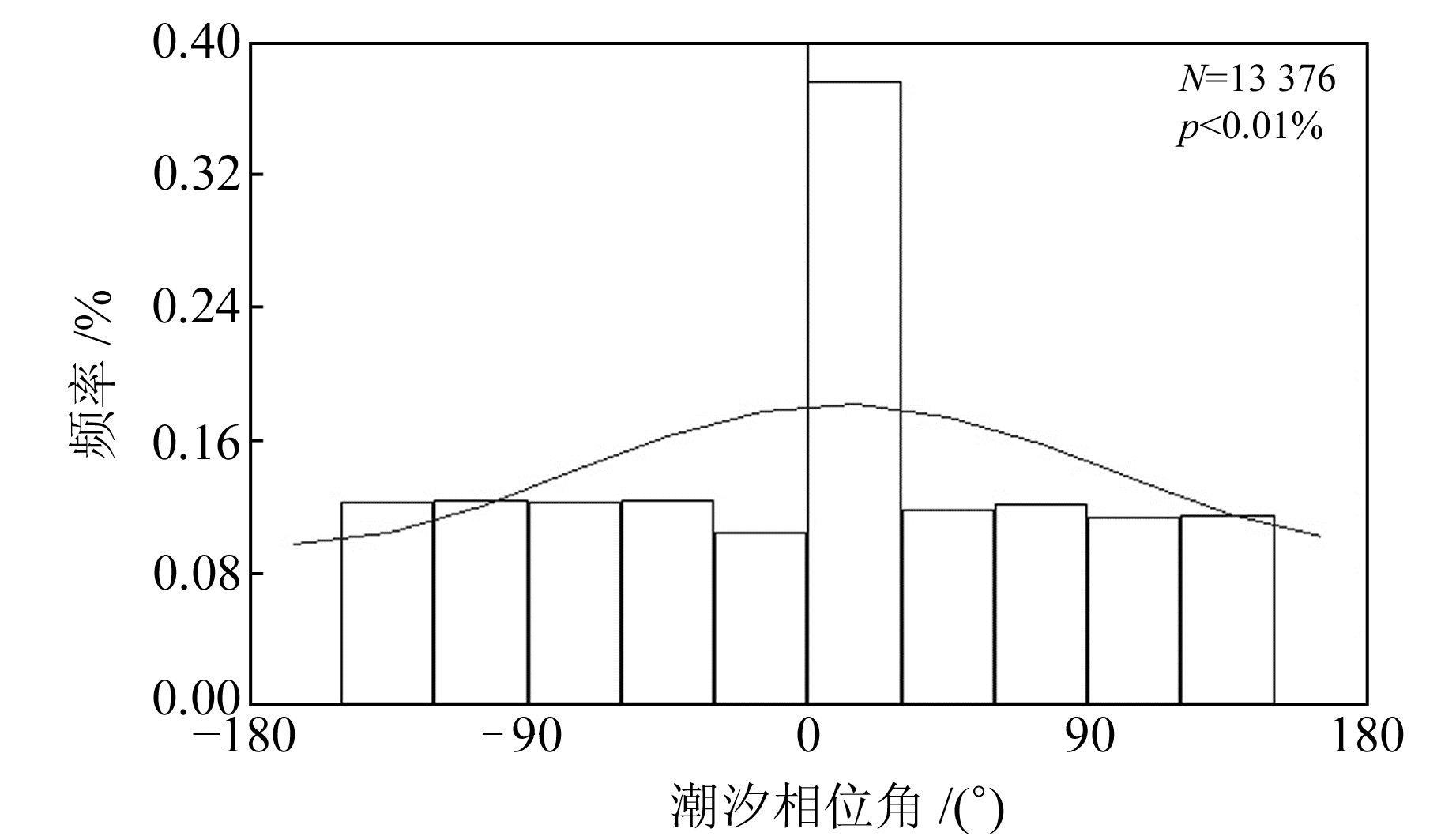
由表 1可知,利用同一数据来源(http://www.jma.go.jp/jma/index.html)进行地震目录下载,本文所选取的地震目录持续年限较长,但地震总数较少,由于采用了Schuster检验(图 3)和Schuster谱检验,得到22个子区域满足p < 5%,更清晰地反映了日本及邻区地震活动与潮汐的相关性。
选取同一子区域(139°~140°E,34°~35°N),将本文结果与Tanaka等[8]的结果进行对比,结果见图 6,二者在该区域的p值都满足p < 5%,说明本文数据使用合理。
|
图 6 日本子区域潮汐相位角频率分布 Fig. 6 Frequency distribution of tidal phase angle in subarea of Japan |
对比图 4(a)和5(a)可以看出,相位角为零处并不与地震发生频率最多的点对应,这是由于地球潮汐引起的应力振荡叠加在构造应力上,潮汐应力的幅值与构造应力相比较小,但潮汐应力的周期振荡特性对断层的影响更显著,一般地震活动多发生于潮汐应力的加载阶段(即图 2中相位角为-180°~0°阶段)。对比图 4(b)和5(b)可以看出,Schuster谱检验结果显示,该地区地震活动具有内在周期性,这些周期有的可能是受潮汐应力的调制和触发作用,如0.5 d;有的可能是受该地区其他因素的影响,如图中出现的1.6~2.0 d的周期成分。
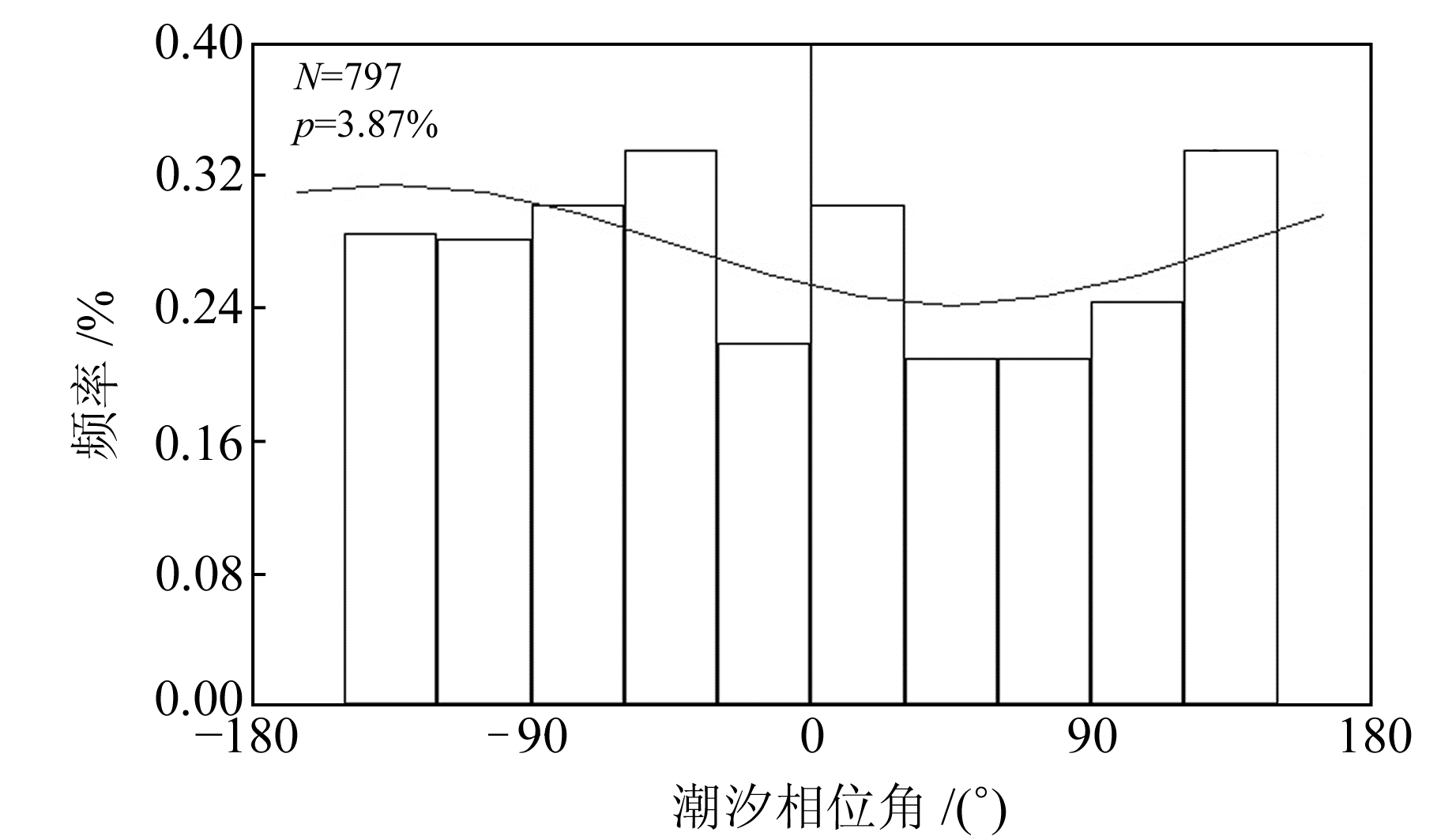
Yoshida[15]给出日本九州地区(131°~132°E,32°~33°N)的区域构造应力场,P轴走向近乎西南方向,结合2016年熊本7级地震的震源机制(http://www.data.jma.go.jp/svd/eqev/data/mech/pdf/mc201604.pdf),计算该地区潮汐库仑应力与地震活动的相关性,μ取0.4,结果见图 7。
|
图 7 日本九州地区库仑应力潮汐相位角频率分布 Fig. 7 Frequency distribution of tidal phase angle for CFS in Kyushu, Japan |
对比图 7和图 3的相同位置(131°~132°E,32°~33°N)可以发现,采用潮汐库仑应力分析的结果与体应变计算的结果一致,均反映该地区的地震活动具有潮汐相关性。
5 结语选取日本及邻区作为研究区域,采用日本1990~2018年28 a的地震目录,并对整个研究区进行分区。首先采用Schuster统计方法,以p值对日本的地震活动进行潮汐相关性分析,初步研究这些区域地震的发生是否受潮汐的影响;再利用Schuster谱对p<5%的地区进行分析,研究影响该地区地震活动的潮汐的主要周期,以探索日本及邻区地震活动与潮汐的相关性。通过分析计算得出如下结论:
1) 在日本及邻区划分的75个子区域中,有22个子区域满足p<5%,说明这些地区地震受潮汐的触发,这与Tanaka等[8]的研究结果基本一致。但本文显示出更多区域存在潮汐相关性,其原因可能是二者所选用的地震目录时间跨度及地震数量等不一致,采用的统计方法也不同。
2) 在22个满足p<5%的子区域中,对其中2个子区域进行Schuster谱的研究发现,0.5 d潮汐在谱图结果中比较明显,说明该地区地震活动受0.5 d潮周期成分的控制。
3) McNutt等[16]的研究已经考虑了海潮的作用,但在应力的变化上忽略了震源深度的影响。利用GOTIC2这个包含海潮模型NAO.99b的数据库,结合固体潮进行潮汐相位角的统计,计算在震源深度上的海潮加载效应,得到的结果更加可靠。
4) 这些结果表明,日本地区的地震活动确实存在一定的潮汐触发相关性,且某些区域的地震活动率存在着周期性的变化,为研究日本地区地震机理提供了一定的理论依据。
| [1] |
Tanaka S. Tidal Triggering of Earthquakes Prior to the 2011 Tohoku-Oki Earthquake(MW9.1)[J]. Geophysical Research Letters, 2012, 39(7): L00G26
(  0) 0) |
| [2] |
Tanaka S, Sato H, Matsumura S, et al. Tidal Triggering of Earthquakes in the Subducting Philippine Sea Plate Beneath the Locked Zone of the Plate Interface in the Tokai Region, Japan[J]. Tectonophysics, 2006, 417(1-2): 69-80 DOI:10.1016/j.tecto.2005.09.013
(  0) 0) |
| [3] |
Tsuruoka H, Ohtake M, Sato H. Statistical Test of the Tidal Triggering of Earthquakes:Contribution of the Ocean Tide Loading Effect[J]. Geophysical Journal International, 1995, 122(1): 183-194 DOI:10.1111/j.1365-246X.1995.tb03546.x
(  0) 0) |
| [4] |
Klein F W. Earthquake Swarms and the Semidiurnal Solid Earth Tide[J]. Geophysical Journal of the Royal Astronomical, 1976, 45(2): 245-295 DOI:10.1111/j.1365-246X.1976.tb00326.x
(  0) 0) |
| [5] |
Heaton T H. Tidal Triggering of Earthquakes[J]. Geophysical Journal of the Royal Astronomical, 1975, 43(2): 307-326 DOI:10.1111/j.1365-246X.1975.tb00637.x
(  0) 0) |
| [6] |
Wilcock W S D. Tidal Triggering of Microearthquakes on the Juan de Fuca Ridge[J]. Geophysical Research Letters, 2001, 28(20): 3 999-4 002 DOI:10.1029/2001GL013370
(  0) 0) |
| [7] |
Tanaka S, Ohtake M, Sato H. Evidence for Tidal Triggering of Earthquakes as Revealed from Statistical Analysis of Global Data[J]. Journal of Geophysical Research: Solid Earth, 2002, 107(B10)
(  0) 0) |
| [8] |
Tanaka S, Ohtake M, Sato H. Tidal Triggering of Earthquakes in Japan Related to the Regional Tectonic Stress[J]. Earth, Planets and Space, 2004, 56(5): 511-515 DOI:10.1186/BF03352510
(  0) 0) |
| [9] |
Ader T J, Avouac J P. Detecting Periodicities and Declustering in Earthquake Catalogs Using the Schuster Spectrum, Application to Himalayan Seismicity[J]. Earth and Planetary Science Letters, 2013, 377-378: 97-105 DOI:10.1016/j.epsl.2013.06.032
(  0) 0) |
| [10] |
Matsumoto K, Sato T, Takanezawa T, et al. GOTIC2: A Program for Computation of Oceanic Tidal Loading Effect[J]. Journal of the Geodetic Society of Japan, 2001, 47(1): 243-248
(  0) 0) |
| [11] |
Sato T. A Program for the Computation of Oceanic Tidal Loading Effects 'GOTIC'[J]. Publications of the International Latitude Observatory of Mizusawa, 1984, 18: 29-47
(  0) 0) |
| [12] |
Dziewonski A M, Anderson D L. Preliminary Reference Earth Model[J]. Physics of the Earth and Planetary Interiors, 1981, 25(4): 297-356 DOI:10.1016/0031-9201(81)90046-7
(  0) 0) |
| [13] |
熊子瑶, 解朝娣, 雷兴林, 等. 云南大姚、姚安及附近地区地震活动与潮汐应力的触发关系[J]. 地震研究, 2015, 38(1): 66-74 (Xiong Ziyao, Xie Chaodi, Lei Xinglin, et al. Triggering Relationship between Seismic Activity and Tidal Stress in Dayao-Yao'an and Its Adjacent Area of Yunnan Province[J]. Journal of Seismological Research, 2015, 38(1): 66-74 DOI:10.3969/j.issn.1000-0666.2015.01.009)
(  0) 0) |
| [14] |
Xie C D, Lei X L, Zhao X Y, et al. Tidal Triggering of Earthquakes in the Ning'er Area of Yunnan Province, China[J]. Journal of Asian Earth Sciences, 2017, 138(1): 477-483
(  0) 0) |
| [15] |
Yoshida M. Re-Evaluation of the Regional Tectonic Stress Fields and Faulting Regimes in Central Kyushu, Japan, behind the 2016 MW7.0 Kumamoto Earthquake[J]. Tectonophysics, 2017, 712-713: 95-100 DOI:10.1016/j.tecto.2017.05.011
(  0) 0) |
| [16] |
McNutt S R, Beavan R J. Patterns of Earthquakes and the Effect of Solid Earth and Ocean Load Tides at Mount St Helens Prior to the May 18, 1980, Eruption[J]. Journal of Geophysical Research: Solid Earth, 1984, 89(B5): 3 075-3 086 DOI:10.1029/JB089iB05p03075
(  0) 0) |
2. Shanghai Earthquake Agency, 87 Lanxi Road, Shanghai 200062, China
 2019, Vol. 39
2019, Vol. 39


