在构造应力场作用下,地壳岩石介质发生差异运动与变形,并逐渐产生能量积累,最终导致局部地壳的破裂,即为地震。连续监测地壳应力、应变场的动态变化过程,对于认识地震孕育过程的动力学特征及探索地震预报具有重要意义。佘山台YRY-4元件式钻孔应变仪自2006-05安装并正式运行至今,仪器的工作状态良好,为地震研究提供了长期的观测资料。本文采用佘山台2013~2018年观测资料的变化值(原始观测值)和差分值(通过一阶差分得到的结果),经实地相对标定检验并校正[1]后,运用邱泽华[2]的观测理论,采用“钻孔加衬模型”公式[3],参考主应变[4]、主方向[5]及剪切应变[6]的分析方法,借鉴刘序俨等[7]提出的以应变不变量为标尺,通过无校正、变化校正和差分校正等3种应变换算方式,对佘山台历史应变资料进行计算分析,研究佘山地区应变场主应力方向的变化特征。
1 观测背景 1.1 地理环境及地质构造环境佘山台坐落于上海市西南的西佘山南麓,地理坐标为121°11′12″E、31°05′44″N。台站地处扬子地块东北段的东南缘,位于青浦-龙华断裂和枫泾-川沙断裂夹持的天马山火山岩构造盆地中央,台站附近发育有姚家港-白鹤断裂,第四纪以来地震活动较弱。
1.2 仪器安装情况佘山台YRY-4元件式钻孔应变仪探头安装于2006-03-24,钻井深度为42 m,地面至钻井用136 mm的标准钢套管保护,并用水泥浆压力封井,将护井套管与岩壁紧密固结,护井套管底部垫入30 mm小石子,探头安装在40 m深处,探头周边均匀灌入水泥石英砂进行固定耦合。表 1为钻孔应变仪传感器安装情况。
|
|
表 1 传感器安装情况 Tab. 1 Process of sensor installation |
本文观测数据采用一阶差分的方法,可有效消除部分坏点,得到差分值。
1) 设有等距节点Xk=X0+kh(k=0, 1, …, n),其中,步长h为常数。
2) 记fk=f(Xk),称相邻两个节点Xk和Xk+1函数值的增量fk+1-fk(k=0, 1, …, n-1)为函数f(x)在点Xk处以h为步长的一阶差分,记为Δfk,则有Δf0=f1-f0、Δf1=f2-f1等。
差分校正和变化校正则引入实地相对标定的方法,求取元件的相对灵敏度后,分别用原始观测值和差分值进行校正。
1) 元件i的孔径相对变化测值为:
| $ {\mathit{S}_\mathit{i}}\mathit{ = }{\mathit{K}_\mathit{i}}\mathit{ }{\mathit{R}_\mathit{i}} $ | (1) |
式中,Ri为元件i的观测读数,Ki为元件i的灵敏度。
2) 利用自检方程:
| $ {\mathit{S}_1}{\rm{ + }}{\mathit{S}_{\rm{3}}}{\rm{ = }}{\mathit{S}_2}{\rm{ + }}{\mathit{S}_4} $ | (2) |
将式(1)代入式(2),得:
| $ {K_1}{R_1} - {K_2}{R_2} - {K_3}{R_3} - {K_4}{R_4} = 0 $ | (3) |
当4个方向的元件同时记录到4个读数时,就可利用其与各个元件实际灵敏度之间的关系对元件进行实地标定。式(3)只含一次项,严格地说这种标定只能确定灵敏度之间的相对大小,因而称为相对标定。在相对标定中,取任意一个未知的相对灵敏度为1,就可解出其他3个未知相对灵敏度。如式(3)两边同除以K1,得:
| $ {K_{11}}{R_1} - {K_{21}}{R_2} + {K_{31}}{R_3} - {K_{41}}{R_4} = 0 $ | (4) |
其中,K11=K1/K1=1,K21=K2/K1,K31=K3/K1,K41=K4/K1。从数学角度来看,只要有3次记录就可求出K21、K31和K41,但实际上这样得到的结果是不可靠的。并且,读数Ri(i=1,2,3,4)都可以看成列向量,能利用大量的观测值来统计确定K21、K31和K41,但这样的解法仍然存在一个问题,就是所有元件并不对称。当一个元件的灵敏度非常高时,取它为1就可能给出相当理想的结果,但无法判断是否存在这样的元件,甚至难以确定哪个元件比其他的好,当被取为1的元件灵敏度出现问题时,就会导致结果不准确。解决这个问题的方法是,分别取4个元件的灵敏度为1,并依次对K进行求解,然后取平均值。仿照式(4)分别在式(3)两边同除以K2、K3、K4,得:
| $ {K_{12}}{R_1} - {K_{22}}{R_2} + {K_{32}}{R_3} - {K_{42}}{R_4} = 0 $ | (5) |
| $ {K_{13}}{R_1} - {K_{23}}{R_2} + {K_{33}}{R_3} - {K_{43}}{R_4} = 0 $ | (6) |
| $ {K_{14}}{R_1} - {K_{24}}{R_2} + {K_{34}}{R_3} - {K_{44}}{R_4} = 0 $ | (7) |
其中,Kij=Ki/Kj(i, j=1, 2, 3, 4)。利用式(4)~(7)求解元件的相对灵敏度,取平均值:
| $ {K_i} = \frac{1}{4}\sum\limits_{j = 1}^4 {{K_{ij}}\;} , (i = 1, 2, 3, 4) $ | (8) |
这样求出的相对灵敏度为确定值,大小都在1附近,满足式(3)。根据式(8),利用变化值及差分值分别计算出2组相对标定的灵敏度K1、K2、K3、K4。利用变化值,运用实地相对标定理论得到的相对灵敏度对原始观测值进行校正,则为变化校正;利用差分值,运用实地相对标定理论得到的元件相对灵敏度对差分值进行校正,则为差分校正;无校正则是原始观测值没有进行计算校正。
佘山台钻孔应变仪的原始观测值及将原始观测值进行一阶差分得到的结果,相邻元件夹角都是45°,当观测元件可信时,有一种综合而具有对称性的应变换算方法,该换算方法的初步操作为:设Si(i=1, 2, 3, 4)是观测值(变化值),观测数据换算成应变的公式为:
| $ \left\{ \begin{array}{l} {S_{13}} = {S_1} - {S_3}\\ {S_{24}} = {S_2} - {S_4}\\ Sa = ({S_1} + {S_2} + {S_3} + {S_4})/2 \end{array} \right. $ | (9) |
式中,S13、S24、Sa称为替代观测值。这样一来,就把4个直接观测值转化成了3个间接观测值,可以用3个已知观测值来求解未知分量值。
目前,一般的钻孔应变仪实际测量给出的是孔径相对变化,根据钻孔加衬模型,当远处有均匀水平主应力ε1和ε2时,钻孔θ方向的理论孔径相对变化为:
| $ {S_\theta } = A({\mathit{\varepsilon }_1} + {\mathit{\varepsilon }_2}) + B({\mathit{\varepsilon }_1} - {\mathit{\varepsilon }_2})\cos 2(\theta - \varphi ) $ | (10) |
式中,φ为ε1的方位角;A和B为2个待定常数,称为耦合系数,其值的大小与套筒的材料、尺寸及周围岩石的性质存在着复杂的关系。由式(9)可知,主应变和主方向与观测值有最直接的关系。四元件钻孔应变观测值公式为:
| $ \left\{ \begin{array}{l} {S_1} = {S_{{\theta _1}}} = A({\varepsilon _1} + {\varepsilon _2}) + B({\varepsilon _1} - {\varepsilon _2})\cos 2({\theta _1} - \varphi )\\ {S_2} = {S_{{\theta _1} + {\raise0.5ex\hbox{$\scriptstyle \pi $} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 4$}}}} = A({\varepsilon _1} + {\varepsilon _2}) - B({\varepsilon _1} - {\varepsilon _2})\sin 2({\theta _1} - \varphi )\\ {S_3} = {S_{{\theta _1} + {\raise0.5ex\hbox{$\scriptstyle \pi $} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}}} = A({\varepsilon _1} + {\varepsilon _2}) - B({\varepsilon _1} - {\varepsilon _2})\cos 2({\theta _1} - \varphi )\\ {S_4} = {S_{{\theta _1} + {\raise0.5ex\hbox{$\scriptstyle {3\pi }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 4$}}}} = A({\varepsilon _1} + {\varepsilon _2}) + B({\varepsilon _1} - {\varepsilon _2})\sin 2({\theta _1} - \varphi ) \end{array} \right. $ | (11) |
式中,θ1为S1的方位角。式(9)可写为:
| $ \left\{ \begin{array}{l} {S_{_{13}}} = 2B({\varepsilon _1} - {\varepsilon _2})\cos 2({\theta _1} - \varphi )\\ {S_{_{24}}} = - 2B({\varepsilon _1} - {\varepsilon _2})\sin 2({\theta _1} - \varphi )\\ {S_a} = 2A({\varepsilon _1} + {\varepsilon _2}) \end{array} \right. $ | (12) |
利用三角公式sin2θ+cos2θ=1可得:
| $ \left\{ \begin{array}{l} \frac{1}{{2B}}\sqrt {{S^{{}^2}}_{13} + {S^{{}^2}}_{24}} = {\varepsilon _1} - {\varepsilon _2}\\ \frac{1}{{2A}}{S_a} = {\varepsilon _1} + {\varepsilon _2} \end{array} \right. $ | (13) |
| $ \frac{{{S_{24}}}}{{{S_{13}}}} = - \tan 2({\theta _1} - \varphi ) $ | (14) |
由式(13)和式(14)可以解出主应变和主方向。
3 分析结果收集2013-01-01~2018-08-31佘山台数字化钻孔应变观测资料,利用MATLAB分别对变化值和差分值进行计算,分别求取2013~2018每年的面应变εα、最大剪应变εs及主方向φ,结果见表 2,其中,1 ns=1×10-9应变量,1 ms=1×10-6应变量。变化值换算是在进行应变换算后,对计算结果不进行差分,直接直线拟合求取变化趋势的均值;差分值换算是在应变换算结果的基础上进行差分运算,最后通过平均值拟合求取均值。
|
|
表 2 佘山台观测数据历年的应变换算结果(2013~2018年) Tab. 2 Strain conversion results of Sheshan observatory data during 2013-2018 |
图 1分别列出佘山台无校正、变化校正、差分校正后用于应变换算的3个替代观测值(Sa、S13、S24)。由图可知,2条替代观测剪应变(S13和S24)曲线整体呈下降趋势,即S13<0及S24<0。根据式(9),S13<0的物理意义是,元件1的伸长量小于元件3的伸长量。与其对应,可以想象一个变形椭圆,其长轴在元件3方位上,短轴在元件1方位上。同理,对于S24<0,也可想象一个变形椭圆,其长轴在元件4方位上,短轴在元件2方位上。实际的变形是二者的叠加,当S13<0和S24<0时可以判定,实际应变变化的主方向(即最大主应变变化方向)应该在元件3和元件4的夹角范围内。由表 1可知,佘山台钻孔应变仪元件3的方位角为65°,元件4的方位角为110°,因此,佘山台实际应变变化的主方向(即最大主应变变化方向)应该在65°~110°范围内。
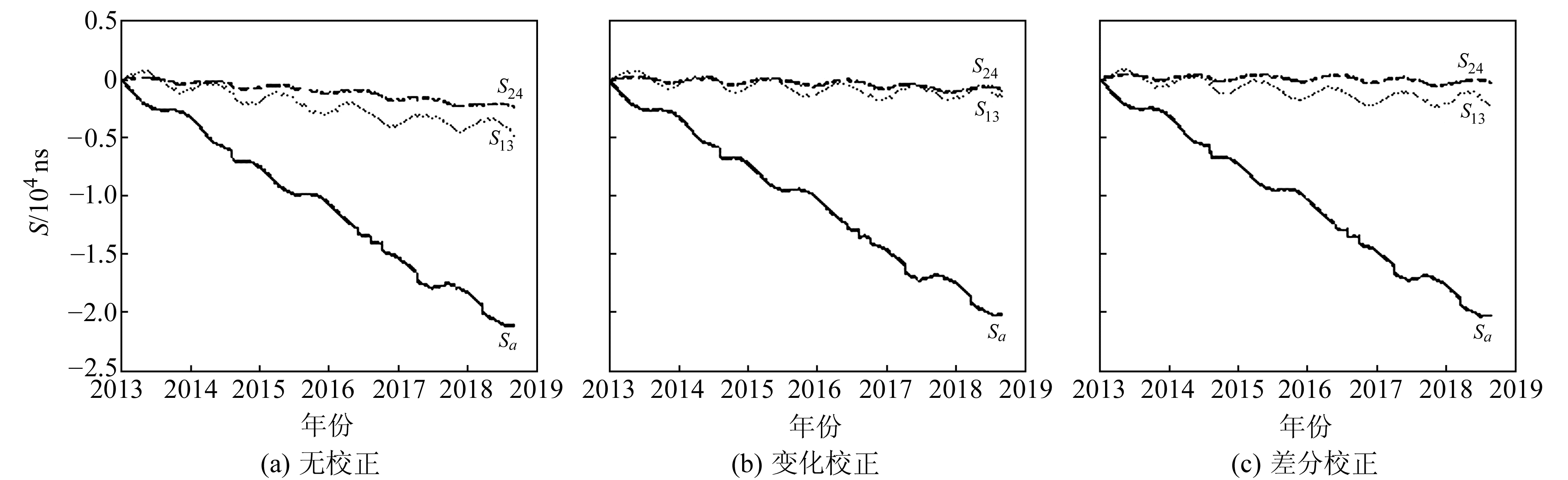
|
图 1 佘山台用于应变换算的3个替代观测值(Sa、S13、S24)曲线 Fig. 1 Three alternative observations (Sa, S13, S24) for strain conversion at Sheshan station |
利用表 2的数据绘制图 2,得到佘山台测点2013~2018年变化值及差分值通过无校正、变化校正、差分校正等计算的主方向φ。图 2表明,差分值得出的主方向不受校正影响,结果比较一致,平均值为95°,符合图 1所示,介于65°~110°之间,并且靠近元件4;而采用变化值进行拟合,得到的主方向φ比较离散,平均值为118°~126°,和差分值相差20°~30°,明显不符合图 1得出的结果。由此可知,在主方向φ的确定上,应使用差分值,观测数据是否进行变化校正或差分校正对主方向的结果判定影响不大。

|
图 2 差分值及变化值计算得到的历年主方向 Fig. 2 The main direction of the calendar year calculated by the difference value and the change value |
图 3为佘山台2013年以来在无校正情况下面应变εa和最大剪应变εs的变化曲线。由图可知,佘山台的面应变整体呈下降趋势,即压缩越来越强烈;同时,最大剪应变在逐步增大。计算得到佘山台最大剪应变εs的变化量约为116 ns/a,面应变变化εa的变化量约为-3 159 ns/a。
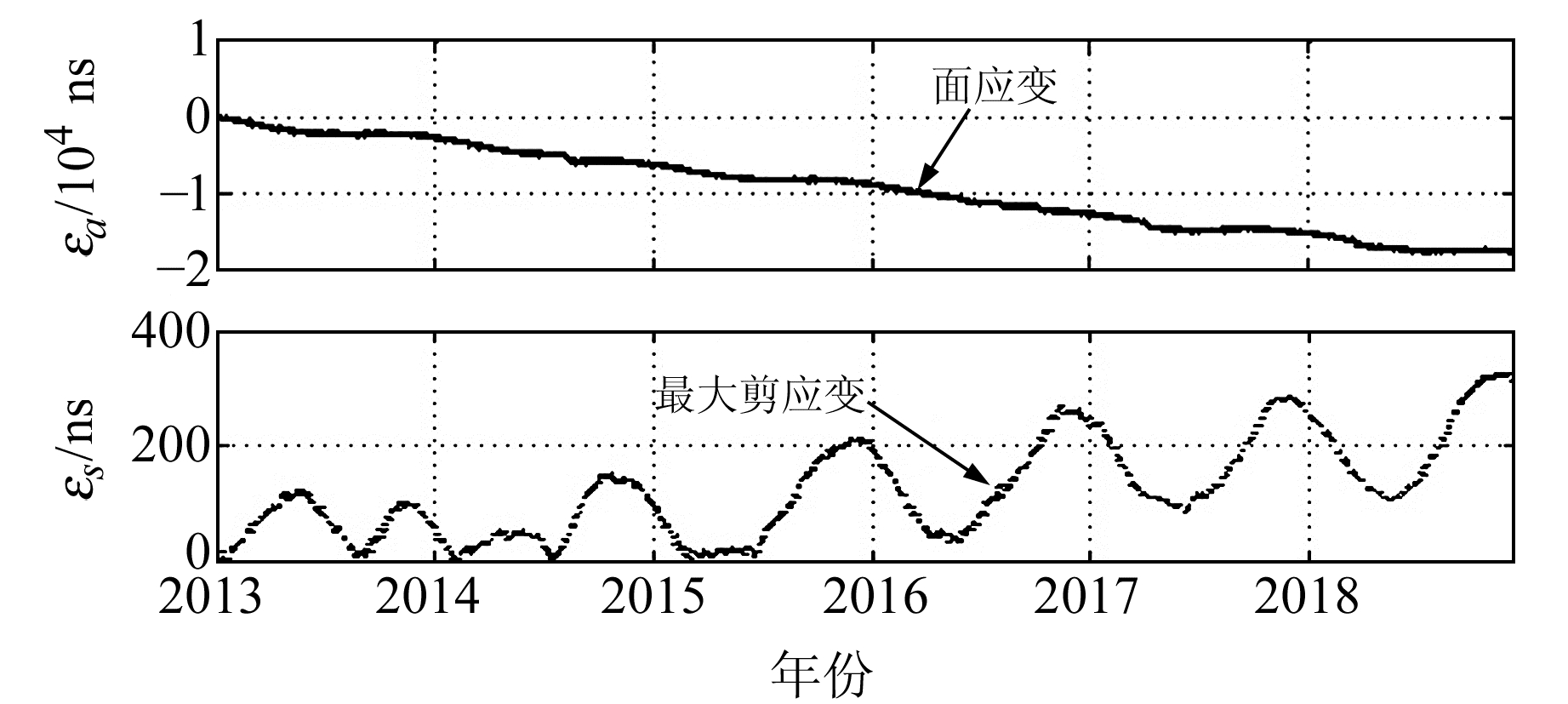
|
图 3 佘山台小时值面应变、最大剪应变曲线(无校正) Fig. 3 Hour strain and maximum shear strain curvs of Sheshan station (no correction) |
图 4为佘山台2013年以来在变化校正情况下面应变εa和最大剪应变εs的变化曲线。由图可知,变化校正后的面应变整体变化趋势和无校正前一致,一直在下降;同时,最大剪应变在逐渐增大。计算得到佘山台最大剪应变εs的变化量约为29ns/a,与无校正结果相差5倍,面应变εa的变化量约为-3 102 ns/a,与无校正结果差别不大,表明数据经过变化校正后,最大剪应变的变化速率更小了。

|
图 4 佘山台小时值面应变、最大剪应变曲线(变化校正) Fig. 4 Hour strain and maximum shear strain curves of Sheshan station (change correction) |
图 5为佘山台2013年以来在差分校正情况下面应变εa、最大剪应变εs的变化曲线。由图可知,差分校正后的面应变整体变化趋势与无校正前一致,一直在下降;同时,最大剪应变在逐步增大。计算得到佘山台最大剪应变εs的变化量约为42 ns/a,与无校正的结果相差3倍,面应变εa的变化量约为-3 388 ns/a,与无校正的结果差别不大。结果表明,经过差分校正后,最大剪应变的年变化速率也变小了。由图 3~5可知,佘山台的应变换算受校正影响较大。
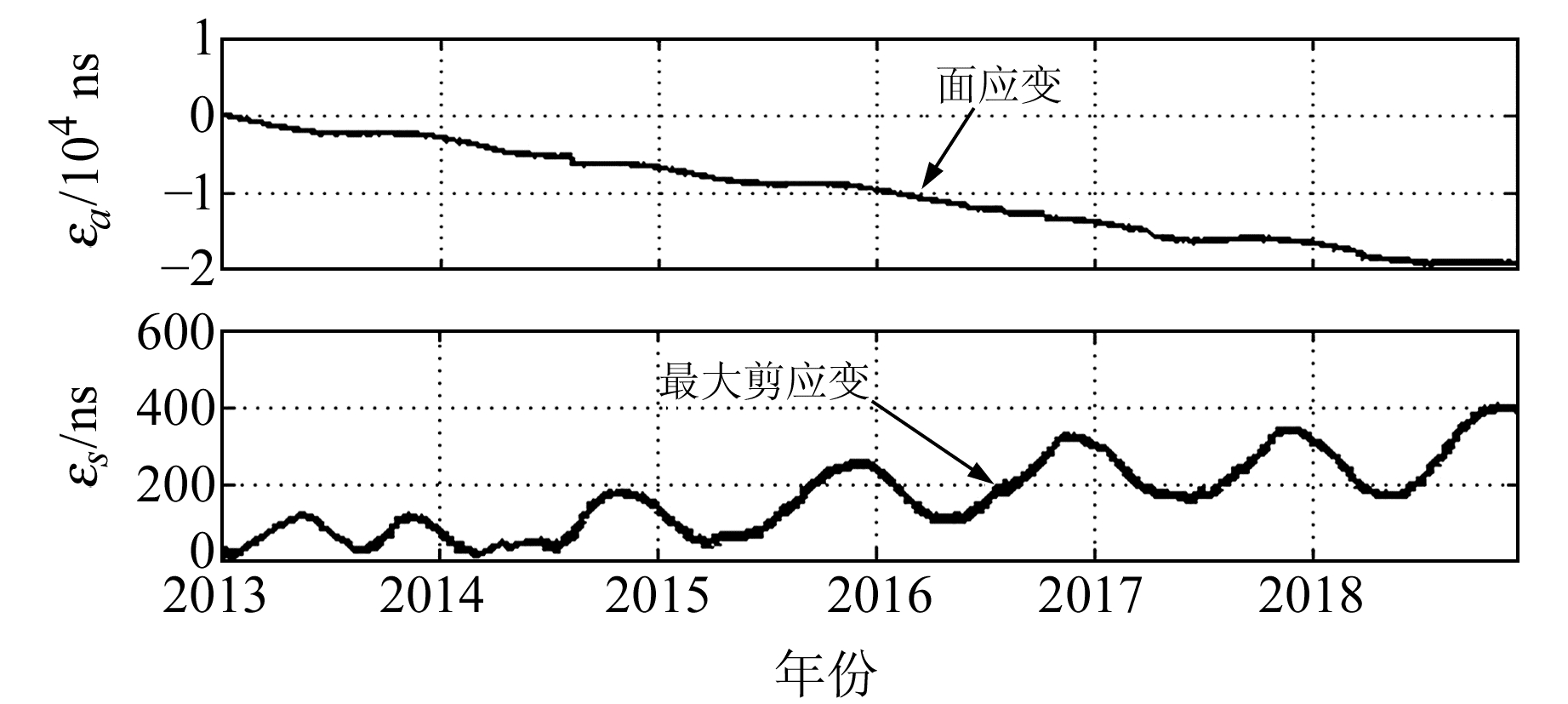
|
图 5 佘山台小时值面应变、最大剪应变曲线(差分校正) Fig. 5 Hour surface strain and maximum shear strain curves of Sheshan station (differential correction) |
利用表 2计算结果作图 6,得到佘山台2013年以来面应变和最大剪应变的年变化速率趋势。
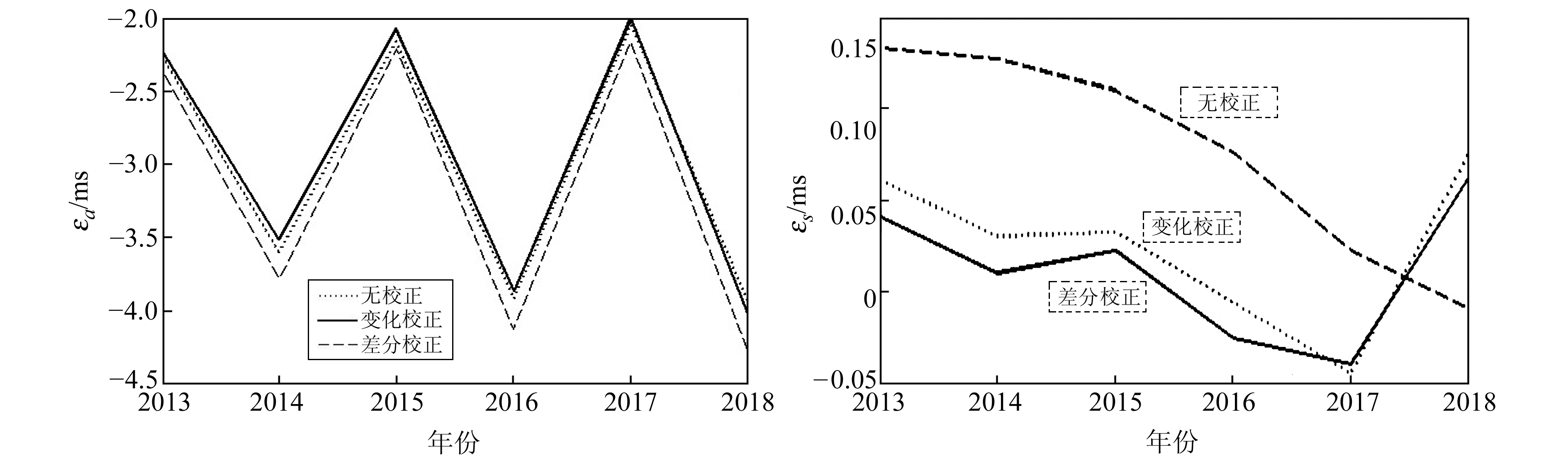
|
图 6 佘山台应变换算结果εa、εs年变化速率趋势分析 Fig. 6 Trend analysis of strain rate εa and εs at Sheshan station |
由图可知,面应变εa的年变化速率相对稳定,速率值保持在-2 ~-4.5ms/a;最大剪应变εs的年变化速率在2013~2017年校正后明显变小,但从2017年开始变大,且校正后的速率逐渐大于校正前,该现象值得进一步探讨。
4 结语1) 在主方向φ的确定上,应使用差分值,观测数据是否进行校正对于主方向的结果判定影响不大。通过差分方法得到的3组主方向φ结果基本一致,2013年以来基本维持在95°左右。
2) 2013年以来,佘山台的面应变整体呈下降趋势,最大剪应变在逐步增大。校正前后面应变的年变化速率差别不大;2013~2017年,校正后最大剪应变的年变化速率明显变小,但从2017年开始,校正后最大剪应变的年变化速率大于校正前。
| [1] |
邱泽华, 石耀霖, 欧阳祖熙. 四分量钻孔应变观测的实地相对标定[J]. 大地测量与地球动力学, 2005, 25(1): 118-122 (Qiu Zehua, Shi Yaolin, Ouyang Zuxi. Relative In-Situ Calibration of 4-Component Borehole Strain Observation[J]. Journal of Geodesy and Geodynamics, 2005, 25(1): 118-122)
(  0) 0) |
| [2] |
邱泽华. 钻孔应变观测理论和应用[M]. , 北京: 地震出版社, 2017 (Qiu Zehua. Theory and Application of Borehole Strain Observation[M]. Beijing: Seismological Press, 2017)
(  0) 0) |
| [3] |
苏恺之, 张钧, 李秀环, 等. 钻孔环境在钻孔地形变观测中的作用[J]. 地震地磁观测与研究, 2005, 26(6): 46-55 (Su Kaizhi, Zhang Jun, Li Xiuhuan, et al. The Effect of Borehole Environment at Borehole Deformation Observation[J]. Seismological and Geomagnetic Observation and Research, 2005, 26(6): 46-55 DOI:10.3969/j.issn.1003-3246.2005.06.008)
(  0) 0) |
| [4] |
钟继茂, 李祖宁, 谢志招, 等. 用多分量钻空应变仪资料推算测区附加应变场方向[J]. 大地测量与地球动力学, 2011, 31(1): 29-33 (Zhong Jimao, Li Zuning, Xie Zhizhao, et al. Determination of Direction of Additional Strain Field in Observation Area from Data of Multi-Component Borehole Strainmeter[J]. Journal of Geodesy and Geodynamics, 2011, 31(1): 29-33)
(  0) 0) |
| [5] |
刘序俨. 应变固体潮主应变及剪应变的计算——四川姑咱台应变固体潮分析[J]. 地球物理学报, 1994, 37: 213-221 (Liu Xuyan. Analysis on Earth Strain Tide of Guza Seismic Station[J]. Acta Geophysica Sinica, 1994, 37(S1): 213-221)
(  0) 0) |
| [6] |
邱泽华, 池顺良. YRY-4型钻孔应变仪观测的P波剪应变[J]. 地震, 2013, 33(4): 64-70 (Qiu Zehua, Chi Shunliang. Shear Strains of P Wave Observed with YRY-4 Borehole Strainmeter[J]. Earthquake, 2013, 33(4): 64-70 DOI:10.3969/j.issn.1000-3274.2013.04.007)
(  0) 0) |
| [7] |
刘序俨, 王紫燕, 方宏芳, 等. 对当前四分量钻孔应变观测的审视——以应变不变量为标尺[J]. 地球物理学报, 2014, 57(10): 3332-3346 (Liu Xuyan, Wang Ziyan, Fang Hongfang, et al. Analysis of 4-Component Borehole Strain Observation Based on Strain Invariant[J]. Chinese Journal of Geophysics, 2014, 57(10): 3332-3346 DOI:10.6038/cjg20141020)
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39

