大坝变形受温度、水位和时间效应等多因素影响，很难直接建立较为准确的变形量与影响因素之间的非线性关系模型。目前常用的预测方法主要有多元线性回归、时间序列模型、灰色理论和神经网络等^[1-2]，但大坝变形具有非平稳性和非线性，传统方法的应用受到一定限制。奇异谱分析(singular spectrum analysis，SSA)从时间序列向空间动力结构出发，以经验正交的方式展开时间序列子空间，不基于正弦波假定前提，不需要先验信息，能够准确识别时间序列中的周期信号^[3]。在使用GPS进行大坝变形监测时，根据SSA理论准确提取大坝变形信号，可提高变形监测的精度，准确获取大坝的真实变形信息，进一步分析各影响因子对大坝变形的贡献情况，深入研究大坝变形的内在规律并进行预测^[4-5]。考虑到SSA提取信号的优势，在准确分析序列提取信号的基础上，基于SSA迭代法对大坝变形进行预测，并与高斯过程模型、多元回归分析方法进行对比，期望能够更好地预测大坝的变形情况。

1 SSA预测方法 1.1 SSA原理

SSA是根据所观测到的时间序列构造出轨迹矩阵，对矩阵进行分解、重构，提取代表原时间序列不同成分的信号，通过分析时间序列的结构进行预测^[3]。首先，对于中心化后的时间序列x_i(1≤i≤N)，根据窗口L按照式(1)构造L×(N－L+1)的轨迹矩阵X：

$ \mathit{\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} {{x_1}}&{{x_2}}& \cdots &{{x_{i + 1}}}& \cdots &{{x_{N - L + 1}}}\\ {{x_2}}&{{x_3}}& \cdots &{{x_{i + 2}}}& \cdots &{{x_{N - L + 2}}}\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {{x_L}}&{{x_{L + 1}}}& \cdots &{{x_{i + 1}}}& \cdots &{{x_N}} \end{array}} \right] $

(1)

可得滞后协方差阵为C=XX^T，对其进行特征值分解：

$ \mathit{\boldsymbol{C}} = \mathit{\boldsymbol{V \boldsymbol{\varLambda} }}{\mathit{\boldsymbol{V}}^{\rm{T}}} $

(2)

式中，Λ为特征值λ_k构成的对角阵，λ_k为C的特征值并按降序排列，v_k为正交矩阵V的行向量。主成分矩阵A计算公式如下：

$ \mathit{\boldsymbol{A}}{\rm{ = }}\mathit{\boldsymbol{VX}} $

(3)

A的第k行(a_k)即为第k个主成分，其中每个数值a_{k, i}为：

$ {a_{k, i}} = \sum\limits_{j = 1}^L {{x_{i + j - 1}}} {v_{k, j}}, 1 \le i \le N - L + 1 $

(4)

其中, v_{k, j}是v_k的第j个元素。时间序列第k个重构分量可以写为：

$ x_{i}^{k}=\\\left\{ {\begin{array}{*{20}{l}} {\frac{1}{i}\sum\limits_{j = 1}^i {{a_{k, i - j + 1}}} {v_{k, j}}, 1 \le i \le L - 1}\\ {\frac{1}{L}\sum\limits_{j = 1}^L {{a_{k \cdot - j + 1}}} {v_{k, j}}, L \le i \le N - L + 1}\\ {\frac{1}{{N - i + 1}}\sum\limits_{j - i - N + L}^L {{a_{k, i - j + 1}}} {v_{k, j}}, \quad N - L + 2 \le i \le N} \end{array}} \right. $

(5)

SSA的特征值是按降序排列的，因此时间序列可由前几个主成分分量重构，其余则视为噪声，即信号${\hat x}$可以由前q个主成分得到：

$ \hat x = \sum\limits_{k = 1}^q {x_i^k} , i = 1, 2, \cdots , N $

(6)

1.2 SSA预测原理

SSA迭代预测法建立在重构序列基础上，具体步骤如下。

定义矩阵${\mathit{\boldsymbol{X}}_\mathit{M}} = [{{\hat X}_1}, \cdots , {{\hat X}_K}, {Z_{K + 1}}, \cdots {Z_{K + M}}]$，其中，$ [{{\hat X}_1}, \cdots , {{\hat X}_K}]$为基于原有数据序列构建的重构轨迹矩阵，[Z_K+1, …, Z_K+M]设为未来预测序列构建的相应矩阵向量。因此，只要获得X_M便可对其进行对角平均，得到预测序列。定义R=(a_L－1, …, a₁)^T，设I为选取的重构特征值，P_i∈R^L(i∈I)为对应的特征向量, P_i为P_i的前(L-1)行，π_i是P_i的最后一个元素，${v^2} = \sum\nolimits_{i \in I} {\mathit{\pi }_i^2} $。

$ \boldsymbol{\mathit{R}}=\frac{1}{1-{{v}^{2}}}\sum\limits_{i\in I}{{{\pi }_{i}}}\underline{{{\boldsymbol{\mathit{P}}}_{i}}} $

(7)

定义线性算子${p_{{\rm{vec}}}}\mathit{\boldsymbol{Y}} = \left( {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\overline Y}} }\\ {{\mathit{\boldsymbol{R}}^{\rm{T}}}\mathit{\boldsymbol{\overline Y}} } \end{array}} \right)$，${\mathit{\boldsymbol{\overline Y}} }$为Y的后(L-1)行，写成向量形式即为：

$ {{\boldsymbol{\mathit{Z}}}_{i}}=\left\{ \begin{array}{*{35}{l}} {{{\hat{X}}}_{i}}, i=1, \cdots , K \\ {{p}_{vex}}{{\boldsymbol{\mathit{Z}}}_{i-1}}, i=K+1, \cdots , K+M \\ \end{array} \right. $

(8)

对式(8)进行对角平均可以计算出预测序列，式(8)的等价形式为：

$ {{y}_{i}}=\left\{ \begin{array}{*{35}{l}} {{{\tilde{x}}}_{i}}, i=1, \cdots , N \\ \sum\limits_{j=1}^{L-1}{{{a}_{j}}}{{y}_{i-j}}, i=N+1, \cdots , N+M \\ \end{array} \right. $

(9)

式中，${{\tilde x}_i}$为重构序列的第i个元素。本文利用蒙特卡洛模拟算法^[6]估计预测序列的95%可信区间，具体预测原理见文献[3]。

2 大坝变形成因分析

在西南某蓄能水电厂的下库混凝土大坝上布设正倒垂线及4个位移监测点，坝体内安装18处电阻式温度计，于2006-11~2010-08对温度、水位、时间和位移变化量进行1 400次记录。由于各监测点变化规律大致相同，本文选择其中一个点进行分析。对采集数据作粗差探测预处理，并通过平滑处理(平滑半径为7 d)得到200期数据集。

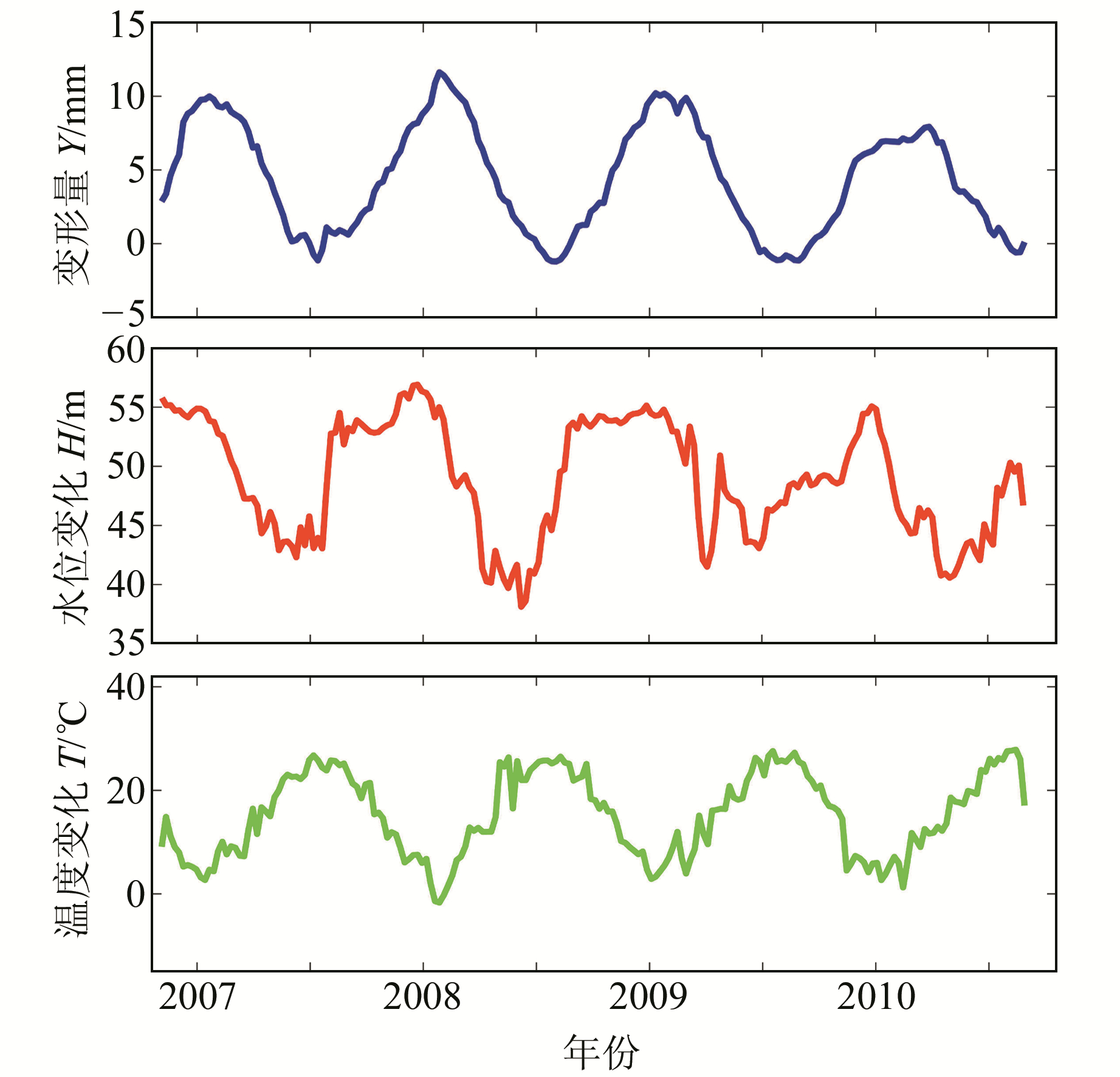
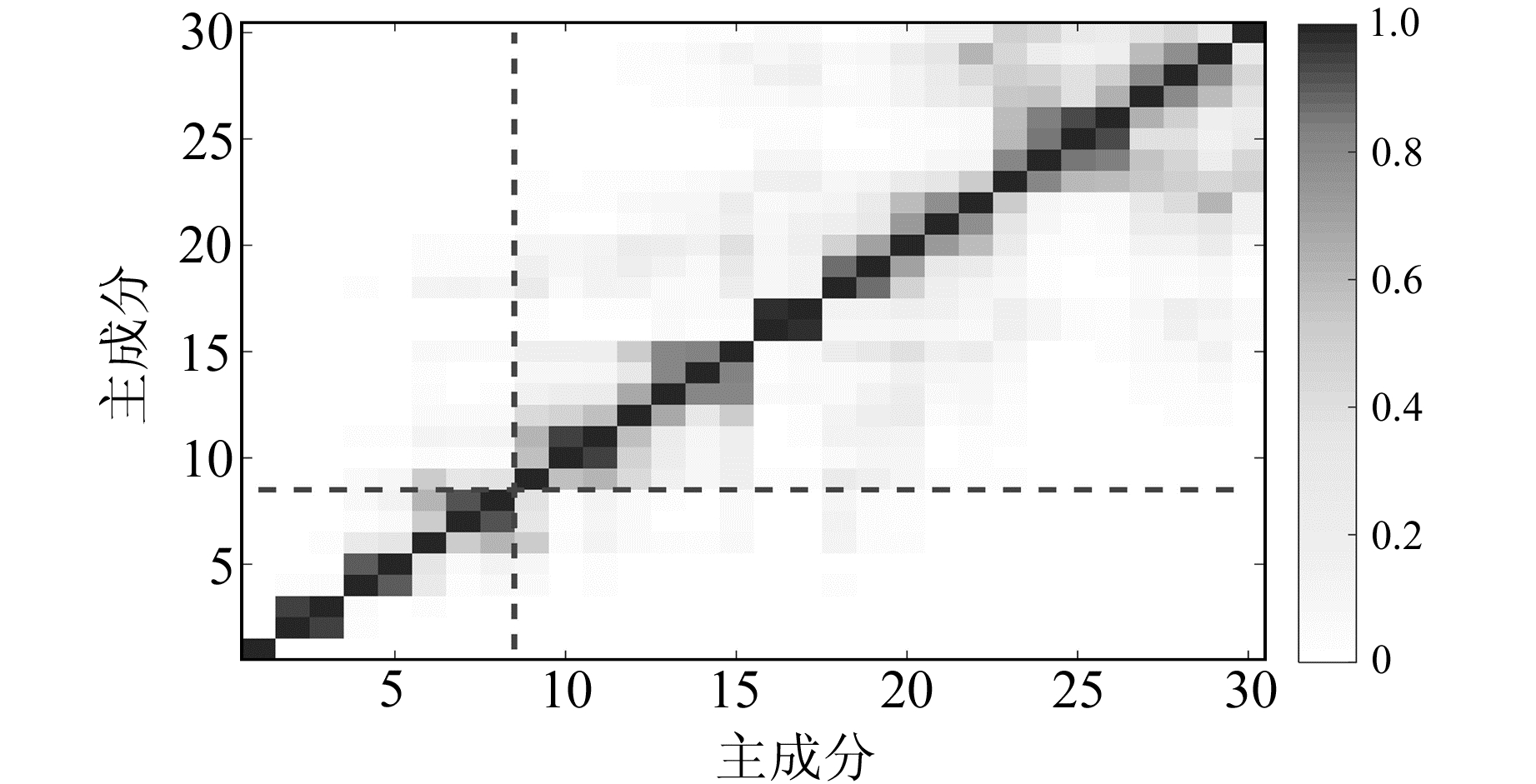
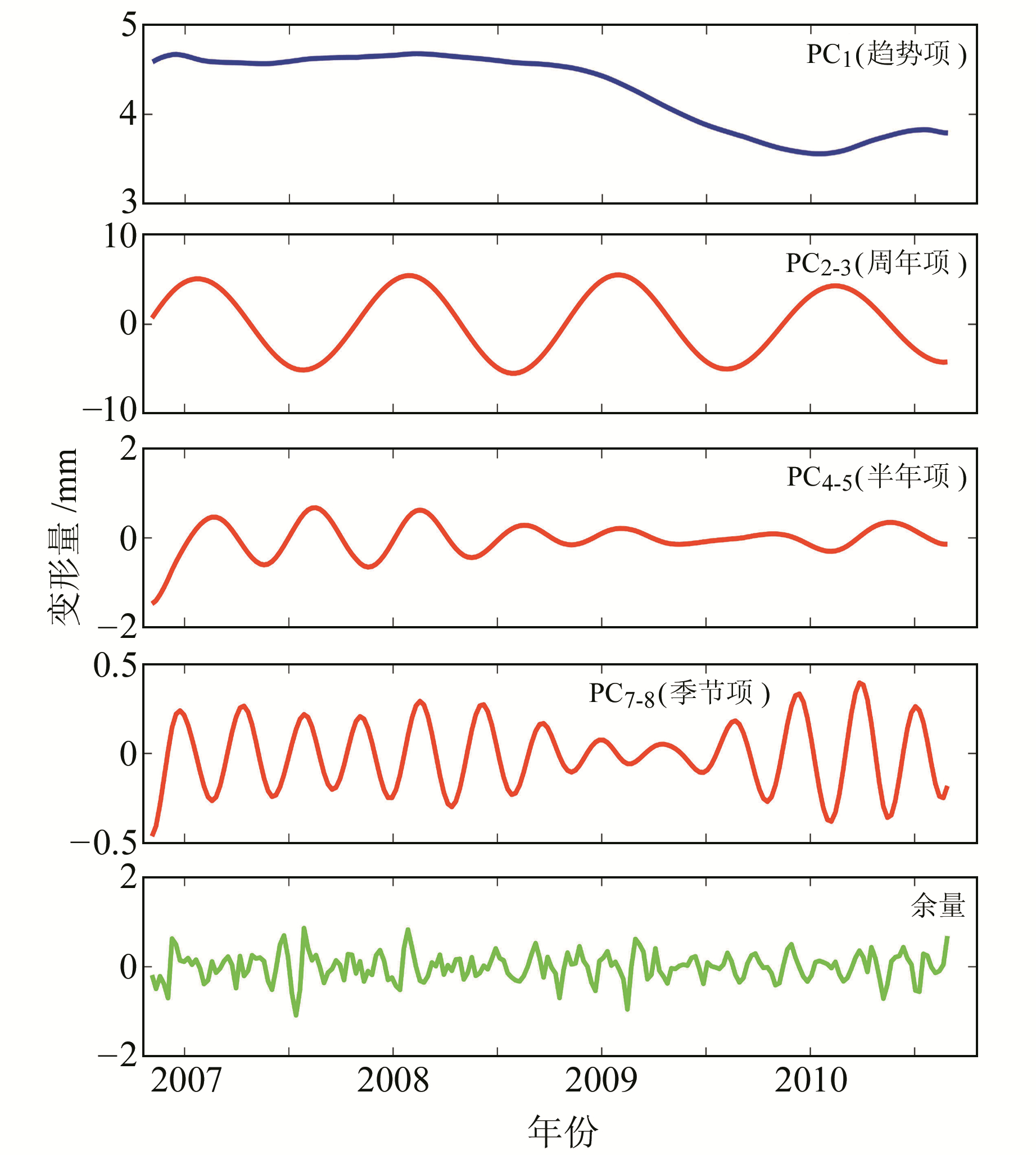
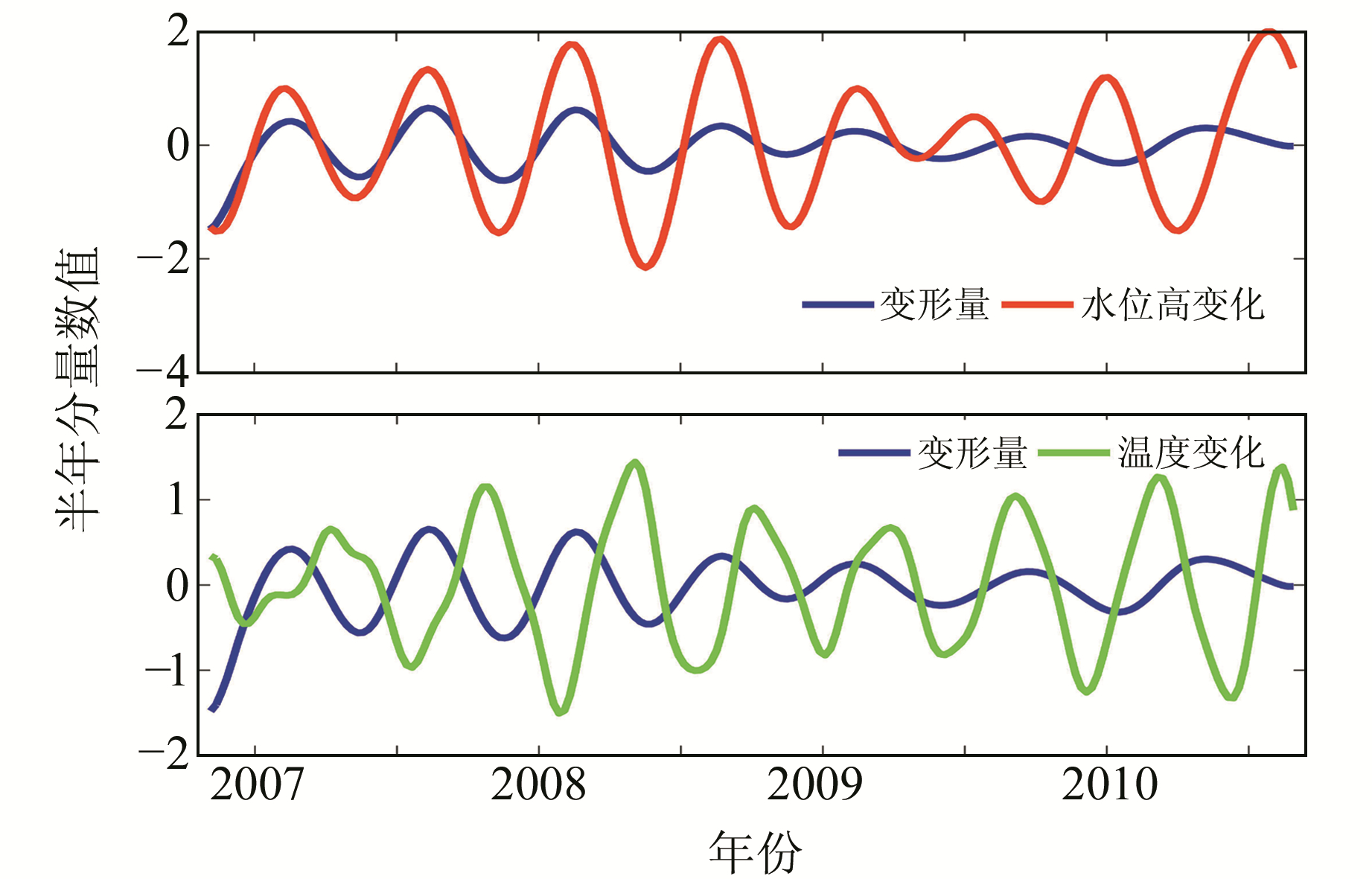
由图 1可知，大坝位移变形随时间、温度、水位的变化具有一定的规律性，分析变形量与影响因素的关联性，可以为变形预测打下良好基础。对原始序列利用SSA进行分析，根据先验信息得知大坝变形存在周年、半年和季节性周期，因此窗口长度取1 a(即52周)，并给出前30个主成分的W-correlations图(图 2)，具体公式见文献[5]。由图 2可知，PC₁是趋势项，能量占比最大，为57.29%；PC_2-3为年周期分量，能量占比为41.79%；PC_4-5为半年周期分量，能量占比为0.39%；PC_7-8为季节性周期分量，能量占比为0.13%。前8个主成分能量占比超过总能量的99%，剩余的分量被视为噪声予以忽略，具体的各成分见图 3。

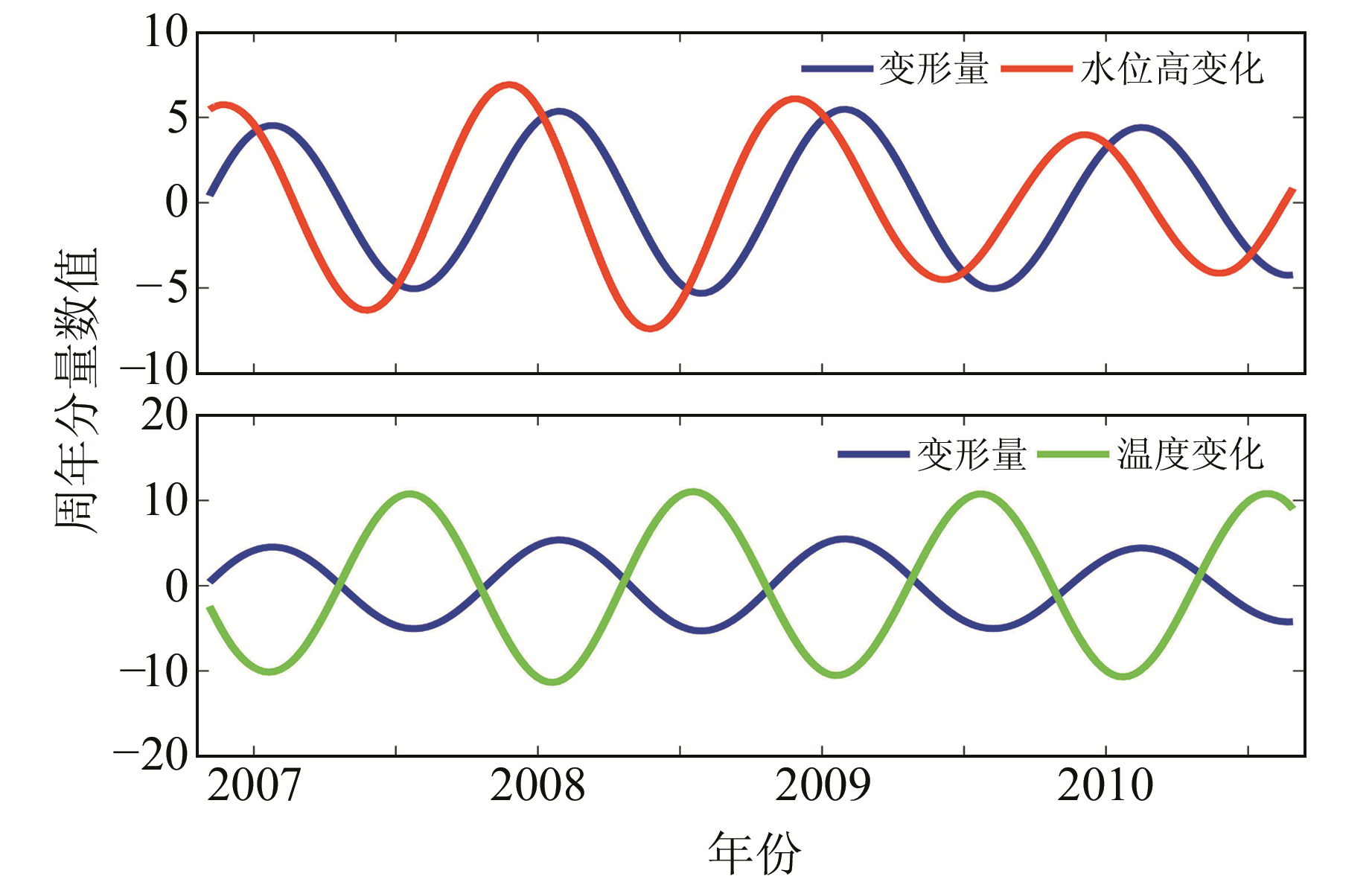
为分析水位、温度和时效因子对大坝变形的贡献情况，将提取的趋势、周期和余量与影响因子之间进行相关性分析，并利用奇异谱分析提取水位变化中相应的趋势和周期成分(表 1)，同时给出变形量、水位和温度变化的周年和半年分量对比情况(图 4、图 5)。由表 1和图 3可知，大坝变形的每个主成分分量都包含原序列中的不同特征信息，PC₁分量变化平缓，主要包含长期变形信息，与水位因子趋势成分相关系数为0.86，与时效因子相关系数为-0.88，即大坝变形长期趋势成分主要与水位的长期趋势变化和时效因子有关，受温度等其他因素的影响较小。大坝周期分量与水位的相应周期分量相关系数为0.38，为正相关；与温度因子相关系数为-0.92，为负相关，即与温度的变化趋势恰好相反，这与混凝土坝体由温度变化引起的坝体变形规律相符合，也与图 4和图 5显示的结果一致。由图 4还可以发现，大坝变形与水位及温度的变化存在一定的相位差，这与大坝变形具有滞后效应的规律一致。余量数据关联性较弱，与水位、温度和时效因子的相关性不强，能量占比较小，此处不再考虑。

3 大坝变形预测

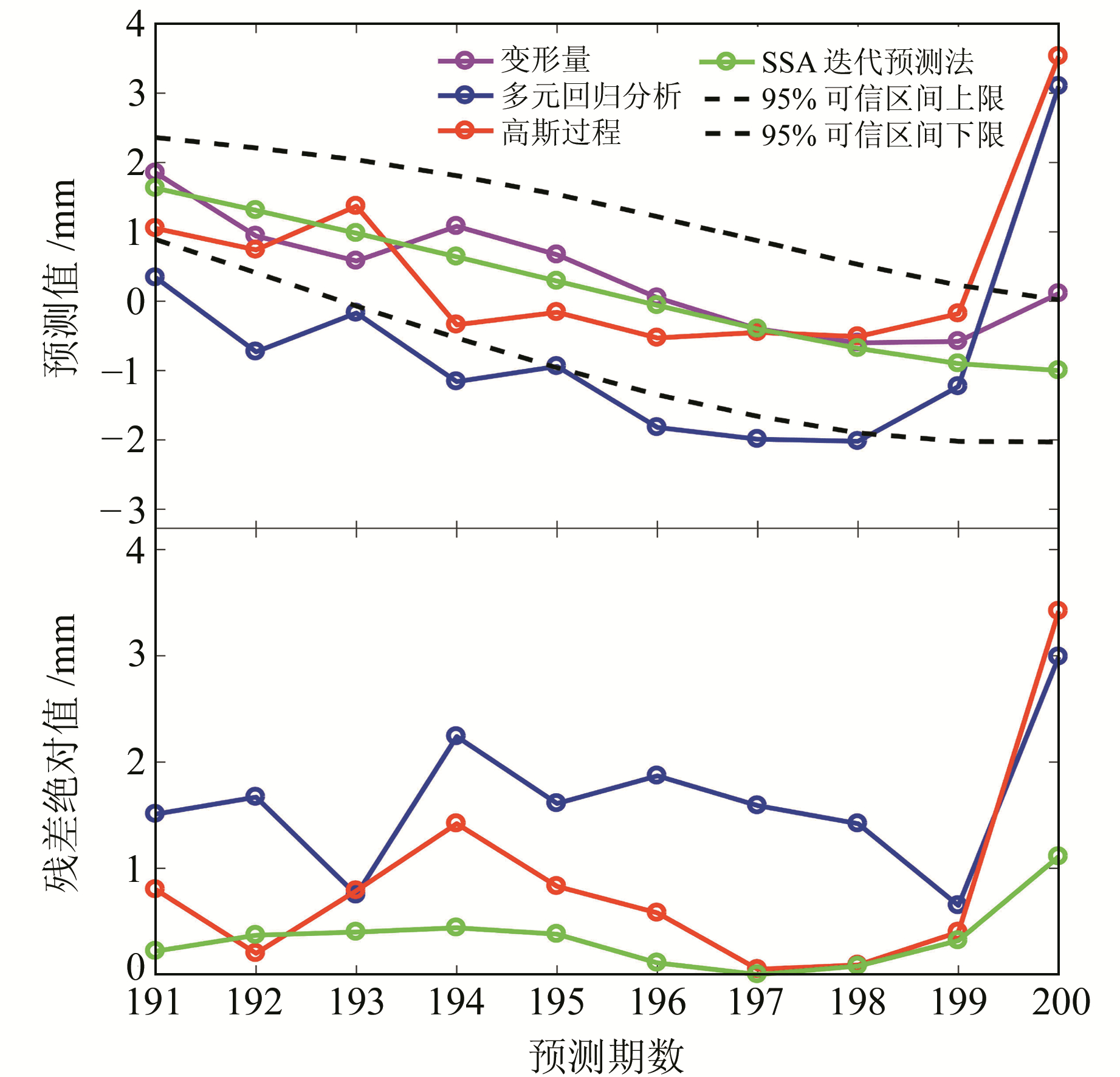
将前190期变形数据{X_i=(t_i, H_i, T_i), Y_i(i=1, 2, …, 190)}作为建模数据集，191~120期变形数据{X_j=(t_j, H_j, T_j), Y_j}作为测试数据集。安全监测因果模型的一项重要工作就是将合理有效的影响因子引入模型，以达到准确预测的目的。运行期间大坝变形的主要影响因素是水位、温度和时效。本文使用多元回归分析方法、高斯过程模型(其中高斯过程模型选择的神经网络核函数及均值函数采用MeanZero)和SSA迭代法^[7]进行预测建模比较分析，并利用蒙特卡洛模拟算法^[6]估计SSA预测序列的95%可信区间，具体预测结果见表 2。

由表 2和图 6可知，多元回归分析方法预测效果较差，表明针对多因素主导的大坝变形监测，其预测模型未能较好地建立大坝变形的因果关系；高斯过程模型在处理高维数、小样本、非线性等复杂问题上具有很好的适应性，预测效果明显更接近于实测值^[8]。与前两种方法相比，SSA能够准确分析并提取大坝变形的趋势和周期信号，并利用迭代法进行预测，预测精度明显提升。

为了进一步对比不同预测模型的预测精度，采用均方根误差和平均绝对误差^[9]检验预测模型的精度：

$ \text{RMSE}=\sqrt{\frac{1}{N}\sum\limits_{i=1}^{N}{{{\left( {{s}_{i}}-{{{\hat{s}}}_{i}} \right)}^{2}}}} $

(10)

$ \text{MAE}=\frac{1}{N}\sum\limits_{i=1}^{N}{\left| {{s}_{i}}-{{{\hat{s}}}_{i}} \right|} $

(11)

式中，${{\hat s}_i}$为模型预测值，s_i为大坝变形实测值，N为预测序列长度。

经计算，SSA迭代预测法的RMSE和MAE分别为0.45 mm和0.34 mm，明显优于高斯过程的1.28 mm和0.86 mm及多元回归分析模型的1.75 mm和1.63 mm。由此可知，基于SSA的迭代预测法结果明显小于传统的多元回归分析及高斯过程预测方法，与表 2和图 6的结果一致。文中利用蒙特卡洛模拟算法计算了预测序列的可信区间，真实数据基本上处于可信区间内，表明SSA迭代预测法可以有效地预测大坝变形，为大坝安全监测提供保障。

4 结语

利用SSA法分析大坝变形数据并建立大坝变形预测模型，通过实例验证分析可得：1)SSA可以有效分离并提取序列中的趋势和周期成分，发现大坝变形存在年周期、半年周期和季节性周期，并分别分析与相应变形因子之间的相关性。大坝变形的趋势项主要与水位趋势变化和时效因子有关，温度变化对大坝变形的周期成分贡献最大，其次为水位变化。2)考虑到SSA提取信号的优势，在SSA重构序列基础上，利用迭代法对大坝变形进行预测，并与高斯过程和多元回归分析进行对比。结果表明，基于SSA的迭代预测法预测精度均方根误差和平均绝对误差分别为0.45 mm和0.34 mm，明显高于高斯过程模型和多元回归分析方法，且给出了95%可信区间，适合对大坝变形进行短中期预测。

如何根据大坝实时监测数据对其进行动态预测，进一步利用新信息建模，是接下来研究的重点。