由于受到集装箱遮挡,GNSS卫星可见性变差,难以为港口内的各种设备提供可靠、准确、连续的导航定位服务,已成为码头自动化改造的难题。而独立组网的地基伪卫星定位系统可根据需求和地形合理部署基站,在不依赖卫星导航的情况下独立自主地为港口内的设备提供高精度、高可靠性的定位服务。考虑到港口环境的复杂性以及对定位可靠性的要求,通常会在港口内布设一定数量的冗余基站,以此提高定位的连续性,减少定位盲区。在此情况下,若还以传统卫星导航定位算法进行解算,不仅会导致接收机计算量增加、硬件成本提升,还会使伪距测量误差较大的观测值参与定位解算,降低系统的定位精度。为了减轻接收机的计算负担、提高定位精度和实时性,需要从可视基站中选择定位精度较高的基站组合进行信号接收和定位解算。
目前,独立组网的地基伪卫星系统尚处于研发和完善的阶段,对于实际应用中出现的基站选择问题的研究并不多,因此可以参考卫星导航中的选星算法设计伪卫星基站的选择方法。在卫星导航系统中,接收机通常采用精度因子(DOP)最优标准作为接收机选择定位卫星的依据。但是与GNSS系统中接收机到各卫星距离大致相同、测量误差差异不明显的应用场景不同,地基伪卫星系统基站布设在地面上,接收机到各基站的距离不同,测距误差存在明显的差异,不再满足DOP值对各单元测距误差基本相同的要求,所以DOP最优准则并不适用。为解决组合导航定位系统接收机选星时遇到的类似问题,文献[1-2]提出将加权精度因子(WDOP)最优标准作为接收机定位卫星选择的依据,削弱伪距测量误差不同对选星和定位结果造成的影响。然而,组合卫星导航中观测量误差的差异是系统级的,基于经验值确定的加权矩阵可以很好地反映系统的特性;而在伪卫星系统中观测量误差的差异是单元级的,无法基于经验值确定系统加权矩阵,需要对系统的测距误差建模分析。此外,伪卫星系统WDOP值随接收机位置变化明显,为提高定位精度需要实时地对基站进行选择,文献中所采用的遍历选星法速度慢、计算量大,在此应用背景下将严重影响定位的实时性。
鉴于上述分析,本文在对地基伪卫星系统测距误差建模分析的基础上,尝试提出伪卫星基站选择的加权水平精度因子(WHDOP)最优准则,确定适用于伪卫星系统的加权矩阵。在此基础上,提出基于基站对WHDOP贡献的选站方法,以降低基站选择算法的计算量,提高定位的实时性。
1 加权精度因子简介 1.1 精度因子在定位导航系统中,定位误差可表示为测距误差与精度因子(DOP)的乘积,其中DOP表示卫星/用户的相对几何布局对定位误差的复合影响,其数值越小,定位精度越高[3]。因此,DOP的大小成为卫星导航系统最佳星座选择、定位精度评估和完好性检测的重要依据[4]。一般来说,DOP是用定位误差协方差矩阵各分量之和与基准均方根伪距误差σUERE2的比值来定义的。定位误差协方差矩阵为:
| $ {\mathop{\rm cov}} ({\rm{d}}x) = {\left( {{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{H}}} \right)^{ - 1}}\mathit{\sigma }_{{\rm{UERE}}}^2 = \mathit{\boldsymbol{D}}\mathit{\sigma }_{{\rm{UERE}}}^2 $ | (1) |
| $ \mathit{\boldsymbol{H}} = \left[ {\begin{array}{*{20}{c}} {a_x^1}&{a_y^1}&{a_z^1}&1\\ {a_x^2}&{a_y^2}&{a_z^1}&1\\ \vdots & \vdots & \vdots & \vdots \\ {a_x^n}&{a_y^n}&{a_z^n}&1 \end{array}} \right] $ | (2) |
式中,H为系统的观测矩阵(axi, ayi, ayi)(i=1, 2, 3, …, n,表示第i颗卫星的方向余弦),n表示可见星数目。几种常用的精度因子可以表示为:
| $ {\rm{GDOP}} = \sqrt {{D_{11}} + {D_{22}} + {D_{33}} + {D_{44}}} $ | (3) |
| $ {\rm{PDOP}} = \sqrt {{D_{11}} + {D_{22}} + {D_{33}}} $ | (4) |
| $ {\rm{HDOP}} = \sqrt {{D_{11}} + {D_{22}}} $ | (5) |
式中,GDOP称为几何精度因子,表示位置和时间解的精度;PDOP称为位置精度因子,表征三维方向上定位的精度;HDOP为水平精度因子,只表征系统的水平定位精度。
文献[5]通过对导航系统定位误差协方差的分析,给出DOP的推导过程。不难发现,各卫星的测距误差相等是保证DOP能准确地衡量系统定位精度的前提。在单系统卫星导航中,由于卫星所处轨道高度相同且与用户之间的距离很远,各卫星测距误差差异不大,所以可以将DOP作为最佳星座的选择依据。而在伪卫星定位系统中,基站布设在地面上,到用户之间的距离不同,信号衰减程度各异,各观测量的伪距测量误差存在明显差异,DOP值并不适合作为系统基站选择的依据,需要对加权精度因子(WDOP)进行研究。
1.2 加权精度因子虽然DOP值不能对伪卫星系统的定位性能作出准确评价,但是伪卫星定位系统定位精度可以表示为测距误差与加权精度因子(WDOP)的乘积。WDOP的本质是给予每个观测值不同的权值,削弱误差大的结果对系统的影响。
文献[6]给出了组合卫星导航中WDOP的定义。假设每颗卫星的伪距测量误差是独立的、具有零均值的正态分布,则n个卫星的测量误差的协方差矩阵可以表示为:
| $ {\mathop{\rm cov}} ({\rm{d}}\rho ) = {\mathit{\boldsymbol{W}}_n}\mathit{\sigma }_{{\rm{UERE}}}^2 $ | (6) |
其中,Wn为系统测距误差的加权矩阵。用dx表示定位系统位置/时间估计的净误差,则协方差矩阵为:
| $ \begin{array}{l} \;\;{\mathop{\rm cov}} ({\rm{d}}x) = {\left( {{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{W}}_n^{ - 1}\mathit{\boldsymbol{H}}} \right)^{ - 1}}{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{W}}_n^{ - 1}{\mathop{\rm cov}} ({\rm{d}}\mathit{\rho }) \cdot \\ \mathit{\boldsymbol{W}}_n^{ - 1}\mathit{\boldsymbol{H}}{\left( {{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{W}}_n^{ - 1}\mathit{\boldsymbol{H}}} \right)^{ - 1}} = {\left( {{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{W}}_n^{ - 1}\mathit{\boldsymbol{H}}} \right)^{ - 1}}\mathit{\sigma }_{{\rm{UERE}}}^2 = \mathit{\boldsymbol{Q}}\mathit{\sigma }_{{\rm{UERE}}}^2 \end{array} $ | (7) |
参考DOP值的定义方式,几种常用的WDOP值可以表示为:
| $ {{\rm{WGDOP}} = \sqrt {{Q_{11}} + {Q_{22}} + {Q_{33}} + {Q_{41}}} } $ | (8) |
| $ {{\rm{WPDOP }} = \sqrt {{Q_{11}} + {Q_{22}} + {Q_{33}}} } $ | (9) |
| $ {{\rm{ WHDOP }} = \sqrt {{Q_{11}} + {Q_{22}}} } $ | (10) |
伪卫星定位系统与组合卫星导航系统情况类似,各观测量的伪距测量误差是独立的、具有零均值的正态分布,满足WDOP定义时对观测量作出的假设。因为目前高程定位结果对码头自动化改造的应用价值不明显,定位过程中通常会锁定高程进行水平方向上的定位,所以本文最终将WHDOP最优标准作为伪卫星定位系统基站选择的依据。
2 伪卫星系统加权矩阵将WHDOP最优标准作为伪卫星系统基站选择的依据,首先要确定系统的加权矩阵Wn。在多星座组合导航定位中,往往根据经验值对卫星观测量进行系统级的加权[7]。而在伪卫星定位系统中,加权矩阵Wn与接收机和基站间的相对位置有关,无法根据经验值确定各观测值的权值,需要分析伪距测量误差的数学模型来确定系统的加权矩阵。
2.1 基站测距误差伪卫星接收机观测误差主要有以下几个来源:基站时钟同步误差、大气层延迟效应、接收机热噪声以及多路径误差。其中伪卫星各基站间采用TimeLoc时间同步法,同步精度优于1 ns,甚至可以达到ps级。此外,由于伪卫星基站布设在地面,信号的传播不经过电离层,本身影响较小的对流层延时可采用文献[8]中的模型校正。因此,基站时钟同步误差和大气层延时误差对伪距测量误差和定位精度的影响很小。考虑到伪卫星的特殊性,多路径误差较为严重,尤其是在码头集装箱堆场这种特殊环境下,抵制和消除多路径效应是独立组网的伪卫星定位系统提供可靠位置服务的重要环节。多路径效应的预处理主要从信号设计、天线设计、数字信号处理以及定位导航计算4个方面进行[9]。目前最成熟的地基伪卫星定位系统Locata基于空间分集、频率分集以及TimeTena天线技术,削弱多路径效应对接收机定位的影响[10]。
在充分抵制多路径效应、校正对流层延时的基础上,测距误差将主要取决于接收机热噪声误差,其导致的伪距测量误差主要取决于热噪声距离误差颤动和动态应力误差。当接收机使用相干DLL鉴别器时测量误差均方根可以表示为:
| $ {\mathit{\sigma }_{th}} = \sqrt {\frac{{{B_n}D}}{{2C/{N_0}}}} $ | (11) |
式中,Bn表示码跟踪环的噪声带宽;D表示超前减滞后相关器的间距;C/N0表示载噪比,指解调前的射频信号与噪声功率的比值。将伪卫星系统基准测距误差均方差设定为接收机距离基站1 m时的测距误差σ1m,则各基站测量误差标准差σi与σ1m存在以下关系:
| $ \frac{{\mathit{\sigma }_i^2}}{{\mathit{\sigma }_{1{\rm{m}}}^2}} = \frac{{\frac{{{B_n}D}}{{2{C_i}/{N_0}}}}}{{\frac{{{B_n}D}}{{2{C_{1{\rm{m}}}}/{N_0}}}}} = \frac{{{C_{1{\rm{m}}}}}}{{{C_i}}} $ | (12) |
可见,观测量误差的大小主要取决于接收信号功率,而接收信号功率可以根据信号的自由空间衰减模型确定:
| $ {C_R}(d) = \frac{{{C_T}{G_T}{G_R}{\lambda ^2}}}{{{{(4{\rm{ \mathsf{ π} }})}^2}{d^2}L}} $ | (13) |
式中,CR(d)是距离发射源d m处天线的接收功率,CT表示信号的发射功率,GT和GR表示发射和接收天线的增益,λ为信号波长,L表示硬件损耗因子。由于基站所采用的硬件设备以及发射的信号波长和功率完全相同,所以σi2可以化简为:
| $ \sigma _i^2 = d_i^2\sigma _{1{\rm{m}}}^2 $ | (14) |
可见,伪卫星接收机观测量误差与接收机到基站之间的距离的平方近似成正比。
2.2 加权矩阵假设伪卫星系统观测量误差是相互独立的、零均值的高斯分布,则其协方差矩阵一般表示为:
| $ {\mathop{\rm cov}} ({\rm{d}}\mathit{\rho }) = {\mathop{\rm diag}\nolimits} \left[ {\begin{array}{*{20}{c}} {\mathit{\sigma }_1^2}&{\mathit{\sigma }_2^2}& \cdots &{\mathit{\sigma }_n^2} \end{array}} \right] $ | (15) |
文献[7]的研究表明,轻微的权值变化对基站选择以及系统的定位性能影响不大,因此可以只考虑接收机热噪声误差,则伪卫星定位系统测距误差的协方差矩阵为:
| $ {\mathop{\rm cov}} ({\rm{d}}x) = {\mathop{\rm diag}\nolimits} \left[ {d_1^2\quad d_2^2\quad \cdots \quad d_n^2} \right]\mathit{\sigma }_{1{\rm{m}}}^2 $ | (16) |
对比式(6)和式(16)可以得到伪卫星系统加权矩阵Wn的表达式:
| $ {\mathit{\boldsymbol{W}}_n} = {\mathop{\rm diag}\nolimits} \left[ {\begin{array}{*{20}{l}} {d_1^2}&{d_2^2}& \cdots &{d_n^2} \end{array}} \right] $ | (17) |
在伪卫星系统中,WHDOP随接收机位置变化非常明显,每次定位前都需要重新选择基站,对基站选择的实时性提出了很高的要求。而由于在WHDOP求解的过程中存在矩阵相乘和矩阵求逆运算,通过对所有潜在基站组合求WHDOP,从中选取最小值和对应基站组合的遍历法计算量较大,难以满足伪卫星系统对定位实时性的要求。为了提高定位的实时性,降低基站选择的时间,参考卫星导航领域中以DOP次优标准为依据的快速选星法,设计了基于基站对WHDOP贡献的选站方法。
假设Hn是可视基站数为n时的观测矩阵,从中去掉一个基站,剩余n-1个基站的观测矩阵是Hn-1,两者的关系如下:
| $ \mathit{\boldsymbol{H}}_n^{\rm{T}}{\mathit{\boldsymbol{W}}_n}{\mathit{\boldsymbol{H}}_n} = \mathit{\boldsymbol{H}}_{n - 1}^{\rm{T}}{\mathit{\boldsymbol{W}}_{n - 1}}{\mathit{\boldsymbol{H}}_{n - 1}} + {\mathit{\boldsymbol{h}}^{\rm{T}}}\mathit{\boldsymbol{wh}} $ | (18) |
式中,h为去掉的基站的观测量,w是其对应的权值。采用Sherman-Morrison-Woodbury展开式(18)得:
| $ \begin{array}{l} {\mathit{\boldsymbol{A}}_{n - 1}} = {\left( {\mathit{\boldsymbol{H}}_{n - 1}^{\rm{T}}{\mathit{\boldsymbol{W}}_{n - 1}}{\mathit{\boldsymbol{H}}_{n - 1}}} \right)^{ - 1}} = \left( {\mathit{\boldsymbol{H}}_n^{\rm{T}}{\mathit{\boldsymbol{W}}_n}{\mathit{\boldsymbol{H}}_n} - } \right.\\ \;\;\;{\left. {{\mathit{\boldsymbol{h}}^{\rm{T}}}\mathit{\boldsymbol{wh}}} \right)^{ - 1}} = {\mathit{\boldsymbol{A}}_n} + \mathit{\boldsymbol{A}}_n^{\rm{T}}h\mathit{S}\mathit{\boldsymbol{h}}{\mathit{\boldsymbol{A}}_n} = {\mathit{\boldsymbol{A}}_n} + \mathit{\boldsymbol{E}} \end{array} $ | (19) |
式中,S=(1/w-hAnhT)-1是一个标量。对比式(8),此时剩余n-1个基站和接收机形成的几何结构的加权水平精度因子为:
| $ \begin{array}{l} {\rm{WHDOP}}_{n - 1}^2 = {\mathit{\boldsymbol{A}}_{{n_{11}}}} + {\mathit{\boldsymbol{A}}_{{n_{22}}}} + {\mathit{\boldsymbol{E}}_{11}} + {\mathit{\boldsymbol{E}}_{22}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{WHDOP}}_n^2 + {\mathit{\boldsymbol{E}}_{11}} + {\mathit{\boldsymbol{E}}_{22}} \end{array} $ | (20) |
所以去掉的基站对WHDOPn的贡献为:
| $ \Delta {\mathit{\boldsymbol{A}}_n} = {\mathit{\boldsymbol{E}}_{11}} + {\mathit{\boldsymbol{E}}_{22}} $ | (21) |
可见,ΔAn越小,去掉基站后剩余基站的WHDOP越小,定位精度越高。所以在基站选择时,ΔAn较小的基站将不会被选中。以此为根据,基于基站对WHDOP贡献的基站选择方法具体步骤如下:
1) 根据接收机通道数量和用户对定位精度的要求确定选择基站的数目;
2) 计算每个基站对WHDOP的贡献值ΔAn;
3) 确定ΔAn的最小值,并去掉其对应的基站;
4) 对剩余基站执行步骤2)~3),直到剩余基站数目等于m时停止。
3.2 算法分析如上所述,基站选择的第一步是确定选择基站的数目m。在只进行水平二维定位的情况下,假设接收机通道数目为k,则m取值范围为[3, k],具体取值需对实际的基站布设情况仿真,确定满足用户定位精度的WHDOP最大值,进而确定满足该WHDOP值的最小基站数目m。分析地基伪卫星定位系统在港口的实际测试结果可以发现,6个基站能够很好地满足港口自动化对设备定位精度的要求,因此m可以暂定为6。
假设接收机可视基站总数为n,遍历法需要执行Cn6次包含矩阵乘法和矩阵求逆的WHDOP求解过程;基于基站对WHDOP贡献的基站选择方法,需要执行n-6次WHDOP和n+n-1+…+7次只包含矩阵乘法的ΔAn求解过程。当n>7时,与遍历法相比,基于基站对WHDOP贡献选站法计算量小,基站选择速度快,定位实时性提升明显。
4 仿真与分析 4.1 WHDOP选站性能仿真和与GNSS组合定位的伪卫星可以提升高程定位精度不同,独立组网的地基伪卫星系统在码头应用时,基站的布设高度一般在30~50 m,不论怎样调节各基站间的高度差,VDOP值都很大,高程定位精度较差;而且高程定位结果对码头设备的自动化改造应用价值有限,因此本文的仿真基于二维平面进行。在4 000 m×1 000 m的区域两侧,每隔500 m布置一个基站。仿真中假定接收机与基站间钟差为0.05 s,接收机单位距离热噪声误差的标准差σ1m为10-4 m,其余误差来源造成的测量误差等效为标准差σ=10-6 m的高斯噪声,结合接收机和基站的真实距离可以确定接收机到各个基站间的伪距。
表 1(单位m)和表 2(单位m)分别给出定位区域内6个具有代表性的位置采用最小二乘法定位1 000次所得定位误差的统计值。对比3种方法在6个位置定位的统计结果可以看出,由于采用WHDOP选择基站,降低了观测误差较大的基站参与定位的可能性,因此其定位精度不仅远优于采用HDOP选择基站定位的精度,而且比采用全部基站观测值定位时还要高,这种定位精度的提升在定位区域边缘更加明显。
|
|
表 1 定位误差平均值 Tab. 1 Mean of positioning error |
|
|
表 2 定位误差标准差 Tab. 2 Standard deviation of positioning error |
纵向对比每一种方法在6个点的定位误差的平均值和标准差可以发现,采用全部基站观测值定位以及采用HDOP选择基站的定位结果在不同位置定位精度差异非常大,而采用WHDOP选择基站各点定位精度更加接近。当接收机在定位区域的各个位置出现的概率相近时,定位精度取决于区域内定位误差的最大值,此时采用WHDOP选择基站,能够更大程度地提高接收机定位的精度和稳定性。
为了评价接收机动态运动时WHDOP选站的性能,表 3(单位m)给出接收机按正弦轨迹运动时2 000个采样点定位误差的统计值。可以发现,采用WHDOP最优标准选择基站,定位误差的最大值、平均值和标准差都有不同程度的减小,定位精度更高。图 1给出了接收机运动轨迹和2 000个定位点定位误差的频数分布。如图所示,采用全部基站观测值定位时,定位误差大于10 cm的概率为15%;采用HDOP最优标准选择基站定位,定位误差大于10 cm的概率增加到20%,同时部分位置定位误差超过30 cm,定位的精度无法保证;而以WHDOP最小准则选择基站定位,定位误差大于10 cm的概率降低到5%,定位精度有较明显的提高。
|
|
表 3 动态过程定位误差统计量 Tab. 3 Statistical magnitude of positioning error in dynamic simulate process |

|
图 1 运动轨迹、定位误差频数分布 Fig. 1 The graphic of movement path, frequency distribution histogram of position error |
综上,通过对比两种场景下所选基站的定位结果可以看出,采用WHDOP最优标准选择伪卫星系统定位基站,可以减小误差较大的观测值参与定位的概率,提升基站选择的稳定性和准确性,提高系统的定位精度,具有很高的工程实用价值。
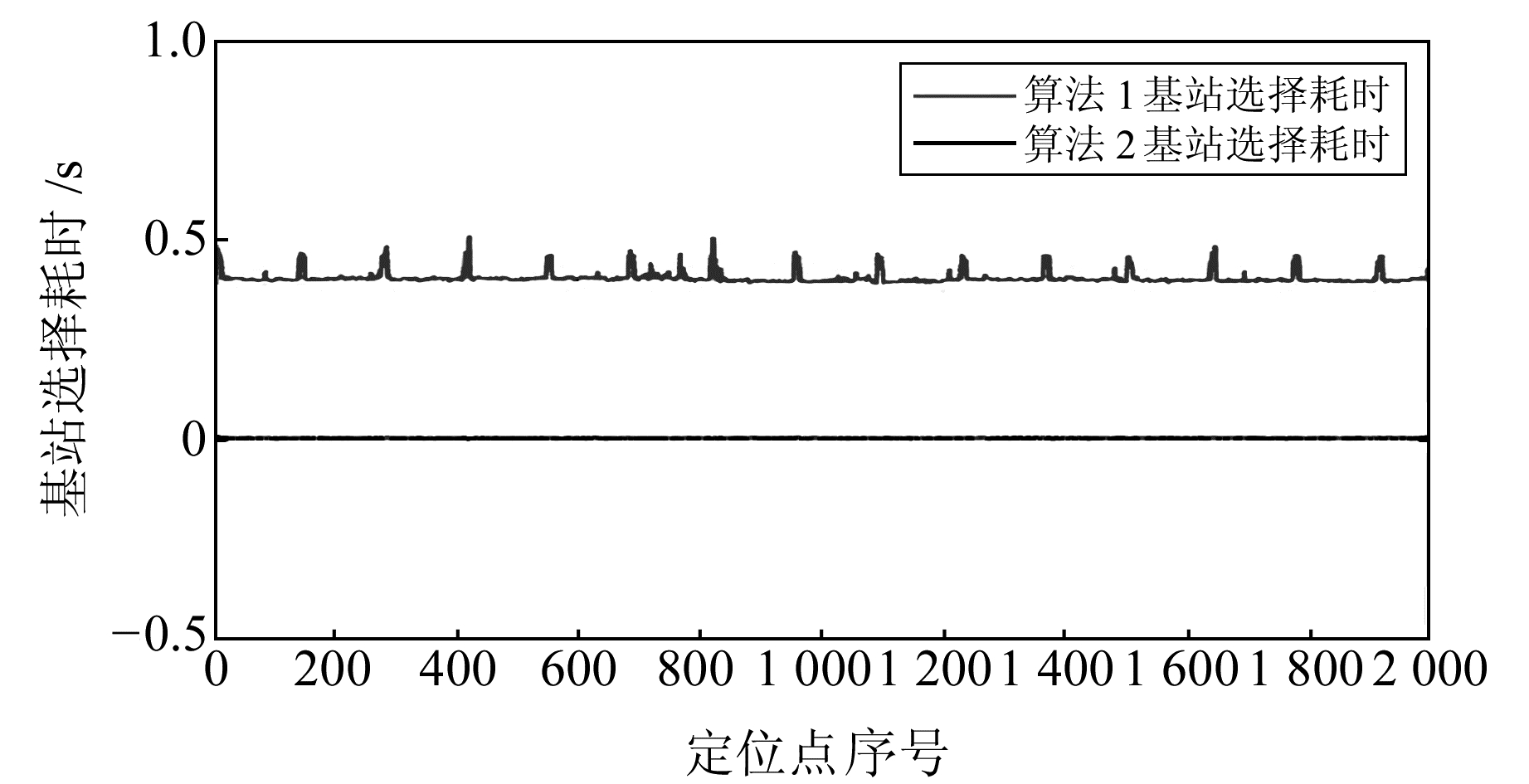
4.2 基站对WHDOP贡献选站法仿真分别采用遍历法(算法1)和基于基站对WHDOP贡献选站法(算法2)对§4.1中的动态仿真场景选站定位。由图 2可知,本文提出的基于基站对WHDOP贡献基站选择方法,在多数情况下与遍历法的基站选择结果相同,即使出现差别,WHDOP的差值也很小。图 3给出两种算法在各个定位点执行一次基站选择算法所需要消耗的时间。可以看出,基于基站对WHDOP贡献的选站法(算法2)耗时远小于遍历法(算法1),单次耗时在2 ms左右。综合考虑系统的定位精度和实时性,基于基站对WHDOP贡献的基站选择方法优势明显。

|
图 2 算法2与算法1的WHDOP值与差值曲线 Fig. 2 The WHDOP values and difference curves of algoeithm 2 and algorithm 1 |
|
图 3 算法1与算法2基站选择耗时曲线 Fig. 3 Selection time curves of algoeithm 2 and algorithm 1 |
在伪卫星定位系统中,各个观测量的测距误差不同,因此需要根据实际情况选择效率高的基站选择算法。本文将WHDOP最优标准作为基站选择的依据,从分析各观测量测距误差的协方差开始,确定适用于伪卫星系统的加权矩阵;参考卫星导航中的方法,提出基于基站对WHDOP贡献的选站法。仿真结果表明,以WHDOP为依据选择基站,能够降低误差较大的观测值参与定位的可能性,在降低接收机计算量的同时提高定位的精度,动态、静态定位误差的平均值和标准差均小于采用HDOP选择定位基站和采用全部基站观测值定位的定位误差;基于基站对WHDOP贡献的基站选择方法,所选基站性能几乎与遍历法相同,而选站耗时有了明显改善。在本文仿真条件下,单次选站时间耗时2 ms,远小于遍历法0.5 s的选站时间,提高了系统定位的实时性,符合伪卫星系统工程应用的需求。
虽然文中提到的多路径效应预处理方法、结合工程实际应用、加高收发天线等措施能够有效地削弱多路径效应,将多路径误差控制在可接受的范围内,以保证本文算法的正确性,但是,这些方法都不能完全消除多路径效应。因此,在基站选择时考虑残留多路径误差带来的影响是后续研究的重点。
| [1] |
Blanco-Delgado N, Nunes F D. Satellite Selection Method for Multi-Constellation GNSS Using Convex Geometry[J]. IEEE Transactions on Vehicular Technology, 2010, 59(9): 4
(  0) 0) |
| [2] |
Bo X, Shao B. Satellite Selection Algorithm for Combined GPS-Galileo Navigation Receiver[C].International Conference on Autonomous Robots and Agents, IEEE, 2009
(  0) 0) |
| [3] |
Blanco-DelgadoN, Nunes F D, Seco-Granados G. Relation between GDOP and the Geometry of the Satellite Constellation[C]. International Conference on Localization and GNSS, IEEE, 2011
(  0) 0) |
| [4] |
王梦丽, 孙广富, 王飞雪, 等. 混合星座导航系统的加权几何精度因子分析[J]. 中国空间科学技术, 2007, 27(5): 50-56 (Wang Mengli, Sun Guangfu, Wang Feixue, et al. Weight Geometric Dilution of Precision's Analysis for Mixed Constellation Navigation System[J]. Chinese Space Science and Technology, 2007, 27(5): 50-56 DOI:10.3321/j.issn:1000-758X.2007.05.009)
(  0) 0) |
| [5] |
王玮, 刘宗玉, 谢荣荣. 伪卫星辅助的北斗定位系统的GDOP研究[J]. 空间科学学报, 2005(1): 57-62 (Wang Wei, Liu Zongyu, Xie Rongrong, et al. The Research on GDOP of PL-Aided Beidou Positioning System[J]. Chinese Journal of Space Science, 2005(1): 57-62 DOI:10.3969/j.issn.0254-6124.2005.01.009)
(  0) 0) |
| [6] |
Chen C S. Weighted Geometric Dilution of Precision Calculations with Matrix Multiplication[J]. Sensors, 2015, 15(1): 803 DOI:10.3390/s150100803
(  0) 0) |
| [7] |
蔡昌盛, 戴吾蛟, 匡翠林, 等. 单频GPS/GLONASS组合单点定位的精度评估[J]. 大地测量与地球动力学, 2011, 31(3): 85-89 (Cai Changsheng, Dai Wujiao, Kuang Cuilin, et al. Accuracy Assessment of Combined Single-Frequency GPS/GLONASS Single Point Positioning[J]. Journal of Geodesy and Geodynamics, 2011, 31(3): 85-89)
(  0) 0) |
| [8] |
Meng X, Roberts G W, Dodson A H, et al. Impact of GPS Satellite and Pseudolite Geometry on Structural Deformation Monitoring: Analytical and Empirical Studies[J]. Journal of Geodesy, 2004, 77(12): 809-822 DOI:10.1007/s00190-003-0357-y
(  0) 0) |
| [9] |
谢钢. GPS原理与接收机设计[M]. 北京: 电子工业出版社, 2009 (Xie Gang. Principles of GPS and Receiver Design[M]. Beijing: Publishing House of Electronics Industry, 2009)
(  0) 0) |
| [10] |
Cheong J W. Signal Processing and Collective Detection for Locata Positioning System[D]. The University of New South Wales, 2012 http://unsworks.unsw.edu.au/fapi/datastream/unsworks:10667/SOURCE01
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39

