2. 山东电力工程咨询院有限公司,济南市闵子骞路106号,250013;
3. 青岛海洋科学与技术试点国家实验室海洋矿产资源评价与探测技术功能实验室,青岛市福州路62号,266071
使用GPS系统获取载体速度具有全天候、全时段、精度高等优点,已经在航空重力测量、地震学、海洋科研及军事领域得到应用[1-3]。常用的GPS测速方法包括位置差分法[3]和多普勒测速法[4-11]。位置差分法是把接收机位置在前后历元之间求差分,其测速精度受限于GPS动态定位精度及载体的运动状态,解算的速度精度不高。多普勒测速法是基于严格的多普勒测速数学模型,使用多普勒观测值得到接收机的运动速度。根据作业模式的不同,多普勒测速可分为相对测速[4-5]和单站测速[6-11]。相对测速是至少使用两台接收机同步观测相同的卫星,确定两台接收机之间的相对速度,其速度精度较高,但难以在大范围或复杂地形中应用;单站测速是只使用一台接收机和卫星之间的多普勒观测值直接确定用户接收机在WGS84坐标中的绝对速度,其原理简单,但需要更精确的数学模型。目前,大多数的研究仅针对相对测速或单站测速中的一种,很少有研究对这两种测速模式的基本原理、误差对测速精度的影响以及两者的测速精度作详细对比分析。
本文首先介绍单站测速和相对测速的数学模型,然后从影响测速精度的误差角度分析两者的区别,最后分别使用静态数据和低动态数据对两种测速模式的精度进行比较。
1 GPS测速的基本原理 1.1 单站测速的基本原理GPS单站测速的观测方程为:
| $ \lambda D = \dot \rho + c{\dot t_u} - c{\dot t^j} + \dot T - \dot I + \dot \varepsilon $ | (1) |
式中,λ为载波波长,D为多普勒观测值,c为光速,
本文的随机模型如下:
| $ \omega = {\sin ^2}E $ | (2) |
式中,ω为多普勒观测值的权重,E为观测时刻卫星的高度角。理论上,当观测到4颗以上GPS卫星时,利用单历元最小二乘就能解算接收机的速度和接收机钟速。
1.2 相对测速的基本原理设基准站为r,流动站为u,则相对多普勒测速模式的站间单差方程为:
| $ \lambda \Delta D = \Delta \dot \rho + c\Delta {{\dot t}_u} + \Delta \dot T - \Delta \dot I + \Delta \varepsilon $ | (3) |
式中,Δ为流动站和基准站之间的单差,其他参数与式(1)相同。
站间单差观测方程消去了卫星钟速,当基准站处于静止状态时,即
GPS测速的误差主要分为3类,一是与卫星相关的误差,主要有卫星位置误差、卫星速度误差、卫星钟速误差、卫星天线相位中心误差和相对论效应;二是与信号传播相关的误差,分为电离层变化率、对流层变化率和多路径效应;三是与接收机相关的误差,包括接收机位置误差、接收机钟速误差、接收机天线相位中心误差和接收机噪声。
卫星和接收机的天线相位中心经模型改正后产生的误差可忽略;相对论效应产生的误差经公式改正之后对测速精度的影响很小;多路径效应和接收机噪声都属于随机噪声;此外,测速误差还包括相位缠绕、固体潮和海潮等,这3个误差对测速的影响可忽略。
波长乘以多普勒观测值表示的是卫星到接收机距离的变化率,本文以式(1)、式(3)作为基础,首先分析各误差对站星距离变化率的影响。
2.1 多普勒观测值误差多普勒观测值分为原始多普勒观测值和载波相位导出多普勒观测值。原始多普勒观测值是某一段时间间隔内多普勒频移的积分,噪声大小受接收机类型的影响,通常优于2 cm/s;载波相位导出多普勒观测值可以通过一阶中心差分法获取[3]:
| $ D = \left\{ {\begin{array}{*{20}{c}} {\int {{S(t)\rm{d}}t} , 原始多普勒值}\\ {\frac{{{\varphi _{t - \delta t}} - {\varphi _{t + \delta t}}}}{{2\delta t}}, 导出多普勒值} \end{array}} \right. $ | (4) |
式中,S(t)为多普勒频移[12],t为观测时刻,δt为采样间隔,φt-δt、φt+δt分别为t-δt和t+δt时刻的载波相位观测值。一般认为,GPS载波相位观测值误差为波长的1%左右,当采样间隔为1 s时,由误差传播率可得导出多普勒观测值的噪声对站星距离变化率的影响约为1.5 mm/s。
2.2 卫星位置误差卫星位置误差是指由星历得到的卫星位置与卫星真实位置之差,对式(1)求偏微分得到单站测速模式下卫星位置误差对站星距离变化率的影响:
| $ {\rm{d}}\dot \rho = - \frac{{{{\mathit{\boldsymbol{\dot r}}}_u} - {{\mathit{\boldsymbol{\dot r}}}^j}}}{{\rho _u^j}} \cdot {\rm{d}}{{\mathit{\boldsymbol{\dot r}}}^j} $ | (5) |
从式(5)可知,卫星的位置误差d
GPS系统MEO卫星轨道高度在20 000 km左右,运行速度约为3 km/s,广播星历精度为1~2 m[13],故卫星的位置误差对站星距离变化率的影响优于0.3 mm/s,小于导出多普勒观测值噪声的影响,远小于原始多普勒观测值噪声的影响。
对式(3)求偏微分得到相对测速模式下卫星位置误差对站星距离变化率的影响:
| $ {\rm{d}}\Delta \dot \rho = \frac{{{{\mathit{\boldsymbol{\dot r}}}^j}}}{{\rho _r^j}} \cdot {\rm{d}}{{\mathit{\boldsymbol{\dot r}}}^j} + \frac{{{{\mathit{\boldsymbol{\dot r}}}_u} - {{\mathit{\boldsymbol{\dot r}}}^j}}}{{\rho _u^j}} \cdot {\rm{d}}{{\mathit{\boldsymbol{\dot r}}}^j} $ | (6) |
其中,基准站r与卫星j之间的距离ρrj和流动站u与卫星j之间的距离ρuj接近,故
| $ {\rm{d}}\Delta \dot \rho = \frac{{{{\mathit{\boldsymbol{\dot r}}}_u} - {{\mathit{\boldsymbol{\dot r}}}_r}}}{{\rho _u^j}} \cdot {\rm{d}}{{\mathit{\boldsymbol{\dot r}}}^j} $ | (7) |
本文仅考虑载体低速运动的情况。低速载体速度
对式(1)求偏微分得到卫星速度误差对单站测速的影响:
| $ {\rm{d}}\dot \rho = \frac{{{{\mathit{\boldsymbol{\dot r}}}_u} - {{\mathit{\boldsymbol{\dot r}}}^j}}}{{\rho _u^j}} \cdot {\rm{d}}{{\mathit{\boldsymbol{\dot r}}}_u} $ | (8) |
由式(8)可知,卫星的速度误差通过站星距离的方向余弦作用于站星距离的变化率,使平差观测量L产生误差。
基于广播星历计算的GPS卫星速度精度优于1 mm/s[14],则卫星速度误差对站星距离变化率的影响小于1 mm/s。
同理,对式(3)求偏微分得到卫星速度误差对相对测速的影响:
| $ {\rm{d}}\Delta \dot \rho = - \frac{{{{\mathit{\boldsymbol{\dot r}}}_r} - {{\mathit{\boldsymbol{\dot r}}}^j}}}{{\rho _r^j}} \cdot {\rm{d}}{{\mathit{\boldsymbol{\dot r}}}^j} + \frac{{{{\mathit{\boldsymbol{\dot r}}}_u} - {{\mathit{\boldsymbol{\dot r}}}^j}}}{{\rho _u^j}} \cdot {\rm{d}}{{\mathit{\boldsymbol{\dot r}}}^j} $ | (9) |
在相对测速模式下,基准站到卫星的距离和流动站到卫星的距离近似相等,即ρuj≈ρrj,式(9)变为:
| $ {\rm{d}}\Delta \dot \rho = \frac{{{{\mathit{\boldsymbol{\dot r}}}_u} - {{\mathit{\boldsymbol{\dot r}}}_r}}}{{\rho _u^j}} \cdot {\rm{d}}{{\mathit{\boldsymbol{\dot r}}}^j} $ | (10) |
由式(10)可知,卫星的速度误差对站星距离变化率的影响取决于基线长度、站星之间的距离以及卫星的速度误差。当基线长度小于1 000 km,速度误差小于1 mm/s时,dΔ小于0.05 mm/s。
2.4 卫星的钟速误差卫星钟速误差对测速的影响主要体现在平差观测值中,对平差观测值求偏微分得
首先分析单站测速模式的情况。对式(1)求偏微分得到:
| $ {\rm{d}}\dot \rho = \frac{{{{\mathit{\boldsymbol{\dot r}}}_u} - {{\mathit{\boldsymbol{\dot r}}}^j}}}{{\rho _u^j}} \cdot {\rm{d}}{{\mathit{\boldsymbol{\dot r}}}_u} $ | (11) |
由式(11)可知,接收机的位置误差对站星距离变化率的影响与卫星位置误差的影响类似,都是通过系数作用于站星距离变化率,而且两者的系数绝对值相等。此外,接收机位置误差还通过站星方向余弦对设计矩阵产生影响。
当观测条件良好时,基于广播星历的GPS伪距单点定位精度优于10 m[16],MEO卫星轨道高度约为20 000 km,速度约为3 km/s,则接收机位置误差对站星距离变化率的影响优于1.5 mm/s,该误差对站星距离变化率的影响与导出多普勒观测值噪声的影响相近,低于原始多普勒观测值噪声的影响。
同理,在相对测速模式下,接收机的位置误差对站星距离变化率的影响为:
| $ {\rm{d}}\Delta \dot \rho = \frac{{ - {{\mathit{\boldsymbol{\dot r}}}^j}}}{{\rho _r^j}} \cdot {\rm{d}}{{\mathit{\boldsymbol{\dot r}}}_r} - \frac{{{{\mathit{\boldsymbol{\dot r}}}_u} - {{\mathit{\boldsymbol{\dot r}}}^j}}}{{\rho _u^j}} \cdot {\rm{d}}{{\mathit{\boldsymbol{\dot r}}}_u} $ | (12) |
与上文分析类似,本文仅考虑低速载体的运动情况,即-
| $ {\rm{d}}\Delta \dot \rho = - \frac{{{{\mathit{\boldsymbol{\dot r}}}^j}}}{{\rho _r^j}} \cdot {\rm{d}}\Delta \mathit{\boldsymbol{r}} $ | (13) |
由式(13)可知,站星距离变化率的大小取决于基线向量的精度、站星之间的距离和卫星的速度。当基准站的坐标精确已知,即dr=0,此时接收机位置误差对站星距离变化率的影响和单站模式相同,不再赘述。
2.6 对流层和电离层的变化率通常情况下对流层的变化十分缓慢,但Graas等[9]指出,对流层变化异常可对测速产生mm/s级误差。因此,为提高测速精度,需要对对流层变化率误差进行改正。对流层延迟误差与信号频率无关[17],常用的改正模型并没有给出对流层的变化率,本文基于UNB3M模型[18-19],利用一阶中心差分获取对流层的变化率。
电离层变化率主要使平差观测值产生误差,进而对测速精度产生影响。Graas等[9]认为,当电离层活动激烈时电离层变化率对测速产生的误差可达到mm/s级。为消除电离层的影响,在使用载波相位导出多普勒观测值进行解算时,先使用双频载波相位观测值构成消电离层组合,之后再使用一阶中心差分获取载波相位导出多普勒观测值;在使用原始多普勒观测值进行解算时,由于其噪声较大,不再进行电离层的改正。
对流层变化率和电离层误差经上述方法处理后,对测速精度的影响可以忽略。此外,从理论上分析,对流层和电离层变化率对相对测速精度的影响小于对单站测速精度的影响,主要因为电离层误差和对流层误差在空间上存在相关性,在相对测速中经基准站和流动站单差后只剩下站间残余误差,对测速精度产生影响。
由以上的分析可知,结合广播星历基于单站模式解算速度时,多普勒观测值噪声对测速影响最大,卫星速度误差和接收机位置误差对测速的影响为亚mm/s~mm/s级,卫星位置误差、钟速误差、经模型改正后的对流层和电离层变化率误差对测速影响可以忽略;基于相对模式解算速度时,多普勒观测值噪声对测速影响最大,而且观测噪声对相对测速的影响大于对单站测速的影响,卫星位置、卫星速度、对流层和电离层变化率等误差对相对测速的影响小于对单站测速的影响。
3 实验测试及结果分析结合广播星历,本文分别用静态数据和低动态数据分析比较单站测速和相对测速的精度。
3.1 静态实验在静态实验中,静态观测值取自2012-06-08欧洲GEOHALO实验[2]的RENON测站和REF6测站,2个测站相距约605 km,数据采样间隔为1 s。分别采用原始多普勒观测值和载波相位消电离层导出多普勒观测值求解接收机速度,并将其转换到站心地平坐标系NEU。由于接收机的速度真值为0,每个历元解算的接收机速度与真值进行比较,以评定单站测速和相对测速的精度。在单站测速模式下,直接解算REF6测站的速度;在相对测速模式下,以RENON测站为基准站,通过站间单差解算REF6测站的速度。
在静态环境下解算的速度误差包括没有模型化的误差、模型化后残余的误差、多普勒观测值噪声。由图 1~4及表 1可得单站测速的2个结论:
1) 东西方向速度误差最小,南北方向速度误差次之,垂直方向速度误差最大。采用原始多普勒观测值解算的速度,南北、东西、垂直方向误差极值绝对值都在cm/s级,南北、东西方向RMS值在亚cm/s级,垂直方向RMS为cm/s级;采用导出多普勒观测值解算的速度,南北方向和东西方向极值绝对值为亚cm/s级,垂直方向为cm/s级,3个方向的RMS都为mm级。
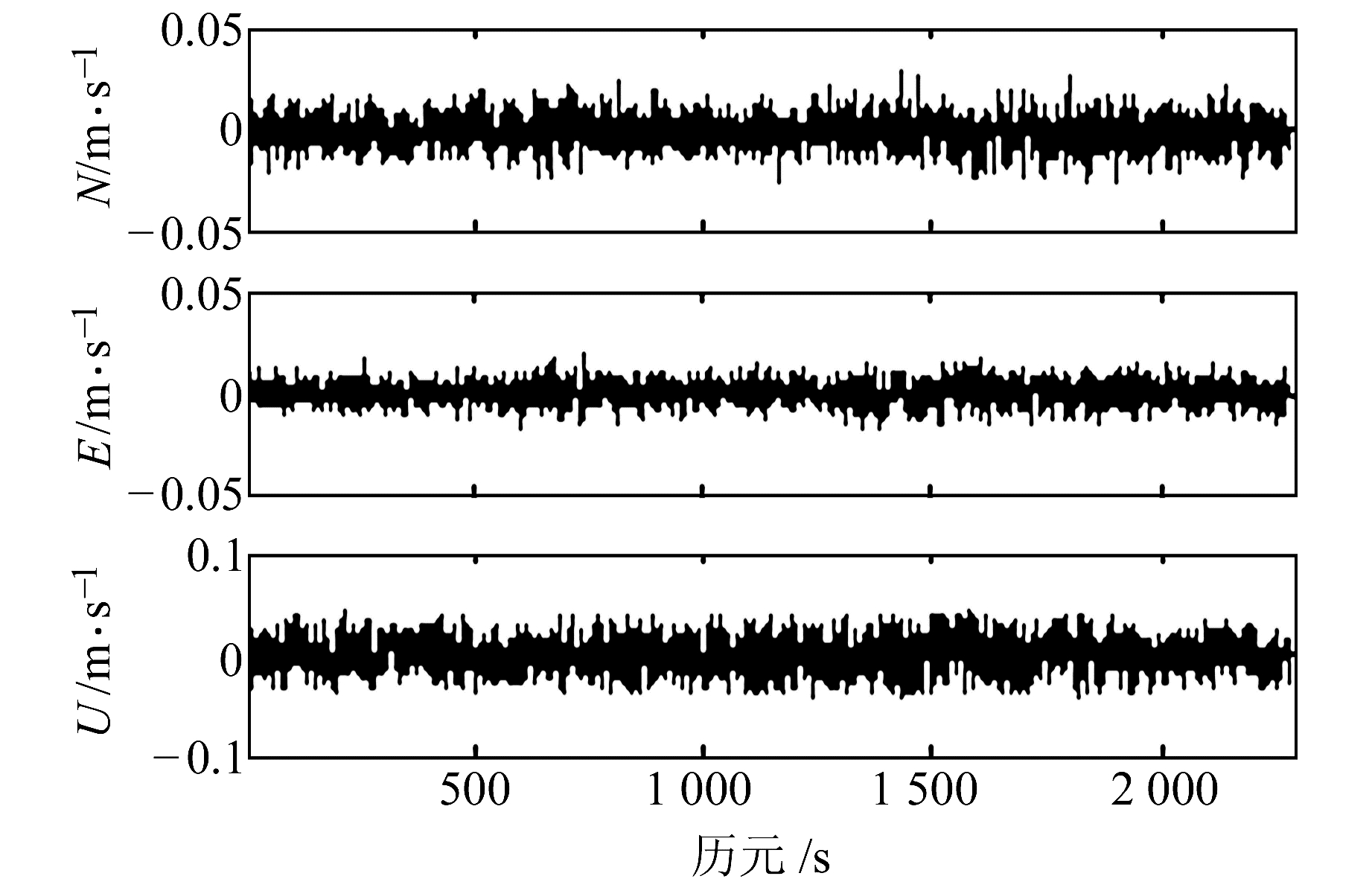
|
图 1 单站模式下原始多普勒观测值解算的速度 Fig. 1 The stand-alone velocity using raw Doppler |
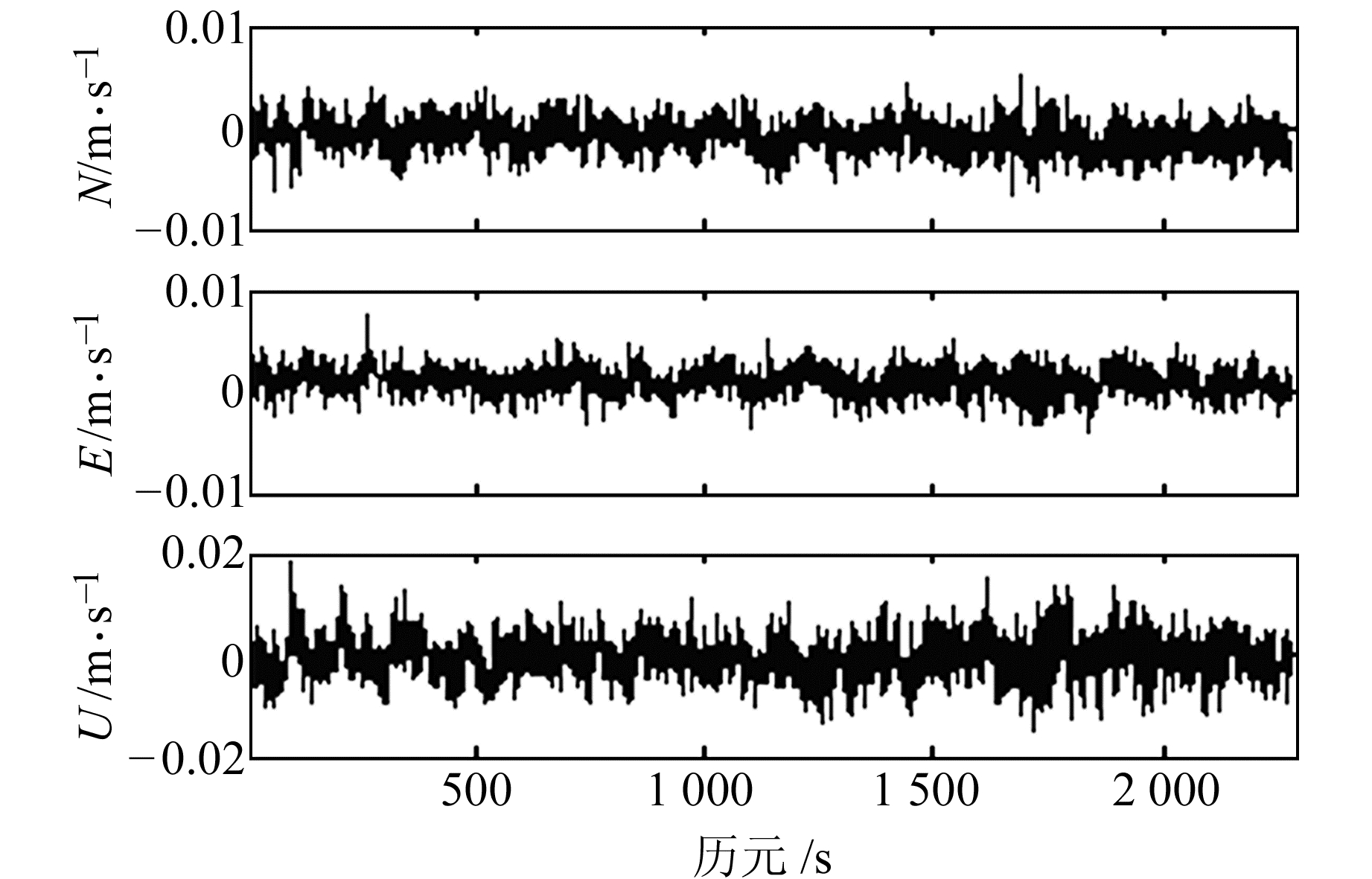
|
图 2 单站模式下导出多普勒观测值解算的速度 Fig. 2 The stand-alone velocity using phase-derived Doppler |
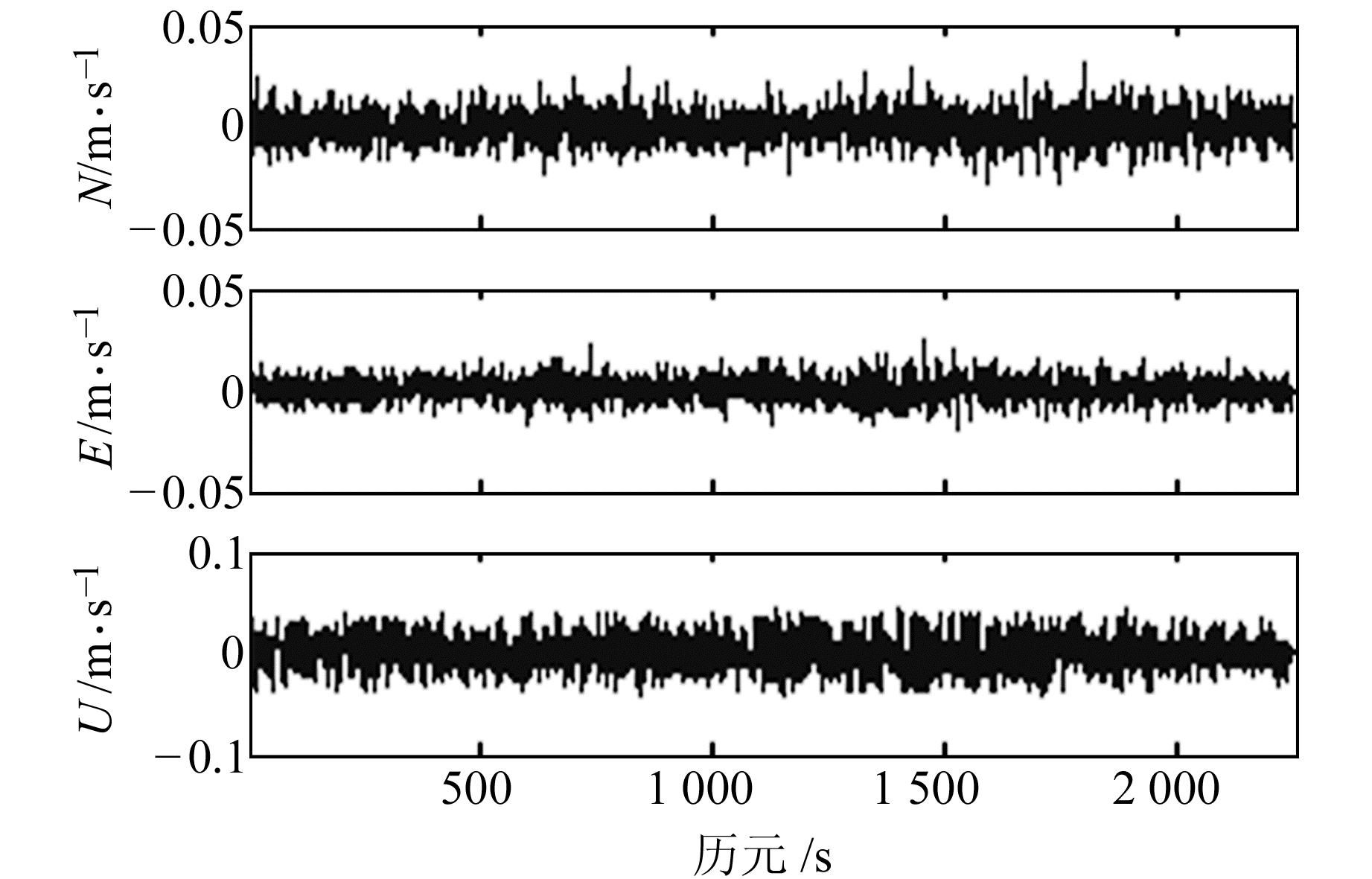
|
图 3 相对模式下原始多普勒观测值解算的速度 Fig. 3 The relative velocity using raw Doppler |
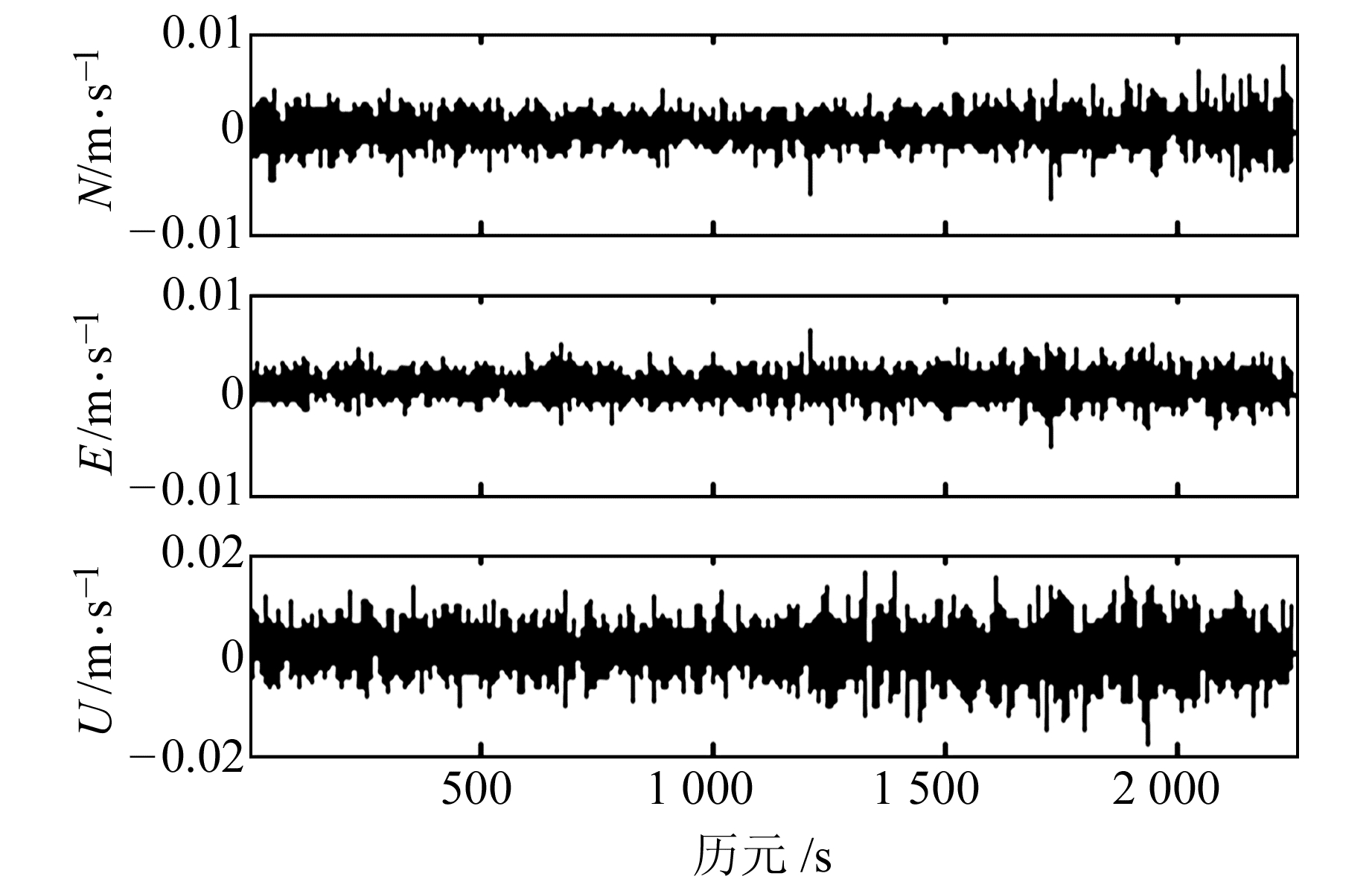
|
图 4 相对模式下导出多普勒观测值解算的速度 Fig. 4 The relative velocity using phase-derived Doppler |
|
|
表 1 静态环境下单站测速和相对测速结果统计 Tab. 1 Statistics of velocity estimation errors of stand-alone velocity and relative velocity in static environments |
2) 采用载波相位导出多普勒观测值得到的速度误差极值绝对值比原始多普勒观测值解算的结果3个方向都明显减小,且RMS值也小,主要原因是载波相位导出多普勒观测值比原始多普勒观测值的观测噪声小。
在相对测速模式下,以上2个结论也成立。将相对测速的结果与单站测速的结果进行对比,有如下结论:
1) 采用原始多普勒观测值测速时,相对测速的南北、东西、垂直方向极值绝对值比单站测速结果大,且RMS值也略大。主要原因是,在相对测速模式下,虽然卫星位置误差、卫星速度误差、电离层和对流层误差得到削弱,但它们对测速的影响都小于mm/s级,远小于原始观测噪声cm/s级的影响,同时采用站间单差观测方程解算进一步放大了观测噪声。
2) 当采用载波相位导出多普勒观测值测速时,相对测速3个方向的RMS值略优于单站测速的RMS值,主要因为载波相位导出多普勒观测值噪声对单站测速和相对测速的影响都为mm/s级,但卫星位置、速度和对流层、电离层等误差对相对测速的影响比对单站测速的影响小。
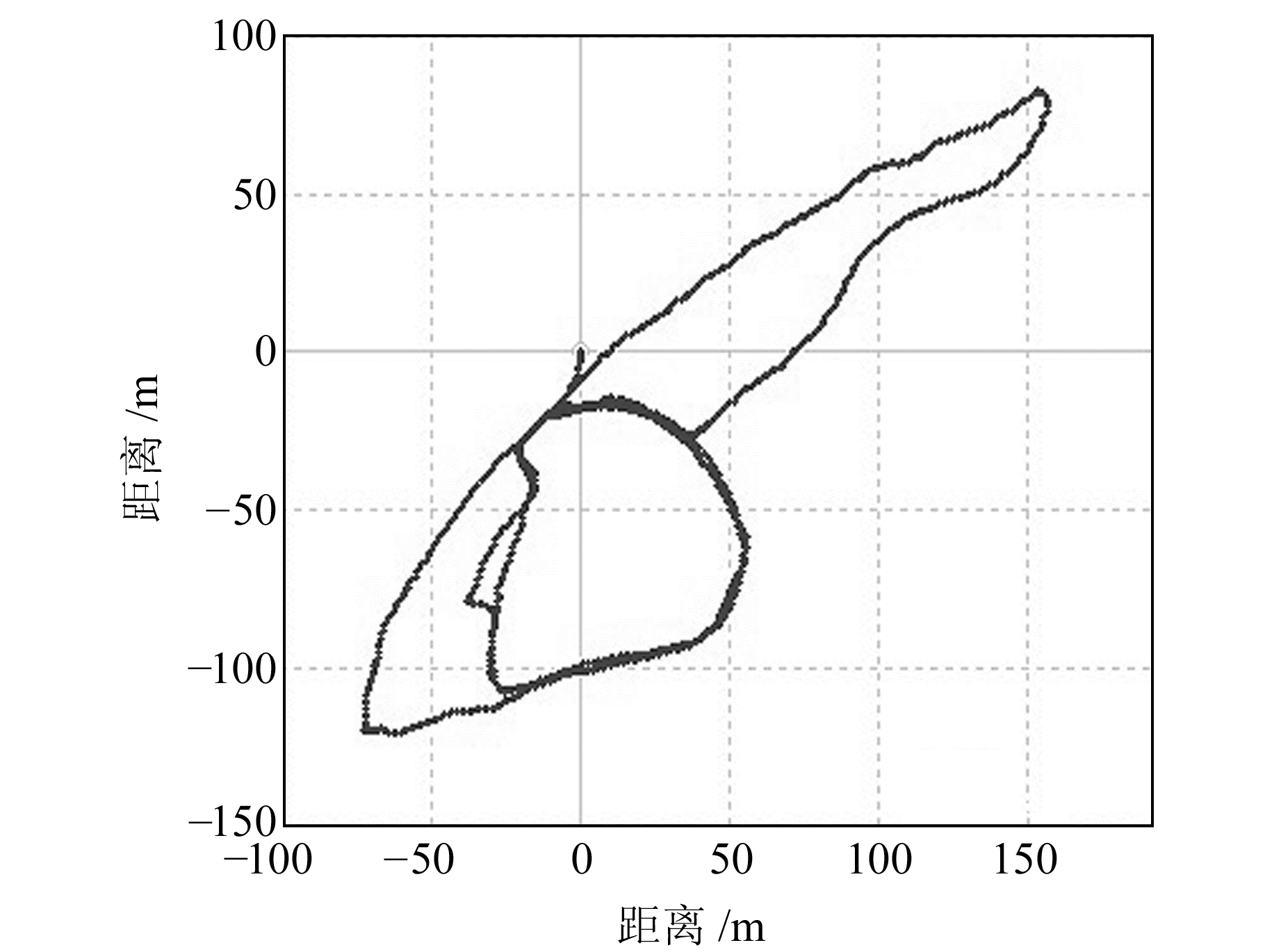
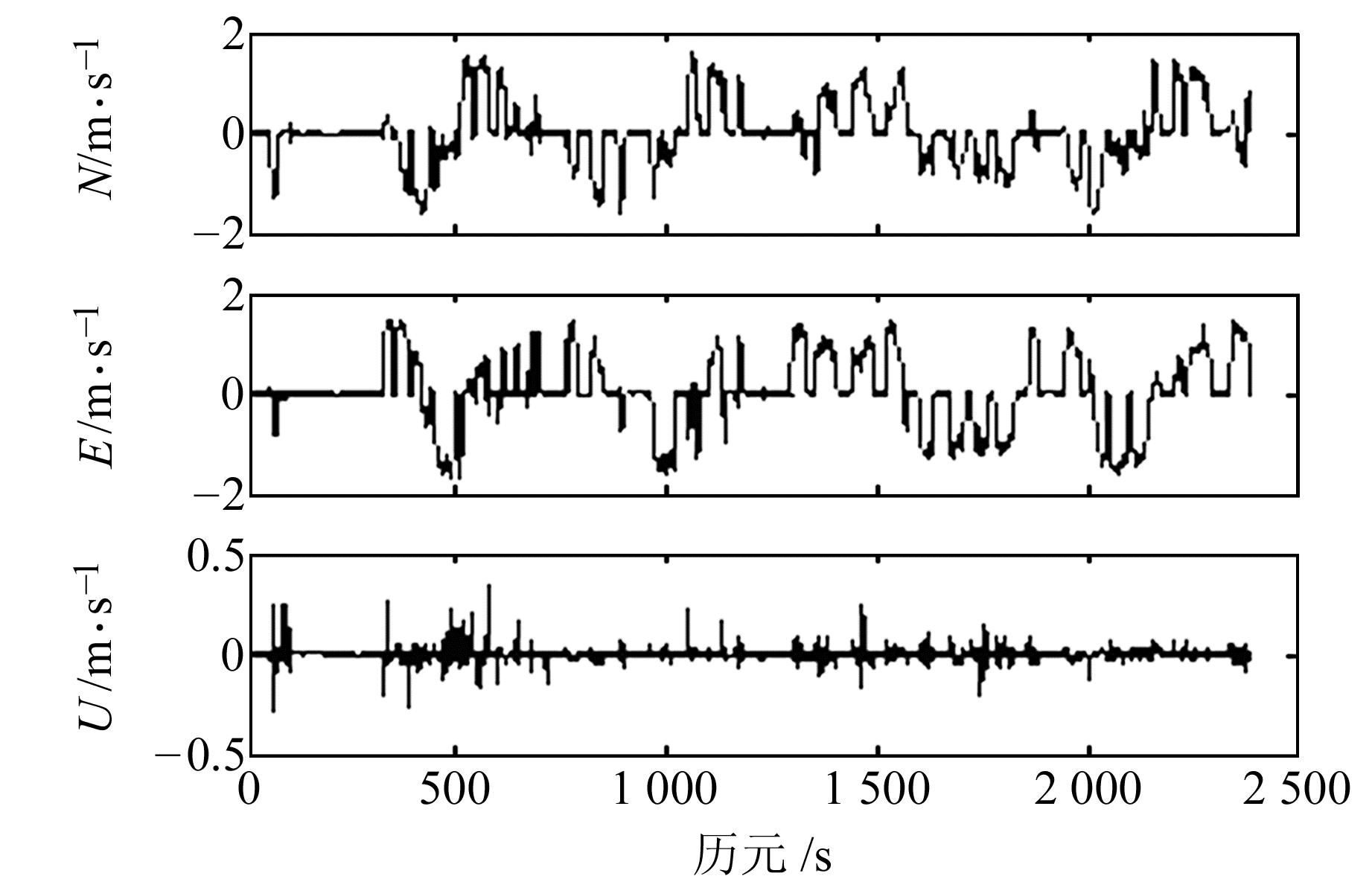
3.2 低动态实验低动态实验数据来自2015-08-02在中国石油大学(华东)南门唐岛湾滨海公园进行的外业实验,本次实验基准站接收机编号为2017,流动站接收机编号为1670,其中流动站固定在低动态载体上,数据采样间隔为1 s。限于实验条件,为评价低动态情况下测速的外符合精度,该实验首先采用RTK模式计算1670移动站的位置,然后使用一阶中心差分获得速度并将其作为真值,把相对测速模式和单站测速模式解算的流动站速度与真值作差,再进行统计分析。若实验条件允许,可以使用INS实测的速度作为真值相比较。图 5是本次动态实验载体的运动轨迹,图 6是采用RTK位置差分解算的载体速度。
|
图 5 载体的运动轨迹 Fig. 5 The running route of vehicle |
|
图 6 RTK位置差分解算的速度 Fig. 6 Velocity calculated by differencing RTK |
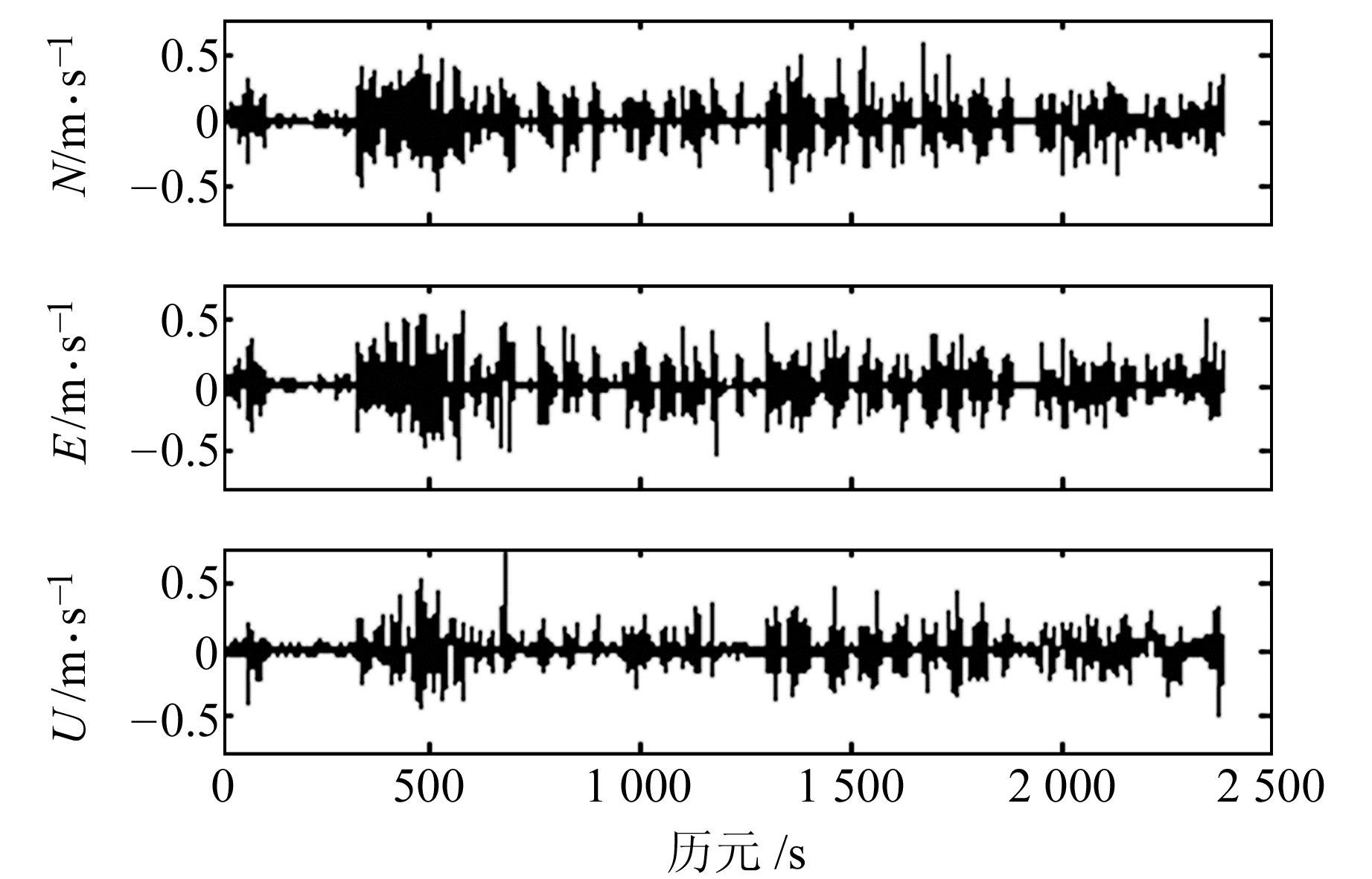
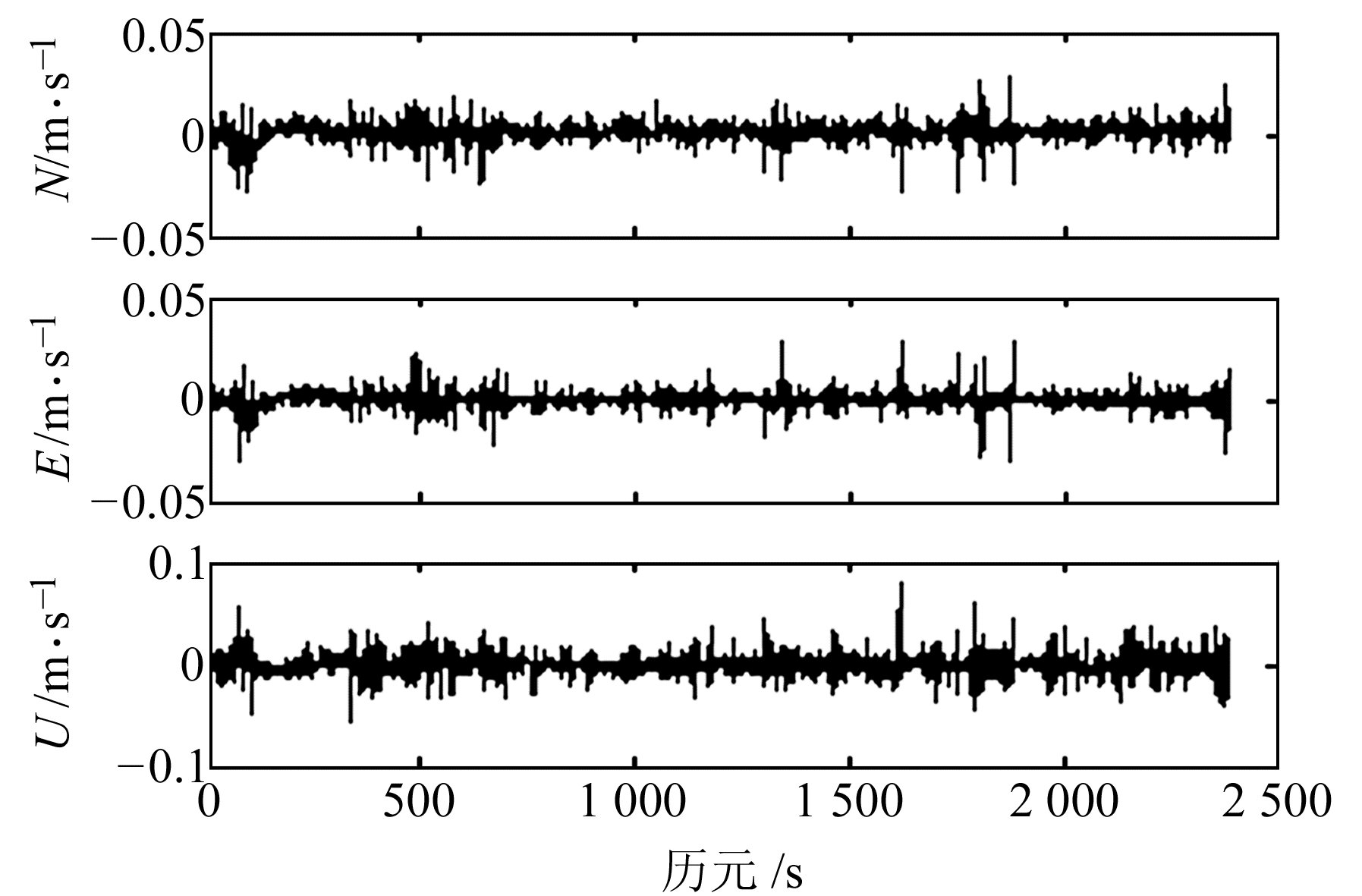
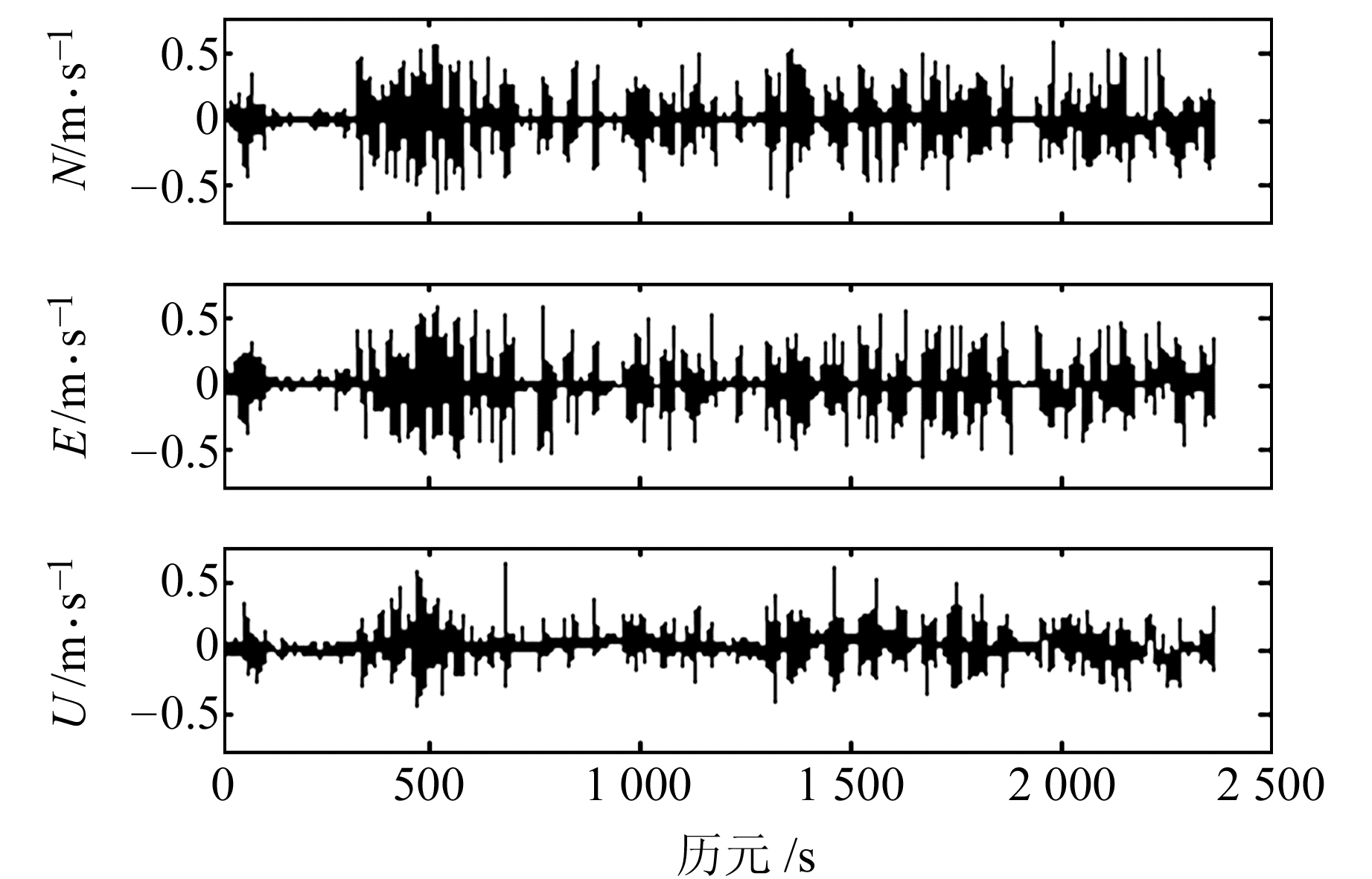
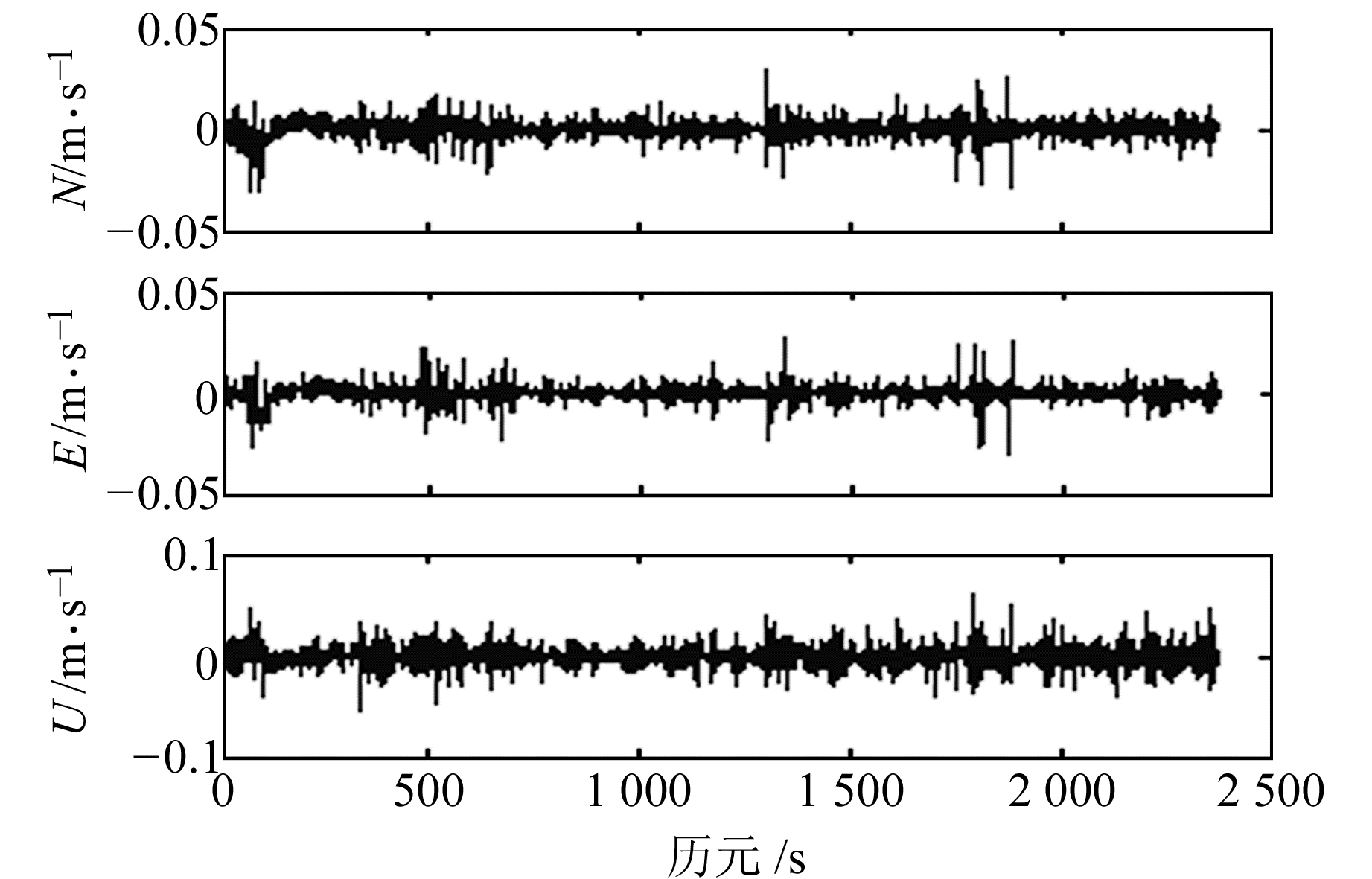
从图 7~10以及表 2可得,采用原始多普勒观测值解算的3个方向速度的RMS值都在dm级,而且单站测速的RMS值小于相对测速的RMS值;采用导出多普勒值获得的N、E方向速度的RMS值为亚cm/s~mm/s级,且相对测速RMS值略小于单站测速RMS值。
|
图 7 基于原始多普勒观测值的单站速度与RTK位置差分速度之差 Fig. 7 Difference between stand-alone velocity and RTK velocity using raw Doppler |
|
图 8 基于导出多普勒观测值的单站速度与RTK位置差分速度之差 Fig. 8 Difference between stand-alone velocity and RTK velocity using phase-derived Doppler |
|
图 9 基于原始多普勒观测值的相对测速与RTK位置差分速度之差 Fig. 9 Difference between relative velocity and RTK velocity using raw Doppler |
|
图 10 基于导出多普勒观测值的相对测速与RTK位置差分速度之差 Fig. 10 Difference between relative velocity and RTK velocity using phase-derive Doppler |
|
|
表 2 低动态环境下单站测速和相对测速结果统计 Tab. 2 Statistics of velocity estimation errors of stand-alone velocity and relative velocity in low-dynamic environments |
与静态环境相比,基于原始多普勒观测值的测速RMS值变大较明显,基于载波相位导出多普勒观测值的测速RMS值略微变大,主要有以下2个原因:
1) 利用原始多普勒观测值计算的是载体的瞬时速度,利用载波相位导出多普勒值获得的是平均速度,RTK位置差分法获取的也是平均速度。在静态环境下,以上3种方法的理论模型误差基本为零[20],但在动态环境下,RTK位置差分法和
基于载波相位导出多普勒值法都存在模型误差,且两者的模型误差近似。在本次实验中,把RTK位置差分法的平均速度作为真值,此时统计的误差实际是瞬时速度与平均速度之差以及不同方法获取的平均速度之差。
2) 载体在运动条件下,由于周围建筑物、树木等物体的遮挡,观测数据的噪声通常比静态条件下的大,这是基于载波相位导出多普勒观测值测速时RMS值变大的主要原因。
4 结语本文对比基于广播星历的GPS单站测速和相对测速的数学模型,主要分析卫星位置误差、卫星速度误差、卫星钟速误差、接收机位置误差、电离层和对流层变化率误差以及多普勒观测值噪声等误差对单站测速和相对测速精度的影响,其中多普勒观测值噪声对两种测速模式的精度影响最大。实验证明,在静态条件下2种测速模式的测速精度在相同水平,但使用原始多普勒观测值解算时,单站测速的RMS值比相对测速结果略小,主要是因为原始多普勒观测值噪声较大,使用站间单差解算放大了噪声;使用载波相位导出多普勒观测值解算时,相对测速的RMS值比单站测速结果略小。在低动态条件下采用高频载波相位导出多普勒观测值解算,单站测速和相对测速的精度都可以达到cm/s级,采用原始多普勒观测值解算两者的精度可达dm级。
由于实验条件所限,在动态条件下本文把RTK位置差分速度作为真值,但该真值只是历元间平均速度,以至于基于原始多普勒值解算的速度外符合精度不高,因此基于原始多普勒值解算的速度外符合精度还需要进一步验证。
| [1] |
刘腾, 欧吉坤, 袁运斌. 基于拟准检定的实时单站GPS提取同震速度的改进算法研究[J]. 地球物理学报, 2014, 57(8): 2 (Liu Teng, Ou Jikun, Yuan Yunbin. An Improved Algorithm of Real-Time Coseismic Velocity Extraction with a Stand-Alone GPS Receiver Based on QUAD Method[J]. Chinese J Geophys, 2014, 57(8): 2)
(  0) 0) |
| [2] |
He K F. GPS Kinematic Position and Velocity Determination for Airborne Gravimetry [D]. German Research Centre for Geosciences, 2015 http://www.ingentaconnect.com/content/doaj/10011595/2015/00000044/00000010/art00017
(  0) 0) |
| [3] |
范龙, 翟国君, 白鸽. 基于抗差最小二乘估计的载体速度计算方法[J]. 测绘学报, 2011(增1): 95-99 (Fan Long, Zhai Guojun, Bai Ge. Calculating the Carrier Velocity Based on Robust Least Square Estimation[J]. Acta Geodaetica et Cartographica Sinica, 2011(S1): 95-99)
(  0) 0) |
| [4] |
Serrano L, Kim D, Langley R B. A Single GPS Receiver as a Real-Time, Accurate Velocity and Acceleration Sensor[C].The 17th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2004), Long Beach, USA, 2004
(  0) 0) |
| [5] |
何海波, 杨元喜, 孙中苗, 等. GPS多普勒频移测量速度模型与误差分析[J]. 测绘学院学报, 2003, 20(2): 79-82 (He Haibo, Yang Yuanxi, Sun Zhongmiao, et al. Mathematic Model and Error Analyses for Velocity Determination Using GPS Doppler Measurements[J]. Journal of Institute of Surveying and Maping, 2003, 20(2): 79-82 DOI:10.3969/j.issn.1673-6338.2003.02.001)
(  0) 0) |
| [6] |
Kuusniemi H, Lachapelle G, Takala J H. Position and Velocity Reliability Testing in Degraded GPS Signal Environments[J]. GPS Solutions, 2004, 8(4): 226-237 DOI:10.1007/s10291-004-0113-7
(  0) 0) |
| [7] |
王甫红, 张小红, 黄劲松. GPS单点测速的误差分析及精度评价[J]. 武汉大学学报:信息科学版, 2007, 11(6): 515-519 (Wang Fuhong, Zhang Xiaohong, Huang Jinsong. Error Analysis and Accuracy Assessment of GPS Absolute Velocity Determination with SA off[J]. Geomatics and Information Science of Wuhan University, 2007, 11(6): 515-519)
(  0) 0) |
| [8] |
郭爱智, 王勇, 刘根友, 等. 高频GPS实时单点测速误差分析[J]. 大地测量与地球动力学, 2013, 33(5): 34-38 (Guo Aizhi, Wang Yong, Liu Genyou, et al. Error Analysis of High-Rate GPS Data Real-Time Single-Point Velocity-Determination[J]. Journal Geodesy and Geodynamics, 2013, 33(5): 34-38)
(  0) 0) |
| [9] |
Graas F V, Soloviev A. Precise Velocity Estimation Using a Stand-Alone GPS Receiver[J]. Navigation, 2004, 51(4): 283-292 DOI:10.1002/j.2161-4296.2004.tb00359.x
(  0) 0) |
| [10] |
Zhang J.Precise Velocity and Acceleration Determination Using a Standalone GPS Receiver in Real Time[D].RMIT University, 2007
(  0) 0) |
| [11] |
Zhou Z, Shen Y, Li B. Stochastic Model of GPS Doppler: Evaluation, Modeling and Performance[J]. Lecture Notes in Electrical Engineering, 2012, 159: 395-406
(  0) 0) |
| [12] |
Zhou Z, Li B. Optimal Doppler-Aided Smoothing Strategy for GNSS Navigation[J]. GPS Solutions, 2016, 21(1): 1-14
(  0) 0) |
| [13] |
Montenbruck O, Steigenberger P, Hauschild A. Broadcast Versus Precise Ephemerides: A Multi-GPS Perspective[J]. GPS Solutions, 2014, 19(2): 321-333
(  0) 0) |
| [14] |
Serrano L, Kim D, Langley R B, et al. A GPS Velocity Sensor: How Accurate Can It Be?-A First Look[C].ION NTM, 2004
(  0) 0) |
| [15] |
黄观文. GPS星载原子钟质量评价及精密钟差算法研究[D].西安: 长安大学, 2012 (Huang Guanwen. Research on Algorithms of Precise Clock Offset and Quality Evaluation of GNSS Satellite Clock[D]. Xi'an: Chang'an University, 2012) http://d.wanfangdata.com.cn/Thesis/D308081
(  0) 0) |
| [16] |
唐卫明, 徐坤, 金蕾, 等. 北斗/GPS组合伪距单点定位性能测试和分析[J]. 武汉大学学报:信息科学版, 2015, 40(4): 529-533 (Tang Weiming, Xu Kun, Jin Lei, et al. Test and Analysis of Beidou/GPS Combined Pseudo-Range Point Positioning Performance[J]. Geomatics and Information Science of Wuhan University, 2015, 40(4): 529-533)
(  0) 0) |
| [17] |
范士杰, 刘焱雄, 高兴国, 等. 海上动态GPS大气可降水量信息反演[J]. 中国石油大学学报:自然科学版, 2012, 36(3): 84-87 (Fan Shijie, Liu Yanxiong, Gao Xingguo, et al. Retrieval Method of Marine Kinematic GPS Precipitable Water Vapor[J]. Journal of China University of Petroleum:Edition of Natural Science, 2012, 36(3): 84-87)
(  0) 0) |
| [18] |
陈猛, 陈俊平, 胡丛玮. 对流层模型评估及其在GNSS精密单点定位中的应用[J]. 大地测量与地球动力学, 2016, 36(3): 229-234 (Chen Meng, Chen Junping, Hu Congwei. Performance Evaluation of Troposphere Models and Application in GNSS Precise Point Positioning[J]. Journal of Geodesy and Geodynamics, 2016, 36(3): 229-234)
(  0) 0) |
| [19] |
Leandro R F, Langley R B, Santos M C. UNB3m_pack: A Neutral Atmosphere Delay Package for Radiometric Space Techniques[J]. GPS Solutions, 2007, 12(1): 65-70
(  0) 0) |
| [20] |
王潜心.机载GPS动态定位定速与定姿理论研究及软件开发[D].长沙: 中南大学, 2011 (Wang Qianxin. Research of Airborne GPS Kinematic Position Velocity and Attitude Determination and Software Development[D]. Changsha: Central South University, 2011) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1918117
(  0) 0) |
2. Shandong Electric Power Engineering Consulting Institute Co Ltd, 106 Minziqian Road, Jinan 250013, China;
3. Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, 62 Fuzhou Road, Qingdao 266071, China
 2019, Vol. 39
2019, Vol. 39

