2. 沈阳市勘察测绘研究院,沈阳市南三好街1号,110004;
3. 新疆维吾尔自治区测绘科学研究院,乌鲁木齐市中山路462号,830002
速度场模型是现代测绘基准体系得以持续应用的支撑,是板块运动、地壳形变等研究领域不可或缺的基础数据。速度场建模的方法分为欧拉矢量法和拟合法[1]。欧拉矢量法将板块看作绕地心进行定轴运动的刚体,利用板块内观测点位置变化计算其欧拉矢量。魏子卿等[2]和任雅奇[3]基于局域欧拉矢量法建立了全国速度场模型,实用价值较大,但欧拉矢量法对参与建模点的数量和分布要求较高。与欧拉矢量法相比,恰当的拟合法更能体现块体的细微变化,主要包括多面函数法、Kriging插值法、最小二乘配置法等。刘经南等[4-5]利用多面函数法模拟大陆水平运动,但多面函数节点的选择、核函数的确定需要大量的实验。于亮等[6]基于Kriging插值构建了中国大陆速度场模型。最小二乘配置能较好地解决速度场中倾向性、随机性因素问题[7-8],但初始观测噪声协方差矩阵与信号协方差矩阵关系的不合理会导致速度场模型拟合精度降低。Helmert方差分量估计[9]可以对各类观测量的验前方差和协方差进行估计,并依此定权,协调观测噪声与信号协方差矩阵的不合理关系。作为速度场建模的基础,测站时间序列获取常用的方法是双差定位,但双差定位需要解算大型矩阵,计算效率低。相对于双差定位,精密单点定位模型简单,不受基准站选择、网平差策略的影响,获得的速度信息与双差定位基本一致[10]。本文以新疆陆态网络2011~2017年连续运行基准站为例,利用GNSSer精密单点定位方式解算测站坐标时间序列,提高GNSS数据处理的效率,并利用自适应最小二乘配置,构建新疆水平速度场格网模型。
1 GNSSer软件GNSSer是一款高精度GNSS解算软件,可进行精密单点定位和双差定位,支持GPS、GLONASS、BDS和Galileo系统的解算,软件基于多核并行和分布式网络技术设计,运算能力强[11-13]。为检验软件精密单点定位精度和计算速度,软件设计者选取全球420个IGS站2013-12-29~2014-01-31的观测数据,以IGS公布的单日解坐标为真值,进行差值统计,主要参数设置见表 1。结果表明,利用GNSSer进行精密单点定位时,非差浮点解水平方向精度优于3 mm,高程方向精度优于6 mm,且多天解精度稳定性较好。此外,多节点多核环境下的非差计算效率得到较大提高。
|
|
表 1 主要参数设置 Tab. 1 Main parameters setting |
给定历元ti(i=1, 2, …, n)的测站北方向坐标N的单日解Ni和方差σi2。假定测站坐标随时间呈线性变化,且伴有周期为1 a和0.5 a的周期性波动,忽略坐标误差之间的相关性,坐标N用以下函数表示:
| $ \begin{array}{c} {N_i} = a\Delta t + b + {A_{\rm{1}}}{\rm{sin}}(2{\rm{ \mathsf{ π} }}\Delta t) + {B_1}\cos (2{\rm{ \mathsf{ π} }}\Delta t) + \\ {A_2}\sin (4{\rm{ \mathsf{ π} }}\Delta t) + {B_2}\cos (4{\rm{ \mathsf{ π} }}\Delta t) \end{array} $ | (1) |
式中,Δt=t-t0,t为观测历元,t0为参考历元;a为一次项系数,代表测站线性速度,b为一次项截距,代表t0历元的坐标;A1、B1为年周期项的振幅,A2、B2为0.5 a周期项的振幅。
根据坐标N的单日解序列,利用抗差最小二乘估计式(1)中的6个未知参数。在抗差估计过程中,权因子ω采用IGG[14]等价权函数确定,观测值初始权矩阵依据测站单日解的方差σi2确定。同理,根据东方向坐标E的单日解序列,可获得相应未知参数的抗差最小二乘估值。至此,可获得各个测站北方向和东方向的线性速度。
3 格网速度场建模最小二乘配置将观测量分为固定效应和随机效应2个部分,能较好地解决具有倾向性、随机性因素的问题[9]。以各个测站的线性速度作为观测值,构建如下模型:
| $ \mathit{\boldsymbol{L}} = \mathit{\boldsymbol{AX}} + \mathit{\boldsymbol{BS}} + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }} $ | (2) |
式中,L为观测向量,表示测站N方向或者E方向的速度;A为确定性参数系数矩阵;B为随机效应部分系数矩阵,一般为单位矩阵;X为确定性参数向量;S为信号向量,表示测站速度中含有的系统误差;Δ为观测误差向量。
最小二乘配置的估计值和信号值分别为:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\hat X}} = {{({\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_L^{ - 1}\mathit{\boldsymbol{A}})}^{{\rm{ - }}1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_L^{{\rm{ - }}1}\mathit{\boldsymbol{L}}}\\ {\mathit{\boldsymbol{\hat S}} = {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_S}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_L^{{\rm{ - }}1}(\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{A\hat X}})}\\ {\mathit{\boldsymbol{\hat S'}} = {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{S'S}}\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_S^{ - 1}\mathit{\boldsymbol{\hat S}}} \end{array}} \right. $ | (3) |
式中,ΣL=BΣSBT+ΣΔ,ΣS为已知点间信号的协方差矩阵,ΣS′S是已知点信号与未知点信号的互协方差矩阵,ΣΔ为观测噪声的协方差矩阵。
由于初始观测噪声协方差矩阵与信号协方差矩阵关系不合理,会导致拟合的速度场精度降低。因此,引入Helmert方差分量估计构造自适应因子,通过调整自适应因子平衡观测噪声协方差矩阵与信号协方差矩阵之间的关系。自适应因子定义为[9]:
| $ \alpha = \frac{{\hat \sigma _{0S}^{2(i)}}}{{\hat \sigma _{0\Delta }^{2(i)}}} $ | (4) |
式中,
| $ \mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{\Delta} ^{^{(i + 1)}} = \frac{1}{\alpha }\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{\Delta} ^{^{(i)}} $ | (5) |
将新确定的协方差矩阵代入式(3),重新解算倾向部分和随机信号部分,直至自适应因子α趋近于1.0。
4 实验及分析 4.1 数据处理及分析数据来源于新疆陆态网络2011~2017年26个连续运行基准站,站点分布见图 1。利用GNSSer精密单点定位方式计算测站单日解坐标。为了检验GNSSer精密单点定位结果用于测站速度计算的精度,利用GAMIT/GLOBK解算同样的数据,并联合全球H文件进行平差。在解算过程中,主要参数设置及改正项参照表 1。

|
图 1 新疆连续运行基准站站点分布 Fig. 1 The distribution of continuously operating reference stations in Xinjiang |
表 2为GAMIT和GNSSer解算采样率为30 s的单天观测文件的用时情况。计算机配置为:型号Think Centre M8400t,操作系统Suse Linux11.4 Server/Windows7,运行内存16.0 GB,处理器Intel Core i7-3770@3.40 GHz。由表 2可知,相对于GAMIT,GNSSer解算效率提升约6倍。
|
|
表 2 GAMIT、GNSSer解算用时统计 Tab. 2 The time spending on solving observation files by GAMIT and GNSSer |
在获得测站单日解的基础上,依据单日解方差、线性拟合后残差与3σ的关系剔除粗差解,通过滤波[15-16]减弱时间序列中的共模误差,拟合各个测站水平方向上的线性速度。以GAMIT/GLOBK为参考,比较GNSSer获得的测站速度差异。图 2为N方向和E方向速度的差值。统计上述测站的速度差值,结果见表 3。

|
图 2 GNSSer与GAMIT/GLOBK获得的测站速度在N、E方向的差值 Fig. 2 Station velocity difference obtained by GNSSer and GAMIT/GLOBK in the N and E direction |
|
|
表 3 测站速度差值统计 Tab. 3 Statistics of station velocity difference |
从图 2可以看出,2种方式获得的测站速度在N方向和E方向的差异均在1.5 mm/a以内。结合表 3可知,N、E方向上RMS分别为0.2 mm/a、0.5 mm/a,比较稳定。由此可知,2种方式计算得到的测站速度差异很小,精密单点定位与双差计算拟合得到的速度信息基本一致,GNSSer精密单点定位结果可用于测站速度计算。
4.2 新疆速度场利用各个测站的速度,基于以下3种方案建立新疆格网速度场模型:1)多面函数(HAR);2)最小二乘配置(CO);3)自适应最小二乘配置(HCO)。3种方案拟合的速度场格网模型精度见表 4(单位mm/a)。
|
|
表 4 速度场格网模型精度 Tab. 4 The precision of velocity field grid model |
从表 4可以看出,3种方案均能较好地建立水平方向速度场模型。相对于多面函数方法,最小二乘配置能够估计测站速度中的随机信号,提高速度场建模精度。相对于最小二乘配置,自适应最小二乘配置利用Helmert方差分量估计方法构造自适应因子,调整观测噪声与信号协方差矩阵的关系,可进一步提高速度场模型精度。
利用自适应最小二乘配置建立新疆1°×1°水平速度场格网模型(图 3),然后双线性内插参与建模的测站速度,并与测站时间序列拟合得到的速度作差(图 4)。
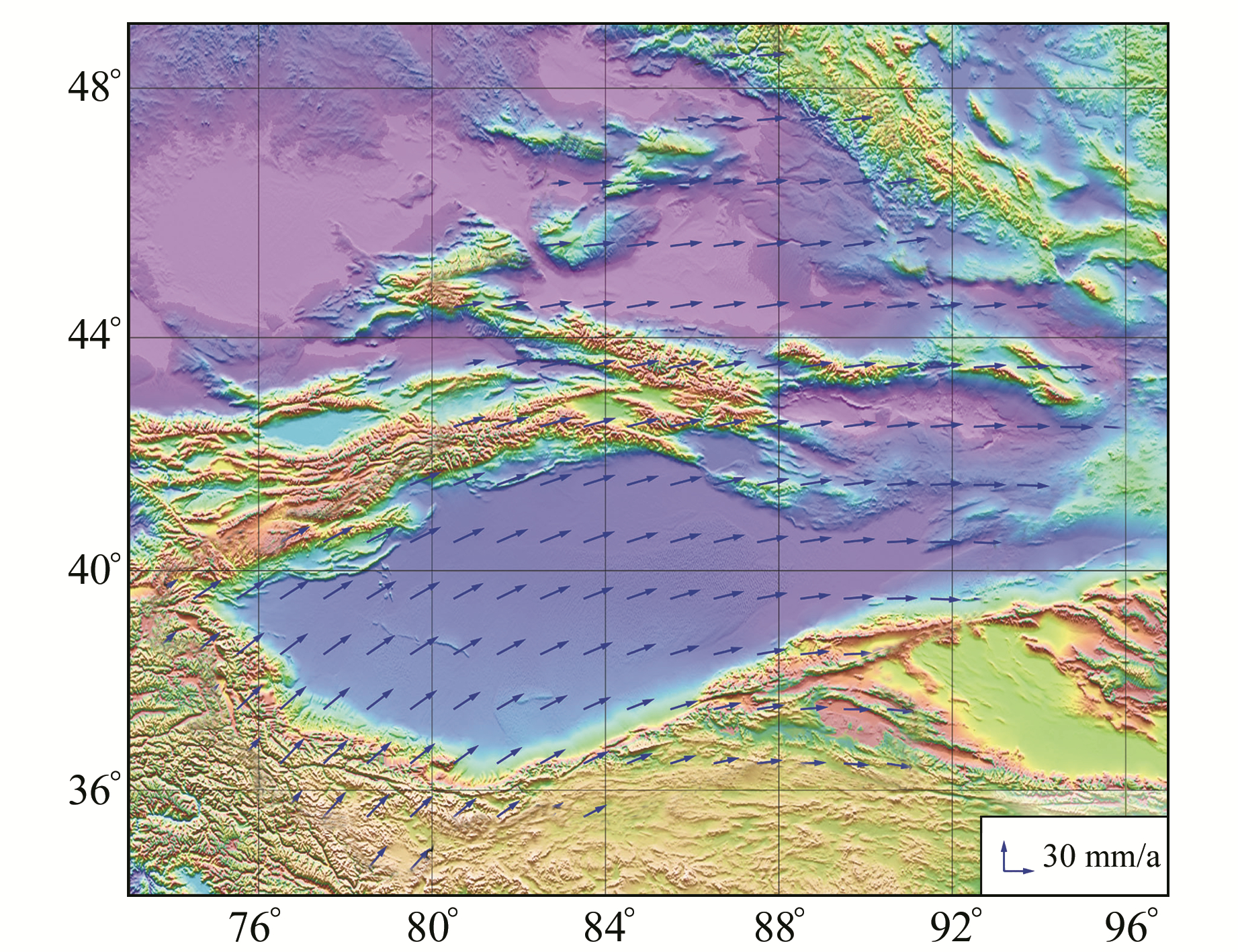
|
图 3 新疆水平方向格网速度场模型 Fig. 3 Horizontal velocity field grid model in Xinjiang |
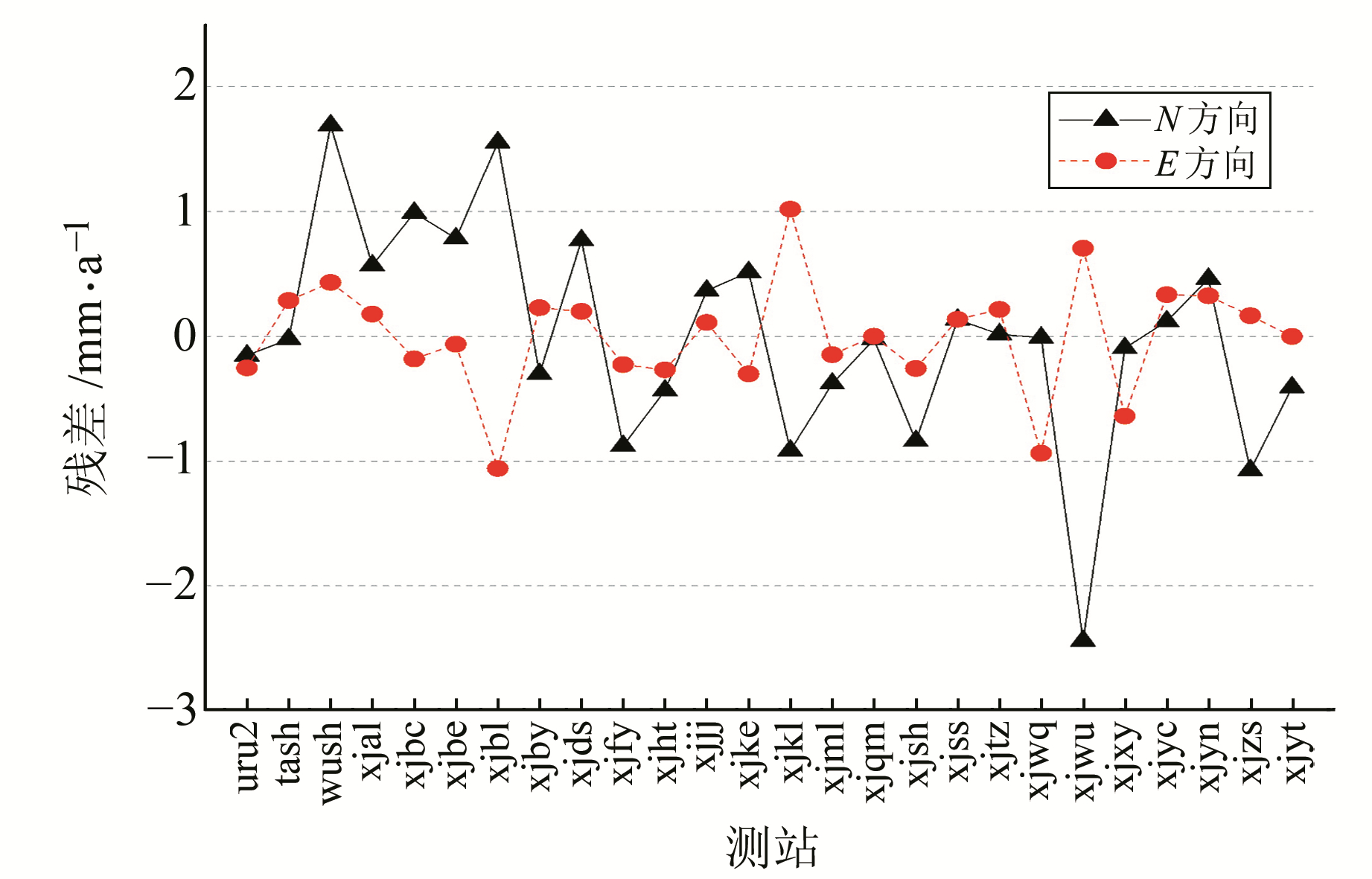
|
图 4 测站拟合残差 Fig. 4 Station fitting residuals |
从图 3可以看出,新疆存在明显的北偏东运动趋势,速度大小为27.1~34.8 mm/a。在新疆西南部,其主要运动方向为北偏东;而在新疆北部及东部,其运动方向主要为东向。在整个新疆,自西南向东北,形成顺时针旋转的运动趋势,这与曾安敏等[5]的结论一致。
从图 4可以看出,N、E方向测站的模型拟合残差基本在2 mm/a以内,且波动性较小,证明了自适应最小二乘配置用于速度场建模的稳定性。
5 结语利用GNSSer精密单点定位方式解算新疆陆态网络连续运行基准站站点坐标,获取测站速度,以GAMIT/GLOBK解算结果作为参照对象进行对比。结果表明,利用GNSSer获得的测站速度在N、E方向精度分别为0.2 mm/a、0.5 mm/a,与GAMIT/GLOBK计算结果在同一量级,结果可信。对于长时间大型网的数据解算,可以充分发挥GNSSer并行计算和分布式计算的优势,提高速度场计算效率。充分发挥自适应最小二乘配置能较好地解决倾向性、随机性因素问题以及观测噪声与信号协方差不协调问题的优势,建立了N、E方向上的精度分别为0.8 mm/a、0.5 mm/a的新疆水平方向格网速度场。速度场模型表明,新疆具有顺时针旋转的运动趋势,大小为27.1~34.8 mm/a。
新疆速度场模型的建立为新疆高精度坐标框架的可持续应用提供了支撑,为板块运动、地壳形变监测研究、丝绸之路经济带核心区建设等提供了重要的参考资料,具有重要意义。
致谢: 感谢信息工程大学地理空间信息学院提供GNSSer软件,感谢陆态网络中心提供GNSS实验观测数据。
| [1] |
刘经南, 姚宜斌, 施闯, 等. 多面函数拟合法及其在建立中国地壳平面运动速度场模型中的应用研究[J]. 武汉大学学报:信息科学版, 2001, 26(6): 500-503 (Liu Jingnan, Yao Yibin, Shi Chuang, et al. Hardy Function Interpolation and Its Applications to the Establishment of Crustal Movement Speed Field[J]. Geomatics and Information Science of Wuhan University, 2001, 26(6): 500-503)
(  0) 0) |
| [2] |
魏子卿, 刘光明, 吴富梅. 2000中国大地坐标系:中国大陆速度场[J]. 测绘学报, 2011, 40(4): 403-410 (Wei Ziqing, Liu Guangming, Wu Fumei. China Geodetic Coordinate System 2000: Velocity Field in Mainland China[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 403-410)
(  0) 0) |
| [3] |
任雅奇.基于GPS数据的中国地壳运动速度场模型的建立[D].郑州: 信息工程大学, 2012 (Ren Yaqi. Establishment of Chinese Crustal Movement Velocity Model Based on the GPS Data[D]. Zhengzhou: Information Engineering University, 2012) http://cdmd.cnki.com.cn/Article/CDMD-90005-1013161053.htm
(  0) 0) |
| [4] |
刘经南, 姚宜斌, 施闯. 中国地壳运动整体速度场模型的建立方法研究[J]. 武汉大学学报:信息科学版, 2002, 27(4): 331-336 (Liu Jingnan, Yao Yibin, Shi Chuang. Method for Establishing the Speed Field Model of Crustal Movement in China[J]. Geomatics and Information Science of Wuhan University, 2002, 27(4): 331-336)
(  0) 0) |
| [5] |
曾安敏, 秦显平, 刘光明, 等. 中国大陆水平运动速度场的多面函数模型[J]. 武汉大学学报:信息科学版, 2013, 38(4): 394-398 (Zeng Anmin, Qin Xianping, Liu Guangming, et al. Hardy Multi-Quadric Fitting Model of Chinese Mainland Horizontal Crustal Movement[J]. Geomatics and Information Science of Wuhan University, 2013, 38(4): 394-398)
(  0) 0) |
| [6] |
于亮, 朱璇, 陈永祥, 等. 基于CMONOC建立和评估中国大陆地壳运动速度场模型[J]. 大地测量与地球动力学, 2017, 37(7): 704-708 (Yu Liang, Zhu Xuan, Chen Yongxiang, et al. The Building and Estimating of Velocity Field in Mainland China Based on CMONOC[J]. Journal of Geodesy and Geodynamics, 2017, 37(7): 704-708)
(  0) 0) |
| [7] |
柴洪洲, 崔岳, 明锋. 最小二乘配置方法确定中国大陆主要块体运动模型[J]. 测绘学报, 2009, 38(1): 61-65 (Chai Hongzhou, Cui Yue, Ming Feng. The Determination of Chinese Mainland Crustal Movement Model Using Least-Squares Collocation[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(1): 61-65 DOI:10.3321/j.issn:1001-1595.2009.01.011)
(  0) 0) |
| [8] |
江在森, 刘经南. 应用最小二乘配置建立地壳运动速度场与应变场的方法[J]. 地球物理学报, 2010, 53(5): 1 109-1 117 (Jiang Zaisen, Liu Jingnan. The Method in Establishing Strain Field and Velocity Field of Crustal Movement Using Least Squares Collocation[J]. Chinese Journal of Geophysics, 2010, 53(5): 1 109-1 117)
(  0) 0) |
| [9] |
张菊清, 张亮. 基于Helmert方差分量估计的拟合推估法及其在地图数字化误差纠正中的应用[J]. 测绘通报, 2008(2): 35-37 (Zhang Juqing, Zhang Liang. The Collocation Method Based on Helmert Variance Component Estimation and Its Application in Errors Correction of Digital Maps[J]. Bulletin of Surveying and Mapping, 2008(2): 35-37)
(  0) 0) |
| [10] |
程义军, 程广义, 刘威. 精密单点定位在GNSS区域网监测中的应用[J]. 大地测量与地球动力学, 2015, 35(1): 97-99 (Cheng Yijun, Cheng Guangyi, Liu Wei. Application of Precise Point Positioning on GNSS Regional Network Monitoring[J]. Journal of Geodesy and Geodynamics, 2015, 35(1): 97-99)
(  0) 0) |
| [11] |
崔阳, 吕志平, 张友阳, 等. 一种GNSS大网数据快速高效处理策略[J]. 大地测量与地球动力学, 2015, 35(3): 383-386 (Cui Yang, Lü Zhiping, Zhang Youyang, et al. Study of Cycle-Slip Detection Using BDS Triple-Frequency Geometry-Free and Ionosphere-Free Combination[J]. Journal of Geodesy and Geodynamics, 2015, 35(3): 383-386)
(  0) 0) |
| [12] |
陈正生, 吕志平, 崔阳, 等. 大规模GNSS数据的分布式处理与实现[J]. 武汉大学学报:信息科学版, 2015, 40(3): 384-389 (Chen Zhengsheng, Lü Zhiping, Cui Yang, et al. Implementation of Distributed Computing with Large-Scale GNSS Data[J]. Geomatics and Information Science of Wuhan University, 2015, 40(3): 384-389)
(  0) 0) |
| [13] |
李林阳.大规模GNSS网云计算方法与实践[D].郑州: 信息工程大学, 2016 (Li Linyang. Cloud Computing Method and Practice of Large Scale GNSS Network[D].Zhengzhou: Information Engineering University, 2016)
(  0) 0) |
| [14] |
杨元喜. 抗差估计理论及其应用[M]. 北京: 八一出版社, 1993 (Yang Yuanxi. Robust Estimation and Its Applications in Geodesy[M]. Beijing: Bayi Publishing House, 1993)
(  0) 0) |
| [15] |
Dong D, Fang P, Bock Y, et al. Spatiotemporal Filtering Using Principal Component Analysis and Karhunen-Loeve Expansion Approaches for Regional GPS Network Analysis[J]. Journal of Geophysical Research: Solid Earth, 2006, 111(B3)
(  0) 0) |
| [16] |
Wdowinski S, Bock Y, Zhang J, et al. Southern California Permanent GPS Geodetic Array: Spatial Filtering of Daily Positions for Estimating Coseismic and Postseismic Displacements Induced by the 1992 Landers Earthquake[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B8): 18 057-18 070 DOI:10.1029/97JB01378
(  0) 0) |
2. Shenyang Geotechnical Investigation and Research Institute, 1 South-Sanhao Street, Shenyang 110004, China;
3. Academy of Surveying and Mapping of Xinjiang Uygur Autonomous Region, 462 Zhongshan Road, Urumqi 830002, China
 2019, Vol. 39
2019, Vol. 39

