2. 中国测绘科学研究院,北京市莲花池西路28号,100830
整体经验模式分解(EEMD)是基于经验模式分解(EMD)存在模态混叠现象进行改进的方法[1],虽解决了EMD的一些缺陷,但仍存在分解后信噪比降低、模态混叠等问题[2-4]。
本文提出基于K均值聚类EEMD的CORS高程时间序列信号分析方法,添加正负白噪声提高信噪比,引入统计学中的K均值(K-means)对CORS高程时间序列进行聚类分析[5-6],并用2个CORS站连续多年的高程时间序列验证该方法的适用性。
1 改进的EEMD算法 1.1 基于正负白噪声的EEMD算法 1.1.1 EEMD算法EEMD的基本思路是在分解前将原始序列信号加入高斯白噪声生成新的待分解信号,对多个本征模态函数(IMF)分量进行平均处理,进而保留具有物理意义的IMF分量,同时消除加入的噪声。对CORS高程序列添加白噪声:
| $ {X_i}\left( t \right) = X\left( t \right) + {w_i}\left( t \right) $ | (1) |
式中,下标i为第i次EMD分解。该过程的循环次数可以取100,噪声与信号的标准差之比可以取0.1、0.2、0.4等[1, 4]。经过EMD生成一系列IMF分量,由于每次随机生成的白噪声都是不同的,可以通过重复分解过程得到信号多次分解的分量,将对应相同分解尺度的分量取平均值,得到最终信号分解的分量。采用式(2)判定产生IMF分量的个数:
| $ {n_{{\rm{max}}}} = {\rm{fix}}({\rm{lo}}{{\rm{g}}_2}N) - 2 $ | (2) |
式中,N为CORS高程时间序列的长度。
1.1.2 添加正负白噪声白噪声的加入会影响原始时间序列的纯净程度,污染原始信号。分解后的IMF分量中存在消除不完全的噪声,使时间序列的信噪比降低,导致信号的重构误差较大。因此采用在加入白噪声的过程中随机添加正、负白噪声[2]:
| $ {X_i}\left( t \right) = X\left( t \right) + {\left( { - 1} \right)^q}{d_0}{w_i}\left( t \right) $ | (3) |
式中,X(t)为原始CORS高程时间序列,d0为白噪声的幅值标准差。当q为奇数时,加入负的白噪声;当q为偶数时,加入正的白噪声,保证所加入的正白噪声总和与负白噪声总和相等。
1.2 K均值聚类算法K均值聚类分析的EEMD算法采用划分聚类方法中的K均值算法,将每次EEMD循环产生的IMF分量进行聚类分析,保留聚类个数多的一类,取该类中IMF分量的平均值作为分解产生的IMF。K均值聚类算法首先要确定常数K为最终分类的数量。令K从2到某个固定值,在每个K值上运行数次K聚类,避免局部最优解,计算K的轮廓系数,最后选取轮廓系数最大的值对应的K作为最终分类个数[7]。轮廓系数计算方法为:
| $ S\left( \mathit{\boldsymbol{i}} \right) = \frac{{o\left( \mathit{\boldsymbol{i}} \right) - p\left( \mathit{\boldsymbol{i}} \right)}}{{{\rm{max}}\left[ {p\left( \mathit{\boldsymbol{i}} \right), o\left( \mathit{\boldsymbol{i}} \right)} \right]}} $ | (4) |
式中,o(i)为i向量到所有它属类中其他点的距离,p(i)为i向量到所有非本身所在类的点的平均距离。
常数K确定后,选取初始点作为质心,分成几类则选择几个初始点。通过计算每个样本与质心的距离来判定样本之间的相似程度,将样本点归到最相似的类中,完成一次聚类。继续计算新生成的各个类的质心,重复计算距离直到质心不再改变,最终确定按所需分成的各类中的样本和各个类的质心。算法本质就是不断更新质心向量,寻找目标函数最小化的过程,通常采用式(5)计算最小方差函数[8]:
| $ E({a_1}, \ldots , {a_k}) = \frac{1}{n}\sum\limits_{i = 1}^k {\sum\limits_{m \in {a_i}} {{{\left\| {{m_j} - {a_i}} \right\|}^2}} } $ | (5) |
式中,m为每一个元素,ai为第i个聚类中心,k为聚类中心数目。
本文采用欧氏距离作为判断2个IMF分量相似程度大小的依据,距离越小则相似度越高,距离越大则相似度越低。对于一个N维数组,数组A(A1, A2, A3,…,An)与数组B(B1, B2, B3,…,Bn)之间的欧氏距离为:
| $\begin{array}{*{20}{c}} {{D_{(A, B)}} = }\\ {\sqrt {{{({A_1} - {B_1})}^2} + {{({A_2} - {B_2})}^2} + \ldots + {{({A_n} - {B_n})}^2}} } \end{array} $ | (6) |
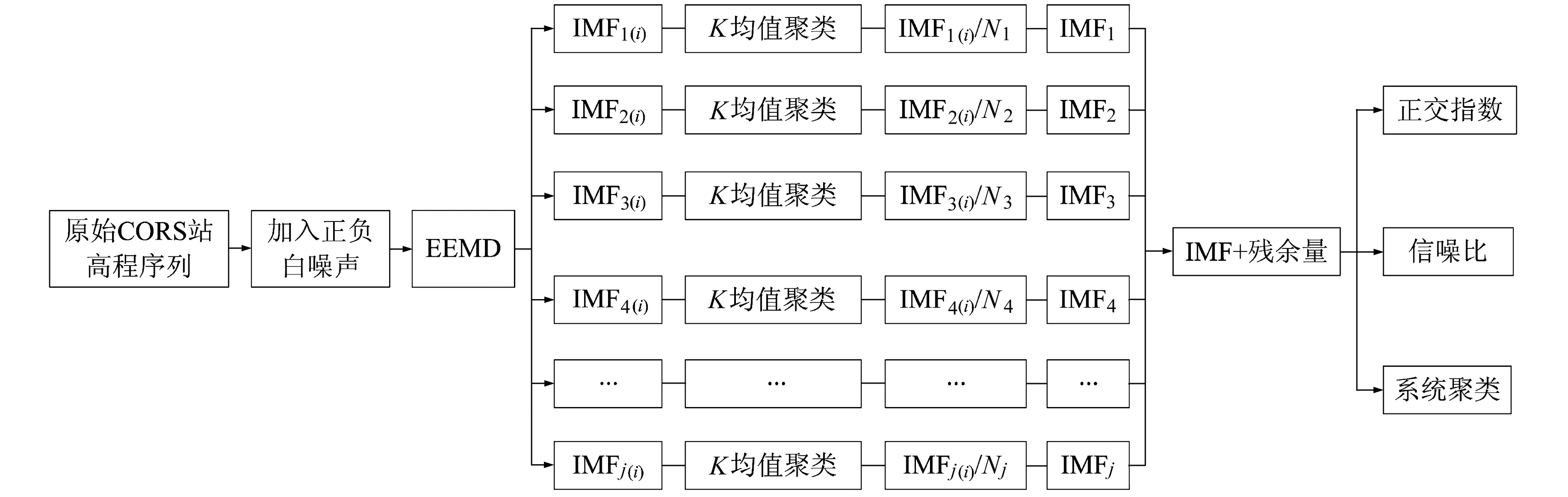
针对EEMD算法100次迭代计算产生的IMF分量矩阵进行K均值聚类分析,选取IMF聚类中成员多的那类作为IMF的合集。聚类过程如下:1)对IMF1进行聚类,选取第1个和第50个矩阵作为起始聚类中心,计算剩余矩阵分别到这2个聚类中心的欧氏距离;2)根据距离的大小将各个矩阵中的IMF1聚类到距离最近的一类中,取各类的平均值作为新的聚类中心,再次计算各矩阵到聚类中心的距离;3)不断重复这个过程,直到聚类中心不再发生改变;4)选取IMF1聚类完成后对象多的一类,继续将IMF各个其他分量和最后的残余项按照上述过程进行K均值聚类,得到每个IMF分量和残余项的聚类结果;5)对聚类结果分别取平均值,即为K均值EEMD分解的各个IMF分量和残余项(图 1)。
|
图 1 K均值聚类EEMD流程 Fig. 1 K-means clustering EEMD flowchart |
正交指数(IO)指标是衡量模式分解结果精度的标准[9],正交指数越小分解得到的精度越高。在CORS高程时间序列分解的结果中,正交指数可以用来衡量任意2个IMF分量:
| $ {{\rm{IO}}_{ij}} = \sum\limits_t {\frac{{{C_i}\left( t \right){C_j}\left( t \right)}}{{{C}_i^2\left( t \right) + {C}_j^2\left( t \right)}}} $ | (7) |
式中,IOij为第i个和第j个IMF分量之间所求得的正交指数,Ci为对应的IMF分量。
CORS高程时间序列信号的信噪比(SNR)计算的是EEMD加入白噪声分解前后的去噪效果,计算公式为:
| $ {\rm{SNR}} = 10{\rm{lo}}{{\rm{g}}_{10}}\left( {\frac{{E\left[ {y{{\left( n \right)}^2}} \right]}}{{E\{ {{\left[ {y\left( n \right) - \hat y\left( n \right)} \right]}^2}\} }}} \right) $ | (8) |
式中,y(n)为没有加入白噪声的原始高程序列,
方差贡献率是各个IMF分量的方差与分解得到的IMF分量方差之和的百分比,IMF分量方差贡献率的大小反映该频率的分解信号在整个序列信号运动能量中的贡献大小[10],统计任一IMF分量的方差公式为:
| $\rho _x^2 = E({x^2}) - {E^2}\left( x \right) $ | (9) |
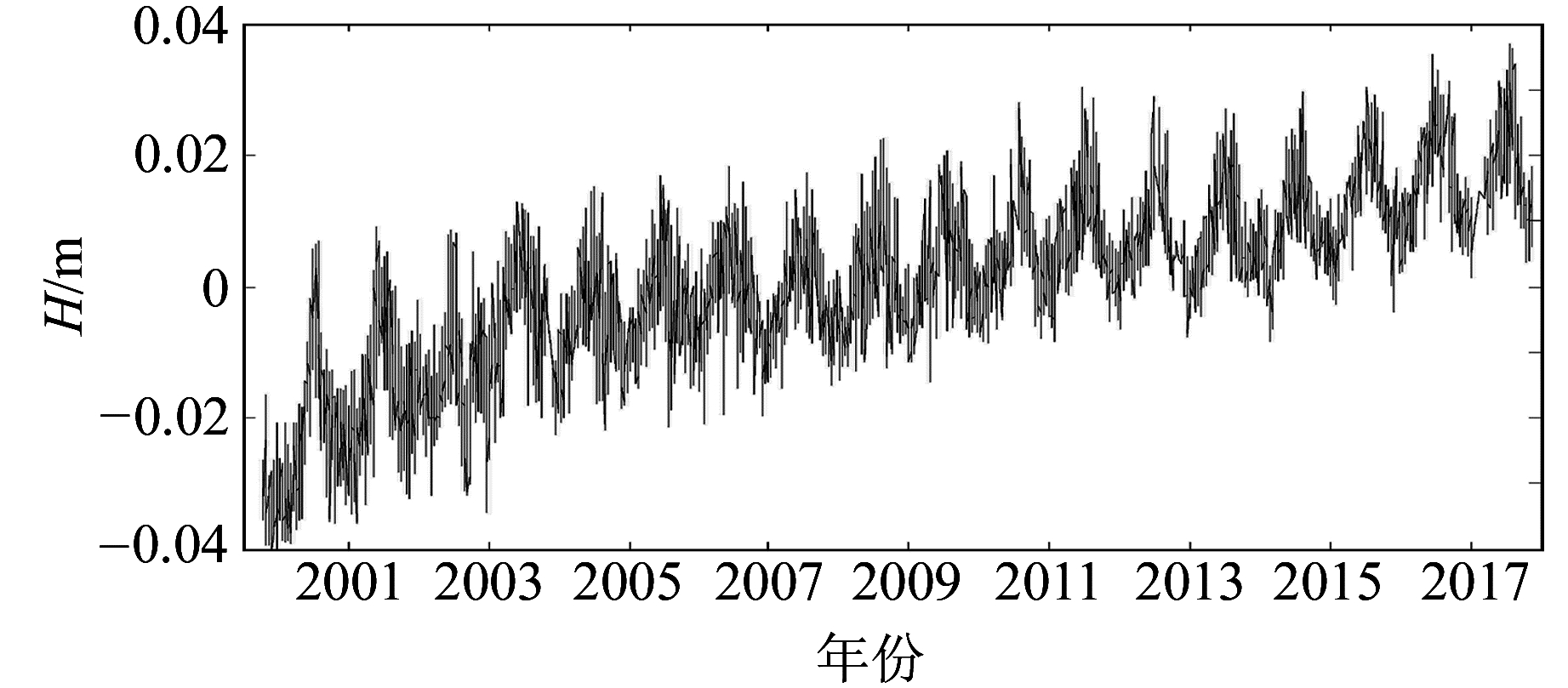
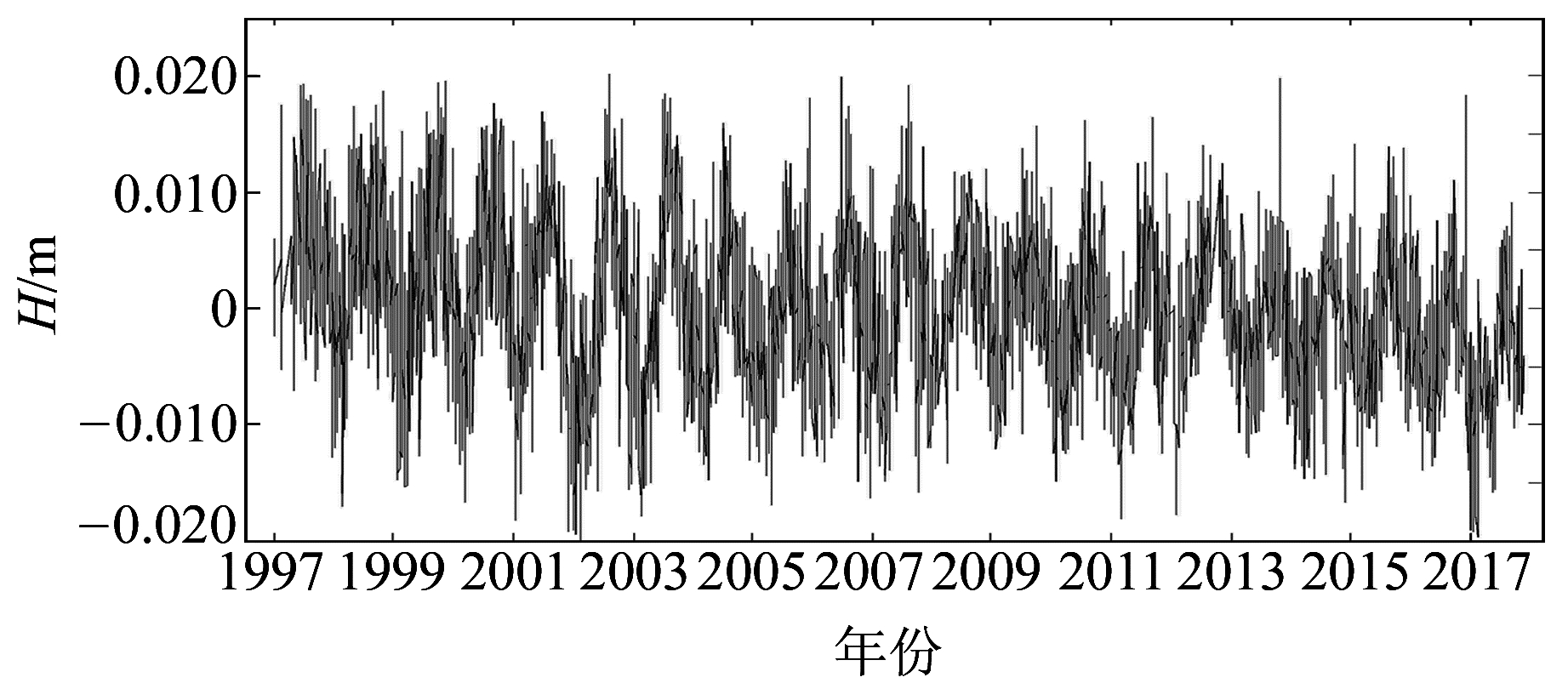
利用BJFS站和国外BOGO站近20 a的高程时间序列进行实验。实验数据来自SOPAC网站,已进行去常数处理,并利用3倍中误差法剔除粗差。图 2、图 3分别为BJFS站和BOGO站的原始高程时间序列,2个站分别进行EEMD和K均值聚类EEMD(K-EEMD)实验。
|
图 2 BJFS站原始高程序列 Fig. 2 Height time series of BJFS station |
|
图 3 BOGO站原始高程序列 Fig. 3 Height time series of BOGO station |
根据Wu等[1]的建议,EEMD迭代次数设置为100,噪声与信号标准差之比设置为0.1。李鹏[5]指出,K均值聚类分析的迭代终止条件一般是聚类中心点收敛或达到最大的迭代次数。本文实验发现,2个CORS站的聚类迭代次数均为12时聚类中心不再发生改变,即完成聚类过程。
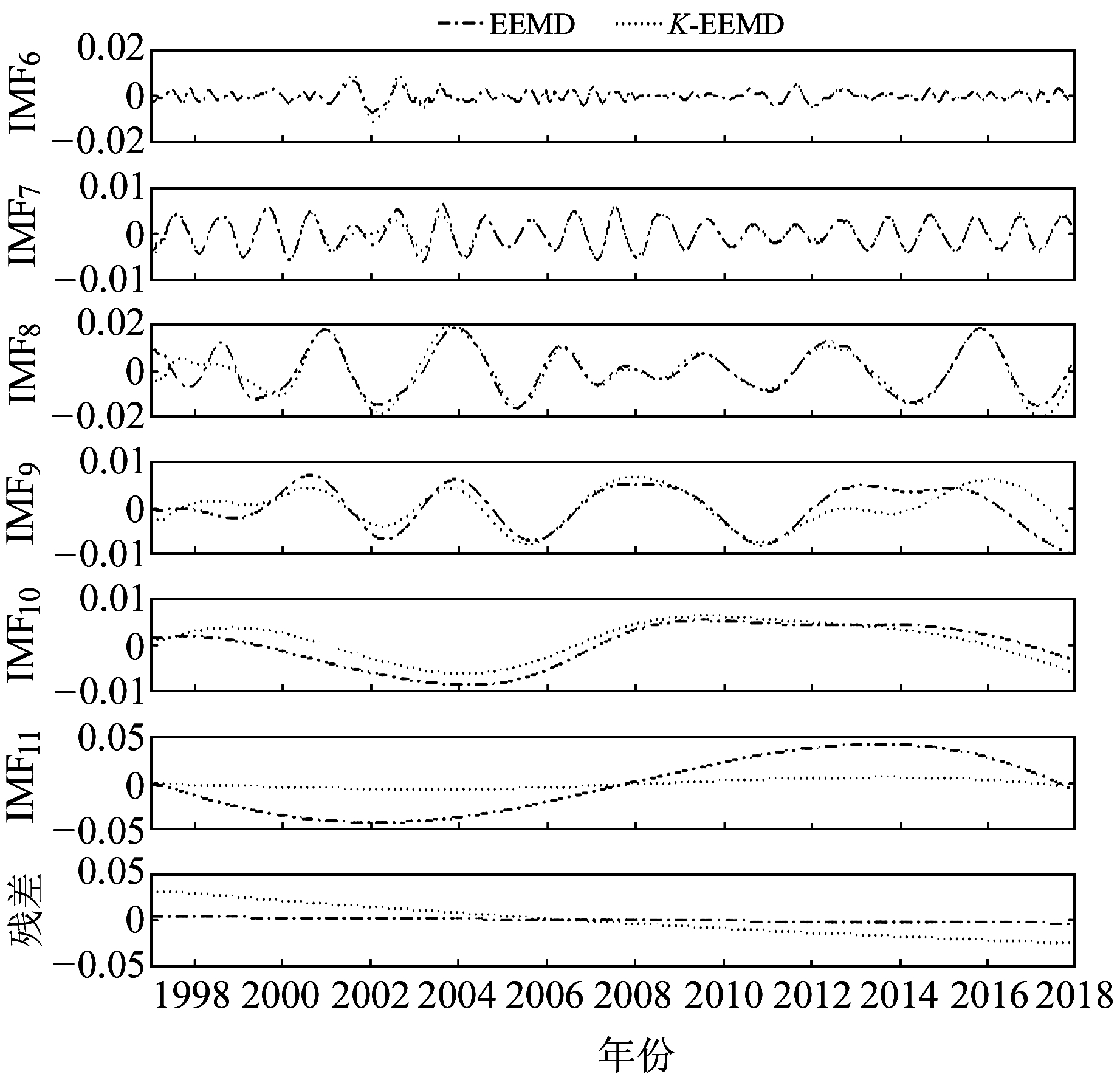
图 4、图 5分别是BJFS站和BOGO站基于2种分解方法得到的IMF分量,图中仅给出中低频的IMF分量。各个IMF分量的方差贡献率如表 1 (单位%)所示。

|
图 4 BJFS站IMF6~IMF11分量 Fig. 4 IMF6-IMF11 components of BJFS station |
|
图 5 BOGO站IMF6~IMF11分量 Fig. 5 IMF6-IMF11 components of BOGO station |
|
|
表 1 2个测站各IMF分量的方差贡献率 Tab. 1 The variance contribution rate of each IMF |
BJFS站IMF1~IMF3为明显高频分量,主要是信号中的有色噪声;IMF4~IMF5的方差贡献率分别为5.43%和3.59%,在序列中占比较小;IMF6与IMF7的方差贡献率分别为21.19%、30.59%,在序列中占比最大,为序列主要周期项。从图 4可以看出,IMF6为近似0.5 a周期项,IMF7为近似1 a周期项,IMF8为近似2 a周期项,IMF9~IMF11周期明显变长,趋势项单调性明显,符合经验模式分解的要求。
BOGO站分解后与BJFS站类似,IMF6与IMF7的方差贡献率分别为20.12%、22.86%,分别为近似0.5 a和1 a的主要周期贡献项;IMF8方差贡献率2.85%,为近似2 a周期项。除IMF1~IMF3为高频分量外,其余各分量方差贡献率大致相同。
2.2 精度对比对BJFS站和BOGO站分解后产生的IMF分量进行正交指数检验。由于IMF6与IMF7是主要的周期贡献量,对这2个分量进行正交指数计算,结果见表 2。
|
|
表 2 2种分解方法的正交指数与信噪比 Tab. 2 IO67 and SNR of EEMD and K-EEMD |
可以看出,K-EEMD算法计算的BJFS站和BOGO站IMF6与IMF7之间的正交指数均小于EEMD算法,正交指数分别减小26%和29%。K-EEMD算法的信噪比明显大于EEMD算法,分别提高6%和3%。
2.3 IMF系统聚类分析判断IMF分量之间是否存在相似性,可利用聚类分析画出系统聚类图,若出现模态混叠现象则存在相似性。
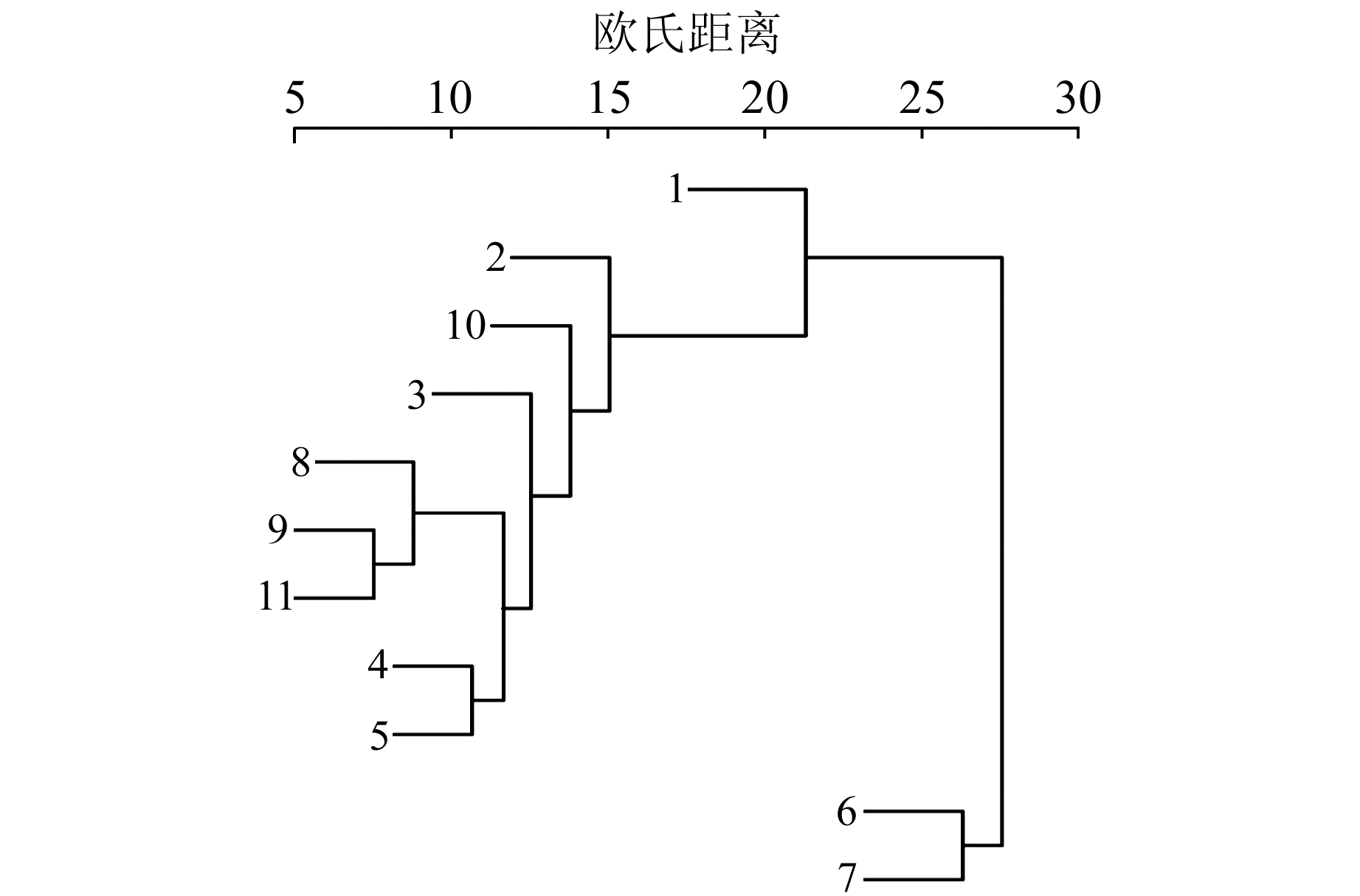
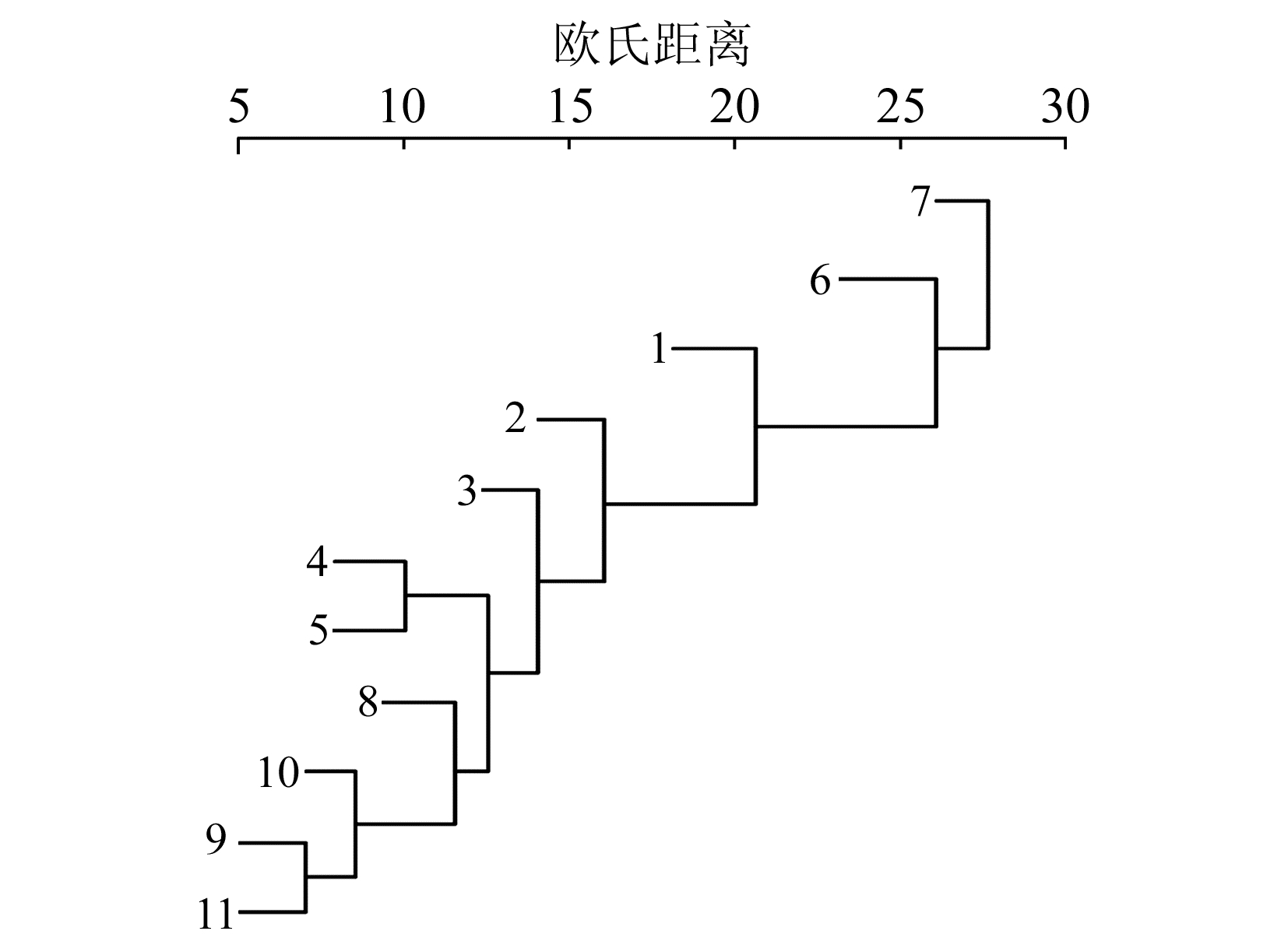
图 6、图 7分别是BJFS站EEMD方法与K-EEMD方法的IMF分量系统聚类图。当欧氏距离为25时,EEMD方法出现模态混叠,IMF6和IMF7被分成一类,具有相似性;当欧氏距离为10时,EEMD方法的IMF4与IMF5同样被分成了一类。K-EEMD方法的11个IMF分量在同等欧氏距离条件下没有出现模态混叠现象,但当欧氏距离小于10时,高频的IMF4与IMF5混叠,可能是聚类分析过程中起始质心点的选择与欧氏距离选择过小引起。
|
图 6 EEMD方法BJFS站IMF聚类图 Fig. 6 IMF clustering by EEMD of BJFS station |
|
图 7 K-EEMD方法BJFS站IMF分量聚类图 Fig. 7 IMF clustering by K-EEMD of BJFS station |
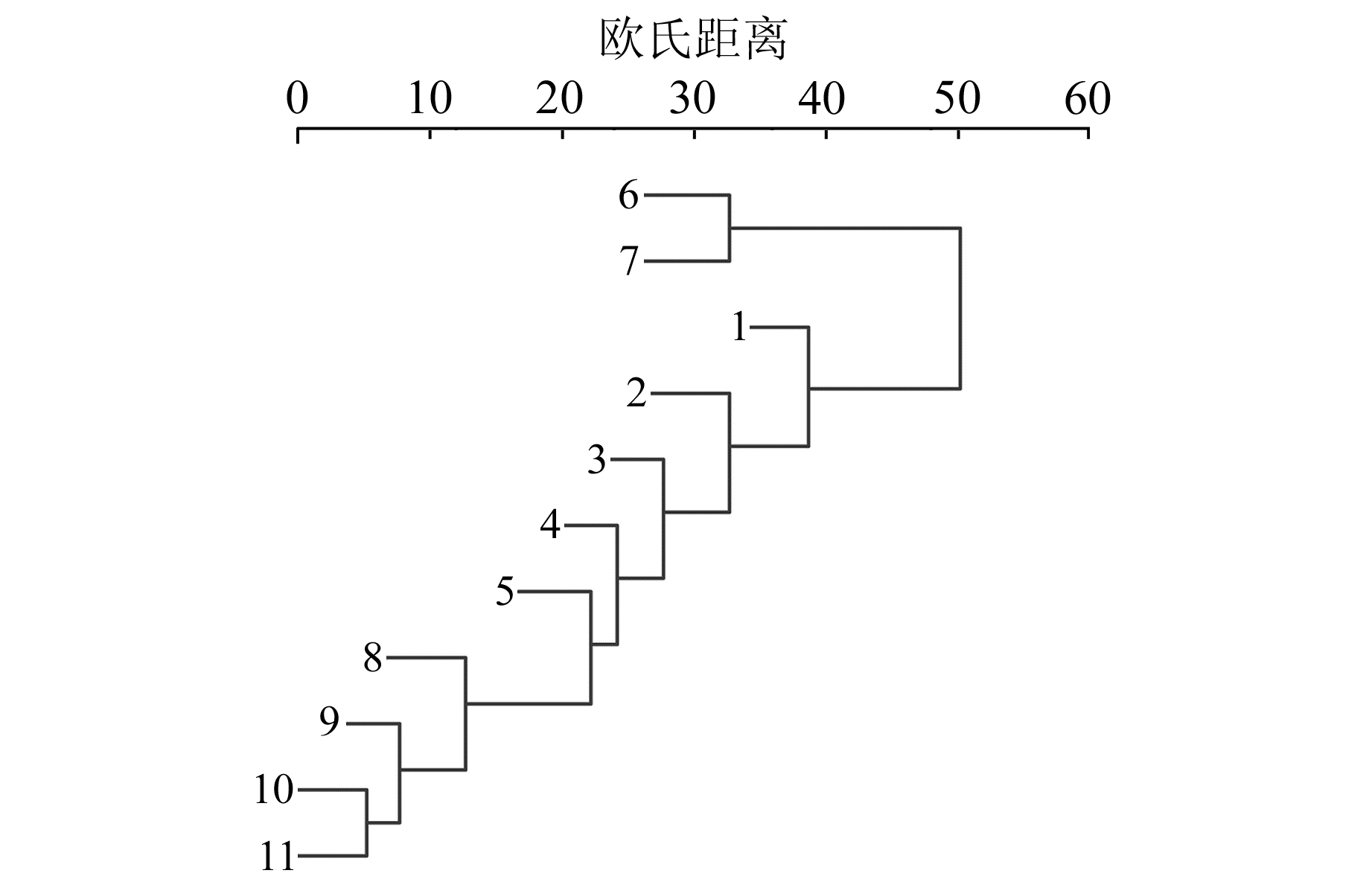
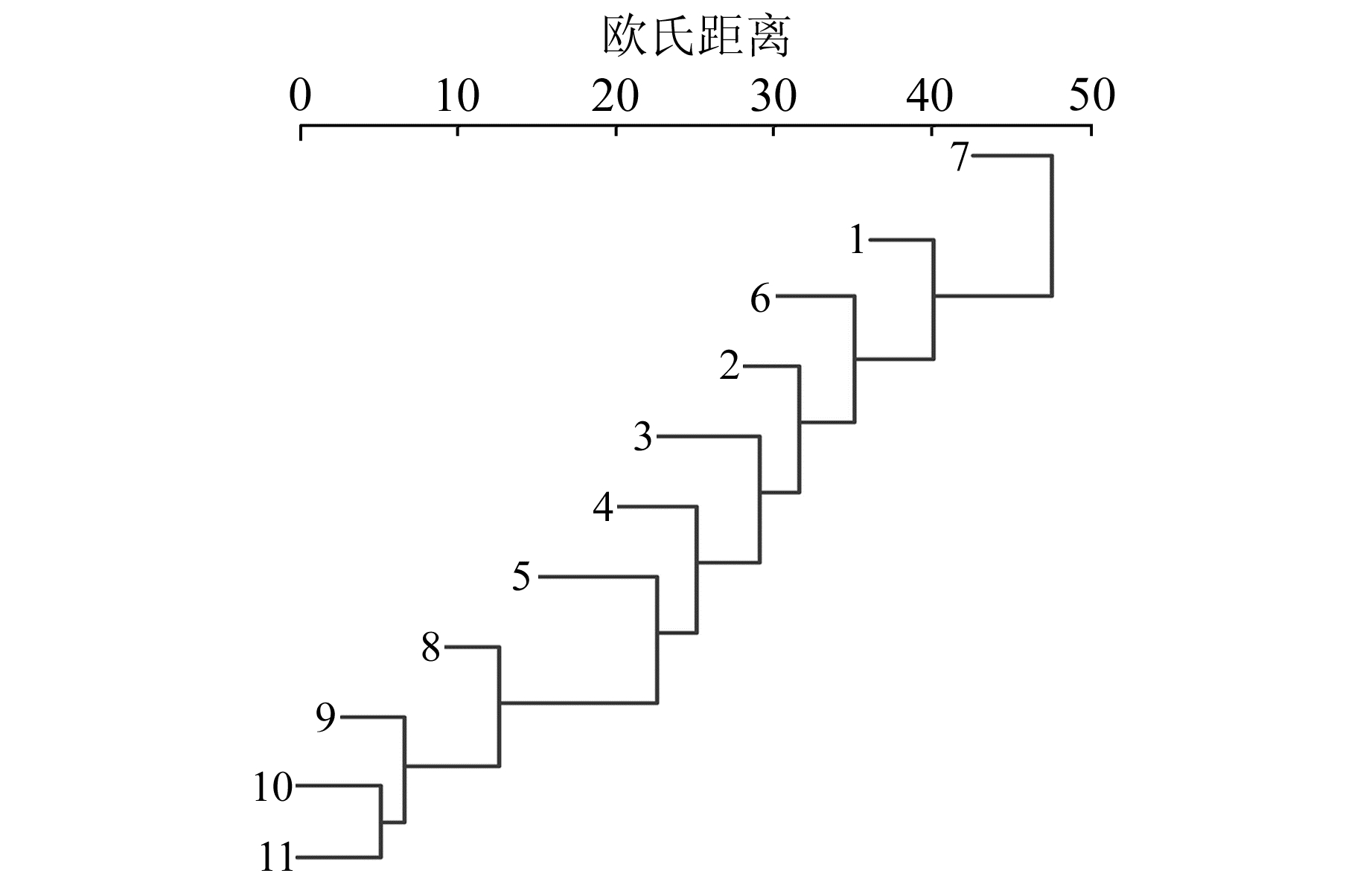
图 8、图 9分别是BOGO站EEMD与K-EEMD的IMF分量系统聚类图。当欧氏距离在30以上时,EEMD方法的IMF6与IMF7分量发生模态混叠,而K-EEMD方法的各个IMF分量在与EEMD同等欧氏距离条件下,没有出现模态混叠,不存在相似性。
|
图 8 EEMD方法BOGO站IMF聚类图 Fig. 8 IMF clustering by EEMD of BOGO station |
|
图 9 K-EEMD方法BOGO站IMF聚类图 Fig. 9 IMF clustering by K-EEMD of BOGO station |
2个CORS站的实验结果表明,EEMD分解后IMF6与IMF7之间存在模态混叠现象,而K均值聚类EEMD在同等条件下不存在模态混叠现象。CORS高程时间序列的IMF分量包含高频噪声项、周期项和低频趋势项。中低频IMF分量对高程时间序列信号的周期运动给出清晰的解释,包含明显的季节性、1 a和2 a周期变化、长周期变化。已有研究表明,IMF周期信号通过Hilbert变换后的频率并不是一个常数,而是瞬时频率,说明IMF的周期随时间而变化,这个问题需要进一步研究。
3 结语利用2个CORS站近20 a的高程时间序列,采用EEMD和K均值聚类EEMD方法进行CORS高程时间序列分解,获取频率从高到低的IMF分量,识别出近似0.5 a、1 a、2 a周期项,有效减少了IMF分量中近似1 a与0.5 a周期信号间存在的模态混叠现象,将信噪比提高3%以上,分解精度提高26%以上。对于分解结果中部分分量之间存在的模态混叠现象,是否是聚类分析过程中起始聚类点和聚类终止条件的选择问题,仍需进一步研究。
| [1] |
Wu Z H, Huang N E. Ensemble Empirical Mode Decomposition: A Noise-Assisted Data Analysis Method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41
(  0) 0) |
| [2] |
徐健, 周志祥, 唐亮, 等. 基于总体平均经验模态分解算法的自适应改进[J]. 振动与冲击, 2017, 36(11): 215-223 (Xu Jian, Zhou Zhixiang, Tang Liang, et al. Adaptive Improvement of EEMD Algorithm[J]. Journal of Vibration and Shock, 2017, 36(11): 215-223)
(  0) 0) |
| [3] |
郑近德, 程军圣, 杨宇. 改进的EEMD算法及其应用研究[J]. 振动与冲击, 2013, 32(21): 21-26 (Zheng Jinde, Cheng Junsheng, Yang Yu. Modified EEMD Algorithm and Its Applications[J]. Journal of Vibration and Shock, 2013, 32(21): 21-26 DOI:10.3969/j.issn.1000-3835.2013.21.004)
(  0) 0) |
| [4] |
施闯, 牛玉娇, 魏娜, 等. HHT-EEMD用于IGS站高程时间序列分析[J]. 大地测量与地球动力学, 2018, 38(7): 661-667 (Shi Chuang, Niu Yujiao, Wei Na, et al. Application of the HHT-EEMD Approach in Analysis of GPS Height Time Series[J]. Journal of Geodesy and Geodynamics, 2018, 38(7): 661-667)
(  0) 0) |
| [5] |
李鹏.基于层次K均值的聚类算法的研究[D].哈尔滨: 哈尔滨工程大学, 2015 (Li Peng. The Study and Development of Hierarchical K-Means Based Clustering Algorithm[D]. Harbin: Harbin Engineering University, 2015)
(  0) 0) |
| [6] |
Chung K L, Lin J S. Faster and More Robust Point Summetry-Based K-Means Algorithm[J]. Pattern Recognition, 2007, 40(2): 410-422 DOI:10.1016/j.patcog.2005.09.015
(  0) 0) |
| [7] |
Rousseeuw P J. Silhouettes: A graphical Aid to the Interpretation and Validation of Cluster Analysis[J]. Journal of Computational and Applied Mathematics, 1987, 20: 53-65 DOI:10.1016/0377-0427(87)90125-7
(  0) 0) |
| [8] |
唐东明.聚类分析及其应用研究[D].成都: 电子科技大学, 2010 (Tang Dongming. Study on Clustering Algorithm and Its Applications[D]. Chengdu: University of Electronic Science and Technology, 2010) http://cdmd.cnki.com.cn/Article/CDMD-10614-2010234406.htm
(  0) 0) |
| [9] |
Huang N E, Shen Z, Long S R, et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis[J]. The Royal Society, 1998, 454(1 971): 903-995
(  0) 0) |
| [10] |
张恒璟, 程鹏飞. 基于经验模式分解的CORS站高程时间序列分析[J]. 大地测量与地球动力学, 2012, 32(3): 129-134 (Zhang Hengjing, Cheng Pengfei. Analysis on Time Series of Two CORS Stations' Height Based on EMD[J]. Journal of Geodesy and Geodynamics, 2012, 32(3): 129-134)
(  0) 0) |
2. Chinese Academy of Surveying and Mapping, 28 West-Lianhuachi Road, Beijing 100830, China
 2019, Vol. 39
2019, Vol. 39


