2. 地球空间信息技术协同创新中心,武汉市珞喻路129号,430079;
3. 武汉大学地球空间环境与大地测量教育部重点实验室,武汉市珞喻路129号,430079
截至2018年初,BD-2在轨工作的卫星一共有15颗,分别为6颗地球静止轨道(GEO)卫星、6颗倾斜地球同步轨道(IGSO)卫星和3颗中地球轨道(MEO)卫星。每颗卫星装备4颗铷钟,其中2颗保持开机运行状态,1颗为工作主钟,1颗为热备份钟。星载原子钟作为星上时间基准,是卫星的重要载荷之一,其性能水平直接影响卫星导航系统的定位、导航和授时服务质量[1],对卫星系统的发展举足轻重。
前人对GPS卫星钟的评估已经作了大量研究工作[2-8],而对北斗卫星钟性能评估的研究较少[9-13],主要集中在单一指标或某一特性上,且多为短期或中短期的性能评估。BD-2卫星经过较长时间的运行,积累了大量数据,可以对其长期特性进行分析,而且有些卫星处于设计寿命后期,评估其星载原子钟的性能对于了解掌握原子钟性能的变化更加重要。
本文利用2013-01-01~2018-05-01的BD-2精密钟差数据,分析北斗星载原子钟的相位、频漂、准确度、稳定度等指标,以期探究其性能的长期变化特征,并判断切钟对卫星原子钟性能的影响。
1 原子钟性能指标 1.1 卫星钟差模型为了较为准确且稳定地表示和估计精密钟差变化序列,通常采用包含表征卫星钟时频特性的相位、频率和频漂的二次多项式模型作为钟差模型,GPS导航文件的卫星钟差也正是基于这3种因素构成。模型表达式为[14]:
| ${l_i} = {a_0} + {a_1}({t_i} - {t_0}) + {a_2}{({t_i} - {t_0})^2} + {\Delta _i} $ | (1) |
式中,t0为卫星钟参数的参考时刻,ti为历元时刻(i=1, 2, …, N),li为ti时刻的卫星钟差,待估参数a0、a1和a2分别为参考时刻t0的相位(钟差)、频率(钟速)及频率漂移率(频漂,也称钟的老化率),Δi为观测误差。当已知钟差数据不少于3个时,便可通过式(1)对卫星钟钟差序列进行最小二乘拟合,求得待估参数。
1.2 频率准确度准确度描述测量值和理想值之间的相对关系,是反映原子钟性能的一项重要指标。但由于原子钟钟差实际值无法精确测量,一般通过时差比对的方法来计算频率准确度。将精密钟差数据标记为xi(i=1, 2, …, N),N为采样个数,设采样周期长度为T,基于最小二乘法,通过线性函数x=x+KT(t-t)便可求得此段时间的频率准确度KT[15]:
| $ {K_T} = \frac{{\sum\limits_{i = 1}^N {\left( {{x_i} - \bar x} \right)} \left( {{t_i} - \bar t} \right)}}{{\sum\limits_{i = 1}^N {{{\left( {{t_i} - \bar t} \right)}^2}} }} $ | (2) |
式中,
考虑到铷钟存在明显的频率漂移,本文采用不受频漂影响的重叠哈达玛方差评估其频率稳定度。基于时差数据的重叠,哈达玛方差可表示为:
| $ \begin{array}{c} H\sigma _y^2\left( \tau \right) = \frac{1}{{6{\tau ^2}\left( {N - 3m} \right)}} \cdot \\ \sum\limits_{i = 1}^{N - 3m} {{{\left[ {{x_{i + 3m}} - 3{x_{i + 2m}} + 3{x_{i + m}} - {x_i}} \right]}^2}} \end{array} $ | (3) |
式中,xi为时差数据,m为平滑因子,一般取1≤m≤
为了对卫星钟进行尽可能长时间的性能评估,利用WHU提供的2013-01-01~2017-06-27精密钟差产品及GFZ提供的2017-06-28~2018-05-01精密钟差产品数据对BD-2星载原子钟性能进行评估分析。BD-2卫星在轨状态统计见表 1。
|
|
表 1 BD-2卫星在轨状态统计(至2018-04-10) Tab. 1 State statistics of BD-2 in-orbit satellites (up to April 10, 2018) |
由表 1可知,BD-2卫星中有2颗(C02、C13)进行了二次发射。截至2018-05,15颗BD-2卫星均正常提供卫星服务,其中C17卫星钟差数据较少,不纳入统计分析。利用精密钟差相位数据进行原子钟性能指标评估的主要步骤如下:
1) 对原始钟差相位数据进行预处理,剔除钟差数据中的异常值,对于剔除后的历元和短期数据间断的历元插值补齐数据;
2) 以1 d为单元进行二次拟合,获取逐天的频漂值,分析频漂序列长期变化规律和异常现象;
3) 以1 d为单元计算卫星钟频率准确度,分析其长期变化规律;
4) 对钟差序列进行万秒频率稳定度计算,探究万秒稳定度序列精度和变化规律;
5) 根据BD-2卫星钟频漂、频率准确度和频率稳定度指标的变化特性和异常现象,结合已有的北斗卫星切钟资料,探究原子钟切换与性能指标的相关性,并以此推断统计BD-2原子钟星上的切钟操作。
2.2 钟差数据预处理星载原子钟在长期运行过程中会受到各种不确定因素的影响,卫星钟差数据时常会出现粗差、相位跳变和数据中断等异常情况,这会直接影响原子钟性能评估指标计算结果的可靠性,所以需要对钟差数据进行预处理。由于相位数据量级较大,异常点并不明显,为便于剔除粗差,需要将相位数据(xi, i=1, 2, …, N)转为频率数据(yi, i=1, 2, …, N-1),公式为:
| $ {y_i} = \frac{{{x_{i + 1}} - {x_i}}}{{{\tau _0}}} $ | (4) |
考虑到频率数据较多,为提高效率,采用基于中位数(MAD)的抗差估计来剔除粗差。以1 d为1个时段,当观测量|yi|>(m+nMAD)时(n可根据需要确定,本文取3),则剔除该观测值。其中,m为频率序列中间数,m=median{yi},中位数MAD=median{|yi-m|/0.674 5}。
在原子钟观测中,相位跳变和频率跳变不可避免,跳变点可以通过移动窗口法查找窗口前后数据均值的变化点来定位。通常需要将跳变前后的数据分成2段处理,本文计算的时段以1 d为单元,时段很短,对跳变当天的数据可以选取数据量较多的一段计算评估指标。
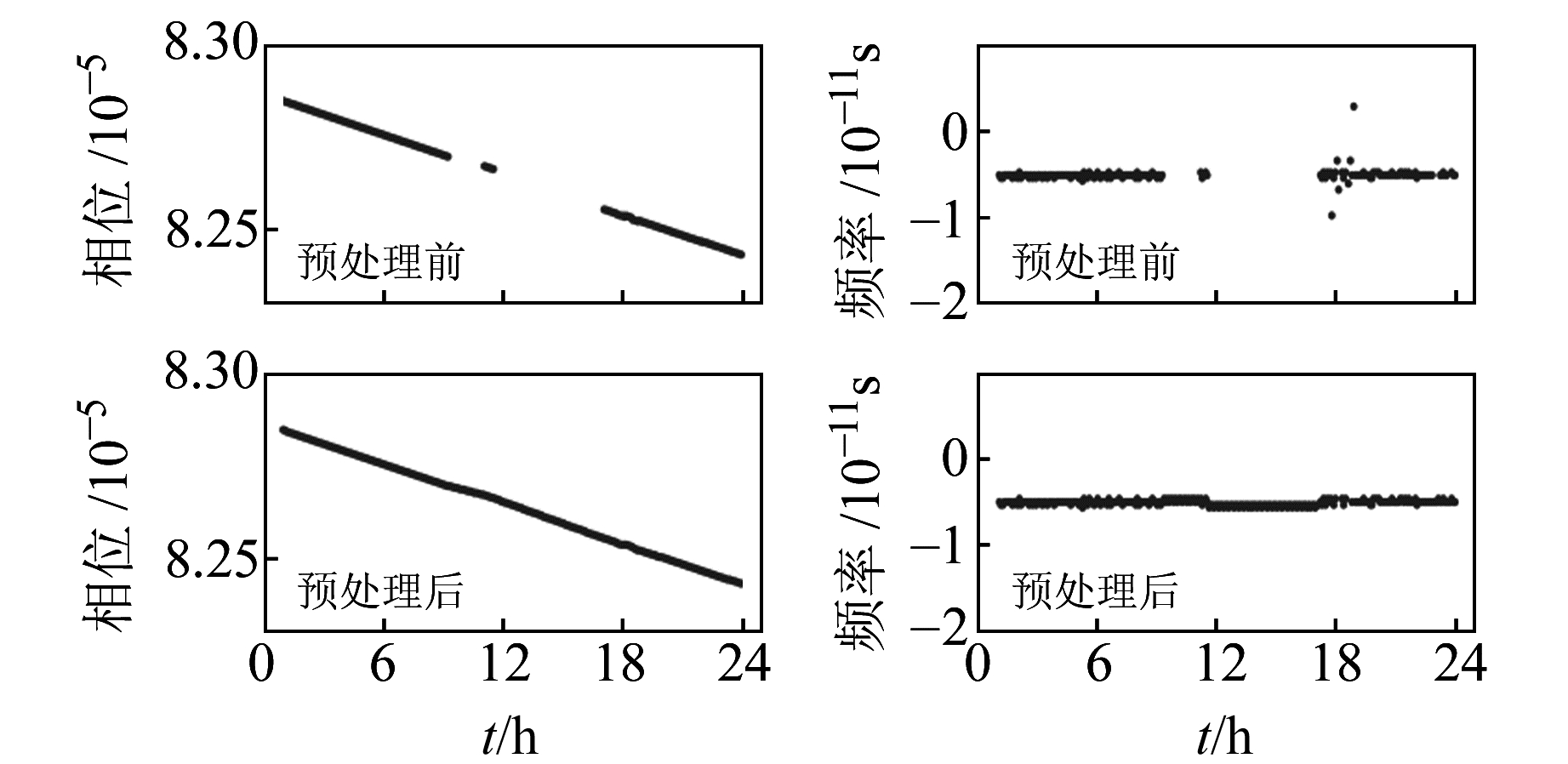
钟差数据中常出现数据间断的情况,当间断时间较短时,可采用线性拟合的方法进行插值补充[16]。以2013-01-01 C14卫星钟差相位序列为例,预处理前钟差相位有2次中断,1次差分频率在18 h有些许波动,预处理后剔除了频率波动较大时刻的粗差,并插值补齐了空缺时刻的钟差相位,为接下来的钟差模型拟合和性能指标计算作准备(图 1)。
|
图 1 C14卫星2013-01-01钟差预处理前后相位与频率序列 Fig. 1 Phase and frequency diagrams before and after clock preprocessing of C14 satellite on January 1, 2013 |
数据处理以1 d为单元,利用当天的钟差数据,根据式(1)拟合得到相位、频率和频漂值。因篇幅有限,选取C03、C06、C09和C13卫星展示相位和频漂的变化序列,结果见图 2、图 3。

|
图 2 BD-2载钟相位序列 Fig. 2 Phase series of BD-2 on-board clocks |
|
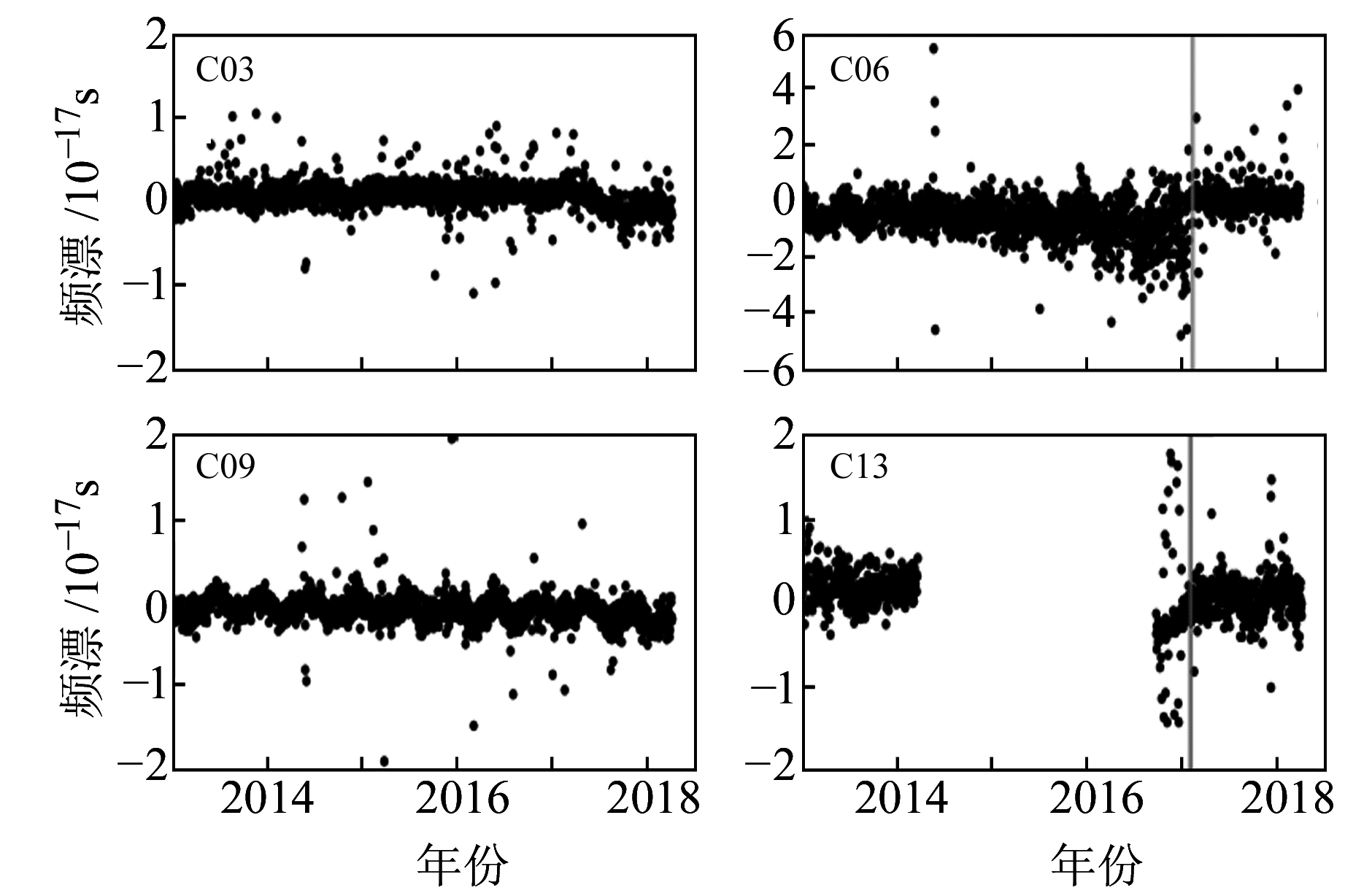
图 3 BD-2载钟频漂序列 Fig. 3 Frequency drift rate series of BD-2 on-board clocks |
观察所有卫星的频漂序列可以发现,大部分北斗卫星钟频漂比较稳定,没有显著的趋势项,类似随机噪声,即使是短期内频漂值也并非连续值。少数卫星的原子钟频漂表现出周期性,如图 3中C09卫星频漂序列有较明显的类似正弦曲线的变化特性,周期为0.5 a或1 a,C06卫星在2017年之前也有类似的周期变化但不明显。此外,C06卫星在2015年后随时间推移频漂开始逐渐发散,波动幅度增大,在2017-02频漂突然收敛,也更加稳定。C13卫星在2017-01前频漂异常值较多,在此之后异常值相对较少,这与该卫星原子钟切换前后的性能有关[9]。
表 2对BD-2卫星2013-01-01~2018-05-01频漂进行整体统计,频漂均值整体维持在4× 10-19~5×10-18/s量级,标准差在10-18~10-17/s量级。MEO卫星钟频漂指标最稳定,C11和C12卫星频漂均值在4×10-19~6×10-19/s量级,标准差在10-18/s量级;C14卫星相对C11和C12卫星来说较差,频漂基本维持在(2~6)×10-18/s。IGSO卫星钟频漂性能稍优于GEO卫星,其中C02和C08频漂性能较差,均值都在3×10-18/s量级,标准差在10-17/s量级。
|
|
表 2 BD-2卫星钟总时段频漂统计 Tab. 2 Full-time frequency drift rate statistics of BD-2 satellite clocks |
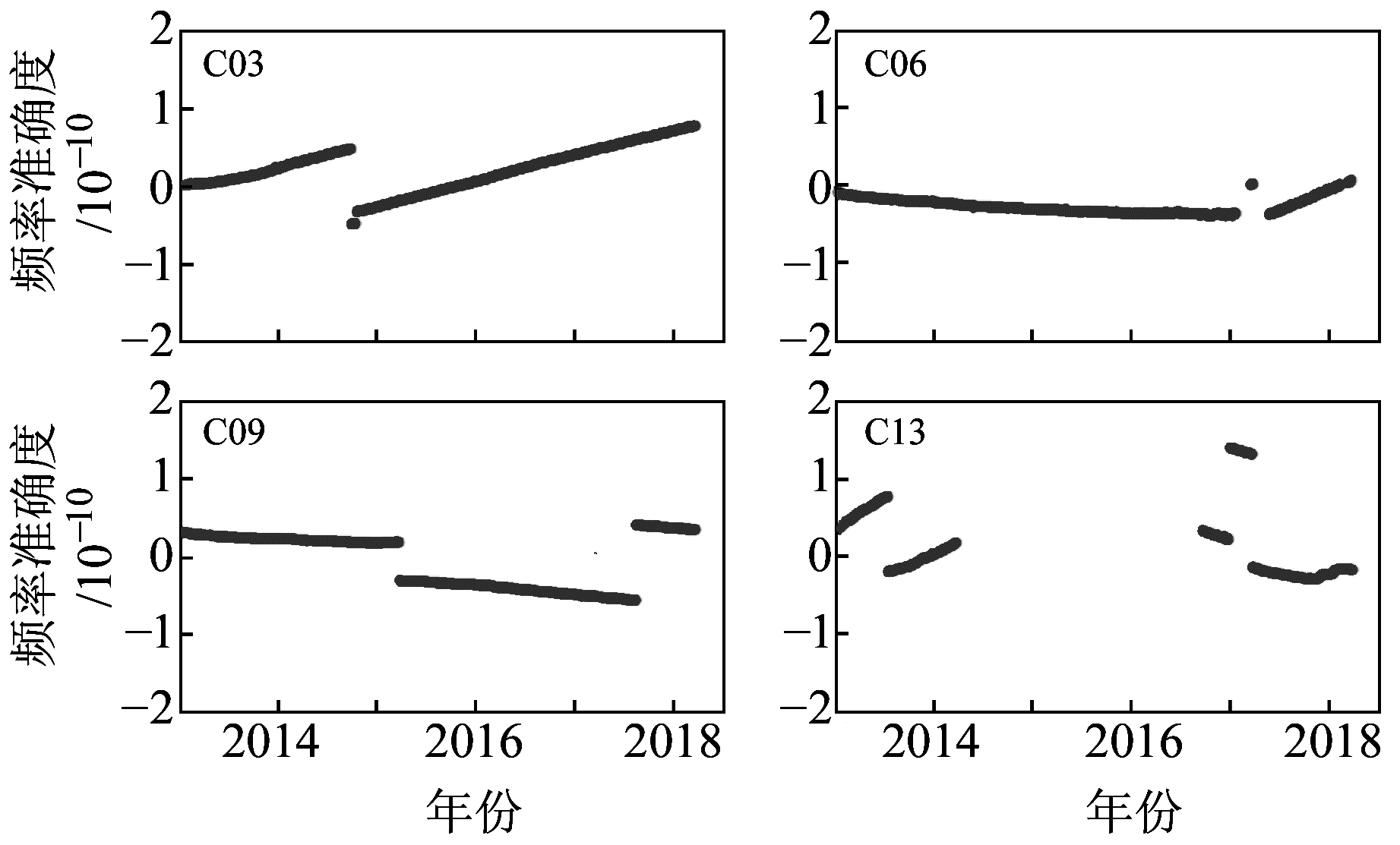
准确度仍以1 d为计算单元,利用式(2)计算获得2013-01-01~2018-05-01逐天的准确度序列。由图 4可知,北斗星载原子钟频率准确度比较稳定,连续性较好,整体处于10-11量级。频率准确度与钟频率相关,频率跳变会引起相应的频率准确度跳变,BD-2卫星大多进行了1~2次的调频操作,主要是为了控制准确度误差小于预定的阈值范围。
|
图 4 BD-2载钟频率准确度序列 Fig. 4 Frequency accuracy series of BD-2 on-board clocks |
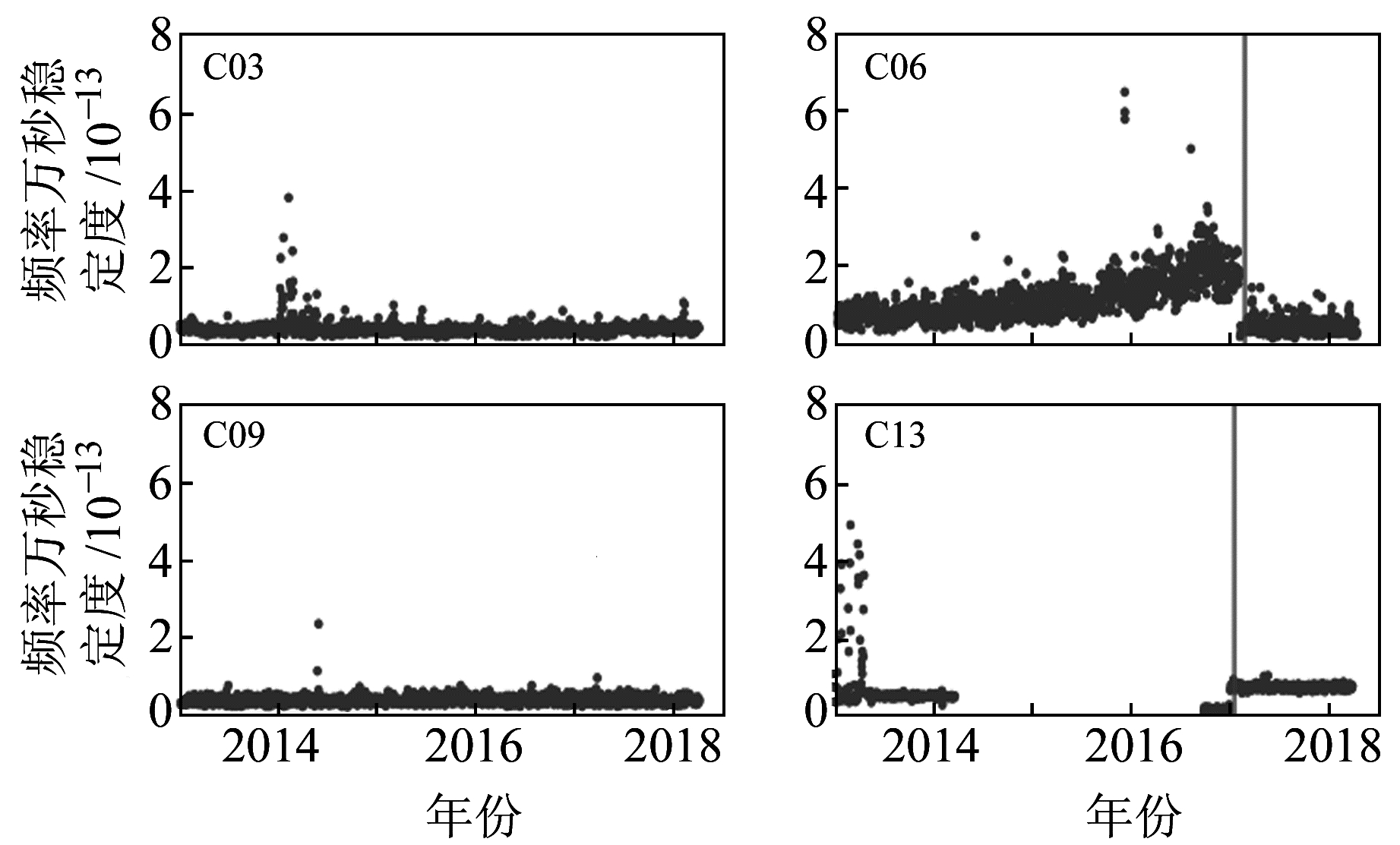
稳定度采用重叠哈达玛方差进行评估,以1 d为计算单元,利用所有的钟差数据,以10 000 s为一个平滑弧段计算得到卫星钟万秒稳定度。由图 5和表 3可以看出,BD-2星载原子钟万秒稳定度在10-14~10-13量级,总体比较平稳,没有明显的趋势项和周期,与文献[8-11]结果比较吻合。C06卫星万秒稳定度在2015年后有明显的上升且发散趋势,在2017-02稳定度忽变平稳;C13卫星万秒稳定度在2017-01也发生跳变。MEO卫星星载原子钟稳定度相对来说更加稳定,万秒稳定度在5×10-14量级,GEO和IGSO卫星万秒稳定度在5×10-14~10-13量级,个别卫星如C02、C06和C08星载原子钟万秒稳定度相对较差,达到10-13量级。
|
图 5 BD-2载钟万秒稳定度序列 Fig. 5 Frequency stability in ten-thousand s series of BD-2 on-board clocks |
|
|
表 3 BD-2卫星钟总时段稳定度统计 Tab. 3 Full-time frequency stability statistics of BD-2 satellite clocks |
卫星钟的切换会对钟差预报模型的构建和定轨产生影响。导航卫星原子钟在轨运行时可根据需要进行合理调相和调频,但一般情况下,原子钟的频漂不能被人为调控。本文从频漂、频率准确度和频率稳定度3个方面分析北斗星载原子钟主备钟切换对其性能的影响。
由图 3~5可知,在使用WHU和GFZ机构的钟差数据切换后,性能指标没有异常变化,可以认为不同机构的数据不会对分析结果产生影响。C06和C13卫星分别在2017-02-14和2017-01-20切换了原子钟[9],通过图 3可以看到,C06卫星频漂在2017-02出现跳变,在这之前频漂波动幅度变大,切钟后频漂值变小也更加稳定;而C13卫星在2017-01之前数据量太少,影响频漂指标的观测。BDS系统星载原子钟频漂均不可调整,因此调相和调频操作不会使频率序列斜率发生变化。频率准确度可以反映频率的变化特性,图 4中C06和C13卫星分别在2017-02-14和2017-01-20之后发生频率准确度的跳变和斜率的改变,C13卫星在二次发射之后斜率与2015年之前不同也可以证明这一点。图 5中C06和C13卫星也在相应时间发生了稳定度的跳变,统计C06卫星切钟前1 a、C13切钟前3个月与切钟后的稳定度指标,结果见图 6。C06卫星的频率稳定度均值从1.90×10-13 变为5.95×10-14 ,标准差也减小很多;C13卫星频率稳定度均值从5.45×10-14 变为2.32×10-13 ,标准差有一定减小,这种频率稳定度指标的跳变很明显。由此可知,卫星切钟通常会带来钟频漂值和离散程度、频率准确度和斜率以及稳定度均值和标准差的变化,可以根据星载钟频漂、频率准确度和频率稳定度的变化情况来判断卫星是否切钟。
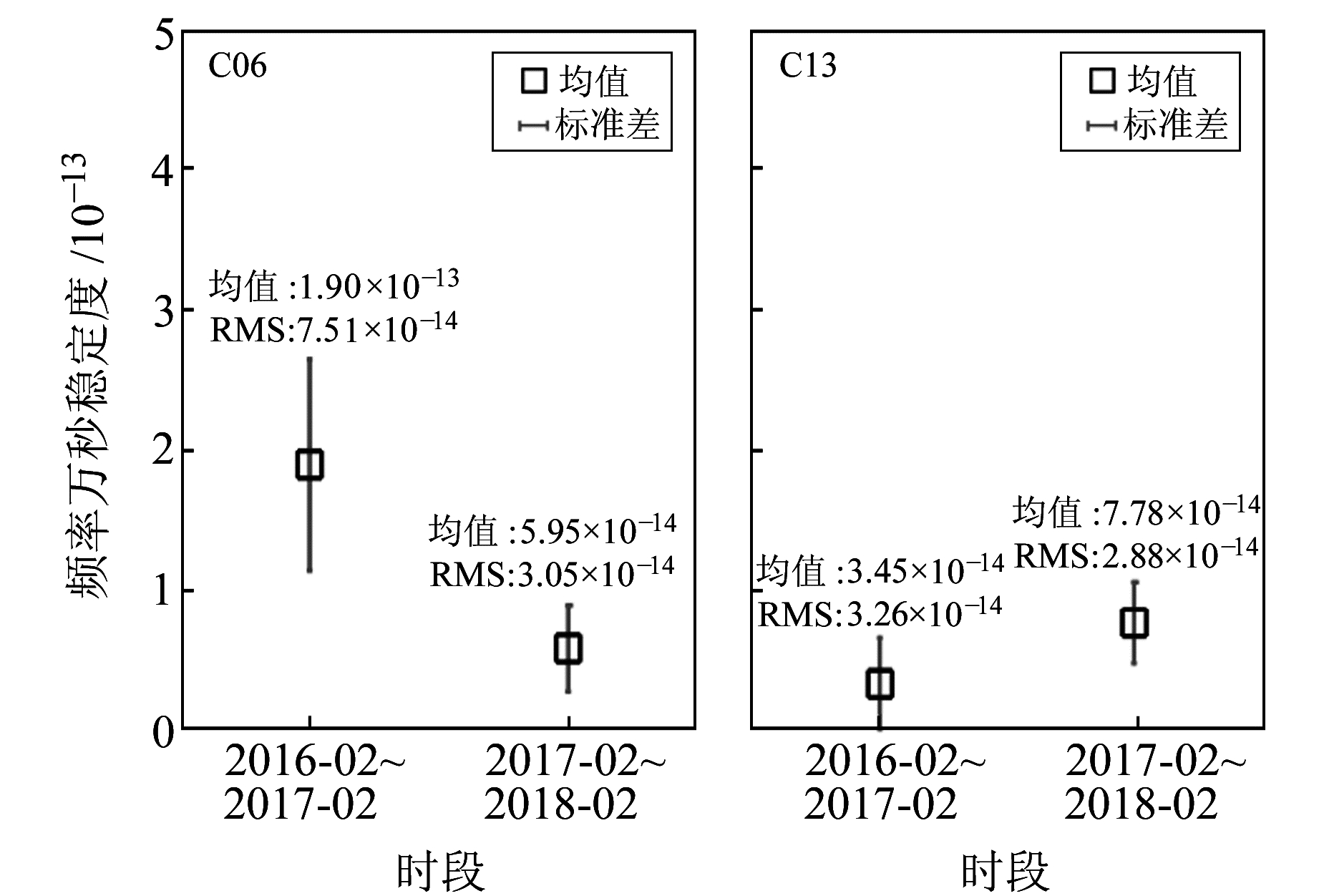
|
图 6 C06和C13卫星切钟前后频率稳定度的变化 Fig. 6 Frequency stability variations before and after C06 and C13 on-board clocks switching |
以上述指标变化为判断依据,推断本文评估期内BD-2部分卫星钟是否进行星上主备钟切换操作。由图 7可以看出,切钟前后卫星钟性能指标变化明显。以C02卫星为例,切钟前频漂比较离散,切钟后频漂变得收敛且稳定,频率稳定度量级变小,由波动较大变得收敛稳定,频率准确度在切钟时有显著跳变,斜率也发生改变。表 4统计了本文评估期内BD-2卫星切钟的次数和时间,GEO的C02和C05卫星各切换1次原子钟,C04卫星共有2次切钟操作,分别在2013-05-15和2014-02-16;IGSO的C06、C08和C13卫星各有1次星上切钟操作;MEO卫星相对来说一直比较稳定,统计期内没有发生切钟现象。
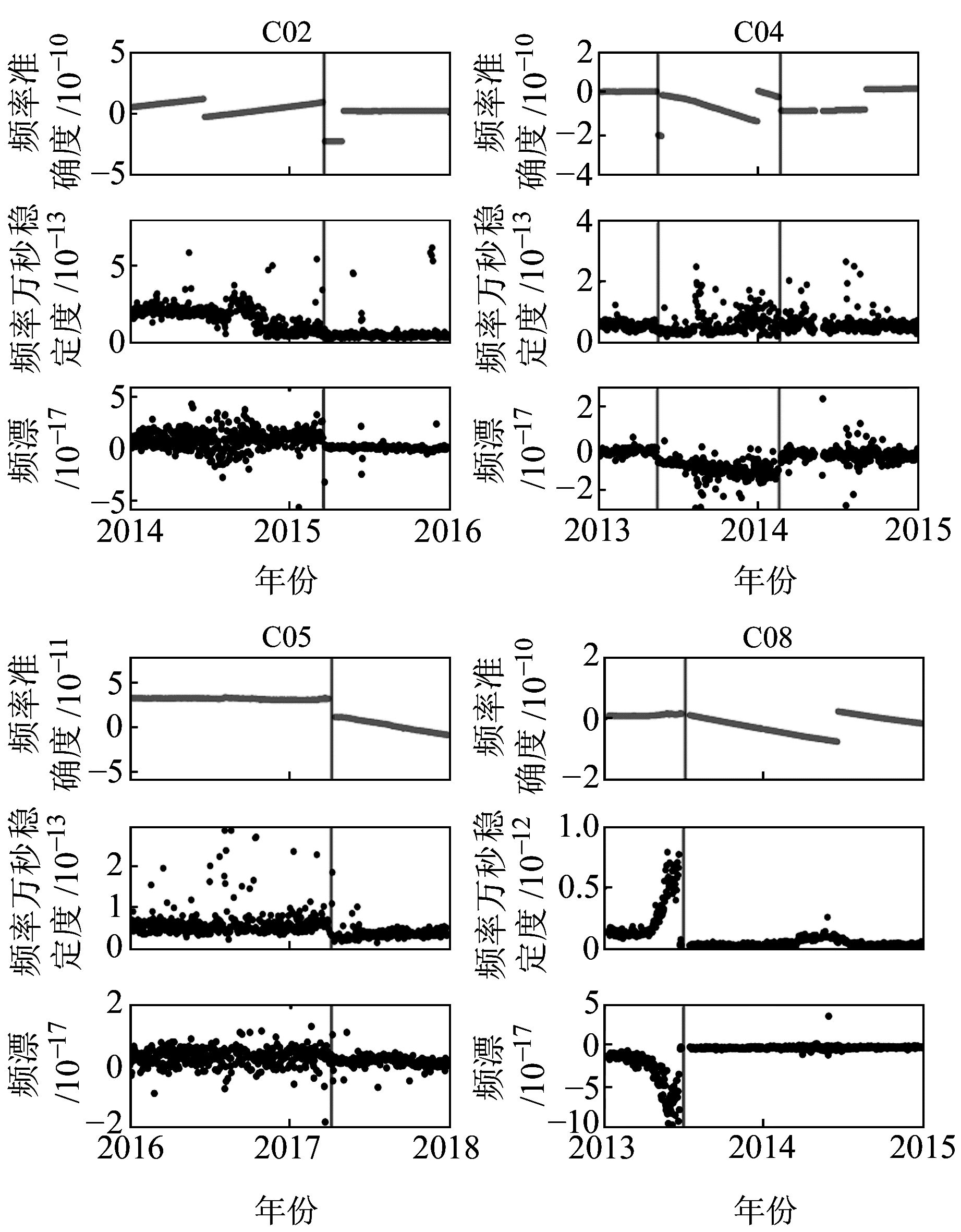
|
图 7 BD-2卫星切钟前后性能指标变化 Fig. 7 Performance index variations before and after BD-2 on-board clocks switching |
|
|
表 4 BD-2卫星切钟信息 Tab. 4 Clock switching information of BD-2 satellite clock |
本文基于BD-2卫星2013-01-01~2018-05-01的精密钟差数据,从原子钟相位、频漂、频率准确度和频率稳定度等方面对其星载原子钟长期在轨性能进行较为全面的分析,主要得到以下结论:
1) BD-2卫星钟相位数据连续性和稳定性不佳,调相操作频繁;频漂整体维持在10-18~10-17/s量级,比较稳定,少数卫星频漂序列存在0.5 a或1 a的长周期变化,MEO卫星的频漂指标相对较小。
2) BD-2卫星钟频率准确度比较稳定,连续性较好,整体处于10-11量级,期间大多数卫星频率准确度发生过1~2次跳变。
3) 利用重叠哈达玛方差计算的北斗卫星钟万秒稳定度在10-14~10-13量级,比较稳定。GEO和IGSO卫星万秒稳定度在5×10-14~10-13量级,MEO卫星为5×10-14量级。
4) 原子钟的频漂、频率准确度和频率稳定度存在一定的相关性。当北斗卫星切换原子钟时,通常会引起卫星钟频漂数值和离散程度、频率准确度和斜率及频率稳定度的改变,利用C06和C13卫星的切钟信息验证上述指标变化,并推断出在本文评估期内C02、C05和C08卫星各进行1次星上切钟操作,C04卫星切换了2次原子钟。
本文给出的BD-2切钟时刻与官方提供的切钟时刻是否一致还需要进一步验证。
致谢: 感谢长安大学黄观文老师和中国科学院上海天文台王彬老师对本文的指导和帮助。
| [1] |
郭海荣, 杨元喜. 导航卫星原子钟时域频率稳定性影响因素分析[J]. 武汉大学学报:信息科学版, 2009, 34(2): 218-221 (Guo Hairong, Yang Yuanxi. Analyses of Main Error Sources on Time-Domain Frequency Stability for Atomic Clocks of Navigation Satellites[J]. Geomatics and Information Science of Wuhan University, 2009, 34(2): 218-221)
(  0) 0) |
| [2] |
王宇谱, 吕志平, 李林阳, 等. GPS BLOCK ⅡF星载原子钟长期性能分析[J]. 天文学报, 2017, 58(3): 11-21 (Wang Yupu, Lü Zhiping, Li Linyang, et al. Analysis of the Long-Term Performance of GPS BLOCK ⅡF Satellite Atomic Clocks[J]. Acta Astronomica Sinica, 2017, 58(3): 11-21)
(  0) 0) |
| [3] |
Huang G W, Zhang Q, Li H, et al. Quality Variation of GPS Satellite Clocks On-Orbit Using IGS Clock Products[J]. Advances in Space Research, 2013, 51(6): 978-987 DOI:10.1016/j.asr.2012.09.041
(  0) 0) |
| [4] |
Fu W J, Huang G W, Liu Y L, et al. The Analysis of the Characterization for GLONASS and GPS On-Board Satellite Clocks[C]. China Satellite Navigation Conference, Wuhan, 2013 https://link.springer.com/chapter/10.1007/978-3-642-37404-3_44
(  0) 0) |
| [5] |
周佩元, 杜兰, 路余, 等. 多星定轨条件下北斗卫星钟差的周期性变化[J]. 测绘学报, 2015, 44(12): 1 299-1 306 (Zhou Peiyuan, Du Lan, Lu Yu, et al. Periodic Variations of Beidou Satellite Clock Offsets Derived from Multi-Satellite Orbit Determination[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(12): 1 299-1 306)
(  0) 0) |
| [6] |
Chen M L, Zhan X Q, Du G, et al. Compass/Beidou-2 Spaceborne Clock Performance Assessment and Its Error Detection, Mitigation[J]. IEEJ Transactions on Electrical and Electronic Engineering, 2015, 10(4): 438-446 DOI:10.1002/tee.22103
(  0) 0) |
| [7] |
Steigenberger P, Hugentobler U, Hauschild A, et al. Orbit and Clock Analysis of Compass GEO and IGSO Satellites[J]. Journal of Geodesy, 2013, 87(6): 515-525 DOI:10.1007/s00190-013-0625-4
(  0) 0) |
| [8] |
王宁, 王宇谱, 李林阳, 等. BDS星载原子钟频率稳定性分析[J]. 武汉大学学报:信息科学版, 2017, 42(9): 1 256-1 263 (Wang Ning, Wang Yupu, Li Linyang, et al. Stability Analysis of the Space-Borne Atomic Clock Frequency for BDS[J]. Geomatics and Information Science of Wuhan University, 2017, 42(9): 1 256-1 263)
(  0) 0) |
| [9] |
黄观文, 余航, 郭海荣, 等. 北斗在轨卫星钟中长期钟差特性分析[J]. 武汉大学学报:信息科学版, 2017, 42(7): 982-988 (Huang Guanwen, Yu Hang, Guo Hairong, et al. Analysis of the Mid-Long Term Characterization for BDS On-Orbit Satellite Clocks[J]. Geomatics and Information Science of Wuhan University, 2017, 42(7): 982-988)
(  0) 0) |
| [10] |
王省超, 贾小林, 沈洪霞, 等. BDS在轨卫星原子钟性能评估分析[J]. 导航定位学报, 2018, 6(1): 60-66 (Wang Shengchao, Jia Xiaolin, Shen Hongxia, et al. Performance Evaluation and Analysis of BDS in Orbit Satellite Atomic Clock[J]. Journal of Navigation and Positioning, 2018, 6(1): 60-66)
(  0) 0) |
| [11] |
王宇谱, 吕志平, 王宁. BDS星载原子钟长期性能分析[J]. 测绘学报, 2017, 46(2): 157-169 (Wang Yupu, Lü Zhiping, Wang Ning. The Long-Term Performance Analysis for On-Board Atomic Clocks of BDS[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(2): 157-169)
(  0) 0) |
| [12] |
王彬. BDS在轨卫星钟特征分析、建模及预报研究[D].武汉: 武汉大学, 2016 (Wang Bin.Analysis of BDS Satellite Clocks in Orbit, Modeling and Its Prediction Research[D]. Wuhan: Wuhan University, 2016) http://cdmd.cnki.com.cn/Article/CDMD-10486-1016131995.htm
(  0) 0) |
| [13] |
孙大伟. GNSS星载原子钟性能分析理论与算法研究[D].西安: 长安大学, 2016 (Sun Dawei. Research on the Performance Analysis of GNSS On-Board Clock[D]. Xi'an: Chang'an University, 2016) http://cdmd.cnki.com.cn/Article/CDMD-10710-1016748887.htm
(  0) 0) |
| [14] |
王宇谱, 吕志平, 孙大双, 等. 一种改进钟差二次多项式模型的导航卫星钟差预报方法[J]. 天文学报, 2016, 57(1): 78-90 (Wang Yupu, Lü Zhiping, Sun Dashuang, et al. A New Navigation Satellite Clock Bias Prediction Method Based on Modified Clock-Bias Quadratic Polynomial Model[J]. Acta Astronomica Sinica, 2016, 57(1): 78-90)
(  0) 0) |
| [15] |
高为广, 蔺玉亭, 陈谷仓, 等. 北斗系统在轨卫星钟性能评估方法及结论[J]. 测绘科学技术学报, 2014, 31(4): 342-346 (Gao Weiguang, Lin Yuting, Chen Gucang, et al. The Performances Assessment Methods and Results of In-Orbit Atomic Clocks of BDS[J]. Journal of Geomatics Science and Technology, 2014, 31(4): 342-346 DOI:10.3969/j.issn.1673-6338.2014.04.003)
(  0) 0) |
| [16] |
田婕, 黄观文, 王利, 等. 一种北斗二代卫星钟差的数据质量控制方法[J]. 大地测量与地球动力学, 2017, 37(2): 215-220 (Tian Jie, Huang Guanwen, Wang Li, et al. A Data Quality Control Method for the Beidou-2 Satellite Clock Bias[J]. Journal of Geodesy and Geodynamics, 2017, 37(2): 215-220)
(  0) 0) |
2. Collaborative Innovation Center of Geospatial Technology, 129 Luoyu Road, Wuhan 430079, China;
3. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, 129 Luoyu Road, Wuhan 430079, China
 2019, Vol. 39
2019, Vol. 39


