2. 地理信息工程国家重点实验室,西安市雁塔路中段1号,710054;
3. 陆军工程大学国防工程学院,南京市后标营路88号,210007;
4. 32139部队,北京市,101211;
5. 信息工程大学地理空间信息学院,郑州市科学大道62号,450001
电离层延迟在GNSS测量误差中仅次于钟差的影响,是单频GNSS测量中必须考虑的误差源。电离层延迟变化复杂,和卫星、测站经纬度、太阳方位等相关。目前各大GNSS系统采用的电离层模型是对电离层的一种近似推估和拟合[1-3]。对于变化连续的测量数据,最小二乘多项式拟合可以有效地减弱观测噪声,并且已经广泛应用于测量数据处理中[4-5]。对于趋势性较为复杂的时变数据,通常在选择的一定时间窗口内逐个处理,得到更接近真值曲线的结果,通常称之为移动开窗或滑动窗口法[6-7]。本文将基于移动开窗的逐历元拟合算法简称为逐历元法。逐历元法可以有效利用与当前历元时间最近、最相关的数据,从而避免由时间积累带来的误差,得到比整体拟合更佳的拟合效果。但是如果观测数据量较大且窗口较大,常规逐历元法的计算量将变得非常庞大,甚至使计算机难以计算,或者难以在有效时间内完成计算。另一种常用的算法是将整体数据进行独立分段,对各个分段分别进行处理[8-9]。这种算法在处理大批量数据时,在计算效率上具有明显的优势,但是这种算法用于分段拟合时,各个分段之间并不连续,会造成节点的断裂。针对这两种常用方法的特点和不足,本文提出一种基于分段的重叠滑动窗口拟合算法,将窗口进行再次分区,并重叠相邻窗口,采用加权平均法使得窗口间拟合数据连续,拟合效率较高。
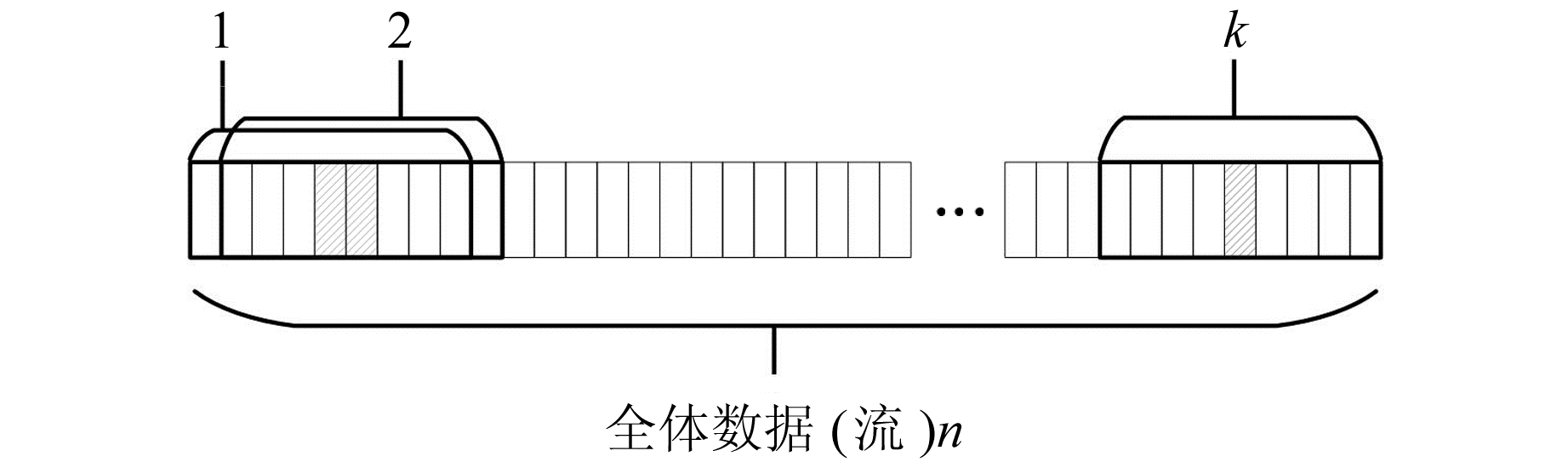
1 常规开窗算法 1.1 逐历元滑动窗口以处理历元数量为n的数据块或历元数据流为例,以某历元为中心向前向后扩展为m个历元的数据块,称之为大小为m的窗口数据。如图 1所示,其中一个小格代表一个历元的数据,斜线填充的小格为当前历元。在处理数据时,逐个历元向前或向后移动,直到处理完所有数据,这种方法称之为逐历元滑动窗口法,简称逐历元法。
|
图 1 逐历元滑动窗口 Fig. 1 Epoch-by-epoch sliding window |
这种方法的优点是能够确保当前历元所采用的数据为与其最为接近、最相关的数据,利用窗口内数据求平均、拟合等操作会得到比较理想的结果。然而,由于每个历元采用的数据都不一样,每个历元都要进行一次最小二乘平差计算,随着窗口数量的增加,其计算量将越来越大,计算时间也越来越长。
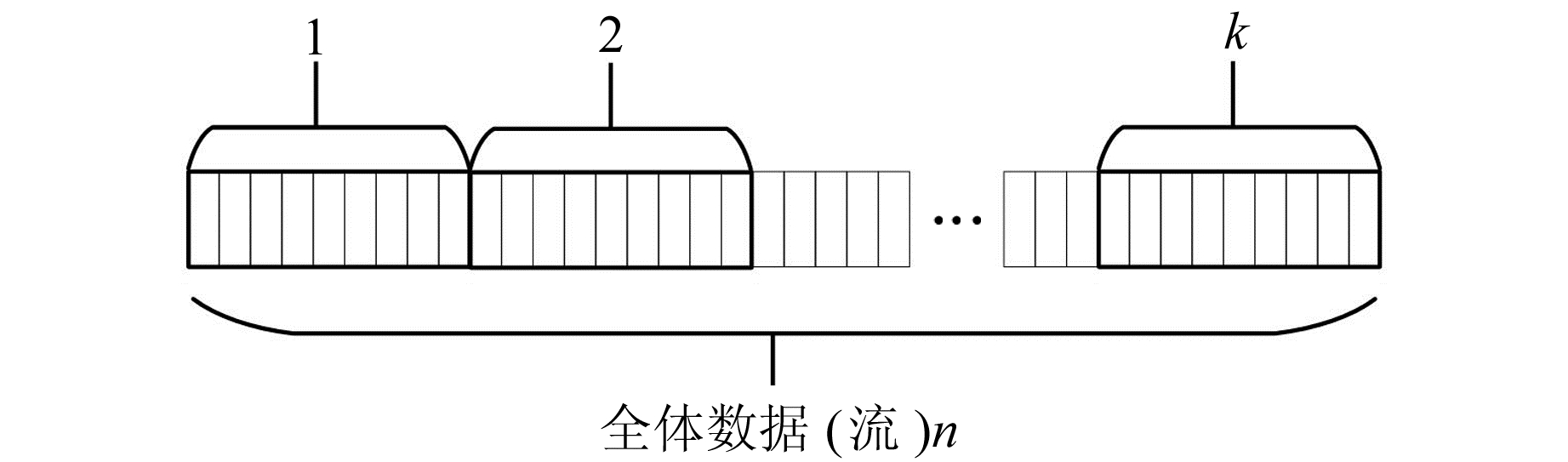
1.2 分段窗口将全体数据按照大小为m个历元的窗口进行分割,称之为独立分段或独立开窗法,如图 2所示,各个窗口并不重叠,首尾相连、互为拼接。
|
图 2 分段开窗示意图 Fig. 2 Schematic diagram of sectional windowing |
与逐历元滑动窗口不同,分段窗口等同对待窗口内的各历元数据。其优点是,对于窗口内的数据,只需一次最小二乘拟合计算,因而计算量较小。通过多次分割,可以快速处理大量数据。不足之处在于,在处理历元相关数据时,独立的窗口之间造成人为的独立分割,导致数据发生“断裂”,其计算精度没有逐历元法高。
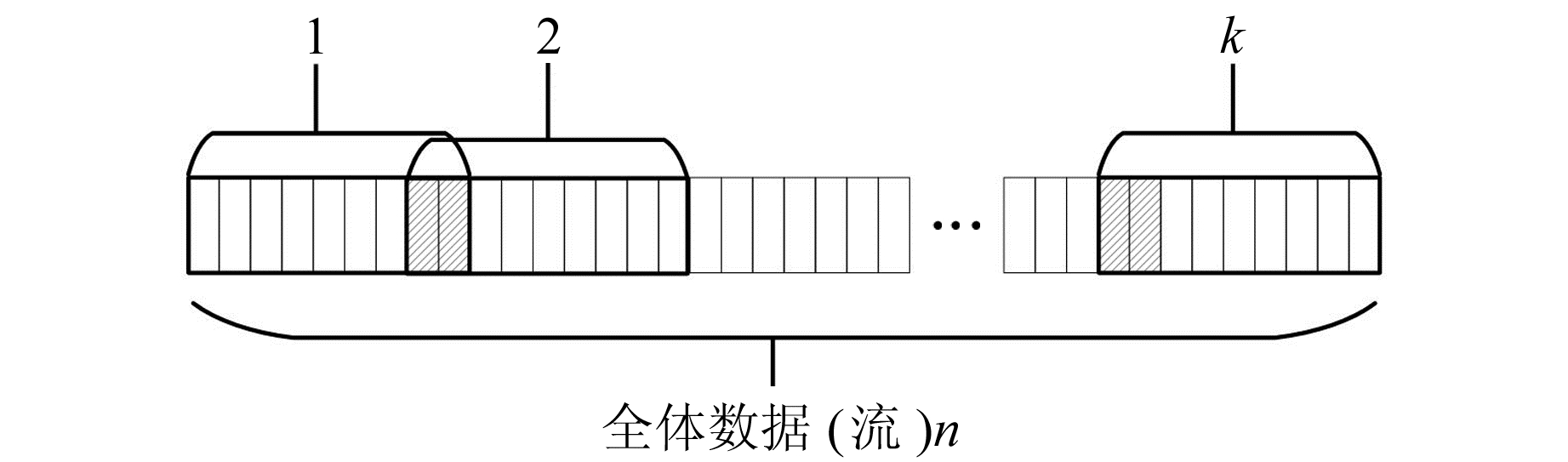
2 分段重叠窗口拟合算法 2.1 部分边界重叠的分段滑动窗口重叠部分边界的分段窗口如图 3所示,斜线填充的是重叠边缘历元数据,即在相邻的窗口中都具有这些历元,从而使得前后窗口的数据并不独立。这种方法兼具逐历元滑动窗口和分段窗口的特点,在减少数据计算量的同时,可确保相邻窗口数据间的连续性。
|
图 3 部分边界重叠的分段滑动窗口 Fig. 3 Segmented sliding window with partially overlapping boundaries |
但是,由于在分段窗口的多项式拟合中,各个窗口拟合函数的不同,造成重叠边界计算数值的不同,即在重叠区域具有2个不同的拟合数据,并且窗口边缘的数据拟合效果通常不如窗口内部的数据拟合效果好。本文设计了具有边缘和重叠拟合区的窗口多项式拟合算法。
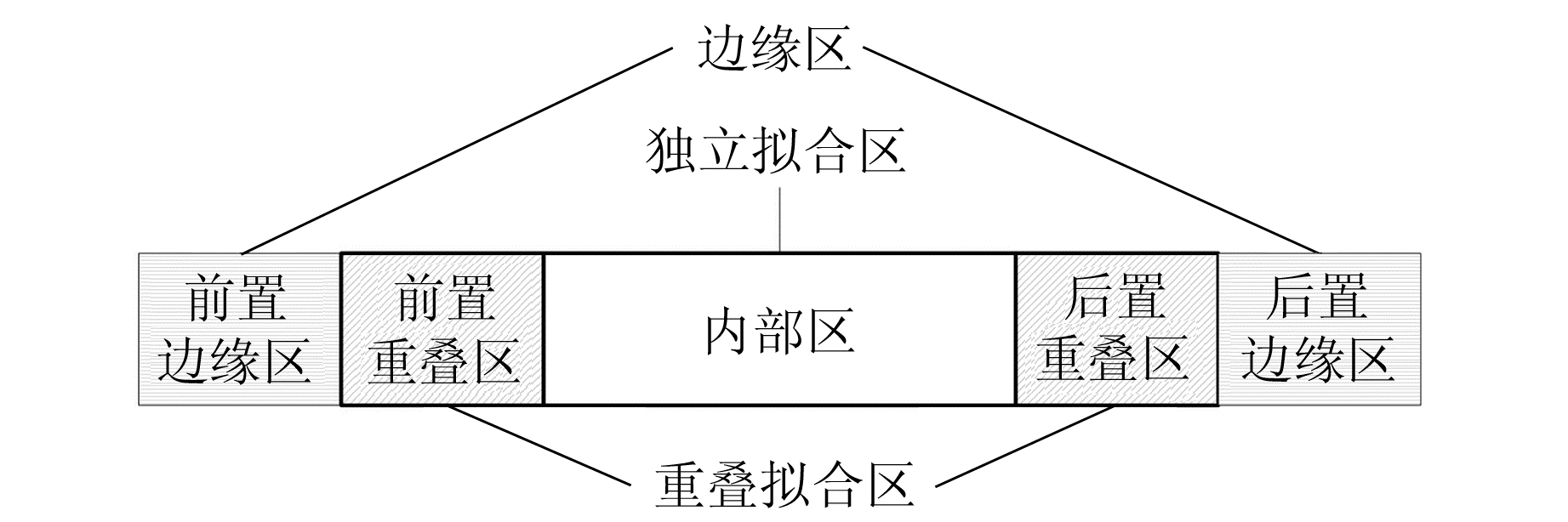
2.2 具有边缘和重叠拟合区的窗口将分段的窗口按照图 4进行分段,一个窗口包括边缘区、重叠区和内部区,其中边缘区和重叠区按照数据方向的不同,分别分为前置和后置两种。在拟合计算时,边缘区的数据只用于计算拟合函数,而不参与拟合求值,这样可以保证拟合精度。
|
图 4 窗口数据分类 Fig. 4 Window data classification |
重叠区和内部区的数据参与拟合函数计算,同时处于该两区的历元可以直接计算拟合值,但是该重叠区要和相邻历元的重叠区进行加权平均,以确保具有唯一的拟合值。相邻两个窗口的前置或后置重叠区的数据相等,如图 5所示。

|
图 5 改进后的时段窗口关系 Fig. 5 Improved time window relationship |
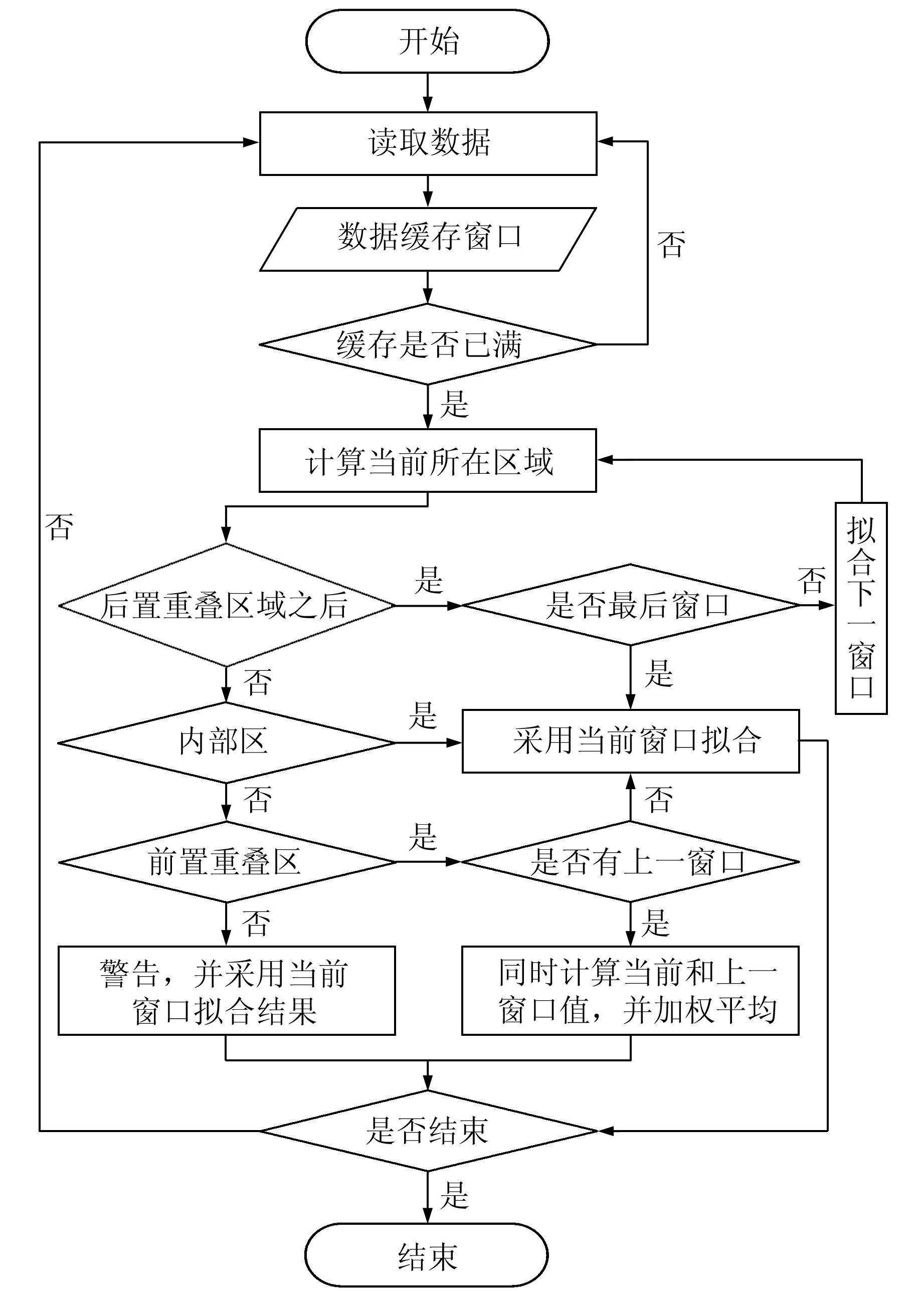
指定拟合历元数为m,边界区历元数为e,重叠区历元数为o。数据读入后,预读缓存历元数为b(b=m-e)。当缓存填满后,开始构建历元数为w(w=m+e)的滑动窗口容器,并开始拟合计算。拟合时,首先计算待拟合历元在窗口数据中的区域位置(图 4)。根据所处位置的不同采用相应的拟合算法(图 6),为从前往后的流式数据重叠窗口拟合算法。
|
图 6 算法流程 Fig. 6 Algorithm flow chart |
当历元达到后置重叠区时,进行下一个拟合窗口的构建,并将当前窗口替换为新建的窗口,将旧窗口赋值为前一窗口,然后计算当前历元位置,判断并计算。对于内部区的数据,直接采用当前窗口拟合计算;对于处于重叠区的窗口,则同时获取相邻2个窗口的拟合值,然后再按照所获得的值与窗口内部区的距离进行加权平均,从而获得一个唯一的值:
| $ \bar x = \frac{{{d_2}{x_1} + {d_1}{x_2}}}{{{d_1} + {d_2}}} $ | (1) |
式中,xi为窗口i的拟合值,di为当前历元距离i窗口内部区的距离。
3 电离层延迟拟合应用分析 3.1 实验环境和数据采用GNSS的实测数据和本文方法,对GNSS信号的电离层延迟进行拟合计算,并对比各种方法的拟合偏差和计算时间。3种算法分别命名为逐历元法、独立分段法、重叠分段法。重叠区设置为拟合窗口的1/3,边界区为1/4。具体应用中,这些参数可以根据实际需求进行设置。实验平台基于GNSSer数据处理软件[10],GNSSer软件是一个国产GNSS数据处理平台,致力于高精度、云模式的GNSS计算服务。实验开发语言为C#,运行平台为. NET 4.5,计算机CPU为Intel i7-7700HQ, 内存为16 GB。
数据来自IGS在2018年第1天的NKLG和SHAO站。NKLG位于非洲中部西海岸加蓬共和国的首都利伯维尔(Libreville),该站位于赤道附近(9.67°E, 0.35°N),对GNSS卫星的平均可见时段较长且电离层影响较为强烈。实验选取NKLG站的G01星,有效观测时段为UTC 06:00~11:39(本地时间为07:00~12:39),作为电离层剧烈变化的代表。SHAO站位于中纬度的中国上海(121.2°E, 31.1°N),分别取G18星的正午时段(有效观测时段UTC 02:30~08:00,即本地时间10:30~16:00)和G01星的夜间时段(时段UTC 14:30~19:27,即本地时间22:30~03:27)作为中纬度地区电离层延迟影响最剧烈和最平缓的时段,来测试各种电离层拟合算法的效果。图 7为分别采用单频伪距和载波组合与双频载波计算的3个时段卫星电离层变化,高度截止角为15°。

|
图 7 3个时段站星电离层延迟变化 Fig. 7 Ionospheric delay variation from station to satellite over three periods |
从图 7可以发现,NKLG站的G01星电离层延迟影响较大,其变化达到了10 m,而中纬度的SHAO站的G01和G18的电离层延迟变化只有1~3 m;电离层延迟历元间变化连续,呈现一定的趋势性;双频载波计算的电离层延迟平滑,而单频伪距和载波组合的电离层延迟具有明显的噪声。站星电离层延迟变化决定于信号传输过程的电子浓度,与卫星高度角、测站经纬度等相关,并不非常规则,若所有观测时段采用整体曲线拟合,通常并不能达到理想的效果,因而实际运用中常采用滑动窗口拟合的方法计算。由于载波观测量的测量精度达mm[11],因此双频载波计算的一阶电离层偏差精度也在mm级别。本文将其作为电离层延迟变化的真值,对单频伪距和载波组合计算的电离层延迟,采用3种滑动窗口拟合算法进行计算,并比较各种算法的计算精度和运行效率。
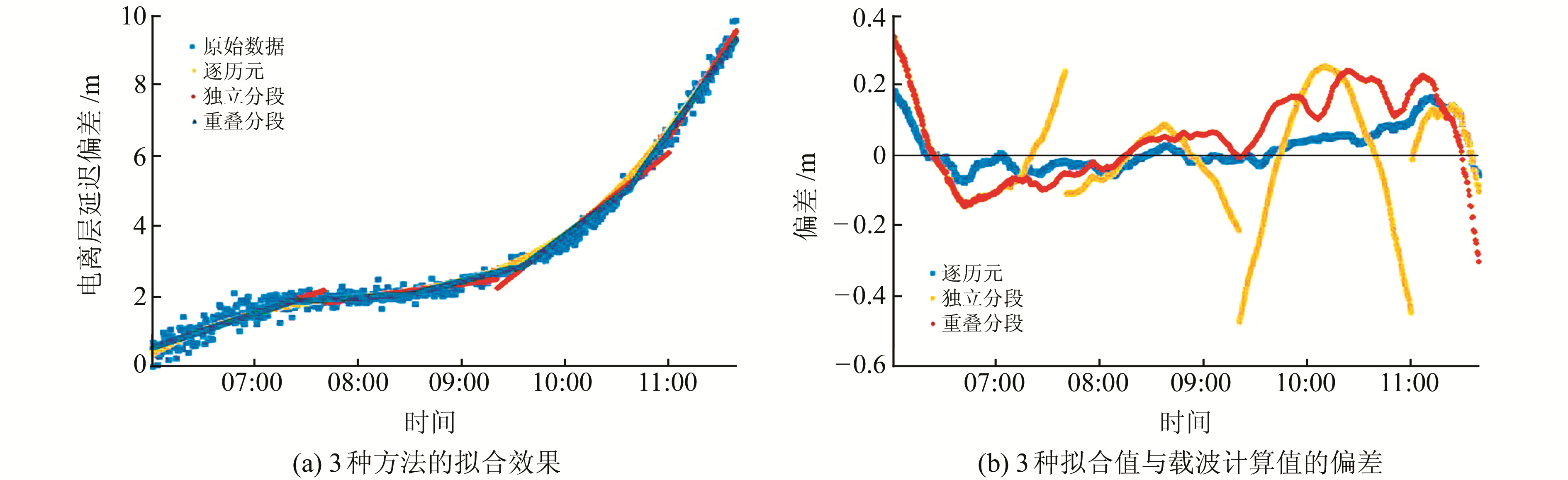
3.2 3种方法的拟合效果分析实验采用NKLG站的G01卫星电离层延迟数据,采样率为30 s,总历元数为678个。为从图形上明显区别各种算法的拟合效果,此处采用大跨度窗口(200历元,100 min),分别采用逐历元、独立分段和重叠分段算法进行一维线性拟合,并对拟合结果进行对比(图 8)。
|
图 8 各种方法的拟合效果与偏差 Fig. 8 Fitting effect and deviation of various methods |
由图 8可见,逐历元法的拟合效果与原始数据的符合程度最好,独立分段方法误差大且具有明显的窗口断裂,而改进的重叠分段法介于二者之间,精度优于独立分段法,同时消除了窗口间的断裂。
3.3 3种方法的拟合精度对比采用3种算法分别对NKLG的G01、SHAO站的G01和G18三个时段的单频伪距和载波计算的站星电离层延迟进行拟合,数据采样率为5 s,以双频载波计算的电离层延迟变化作为真值,统计每种算法的残差中误差,计算结果如表 1所示,其中加粗字体为当前算法的最优精度。根据表 1数据绘制NKLG G01和SHAO G18的三维曲面梯度图(图 9)。
|
|
表 1 3种算法对3段不同站星数据的拟合精度 Tab. 1 Fitting accuracy of three algorithms for three different stations to satellite data |

|
图 9 3种方法拟合精度的曲面梯度图 Fig. 9 Surface gradient map of fitting accuracy with three methods |
可以发现,逐历元滑动窗口拟合算法精度最高,独立分段法拟合精度最差,重叠分段法精度高于独立分段法,而略低于逐历元法。NKLG的G01在200~300历元(40~60 min)取得了最好的精度,SHAO的G01和G18在300~400历元(60~80 min)取得了最好的拟合精度。对比图 7可以发现,最优拟合窗口和电离层变化剧烈程度相关,当电离层变化缓慢时,可采用60~80 min窗口拟合;而变化剧烈时,最好采用40~60 min窗口拟合。
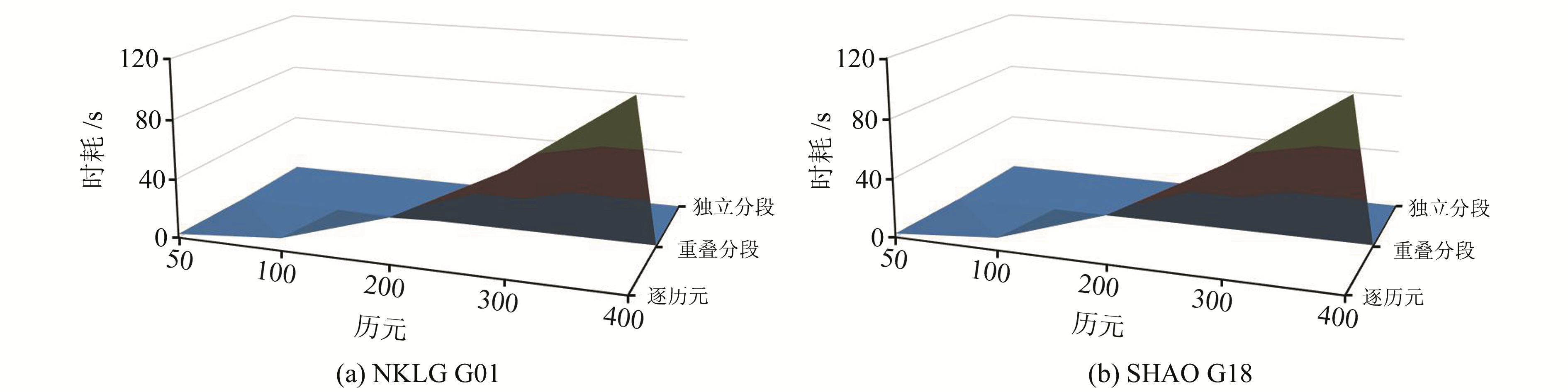
3.4 3种算法的计算效率对比采用§3.3的数据和方法,分别统计各种算法在不同历元窗口的时间消耗,统计结果见表 2。根据表 2数据绘制NKLG G01和SHAO G18的三维曲面梯度图,如图 10所示。
|
|
表 2 3种算法对3段不同站星数据的时耗 Tab. 2 Time-consuming of three algorithms for data of three different stations to satellite |
|
图 10 3种方法拟合时间的曲面梯度图 Fig. 10 Surface gradient map of fitting time with three methods |
可以发现,3个时段的站星数据计算时耗和趋势基本一致,随着总历元数量和窗口历元数量的增加,逐历元法的计算时间呈几何级数增长,而独立分段和重叠分段法的计算时间呈线性增长。以NKLG站的G01为例,在400历元窗口的拟合计算中,逐历元法耗费121.618 s,而独立分段法和重叠分段法分别只用0.396 s和0.985 s,计算效率分别为前者的307倍和123倍。
4 结语通过本文实验可以得出以下结论:1)计算精度上,逐历元法最高,重叠分段法次之,独立分段法最低;2)计算效率上,逐历元法最低,重叠分段法次之,独立分段法最高。
重叠分段法是介于逐历元法和独立分段法之间的一种算法,当将内部区设定为1、重叠区设定为0时,重叠分段法与逐历元法完全相同;当重叠区和边缘同时设定为0时,重叠法和独立分段法完全相同。因此,在运用中根据实际需求,合理地设定重叠区和边缘区,重叠法可以在精度和效率上获得理想的结果。
| [1] |
Klobuchar J A. Ionospheric Time-Delay Algorithm for Single-Frequency GPS Users[J]. IEEE Trans on AES, 1987, 23(3): 325-331
(  0) 0) |
| [2] |
袁运斌, 霍星亮, 张宝成. 近年来我国GNSS电离层延迟精确建模及修正研究进展[J]. 测绘学报, 2017, 46(10): 1 364-1 378 (Yuan Yunbin, Huo Xingliang, Zhang Baocheng. Research Progress of Precise Models and Correction for GNSS Ionospheric Delay in China over Recent Years[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1 364-1 378)
(  0) 0) |
| [3] |
谢杰, 张博, 侯博, 等. Galileo卫星导航系统广播NeQuick模型及其参数拟合[J]. 空间科学学报, 2012, 32(6): 881-886 (Xie Jie, Zhang Bo, Hou Bo, et al. Simulation of NeQuick Parameters of Galileo Satellite Navigation System[J]. Chinese Journal of Space Science, 2012, 32(6): 881-886)
(  0) 0) |
| [4] |
王建强, 李建成, 赵国强, 等. 多项式拟合快速计算扰动引力方法[J]. 大地测量与地球动力学, 2013, 33(4): 52-55 (Wang Jianqiang, Li Jiancheng, Zhao Guoqiang, et al. Fast Calculation of Earth's Disturbing Gravity through Polynomial Fitting[J]. Journal of Geodesy and Geodynamics, 2013, 33(4): 52-55)
(  0) 0) |
| [5] |
吉长东, 徐爱功, 冯磊. GPS精密星历拟合与插值中龙格现象的处理方法[J]. 测绘科学, 2011, 36(6): 169-171 (Ji Changdong, Xu Aigong, Feng Lei. Treatment of Runge's Phenomenon in Fitting and Interpolating GPS Precise Ephemeris[J]. Science of Surveying and Mapping, 2011, 36(6): 169-171)
(  0) 0) |
| [6] |
刘茂华, 尹潇, 吕志鹏, 等. 基于移动窗口的抗差自适应滤波算法研究[J]. 大地测量与地球动力学, 2014, 34(6): 140-143 (Liu Maohua, Yin Xiao, Lü Zhipeng, et al. Research of Robust Adaptive Filtering Based on Moving Window[J]. Journal of Geodesy and Geodynamics, 2014, 34(6): 140-143)
(  0) 0) |
| [7] |
杨元喜, 徐天河. 基于移动开窗法协方差估计和方差分量估计的自适应滤波[J]. 武汉大学学报:信息科学版, 2003(6): 714-718 (Yang Yuanxi, Xu Tianhe. An Adaptive Kalman Filter Combining Variance Component Estimation with Covariance Matrix Estimation Based on Moving Window[J]. Geomatics and Information Science of Wuhan University, 2003(6): 714-718)
(  0) 0) |
| [8] |
陈然, 戴齐. 基于重要点的时间序列固定分段数分段算法[J]. 计算机技术与发展, 2011, 21(9): 103-106 (Chen Ran, Dai Qi. Time Series Segmentation Based on Fixed Number of PIPs Detection[J]. Computer Technology and Development, 2011, 21(9): 103-106 DOI:10.3969/j.issn.1673-629X.2011.09.027)
(  0) 0) |
| [9] |
喻高瞻, 彭宏, 胡劲松, 等. 时间序列数据的分段线性表示[J]. 计算机应用与软件, 2007(12): 17-18 (Yu Gaozhan, Peng Hong, Hu Jinsong, et al. Piecewise Linear Representation of Time Series Data[J]. Computer Applications and Software, 2007(12): 17-18 DOI:10.3969/j.issn.1000-386X.2007.12.008)
(  0) 0) |
| [10] |
Li L Y, Lü Z P, Chen Z S, et al. GNSSer: Objected-Oriented and Design Pattern-Based Software for GNSS Data Parallel Processing[J]. Journal of Spatial Science, 2019, 10
(  0) 0) |
| [11] |
许国昌. GPS理论、算法与应用[M]. 北京: 清华大学出版社, 2011 (Xu Guochang. GPS Theory, Algorithm and Application[M]. Beijing: Tsinghua University Press, 2011)
(  0) 0) |
2. State Key Laboratory of Geo-Information Engineering, 1 Mid-Yanta Road, Xi'an 710054, China;
3. Academy of National Defense Engineering, Army Engineering University, 88 Houbiaoying Road, Nanjing 210007, China;
4. 32139 Troops of PLA, Beijing 101211, China;
5. School of Surveying and Mapping, Information Engineering University, 62 Kexue Road, Zhengzhou 450001, China
 2019, Vol. 39
2019, Vol. 39


