利用重力场位系数模型计算垂线偏差的耗时会随着截断阶次、计算范围、分辨率的增大而增加,难以满足一些工程的需求[1-4]。尽管利用交换积分次序等方法可以减少计算量从而提高计算效率,但随着计算区域和分辨率的增加,上述方法计算耗时显著增加,因为常规串行程序运行过程中仅使用单核计算,极大地浪费运算能力[5]。OpenMP是一个并行运算库,它可用于共享内存并行系统多处理器程序设计编译处理[6],但OpenMP在对复杂程序进行整体并行时,常会造成内存读写冲突,导致并行化失败。本文提出利用OpenMP并行计算方法计算超高阶垂线偏差,并通过数组升维和分区计算的方法解决并行化过程中内存读写冲突的问题,能显著提升计算效率。
1 Belikov递推法与交换积分次序法 1.1 缔合勒让德函数Belikov递推法缔合勒让德函数Belikov递推法公式为:
| $ \left\{ \begin{array}{l} {{\tilde P}_{n0}}\left( {\cos \theta } \right) = t{{\tilde P}_{n - 1, 0}}\left( {\cos \theta } \right) - \\ \;\;\;\frac{u}{2}{{\tilde P}_{n - 1, 1}}\left( {\cos \theta } \right), \;\;\;m = 0\\ {{\tilde P}_{nm}}\left( {\cos \theta } \right) = t{{\tilde P}_{n - 1, m}}\left( {\cos \theta } \right) - \\ \;\;\;u\left[ {\frac{1}{4}{{\tilde P}_{n - 1, m + 1}}\left( {\cos \theta } \right) - {{\tilde P}_{n - 1, m - 1}}\left( {\cos \theta } \right)} \right], \\ \;\;\;m > 0 \end{array} \right. $ | (1) |
将
| $ {\overline P _{nm}}\left( {\cos \theta } \right) = \sqrt {2n + 1} {\tilde N_{nm}}{\tilde P_{nm}}\left( {\cos \theta } \right) $ | (2) |
其中,
| $ \left\{ \begin{array}{l} {{\tilde N}_{nm}} = \sqrt {\left( {2 - \delta _0^m} \right)\frac{{\left( {n + m} \right)!}}{{{2^m}n!}}\frac{{\left( {n - m} \right)!}}{{{2^m}n!}}} \\ \delta _0^m = \left\{ \begin{array}{l} \begin{array}{*{20}{c}} {1, }&{m = 0} \end{array}\\ \begin{array}{*{20}{c}} {0, }&{m \ne 0} \end{array} \end{array} \right. \end{array} \right. $ | (3) |
由位系数模型计算模型垂线偏差的计算公式为:
| $ \left\{ {\begin{array}{*{20}{l}} {\xi _M^{ij} = \sum\limits_{m = 0}^N {(xE_m^i\cos m{\lambda _j} + xF_m^i\sin m{\lambda _j})} }\\ {xE_m^i = - \sum\limits_{n = 0}^N {{{(\frac{R}{{{r_i}}})}^{n + 2}}\bar C_{nm}^ * \frac{d}{{{\rm{d}}\varphi }}{{\bar P}_{nm}}(\sin {\varphi _i})} }\\ {xF_m^i = - \sum\limits_{n = 0}^N {{{(\frac{R}{{{r_i}}})}^{n + 2}}{{\bar S}_{nm}}\frac{d}{{{\rm{d}}\varphi }}{{\bar P}_{nm}}(\sin {\varphi _i})} } \end{array}} \right. $ | (4) |
| $ \left\{ {\begin{array}{*{20}{l}} {\eta _M^{ij} = \sum\limits_{m = 0}^N {(yE_m^i\cos m{\lambda _j} + yF_m^i\sin m{\lambda _j})} }\\ {yE_m^i = - \sum\limits_{n = 0}^N {{{(\frac{R}{{{r_i}}})}^{n + 2}}m{{\bar S}_{nm}}\frac{{{{\bar P}_{nm}}(\sin {\varphi _i})}}{{\cos {\varphi _i}}}} }\\ {yF_m^i = \sum\limits_{n = 0}^N {{{(\frac{R}{{{r_i}}})}^{n + 2}}m\bar C_{nm}^ * \frac{{{{\bar P}_{nm}}(\sin {\varphi _i})}}{{\cos {\varphi _i}}}} } \end{array}} \right. $ | (5) |
式中,(ri, λi, φj)为第i个纬度圈第j个网格中点处地心向径和经纬度(为简单起见,实验中可假定ri=R)。这样,同一纬度圈只需递推勒让德函数及其导数便可一次求得系数xEmi、xFmi、yEmi和yFmi,从而加快其计算速度。而经度的正余弦函数值亦可递推求得。
2 OpenMP多核并行算法单核CPU运算时,串行程序依照编写顺序依次进行计算。多核CPU进行并行运算时,多个CPU可同时对程序各进程进行运算,从而提高程序的运行效率。OpenMP支持Fortran、C/C++的共享存储并行编程。它基于fork-join的并行执行模型,将程序主体划分为并行区和串行区,不同线程间可通过共享变量实现数据交换[6]。本文采用OpenMP多核并行算法,实现依托于超高阶重力场模型的高精度垂线偏差并行运算。
2.1 并行计算的需求分析缔合勒让德函数值在同一纬度上相同,因此在计算格网模型垂线偏差时将纬度作为外层循环、经度作为内层循环来减少缔合勒让德函数的计算次数。考虑到缔合勒让德函数的求解涉及到递推算法,因此无法直接利用并行手段对该过程进行直接改化。本文主要考虑依据纬度的不同对相应格网点进行分组,进行多纬度同时计算以提高计算效率。
2.2 并行方案使用同构并行面临两个问题。一是并行手段的选择问题。在共享存储器环境下,OpenMP多线程技术以其良好的简洁性和可移植性成为共享存储系统并行编程的工业标准[7]。OpenMP可直接在高级语言(如C语言)的串行代码上通过编写并行制导语句实现程序的并行化,而不需要作太大的修改。但如果需要并行化的程序比较复杂,则需要改变程序内部结构以防止并行后内存读写冲突,这一过程相对较为复杂。二是怎样更为有效地提高并行效率, 这个问题将在下节进行讨论。
2.3 并行算法设计本节主要分析讨论利用OpenMP技术进行并行设计的几个关键问题:一是如何将原来复杂的串行程序改为并行程序,避免内存读写冲突;二是如何更为有效地利用计算机的运算能力,提高并行效率。
2.3.1 并行程序实现经过前面的分析可知,计算不同纬度圈上的格网点模型垂线偏差有着天然的可并行性,而缔合勒让德函数因其递推计算的性质不利于并行化,在并行过程中会造成数组和变量的内存读写冲突,即数组和变量在被不同线程调用读写的过程中会产生内存读写冲突导致程序中断,因此需要对它们进行一定的处理以消除内存读写冲突。
使用OpenMP中private数据子句解决简单变量的内存读写冲突问题。private子句可将简单变量声明为本线程的私有变量,每个线程都存有变量的副本,其他线程无法访问。即使在并行区域外有同名的共享变量,此共享变量也不会对并行区域造成影响,且并行区域内部计算也不会改变外部共享变量的值[7]。因此在并行起始语句中加入private(m, f, n, …)即可解决简单变量的内存读写冲突问题。
然而对于数组变量,尤其是二维数组变量,在普通便携式计算机上通过private子句进行变量私有会占用大量的内存空间,针对以上问题本文提出数组升维和区域分组方法。
数组升维是指将一维数组升至二维数组(如将xE[f]、xF[f]、yE[f]、yF[f]升维至xE[v][f]、xF[v][f]、yE[v][f]、yF[v][f]); 将二维数组升至三维数组(如将P[e][f]和dP[e][f]升维至P[v][e][f]和dP[v][e][f])。这样,就可通过循环v实现不同线程在高维数组中调用不同的低维数组。当v等于网格行数时,就可通过一条OpenMP并行语句实现格网点模型垂线偏差的并行计算。
在计算截断阶数为j的超高阶垂线偏差时,如果令v=gw2(gw2为格网行数),则需要开辟多个j×j×gw2的三维数组。假定截断阶数j=2 160,计算区域4°×8°(纬度×经度),分辨率2′×2′,则gw2=120。一个double型数据需要占用8字节内存,则开辟一个double型三维数组需要占用4.17 G内存,这显然不适用于普通计算机,如何使用有限的内存来达到并行效果成为本文另一个研究重点。
为解决以上问题,以8线程为例,对计算格网进行区域分组,将格网以行为单位,8行为1组进行计算。在使用OpenMP进行并行计算时,在每组内进行并行计算,这样只需要开辟2 160×2 160×8的三维数组,此时内存占用仅为之前的1/15。
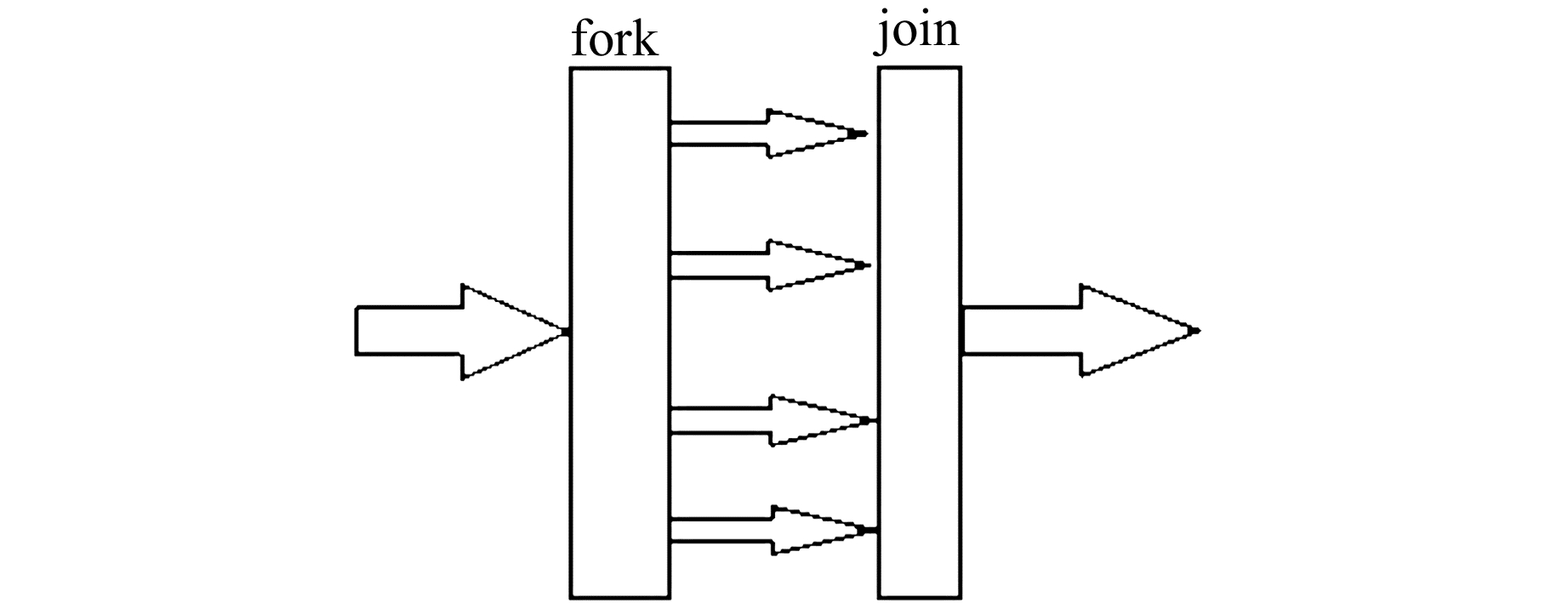
2.3.2 并行程序改进OpenMP是以fork-join(分叉-合并)的形式来执行并行指令,其中fork代表开启新线程,join代表多个线程会合。fork-join模型在运行前只有一个线程存在,称之为“主线程”;在运行过程中,遇到并行开始代码,计算机则调用多个线程来执行并行任务;在并行代码执行结束后,调用的程被释放,不再工作[8](图 1)。
为了减少线程调度的时间消耗,本文提出一种优化算法:当待计算格网行数为gw2、使用线程数为p时,将格网平均分为p组,若gw2与p之比不为整数,余数为q,则将余下q行分配至前q个线程,以保证线程利用率最高。
分别取7线程和8线程为例。首先要对计算区域进行分区,以4°×8°(分辨率为2′×2′)范围格网为例,格网行数gw2为120。7线程时,将区域分为7组,第1组分配18行,后6组分配17行;8线程时,将区域分为8组,每组分配15行,将每组的计算分配给独立的线程。
3 实验计算分析为验证本文所提方法的有效性,利用便携式个人计算机,基于VS2013平台(C语言)对上述方法进行实验。实验所用计算机处理器为Intel®CoreTMi7-4700MQ CPU@ 2.40 GHz,内存为8.00 GB,操作系统为64位Windows 10专业版操作系统。实验采用超高阶地球重力场模型EIGEN6C4[4],拓展阶次为2 160阶,空间分辨率为5′×5′。
3.1 并行程序改进前后对比分析计算范围为4°×8°(纬度×经度),分辨率分别取2′×2′和1′×1′,统计不同线程数下该区域格网模型垂线偏差的求解时间,计算耗时见表 1。
|
|
表 1 程序改进前后格网计算耗时 Tab. 1 Time-consuming grid computing before and after program improvement |
由实验结果可知,多线程任务模式下,改进后的算法(多线程分区计算法)计算时间更短(在计算范围4°×8°、分辨率1′×1′时,改进后算法耗时减少4.34 s),充分证明改进后的算法能减少OpenMP线程调度时间,提高代码运行效率。
因此在接下来的实验中,均采用改进后的分区计算方法进行任务测试。
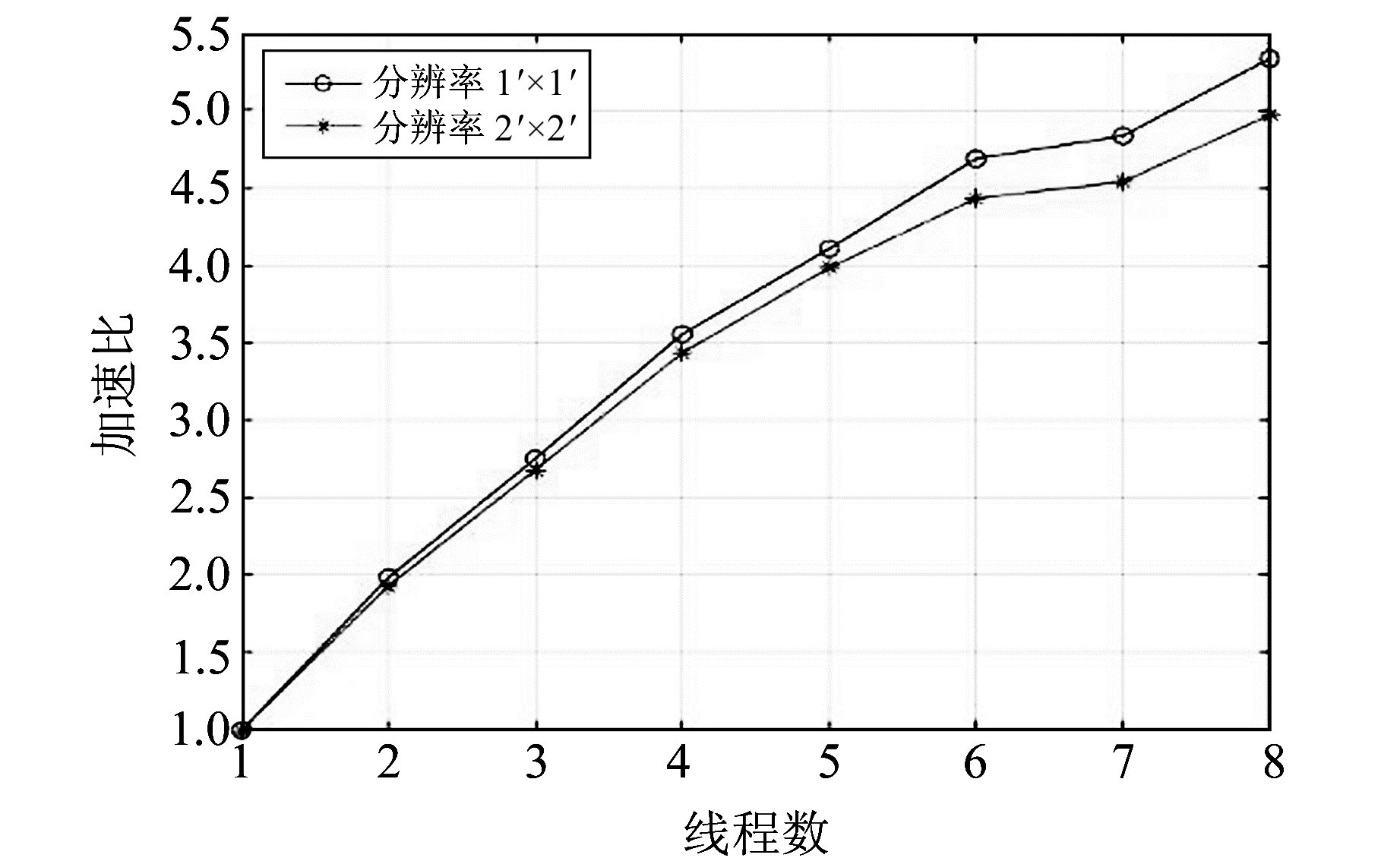
3.2 不同线程数加速效果分析利用上述实验结果,统计改进后程序耗时的加速比(不同线程数与串行程序效率比),结果见表 2和图 2。
|
|
表 2 改进后程序计算的加速比 Tab. 2 Using the improved program to calculate the acceleration ratio |
|
图 2 不同线程数下计算的加速比 Fig. 2 Acceleration ratios computied with different threads |
由测试结果可知:
1) 随着线程数的增加,计算的加速比在提高,加速比在8线程下可达到5.3倍。
2) 加速比会小于对应的线程数(如8线程时加速比为5.3)。因为在程序运算过程中,OpenMP调度线程和同步各个线程计算过程都需要消耗一定的时间,改进后的程序尽管减少了线程调度时间,但没有减少同步线程计算的时间。
3) 由图 2可知,线程数为7时,加速比提高效果不明显,主要原因在于格网数不能整除线程数。按照上述线程分配原则,0号线程分配18行格网、1~6线程分配17行格网,计算耗时以任务量最大的0号线程计算结束为准,因此加速效果不明显。
4) 格网分辨率提高,计算量变大,同等线程数下加速比会提高。
3.3 不同范围计算效果对比在上述实验的基础上,基于8线程组织实验,实验范围分别为实验区1(2°×4°)、实验区2(4°×8°)、实验区3(8°×16°),对应分辨率分别为2′×2′和1′×1′。统计不同线程数下各个实验区格网模型垂线偏差赋值时间,计算耗时和加速比(表 3)。
|
|
表 3 不同范围计算的耗时与加速比 Tab. 3 Time-consuming and acceleration ratio in different ranges |
由测试结果可知,计算效率会随着计算范围的增大而提高,计算范围8°×16°、分辨率为1′×1′的格网串行运算时间为307 s,并行加速后计算耗时仅为54 s,加速比达到5.6倍,计算效率获得大幅提升。
4 结语本文对计算超高阶垂线偏差的并行化问题进行探讨。根据实际计算需求和设备的特点,引入OpenMP并行算法。通过实例阐述并行化过程的关键技术,即数组升维和分区计算技术,并进行数值验证。结果表明,并行计算充分利用现有计算设备的计算能力,在不增加任何多余成本的基础上,提高了模型垂线偏差的解算速度,加速比最高可达5.6倍,为大范围乃至全球计算提供了保障。
本文提出的数组升维和分区计算方法,能有效解决OpenMP算法处理大型复杂程序整体并行过程中的内存读写冲突问题,并通过实验验证这一技术的可行性,为解决重力场数据计算和处理过程中各种复杂程序整体并行问题提供了解决思路,同时也是提高数据处理计算能力的有效途径之一。
| [1] |
范昊鹏, 李姗姗. 局部区域模型重力异常快速算法研究[J]. 大地测量与地球动力学, 2013, 33(6): 28-30 (Fan Haopeng, Li Shanshan. Study on a Fast Algorithm for Model Gravity Anomalies in Local Areas[J]. Journal of Geodesy and Geodynamics, 2013, 33(6): 28-30)
(  0) 0) |
| [2] |
曲政豪, 曾添, 周强. 超高阶地球重力场模型的高程异常优化算法[J]. 海洋测绘, 2014, 34(4): 5-8 (Qu Zhenghao, Zeng Tian, Zhou Qiang. Optimization Algorithm for Height Anomaly of Ultra-High Degree and Order Earth Gravity Field Model[J]. Hydrographic Surveying and Charting, 2014, 34(4): 5-8 DOI:10.3969/j.issn.1671-3044.2014.04.002)
(  0) 0) |
| [3] |
章传银, 郭春喜, 陈俊勇, 等. EGM2008地球重力场模型在中国大陆适用性分析[J]. 测绘学报, 2009, 38(4): 283-298 (Zhang Chuanyin, Guo Chunxi, Chen Junyong, et al. EGM 2008 and Its Application Analysis in Chinese Mainland[J]. Acta Geodaeticaet Cartographica Sinica, 2009, 38(4): 283-298 DOI:10.3321/j.issn:1001-1595.2009.04.001)
(  0) 0) |
| [4] |
欧阳明达, 张敏利, 于亮. 采用Belikov列推和跨阶次递推方法计算超高阶缔合勒让德函数[J]. 测绘工程, 2017, 26(7): 12-15 (Ouyang Mingda, Zhang Minli, Yu Liang. Calculating the Ultra-High-Order Associated Legendre Functions by Belikov Column Method and Recursive Method Between Every Other Order and Degree[J]. Engineering of Surveying and Mapping, 2017, 26(7): 12-15)
(  0) 0) |
| [5] |
黄佳喜.扰动重力场快速(并行)计算方法研究[D].郑州: 信息工程大学, 2017 (Huang Jiaxi. Research on Fast (Parallel) Computing of Disturbing Gravity[D]. Zhengzhou: Information Engineering University, 2017) http://cdmd.cnki.com.cn/Article/CDMD-90005-1018702621.htm
(  0) 0) |
| [6] |
刘文志. 并行算法设计与性能优化[M]. 北京: 机械工业出版社, 2015 (Liu Wenzhi. Parallel Computing and Performance Optimization[M]. Beijing: China Machine Press, 2015)
(  0) 0) |
| [7] |
郁志辉. 高性能计算并行编程技术——MPI并行程序设计[M]. 北京: 清华大学出版社, 2001 (Yu Zhihui. High Performance Parallel Programming with MPI[M]. Beijing: Tsinghua University Press, 2001)
(  0) 0) |
| [8] |
刘胜飞, 张云泉, 孙相征. 一种改进的OpenMP指导调度策略研究[J]. 计算机研究与发展, 2010, 47(4): 687-694 (Liu Shengfei, Zhang Yunquan, Sun Xiangzheng. An Improved Guided Loop Scheduling Algorithm for OpenMP[J]. Journal of Computer Research and Development, 2010, 47(4): 687-694)
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39