2. 信息工程大学地理空间信息学院,郑州市科学大道62号,450001;
3. 伟志股份公司,泉州市迎宾路7-1号,362200
研究地球形状、大小及其内部精细结构是大地测量学的科学任务之一,确定了地球形状即确定了(似)大地水准面的起伏[1]。随着卫星技术的发展,特别是GPS等全球定位导航系统在测绘导航领域中的应用,使得获取测点三维坐标成为可能,进而产生了一种新的(似)大地水准面拟合方法——GPS/水准法[2]。该方法可以获得离散点的观测数据,通过数据拟合内插方法确定未知点的(似)大地水准面高。因此,如何利用离散点拟合未知点的大地水准面高便成为构建高精度、高分辨率(似)大地水准面研究中的关键问题之一。传统的数学拟合方法如多项式拟合、多面函数法和样条函数法等均可应用于该领域:黄良珂等[3]对传统的Kriging方法进行改化,发现改进的Kriging法的拟合精度明显优于Kriging法;杨明清等[4]首次将神经网络法引入到该领域并与传统的曲面拟合方法进行对比发现,其精度优于传统的曲面拟合法,且效果更为稳定。
点质量模型是一种有效的位场逼近方法,根据位场的可叠加原理,将扰动质量看作一大批离散的扰动质点,将这些扰动质点产生的扰动位之和来等效空间扰动位[5-10]。本文将点质量原理应用于区域(似)大地水准面拟合中,提出一种平面位置固定、埋深自由的半自由点质量模型,并通过迭代法确定每个扰动质点的埋深与大小。实验证明,该方法可应用于局部(似)大地水准面拟合。
1 Kriging/Co-Kriging法现阶段确定高程异常主要有如下几种方法:1)利用超高阶地球重力场模型解算,此方法理论上能达到cm级精度,但在重力资料缺失地区精度不够稳定;2)利用GPS/水准法直接测量,此方法精度较高,但传统水准测量作业成本较高,无法大范围开展;3)基于方法2)获得区域内离散点的高程异常,以有限个水准联测点为基础绘制区域内的数学曲面,然后通过内插法确定该区域内其他点的高程异常。该方法在保证一定解算精度的基础上减小了工作量,获得广泛应用。
Kriging法是一种利用局部加权思想对局部区域点位进行拟合的插值方法,当大地水准面差距变化较为平缓时其拟合效果较好,可以对重力场元的低频部分进行较好的描述。该方法是矿产学家Kriging提出的一种地学统计拟合方法,以已知点的空间分布为依据进行插值拟合,从本质上讲,该方法是利用区域原始数据对估计点进行的最优无偏估计,其广泛应用于数据处理及工程应用等领域[11-13]。Kriging法满足以下条件:
| $ \left\{ \begin{array}{l} E(N - {N_i}) = 0\\ C(N - {N_i}) = \min \end{array} \right. $ | (1) |
式中,E与C为数学期望与方差,N与Ni分别为计算点与拟合点的大地水准面高。插值模型为:
| $N = \sum\limits_{i = 1}^{\rm{Num}} {{\lambda _i}{N_i}} $ | (2) |
式中,λi为每个拟合点的权值,通常利用变异函数代替方差元素,即
| $ \gamma (h) = \frac{1}{{2{\rm{Num}}(h)}}\sum\limits_{i = 1}^{{\rm{Num}}(h)} {{{({N_i} - {N_{i + h}})}^2}} $ | (3) |
式中,h为滞后距,Num(h)为滞后距个数,详细推导见文献[14]。
Co-Kriging法是Kriging方法的优化,该方法在原来基础上加入高程信息,凸显重力异常的高频特性,使精度获得一定的提升。在计算变异函数的过程中,通过设置主变量与协变量充分考虑其他信息对计算结果的影响,即将式(3)改为:
| $ \gamma (h) = \frac{1}{{2{\rm{Num}}(h)}}\sum\limits_{i = 1}^{{\rm{Num(}}h)} {({N_i} - {N_{i + h}})({H_i} - {H_{i + h}})} $ | (4) |
式中,H为拟合点的高程。
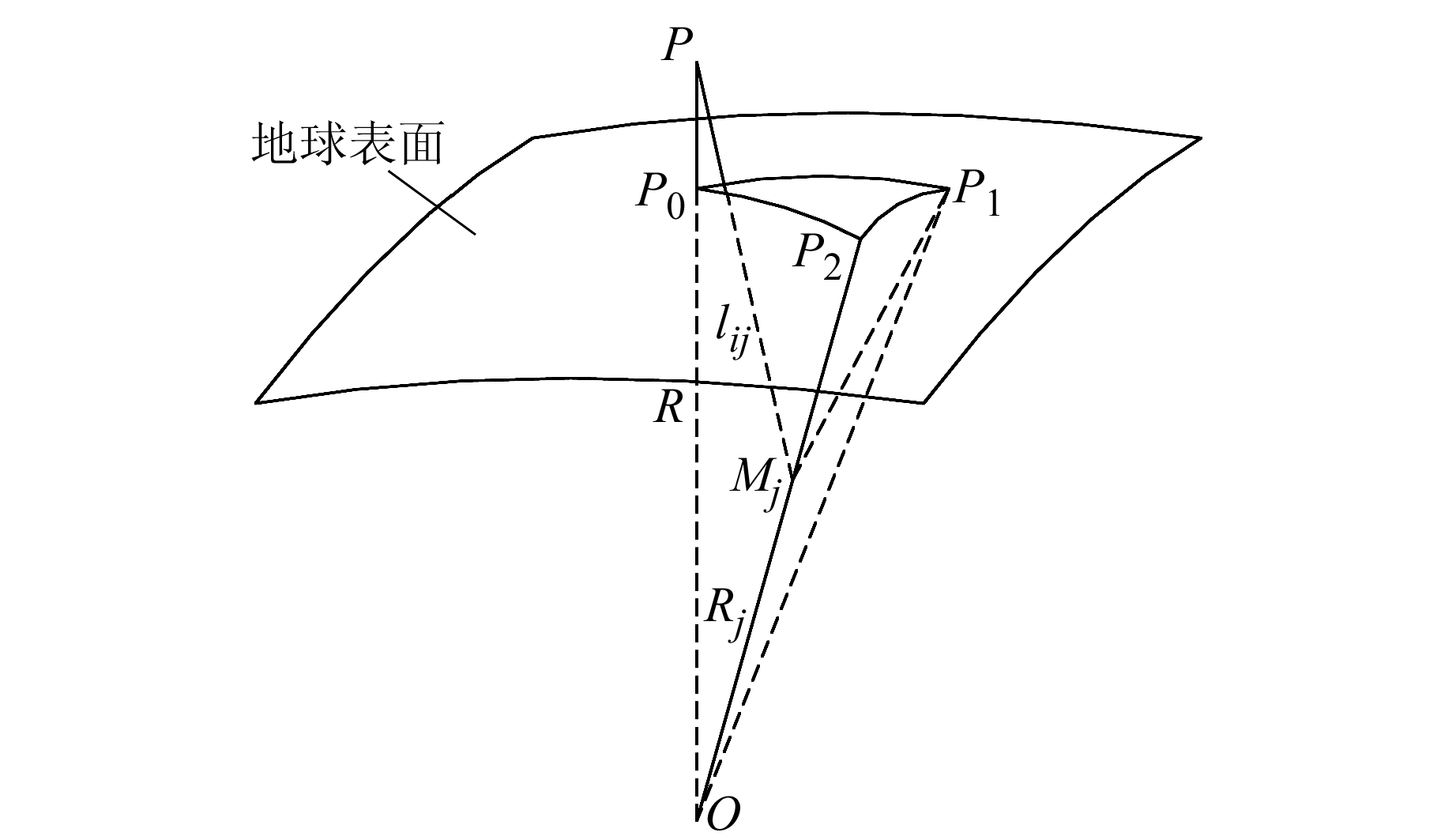
2 传统点质量模型方程记点P为待求点,P0、P1、P2为已知重力场元点,Mj为扰动质点,3种参数的关系见图 1。图中,O为地球球心,R为地球半径,lPj为质量点到计算点距离。
|
图 1 点质量、重力场元点和待求点的关系 Fig. 1 The relation diagram of point mass, point of gravity field and the point to be sought |
将空间的扰动信息看作由一组离散分布在地面以下的扰动质点产生,由万有引力公式可得扰动质点在地表点产生的扰动位TP为:
| $ {T_P} = G\sum\limits_{j = 1}^m {\frac{{{M_j}}}{{{l_{pj}}}}} $ | (5) |
由式(5)可知,确定空间扰动位TP的关键在于扰动质点集M。现实生产过程中,需要利用扰动位的泛函来求解质点集M。考虑到实际测量操作的可行性,一般采用测量成本相对较低的重力异常作为已知数据求解质点集M。扰动位TP与重力异常Δg的关系为:
| $ \Delta g = - \frac{{\partial T}}{{\partial R}} - \frac{{2T}}{R} $ | (6) |
| $ \Delta {g_i} = \sum\limits_{j = 1}^k {(\frac{{R - {R_j}\cos {\psi _{ij}}}}{{l_{ij}^3}}} - \frac{2}{{R{l_{ij}}}}){M_j} $ | (7) |
式中,(R, φi, λi)、(Rj, φj, λj)为重力异常点和点质量的球坐标(球近似情况下),ψij为两点所成的球心角。将式(7)转化为矩阵形式:
| $ {\rm{\Delta }}\mathit{\boldsymbol{g}} = \mathit{\boldsymbol{AM}} $ | (8) |
当观测数据(重力异常)足够且分布合理时,可由最小二乘理论解得质点集M为:
| $ \mathit{\boldsymbol{M}} = \left\{ \begin{array}{l} {\mathit{\boldsymbol{A}}^{{\rm{ - }}1}}{\rm{\Delta }}\mathit{\boldsymbol{g}}, n = k\\ {({\mathit{\boldsymbol{A}}^T}\mathit{\boldsymbol{A}})^{{\rm{ - }}1}}{\mathit{\boldsymbol{A}}^T}{\rm{\Delta }}\mathit{\boldsymbol{g}}, n > k \end{array} \right. $ | (9) |
式中,n、k分别为质点和重力异常的个数。
大地水准面高N与扰动位的关系可由布隆斯公式表示,即
| $ N = \frac{{{T_P}}}{\gamma } $ | (10) |
式中,γ为正常重力。将式(5)代入式(10),得到大地水准面高N的计算公式为:
| $ N = G\sum\limits_{j = 1}^n {\frac{{{M_j}}}{{{l_{pj}}\gamma }}} $ | (11) |
模型在建模过程中对输入数据的分布和数量要求较高。首先,为满足式(9)求解的稳定性,一般需要输入数据按照与质点相同的格网分布,但实际测量过程中很难满足格网化测量的要求,因此会引入一定的格网化方法对实测数据进行处理,此过程会引入一定的平滑误差;再者,为满足最小二乘要求,输入数据的数量必须大于或等于质点数,当建模分辨率较高时,工作量较大;另外,传统点质量模型中质点一般按照等间距格网进行排列,这就使得式(11)的计算结果为简单的线性拟合,理论上这种拟合结果并不是最优的。
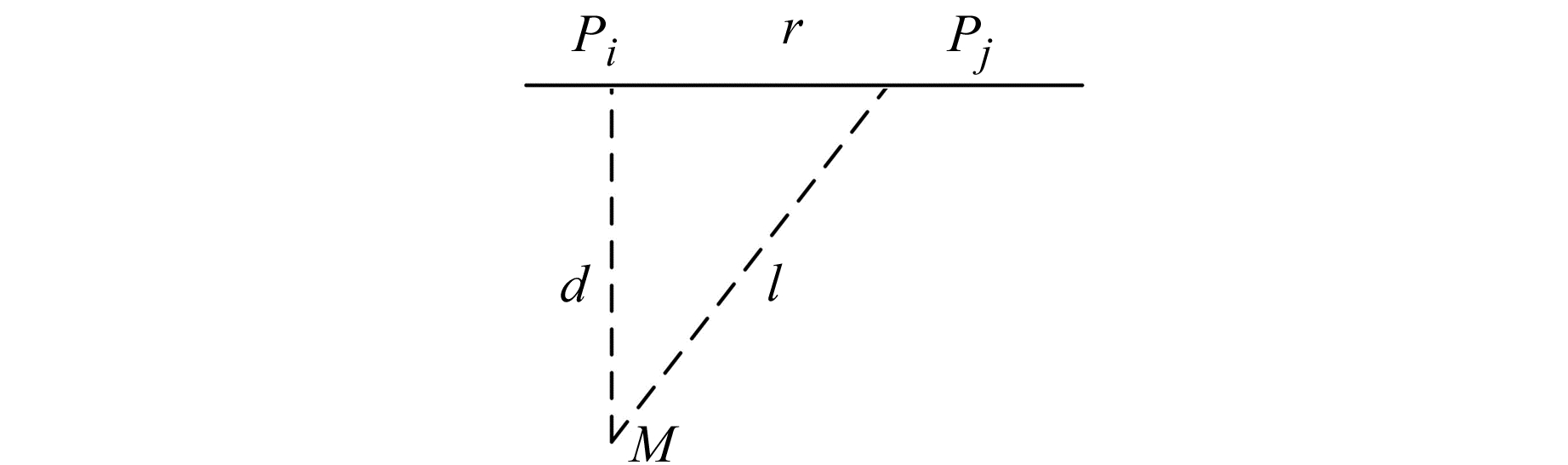
3 半自由点质量模型不同于格网化的扰动质点分布模式,半自由点质量模型是将扰动质点固定于实测GPS/水准点位的下方,即固定扰动质点的平面位置,其埋深作为待求未知量,同时考虑到重力场元的多波段性,设定每个观测点下方有数个不同埋深的质点,从而可以拟合重力场元的不同波段信息,模型示意图见图 2。
|
图 2 半自由点质量模型示意图 Fig. 2 The sketch diaof semi-free point mass model |
图 2中,Pi和Pj为地面两个实测高程异常点,设定某一实测点Pi下有一扰动质点M,l为扰动质点与另一高程异常Pj之间的距离,d为扰动质点M的埋深。可将式(11)改为:
| $ {{N_j} = G\sum\limits_{i = 1}^{GN} {\sum\limits_{m = 1}^{{M_i}N} {\frac{{{M_{im}}}}{{\sqrt {r_{im}^2 + d_{ij}^2} \gamma }}, } } }{j = 1, 2, 3, \cdots , GN} $ | (12) |
由于每一个高程异常点下方可能会有多个扰动质点,所以设定MiN为第i个高程异常点下的扰动质点的总数,GN为已知的实测点个数,Nj为所有质点对Gj点的影响(j=1, 2, 3, …, GN),γ为正常重力值。
由式(12)可知,扰动质点对计算点高程异常的影响与平面距离(埋深)呈负相关,与质点的大小呈正相关。在质点大小确定且平面距离固定的条件下,当质点位于计算点下方时,该质点对计算点的高程异常影响最大。单个质点Mim对Gj的影响N′j为:
| $ N_j' = \left\{ \begin{array}{l} \begin{array}{*{20}{c}} {G\frac{{{M_{im}}}}{{\sqrt {r_{im}^2 + d_{ij}^2} \gamma }}, }&{j \ne i} \end{array}\\ \begin{array}{*{20}{c}} {G\frac{{{M_{im}}}}{{\sqrt {r_{im}^2} \gamma }}, }&{j{\rm{ = }}i} \end{array} \end{array} \right. $ | (13) |
实际求解过程中参考了Cordell[15]的简单迭代算法,认为平面距离最近点的计算结果最为可信。根据式(13)给出如下迭代步骤:
1) 遍历已知观测数据,寻找已知值中绝对值最大的点(如图 2中Pi),并设定其正下方某一深度处有一扰动质点Mim。
2) 确定距离该点平面距离最近的点(如图 2中Pj),根据最近点置信度最大原则,假设Gi和Gj点的高程异常是由Mim引起,根据公式(13)可得到参数k:
| $ k = \frac{{N_j'}}{{N_i'}} = \frac{{{r_{im}}}}{{\sqrt {r_{im}^2 + d_{ij}^2} }}, 0 < k < 1 $ | (14) |
3) 求解rim:
| $ {r_{im}} = \frac{{{d_{ij}}k}}{{\sqrt {1 - {k^2}} }} $ | (15) |
4) 求定Mim:
| $ {M_{im}} = {N_i}\sqrt {r_{im}^2 + d_{ij}^2} \gamma /G $ | (16) |
5) 求定Mim对实验区内每一个实测点高程异常的影响。
6) 将实测值与步骤5)中的拟合值之差作为新的已知值,设定限差并循环以上步骤进行迭代。为实现cm级大地水准面的建模要求,一般迭代过程中设定限差为1 mm。
4 数值实验选取不同地形条件下、不同点位分布的3个区域进行模型结构分析及拟合精度评估,各区域分布示意图见图 3。图中,圆点为拟合点,三角点为模型精度检核点,检核点随机分布在区域内部。

|
图 3 3个区域的GPS/水准点分布示意图 Fig. 3 GPS/leveling points distribution chart in three regions |
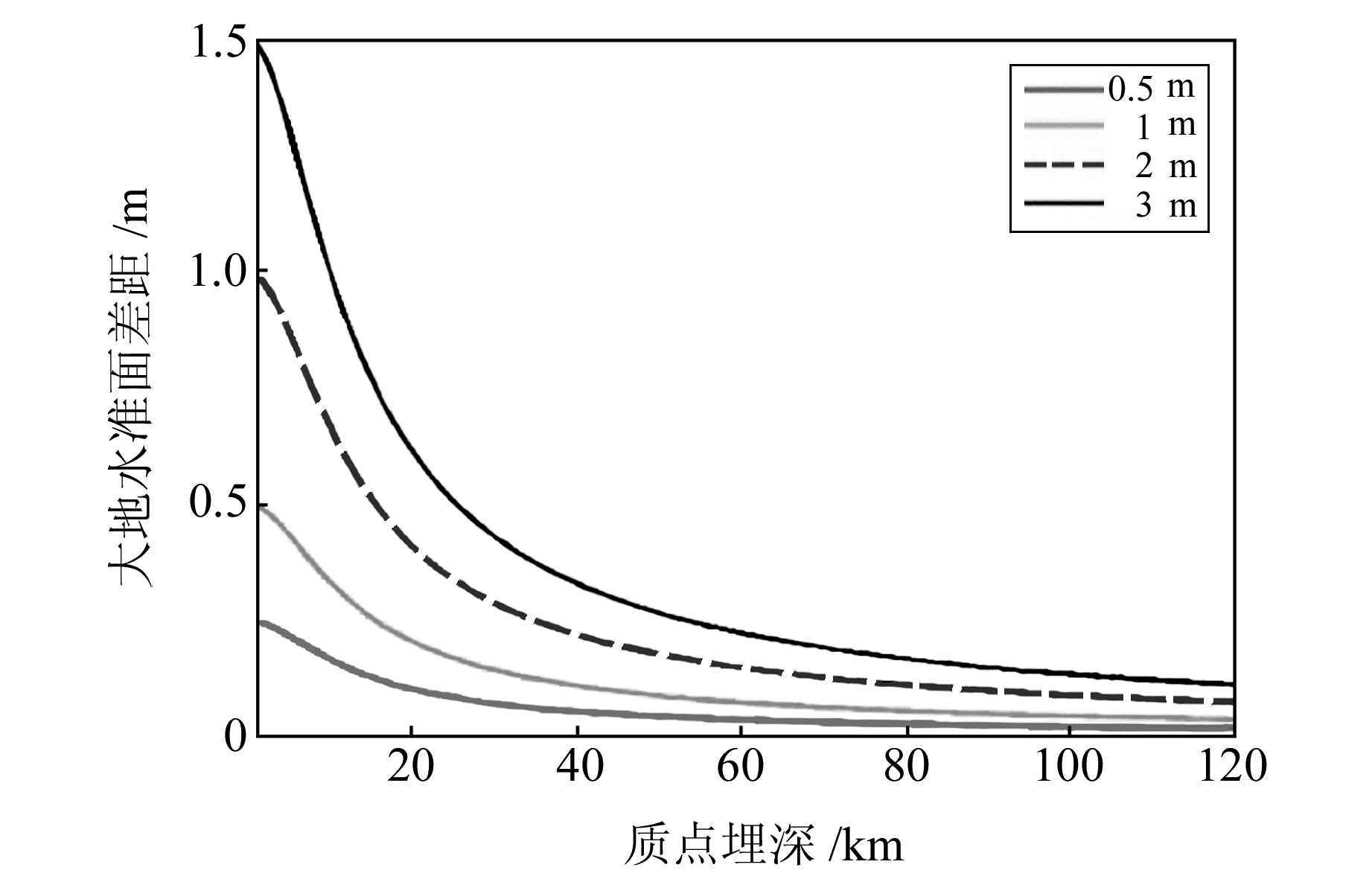
半自由点质量模型的未知参量为质点大小与质点埋深,大地水准面差距与质点埋深及质点大小之间的关系见图 4。
|
图 4 大地水准面差距与质点埋深及质点大小之间的关系 Fig. 4 Relation between geoid gap and particle depth and particle size |
由图 4可知,某质点埋深一定时,质点对计算点大地水准面差距的影响随着质点质量的增大而增大。当该质点质量确定时,其对(似)大地水准面的影响与埋深成反比,即深层的质点引起的大地水准面差距变化较为平缓,可以突出(似)大地水准面的低频特性;相反,当埋深较浅时,其影响较为剧烈,可以反映(似)大地水准面的高频影响。
传统分频余差点质量模型中,在除去“移去-恢复”所需背景场的基础上,不同埋深层的质点对应重力场的不同频段,其叠加可以实现重力场的多频组合。由表 1可知,每一个建模点下方会生成多个扰动质点,且质点的埋深不同。由于扰动质点恢复重力场的频段与其埋深有关,这些不同埋深的质点可以通过不同频段的组合恢复地球重力场的多尺度特性。
|
|
表 1 3个区域内生成质点数统计 Tab. 1 Statistical table of mass points in three regions |
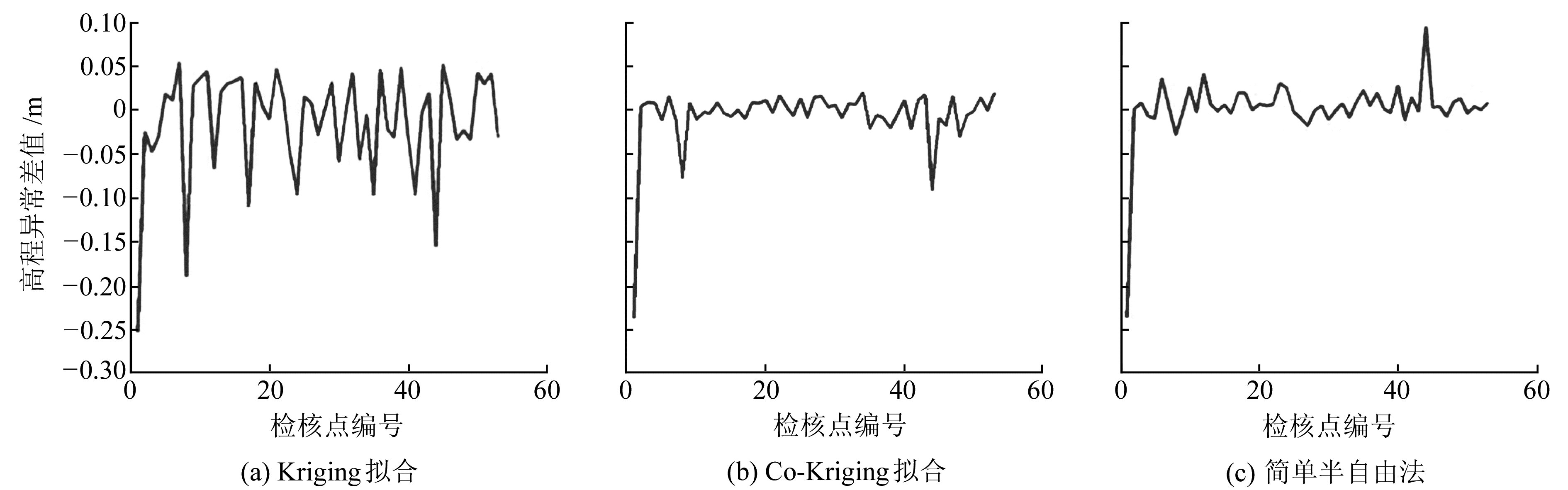
为分析半自由点质量法的拟合效果,分别利用Kriging和Co-Kriging作对比实验,实验区1内3种方法的拟合效果统计信息见表 2(单位m),各个检核点的计算差值统计见图 5。
|
|
表 2 实验区1内3种方法外部校核效果统计 Tab. 2 Statistical results of three methods for external checking in regionone |
|
图 5 实验区1内3种方法外部检核图 Fig. 5 Three methods for external checking in region 1 |
根据以上统计信息可知,3种方法恢复大地水准面的效果呈现依次变好的趋势。在该实验区内,相比于Kriging拟合方法,其他两种方法的精度提高了近1倍;编号为1的检核点恢复效果最差,因为该点为图 5(a)~5(c)中左下方受约束较小的“飞点”,实验采用的3种方法都无法对其进行有效的计算;在该平原区域内,简单半自由点质量法达到了与Co-Kriging拟合相当的精度,表明利用本文提出的简单半自由点质量法来恢复高程异常是可行的。
利用相同的方法处理实验区2中的数据,其拟合效果统计信息见表 3(单位m),各个检核点的高程异常差值见图 6。
|
|
表 3 实验区2内3种方法外部校核效果统计 Tab. 3 Statistical results of three methods for external checking in region 2 |
|
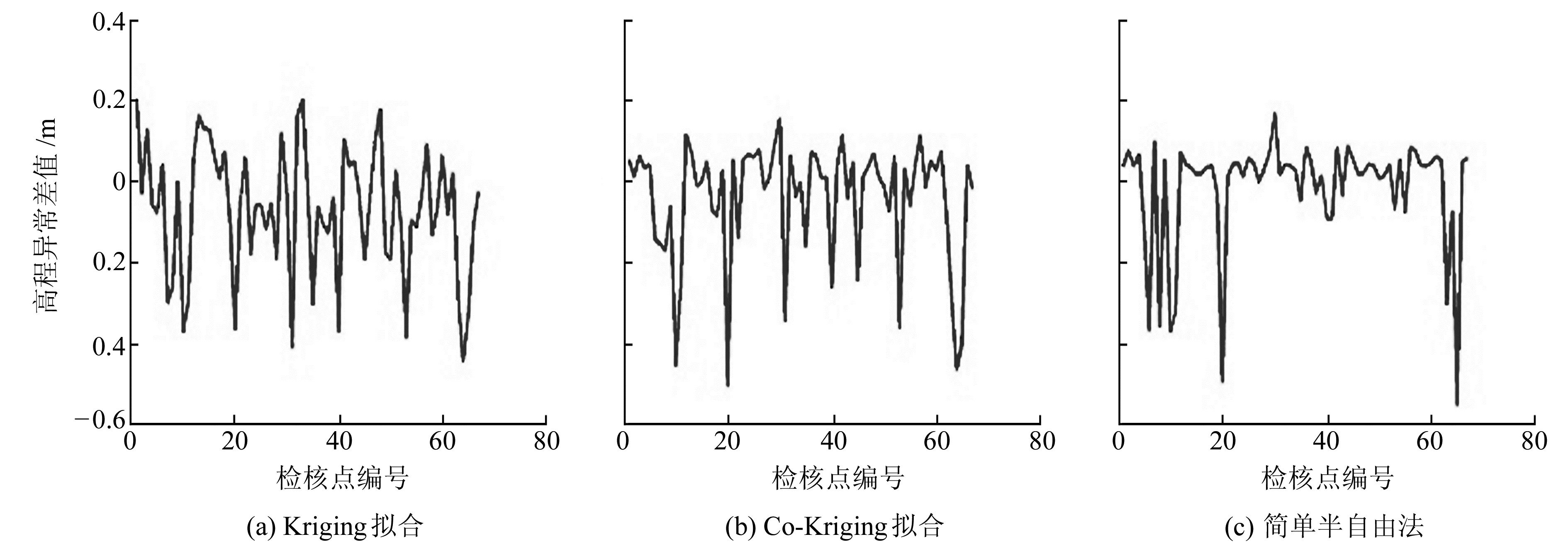
图 6 实验区2内3种方法外部检核图 Fig. 6 Three methods for external checking in region 2 |
相比于实验区1,本实验区内高程变化较为剧烈。由以上统计信息可知,3种方法恢复高程异常的效果依次变好,简单半自由点质量法相比于Kriging拟合精度提高了约13.7%。
利用GPS/水准点进行(似)大地水准面拟合从根本上讲是一种数学逼近,逼近精度受点位分布、实验区地形及已知测点数量等方面的影响。该区域内高程信息变化剧烈、已知点位较少且不均匀,仅单纯利用拟合方法确定高精度的(似)大地水准面是不现实的,但相比于其他两种方法,本文方法在精度上仍能有所提高,这一点是难得可贵的。
4.3 利用格网点进行拟合与§4.2实验方法相同,利用3种计算方法对实验区3的点位进行拟合计算,拟合差值信息统计见表 4(单位m)和图 7。
|
|
表 4 实验区3内3种方法外部校核效果统计 Tab. 4 Statistical results of three methods for external checking in region three |

|
图 7 实验区3内3种方法外部检核图 Fig. 7 Three methods for external checking in region 3 |
由表 4可知,本文的简单半自由法相比于2种传统的数学拟合方法在精度上有大幅提高,说明在利用格网化的点位进行高程异常拟合时,本文方法占优。由图 6可知,在利用传统数学拟合方法进行计算时,各个点位的恢复精度相差较大,使得图 7(a)和7(b)中出现很多“毛刺”,大大降低了拟合效果,而本文方法将“毛刺”个数减少到2个,其余点位的最大误差控制在5 cm。相比于§4.2的实验,本实验中格网化的拟合点位提供了更多的有效信息,说明本文提出的算法能够有效地利用已知信息对区域(似)大地水准面进行拟合。
5 结语将改进的点质量模型应用于(似)大地水准面拟合,通过对不同地形、不同点位分布的区域数据进行实验,并结合Kriging与Co-Kriging方法进行对比分析表明,本文提出的方法可以应用于(似)大地水准面拟合。
| [1] |
Moritz H. Advanced Physical Geodesy[M]. Karisruhe: Abacus Press, 1980
(  0) 0) |
| [2] |
姚吉利, 曲国庆, 刘科利, 等. 拟合点分布与GPS水准面拟合精度关系研究[J]. 大地测量与地球动力学, 2008, 28(5): 50-54 (Yao Jili, Qu Guoqing, Liu Keli, et al. Research on Accuracy of Quasi-Geoid with Fitting Methods under Different Distribution of GPS Points[J]. Journal of Geodesy and Geodynamics, 2008, 28(5): 50-54)
(  0) 0) |
| [3] |
黄良珂, 刘立龙, 唐艳新, 等. 基于改进的Kriging法区域似大地水准面精化[J]. 桂林理工大学学报, 2012, 32(4): 532-536 (Huang Liangke, Liu Lilong, Tang Yanxin, et al. Area Quasi-Geoid Refine Based on Improved Kriging Method[J]. Journal of Guilin University of Technology, 2012, 32(4): 532-536 DOI:10.3969/j.issn.1674-9057.2012.04.015)
(  0) 0) |
| [4] |
杨明清, 靳蕃, 朱达成, 等. 用神经网络方法转换GPS高程[J]. 测绘学报, 1999, 28(4): 301-307 (Yang Mingqing, Jin Fan, Zhu Dacheng, et al. Conversion of GPS Height by Artifical Neural Network Method[J]. Acta Geodaetica et Cartographica Sinica, 1999, 28(4): 301-307 DOI:10.3321/j.issn:1001-1595.1999.04.005)
(  0) 0) |
| [5] |
吴晓平. 局部重力场的点质量模型[J]. 测绘学报, 1984, 13(4): 249-258 (Wu Xiaoping. Point-Mass Model of Local Gravity Field[J]. Acta Geodaetica et Cartographica Sinica, 1984, 13(4): 249-258 DOI:10.3321/j.issn:1001-1595.1984.04.002)
(  0) 0) |
| [6] |
晁定波, 宁津生, 邱卫根. 整体大地测量的虚拟点质量模型[J]. 武汉测绘科技大学学报, 1992, 17(2): 1-7 (Chao Dingbo, Ning Jinsheng, Qiu Weigen. Quasi-Point Mass Model of Integrated Geodesy[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1992, 17(2): 1-7)
(  0) 0) |
| [7] |
Antunes C, Pail R, Catalāo J. Point Mass Method Applied to the Regional Gravimetric Determination of the Geoid[J]. Studia Goephysica et Geodaetica, 2003, 47(3): 495-509 DOI:10.1023/A:1024836032617
(  0) 0) |
| [8] |
王建强, 李建成, 赵国强, 等. 重力三层点质量模型的构造与分析[J]. 测绘学报, 2010, 39(5): 503-507 (Wang Jianqiang, Li Jiancheng, Zhao Guoqiang, et al. The Construction and Analysis for Three-Tier Point Mass Model of Gravity[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 503-507)
(  0) 0) |
| [9] |
Lin M, Denker H, Müller J. Regional Gravity Field Modeling Using Free-Positioned Point Masses[J]. Studia Geophysica et Geodaetica, 2014, 58(2): 207-226 DOI:10.1007/s11200-013-1145-7
(  0) 0) |
| [10] |
吴怿昊, 罗志才, 周波阳. 基于泊松小波径向基函数融合多源数据的局部重力场建模[J]. 地球物理学报, 2016, 59(3): 852-864 (Wu Yihao, Luo Zhicai, Zhou Boyang. Regional Gravity Modeling Based on Heterogeneous Data Sets by Using Poisson Wavelets Radial Basis Functions[J]. Chinese Journal of Geophysics, 2016, 59(3): 852-864)
(  0) 0) |
| [11] |
刁鑫鹏, 吴侃. 基于Kriging算法与曲面拟合的三维激光扫描点云数据插值研究[J]. 大地测量与地球动力学, 2012, 32(1): 110-113 (Diao Xinpeng, Wu Kan. Interpolation of 3D Laser Point Clouds Data Based on Kriging Interpolation and Surface Fitting[J]. Journal of Geodesy and Geodynamics, 2012, 32(1): 110-113)
(  0) 0) |
| [12] |
Atalay F, Ertunc G. Metaheuristic Kriging: A New Spatial Estimation Method[J]. Hacettepe Journal of Mathematics and Statistics, 2017, 46(2): 483-492
(  0) 0) |
| [13] |
Simpson T W, Mauery T M, Korte J J, et al. Kriging Models for Global Approximation in Simulation-Based Multidisciplinary Design Optimization[J]. AIAA Journal, 2011, 39(12): 2 233-2 241
(  0) 0) |
| [14] |
陈宝政, 蔡德利. 普通Kriging插值算法研究[J]. 测绘与空间地理信息, 2009, 32(3): 7-9 (Chen Baozheng, Cai Deli. Algorithm and Application of Kriging[J]. Geomatics and Spatial Information Technology, 2009, 32(3): 7-9 DOI:10.3969/j.issn.1672-5867.2009.03.003)
(  0) 0) |
| [15] |
Cordell L. A Scattered Equivalent-Source Method for Interpolation and Gridding of Potential-Field Data in Three Dimensions[J]. Geophysics, 1992, 57(4): 629-636 DOI:10.1190/1.1443275
(  0) 0) |
2. School of Surveqing and Mapping, Information Engineering University, 62 Kexue Road, Zhengzhou 450001, China;
3. Weizhi Co Ltd, 7-1 Yingbin Road, Quanzhou 362200, China
 2019, Vol. 39
2019, Vol. 39

