2. 中国地震局地震研究所,武汉市洪山侧路40号,430071
地球具有一系列的本征模态(normal modes),其频率与地球介质的密度分布、横向结构、异质性、自转和椭率等相关,一旦被地震等外部震源激发,这些模态会使地球发生相应的振荡,即地球的自由振荡。地球自由振荡通常指周期低于54 min的本征振荡,通过地球自由振荡的实测值与理论值之间的差异对比,可对地球的密度结构等进行有效约束。已有很多学者对各个频段的自由振荡信号进行观测及理论分析[1-9],但给出的模态在不同观测值之间存在差异,现阶段仍需要开展进一步研究。
本文关注的是地球径向模态0S0,通常被称为呼吸模态。对于各向同性球对称地球模型而言,该模态在地表的各处被激发的振幅是相同的,不存在模态分裂的现象。如果能够准确地确定0S0模态特征频率f和品质因子Q,就能有效地约束地球介质密度和衰减模型。由于0S0模态的品质因子Q相对较高(约5 200)[10],被激发的振幅也相对较强[8],相比于其他模态,该模态的特征频率f和品质因子Q更有可能被精确测定。虽然前人对0S0模态进行过一些相关研究,但各项研究检测到的特征频率f和品质因子Q之间仍存在一定差异[8]。本文基于2011-03-11日本MW9.3地震后全球500多个宽频带地震台站记录的地震波数据,通过频域方法估计0S0的特征频率f和品质因子Q,以期得到更为精确的估值,从而更好地约束地球介质密度和衰减结构[11]。
1 数据与方法 1.1 数据集2011-03-11日本近海发生MW9.3地震,产生了强烈的地球自由振荡信号[8]。本文从IRIS网站下载800多个台站10 s采样的地震波数据,经常规去除仪器响应等步骤后,转换为加速度记录数据,剔除一些质量较差(有较大间断和突跳)的台站数据,最终选用了545个质量较好的台站的垂直分量记录数据,所选台站几乎覆盖了全球的陆地,但大多数台站布设在美国与欧洲地区。由于0S0模态被激发的信号在地震结束后会快速衰减[12],综合考虑信噪比(signal-noise-ratio, SNR)等因素,选取地震后1~221 h时间段内地震波数据作为最终数据集。
1.2 估计方法估计自由振荡信号的频率f和品质因子Q有许多方法,如Chao等[3]提出频率域的自回归(AR)估计方法,Masters等[13]提出非线性最小二乘拟合方法,Rosat等[14]提出非线性衰减谐波分析方法。每种方法都有其优势与适用范围,也都取得了较理想的结果,各种方法的综述可参见文献[8]。本文选用Chao等[3]提出的频域AR方法来估计0S0模态的特征频率f和品质因子Q,基本原理如下[3]。
以地表观测的垂直加速度记录为例,通常可以表示为一组衰减余弦函数的叠加形式[3, 10]:
| $ a(t)=\sum\limits_{j}^{M} A_{j} \cos \left(\omega_{j} t+\varphi_{j}\right) \mathrm{e}^{-\alpha_{j} t} $ | (1) |
式中,Aj为振幅,αj为衰减因子,ωj和φj分别为角频率和相位。品质因子Q可通过所估计的角频率和衰减因子得到,即
| $ Q_{j}=\frac{\omega_{j}}{2 \alpha_{j}} $ | (2) |
对于离散时间序列a(n),记σj=ωj+iαj和Aj=Ajeiφj,则式(1)可表示为:
| $ \begin{array}{l} a(n) = \sum\limits_{j = 1}^M {\left[ {{\mathit{\boldsymbol{A}}_j}\exp \left( {{\rm{i}}n{\sigma _j}} \right) + \mathit{\boldsymbol{A}}_j^*\exp \left( { - {\rm{i}}n\sigma _j^*} \right)} \right]} , \\ n = 1, 2, \cdots , N \end{array} $ | (3) |
式中,*为复共轭,N为数据点个数。式(3)中,a(n)可表示为差分方程的形式,即
| $ \begin{array}{l} a(n) = \sum\limits_{i = 1}^{2M} {{S_i}} a(n - i), \\ n = 2M + 1, \cdots , N \end{array} $ | (4) |
式中,系数Si为实常数(i=1, 2, …, 2M)。Si和σj的关系可通过Prony多项式来构造[3],一旦求得Si,σj即可通过式(3)得到。
然而,对于震后地震仪记录的时间序列,M通常是未知的,这意味着很难在时域求解式(4)中的Si。不同的模态在频域通常可被分离开,即呈现为不同的谱峰,因此利用离散傅氏变换,将式(4)转化到频率域上,可得:
| $ X_{0}\left(\omega_{k}\right)=\sum\limits_{i=1}^{2 M} X_{i}\left(\omega_{k}\right) S_{i}, k=1, 2, \cdots, K $ | (5) |
其中,Xi(ωk)(i=0, 1, …, 2M)对应于a(n-i)(n=2M+1, …, N)的傅里叶变换,可将式(5)表示为矩阵的形式:
| $ \left[\begin{array}{cccc}{X_{1}\left(\omega_{1}\right)} & {X_{2}\left(\omega_{1}\right)} & {\cdots} & {X_{2 M}\left(\omega_{1}\right)} \\ {X_{1}\left(\omega_{2}\right)} & {X_{2}\left(\omega_{2}\right)} & {\cdots} & {X_{2 M}\left(\omega_{2}\right)} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {X_{1}\left(\omega_{K}\right)} & {X_{2}\left(\omega_{K}\right)} & {\cdots} & {X_{2 M}\left(\omega_{K}\right)}\end{array}\right]\left[\begin{array}{c}{S_{1}} \\ {S_{2}} \\ {\vdots} \\ {S_{2 M}}\end{array}\right]=\\ \left[\begin{array}{c}{X_{0}\left(\omega_{1}\right)} \\ {X_{0}\left(\omega_{2}\right)} \\ {\vdots} \\ {X_{0}\left(\omega_{K}\right)}\end{array}\right] $ | (6) |
需要注意,在进行傅里叶变换之前,可采取加汉宁窗来抑制能量泄露造成的影响。对于一个单独的谱峰,M可视为1,此时只需求解2个AR系数S1和S2,同时Xi(ωk)也具有实部和虚部,即使只取一个频率点,即K=1,也可得如下形式:
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{\mathop{\rm Re}\nolimits} \left[ {{X_1}\left( {{\omega _1}} \right)} \right]}&{{\mathop{\rm Re}\nolimits} \left[ {{X_2}\left( {{\omega _1}} \right)} \right]}\\ {{\mathop{\rm Im}\nolimits} \left[ {{X_1}\left( {{\omega _1}} \right)} \right]}&{{\mathop{\rm Im}\nolimits} \left[ {{X_2}\left( {{\omega _1}} \right)} \right]} \end{array}} \right]·\left[ {\begin{array}{*{20}{l}} {{S_1}}\\ {{S_2}} \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} {{\mathop{\rm Re}\nolimits} \left[ {{X_0}\left( {{\omega _1}} \right)} \right]}\\ {{\mathop{\rm Im}\nolimits} \left[ {{X_0}\left( {{\omega _1}} \right)} \right]} \end{array}} \right] \end{array} $ | (7) |
足以求解所有的Si;如果取K>1,则可用最小二乘的方法求解式(6)。得到Si后,便可得出特征频率f和品质因子Q。
由于0S0模态在频域里只有一个独立的谱峰,因此M=1,本文统一选取K=3(3个频率点,即谱峰最大值及其左右2个点)来求解式(6)。
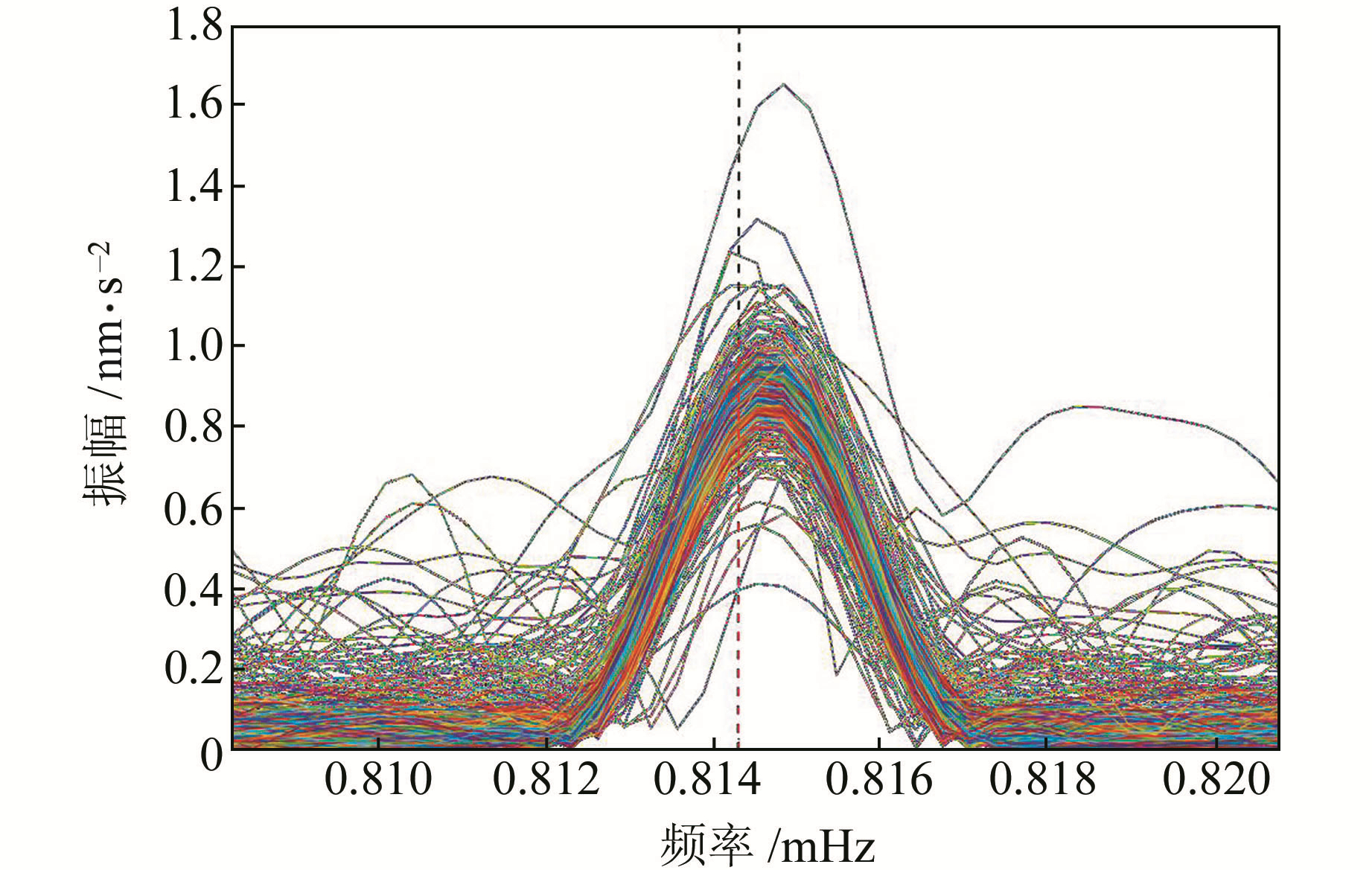
2 结果及分析基于所选545个地震波垂向观测数据对0S0模态检测得到的振幅谱见图 1,其中红色垂线为PREM模型的0S0模态理论值[15]。由图可知,谱图的最大值与理论值存在明显偏差,这表明PREM模型的理论值与真实值也存在一定差异。图 1还显示,不同的台站在目标频段(0.808~0.821 mHz)的噪音水平存在明显差异。选取0.808~0.812 mHz和0.817~0.821 mHz 2个频段内振幅的均值作为台站在此频段的噪音水平,选择0.814~0.815 mHz内的最大值作为信号值,利用信号值与噪音水平的比值作为台站在目标频段内的信噪比(SNR),通过计算得到的SNR结果见图 2。
|
图 1 所选545个台站地震波垂向序列的振幅谱 Fig. 1 Amplitude spectra of vertical components of seismic waves of selected 545 sets |

|
图 2 所选545个台站地震波垂向序列在目标频段(0.808~0.821 mHz)的SNR分布 Fig. 2 The SNR of vertical components of seismic waves of 545 sets on the frequency band 0.808-0.821 mHz |
由图 2可知,所选545个台站垂向观测数据的SNR都大于2,可认为所有台站都可以用于识别0S0模态。为进一步提高0S0模态的特征频率f和品质因子Q的估计精度,选出满足SNR>10的台站,最终得到448个台站,其垂向观测数据用于计算各项估值。
基于频率域AR方法,对所选的448个台站序列进行计算,得到各个台站的0S0模态特征频率f和品质因子Q的估值(图 3)。由于品质因子Q应当为正值,因此剔除了13个因估计误差过大而导致负值的Q估值。在给出特征频率f和品质因子Q估值的同时,也给出相应的估值误差,计算方法采用与文献[8]相同的蒙特卡洛过程。

|
图 3 各个台站得到的0S0模态的特征频率f和品质因子Q估值 Fig. 3 The estimated frequency and quality factor of 0S0 at different stations |
根据各个台站的估值,本文采用以信噪比SNR为权重的加权平均法,得到0S0模态的特征频率f和品质因子Q的最终估值:
| $ \left\{ {\begin{array}{*{20}{l}} {f = \sum\limits_i {\left( {{f_i} \cdot {{{\mathop{\rm SNR}\nolimits} }_i}/\sum\limits_i {} {\rm{SN}}{{\rm{R}}_i}} \right)} }\\ {Q = \sum\limits_i {\left( {{Q_i} \cdot {\rm{SN}}{{\rm{R}}_i}/\sum\limits_i {{\rm{SN}}{{\rm{R}}_i}} } \right)} } \end{array}} \right. $ | (8) |
式中,fi、SNRi、Qi分别为第i个台站的特征频率估计结果、信噪比及品质因子估值,最终估值的误差也可由式(8)得到,估值结果及其与已有研究成果的对比见表 1。
|
|
表 1 本文所得0S0模态特征频率f和品质因子Q的估值与前人及模型值的比较 Tab. 1 Comparison of the estimated frequency f and quality factor Q of 0S0 with the PREM prediction and previous estimates |
由表 1可知,本文结果相比于前人的研究,具有较高的估计精度,而其估值与PREM模型理论值的差异说明本文研究具有实际意义。由于地球模型本身就是一个建模过程,与时刻处于变化的真实地球相比,地球模型必然会存在差异,检测得到的模态也是动态的,各种地球模型仍需进一步精化,而本文结果为这种精化提供了有意义的约束数据。
3 结语基于2011年日本MW9.3地震后全球宽频地震台站记录的220 h地震波垂直分量数据,选用545个质量较好的台站的观测数据,并在目标频段内筛选出满足SNR>10的448个台站的高质量观测数据;采用频域AR方法对0S0模态特征频率f和品质因子Q进行检测,得到精度较高的估值。选用的地震台站具有高质量的观测数据,使获得的0S0模态特征频率f和品质因子Q具有更高的精度,可为构建更真实的地球模型提供有效的数据源。
| [1] |
Buland R, Berger J, Gilbert F. Observations from the IDA Network of Attenuation and Splitting during a Recent Earthquake[J]. Nature, 1979, 277(5 695): 358-362
(  0) 0) |
| [2] |
Sailor R V, Dziewonski A M. Measurements and Interpretation of Normal Mode Attenuation[J]. Geophysical Journal International, 1978, 53(3): 559-581 DOI:10.1111/j.1365-246X.1978.tb03760.x
(  0) 0) |
| [3] |
Chao B F, Gilbert F. Autoregressive Estimation of Complex Eigenfrequencies in Low Frequency Seismic Spectra[J]. Geophysical Journal International, 1980, 63(3): 641-657 DOI:10.1111/j.1365-246X.1980.tb02643.x
(  0) 0) |
| [4] |
Roult G, Rosat S, Clévédé E, et al. New Determinations of Q Quality Factors and Eigenfrequencies for the Whole Set of Singlets of the Earth's Normal Modes 0S0, 0S2, 0S3 and 2S1 Using Superconducting Gravimeter Data from the GGP Network[J]. Journal of Geodynamics, 2006, 41(1-3): 345-357 DOI:10.1016/j.jog.2005.08.020
(  0) 0) |
| [5] |
Rosat S, Watada S, Sato T. Geographical Variations of the 0S0 Normal Mode Amplitude: Predictions and Observations after the Sumatra-Andaman Earthquake[J]. Earth, Planets and Space, 2007, 59(4): 307-311 DOI:10.1186/BF03353109
(  0) 0) |
| [6] |
唐磊, 邱泽华, 阚宝祥. 对两次印尼地震环型振荡剪应变方向的分析[J]. 大地测量与地球动力学, 2008, 28(2): 56-60 (Tang Lei, Qiu Zehua, Kan Baoxiang. Analysis of Shear Strain Orientation of Earth's Torsional Oscillation Excited by Two Indonesia Earthquakes[J]. Journal of Geodesy and Geodynamics, 2008, 28(2): 56-60)
(  0) 0) |
| [7] |
张致伟, 程万正, 阮祥. 用SSY伸缩仪资料研究巨大远震引起的振荡波及谱[J]. 大地测量与地球动力学, 2008, 28(5): 27-33 (Zhang Zhiwei, Cheng Wanzheng, Ruan Xiang. On Oscillation Waves Induced by Great Far-Field Earthquake and Its Spectrum from SSY Extensometer Data[J]. Journal of Geodesy and Geodynamics, 2008, 28(5): 27-33)
(  0) 0) |
| [8] |
Ding H, Shen W B. Determination of the Complex Frequencies for the Normal Modes below 1 mHz after the 2010 Maule and 2011 Tohoku Earthquakes[J]. Annals of Geophysics, 2013, 56(5): S0563
(  0) 0) |
| [9] |
许闯, 罗志才, 周波阳, 等. 利用超导重力数据检测汶川地震激发的球型地球自由振荡[J]. 测绘学报, 2013, 42(4): 501-507 (Xu Chuang, Luo Zhicai, Zhou Boyang, et al. Detecting Spheroidal Modes of Earth's Free Oscillation Excitated by Wenchuan Earthquake Using Superconducting Gravity Observations[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(4): 501-507)
(  0) 0) |
| [10] |
Masters T G, Widmer R. Free Oscillation: Frequencies and Attenuations[A]//Ahrens T J. Global Earth Physics: A Handbook of Physical Constants[M]. Washington D C: American Geophysical Union, 1995
(  0) 0) |
| [11] |
Häfner R, Widmer-Schnidrig R. Signature of 3-D Density Structure in Superconducting Gravimeter Spectra of the 0S2 Multiplet[J]. Geophysical Journal International, 2013, 192(1): 285-294 DOI:10.1093/gji/ggs013
(  0) 0) |
| [12] |
Xu Y, Crossley D, Herrmann R B. Amplitude and Q of 0S0 from the Sumatra Earthquake as Recorded on Superconducting Gravimeters and Seismometers[J]. Seismological Research Letters, 2008, 79(6): 797-805 DOI:10.1785/gssrl.79.6.797
(  0) 0) |
| [13] |
Masters G, Gilbert F. Attenuation in the Earth at Low Frequencies[J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1983, 308(1504): 479-522 DOI:10.1098/rsta.1983.0016
(  0) 0) |
| [14] |
Rosat S, Fukushima T, Sato T, et al. Application of a Non-Linear Damped Harmonic Analysis Method to the Normal Modes of the Earth[J]. Journal of Geodynamics, 2008, 45(1): 63-71 DOI:10.1016/j.jog.2007.06.001
(  0) 0) |
| [15] |
Dziewonski A M, Anderson D L. Preliminary Reference Earth Model[J]. Physics of the Earth and Planetary Interiors, 1981, 25(4): 297-356 DOI:10.1016/0031-9201(81)90046-7
(  0) 0) |
| [16] |
Riedesel M A, Agnew D, Berger J, et al. Stacking for the Frequencies and Qs of 0S0 and 1S0[J]. Geophysical Journal International, 1980, 62(2): 457-471 DOI:10.1111/j.1365-246X.1980.tb04867.x
(  0) 0) |
| [17] |
El-Gelil M A, Pagiatakis S, El-Rabbany A. Normal Mode Detection and Splitting after Sumatra–Andaman Earthquake[J]. Journal of Geodynamics, 2010, 50(2): 49-56 DOI:10.1016/j.jog.2010.02.003
(  0) 0) |
| [18] |
Zábranová E, Matyska C, Hanyk L, et al. Constraints on the Centroid Moment Tensors of the 2010 Maule and 2011 Tohoku Earthquakes from Radial Modes[J]. Geophysical Research Letters, 2012, 39(18)
(  0) 0) |
2. Institute of Seismology, CEA, 40 Hongshance Road, Wuhan 430071, China
 2019, Vol. 39
2019, Vol. 39


