2003-07-13长江支流青干河左岸的千将坪村发生大型滑坡,滑坡体积约2 ×107 m3,造成人民生命与财产的巨大损失。此次滑坡是我国乃至世界上典型的水库型顺层岩质滑坡之一[1],受到工程界和学术界高度关注。
对千将坪滑坡的大部分研究均是分析其成因和失稳机制,只有少数学者通过数值模拟、地震监测资料等途径对滑坡的运动特性进行分析[2-5]。国际上对包括火山岩屑崩滑和雪崩在内的多起大型高速滑坡事件的地震图进行深入研究,主张将滑坡地震信号划分为高频和低频2个部分[6-7],其中低频信号是由巨大滑体进行整体滑行运动时对地面施加的变化的压力以及摩擦力激发产生的。反演低频滑坡地震信号可以得到滑源区的受力-时间函数,对此受力-时间函数进行经典力学分析[6-8],即可得到滑体的运动特性。
由于滑坡与普通震源过程有着根本的区别,无法用双力偶点源模型来解释,学者们改用类正弦单力点源模型来描述滑源区的受力-时间函数[6, 9-10]。如果以滑体运动方向为正,类正弦函数的正值部分表示滑体进行加速运动,负值部分表示滑体进行减速运动。但是,高速滑坡是一个复杂的过程,包含多种能量转换和多起滑坡子事件,仅用一个简单的类正弦模型来描述仍是不够的。同时,已有的研究也并未划定“高频”与“低频”的分界频率,低频地震波仍然对应一个非常宽泛的范围,在并不确知受力-时间函数所在的具体频段之前,盲目滤波会导致信号提取不完整或是将多个不同滑坡子事件激发的地震信号混杂在一起,从而影响之后的滑坡运动分析。
基于以上问题,本文首先对千将坪滑坡概况进行介绍;接着在一个较宽的频段反演得到滑源区地面的受力-时间函数,将这个受力-时间函数视为多起滑坡子事件的受力-时间函数与噪声的集合,再使用时频分析对宽频带内的时间函数进行处理,依据时频图的能量分布划分滑坡子事件的时间域与频段,结合不同子事件的运动特性,推断滑坡整体运动的相关参数,还原千将坪滑坡过程。
1 千将坪滑坡概况滑坡位于湖北秭归千将坪村所在的向东南倾斜的斜坡上,约发生于当地时间00:20。滑体平面形态呈舌状(图 1),总体上薄下厚。滑体顶高450 m,剪出口高程约100 m,被青干河高水位淹没,高差约350 m,被剪出的部分滑体在受到对岸坚硬岩壁阻挡后,形成高程149~178 m的过江堆积体[11]。滑床上陡下缓,坡度自上而下为35°~10°(图 1(c))。滑坡主体运动方式为高速整体滑行,主滑方向指向N130°E[12]。
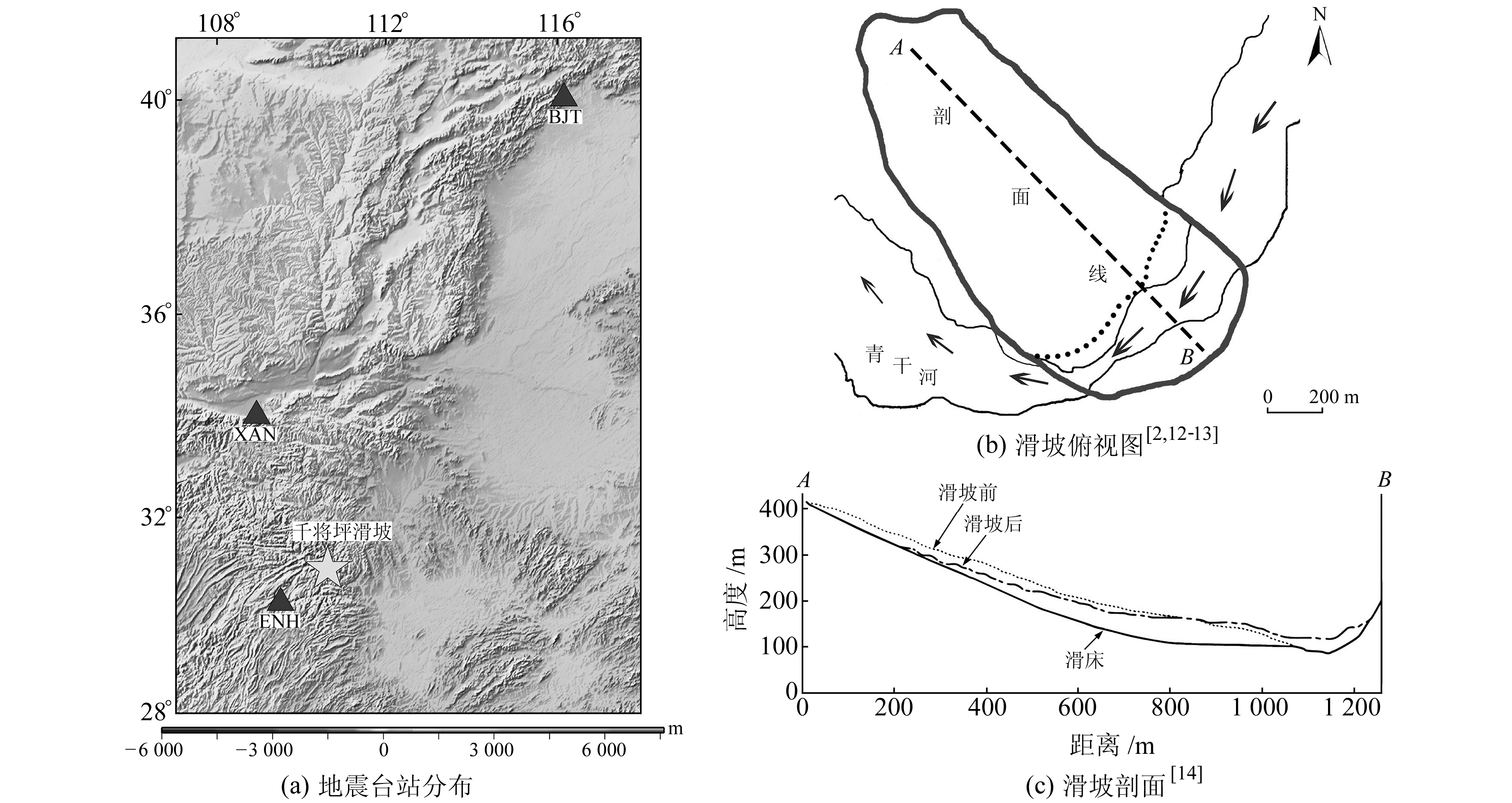
|
图(a)中,白色五角星表示千将坪滑坡所在地,黑色三角形表示地震台站所在地,其中BJT台位于北京,XAN台位于西安,ENH台位于恩施;图(b)中粗实线表示滑坡边界线,点线表示滑坡前滑体前缘体;图(c)剖面为沿图(b)中剖面线AB所得,实线表示滑床,点线为滑坡前地面线,点划线为滑坡后地面线 图 1 千将坪滑坡概况 Fig. 1 General situation of Qianjiangping landslide |
采集3个地震台站的数据(图 1(a)),为便于分析,文中所有时间轴的零点对应时刻都为00:19,比目击滑坡时间提前1 min。由于希望获得的受力-时间函数处于信号的低频段,故将原始数据进行预滤波,并将频段限制到0.600 Hz以下(图 2(a))。

|
图 2 滤波后波形和受力-时间函数 Fig. 2 Filtered seismograms and force-time function |
如式(1)所示,将滑坡区域的受力-时间函数f(t)与滑源至台站间的格林函数g(t)进行卷积,可获得地震台站处可观测到的地震波d(t);在已知d(t)和g(t)的前提下,通过反卷积求得f(t):
| $ d(t)=g(t) * f(t) $ | (1) |
以2个地震台的观测数据进行计算。将各地震数据与格林函数分量代入式(1),得:
| $ \left[ {\begin{array}{*{20}{c}} {d_Z^1}\\ {d_R^1}\\ {d_T^1}\\ {d_Z^2}\\ {d_R^2}\\ {d_T^2} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {Z{\rm{V}}{{\rm{F}}^1}}&{Z{\rm{H}}{{\rm{F}}^1}\cos \varphi }&{Z{\rm{H}}{{\rm{F}}^1}\sin \varphi }\\ {{\rm{RV}}{{\rm{F}}^1}}&{{\rm{RH}}{{\rm{F}}^1}\cos \varphi }&{{\rm{RH}}{{\rm{F}}^1}\sin \varphi }\\ 0&{{\rm{TH}}{{\rm{F}}^1}\sin \varphi }&{ - {\rm{TH}}{{\rm{F}}^1}\cos \varphi }\\ {Z{\rm{V}}{{\rm{F}}^2}}&{{\rm{ZH}}{{\rm{F}}^2}\cos \omega }&{{\rm{RH}}{{\rm{F}}^2}\sin \omega }\\ {{\rm{RV}}{{\rm{F}}^2}}&{{\rm{RH}}{{\rm{F}}^2}\cos \omega }&{{\rm{RH}}{{\rm{F}}^2}\sin \omega }\\ 0&{{\rm{TH}}{{\rm{F}}^2}\sin \omega }&{ - {\rm{TH}}{{\rm{F}}^2}\cos \omega } \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{l}} {{f_Z}}\\ {{f_N}}\\ {{f_E}} \end{array}} \right] $ | (2) |
式中,ZVF、RVF、ZHF、RHF、THF由CPS软件[15]基于CRUST1.0地壳模型计算而得;格林函数矩阵中,Z为格林函数的垂直分量,R为径向分量,T为切向分量,V为竖直方向作用的单力,H为水平方向作用的单力;受力-时间函数中,Z为垂直分量,N为南北向分量,E为东西向分量;上标1、2为台站编号,φ和ω为2个台站相对滑坡区域的方位角。为使卷积计算的矩阵维数互相对应,长度不够的分量需在末尾补0。
由于3个台站中BJT台与滑源地点之间的距离超过1 000 km,地震数据截取时间较长,虽然已降采样至2 Hz,基于式(1)进行时域反卷积计算的矩阵维数仍然超出使用MATLAB软件进行处理时的内存限制。为了减小内存消耗,加快运算速度,可将数据转至频域进行处理[16]。在[0.003,0.600] Hz频段内的反演结果如图 2(b)所示。
2.1.2 时频分析时频分析方法常用于观察反演前地震信号的能量分布,本文将其用于反演后得到的受力-时间函数。基于S变换的时频分析[17]结果如图 3所示。观察其能量分布,可划分出3个频段,分别为最低频段[0.012, 0.040] Hz、中间频段[0.040, 0.150] Hz和最高频段[0.150, 0.500] Hz。将图 2(b)的结果经以上3个频段滤波,得到如图 4所示的3组波形。
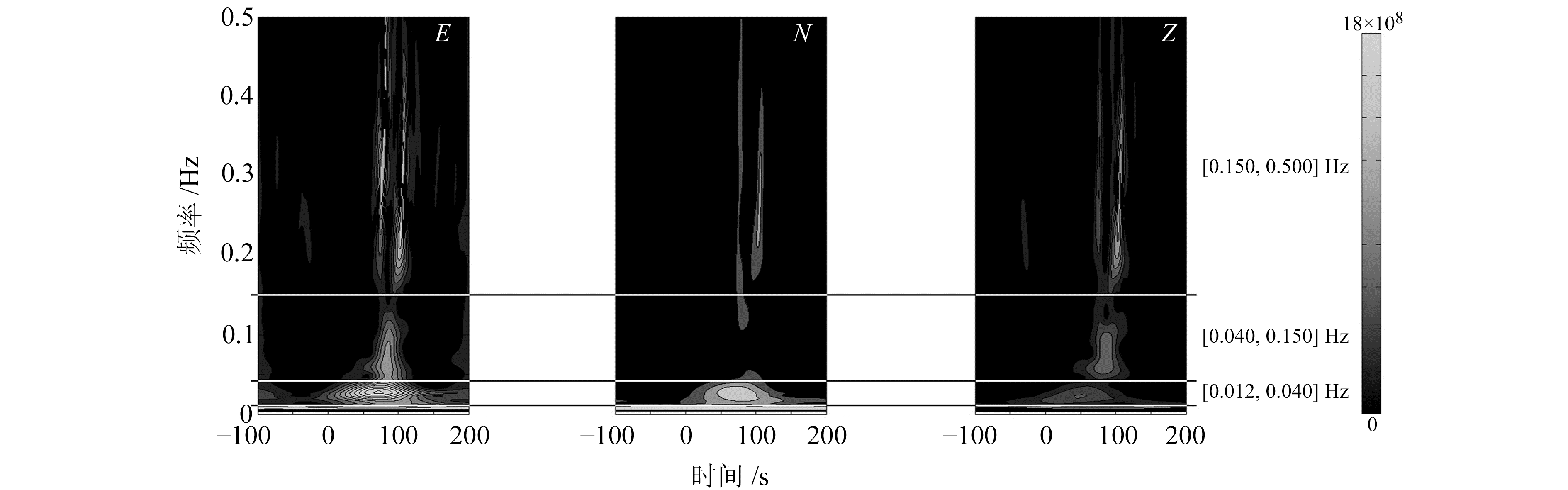
|
图 3 反演结果的时频分析 Fig. 3 Time-frequency analysis results |

|
图 4 滤波后的三频段波形 Fig. 4 Filtered triband waveforms |
最低频段的波形与学者们提出的类正弦函数模型(图 5(a))吻合,可将其视为因滑体作整体滑行运动而产生的力。中间频段有效波形持续时间较短且幅度也较小,但同样与类正弦函数模型类似,初步猜测为较小规模的滑坡产生的力。最高频段波形无法对应类正弦函数模型,归类为“高频信号”,是因滑体与坡壁、河堤碰撞,以及滑体内部的相互碰撞而产生,与巨大滑体的整体滑行运动无关。
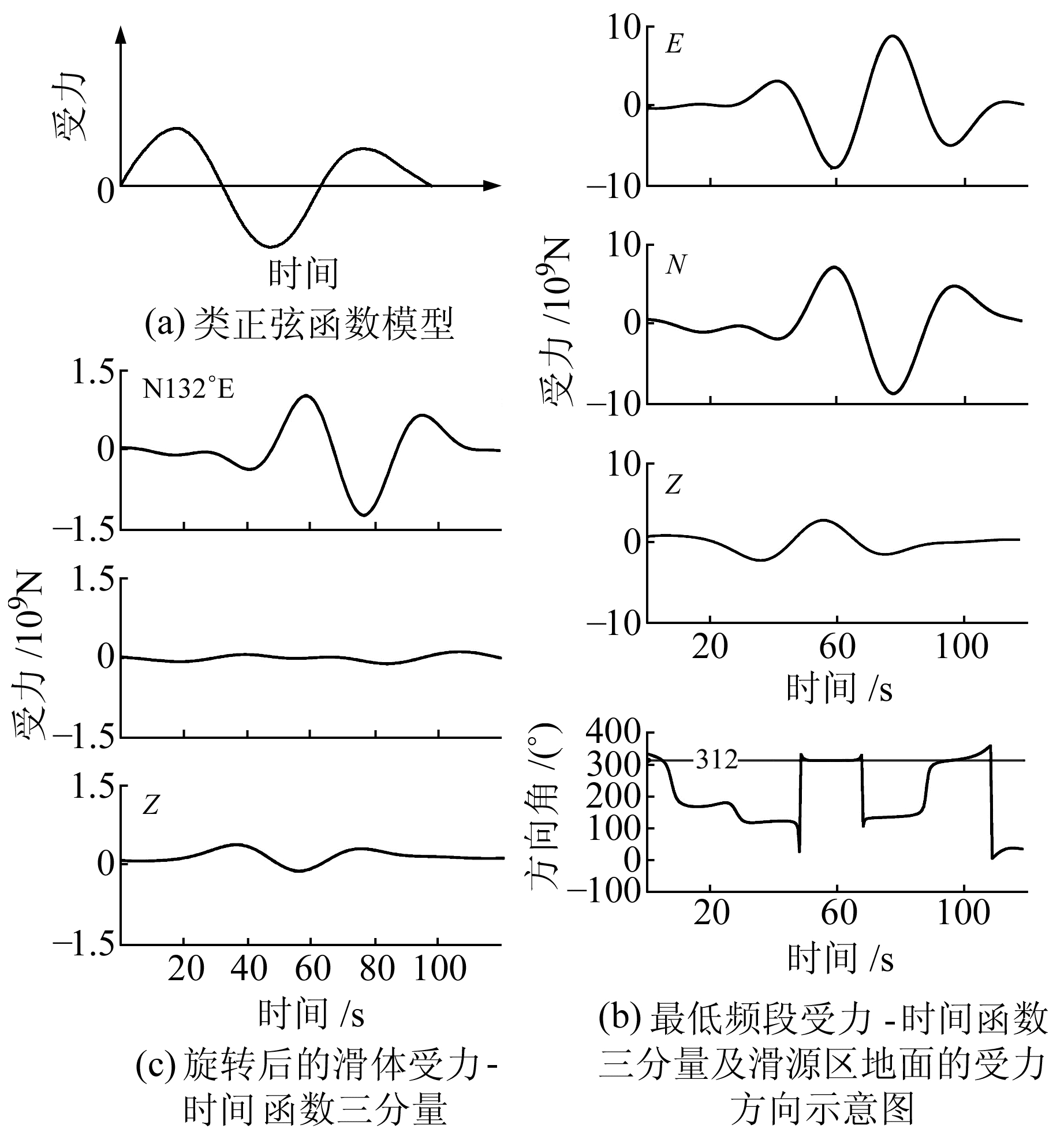
|
图 5 受力-时间函数三分量和类正弦函数模型 Fig. 5 Three-components of force-time function and sinusoidal model |
滑体最初作加速运动,其受力方向与运动方向相同。基于最低频段受力-时间函数2个水平分量的幅值,可计算出滑体的受力(运动)方位角随时间而变化的函数。从图 5(b)可知,在千将坪滑坡中滑体的初始运动方向约为N132°E,与现场调查所得结果相符合。在时间轴约68 s处,大地受力方向突然改变近180°,滑体此时由加速运动变为减速运动。可认为滑坡的开始时刻位于类正弦曲线的第1个零点(即47.5 s处),停止于第4个零点(即120.5 s处),滑坡整体运动持续时间约为73 s,符合目击者证词。滑坡启动后,滑体受到沿滑动方向的合力先增大后减小,直至反向。第一次加速结束于类正弦函数的第2个零点处,加速时长约为20.5 s。
由于最低频段时间函数的E、N分量的变化几乎完全同步,为方便计算,将2个水平分量逆时针旋转48°,得到沿滑体滑行方向(N132°E)和垂直于滑体滑行方向的2个分量,Z分量维持不变(图 5(c))。可以看到,垂直于滑体滑行方向的水平分量起伏非常小,计算时可忽略不计。
依照牛顿第二定律,滑体的加速度可由受力时间函数F(t)除以滑体质量m求得。而速度v(t)、位移D(t)又分别为加速度函数在时间上的积分和双重积分:
| $ {v(t) = {v_0} + \frac{1}{m}\int_0^t F (\tau ){\rm{d}}\tau } $ | (3) |
| $ {D(t) = \int_0^t {{\nu _0}} (\tau ){\rm{d}}\tau + \frac{1}{m}\mathop \int\!\!\!\int \nolimits_0^t F(\tau ){\rm{d}}\tau } $ | (4) |
式中,m为滑体质量,v0为启动速度,根据程谦恭等[18]的计算公式以及肖诗荣等[3]的千将坪滑坡参数,计算得到v0=2.20 m/s。取滑体物质密度2 000 kg/m3、体积2×107 m3代入计算。滑体加速度-时间、速度-时间函数、位移-时间函数如图 6所示。最终可得千将坪滑坡的最大速度为5.5 m/s,(质心)滑距为247 m。

|
图 6 滑体加速度-时间、速度-时间及位移-时间函数图 Fig. 6 Acceleration-time, velocity-time, and position-time curves of the landslide |
在计算启动速度时,假设变形滑体的弹性能100%转化为滑体动能。但实际情况下,弹性能还会转化为声、光、电、热等能量形式,仅有一部分成为滑体的初始动能,相应求得的值要小得多。同时,求得的速度是滑体质心的最大运动速度,和数值模拟[3]中得到的滑坡某一点的最大速度16 m/s不同。滑坡体上某一点的速度远大于质心运动速度是完全可能的,且按照计算所得的质心速度求得的滑距247 m与根据滑坡现场公路断开处2点GPS距离估算出的滑距250 m[19]一致。
2.2.2 滑床坡度及滑动摩擦系数取滑体加速阶段50~62 s的数据计算滑床坡度和滑动摩擦系数(滑体减速时受对岸阻力,影响式(5)的计算结果)。坡度可由受力-时间函数水平方向分量和垂直方向分量幅值比值的反正切得到。其滑动摩擦系数可根据式(5)求得,其中θ为前面已经求得的滑床坡度,μ为滑动摩擦系数:
| $ F=m g(\sin \theta-\mu \cos \theta) $ | (5) |
滑床坡度实际测量值为10°~35°,本文计算得到的值(图 7(a))基本反映了滑动过程中的坡度角变化。滑动摩擦系数在滑坡启动后迅速减小至0.21左右(图 7(b)),这与高速滑坡中气垫擎托持速效应以及滑床触变液化持速效应[20]等因素有关,较小的滑动摩擦系数可以使滑体保持高速滑行。
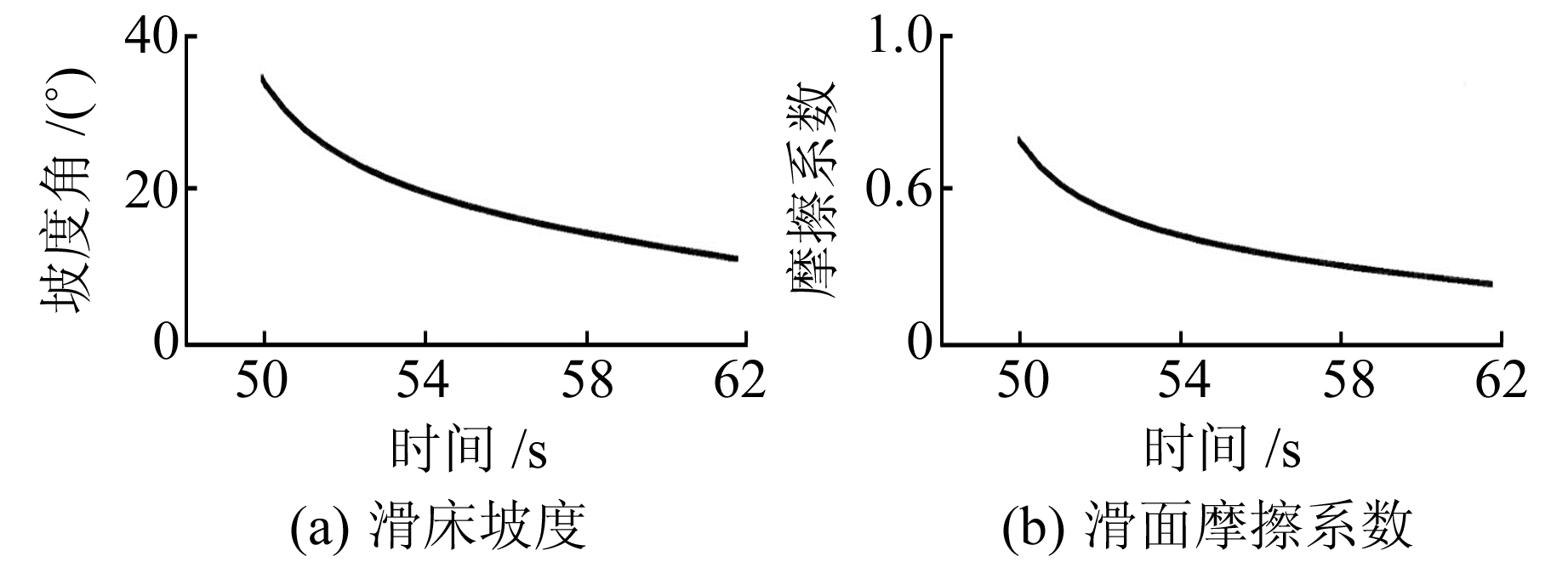
|
图 7 滑床坡度和滑面摩擦系数 Fig. 7 Slope of the sliding surface and friction coefficient during landslide |
在邬爱清等[2]的数值模拟实验中,设置主滑面摩擦系数为0.21~0.27,其最小值与我们求得的数值较接近。依照Lucas等[21]提出的经验公式:
| $ \mu=V^{-0.0774} $ | (6) |
平均滑动摩擦系数μ可由滑坡体积V求得。当V的数值等于2 ×107时,μ约等于0.27,与邬爱清等[2]设置的摩擦系数最大值一致。
2.2.3 讨论与分析从图 4可以看出,中间频段的时间函数同样具有类正弦函数模型的特点。滑体先加速再减速直至最终停止,但其运动方向偏西,与滑坡整体运动方向相反。从时间上来看,中间频段波形滞后于最低频段的波形,出现在滑坡整体运动受到最大阻力的时刻。当中间频段对应的滑坡事件发生后,滑坡整体运动的阻力减小,且再次产生一个短暂的加速阶段,直至最终静止。千将坪滑坡为典型的库岸滑坡,滑体受到的主要阻力来自于河岸,当滑体受到最大阻力时,地面的受力为阻力的相反方向,即N132°E方向,这与图 4和图 5(a)展示的地面受力波形相符。
当滑体受到最大阻力时(77 s左右),分析图 4波形发现,其包含了与滑坡主体体积相比较小的两起滑坡事件。其中一起事件在图 3的时频分析图中仅有南北向分量较明显;另一起事件能量更显著,且从其水平受力的振幅判断,滑体初始滑行方向与主滑体初始滑行方向相反,极可能是因河堤阻挡,使得主滑体前缘破裂,一部分滑体向回滑动,产生反倾运动。结合现场勘踏得到的沉积情况[12]可知,在滑坡区域的河道内,确实存在一个前缘反翘区,在对面河岸陡崖下形成逆冲反翘地形,这与本文分析结果一致。
据此,可将千将坪滑坡过程描述如下:在锁固段断裂后,滑体向N132°E方向作整体滑行,加速度不断增大,滑体前缘进入青干河,并到达对岸河堤;受摩擦力和对岸河堤的阻力影响,滑体加速度不断减小,直至滑体转为减速运动,到达对岸河堤的岩土逐渐累积,沿着河堤向上爬升;当滑体受到最大阻力无法前进时,爬升至对岸河堤高处的部分岩土开始向偏西北的方向作反倾运动;滑体主体受到的阻力因此减小,并再次加速滑行了一段距离,直至达到最终稳定状态。
3 结语本文基于地震信号反演求取千将坪滑坡过程中滑坡区域的受力状态,使用时频分析划分出不同滑坡子事件的频段,并结合经典力学分析还原滑坡过程。计算可知,在千将坪滑坡中,滑体的运动方向为N132°E,整体运动的持续时间约为73 s;滑体质心的最大速度达到约5.5 m/s;滑距约247 m,与地质分析结论相近。基于受力-时间函数还可以计算滑坡过程中摩擦系数随时间变化的曲线,在滑坡启动后,滑动摩擦系数值迅速减小至0.2左右,为滑体高速运动创造了条件。观察处于不同频段滑坡子事件的受力-时间函数并进行综合分析,可推导出“静止-加速-减速-前端反倾后整体再加速-静止”的滑坡过程。
本文方法可用于远程了解滑坡受灾情况,指导灾后抢险。同时,经由地震波形反演得到滑体滑行期间的受力-时间函数是一种直接获取大地受力状态的方法,其结果可与地质分析的结论、物理模拟以及数值模拟的实验结果进行对照分析,促进高速滑坡运动机制的研究。
致谢: 感谢段翔、付彪、邹凌志、胡德琪、陈星壮、邓胜、李婉婧、冯圣轩等提供帮助。
| [1] |
吴剑, 张振华, 刘依松. 千将坪滑坡中几个高速滑坡问题的探讨[J]. 三峡大学学报:自然科学版, 2007, 29(2): 120-123 (Wu Jian, Zhang Zhenhua, Liu Yisong. Study on High-Speed Mechanism of Qianjiangping Landslide[J]. Journal of China Three Gorges University:Natural Science, 2007, 29(2): 120-123)
(  0) 0) |
| [2] |
邬爱清, 丁秀丽, 李会中, 等. 非连续变形分析方法模拟千将坪滑坡启动与滑坡全过程[J]. 岩石力学与工程学报, 2006, 25(7): 1 297-1 303 (Wu Aiqing, Ding Xiuli, Li Huizhong, et al. Numerical Simulation of Startup and Whole Failure Process of Qianjiangping Landslide Using Discontinuous Deformation Analysis Method[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(7): 1 297-1 303)
(  0) 0) |
| [3] |
肖诗荣, 刘德富, 胡志宇. 三峡库区千将坪滑坡高速滑动机制研究[J]. 岩土力学, 2010, 31(11): 3 531-3 536 (Xiao Shirong, Liu Defu, Hu Zhiyu. Study of High Speed Slide Mechanism of Qianjiangping Landslide in Three Gorges Reservoir Area[J]. Rock and Soil Mechanics, 2010, 31(11): 3 531-3 536)
(  0) 0) |
| [4] |
王秋良, 申学林, 王墩, 等.三峡水库千将坪滑坡地震记录的波形特征研究[C].中国地震学会成立三十年学术研讨会, 北京, 2009 (Wang Qiuliang, Shen Xuelin, Wang Dun, et al. Study of Waveform Characteristics of the Seismic Record of Qianjiangping Landslide in Three Gorges Reservoir Area[C]. Thirty Annual Symposium of the Seismological Society of China, Beijing, 2009)
(  0) 0) |
| [5] |
刘文清, 董建辉, 朱建, 等. 三峡库区千将坪滑坡信息特征分析[J]. 大地测量与地球动力学, 2016, 36(增1): 144-148 (Liu Wenqing, Dong Jianhui, Zhu Jian, et al. Characteristics Analysis of Qianjiangping Landslide Information in Three Gorges Reservior Area[J]. Jourcal of Geodesy and Geodynamics, 2016, 36(S1): 144-148)
(  0) 0) |
| [6] |
Ekström G, Stark C P. Simple Scaling of Catastrophic Landslide Dynamics[J]. Science, 2013, 339(6126): 1 416-1 419 DOI:10.1126/science.1232887
(  0) 0) |
| [7] |
Hibert C, Ekström G, Stark C P. Dynamics of the Bingham Canyon Mine Landslides from Seismic Signal Analysis[J]. Geophysical Research Letters, 2014, 41(13): 4 535-4 541 DOI:10.1002/2014GL060592
(  0) 0) |
| [8] |
Yamada M, Kumagai H, Matsushi Y, et al. Dynamic Landslide Processes Revealed by Broadband Seismic Records[J]. Geophysical Research Letters, 2013, 40(12): 2 998-3 002 DOI:10.1002/grl.50437
(  0) 0) |
| [9] |
Li Z Y, Huang X H, Xu Q, et al. Dynamics of the Wulong Landslide Revealed by Broadband Seismic Records[J]. Earth, Planets and Space, 2017, 69(1): 27 DOI:10.1186/s40623-017-0610-x
(  0) 0) |
| [10] |
Huang X H, Li Z Y, Yu D. Evolution of a Giant Debris Flow in the Transitional Mountainous Region between the Tibetan Plateau and the Qinling Mountain Range, Western China: Constraints from Broadband Seismic Records[J]. Journal of Asian Earth Sciences, 2017, 148: 181-191 DOI:10.1016/j.jseaes.2017.08.031
(  0) 0) |
| [11] |
三峡库区地质灾害防治工作指挥部. 湖北省秭归县沙镇溪镇千将坪滑坡[J]. 中国地质灾害与防治学报, 2003, 14(3): 139 (Geological Disaster Prevention Headquarters of the Three Gorges Reservoir Area. Qianjiangping Landslide in Zigui, Hubei Province[J]. The Chinese Journal of Geological Hazard and Control, 2003, 14(3): 139 DOI:10.3969/j.issn.1003-8035.2003.03.030)
(  0) 0) |
| [12] |
李会中, 潘玉珍, 王团乐. 三峡库区千将坪滑坡成因与机制分析[J]. 人民长江, 2006, 37(7): 12-20 (Li Huizhong, Pan Yuzhen, Wang Tuanle. The Cause and Mechanism Analysis of the Landslide in the Three Gorges Reservoir Area[J]. Yangtze River, 2006, 37(7): 12-20 DOI:10.3969/j.issn.1001-4179.2006.07.005)
(  0) 0) |
| [13] |
杨海平, 王金生. 长江三峡工程库区千将坪滑坡地质特征及成因分析[J]. 工程地质学报, 2009, 17(2): 233-239 (Yang Haiping, Wang Jinsheng. Geological Features and Cause Analysis of Qianjiangping Landslide of July 13, 2003 on Three Gorges Reservoir[J]. Journal of Engineering Geology, 2009, 17(2): 233-239 DOI:10.3969/j.issn.1004-9665.2009.02.013)
(  0) 0) |
| [14] |
Wang F W, Zhang Y M, Huo Z T, et al. Mechanism for the Rapid Motion of the Qianjiangping Landslide during Reactivation by the First Impoundment of the Three Gorges Dam Reservoir, China[J]. Landslides, 2008, 5(4): 379-386 DOI:10.1007/s10346-008-0130-7
(  0) 0) |
| [15] |
Hermann R B.Computer Programs in Seismology, An Overview of Synthetic Seismogram Computation, Version 3.30[Z]. Dept of Earth and Atmospheric Sciences, Saint Louis University, 2002
(  0) 0) |
| [16] |
Zhao J, Moretti L, Mangeney A, et al. Model Space Exploration for Determining Landslide Source History from Long-Period Seismic Data[J]. Pure and Applied Geophysics, 2015, 172(2): 389-413 DOI:10.1007/s00024-014-0852-5
(  0) 0) |
| [17] |
Stockwell R G, Mansinha L, Lowe R P. Localization of the Complex Spectrum: the S Transform[J]. IEEE Transactions on Signal Processing, 1996, 44(4): 998-1 DOI:10.1109/78.492555
(  0) 0) |
| [18] |
程谦恭, 胡厚田, 胡广韬, 等. 高速岩质滑坡临床弹冲与峰残强降复合启程加速动力学机制[J]. 岩石力学与工程学报, 2000, 19(2): 173-176 (Cheng Qiangong, Hu Houtian, Hu Guangtao, et al. A Study of Complex Accelerated Dynamics Mechanism of High-speed Landslide by Elastic Rocky Impulse and Peak-Residual Strength Drop[J]. Chinese Journal of Rock Mechanics and Engineering, 2000, 19(2): 173-176 DOI:10.3321/j.issn:1000-6915.2000.02.010)
(  0) 0) |
| [19] |
王治华, 杨日红. 三峡水库区千将坪滑坡活动性质及运动特征[J]. 中国地质灾害与防治学报, 2005, 16(3): 5-10 (Wang Zhihua, Yang Rihong. The Activity Characteristics and Movement Style of Qianjiangping Landslide in the Three Gorges Reservoir Region[J]. The Chinese Journal of Geological Hazard and Control, 2005, 16(3): 5-10 DOI:10.3969/j.issn.1003-8035.2005.03.002)
(  0) 0) |
| [20] |
胡广韬. 滑坡动力学[M]. 北京: 地质出版社, 1995 (Hu Guangtao. Landslide Dynamics[M]. Beijing: Geological Publishing House, 1995)
(  0) 0) |
| [21] |
Lucas A, Mangeney A, Ampuero J P. Frictional Velocity-Weakening in Landslides on Earth and on Other Planetary Bodies[J]. Nature Communications, 2014(5): 3 417
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39

