微小地震虽然破坏性不大,却是研究大地震和整个地震带应力场的基础[1],其特点是频率高、信噪比低、数量多,若能实现微地震事件的自动识别和初至震相的自动拾取,将对海量微地震数据的自动处理有重要意义[2]。Stevenson[3]首次提出应用长短时窗平均能量比值法(STA/LTA)识取地震初至震相,其后发展出各种基于该方法的时间域、频率域、偏振分析、高阶统计量、模式识别等综合分析震相拾取方法[4];Gelchinsky等[5]提出用相关法自动检测走时曲线初至到时;Schaff等[6]提出基于波形互相关的重复地震检测方法,并在此基础上发展了一种模板匹配技术,用于检测波形相似的地震[7]。由于模板匹配技术能够有效抑制背景噪声、较大地震面波和震荡等造成的低频信号干扰[8],在地震自动识别领域被广泛应用[9-11]。与STA/LTA方法相比,波形互相关法在波形相似度较高的情况下能够检测出更多的地震[10],但当信噪比不高、地震记录信号与噪声频带重叠时,其检测效果并不理想。
小波相似性分析是研究时间序列多尺度相似性的一种新的时频分析方法。该方法基于多尺度分析框架并考虑局部相位,可较好地再现2个序列时间尺度上的相似性,同时也保持了局部的细节特征,进而揭示2个序列间多尺度的相互作用关系[12]。Johnson等[13]首次应用小波相似性算法分析地球物理钻孔数据,并对不同情况下数据的相似性进行讨论。本文提出一种基于小波互相关技术的微地震波形自动检测方法,利用复Morlet小波在特定尺度上对地震波形进行变换,分析其相位角相关性,设置合理的相似度阈值,自动检测微地震。
1 基本原理由于Morlet小波采用时域窗面积最小的高斯窗函数,时域、频域局部化性能都很好,对称性也较好,故本文选用该小波作为母小波进行地震信号检测。地震信号f(x)的连续小波变换CWT[14]为:
| $ \mathrm{CWT}(u, s)=\int_{-\infty}^{\infty} f(t) \frac{1}{|s|^{0.5}} \psi^{*}\left(\frac{t-u}{s}\right) \mathrm{d} t $ | (1) |
式中,s为小波分析尺度,u为位移,ψ为小波母函数,*表示共轭复数。用复Morlet小波作为小波母函数,定义如下[15]:
| $ \psi(x)=\frac{1}{\pi f_{b}} \mathrm{e}^{2 \pi \mathrm{i} f_{c} x} \mathrm{e}^{-x^{2} / f_{b}} $ | (2) |
式中,fb为复Morlet小波的带宽,fc为复Morlet小波的中心频率。
对于地震数据X(t),由于同一地震在同一台站内应具有相同的频率特征,故可以利用连续小波在某些特定尺度上的相位角相似性来检测获得一段时间内的所有地震事件。
定义2个信号的连续交叉小波变换[16]为:
| $ \mathrm{CWT}_{1, 2}=\mathrm{CWT}_{1} \times \mathrm{CWT}_{2}^{*} $ | (3) |
式中,CWT1, 2的幅值A为|CWT1, 2|,相位角θ为
| $ S=\cos ^{n} \theta $ | (4) |
式中,n为大于0的奇数。当S=1时表示数据正相关,S=0时表示数据不相关,S=-1时表示数据负相关。
当信号的背景噪声很大时,相似性的变化对噪声较为敏感,所以考虑信号的幅值信息,2组数据的相似度又可表示为:
| $ S=A \cos ^{n} \theta $ | (5) |
假设有2个时间序列x1、x2分别为:
| $ x_{1}=A \cos \omega_{1} t+A R \times \operatorname{rand} n(1, n) $ |
| $ x_{2}=B \cos \omega_{2} t+B R \times \operatorname{rand} n(1, n) $ |
对x1和x2进行小波相关性分析,波形及分析结果见图 1。图 1(a)为x1数据,是一组10 Hz正弦信号掺杂50 Hz的正弦信号;图 1(b)为x2数据,是一组50 Hz的正弦信号;图 1(c)、1(d)分别为x1、x2数据的复Morlet连续小波变换结果;图 1(e)为2组数据进行Morlet小波相位角相关性分析的结果。从图中可以看出,在2组信号频率相同的地方表现出明显的相关性。
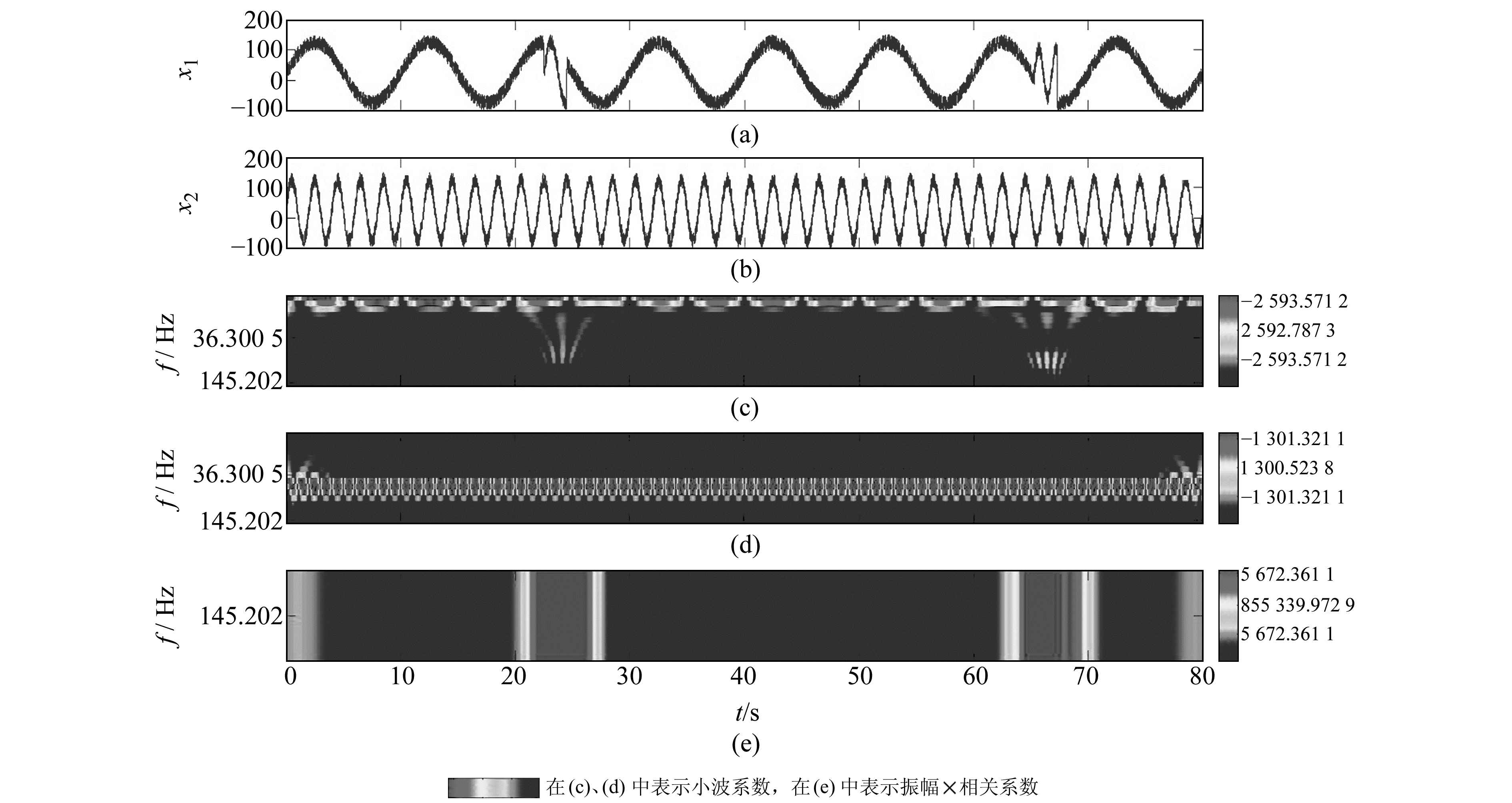
|
图 1 x1和x2小波相关性分析结果 Fig. 1 Results of wavelet correlation analysis of x1 and x2 |
由于小波分析的多尺度特性,小波相关分析具备明显的尺度特征,即可以在不同尺度下进行相关性比较。这给相关性分析带来了很好的频率指向性,从而能够进行更精细的数据相关性分析,因此可以使用统计学方法进行2组波形相似度的定量计算。
假定x1为基准波形,试图从序列x2中寻找与x1最相似的数据段时,可以通过计算x1在不同尺度下的小波系数的能量权重,将该权重引入相似度中。取数据序列中所有数据的平均值,可以标定2组数据序列的定量相似性,表示为:
| $ S_{\mathrm{avg}}=\frac{\sum\limits_{n=1}^{N} K(n) \times S(n)}{(N \times M)} $ | (6) |
式中,K(n)为x1在各尺度下的小波系数的能量权重,S(n)为x1与x2进行相关性分析的结果,N为x1与x2进行相关性分析的每个尺度下的系数数量,M为x1与x2进行相关性分析的尺度。
在x2逐点取得与x1同长度数据,使用式(1)~(6)计算信号x2中任意位置信号片段与信号x1的相关性,得到相关性系数集合,在集合中寻找满足离群条件的数据,则可以找到信号x2中与模板信号x1相关的信号片段。这个过程可以用绝对离差中位数(median absolute deviation,MAD)计算。
对所有数据进行MAD计算,并约定阈值Thr,则可以基本确定序列x2中与x1较为相似的数据段位置,即
| $ \mathrm{MAD}=\operatorname{median}\left(\left|X_{i}-\operatorname{median}(X)\right|\right) $ | (7) |
| $ \mathrm{Thr}>\kappa \mathrm{MAD} $ | (8) |
继续上述实验,在序列x2中寻找与x1相似性的定量分析,结果见图 2。图 2(a)、2(b)分别为用式(4)、(5)对x1和x2进行小波相位角相关性定量分析的结果。从图 2可看出,该方法能直观地确定相关数据的具体位置,从而自动检测强地震后的余震或震群。
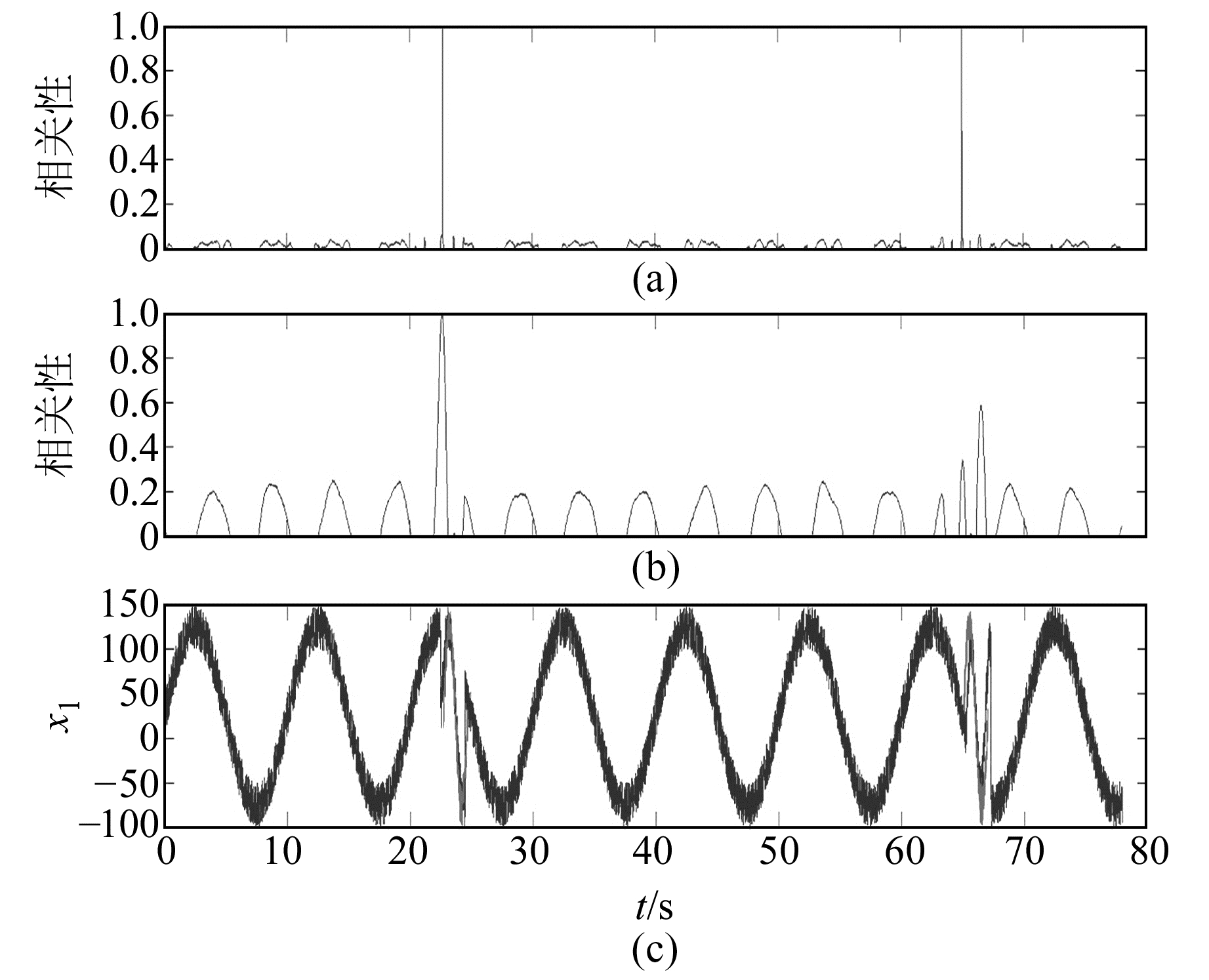
|
图 2 数据相似性定量分析 Fig. 2 Quantitative analysis of data similarity |
2018-05-01 11:14新疆昌吉发生ML4.8地震(43.61°N,86.62°E),其后发生一系列余震。主震与余震通常有共同的发震构造和互相关联的震源机制,波形也具有很好的相似性[17]。为验证本文方法的可靠性,选取离震中最近的STZ、LHG和HTB台记录的2018-05-01 16:00~16:30三分量波形为待检测数据,以信噪比高、记录清晰的地震波形为模板地震。首先用2~8 Hz四阶巴特沃斯(Butterworth)带通滤波器对地震波形进行去均值及归一化处理,然后对模板地震三分量数据进行复Morlet连续小波计算,计算其主要能量集中的尺度范围,并对这个尺度范围内的小波数据进行相位角计算,得出相位角序列。根据此结果截取待检测数据中相似的地震数据,对每一次截取的数据进行复Morlet小波变换,在能量集中的尺度范围内用式(4)或式(5)、式(6)和式(7)进行小波相位角相关性计算。计算MAD时采用三分量数据小波相位角相关系数的平均值,阈值选取根据实际地震不同而有所不同,本文选取40倍MAD作为判别地震的阈值Thr。地震检测结果见表 1,30 min内共检测出11个地震,与中国地震台网中心地震编目结果基本一致,无漏检、错检。比较P波到时,STZ台相差约1 s,LHG台相差约为0.05 s,HTB台相差约为0.26 s。图 3为2018-05-01 16:20:50~16:26:10的地震检测情况,图 3(a)、3(c)及3(e)为在连续波形上检测到的地震P波初至的位置,图 3(b)、3(d)及3(f)为检测波形示意图。STZ台和LHG台记录的波形信噪比高,用式(4)进行计算;HTB台记录波形背景噪声大,用式(5)进行计算,所有结果均能清晰地检测到地震。由此可见,将该方法用于地震序列中微地震检测具有一定的可行性。
|
|
表 1 地震检测结果 Tab. 1 Seismic detection results |
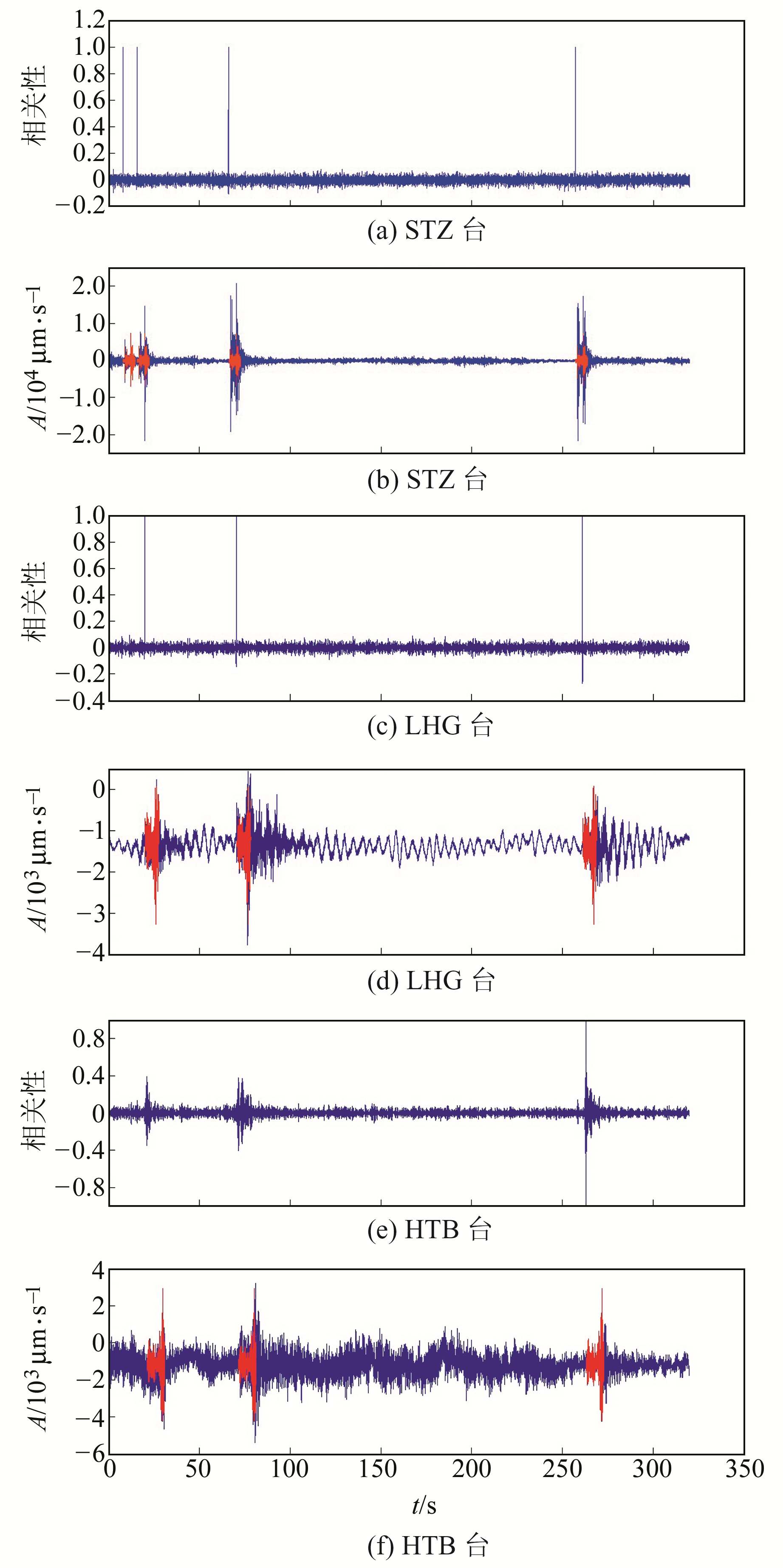
|
蓝色表示连续波形,红色表示波形模板 图 3 3个台站检测结果及该结果在垂直向波形的情况 Fig. 3 Detection results of vertical recording waveform of three stations |
本文利用复Morlet小波相位角互相关变换分析数据的相关性,通过统计学方法对数据相似度进行定量计算,获得原始数据中与模板数据较为相似的数据段初始位置,进而将该方法用于地震序列微地震检测。对2018-05-01新疆昌吉ML4.8地震后30 min的波形进行检测测试,共发现11个微地震事件,并给出其检测台站的P波到时结果。与中国地震台网中心地震编目结果进行对比发现,无漏检、错检,P波到时结果相差基本在1 s之内,认为将该方法用于地震序列微地震检测具有一定的可行性。
本文所用方法的一个显著特点是使用三分量地震波形进行小波变换,利用小波相位角互相关检测地震序列,同时标定检测出的地震序列P波到时。与前人用互相关检测地震的方法[8-9, 11]相比,该方法应用小波变换将时间序列分解到时间频率内,从而得出时间系列显著的相位变化特征。由于小波变换在时频两域都有表征局部特性的能力,对地震噪声有很强的压制作用,即使地震记录信号与噪声频带重叠,也能通过变换尺度突显检测信号的瞬态或奇异点。
本文所用方法选取的模板地震为信噪比大于4、震级ML≥1.5、至少有3个以上的台站清晰记录,若震级太小,则能记录到该地震的台站不多,不具有通用性,如第1个模板地震。作为方法检验仅选择了30 min的数据,用到3个模板地震,对于地震序列较多、待检测波形时间更长的情况,采用该原则选择的模板地震会有很多,若进行实际操作,工作量将非常庞大。在以后的工作中,笔者会选择几个小时的数据进行试算,若有N个地震都被检测到,则确定该地震为模板地震,N的确定要保证不漏检、错检和多检地震。不可否认,在检测过程中,若存在与任何模板地震波形均不互相关的地震,该地震将难以被检测到。
目前,该方法仅用于检测相似微地震的P波初至,对于形成完整的地震序列目录还存在一定的局限性,今后会尝试用该方法检测微地震的S波初至。
致谢: 感谢新疆维吾尔自治区地震局阿克苏中心地震台龚固斌对相关公式给予的指导。
| [1] |
周银兴.微震事件检测及震相自动识别研究[D].北京: 中国地震局地震预测研究所, 2009 (Zhou Yinxing.Research on the Micro-Earthquake Detection and Seismic Phase Automatic Identification[D].Beijing: Institute of Earthquake Forecasting, CEA, 2009) http://cdmd.cnki.com.cn/Article/CDMD-85405-2009237135.htm
(  0) 0) |
| [2] |
Warpinski N. Microseismic Monitoring:Inside and Out[J]. Journal of Petroleum Technology, 2009, 61(11): 80-85 DOI:10.2118/118537-JPT
(  0) 0) |
| [3] |
Stevenson P R. Microearthquakes at Flathead Lake, Montana:A Study Using Automatic Earthquake Processing[J]. Bulletin of the Seismological Society of America, 1976, 66(1): 61-80
(  0) 0) |
| [4] |
武东坡.震相识别的实时方法研究[D].哈尔滨: 中国地震局工程力学研究所, 2004 (Wu Dongpo.Research on the Real-Time Processing Method of Seismic Phase Identification[D].Harbin: Institute of Engineering Mechanics, CEA, 2004) http://cdmd.cnki.com.cn/Article/CDMD-85406-2004102023.htm
(  0) 0) |
| [5] |
Gelchinsky B, Shtivelman V. Automatic Picking of First Arrival and Parameterization of Traveltime Curves[J]. Gephysical Prospecting, 1983, 31(6): 915-928 DOI:10.1111/j.1365-2478.1983.tb01097.x
(  0) 0) |
| [6] |
Schaff D P, Richards P G. Repeating Seismic Events in China[J]. Translated World Seismology, 2004, 303(5 661): 1 176-1 178
(  0) 0) |
| [7] |
Gibbons S J, Ringdal F. The Detection of Low Magnitude Seismic Events Using Array-Based Waveform Correlation[J]. Geophysical Journal International, 2006, 165(1): 149-166 DOI:10.1111/j.1365-246X.2006.02865.x
(  0) 0) |
| [8] |
谭毅培, 曹井泉, 刘文兵, 等. 2013年3月涿鹿微震群遗漏地震事件检测和发震构造分析[J]. 地球物理学报, 2014, 57(6): 1 847-1 856 (Tan Yipei, Cao Jingquan, Liu Wenbing, et al. Missing Earthquakes Detection and Seismogenic Structure Analysis of the Zhuolu Micro-Earthquake Swarm in March 2013[J]. Chinese Journal of Geophysics, 2014, 57(6): 1 847-1 856)
(  0) 0) |
| [9] |
Peng Z G, Zhao P. Migration of Early Afterschocks Following the 2004 Parkfield Earthquake[J]. Nature Geoscience, 2009, 2(12): 877-881 DOI:10.1038/ngeo697
(  0) 0) |
| [10] |
Schaff D. Improvements to Detection Capability by Cross-Correlating for Similar Events:A Case Study of the 1999 Xiuyan, China, Sequence and Synthetic Sensitivity Tests[J]. Geophysical Journal International, 2010, 180(2): 829-846 DOI:10.1111/j.1365-246X.2009.04446.x
(  0) 0) |
| [11] |
王娟, 邱宏茂, 李健, 等. 基于相匹配滤波的面波自动检测算法的实现[J]. 核电子学与探测技术, 2015, 35(5): 426-429 (Wang Juan, Qiu Hongmao, Li Jian, et al. Realization of Surface Wave Automatic Detection Algorithm Based on Phase-Matched Filter[J]. Nuclear Electronics and Detection Technology, 2015, 35(5): 426-429 DOI:10.3969/j.issn.0258-0934.2015.05.003)
(  0) 0) |
| [12] |
俞肇元, 袁林旺, 闾国年, 等. 西北太平洋边缘海区海面变化多尺度解析及空间分布[J]. 地理研究, 2009, 28(6): 1 644-1 655 (Yu Zhaoyuan, Yuan Linwang, Lü Guonian, et al. Multi-Scale Analysis of Sea-Level Change and Its Spatial Characteristics in Northwest Pacific Ocean Marginal Seas[J]. Geographical Research, 2009, 28(6): 1 644-1 655)
(  0) 0) |
| [13] |
Johnson C, Webb S, Cooper G, et al.Wavelet-Based Semblance Analysis Applied to Geophysical Borehole Data[C].11th Saga Biennial Technical Meeting and Exhibition, Swaziland, 2009
(  0) 0) |
| [14] |
Mallat S. A Wavelet Tour of Signal Processing[M]. New York: Academic Press, 1998
(  0) 0) |
| [15] |
Teolis A. Computational Signal Processing with Wavelets[M]. Boston: Birkhauser, 1998
(  0) 0) |
| [16] |
Torrence C, Compo G P. A Practical Guide to Wavelet Analysis[J]. Bulletin of the American Meteorological Society, 1998, 79(1): 61-78 DOI:10.1175/1520-0477(1998)079<0061:APGTWA>2.0.CO;2
(  0) 0) |
| [17] |
刘翰林, 吴庆举. 地震自动识别及震相自动拾取方法研究进展[J]. 地球物理学进展, 2017, 32(3): 1 000-1 007 (Liu Hanlin, Wu Qingju. Developments of Research on Earthquake Detection and Seismic Phases Picking[J]. Progress in Geophysics, 2017, 32(3): 1 000-1 007)
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39

