对地壳应变场的监测是发现地震短临前兆异常的重要途径,而钻孔体应变是监测地壳应变场的有效手段之一,但体应变会受到气压、降雨、荷载、抽水、温度等非地震因素的影响[1]。
分析青岛地震台体应变观测资料发现,青岛台体应变在固体潮背景曲线上经常出现小幅抖动或畸变的现象。参考前人[2-7]对体应变干扰的相关分析,选取青岛台体应变和辅助测项观测资料,利用相关分析、回归分析计算不同周期体应变与气压的相关系数和气压系数,探讨不同周期气压波相关系数和气压系数的变化规律;然后利用交叉小波变换[8-9]研究气压和体应变的相关性,以揭示该台体应变受短周期气压波干扰的客观现象,得出不同周期气压波与体应变相关系数和气压系数,并根据不同尺度下气压系数对各个尺度的气压干扰进行压制,重构数据显示体应变信噪比得到提高。
1 观测井概况青岛地震台紧邻劈石口断裂和王哥庄断裂,劈石口断裂总体走向40°左右,倾角65°~80°,早期活动为左旋走滑,后期活动为右旋走滑,呈现多期活动构造特征[10],最后一次断错地表的活动发生在中更新世中晚期,晚更新世以来没有活动[11];王哥庄断裂走向48°,倾向NW,倾角65°~78°, 也具有多期活动特征,最新活动时代为中更新世中晚期,晚更新世以来没有断错地表的活动[11]。
青岛台应变仪为TJ-2型体积式应变仪,安装钻孔孔径130 mm,钻孔深度66 m,仪器安装深度55 m,具有气压、水位和钻孔温度等3个辅助测项。根据仪器安装报告,钻孔的岩石性质主要为花岗岩。由地表至66 m深处,岩体十分坚硬而破碎,仅在54~55 m、58~59 m深处相对完整,岩石节理面与裂隙的倾角近乎垂直。
2 数据情况和分析方法青岛台体应变资料固体潮形态清晰,变化趋势稳定。本文采用2012~2017年的数据,采样间隔为1 min。
为了研究不同周期气压波对体应变的影响,首先利用离散小波变换将数据分解为不同周期,再利用相关分析和回归分析计算相关系数和气压系数,并结合交叉小波变换在时频域分析二者的相关性。离散小波变换的相关理论可以参照文献[12],在此仅介绍交叉小波变换的计算思路。
交叉小波变换是将连续小波变换和交叉谱分析结合起来的一项时频分析技术[8-9],可以在时频域研究2个时间序列的相关关系。假设WX、WY分别是给定2个时间序列X、Y的连续小波变换谱,定义其交叉小波变换谱为:
| $ W^{X Y}=W^{X} W^{Y *} $ | (1) |
式中,*表示复共轭,|WXY|为交叉小波变换的能量谱,WXY的相位角表示2个时间信号局部位置的相对位相关系,在时频谱图上用方向箭头表示,水平向右表示二者相位角相同,向左表示二者相位角相差180°,向上表示相差-90°,向下表示相差90°。
交叉小波变换能量谱可以揭示2个时间序列共同强能量区域,对能量谱的检验可以利用交叉小波变换能量谱与红色噪声背景谱的大小关系确定。假设2个具有红色背景噪声谱的信号X和Y,其红色噪声谱为PX和PY,利用交叉小波变换谱与红色噪声谱的关系式作为评判标准:
| $ \frac{\left|W_{n}^{X}(s) W_{n}^{Y *}(s)\right|}{\sigma_{X} \sigma_{Y}}=\frac{Z_{v}(P)}{v} \sqrt{P^{X} P^{Y}} $ | (2) |
式中,n为时间序列号,s为尺度变量,σX、σY为时间序列X和Y各自的标准差,Zv(P)为与概率P有关的置信度。由于采用复小波计算,因此ν=2,在显著水平α=0.05的水平下,Z2(95%)=3.999。先求出红色噪声功率谱的95%的置信限上界,当式(3)左端超过置信限,则认为通过了显著水平α=0.05下的红色噪声标准谱的检验。
交叉小波变换能量谱揭示2个信号具有的相同强能量的区域,而交叉小波变换相关谱揭示2个信号在时频域的相关性,相关谱计算公式为:
| $ R_{n}^{2}(s)=\frac{\left|S\left(s^{-1} W_{n}^{X Y}(s)\right)\right|^{2}}{S\left(s^{-1}\left|W_{n}^{X}(s)\right|^{2}\right) S\left(s^{-1}\left|W_{n}^{Y}(s)\right|^{2}\right)} $ | (3) |
式中,s为小波变换的尺度,S为平滑算子,其计算公式为:
| $ S(W)=S_{s}\left(S_{t}\left(W_{n}(s)\right)\right) $ | (4) |
式中,Ss为沿尺度轴方向的平滑,St为沿时间轴方向的平滑,具体计算可以参照文献[9]。需要注意的是,交叉小波变换是基于连续小波变换实现的,由于连续小波变换假设数据是周期数据,但是实际数据是有限长的,因此在小波时频谱边缘会产生误差。为了减小误差,对原始数据在首尾补零,但是同时会产生时频谱不连续的边界,因此只分析边界内的时频谱数据。
3 短周期气压波与体应变相关分析为了避免数据选择的主观性,随机选取2012~2017年每年没有地震、仪器故障和人为干扰的30 d左右的数据(共190 d)进行分析。在定量分析之前,选择气压波动明显的单日数据进行定性分析(图 1)。由图 1可知,矩形框内气压变化较大,体应变小幅度波动在时间上具有同步性,但在固体潮背景下不易判断二者相似性的大小,需要计算相关系数和气压系数。
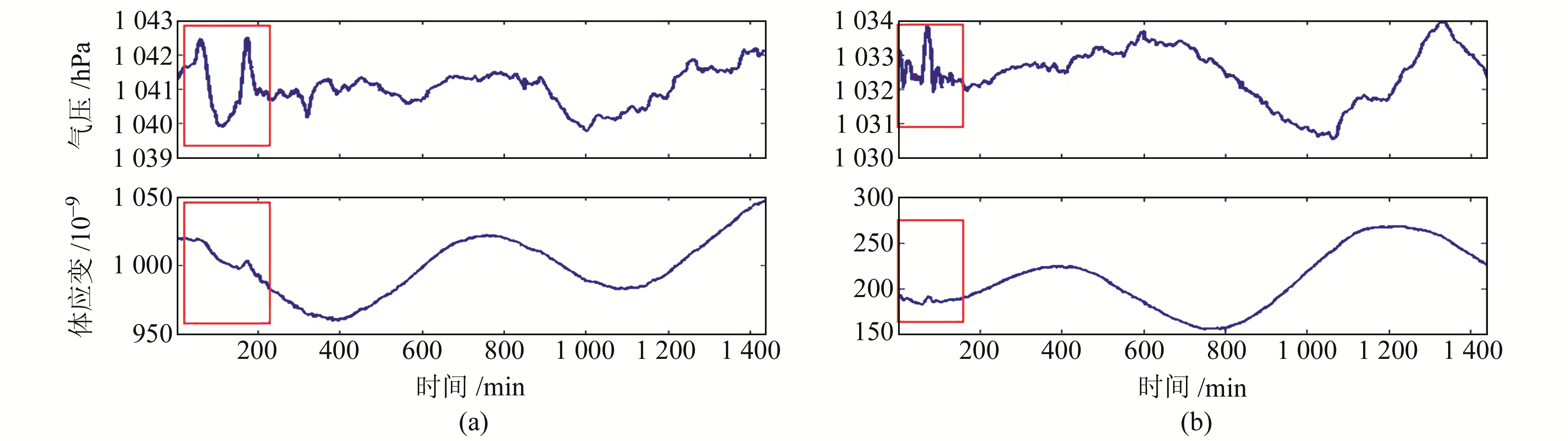
|
图 1 不同日期的气压和体应变数据 Fig. 1 Atmospheric pressure and volume strain data for different dates |
采用db4小波,利用离散小波变换将气压和体应变数据按7层小波变换分解,分解后的周期分别为2~4 min、4~8 min、8~16 min、16~32 min、32~64 min、64~128 min、128~256 min。7个周期分别对应尺度1~7,其中尺度7是为了确定需要进行分析的气压波的周期范围。利用相关分析得到图 1中气压和体应变单日数据的相关系数(图 2)。
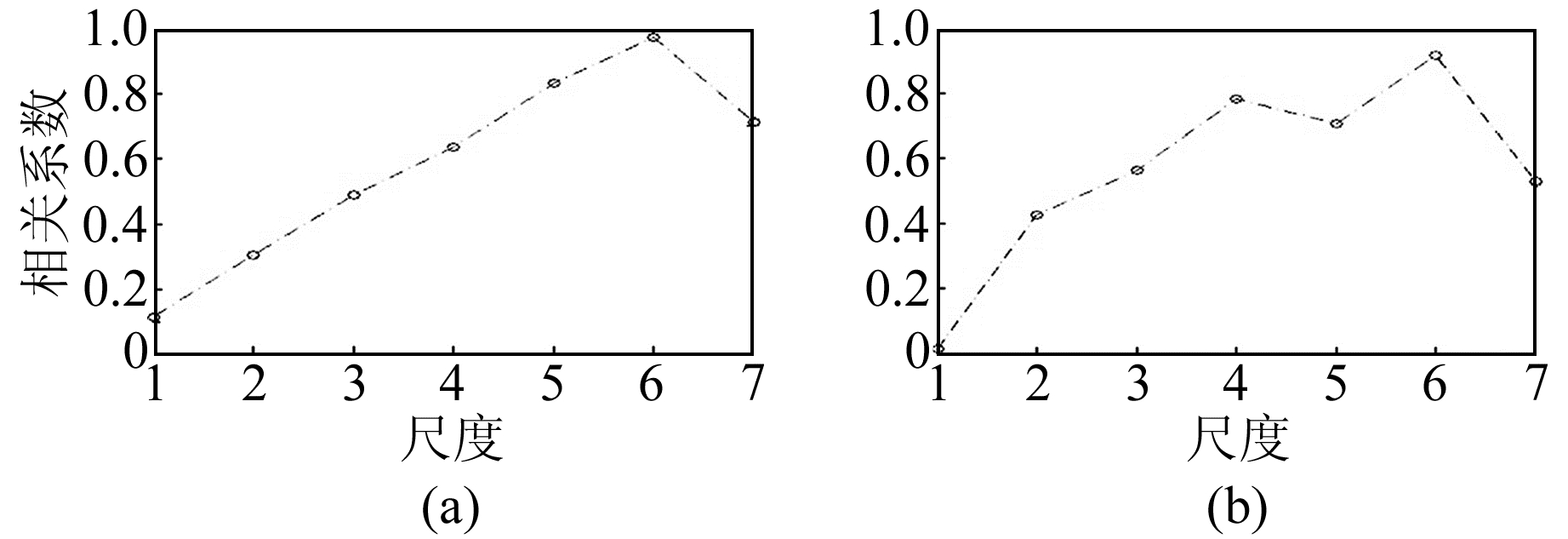
|
图 2 不同尺度的相关系数 Fig. 2 Correlation coefficient of different scales |
如图 2所示,单日数据气压和体应变的相关系数随尺度的变化不完全一致,但是其整体趋势为:尺度1~3(周期为2~16 min)相关系数较低,随尺度递增;尺度4~6(周期为16~128 min)相关系数较高且稳定,表明在尺度4~6上二者强相关;尺度7的相关系数均呈下降趋势。通过单日相关系数推断,气压影响体应变的优势周期为16~128 min。为了进一步确定相关系数的变化规律,计算全部数据各尺度气压波和体应变的相关系数及其平均值和变异系数(图 3、4)。
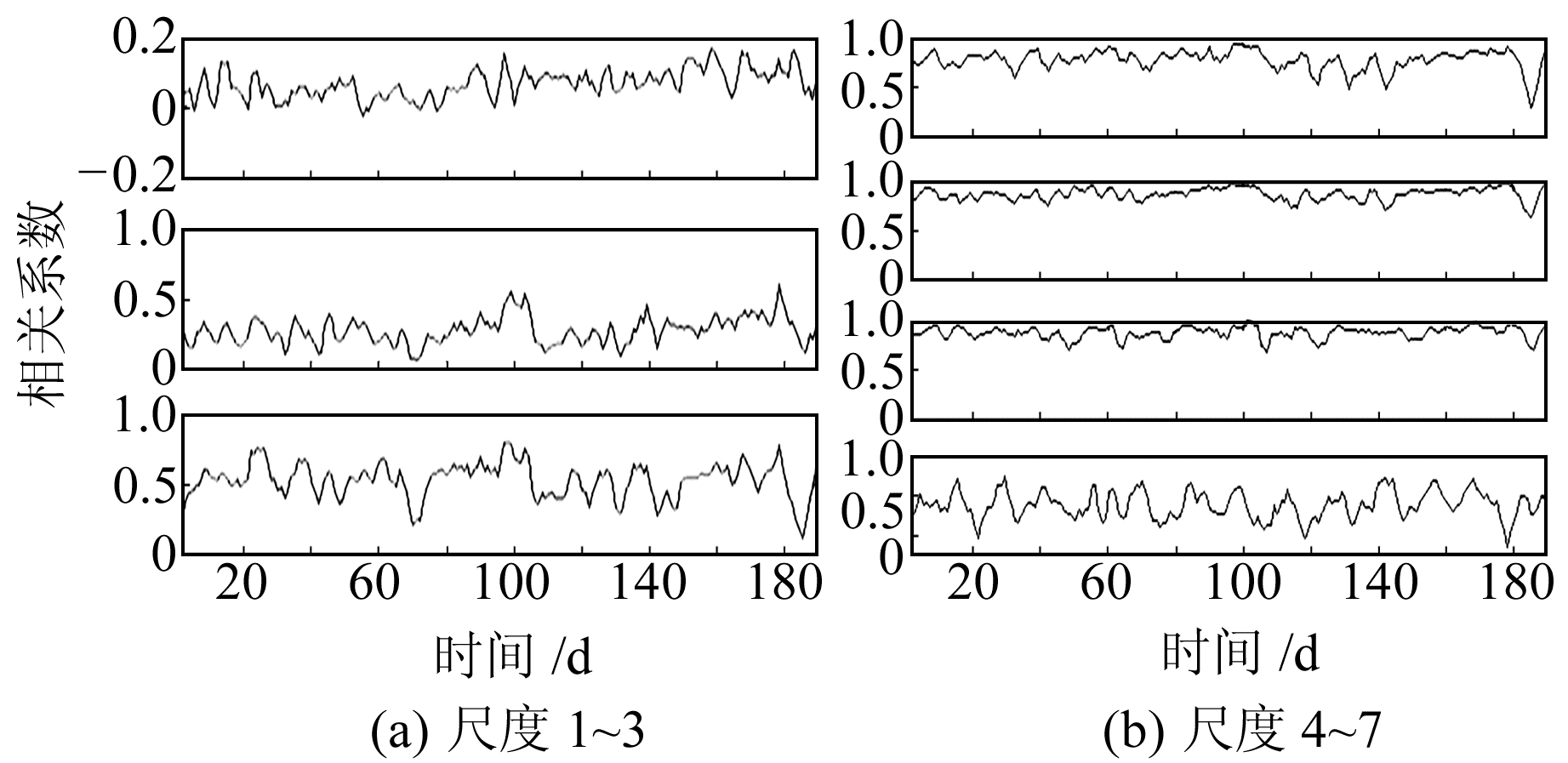
|
图 3 气压与体应变相关系数随时间变化曲线 Fig. 3 Curves of correlation coefficient between air pressure and volumetric strain with time |
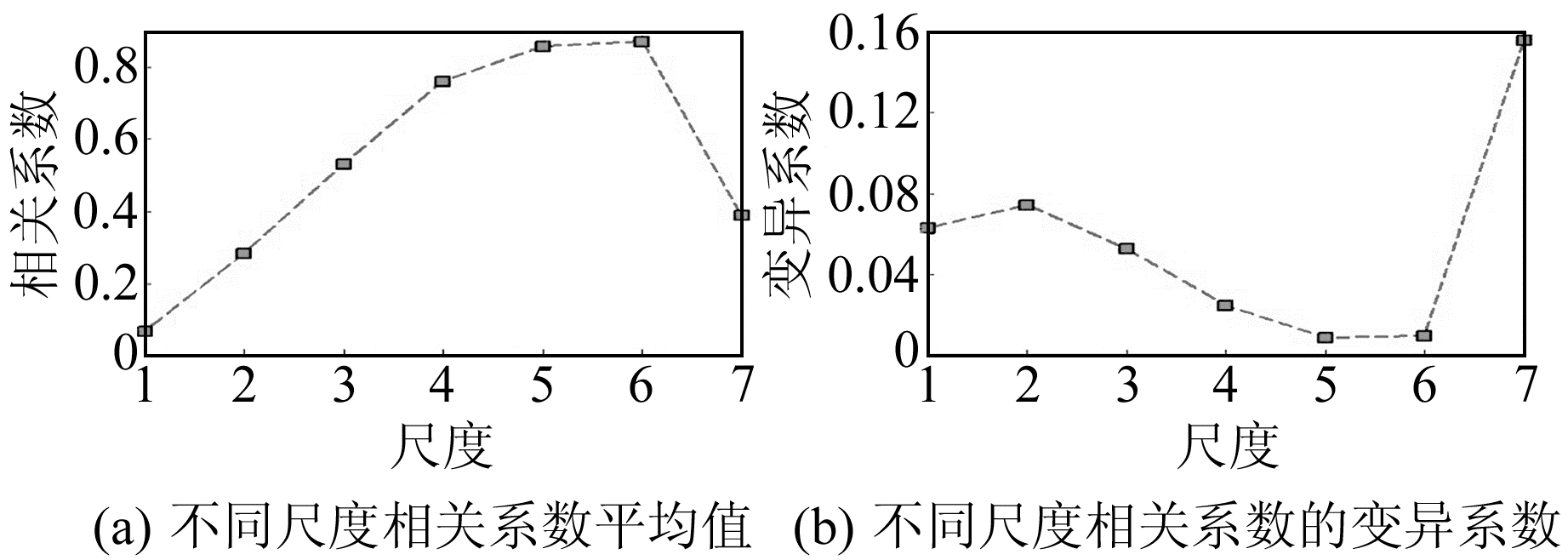
|
图 4 相关系数统计曲线 Fig. 4 Correlation coefficient statistical curve |
由图 3可知,同一尺度的相关系数整体上变化比较平稳,且随着尺度的增大,相关系数逐渐增大;最后几天的相关系数出现一个低值区,可能与该段时间距离体应变井孔10 m处的大型机械钻孔施工有关。由图 4可知,相关系数平均值较大且较平稳的尺度是4~6,即周期为16~128 min,相关系数平均值大于0.75;尺度7相关系数较低,且有正有负波动很大,因此在后续分析过程中主要分析尺度1~6。
在分析过程中,按照上述气压计算思路对水位和钻孔温度进行相同的计算,发现体应变与水位在尺度1~6的相关系数均在0值附近波动,相关系数平均值的绝对值均小于0.10;体应变与温度在尺度1~6的相关系数均在0值附近波动,相关系数平均值的绝对值均小于0.05;而且青岛台位于市区,井孔周边没有抽水、注水等突变性影响,根据体应变和辅助测项的多年观测曲线可知,与短周期气压的变化相比,青岛台相同周期的水位和温度变化相对比较平稳,因此推断,在短周期水位和温度对体应变的影响比气压小,在没有其他人为、仪器故障干扰的情况下,体应变的小幅度波动主要来源于气压干扰。
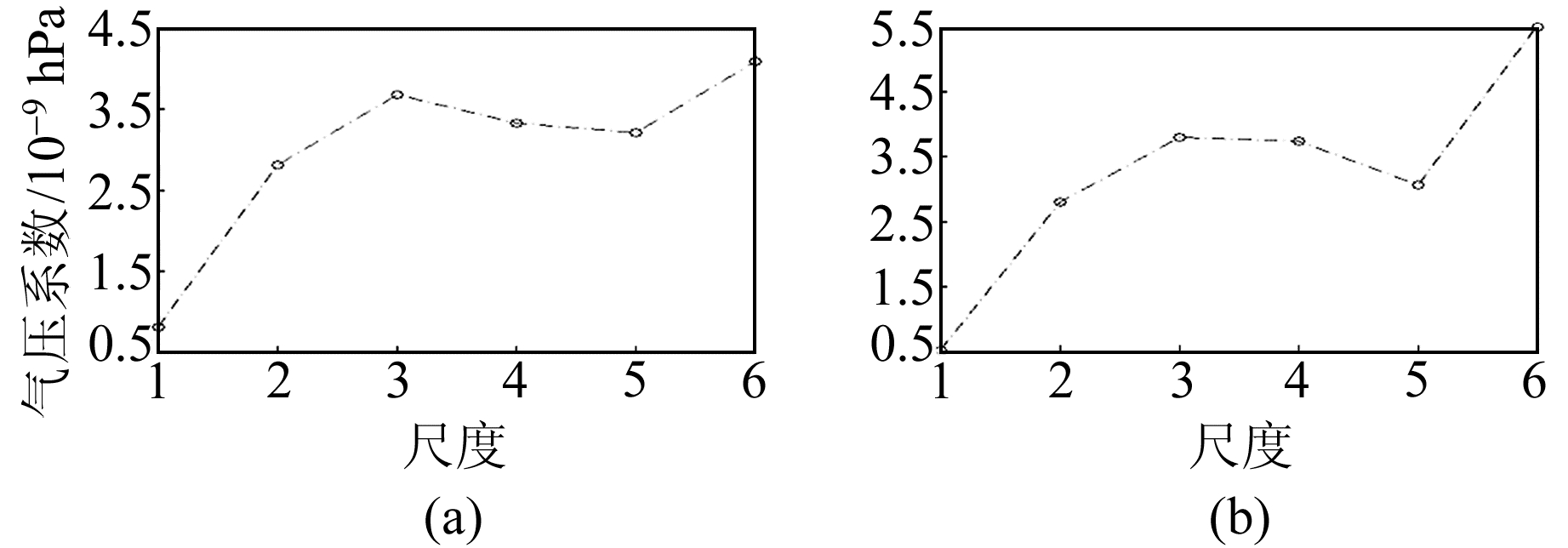
3.2 气压系数分析通过相关系数的计算可得到气压系数随周期的变化规律。采用同样的处理思路,利用回归分析计算尺度1~6的气压系数,得到不同周期气压波对体应变的干扰量,如图 5。
|
图 5 不同尺度的气压系数 Fig. 5 Atmospheric pressure coefficient of different scales |
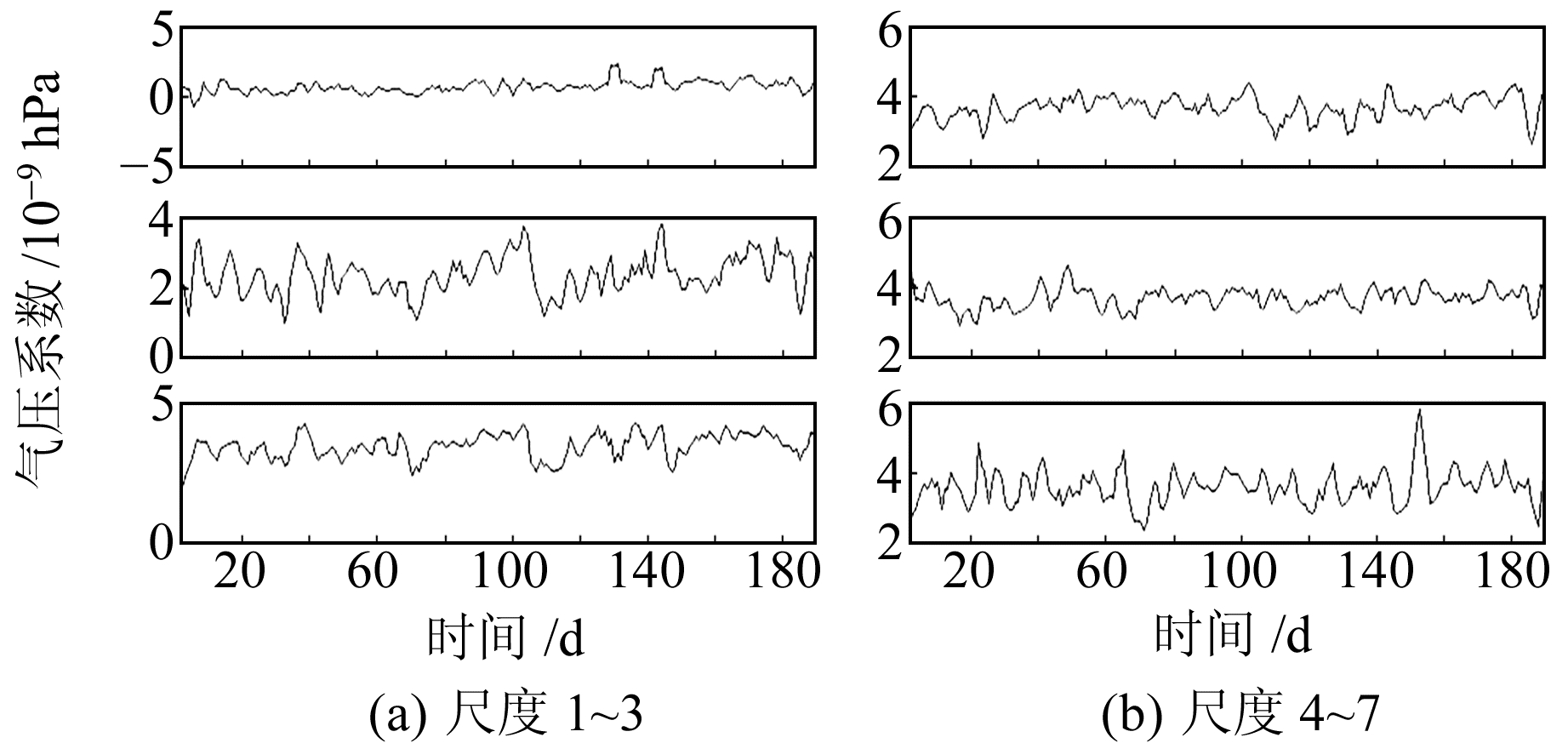
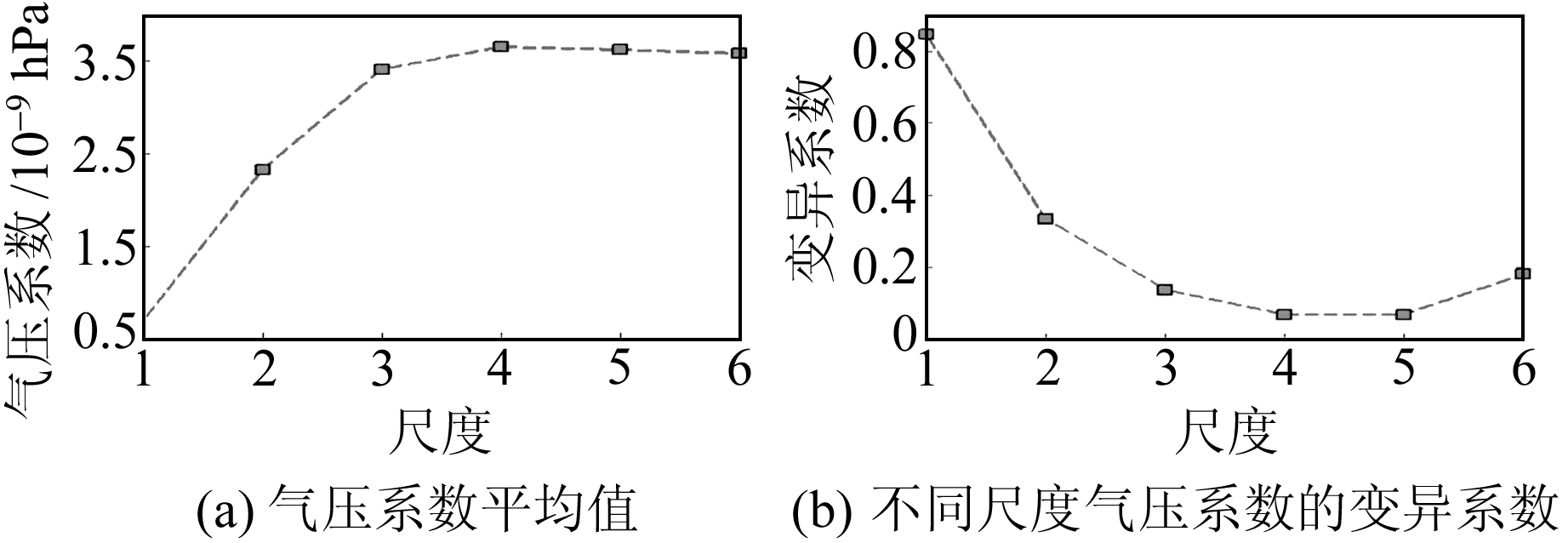
由图 5可知,尺度1~3(周期小于16 min)气压系数随尺度变化较大,尺度4~6(周期为16~128 min)气压系数趋于稳定。为了研究气压系数的变化规律,计算全部数据气压系数的平均值和变异系数,结果如图 6、7。
|
图 6 体应变气压系数随时间变化曲线 Fig. 6 Curves of volume strain pressure coefficient varying with time |
|
图 7 气压系数统计曲线 Fig. 7 Statistical curves of volume strain pressure coefficients |
由图 6、7可知,尺度4~6气压系数趋于稳定,约为(3.5~3.6)×10-9/hPa,其中尺度4~5的气压系数波动最小。
3.3 时频谱相关分析为更细致地分析不同周期气压波和体应变的相关性并对时间域的相关系数加以佐证,以图 1(b)为例,采用交叉小波变换研究气压波和体应变在时频域的相关性。首先利用离散小波变换将图 1(b)周期大于256 min的气压和体应变的信号成分滤除,对滤波后数据作滑动相关和交叉小波变换,得到气压和体应变的滑动相关系数以及交叉小波变换能量谱和相关谱(图 8)。

|
图 8 气压和体应变滑动相关系数及交叉小波变换谱 Fig. 8 Sliding correlation coefficient of atmospheric pressure and volumetric strain and cross wavelet transform spectrum |
由图 8(a)可知,气压和体应变滤波后信号的滑动相关系数在4个时间段上数值较大。由图 8(b)可知,时间为0~180 min、周期为8~128 min和时间为900~1 100 min、周期为90~240 min的2个区域是能量高值区,表明在这2个区域二者能量均较强。结合图 8(c)可以看出,除了图 8(b)的2个能量高值区外,还有3个能量高值区,其周期基本在8~128 min。这些高值区说明在8~128 min的周期内,气压和体应变虽然能量有强有弱,但具有强相关性,而且其时间范围与滑动相关系数高值区基本对应。
通过时频谱的相关性分析可知,气压和体应变相关性强的周期主要集中在16~128 min的范围,虽然周期大于128 min有部分高值区,但相对来说区域较小,且§3.1的统计结果显示,周期128~256 min的气压和体应变相关系数波动较大且数值较小,暂不予考虑。
3.4 短时气压干扰压制利用离散小波变换将单日气压和体应变数据进行回归分析,得到各尺度的气压系数并处理各个尺度下体应变数据的气压干扰,再对处理后各尺度信号进行重构。以图 1数据为例,计算结果如图 9所示。
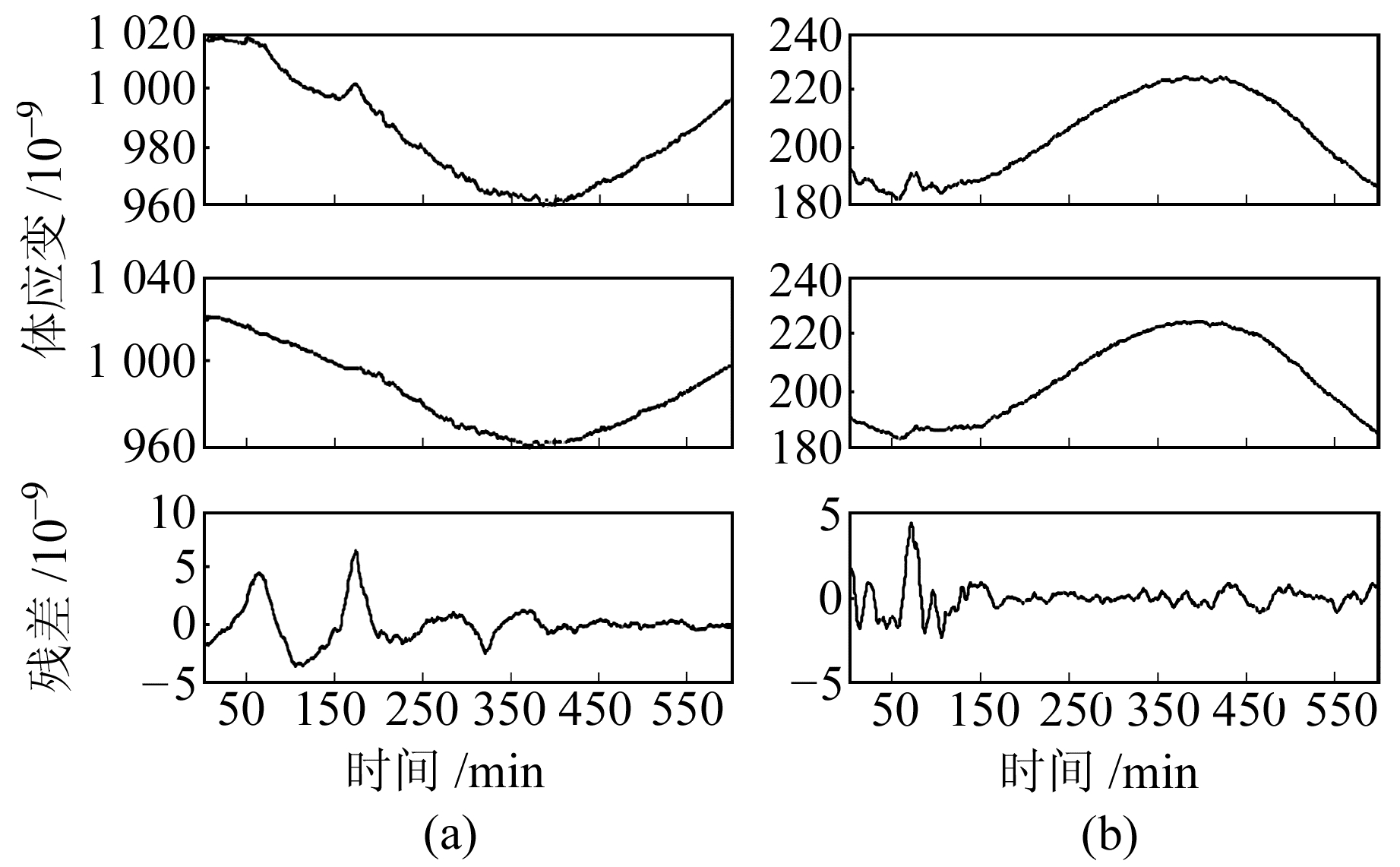
|
自上而下依次为原始信号、重构信号和残差信号 图 9 气压干扰压制效果图 Fig. 9 Results of removing the interference of atmospheric pressure |
对照图 1、9可知,利用离散小波变换可以有效地压制短时剧烈气压变化造成的体应变信号波动,提高体应变信号的信噪比,同时对气压变化平稳的时间段的影响较小,和原始数据基本保持一致,为后续体应变的前兆异常识别提供准确、可靠的资料。
4 结语本文结合相关分析、线性回归、交叉小波变换等几种方法,系统分析了短周期气压波与青岛台体应变的关系,得到如下结论:
1) 青岛台体应变受短周期气压变化影响明显。周期为2~16 min时,气压和体应变的相关系数随周期的增大逐渐增大;周期为16~128 min时,其相关系数趋于稳定;周期为128~256 min时,相关系数波动较大且数值较小,因此短周期气压波对体应变影响较大的周期为16~128 min。
2) 气压系数随周期的变化规律与相关系数相似,当周期为16~128 min时,气压系数波动较小,约为(3.5~3.6)×10-9/hPa。
3) 当周期为16~128 min的气压波变化幅度较大时,相应时间段的体应变与气压在交叉小波变换能量谱上表现出共同的能量高值区,揭示二者具有强相关性;当气压波变化幅度较小时,交叉小波变换能量谱可能无法揭示二者存在相关性的部分,这时可以结合交叉小波变换相关谱来分析在气压变化幅度较小时二者的相关性。
| [1] |
崔青发, 韩晓飞, 张璐, 等. 西安台体应变对汶川大地震的响应分析[J]. 大地测量与地球动力学, 2014, 34(4): 96-101 (Cui Qingfa, Han Xiaofei, Zhang Lu, et al. Analysis of Response of Body Strain Xi'an Seismostation to Wenchuan Earthquake[J]. Journal of Geodesy and Geodynamics, 2014, 34(4): 96-101)
(  0) 0) |
| [2] |
张凌空, 牛安福. 不同周期气压波对钻孔体应变仪观测结果的影响[J]. 中国地震, 2008, 24(4): 415-421 (Zhang Lingkong, Niu Anfu. Analysis on the Influence of Atmospheric Pressure Wave on the Observational Curves of Borehole Volumetric Strain Instrument at Different Periods[J]. Earthquake Research in China, 2008, 24(4): 415-421 DOI:10.3969/j.issn.1001-4683.2008.04.012)
(  0) 0) |
| [3] |
周龙寿, 邱泽华, 唐磊. 地壳应变场对气压短周期变化的响应[J]. 地球物理学进展, 2008, 23(6): 1 717-1 726 (Zhou Longshou, Qiu Zehua, Tang Lei. The Response of Crustal Strain Field to Short-Period Atmospheric Pressure Variation[J]. Progress in Geophysics, 2008, 23(6): 1 717-1 726)
(  0) 0) |
| [4] |
张凌空, 吴利军, 杨颖. 雷暴产生的气压突变对体应变与同井水位干扰的对比研究[J]. 中国地震, 2012, 28(1): 69-77 (Zhang Lingkong, Wu Lijun, Yang Ying. Comparative Study of the Interference of Mutation Pressure Generated by Thunderstorms with Volume Strain and Same Well Water-Level[J]. Earthquake Research in China, 2012, 28(1): 69-77 DOI:10.3969/j.issn.1001-4683.2012.01.008)
(  0) 0) |
| [5] |
卢双苓, 于庆民, 曲保安, 等. 山东数字化钻孔体应变观测的干扰异常分析[J]. 西北地震学报, 2010, 32(2): 186-190 (Lu Shuangling, Yu Qingmin, Qu Bao'an, et al. Analysis on the Disturbances which Cause Undulately Change in Observation Data of Digital Borehole Volume Strainmeter[J]. Northwestern Seismological Journal, 2010, 32(2): 186-190)
(  0) 0) |
| [6] |
张凌空, 王广才, 牛安福. 周期气压波对地壳应变场观测影响的若干因素分析[J]. 地震学报, 2011, 33(3): 351-361 (Zhang Lingkong, Wang Guangcai, Niu Anfu. Analysis on Several Factors of Periodic Air Pressure Wave Affecting Crustal Strain Field[J]. Acta Seismologica Sinica, 2011, 33(3): 351-361 DOI:10.3969/j.issn.0253-3782.2011.03.008)
(  0) 0) |
| [7] |
邢喜民, 杨绍富. 乌什体应变的气压响应特征分析[J]. 大地测量与地球动力学, 2016, 36(10): 930-932 (Xing Ximin, Yang Shaofu. Exploration of the Response Characteristics of Air Pressure to Wushi Body Strain[J]. Journal of Geodesy and Geodynamics, 2016, 36(10): 930-932)
(  0) 0) |
| [8] |
安玉柱, 张韧, 王伟民, 等. 太阳黑子数与电离层TEC的相关性分析[J]. 解放军理工大学学报:自然科学版, 2012, 13(5): 571-576 (An Yuzhu, Zhang Ren, Wang Weimin, et al. Correlation Analysis between Sunspot and TEC[J]. Journal of PLA University of Science and Technology:Natural Science Edition, 2012, 13(5): 571-576)
(  0) 0) |
| [9] |
Grinsted A, Moore J C, Jevrejeva S. Application of the Cross Wavelet Transform and Wavelet Coherence to Geophysical Time Series[J]. Nonlinear Processes in Geophysics, 2004, 11(5/6): 561-566 DOI:10.5194/npg-11-561-2004
(  0) 0) |
| [10] |
栾光忠, 赵淑娟, 王庆帅, 等. 青岛劈石口断裂的构造特征和现代活动性研究[J]. 中国海洋大学学报, 2009, 39(2): 299-303 (Luan Guangzhong, Zhao Shujuan, Wang Qingshuai, et al. The Study of Structural Characteristic and Modern Activity of the Qingdao Pishikou Fault Zone[J]. Periodical of Ocean University of China, 2009, 39(2): 299-303)
(  0) 0) |
| [11] |
潘元生, 侯海锋, 万连初, 等. 2003年6月青岛崂山4级震群序列初步分析[J]. 内陆地震, 2004(1): 77-83 (Pan Yuansheng, Hou Haifeng, Wan Lianchu, et al. The Preliminary Analysis of the Swarm Sequence about the Laoshan Earthquake with MS4 of Qingdao City in June 2003[J]. Inland Earthquake, 2004(1): 77-83 DOI:10.3969/j.issn.1001-8956.2004.01.010)
(  0) 0) |
| [12] |
Mallat S G. A Theory for Multi-Resolution Signal Decomposition:The Wavelet Representation[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1989, 11(7): 674-693
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39

