2. 吉林大学仪器科学与电气工程学院,长春市民主大街938号,130026;
3. 中国地震局地壳应力研究所,北京市安宁庄路1号,100085
地震地下流体数据的处理、分析、成图产出等已有专业的应用软件[1-2],并在监测台网中得到广泛应用。但由于我国地域辽阔、各观测井间存在非常明显的差异性,用统一的软件处理数据有时很难达到理想的产出效果,对于特定问题的分析,这些专业软件往往也难以胜任。而围绕这些特定问题,如果不借助现有成熟的数学软件,而是单纯地进行专业软件的升级,将是一件非常复杂且没有任何创造意义的工作。在众多的数学工具软件中,MATLAB在数值计算方面代表了当今国际科学计算软件的先进水平,它拥有矩阵运算、算法实现、图形产出以及与其他编程语言相连接的功能,广泛应用于工程计算、控制设计、信号分析、图像处理等领域。相比C等其他语言,MATLAB中与计算相关的操作更简捷,且提供丰富的应用工具箱(函数调用),极大提升了处理效率。
虽然MATLAB具有简捷的操作过程以及丰富的函数库,但对于许多刚参加工作、或者非数学专业的监测人员来说,如何将该软件应用到日常工作中一直存在入门难,甚至无从下手的感觉。本文使用MATLAB实现地震地下流体数据处理过程中最基本的数学方法,使监测人员初步掌握MATLAB在流体数据分析过程中的应用,为更好地挖掘地震地下流体数据中隐含的规律提供基础知识。
1 基本处理方法地震地下流体数据基本处理方法主要包括去异常值、提取均值以及去趋势等。
1.1 取均值和去突跳点受供电、人为因素等干扰,台站观测设备难免会出现异常数据或者缺数等现象。地震地下流体原始数据采样频率一般为分钟甚至更高,而实际进行地震预测研究时,往往采用整点值、甚至日均值即可,因此在进行趋势性地震预报分析时,需要先对明显的异常点数据进行剔除,并对高采样数据(秒采样、或分采样)取均值。
下列函数GetMean为按指定数据间隔进行均值降采样的过程,并剔除了超过1倍均方差的异常点数据。
|
|
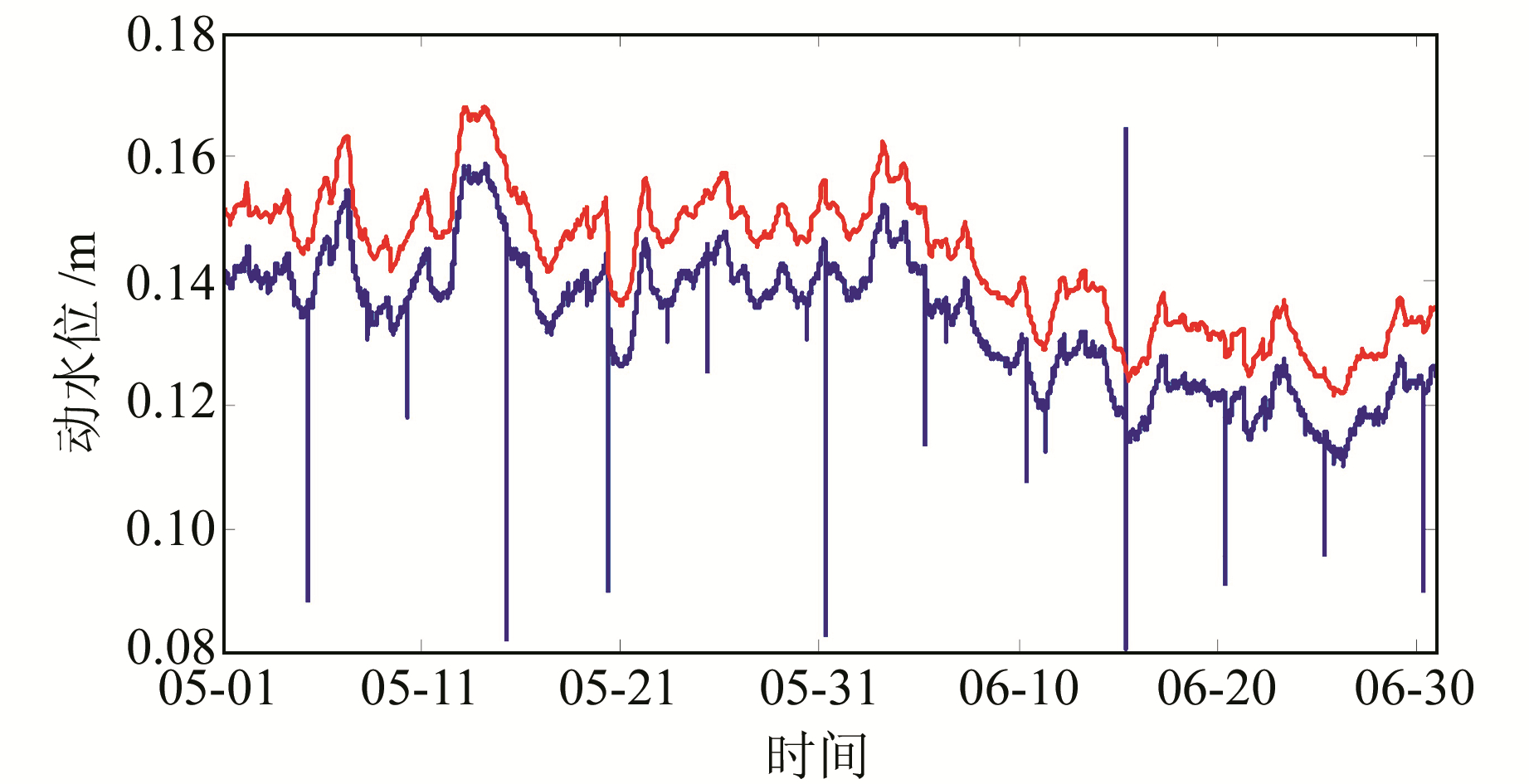
以河北石家庄小马村井为例,其2008-05~06原始数据(图 1中蓝线)中含有较多的干扰数据(突跳点),通过GetMean函数取整点值(图 1中红线,为突出对比效果,将整点数据、红色曲线进行+0.01 m的平移)后可以看出,结果完全保留了原始数据的变化形态,并且对分钟值中的突跳点进行了同步剔除。
|
图 1 取均值、去异常点实例 Fig. 1 The sample of computing average and removing the exception point |
地震地下流体数据存在趋势性变化,这种变化有可能来自仪器本身的漂移,也有可能代表着地壳蠕变的结果[3]。这种趋势性变化容易掩盖较细微的异常信息,因此在进行细节信息提取的过程中,需先进行去趋势。对于等间隔数据(如整点值)直接采用detrend函数即可实现;而对于非等间隔数据,则需采用一元线性回归进行去趋势(可参考回归分析)。
|
|
需要注意的是,利用detrend函数工具进行去趋势前,必须保证原始数据是连续的,如果出现缺数据,要先对数据进行插值补全[4]。以北京市地震局昌平台2008-05~06的数据为例(图 2)进行分析。可以看出,单纯从原始曲线上来看,很难分辨出汶川地震导致的水位同震响应以及震后调整,而对数据进行去趋势分析后,可明显看出汶川地震的同震响应以及震后调整过程。

|
图 2 数据去趋势实例 Fig. 2 The sample of detrending |
回归分析是确定2种或2种以上变量间相互依赖的定量关系的统计分析方法。按照自变量和因变量之间的关系类型,可分为线性回归分析和非线性回归分析。水位潮汐效应分析、气压效应分析可简化为线性回归[5],而水位季节性变化、温度测量时其稳定过程等,都可采用非线性回归分析。线性回归过程主要解决的是如何通过样本来获取最佳的拟合线,最常用的方法便是最小二乘法,通过最小化误差的平方和寻找数据的最佳函数匹配。
|
|
进行一元线性回归之前,要先找出输出量与输入量(不同滞后时间)之间的相关系数,相关系数最大点即表示两者之间的滞后时间关系。以川03井为例,计算2008-03~04井水位与理论固体潮汐以及去潮汐后井水位与气压效应之间的相关系数可得:
corrcoefs1= [0.803 9 0.633 2 0.330 9];
corrcoefs2= [0.435 0.465 0.514 0.582 0.663 0.744 9 0.816 0.865 0.883 0.866 0.820 0.752 0.674]
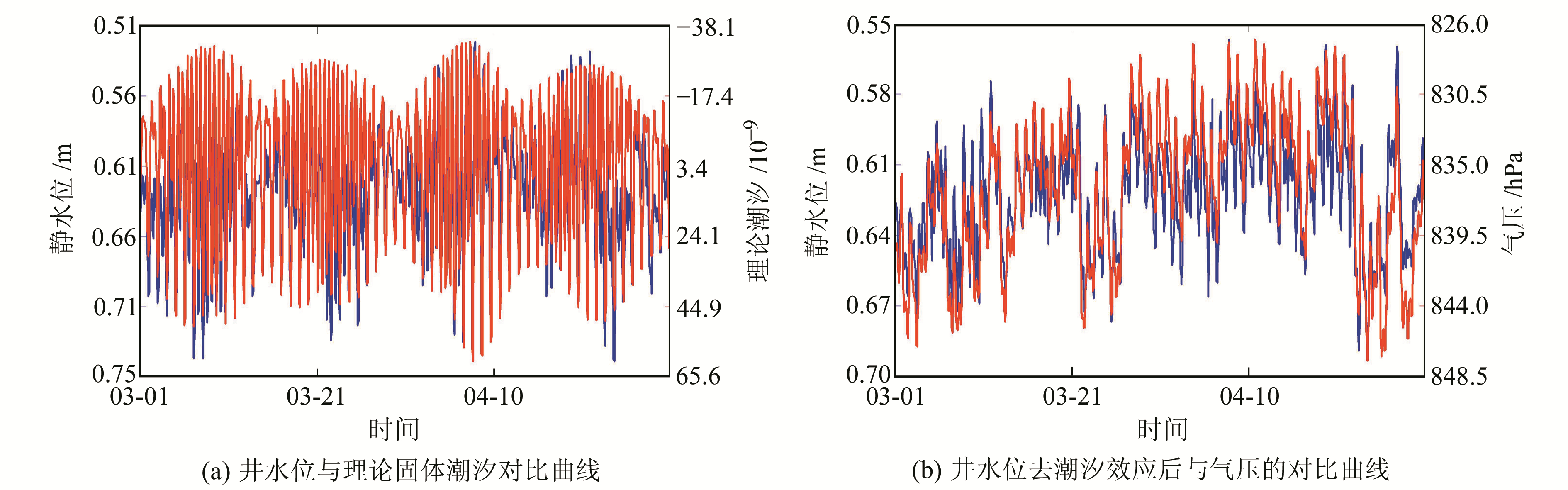
可以看出,井水位与理论潮汐最大相关系数为0.803 9,说明井水位对固体潮汐滞后为0 h;而井水位与气压的最大相关系数为0.883,说明井水位对气压的滞后时间为8 h。进行一元线性回归,需根据最大相关系数得出滞后时间点后,再进行回归系数求解(图 3)。
|
图 3 一元线性回归实例 Fig. 3 The sample of unary linear regression |
多数地震预测预报还处在经验预报与统计预报阶段,从观测数据中提取规律性的总结显得非常重要。而从观测数据中提取规律性的总结往往需要对数据进行自定义函数拟合。
以福建泉州鲤城台水温仪安装为例,对水温传感器的稳定过程进行自定义函数拟合:
|
|
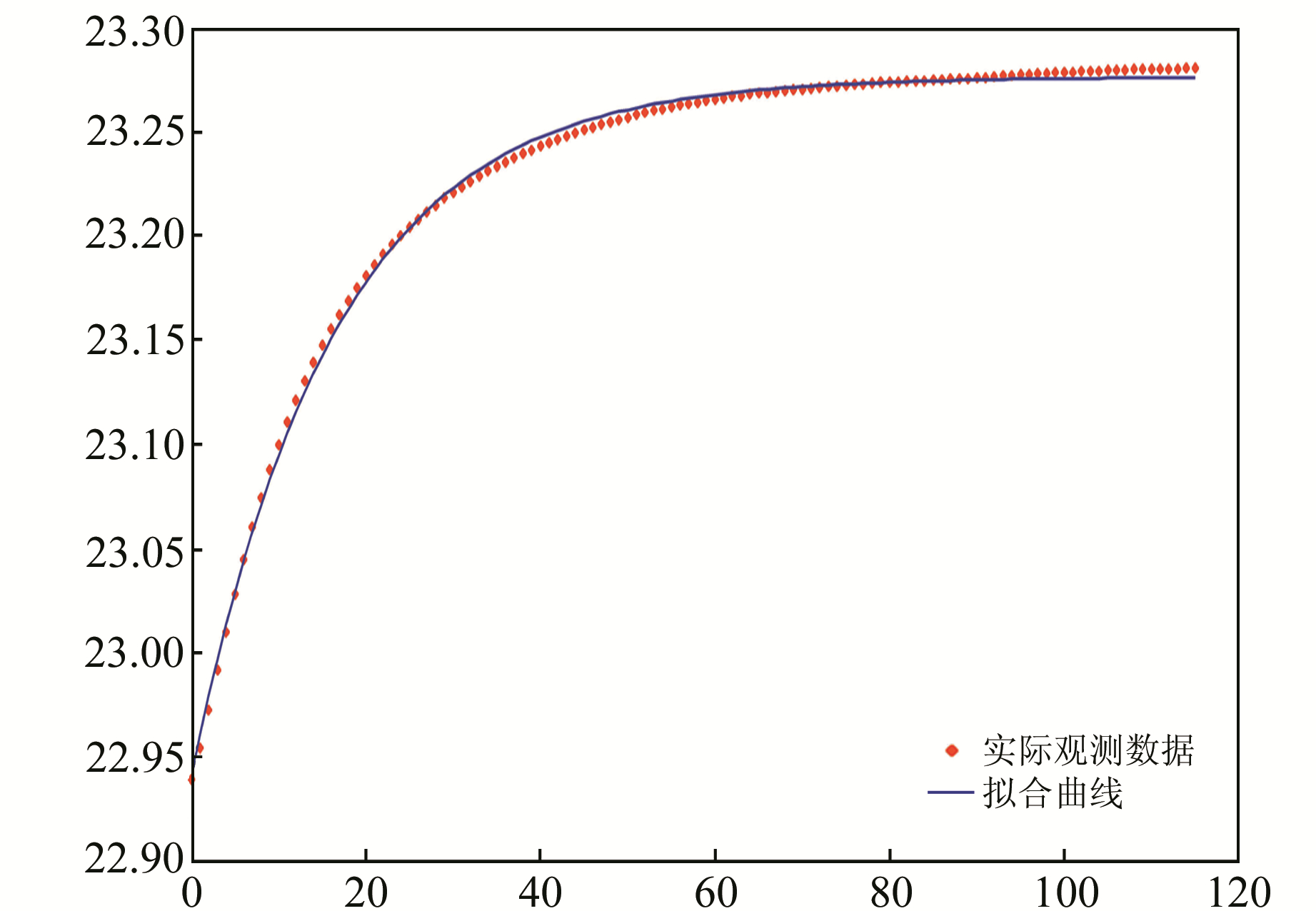
通过自定义函数计算得决定系数R2=0.998 3 (图 4),说明自定义函数拟合较佳。
|
图 4 自定义函数拟合实例 Fig. 4 The sample of fitting with custom function |
温度梯度数据是分析井下温度的基础信息,而一幅好的温度梯度曲线应该融合温度梯度变化趋势、井孔结构、含水层布局等,这可以为进行温度资料分析、井-含水层建模等提供直观的信息。井孔温度梯度测量时,先按学科要求进行步进式温度测量,温度梯度等于两点温度差与两点深度差的比,单位为℃/m(也经常用℃/m进行标示)。
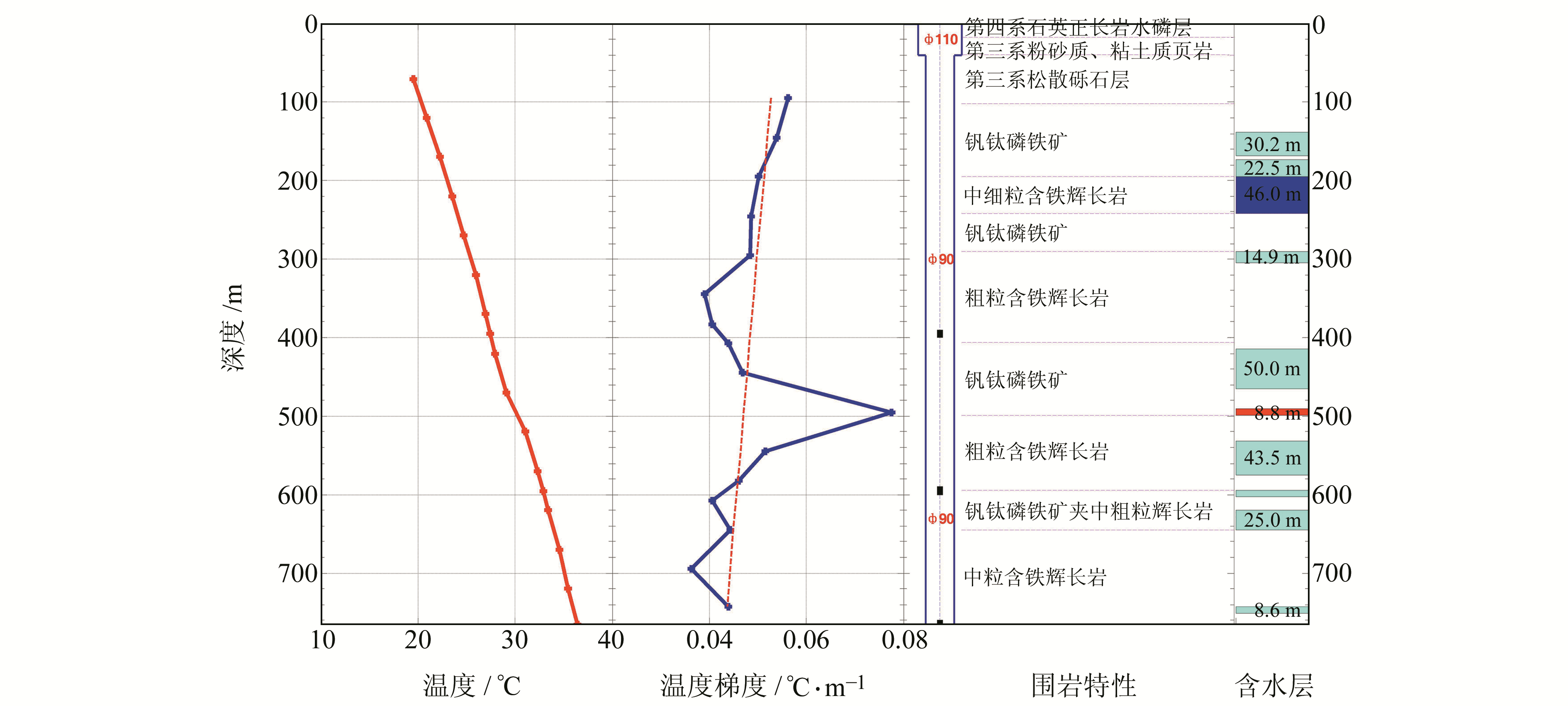
以川03井为例计算温度梯度并绘制于图 5。从图可见,总体上看,水温随深度增加而增加,而水温梯度则随深度而降低;但在井深近500 m处,水温梯度却反常突增。结合井孔地质剖面分析,可断定该深度出现热水的出水带(该项内容代码较长,限于篇幅,不逐行展示。)。
|
图 5 温度梯度曲线[6] Fig. 5 Water temperature gradient |
MATLAB有着非常强大的数据处理功能和丰富的数学工具,极大简化了数据处理的编程工作。本文从地震地下水数据处理的基本方法入手,展示了相关代码,为更复杂的数据处理过程提供了基础。
当然,有关地震地下水数据处理应用远非这些方面,也远非这种难度,如常见的频谱分析、调和分析等内容,文章都未涉及,可参考相关书籍或相应的文献。本文示例程序均在MATLAB R2014a版本下运行通过,文中所有程序和算例均可公开,如有兴趣者,可直接发邮件到dqs_hah@163.com索取。
| [1] |
刘春国, 李正媛, 王建国, 等. 地下流体数据处理与产品加工软件系统设计[J]. 中国地震, 2014, 30(2): 260-271 (Liu Chunguo, Li Zhengyuan, Wang Jianguo, et al. Design of Underground Fluid Data Processing and Product Processing Software System[J]. Eearhquake Research China, 2014, 30(2): 260-271 DOI:10.3969/j.issn.1001-4683.2014.02.014)
(  0) 0) |
| [2] |
王建国, 陈华静, 刘春国. 地下流体学科数据处理软件的研制[J]. 地震地磁观测与研究, 2010, 31(增1): 94-100 (Wang Jianguo, Chen Huajing, Liu Chunguo. Development of Data Processing Software for Underground Fluid Subject[J]. Seismological and Geomagnetic Observation and Research, 2010, 31(S1): 94-100)
(  0) 0) |
| [3] |
何案华, 邓卫平, 李国佑. 青海地热台网温度漂移问题初步分析[J]. 大地测量与地球动力学, 2017, 37(10): 1 083-1 086 (He Anhua, Deng Weiping, Li Guoyou. Analyses of Temperature Drift in Qinghai Geothermal Network[J]. Journal of Geodesy and Geodynamics, 2017, 37(10): 1 083-1 086)
(  0) 0) |
| [4] |
万永革. 数字信号处理的MATLAB实现[M]. 北京: 科学出版社, 2012 (Wan Yongge. Implementation of Digital Signal Processing Based on MATLAB[M]. Beijing: Science Press, 2012)
(  0) 0) |
| [5] |
He A H, Singh R P, Sun Z H, et al. Comparison of Regression Methods to Compute Atmospheric Pressure and Earth Tidal Coefficients in Water Level Associated with Wenchuan Earthquake of 12 May 2008[J]. Pure and Applied Geophysics, 2016, 173(7): 2 277-2 294 DOI:10.1007/s00024-016-1310-3
(  0) 0) |
| [6] |
He A H, Zhao G, Sun Z H, et al. Co-Seismic Multilayer Water Temperature and Water Level Changes Associated with Wenchuan and Tohoku-Oki Earthquakes in the Chuan No.03 Well, China[J]. Journal of Seismology, 2017, 21(4): 719-734 DOI:10.1007/s10950-016-9631-3
(  0) 0) |
2. College of Instrumentation & Electrical Engineering, Jilin University, 938 Minzhu Street, Changchun 130026, China;
3. Institute of Crustal Dynamics, CEA, 1 Anningzhuang Road, Beijing 100085, China
 2019, Vol. 39
2019, Vol. 39


