病态观测方程广泛存在于卫星定位[1-2]、大地测量反演[3-4]和重力场向下延拓[5-7]等解算模型中。由于法矩阵的病态性,常规最小二乘解的方差较大,参数估值极不可靠。为求得稳定、可靠的参数估值,需要根据病态观测方程的特点构建正则化解,常用的正则化方法有Tikhonov正则化和截断奇异值(TSVD)法。利用参数间一些精确已知的先验等式约束信息也可以显著提高解的准确性和精度[8-10]。王乐洋等[11-12]和马洋等[13]针对大地测量反演问题中设计阵呈良态、约束阵呈病态的情形,分别给出模型的岭估计法、奇异值分解法及联合平差法;谢建等[14]建立了附等式约束的病态模型,给出附加参数范数最小的正则化准则,导出约束正则化解计算公式,并证明约束正则化解的均方误差小于约束最小二乘解。
虽然约束正则化法通过对原方程施加等式约束能大幅提高解的精度,但本质同正则化法一样,是通过引入正则化参数来削弱模型的病态性,由于改变了方程的等式结构,其解和残差也是有偏的。因此,利用有偏残差所估的单位权中误差必定也是有偏的,在进行精度评定时,有偏的单位权中误差势必会造成错误的精度估计。沈云中等[15]和Xu等[16]用不同方法导出病态方程正则化解的单位权方差无偏公式,结果表明,无偏公式所估的单位权中误差较传统公式更接近真值;张俊等[17]根据残差矩阵二次型的数学期望公式导出了半参数模型补偿最小二乘解的单位权方差无偏公式。本文在正则化解的单位权中误差无偏估计式的基础上,引入等式约束条件,利用有偏的约束正则化解导出无偏的单位权中误差计算式,并用数值算例和病态测边网算例验证公式的正确性。
1 附有等式约束的Gauss-Markov模型附有等式约束的Gauss-Markov模型[18]为:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{L}} = \mathit{\boldsymbol{AX}} + \mathit{\boldsymbol{e}}}\\ {\mathit{\boldsymbol{KX}} = {\mathit{\boldsymbol{K}}_0}} \end{array}} \right. $ | (1) |
式中,设计矩阵A∈Rm×n,且rank(A)=n,待估参数X∈Rn,观测向量L及其误差向量e∈Rm,约束矩阵K∈Rl×n,且rank(K)=l,常数项K0∈Rl。式(1)的统计性质为:
| $ \begin{array}{*{20}{l}} {E\left( \mathit{\boldsymbol{L}} \right) = \mathit{\boldsymbol{AX}}}\\ {D\left( \mathit{\boldsymbol{L}} \right) = \sigma _0^2{\mathit{\boldsymbol{P}}^{ - 1}}} \end{array} $ | (2) |
式中,P为观测值L的权阵。式(1)参数的最小二乘估值及方差分别为:
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat X}}}_{{\rm{CLS}}}} = \left( {{\mathit{\boldsymbol{N}}^{ - 1}} - {\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{K}}^{\rm{T}}}\mathit{\boldsymbol{N}}_k^{ - 1}\mathit{\boldsymbol{K}}{\mathit{\boldsymbol{N}}^{ - 1}}} \right)\mathit{\boldsymbol{W}} + }\\ {{\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{K}}^{\rm{T}}}\mathit{\boldsymbol{N}}_k^{ - 1}{\mathit{\boldsymbol{K}}_0}} \end{array} $ | (3) |
| $ D\left( {{{\mathit{\boldsymbol{\hat X}}}_{{\rm{CLS}}}}} \right) = \sigma _0^2\left( {{\mathit{\boldsymbol{N}}^{ - 1}} - {\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{K}}^{\rm{T}}}\mathit{\boldsymbol{N}}_k^{ - 1}\mathit{\boldsymbol{K}}{\mathit{\boldsymbol{N}}^{ - 1}}} \right) $ | (4) |
式中,σ02为单位权方差,N=ATPA, Nk= KN-1KT, W=ATPL。当无约束时,式(1)退化为传统的G-M模型,相应的参数估值及方差分别为:
| $ {{\mathit{\boldsymbol{\hat X}}}_{{\rm{LS}}}} = {\mathit{\boldsymbol{N}}^{ - 1}}\mathit{\boldsymbol{W}} $ | (5) |
| $ D\left( {{{\mathit{\boldsymbol{\hat X}}}_{{\rm{LS}}}}} \right) = \sigma _0^2{\mathit{\boldsymbol{N}}^{ - 1}} $ | (6) |
比较式(4)与式(6)可知,对参数施加等式约束使式(4)右端出现负定阵,附有等式约束的参数估值方差小于传统最小二乘估值方差,解的精度更高。
2 附有等式约束病态模型的正则化解及其单位权中误差无偏估计 2.1 附有等式约束病态模型的正则化解由式(3)可知,当设计矩阵A病态时,直接对法矩阵N求逆会使解变得不稳定,为得到稳定解,必须对模型施加某个正则化准则。谢建等[14]根据Tikhonov正则化准则导出附加等式约束病态模型的正则化解,准则为:
| $ {\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{Pe}} + \alpha {\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{RX}} = \min $ | (7) |
式中,α为正则化参数,R为正则化矩阵。根据式(7)及等式约束,构建拉格朗日函数:
| $ \mathit{\Phi }\left( \mathit{\boldsymbol{X}} \right) = {\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{Pe}} + \alpha {\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{RX}} + 2{\mathit{\boldsymbol{\lambda }}^{\rm{T}}}\left( {\mathit{\boldsymbol{KX}} - {\mathit{\boldsymbol{K}}_0}} \right) $ | (8) |
对X求偏导得:
| $ \frac{{\partial \mathit{\Phi }}}{{\partial \mathit{\boldsymbol{X}}}} = \left( {\mathit{\boldsymbol{N}} + \alpha \mathit{\boldsymbol{R}} + {\mathit{\boldsymbol{K}}^{\rm{T}}}\mathit{\boldsymbol{\lambda }}} \right)\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{W}} = 0 $ | (9) |
联立等式约束条件,推导得:
| $ {{\mathit{\boldsymbol{\hat X}}}_R} = \left( {\mathit{\boldsymbol{N}}_r^{ - 1} - \mathit{\boldsymbol{N}}_r^{ - 1}{\mathit{\boldsymbol{K}}^{\rm{T}}}\mathit{\boldsymbol{N}}_c^{ - 1}\mathit{\boldsymbol{KN}}_r^{ - 1}} \right)\mathit{\boldsymbol{W}} + \mathit{\boldsymbol{N}}_r^{ - 1}{\mathit{\boldsymbol{K}}^{\rm{T}}}\mathit{\boldsymbol{N}}_c^{ - 1}{\mathit{\boldsymbol{K}}_0} $ | (10) |
式中,Nr=N+α R, Nc= KNr-1KT。为简化计算,将正则化矩阵取为单位阵In,相应的
引入正则化参数α虽能在一定程度上削弱模型的病态性,但破坏了方程的结构,造成所求参数解有偏。因此,利用传统的最小二乘单位权中误差估计公式所估的单位权中误差也是有偏的。记Mα=Nr-1-Nr-1KTNc-1KNr-1,为推导方便,先给出如下辅助公式:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_\alpha }\mathit{\boldsymbol{N}} = {\mathit{\boldsymbol{M}}_\alpha }\left( {\mathit{\boldsymbol{N}} + \alpha {\mathit{\boldsymbol{I}}_n} - \alpha {\mathit{\boldsymbol{I}}_n}} \right) = }\\ {{\mathit{\boldsymbol{I}}_n} - \mathit{\boldsymbol{N}}_r^{ - 1}{\mathit{\boldsymbol{K}}^{\rm{T}}}\mathit{\boldsymbol{N}}_c^{ - 1}\mathit{\boldsymbol{K}} - \alpha {\mathit{\boldsymbol{M}}_\alpha }} \end{array} $ | (11) |
式(10)可改写成:
| $ {{\mathit{\boldsymbol{\hat X}}}_R} = {\mathit{\boldsymbol{M}}_a}\mathit{\boldsymbol{W}} + \mathit{\boldsymbol{N}}_r^{ - 1}{\mathit{\boldsymbol{K}}^{\rm{T}}}\mathit{\boldsymbol{N}}_c^{ - 1}{\mathit{\boldsymbol{K}}_0} $ | (12) |
约束正则化解的残差为:
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat e}}}_R} = \mathit{\boldsymbol{L}} - \mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{\hat X}}}_R} = }\\ {\left( {{\mathit{\boldsymbol{I}}_m} - \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{M}}_c}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{P}}} \right)\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{AN}}_r^{ - 1}{\mathit{\boldsymbol{K}}^{\rm{T}}}\mathit{\boldsymbol{N}}_c^{ - 1}{\mathit{\boldsymbol{K}}_0}} \end{array} $ | (13) |
其期望为:
| $ \begin{array}{*{20}{c}} {E\left( {{{\mathit{\boldsymbol{\hat e}}}_R}} \right) = \left( {{\mathit{\boldsymbol{I}}_m} - \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{M}}_\alpha }{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{P}}} \right)E\left( \mathit{\boldsymbol{L}} \right) - \mathit{\boldsymbol{AN}}_r^{ - 1}{\mathit{\boldsymbol{K}}^{\rm{T}}}\mathit{\boldsymbol{N}}_c^{ - 1}{\mathit{\boldsymbol{K}}_0} = }\\ {\left( {{\mathit{\boldsymbol{I}}_m} - \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{M}}_\alpha }{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{P}}} \right)\mathit{\boldsymbol{AX}} - \mathit{\boldsymbol{AN}}_r^{ - 1}{\mathit{\boldsymbol{K}}^{\rm{T}}}\mathit{\boldsymbol{N}}_c^{ - 1}{\mathit{\boldsymbol{K}}_0} = }\\ {\left( {\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{M}}_\alpha }\mathit{\boldsymbol{N}}} \right)\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{AN}}_r^{ - 1}{\mathit{\boldsymbol{K}}^{\rm{T}}}\mathit{\boldsymbol{N}}_c^{ - 1}{\mathit{\boldsymbol{K}}_0}} \end{array} $ | (14) |
将式(11)代入式(14)得:
| $ \begin{array}{*{20}{c}} {E\left( {{{\mathit{\boldsymbol{\hat e}}}_R}} \right) = \mathit{\boldsymbol{AN}}_r^{ - 1}{\mathit{\boldsymbol{K}}^{\rm{T}}}\mathit{\boldsymbol{N}}_c^{ - 1}\left( {\mathit{\boldsymbol{KX}} - {\mathit{\boldsymbol{K}}_0}} \right) + }\\ {\alpha \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{M}}_\alpha }\mathit{\boldsymbol{X}} = \alpha \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{M}}_\alpha }\mathit{\boldsymbol{X}}} \end{array} $ | (15) |
根据二次型的期望公式:
| $ \begin{array}{*{20}{c}} {E\left( {\mathit{\boldsymbol{\hat e}}_R^{\rm{T}}\mathit{\boldsymbol{P}}{{\mathit{\boldsymbol{\hat e}}}_R}} \right) = {\rm tr}\left( {\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{D}}_{{{\mathit{\boldsymbol{\hat e}}}_R}}}} \right) + }\\ {{E^{\rm{T}}}\left( {{{\mathit{\boldsymbol{\hat e}}}_R}} \right)\mathit{\boldsymbol{P}}E\left( {{{\mathit{\boldsymbol{\hat e}}}_R}} \right)} \end{array} $ | (16) |
将式(14)代入式(16)右边第2项得:
| $ \begin{array}{*{20}{c}} {{E^{\rm{T}}}\left( {{{\mathit{\boldsymbol{\hat e}}}_R}} \right)\mathit{\boldsymbol{P}}E\left( {{{\mathit{\boldsymbol{\hat e}}}_R}} \right) = {\alpha ^2}{\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_\alpha }{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PA}}{\mathit{\boldsymbol{M}}_\alpha }\mathit{\boldsymbol{X}} = }\\ {{\alpha ^2}{\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_\alpha }\mathit{\boldsymbol{N}}{\mathit{\boldsymbol{M}}_\alpha }\mathit{\boldsymbol{X}}} \end{array} $ | (17) |
根据式(13)和协方差传播定律得:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{D}}_{{{\hat e}_R}}} = \sigma _0^2\left( {{\mathit{\boldsymbol{I}}_m} - \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{M}}_\alpha }{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{P}}} \right){\mathit{\boldsymbol{P}}^{ - 1}}\left( {{\mathit{\boldsymbol{I}}_m} - \mathit{\boldsymbol{PA}}{\mathit{\boldsymbol{M}}_\alpha }{\mathit{\boldsymbol{A}}^{\rm{T}}}} \right) = }\\ {\sigma _0^2\left( {{\mathit{\boldsymbol{P}}^{ - 1}} - 2\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{M}}_\alpha }{\mathit{\boldsymbol{A}}^{\rm{T}}} + \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{M}}_\alpha }\mathit{\boldsymbol{N}}{\mathit{\boldsymbol{M}}_\alpha }{\mathit{\boldsymbol{A}}^{\rm{T}}}} \right)} \end{array} $ | (18) |
顾及矩阵迹的性质得:
| $ \begin{array}{*{20}{c}} {{\rm tr}\left( {\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{D}}_{{{\mathit{\boldsymbol{\hat e}}}_R}}}} \right) = \sigma _0^2 {\rm tr} \left( {{\mathit{\boldsymbol{I}}_m} - 2{\mathit{\boldsymbol{M}}_a}\mathit{\boldsymbol{N}} + {{\left( {{\mathit{\boldsymbol{M}}_a}\mathit{\boldsymbol{N}}} \right)}^2}} \right) = }\\ {\sigma _0^2{\rm tr}\left( {{\mathit{\boldsymbol{I}}_m} - 2\left( {{\mathit{\boldsymbol{I}}_n} - {\mathit{\boldsymbol{T}}_\alpha }} \right) + {{\left( {{\mathit{\boldsymbol{I}}_n} - {\mathit{\boldsymbol{T}}_\alpha }} \right)}^2}} \right) = }\\ {\sigma _0^2{\rm tr}\left( {{\mathit{\boldsymbol{I}}_m} - {\mathit{\boldsymbol{I}}_n} + \mathit{\boldsymbol{T}}_a^2} \right) = }\\ {\sigma _0^2\left( {m - n + {\rm tr} \left( {\mathit{\boldsymbol{T}}_\alpha ^2} \right)} \right)} \end{array} $ | (19) |
式中,Tα=Nr-1KTNc-1K+αMα。将式(17)和式(19)代入式(16)右边,去掉左边期望符号,得单位权中误差无偏估计公式[15, 17]:
| $ {{\hat \sigma }_0} = \sqrt {\frac{{\mathit{\boldsymbol{e}}_R^{\rm{T}}\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{e}}_R} - {\alpha ^2}{\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_\alpha }\mathit{\boldsymbol{N}}{\mathit{\boldsymbol{M}}_\alpha }\mathit{\boldsymbol{X}}}}{{m - n + {\rm tr} \left( {\mathit{\boldsymbol{T}}_\alpha ^2} \right)}}} $ | (20) |
实际计算时,由于参数真值X未知,可用其正则化解
在式(12)和式(13)中,参数估值
| $ \eta = {\left\| {{{\mathit{\boldsymbol{\hat X}}}_R}} \right\|^2},\rho = {\left\| {{{\mathit{\boldsymbol{\hat e}}}_r}} \right\|^2} $ | (21) |
对式(21)两边取对数得:
| $ \hat \eta = \lg \eta = 2\lg \left\| {{{\mathit{\boldsymbol{\hat X}}}_R}} \right\|,\hat \rho = \lg \rho = 2\lg \left\| {{{\mathit{\boldsymbol{\hat e}}}_r}} \right\| $ | (22) |
则L曲线由若干点(
| $ \kappa = 2\frac{{\hat \rho '\hat \eta '' - \hat \rho ''\hat \eta '}}{{{{\left( {{{\left( {\hat \rho '} \right)}^2} + {{\left( {\hat \eta '} \right)}^2}} \right)}^{3/2}}}} $ | (23) |
式中,ρ′、η′、ρ″、η″分别为
对文献[14]的算例1进行改化。算例有10个观测值、5个未知数,真值X=[1 1 1 1 1]T。使用MATLAB中mvnrnd函数对观测值模拟零均值,方差阵为σ02P-1的随机误差,即e~N(0, σ02P-1),其中σ0为单位权中误差,取0.3,P为观测值权阵,为对角阵,其对角元为diag(1.2, 2.4, 1.7, 1.1, 1.3, 0.2, 0.1, 0.6, 0.4, 1)。根据L= AX + e生成观测值,A为系数矩阵,其构成为:
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{r}} {2.0}&{ - 5.0}&{1.0}&{1.00}&{ - 9.50}\\ { - 2.0}&{4.0}&{1.0}&{ - 1.05}&{8.50}\\ { - 2.0}&{1.0}&{1.0}&{ - 1.00}&{2.40}\\ { - 1.0}&{2.5}&{4.0}&{ - 0.50}&{7.00}\\ { - 1.0}&{3.2}&{4.0}&{ - 0.50}&{8.40}\\ {1.0}&{1.0}&{ - 3.0}&{0.40}&{0.49}\\ {5.0}&{7.0}&{ - 2.0}&{1.50}&{12.70}\\ {5.0}&{2.0}&{ - 2.0}&{2.50}&{ - 3.00}\\ {4.0}&{2.0}&{ - 2.0}&{2.01}&{3.00}\\ {4.0}&{3.0}&{ - 2.0}&{2.00}&{5.00} \end{array}} \right] $ | (24) |
法矩阵ATPA的条件数为1.822 3×105,病态性严重。根据真值建立等式约束[14]:
| $ {{\hat X}_i} + {{\hat X}_{i + 1}} = 2,i = 1,2,3,4 $ | (25) |
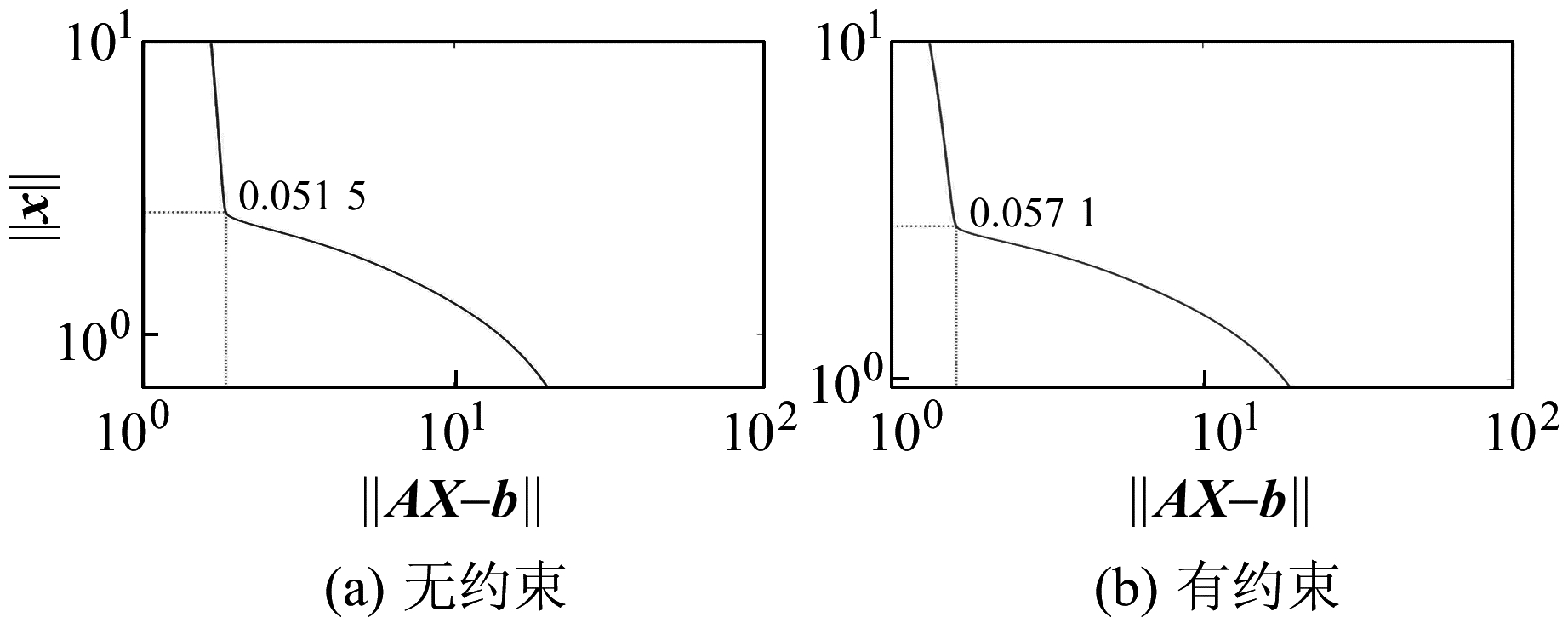
分别采用最小二乘法、约束最小二乘法、正则化法和约束正则化法估计参数,图 1为采用L曲线法确定正则化法和约束正则化法的正则化参数示意图。由图 1可知,2种算法的α分别为0.051 5(无约束)和0.057 1(有约束)。表 1列出了不同算法获得的参数估值
|
图 1 正则化解和约束正则化解的L曲线图 Fig. 1 L-curve diagram of regularized solution and constrained regularized solution |
|
|
表 1 数值算例计算结果 Tab. 1 Results of numerical example |
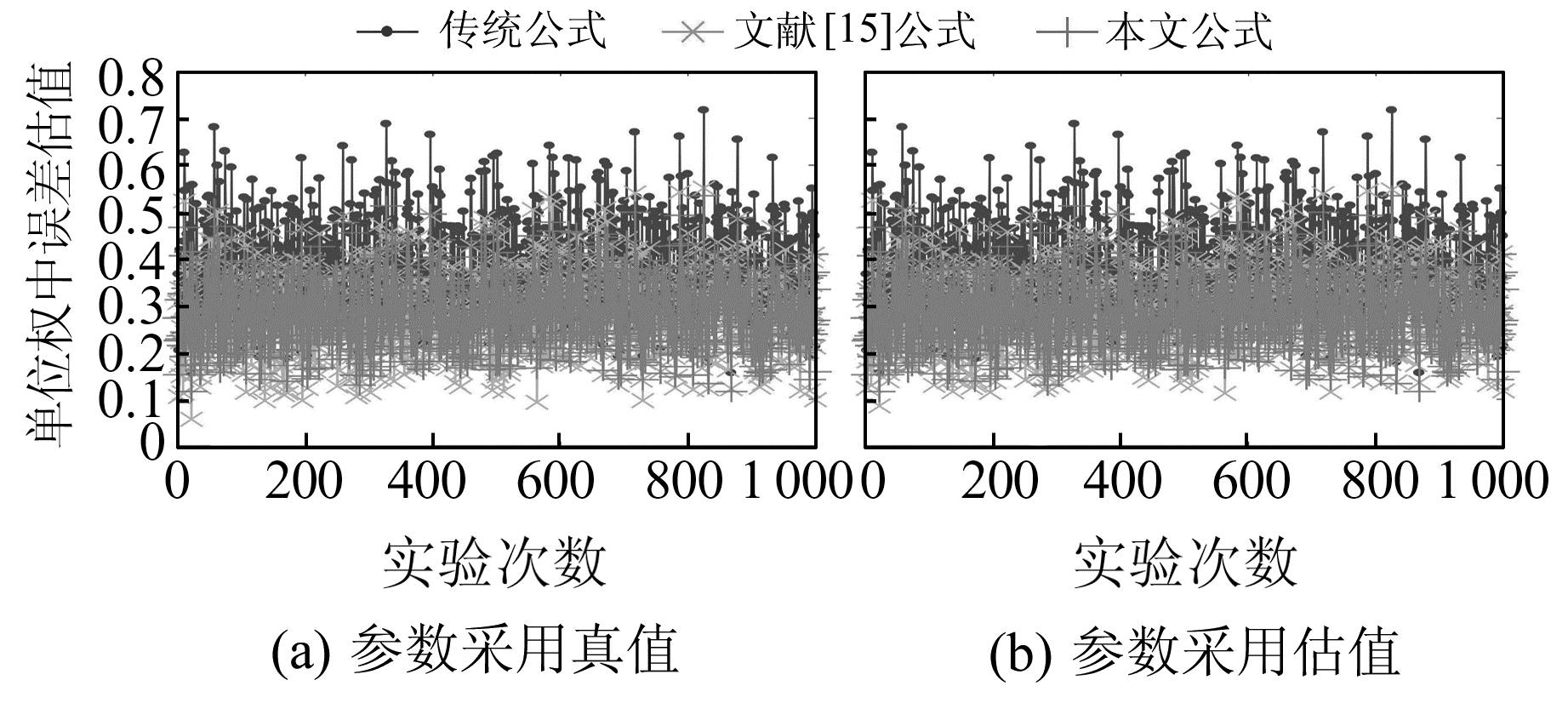
为验证本文提出的无偏单位权中误差计算公式的正确性,模拟1 000组数据,每组数据均按e~N(0, 0.32×P-1)模拟偶然误差,分别使用传统最小二乘公式
|
图 2 3种方式算得的1 000个单位权中误差对比 Fig. 2 Comparison of 1 000 medium errors estimated by three formulas |
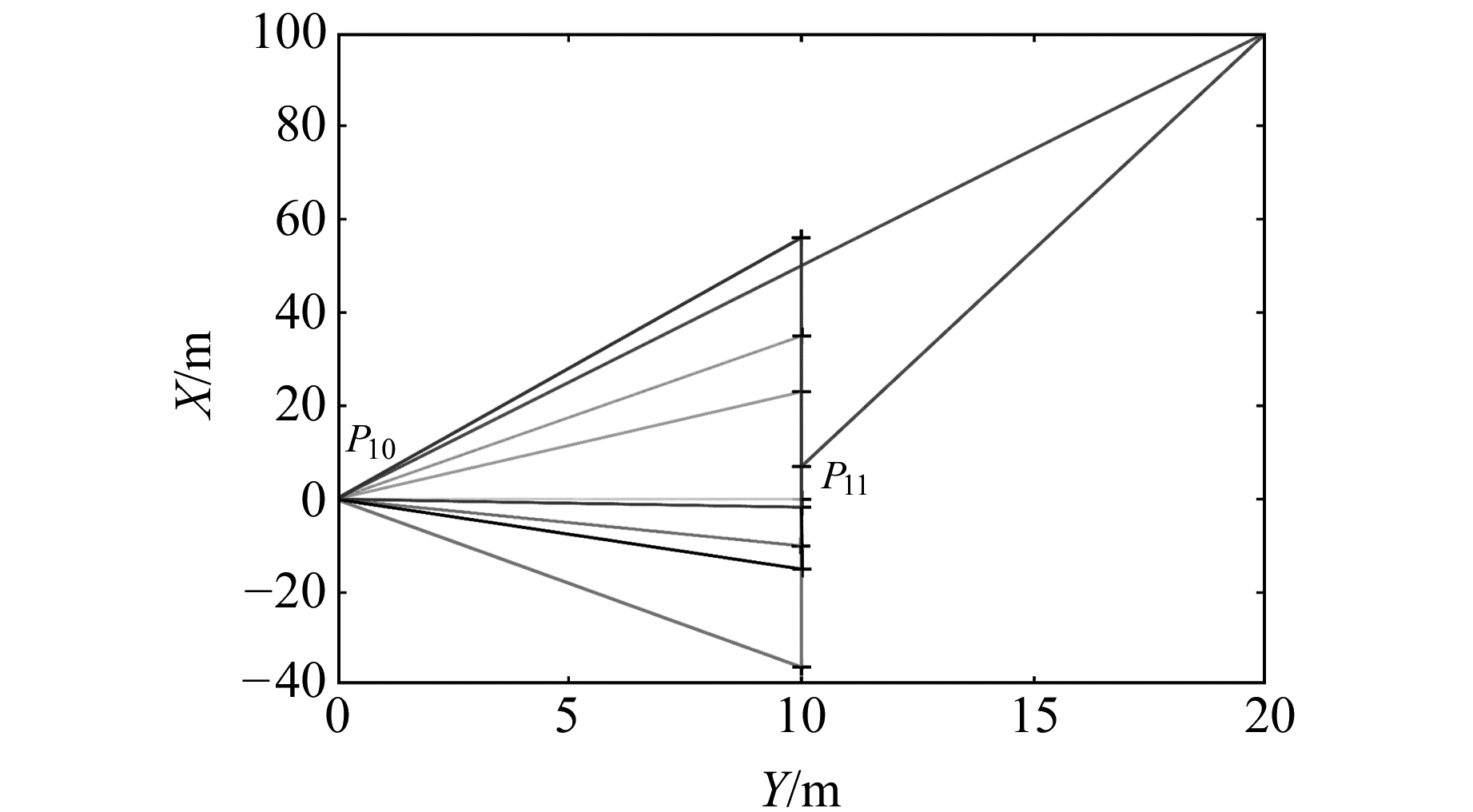
采用文献[20]和[21]中的病态测边网算例,该算例中有9个已知点P1~P9,2个未知点P10、P11,点位平面分布见图 3,已知点坐标及与未知点的距离观测值见表 2。P10和P11的真实坐标分别为(0, 0, 0)和(7, 10, -5),观测距离为d10,11=13.107 8 m,各观测距离均为等精度观测,2个未知点坐标可根据19个距离观测值组建误差方程平差得到。
|
图 3 空间测边网的平面点位分布 Fig. 3 The points distribution map of the space net in plane |
|
|
表 2 控制点的坐标及距离观测值 Tab. 2 The coordinates and distance observations of control points |
算例中,法矩阵ATA的条件数为4.585 1×103,存在病态。根据真实坐标建立等式约束:
| $ \begin{array}{*{20}{c}} {\left( {\begin{array}{*{20}{c}} {{{\hat X}_{10}}}&{{{\hat Y}_{10}}}&{{{\hat Z}_{10}}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{{\hat X}_{11}}}&{{{\hat Y}_{11}}}&{{{\hat Z}_{11}}} \end{array}} \right) = }\\ {\left( {\begin{array}{*{20}{c}} 7&{10}&{ - 5} \end{array}} \right)} \end{array} $ | (26) |
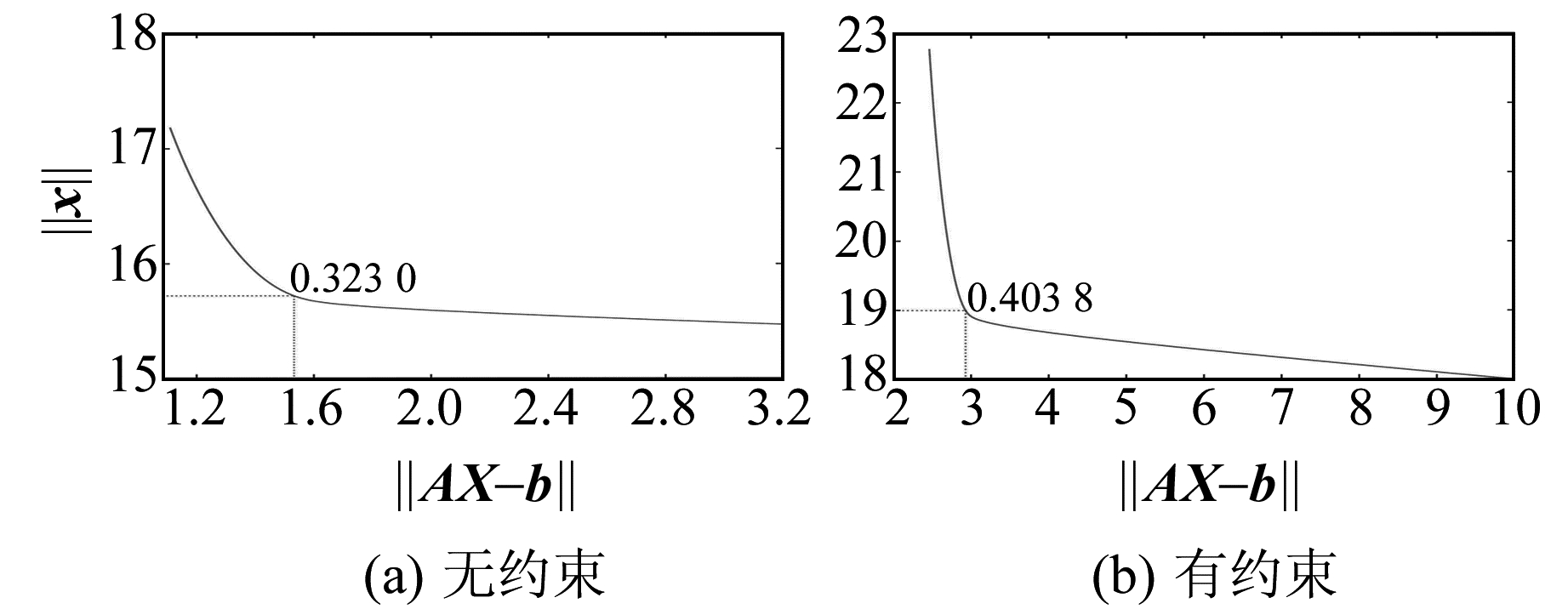
同数值算例,分别采用最小二乘法、约束最小二乘法、正则化法和约束正则化法估计参数,图 4为使用L曲线法确定2种正则化算法的α示意图。由图 4可知,正则化参数分别取为0.323 0(无约束)和0.403 8(有约束)。4种算法求解的参数估值及其与真值的差值范数和相对偏差范数见表 3。由表 3可知,最小二乘解的精度最差,严重偏离真值;当考虑约束条件时,约束最小二乘解精度明显提升;当不考虑约束条件时,正则化解较最小二乘解有明显改善;而约束正则化法既改善了法矩阵的病态性,又考虑了正确的先验信息,所以其精度最高。
|
图 4 正则化解和约束正则化解的L曲线 Fig. 4 L-curve diagram of regularized solution and constrained regularized solution |
|
|
表 3 病态测边网计算结果 Tab. 3 Results of ill-posed trilateration network |
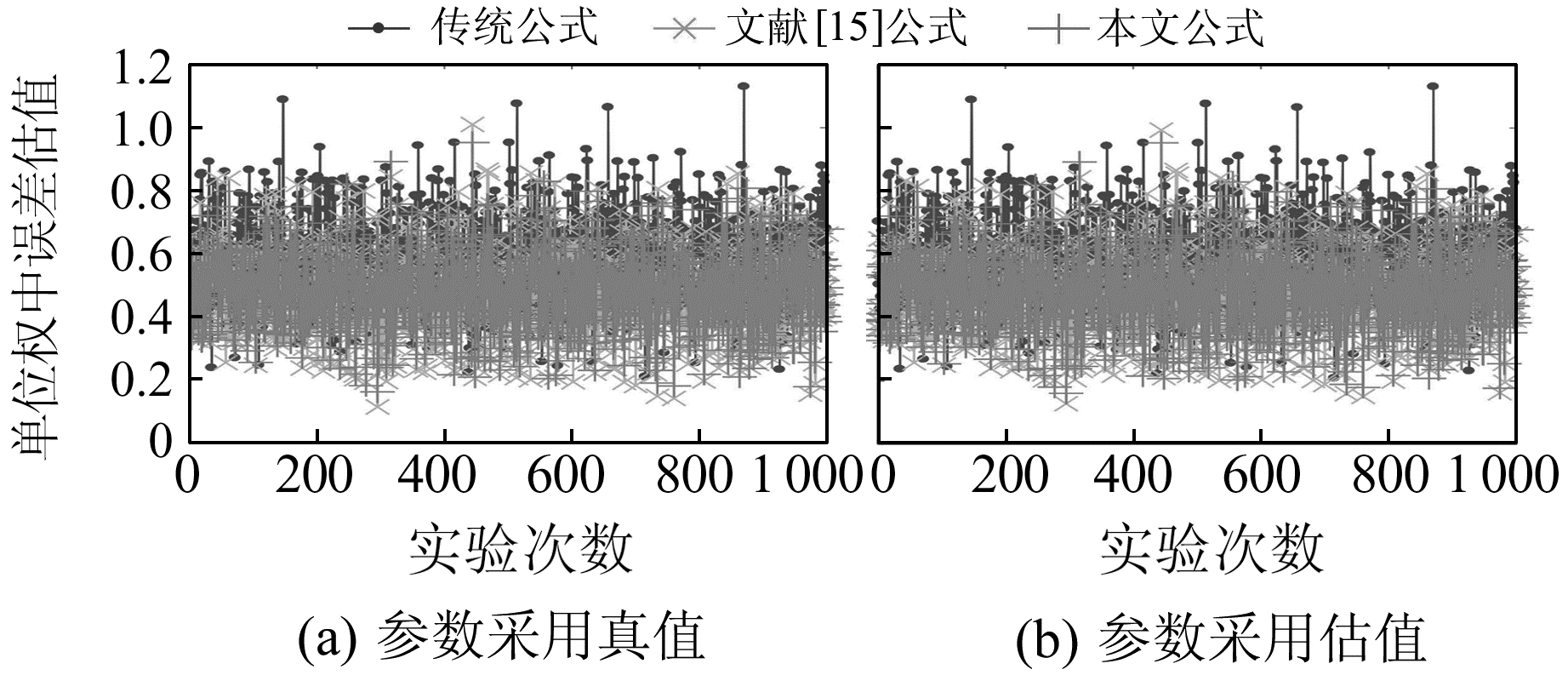
模拟1 000组数据,每组数据均按e~N(0, 0.52×Im)模拟偶然误差,同数值算例,分别采用传统公式、本文公式和文献[15]中公式计算单位权中误差。采用本文公式和文献[15]公式计算时,分别采用参数真值及估值代入计算,结果见图 5。传统公式计算出的1 000个单位权中误差均值为0.585 8,与真值相差17.16%。参数采用真值时,本文公式和文献[15]公式计算的1 000个单位权中误差,均值分别为0.488 9和0.478 2,与真值分别相差2.22%和4.36%。参数采用相应的估值时,文献[15]计算出的单位权中误差均值为0.476 2,与真值相差4.76%;本文公式计算的单位权中误差均值为0.488 8,与真值相差2.24%。从结果来看,使用无偏公式计算单位权中误差时,参数采用真值和估值所得的结果相差极小。
|
图 5 2种公式算得的1 000个单位权中误差对比 Fig. 5 Comparison of 1 000 medium errors estimated by two formulas |
通过对病态模型施加等式约束条件虽能显著提升解的精度,然而其本质仍是通过引入正则化参数来削弱模型的病态性,所得的约束正则化解及残差均有偏,利用有偏残差所估的单位权中误差也有偏。本文在病态模型正则化解的无偏单位权方差估计式的基础上引入等式约束条件,利用有偏的约束正则化解导出附有等式约束病态模型正则化解的无偏单位权中误差估计式,并用数值算例和病态测边网算例加以验证。结果表明,本文公式和文献[15]中公式计算得到的单位权中误差精度均优于传统公式,且当参数估值与真值较为接近时,利用无偏公式计算的单位权中误差相差不大。
| [1] |
Li B F, Shen Y Z, Feng Y M. Fast GNSS Ambiguity Resolution as an Ill-Posed Problem[J]. Journal of Geodesy, 2010, 84(11): 683-698 DOI:10.1007/s00190-010-0403-5
(  0) 0) |
| [2] |
李慕清, 刘正华, 夏传甲, 等. GPS单历元模型病态方程解算方法研究[J]. 大地测量与地球动力学, 2013, 33(增1): 160-162 (Li Muqing, Liu Zhenghua, Xia Chuanjia, et al. Analysis of Ill-Posed Equation Resolution Technique for GPS Positioning in Epoch-Wise[J]. Journal of Geodesy and Geodynamics, 2013, 33(S1): 160-162)
(  0) 0) |
| [3] |
顾勇为, 归庆明, 张璇, 等. 大地测量与地球物理中病态性问题的正则化迭代解法[J]. 测绘学报, 2014, 43(4): 331-336 (Gu Yongwei, Gui Qingming, Zhang Xuan, et al. Iterative Solution of Regularization to Ill-Conditioned Problems in Geodesy and Geophysics[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(4): 331-336)
(  0) 0) |
| [4] |
邓凯亮, 黄谟涛, 暴景阳, 等. 向下延拓航空重力数据的Tikhonov双参数正则化法[J]. 测绘学报, 2011, 40(6): 690-696 (Deng Kailiang, Huang Motao, Bao Jingyang, et al. Tikhonov Two-Parameter Regulation Algorithm in Downward Continuation of Airborne Gravity Data[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 690-696)
(  0) 0) |
| [5] |
许才军, 陈庭, 张丽琴. 地球物理大地测量反演理论与应用[M]. 武汉: 武汉大学出版社, 2015 (Xu Caijun, Chen Ting, Zhang Liqin. Joint Inversion Theory Geophysics and Geodesy and Its Application[M]. Wuhan: Wuhan University Press, 2015)
(  0) 0) |
| [6] |
Save H, Bettadpur S, Tapley B D. Reducing Errors in the GRACE Gravity Solutions Using Regularization[J]. Journal of Geodesy, 2012, 86(9): 695-711 DOI:10.1007/s00190-012-0548-5
(  0) 0) |
| [7] |
Zhou W N. Normalized Full Gradient of Full Tensor Gravity Gradient Based on Adaptive Iterative Tikhonov Regularization Downward Continuation[J]. Journal of Applied Geophysics, 2015, 118: 75-83 DOI:10.1016/j.jappgeo.2015.04.012
(  0) 0) |
| [8] |
Schaffrin B, Felus Y A. An Algorithmic Approach to the Total Least-Squares Problem with Linear and Quadratic Constraints[J]. Studia Geophysica et Geodaetica, 2009, 53(1): 1-16
(  0) 0) |
| [9] |
谢建, 朱建军. 等式约束对病态问题的影响及约束正则化方法[J]. 武汉大学学报:信息科学版, 2015, 40(10): 1 344-1 348 (Xie Jian, Zhu Jianjun. Influence of Equality Constraints on Ill-Conditioned Problems and Constrained Regularization Method[J]. Geomatics and Information Science of Wuhan University, 2015, 40(10): 1 344-1 348)
(  0) 0) |
| [10] |
马下平. 附有约束条件的间接平差扩展模型的参数估计及其精度评定[J]. 工程勘察, 2016, 44(5): 55-59 (Ma Xiaping. Parameter Estimation and Precision Assessment of Extended Indirect Adjustment Model with Constraints[J]. Geotechnical Investigation & Surveying, 2016, 44(5): 55-59)
(  0) 0) |
| [11] |
王乐洋, 许才军, 汪建军. 附有病态约束矩阵的等式约束反演问题研究[J]. 测绘学报, 2009, 38(5): 397-401 (Wang Leyang, Xu Caijun, Wang Jianjun. Research on Equality Constraint Inversion with Ill-Posed Constraint Matrix[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(5): 397-401 DOI:10.3321/j.issn:1001-1595.2009.05.004)
(  0) 0) |
| [12] |
王乐洋, 许才军. 附有病态约束反演问题的岭估计法[J]. 武汉大学学报:信息科学版, 2011, 36(5): 612-616 (Wang Leyang, Xu Caijun. Ridge Estimation Method in Inversion Problem with Ill-Posed Constraint[J]. Geomatics and Information Science of Wuhan University, 2011, 36(5): 612-616)
(  0) 0) |
| [13] |
马洋, 欧吉坤, 袁运斌, 等. 采用联合平差法处理附有病态等式约束的反演问题[J]. 武汉大学学报:信息科学版, 2011, 36(7): 816-819 (Ma Yang, Ou Jikun, Yuan Yunbin, et al. Solving Equality Constraint Inversion with Ill-Posed Constraint Matrix Using United Method[J]. Geomatics and Information Science of Wuhan University, 2011, 36(7): 816-819)
(  0) 0) |
| [14] |
谢建, 朱建军. 等式约束病态模型的正则化解及其统计性质[J]. 武汉大学学报:信息科学版, 2013, 38(12): 1 440-1 444 (Xie Jian, Zhu Jianjun. A Regularized Solution and Statistical Properties of Ill-Posed Problem with Equality Constraints[J]. Geomatics and Information Science of Wuhan University, 2013, 38(12): 1 440-1 444)
(  0) 0) |
| [15] |
沈云中, 刘大杰. 正则化解的单位权方差无偏估计公式[J]. 武汉大学学报:信息科学版, 2002, 27(6): 604-606 (Shen Yunzhong, Liu Dajie. Unbiased Estimation Formula of Unit Weight Mean Square Error in Regularization Solution[J]. Geomatics and Information Science of Wuhan University, 2002, 27(6): 604-606)
(  0) 0) |
| [16] |
Xu P L, Shen Y Z, Fukuda Y, et al. Variance Component Estimation in Linear Inverse Ill-Posed Models[J]. Journal of Geodesy, 2006, 80(2): 69-81 DOI:10.1007/s00190-006-0032-1
(  0) 0) |
| [17] |
张俊, 独知行, 杜宁, 等. 补偿最小二乘解的单位权方差的无偏估计[J]. 大地测量与地球动力学, 2014, 34(1): 153-156 (Zhang Jun, Du Zhixing, Du Ning, et al. Unbiased Estimation Formula of Unit Weight Variance in Solution by Penalized Least Square[J]. Journal of Geodesy and Geodynamics, 2014, 34(1): 153-156)
(  0) 0) |
| [18] |
崔希璋. 广义测量平差[M]. 武汉: 武汉大学出版社, 2009 (Cui Xizhang. Generalized Measurement Adjustment[M]. Wuhan: Wuhan University Press, 2009)
(  0) 0) |
| [19] |
Hansen P C, O'Leary D P. The Use of the L-Curve in the Regularization of Discrete Ill-Posed Problems[J]. SIAM Journal on Scientific Computing, 1993, 14(6): 1 487-1 503 DOI:10.1137/0914086
(  0) 0) |
| [20] |
鲁铁定, 宁津生. 总体最小二乘平差理论及其应用[M]. 北京: 中国科学技术出版社, 2011 (Lu Tieding, Ning Jinsheng. Total Least Squares Adjustment Theory and Its Application[M]. Beijing: Science and Technology of China Press, 2011)
(  0) 0) |
| [21] |
王乐洋, 于冬冬. 病态总体最小二乘问题的虚拟观测解法[J]. 测绘学报, 2014, 43(6): 575-581 (Wang Leyang, Yu Dongdong. Virtual Observation Method to Ill-Posed Total Least Squares Problem[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(6): 575-581)
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39

