2. 中国人民解放军31009部队,北京市,100088
传统精密单点定位(precise point positioning,PPP)需要精密卫星轨道和钟差的支持,但这些精密产品往往存在一定的时延,不能满足实时应用。超快速产品IGU虽然能实时得到,但由于其预报钟差精度较低,不能满足PPP的需求。为此,IGS从2013-04-01起正式运行实时实验计划[1],利用全球GNSS跟踪站观测数据实时生成包含基于广播星历的卫星轨道和钟差改正数,采用符合RTCM标准的状态空间表示(state space representation,SSR)信息格式发布,基于NTRIP(networked transport of RTCM via internet protocol)协议向全球播发[2]。用户可以在任意时间接收IGS及其分析中心播发的数据流产品,并与广播星历结合实时恢复出高精度的卫星轨道与钟差,进而用于实时精密单点定位(real-time PPP,RTPPP)。
本文实时接收法国空间研究中心(Centre National d’Etudes Spatiales, CNES)播发的2018-03-22~03-31的数据流,实时恢复出高精度的卫星轨道与钟差,统计数据流产品自身的完整性;然后以IGS最终产品为参考,分析实时恢复得到的轨道和钟差产品的精度;最后选取10个全球分布的IGS测站,结合实时恢复出的轨道和钟差进行PPP解算,以获得实时数据流在RTPPP中的定位性能。
1 实时产品质量分析实时卫星轨道与钟差恢复的基本原理在文献[3]中已有详细介绍,此处不再赘述。
1.1 实时数据流的获取选择由武汉大学运营的NTRIP播发器来接收实时数据流[4]。选择RTCM3EPH01和CLK93两个挂载点,并通过BNC软件来实时接收SSR数据流,同时结合广播星历流生成定位所需的精密产品。由于GPS实时轨道和钟差数据流运行稳定且精度较高,所以仅对GPS信息进行分析和用于PPP解算。本文实时接收2018-03-22~03-31共10 d的数据,结合广播星历和SSR数据流实时恢复得到SP3星历文件和CLK钟差文件并存于本地,以方便分析实时数据流的完整性和实时轨道与钟差的精度。
1.2 实时数据流完整性分析受数据源本身、播发机构、传输网络以及BNC软件稳定性等因素的影响,实时接收的数据流不一定完整,因此有必要对其完整性进行分析。综合分析连续接收的实时数据流并分卫星进行统计,结果见表 1。
|
|
表 1 GPS卫星数据完整率统计 Tab. 1 Statistics of data integrity rate of GPS satellites |
由表 1可知,实时数据流主要存在2个方面的不完整性:1)没有改正信息,如G04、G18号卫星数据完整率为0.000%,这是因为对应卫星的实时改正数的生成有问题;2)改正信息不连续,如除G04、G18号卫星外的其他卫星数据完整率都没有100%,中间断断续续均存在几个或上千个历元的数据缺失,有的是因为改正信息生成时就缺少部分数据,有的是因为网络故障导致接收不到实时数据。实验时段内的实时数据流较为完整,对于含有改正信息的卫星,数据流接收完整率可达91.769%。
1.3 实时卫星轨道精度分析以IGS发布的最终产品为参考值,为了避免数据内插引起的误差,对相同时刻实时轨道和IGS最终产品的数据进行对比分析,并按式(1)统计每颗卫星在径向、切向和法向方向上的RMS值[5]:
| $ {\rm{RMS}} = \sqrt {{{\mathop \sum \limits_{i = 1}^n \varDelta _i^2/n}}} $ | (1) |
式中,Δi为在第i个历元的轨道互差,n为比较的历元个数。
统计各颗卫星在对应方向上的RMS值,如图 1所示。可以看出,实时轨道的精度在3个方向上的RMS值大多优于3 cm,其中径向误差最小。统计去除G04、G18号卫星后的其他30颗GPS卫星实时轨道精度,可得轨道径向、切向和法向方向的误差平均值分别为2.10 cm、2.84 cm和2.50 cm,轨道三维位置误差平均值为4.37 cm,与超快速IGU产品的预报段星历精度(约5 cm)相当,可以满足实时精密单点定位的需求。
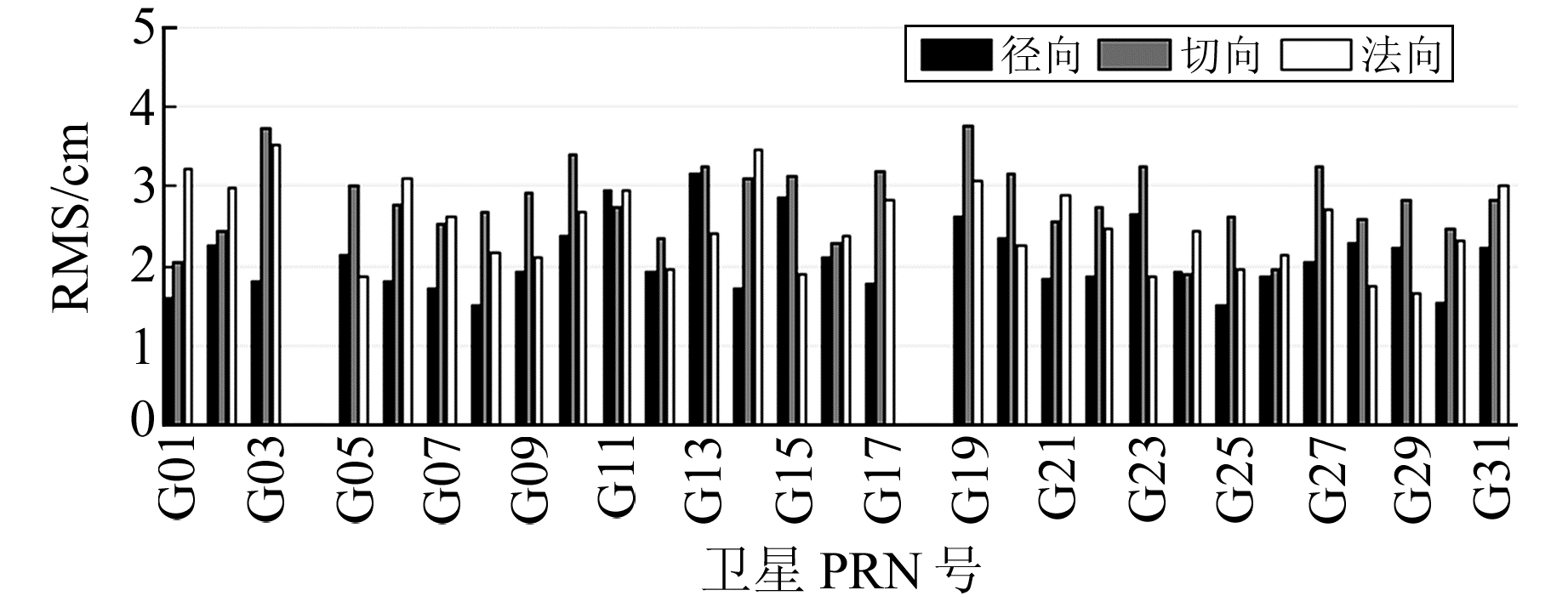
|
图 1 实时卫星轨道精度 Fig. 1 Real-time satellite orbit accuracy |
应用二次差方法对得到的实时卫星钟差进行精度分析[6]。首先在实时钟差与IGS钟差产品中选择同一颗卫星作为参考卫星(本文选择G32号),其他卫星按历元分别与参考卫星作一次差,消除基准钟不同带来的影响;然后对实时钟差和IGS钟差产品的一次差结果作二次差,并采用式(2)计算二次差的RMS值,从而有效反映出实时钟差与IGS钟差之间的符合程度:
| $ {\rm{RMS}} = \sqrt {{{{\mathop \sum \limits_{i = 1}^n {{\left( {{\varDelta _i} - \bar \varDelta } \right)}^2}/n}}} } $ | (2) |
式中,Δi为第i个历元的二次差结果,Δ为二次差的均值。
统计每颗卫星钟差的RMS值,如图 2所示。可以看出,实时卫星钟差精度均优于0.12 ns,平均优于0.09 ns,间接反映出CNES播发的实时钟差改正数精度较高,可以满足RTPPP的需求。
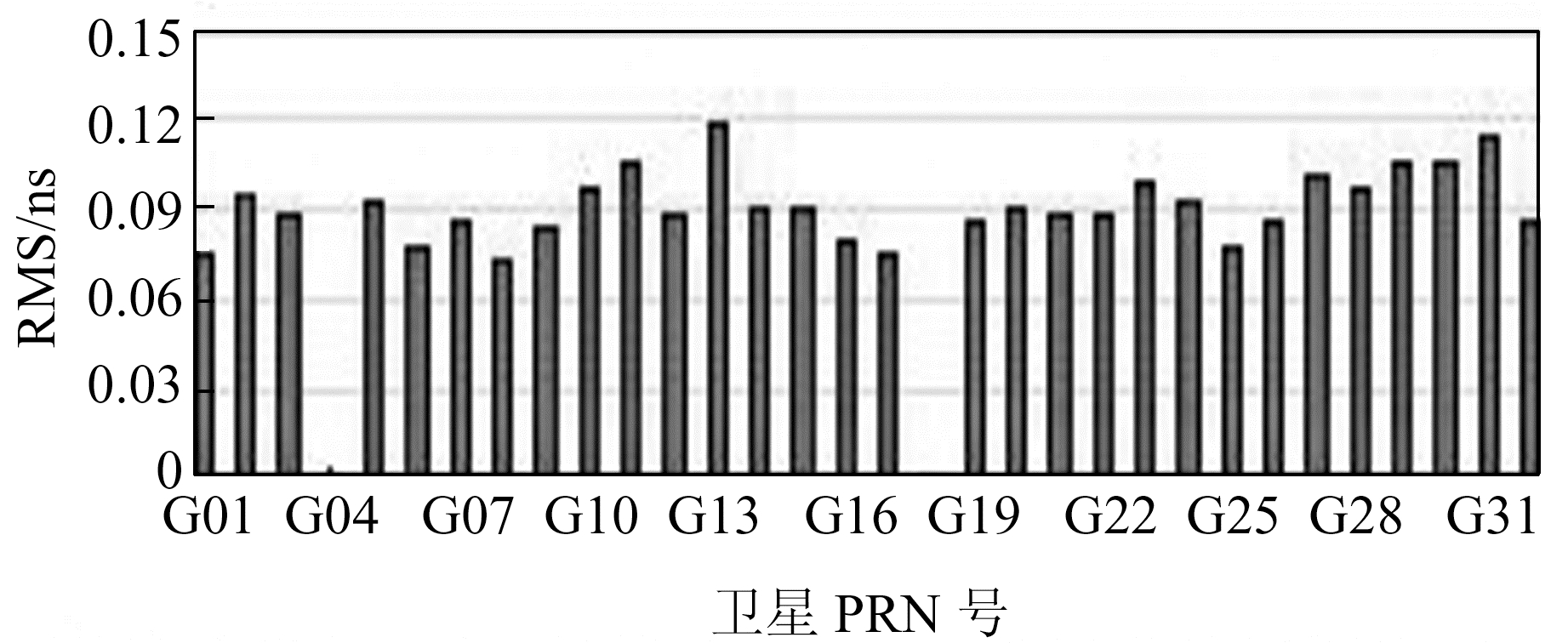
|
图 2 实时卫星钟差精度 Fig. 2 Precision of real-time satellite clock difference |
为了检验实时轨道和钟差在RTPPP中的定位性能,同时使定位结果在时间和空间分辨率上具有参考性,选取10个全球分布的IGS测站(图 3),对其GPS观测数据进行解算。选取的观测时间均为2018-03-22~03-31,对应年积日为081~090。PPP解算采用无电离层组合模型,应用扩展卡尔曼滤波方法进行参数估计,详细的数据处理策略如表 2所示[7]。
|
图 3 测站分布 Fig. 3 Distribution of stations |
|
|
表 2 PPP数据处理策略 Tab. 2 PPP data processing strategy |
分别对10个测站10 d的观测数据以日为单位进行解算,将定位结果与IGS提供的周解坐标作差,求得X、Y、Z方向上的定位误差,并将其转换到ENU坐标系下,统计不同测站不同时段PPP的收敛时间以及收敛后的定位精度。限于篇幅,这里随机选取KZN2、NKLG和UNB3等3个测站不同观测时段作定位误差序列图(图 4),其他测站不同时段的定位误差序列与此相似。
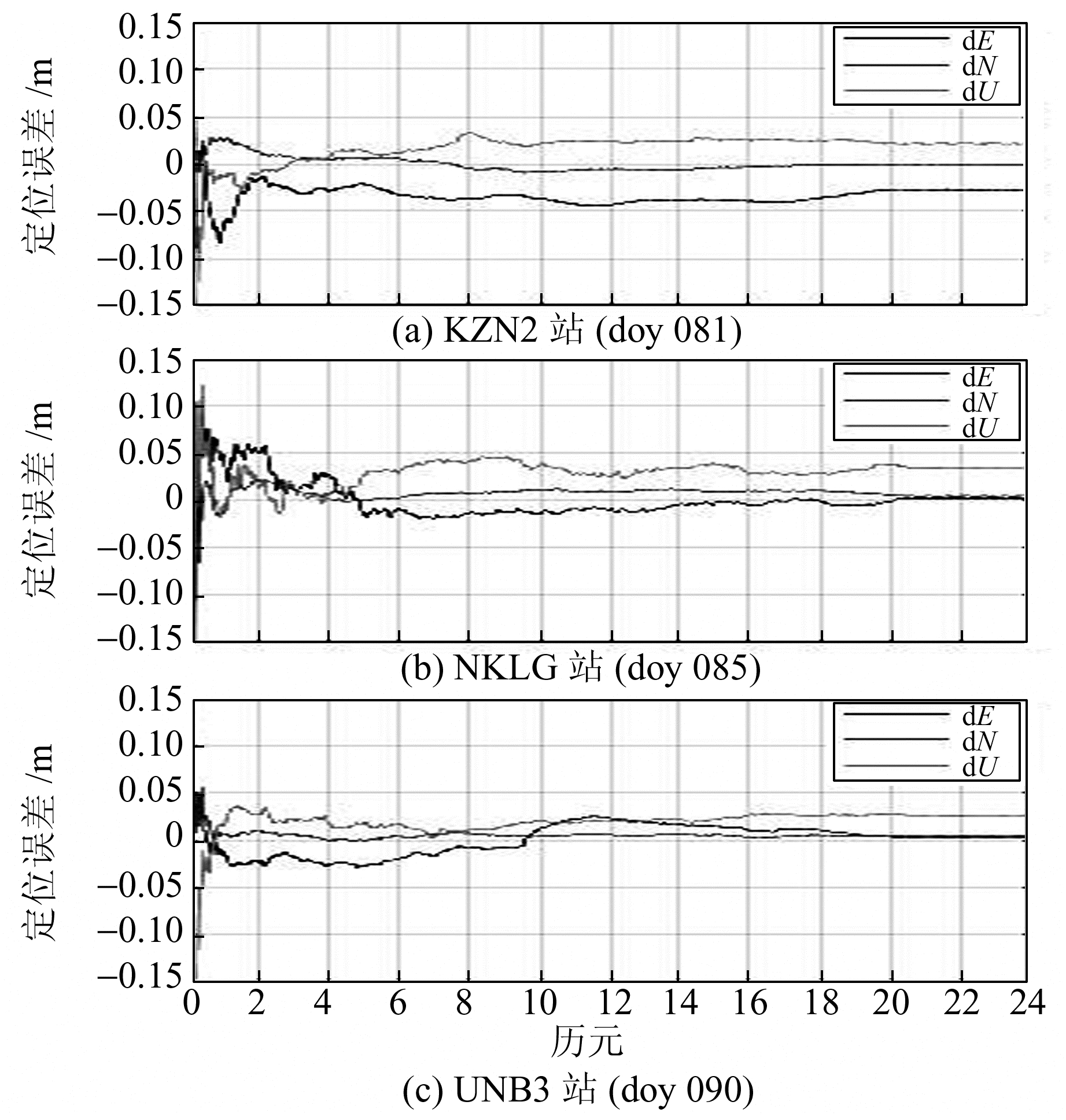
|
图 4 RTPPP定位误差序列 Fig. 4 RTPPP positioning error sequence |
由图 4可知,使用实时轨道与钟差数据进行RTPPP解算均能快速收敛,单天解E、N、U方向的定位精度均优于5 cm。部分测站收敛较慢,且收敛后定位误差波动较大,可能是因为该时段SSR数据缺失使得外推星历和钟差误差较大。
2.1 实时PPP收敛时间分析分别统计各个测站10 d内PPP解算E、N、U方向的收敛时间平均值,结果如图 5所示。这里定义收敛为定位误差小于10 cm,且至少保持15 min。
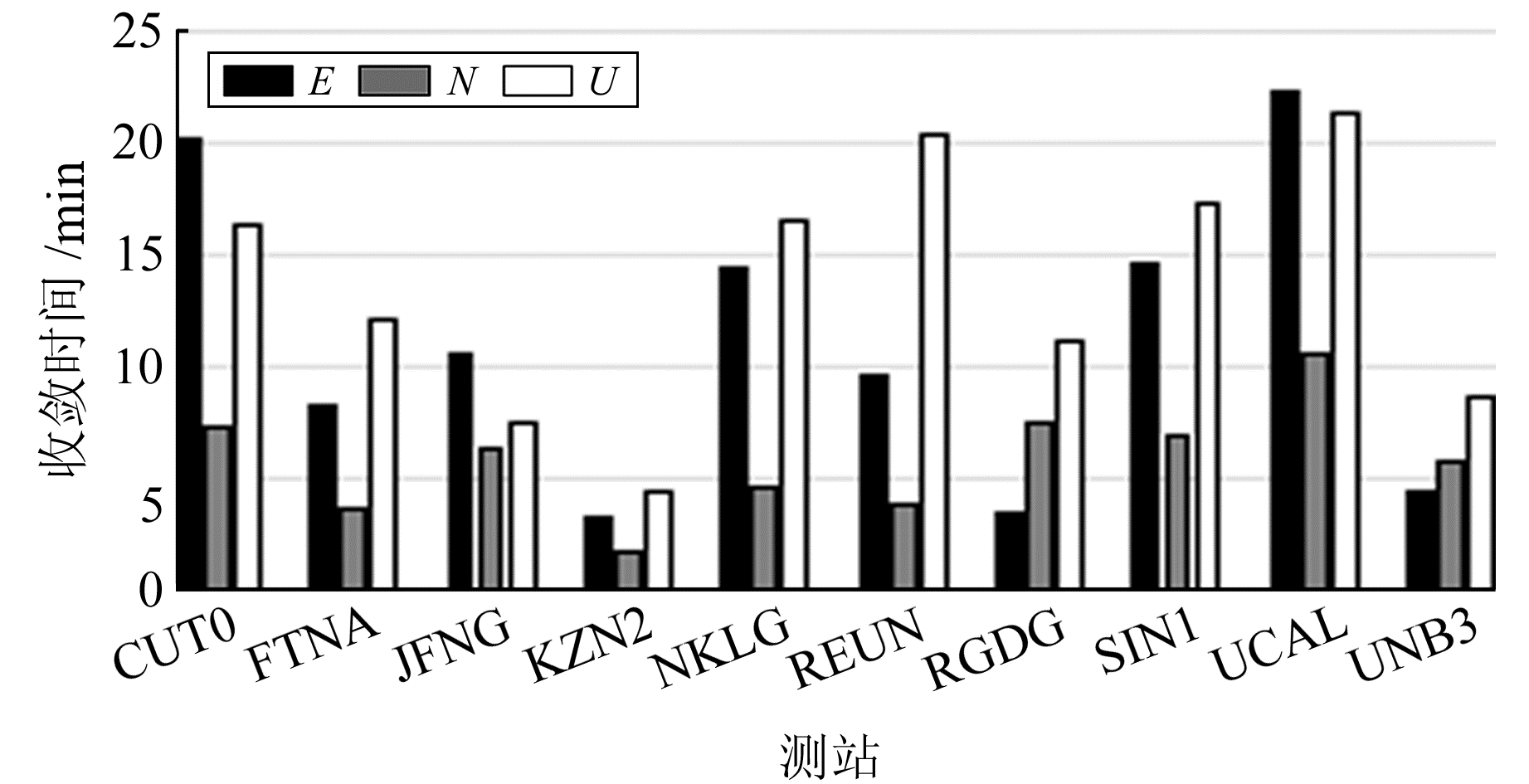
|
图 5 RTPPP收敛时间统计 Fig. 5 RTPPP convergence time statistics |
由图 5可知,每个测站N方向收敛速度最快,不同测站收敛时间存在较大差异,其中KZN2测站收敛速度最快,E、N、U方向平均收敛时间分别为3.28 min、1.84 min、4.48 min;UCAL测站收敛速度最慢,E、N、U方向平均收敛时间分别为22.28 min、10.59 min、21.34 min。这可能与测站周围环境有关,如多路径效应、可视卫星数不同等。
分析可知,基于SSR信息的RTPPP可以实现23 min收敛到10 cm精度的定位性能,同时在某些情况下,RTPPP还可以实现5 min内快速收敛到10 cm的精度水平。
2.2 实时PPP定位精度分析定位误差是基于SSR信息的RTPPP解算结果与IGS给出的周解坐标之间的差值,分别计算各个测站10 d内日解结果的平均值(图 6)。
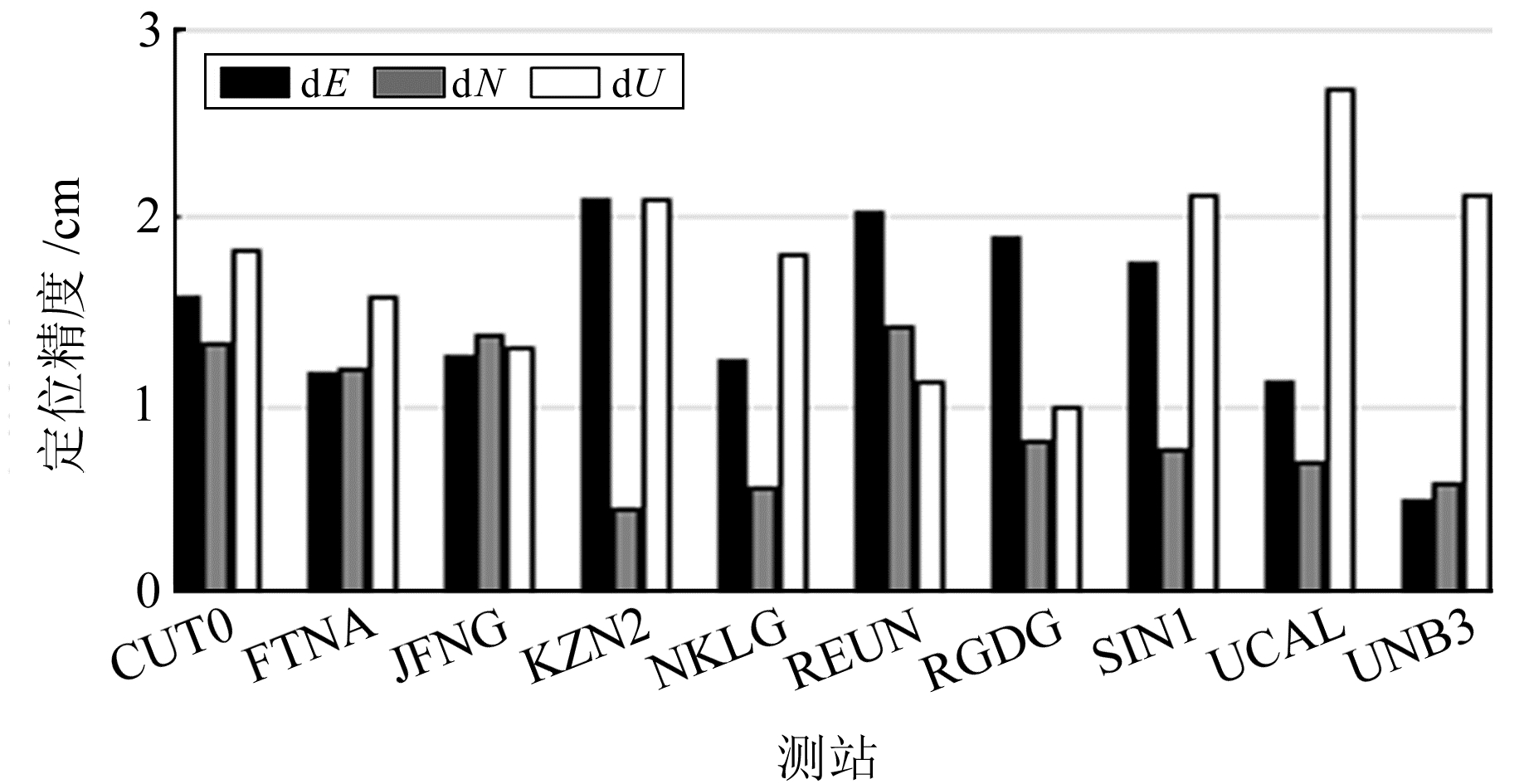
|
图 6 RTPPP定位精度统计 Fig. 6 RTPPP positioning accuracy statistics |
由图 6可知,所有测站的定位误差平均值在E、N、U方向均优于3 cm,N方向定位精度最高,部分测站E、N方向定位误差能达到mm级。表 3(单位cm)给出每个测站E、N、U、水平和三维方向定位误差的平均值。可以看出,每个测站的定位精度相当,其中N方向定位精度优于1.5 cm,最优能达到4.6 mm;E方向定位精度基本分布在1.1~2.1 cm,较优时能达到5.1 mm;U方向定位精度基本分布在1.5~2.7 cm,因此总体上N方向定位精度优于E方向,U方向最差。水平定位精度基本分布在1.3~2.5 cm,三维定位精度基本分布在2.2~3.0 cm。因此基于SSR信息的RTPPP具有较高定位精度,能够满足PPP的精度要求。
|
|
表 3 各测站平均定位误差 Tab. 3 Average positioning errors of each station |
本文以IGS最终产品为参考,对CNES提供的实时轨道和钟差产品质量进行分析。以d为单位,对全球分布的10个IGS测站10 d观测数据进行PPP处理,分别统计PPP定位收敛时间和定位精度,以分析基于SSR信息的RTPPP性能。结果表明,CNES分析中心10 d内GPS实时数据完整率达到91.769%,实时轨道在径向、切向和法向上的精度分别为2.10 cm、2.84 cm和2.50 cm,轨道三维位置误差平均值为4.37 cm,并且实时轨道数据采样率高,能够减小轨道的插值误差;实时钟差产品与IGS最终钟差产品比较的平均RMS值可达0.09 ns,约2.7 cm。
对于RTPPP的定位性能,实验结果表明:1) RTPPP对于10 cm的精度水平能够实现小于23 min的收敛性能,同时某些情况下还可以实现5 min内快速收敛到10 cm的精度水平;2)RTPPP可以实现优于3 cm的定位精度,这些精度对于水平方向大约为1.3~2.5 cm,对于三维方向大约为2.2~3.0 cm。
| [1] |
夏凤雨, 叶世榕, 赵乐文, 等. 基于SSR改正的实时精密单点定位精度分析[J]. 导航定位与授时, 2017, 4(3): 52-57 (Xia Fengyu, Ye Shirong, Zhao Lewen, et al. Real-Time Precise Point Positioning Accuracy Analysis Based on SSR Correction[J]. Navigation Position and Timing, 2017, 4(3): 52-57)
(  0) 0) |
| [2] |
尹倩倩, 楼益栋, 易文婷. IGS实时产品比较与分析[J]. 大地测量与地球动力学, 2012, 32(6): 123-128 (Yin Qianqian, Lou Yidong, Yi Wenting. IGS Real-Time Product Comparison and Analysis[J]. Journal of Geodesy and Geodynamics, 2012, 32(6): 123-128)
(  0) 0) |
| [3] |
赵爽.BDS/GPS实时精密单点定位方法研究[D].郑州: 信息工程大学, 2018 (Zhao Shuang.Research on BDS/GPS Real-Time Precise Point Positioning Method[D].Zhengzhou: Information Engineering University, 2018) http://cdmd.cnki.com.cn/Article/CDMD-91037-1019818853.htm
(  0) 0) |
| [4] |
赖允斌, 赵春梅, 李子申. 不同星历下实时精密单点定位精度分析[J]. 测绘通报, 2015(8): 9-12 (Lai Yunbin, Zhao Chunmei, Li Zishen. Real-Time Precision Single-Point Positioning Accuracy Analysis under Different Ephemeris[J]. Bulletin of Surveying and Mapping, 2015(8): 9-12)
(  0) 0) |
| [5] |
王俊杰, 许杭, 高俊强. 基于广播星历改正的实时精密星历与钟差获取研究[J]. 全球定位系统, 2015, 40(2): 21-25 (Wang Junjie, Xu Hang, Gao Junqiang. Research on Real-Time Precision Ephemeris and Clock Aberration Acquisition Based on Broadcast Ephemeris Correction[J]. GNSS World of China, 2015, 40(2): 21-25)
(  0) 0) |
| [6] |
Kazmierski K, Sošnica K, Hadas T. Quality Assessment of Multi-GNSS Orbits and Clocks for Real-Time Precise Point Positioning[J]. GPS Solutions, 2018, 22(1): 11 DOI:10.1007/s10291-017-0678-6
(  0) 0) |
| [7] |
Wang L, Li Z S, Ge M R, et al. Validation and Assessment of Multi-GNSS Real-Time Precise Point Positioning in Simulated Kinematic Mode Using IGS Real-Time Service[J]. Remote Sensing, 2018, 10(2): 337 DOI:10.3390/rs10020337
(  0) 0) |
2. 31009 Troops of PLA, Beijing 100088, China
 2019, Vol. 39
2019, Vol. 39

