2. 中国科学院大学,北京市玉泉路19号甲,100049
在多系统融合定位中,必须要考虑系统偏差(ISB)[1]对定位结果的影响[2]。近年来,很多学者对ISB进行了广泛研究。Montenbruck等[3]首次提出GPS/Galileo测距码ISB,并从理论上证明ISB与接收机和测距码的类型有关; Tegedor等[4]证明ISB与接收机类型强相关,并指出相同类型接收机的ISB由于天线延迟或者热效应等原因会有微小差异,不同类型接收机之间GPS/BDS的ISB差异最大超过100 ns; Chen等[5]证明ISB能被钟差和模糊度参数吸收,与坐标参数不相关,同时提出一种消去ISB参数的多系统PPP统一模型,并通过双系统验证了模型的正确性。
由于ISB在短期内是稳定的,目前PPP数据处理中,大多对ISB采用常数估计或者分段常数估计的方法[6-7],鲜有学者详细分析不同时段常数估计方法对多系统精密单点定位的影响。本文通过对GPS、BDS、GLONASS和Galileo四系统观测数据进行静态PPP数据测试,采用不同常数弧段估计ISB,比较其对多系统融合PPP收敛时间和定位精度的影响。
1 多系统融合PPP观测模型及数据处理策略 1.1 多系统消电离层组合观测模型为消除一阶电离层影响,以GPS单系统为例,接收机r在t时刻观测卫星s的基于双频消电离层组合伪距和相位观测方程分别为:
| $ \begin{array}{l} P_i^{\rm{G}}(t) = {\rho ^{\rm{G}}}(t) + c\left[{{\rm{d}}{t_{\rm{G}}}(t) - {\rm{d}}{t^{\rm{s}}}(t)} \right] + \\ \;\;\;\;T(t) + {\rm{hd}}_{{\rm{r}}, i}^{\rm{G}}(t) - {\rm{hd}}_i^{\rm{s}}(t) + {\varepsilon _{p, i}}(t) \end{array} $ | (1) |
| $ \begin{array}{l} \mathit{\Phi }_i^{\rm{G}}(t) = {\rho ^{\rm{G}}}(t) + c\left[{{\rm{d}}{t_{\rm{G}}}(t) - {\rm{d}}{t^{\rm{s}}}(t)} \right] + \\ {\lambda _i}{N_i} + T(t) + {\rm{HD}}_{{\rm{r}}, i}^{\rm{G}}(t) - {\rm{HD}}_i^{\rm{s}} + {\varepsilon _{L, i}}(t) \end{array} $ | (2) |
式中,P、Φ分别为消电离层伪距观测值与载波相位观测值(单位m); Φi=λiφi,λi为Φi载波的波长(单位m),φi为Φi载波相位观测值(单位周); ρ为信号发射时刻卫星至接收机的几何距离(单位m); c为真空中的光速(单位m/s); dtG、dts分别为GPS接收机钟差、卫星钟差(单位s); T为对流层延迟(单位m); Ni为Φi载波的整周模糊度(单位周); hdr, iG和hdis分别为消电离层组合的接收机和卫星的伪距硬件延迟(单位m); HDr, iG和HDis分别为消电离层组合的接收机和卫星的相位硬件延迟(单位m); εP, i、εL, i分别为消电离层组合的伪距和相位观测值的其他噪声(单位m)。
PPP一般使用精密钟差产品修正卫星钟差,IGS精密卫星钟差产品中包含了消电离层组合卫星伪距硬件延迟的影响,即
| $ c{\widetilde {{\rm{d}}\mathit{t}}^{\rm{s}}} = c{\rm{d}}{t^{\rm{s}}} + {\rm{hd}}_{{\rm{IF}}}^{\rm{s}} $ | (3) |
接收机伪距硬件延迟与接收机钟差密不可分,因此其被接收机钟差吸收,即
| $ c{\widetilde {{\rm{d}}\mathit{t}}_{\rm{G}}} = c{\rm{d}}{t_{\rm{G}}} + {\rm{hd}}_{{\rm{r}}, {\rm{IF}}}^{\rm{G}} $ | (4) |
对于ΦIF而言,观测方程所包含的硬件延迟与模糊度不可分离,可以被相应的模糊度参数吸收,因此,
| $ {\lambda _{{\rm{IF}}}}{{\tilde N}_{{\rm{IF}}}} = {\lambda _{{\rm{IF}}}}{N_{{\rm{IF}}}} + {\rm{HD}}_{{\rm{r}}, {\rm{IF}}}^{\rm{G}} - {\rm{HD}}_{{\rm{IF}}}^{\rm{s}} - {\rm{hd}}_{{\rm{r}}, {\rm{IF}}}^{\rm{G}} + {\rm{hd}}_{{\rm{IF}}}^{\rm{s}} $ |
以GPS接收机钟差为基准,分别引入BDS、GLONASS、Galileo与GPS系统间偏差,以GPS和BDS为例,其定位模型为:
| $ \left\{ {\begin{array}{*{20}{c}} {{\rm{ }}P_{{\rm{IF}}}^{\rm{C}}(t) = {\rho ^{\rm{C}}}(t) + c{{\widetilde {{\rm{d}}\mathit{t}}}_{\rm{G}}}(t) + {\rm{ISB}}_{\rm{G}}^{\rm{C}} + {\mathit{T}^{\rm{C}}}(t) + \varepsilon _{p, {\rm{IF}}}^{\rm{C}}\left( t \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\\ {\Phi _{{\rm{IF}}}^{\rm{C}}(t) = {\rho ^{\rm{C}}}(t) + c{{\widetilde {{\rm{d}}\mathit{t}}}_{\rm{G}}}(t) + {\rm{ISB}}_{\rm{G}}^{\rm{C}} + \lambda _{{\rm{IF}}}^{\rm{C}}\tilde N_{{\rm{IF}}}^{\rm{C}}{\kern 1pt} + {T^{\rm{C}}}{\rm{(}}t{\rm{)}} + \varepsilon _{\mathit{L}, {\rm{IF}}}^{\rm{C}}(t)\;\;\;\;\;\;\;\;\;\;} \end{array}\;\;} \right. $ | (5) |
其中,
| $ \begin{array}{l} {\rm{ISB}}_{\rm{G}}^{\rm{C}} = c{\widetilde {{\rm{d}}\mathit{t}}_{\rm{G}}} - c{\widetilde {{\rm{d}}\mathit{t}}_{\rm{C}}} = c{\rm{d}}{t_{\rm{G}}} - c{\rm{d}}{t_{\rm{C}}} + \\ {\rm{hd}}_{{\rm{r}}, {\rm{IF}}}^{\rm{G}} - {\rm{hd}}_{{\rm{r}}, {\rm{IF}}}^{\rm{C}} = {\rm{TO}}_{\rm{r}}^{{\rm{G}}, {\rm{C}}} + {\rm{hd}}_{{\rm{r}}, {\rm{IF}}}^{\rm{G}} - {\rm{hd}}_{{\rm{r}}, {\rm{IF}}}^{\rm{C}} \end{array} $ |
式中,TOrG, C为GPS与BDS固有的时间差,其他系统的公式与式(5)类似。GLONASS采用频分多址的信号体制,与GPS之间存在伪距和载波的频间偏差,由于伪距观测值在PPP中权重很小,伪距频间偏差可忽略,载波频间偏差被接收机钟差和模糊度参数吸收[6]。
1.2 数据处理策略采用笔者编写的软件进行数据测试,选用序贯最小二乘[8]作为参数估计方法。消电离层组合消去一阶电离层延迟后,待估参数包括三维坐标、接收机钟差、天顶对流层湿分量延迟、卫星模糊度参数以及BDS、GLONASS、Galileo各系统与GPS系统之间的ISB。静态定位估计坐标时,采用常数估计的方法,对于对流层延迟参数,首先采用Saastmoinen模型加GMF投影函数求出对流层干分量延迟误差和部分湿分量延迟误差,然后对残余天顶对流层湿分量延迟采用分段常数估计的方法求解。模糊度参数在卫星未发生周跳时作为常数估计,发生周跳时重新初始化,初始化方差设为1.0×1010 m2; 接收机钟差采用高斯白噪声模型,噪声方差设为1.0×1010 m2; ISB采用不同估计策略,并对结果进行比较。
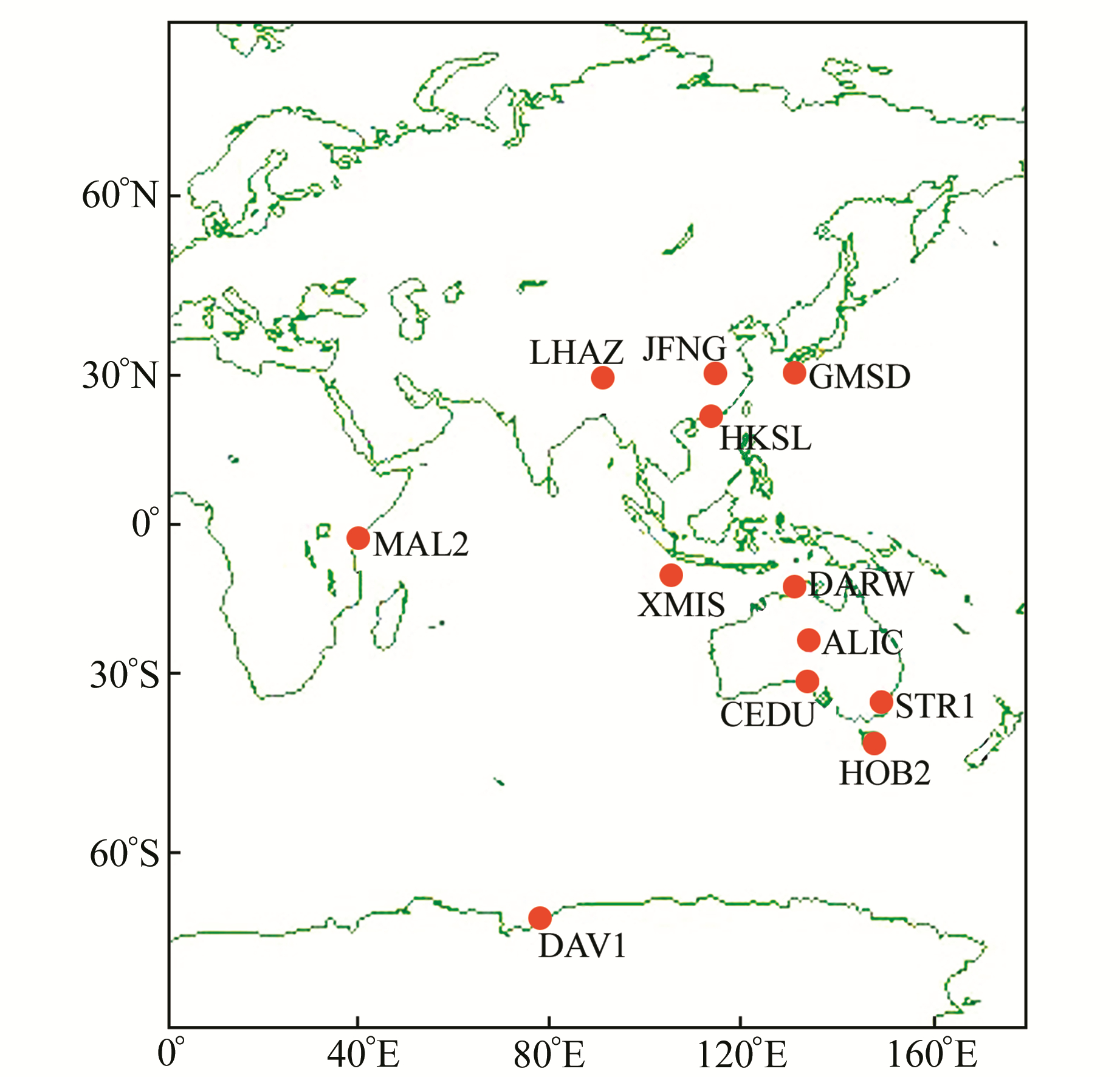
2 实验结果与分析选取MGEX网中分布在亚太地区可同时观测到GPS/BDS/GLONASS/Galileo卫星数据较多的12个测站(图 1)2018年doy 083~089的观测数据进行静态PPP实验,观测数据采样率为30 s。精密产品采用GFZ提供的30 s的精密卫星钟差产品和5 min的精密轨道产品。卫星端和接收机端的PCO与PCV使用IGS提供的igs14.atx文件改正,目前只有BDS的PCO改正参数,因此未对BDS的PCV进行改正。
|
图 1 测站分布 Fig. 1 Distribution of the stations |
实验中,将IGS发布的文件(*.snx)中的测站坐标当作参考值,将ISB按照高斯白噪声、20 min、30 min、1 h与2 h分段常数进行单天静态解,分别获得E、N、U方向上的坐标偏差以分析多系统融合PPP的收敛时间和定位精度,从而比较不同策略下的定位结果。本文收敛条件定义为:E、N、U方向均首次收敛到1 dm且后面连续20个历元均小于1 dm[9]。
2.1 收敛速度分析对12个测站1周的观测数据进行多系统融合静态精密单点定位解算,为比较不同求解策略下收敛时间的具体差异,统计各测站不同ISB求解策略多天收敛时间的平均值,见表 1(单位min,表中最后1行表示各测站的平均收敛时间)。从表 1可以看出,20 min分段常数估计ISB策略的收敛时间与高斯白噪声估计ISB的收敛时间是最短的,在20~30 min。为了更直观地反映各测站不同ISB求解策略收敛速度的差异,统计各测站不同天不同ISB求解策略下静态PPP的收敛时间(图 2)。由于篇幅限制,图 2只展示部分测站的结果,收敛时间截取至180 min。从图 2可以看出,PPP定位结果的收敛时间随着ISB求解弧段的增长而增加,尤其是ISB采取30 min以上常数弧段估计时,收敛时间的增加尤为明显。以doy 084的部分测站为例,E、N、U方向上的坐标偏差见图 3。从图 3可以看出不同ISB弧段求解策略下收敛时间的差异与收敛趋势,尤其在E方向上差异更加明显。因此,从收敛时间来看,高斯白噪声估计与20 min常数估计都可满足精密单点定位的需求,而且相比于其他求解策略,结果最优。
|
|
表 1 各测站不同ISB求解策略下静态PPP的平均收敛时间 Tab. 1 Average convergence time of static PPP per station under different ISB solution strategies |

|
图 2 部分测站doy 083~089不同ISB求解策略下静态PPP的收敛时间 Fig. 2 Covergence time of static PPP part of stations under different ISB solution strategies in doy 083-089 |

|
图 3 部分测站doy 084不同ISB求解策略下静态PPP的3个方向定位偏差 Fig. 3 Position bias in three directions of static PPP part of stations under different ISB solution strategies in doy 084 |
为分析不同ISB求解策略下多系统融合静态PPP的定位精度,统计各测站单天解收敛后定位偏差的RMS值。各测站不同ISB求解策略下的3个方向1周的RMS均值见表 2(单位cm,表中最后1组数据表示各测站在不同求解策略下3个方向的RMS平均值)。以doy 084为例,各测站在不同策略下3个方向的RMS值见图 4。结合图 3可以看出,在不同ISB参数求解策略下,E、N、U方向RMS值都有变化,具体为:
|
|
表 2 各测站doy 083~089不同ISB求解策略下静态PPP的平均RMS Tab. 2 Average RMS of static PPP per station under different ISB solution strategies in doy 083-089 |

|
图 4 部分测站doy 083~089不同ISB求解策略下静态PPP的3个方向的RMS平均值 Fig. 4 Average RMS in three directions of static PPP part of stations under different ISB solution strategies in doy 083-089 |
1) E方向RMS值变化最为明显,整体随ISB常数估计弧段的增长而增加,30 min内(包含30 min)常数估计策略下的RMS值优于2 cm,1 h与2 h常数估计策略下的RMS值在5 cm左右,特别是2 h常数估计策略下精度明显降低;
2) U方向RMS值整体随常数弧段的增长而增加,但变化不明显,整体上优于5 cm;
3) N方向RMS值变化最小且无规律,整体上优于1 cm。
从定位精度来看,采用高斯白噪声估计、20 min及30 min常数估计的ISB结果最优,静态PPP单天解定位精度E方向优于2 cm,N方向优于1 cm,U方向优于5 cm。PPP中模糊度由于保留浮点解,E方向相比于N方向定位精度普遍较低[10],这一点从定位精度的统计结果中可以明显看出。在不同策略下,E方向RMS值相较于N方向变化更加明显,这可能是由于ISB与模糊度参数有关[5]。
3 结语本文利用IGS提供的12个MGEX测站1周的观测数据和GFZ发布的精密轨道与钟差产品,通过设置ISB不同常数估计弧段策略进行多系统融合静态精密单点定位解算,比较不同ISB求解策略下的定位精度和收敛情况,得出以下结论:
1) 将ISB采用30 min以上常数估计策略后,收敛时间明显增加,E方向收敛趋势差异尤为明显。将ISB设置为高斯白噪声估计与20 min常数估计收敛速度最快,收敛时间约为30 min,符合当前精密单点定位结果的规律;
2)对ISB采用高斯白噪声估计、20 min及30 min常数估计时,静态PPP收敛后的定位精度最好,E方向优于2 cm,N方向优于1 cm,U方向优于5 cm。将ISB采用30 min以上常数估计策略后,E方向定位精度明显降低,N、U方向定位精度有所下降。
综上所述,从观测模型强度和保证结果稳定性与可靠性的角度考虑,对ISB采用20 min分段常数估计策略是最优的。
| [1] |
Torre A D, Caporali A. An Analysis of Intersystem Biases for Multi-GNSS Positioning[J]. GPS Solutions, 2015, 19(2): 297-307 DOI:10.1007/s10291-014-0388-2
(  0) 0) |
| [2] |
Li X X, Zhang X H, Ren X D, et al. Precise Positioning with Current Multi-Constellation Global Navigation Satellite Systems: GPS, GLONASS, Galileo and Beidou[J]. Scientific Reports, 2015, 5: 8 328 DOI:10.1038/srep08328
(  0) 0) |
| [3] |
Montenbruck O, Hauschild A, Hessels U. Characterization of GPS/GIOVE Sensor Stations in the CONGO Network[J]. GPS Solutions, 2011, 15(3): 193-205 DOI:10.1007/s10291-010-0182-8
(  0) 0) |
| [4] |
Tegedor J, Øvstedal O, Vigen E. Precise Orbit Determination and Point Positioning Using GPS, GLONASS, Galileo and Beidou[J]. Journal of Geodetic Science, 2014, 4(1): 65-73
(  0) 0) |
| [5] |
Chen J P, Zhang Y Z, Wang J G, et al. A Simplified and Unified Model of Multi-GNSS Precise Point Positioning[J]. Advances in Space Research, 2015, 55(1): 125-134 DOI:10.1016/j.asr.2014.10.002
(  0) 0) |
| [6] |
Cai C S, Gao Y. Modeling and Assessment of Combined GPS/GLONASS Precise Point Positioning[J]. GPS Solutions, 2013, 17(2): 223-236 DOI:10.1007/s10291-012-0273-9
(  0) 0) |
| [7] |
张守建, 王伟. 多系统融合精密单点定位性能分析[J]. 大地测量与地球动力学, 2017, 37(10): 1 065-1 069 (Zhang Shoujian, Wang Wei. Perfor-Mance Analysis on Multi-GNSS Precise Point Positioning[J]. Journal of Geodesy and Geodynamics, 2017, 37(10): 1 065-1 069)
(  0) 0) |
| [8] |
蔡昌盛. 多模GNSS融合精密单点定位理论与方法[M]. 北京: 科学出版社, 2017 (Cai Changsheng. Theory and Method of Multi-GNSS Integrated Precise Point Positioning[M]. Beijing: Science Press, 2017)
(  0) 0) |
| [9] |
Li P, Zhang X H. Integrating GPS and GLONASS to Accelerate Convergence and Initialization Times of Precise Point Positioning[J]. GPS Solutions, 2014, 18(3): 461-471 DOI:10.1007/s10291-013-0345-5
(  0) 0) |
| [10] |
Blewitt G. Carrier Phase Ambiguity Resolution for the Global Positioning System Applied to Geodetic Baselines up to 2 000 km[J]. Journal of Geophysical Research: Solid Earth, 1989, 94(B8): 10 187-10 203 DOI:10.1029/JB094iB08p10187
(  0) 0) |
2. University of Chinese Academy of Sciences, A19 Yuquan Road, Beijing 100049, China
 2019, Vol. 39
2019, Vol. 39

