为保障工程建筑的安全,变形监测越来越有必要。GNSS技术由于具有全天候、全天时、测站间无需通视等其他监测手段不具备的优点,已成为变形监测的重要手段之一。为满足变形监测的高精度要求,需要使用GNSS的载波观测量,这就需要考虑模糊度的问题。目前,运用较广的模糊度固定算法有最小二乘[1]、FARA[2]等,这些方法一般需要多个历元来进行模糊度的初始化,在解算过程中还需要不断进行探测、修复周跳,一旦信号失锁就需要再次初始化。但在实际的工程项目中,受环境等因素的影响与限制,信号失锁较为频繁,影响数据的实时和快速解算。单历元解算可实现数据的快速解算,但单个历元每观测到1颗卫星,就会增加待求的模糊度,再加上3个未知的坐标参数,待求参数多于观测值。因此,将传统的模糊度解算方法直接运用到单历元解算中会造成法方程的秩亏,但模糊度的单历元解算方法可以解决该问题。变形监测中监测站点的变形小、近似坐标已知等特点使单历元高精度解算成为可能。针对变形监测中的特殊情况,同时也为加快解算速度、减小计算量,很多学者提出并完善了适用于变形监测的单历元模糊度求解法,该方法利用近似坐标已有的条件,只需要1个历元的观测数据就可实现变形解算,不需要进行周跳的探测和修复。许多学者针对这种算法进行了大量的实验和研究[3-5],但这些研究工作大多基于单频数据进行解算,未能解释与双频观测数据之间的关系,而且只能处理短基线的数据。唐卫明等[6]在网络RTK基准站间对单历元模糊度解算进行研究。网络RTK基准站间的基线一般很长,可以借鉴到变形监测中,但其与变形监测的情形又有一些不同:网络RTK中的基准站坐标是已知的,变形监测中的监测站点只能获得近似坐标,所以模糊度解算方法有一些不同。本文通过借鉴网络RTK基准站间单历元模糊度解算算法,针对变形监测的特点,提出一种利用双频观测值的单历元数据处理方法。
1 单历元数据处理方法双差观测模型详见文献[7]。
1.1 已有的单历元解算算法已有的单历元模糊度解算算法大多认为观测数据在双差之后,电离层延迟、对流层延迟等误差都已经得到很好的削弱,可以直接利用初始坐标固定模糊度并进行坐标解算。如王新洲等[8]提出的DC算法,直接利用双差后的伪距观测值除以载波波长,再减去双差相位观测值来获取双差模糊度。由于该方法忽略了大气延迟误差对模糊度固定的影响,只适用于基线较短的情形,当基线较长时,仅通过双差很难消除大气延迟的影响,需要一种新的顾及残余大气延迟的模糊度固定方法。
1.2 中长基线的模糊度数学模型本文通过学习和借鉴已有的单历元模糊度固定算法及RTK参考站间的单历元模糊度解算算法,综合考虑观测数据精度, 结合变形监测中监测站点近似坐标已知、变形小等特点,利用电离层延迟与波段的频率平方成反比等特性,实现单历元的数据处理。
由双差模型[7]可得双频双差方程为:
| $ \left. {\begin{array}{*{20}{c}} \begin{array}{l} {\lambda _1}\nabla \Delta {\varphi _1}(t) = \nabla \Delta {\rho ^j}(t) - {\lambda _1}\nabla \Delta {N_1}\left( {{t_0}} \right) + \\ \left( {\frac{{\nabla \Delta I}}{{f_1^2}} + \nabla \Delta {\delta _{{\rm{tro}}{{\rm{p}}_1}}}} \right) + \nabla \Delta {\varepsilon _1} \end{array}\\ \begin{array}{l} {\lambda _2}\nabla \Delta {\varphi _2}(t) = \nabla \Delta {\rho ^j}(t) - {\lambda _2}\nabla \Delta {N_2}\left( {{t_0}} \right) + \\ \left( {\frac{{\nabla \Delta I}}{{f_2^2}} + \nabla \Delta {\delta _{{\rm{tro}}{{\rm{p}}_2}}}} \right) + \nabla \Delta {\varepsilon _2} \end{array} \end{array}} \right\} $ | (1) |
式中,
| $ {\nabla \Delta {N_1} = \frac{{{\lambda _1}}}{{{\lambda _2}}}\nabla \Delta {N_2} + b} $ | (2) |
其中,
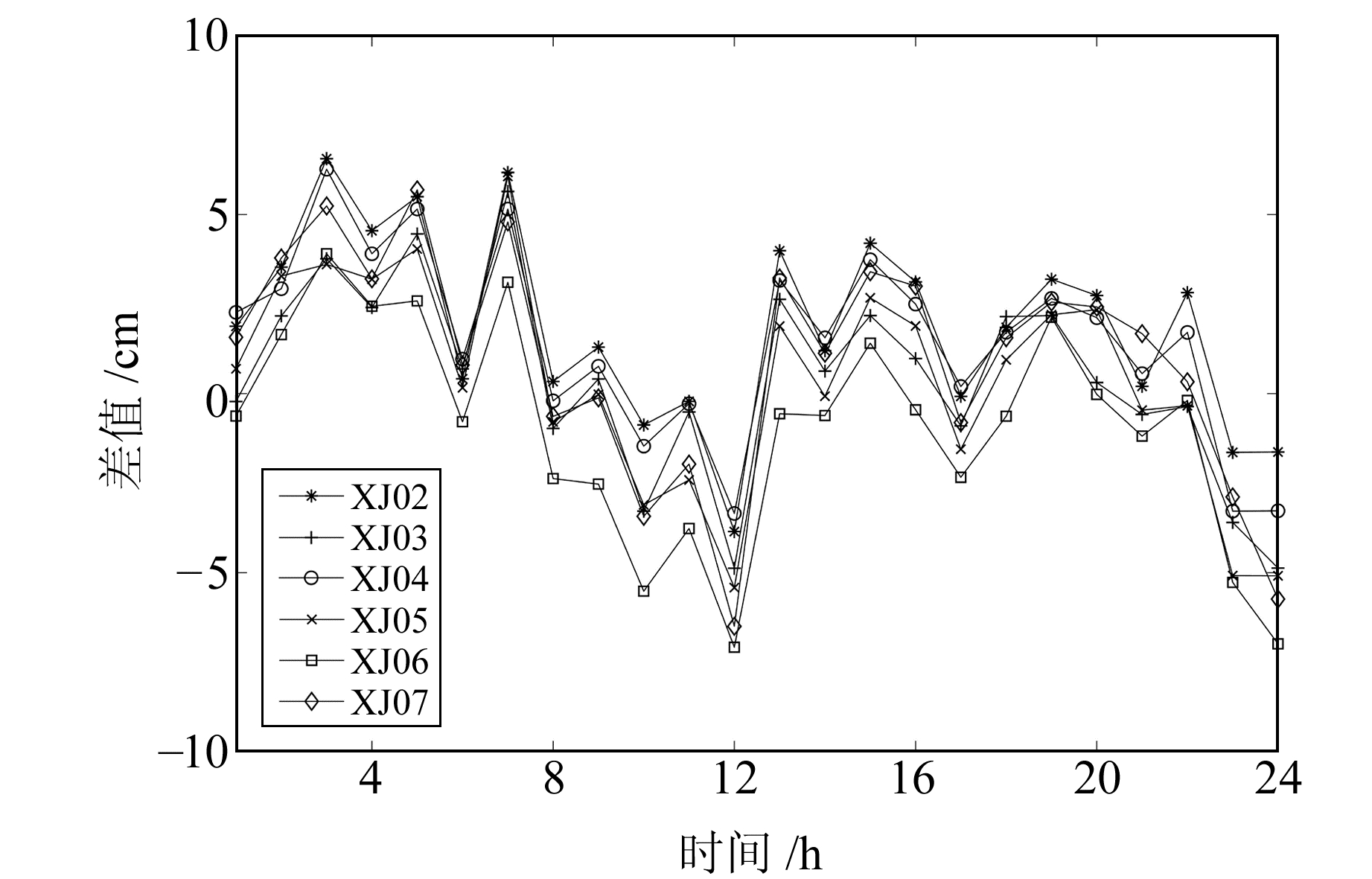
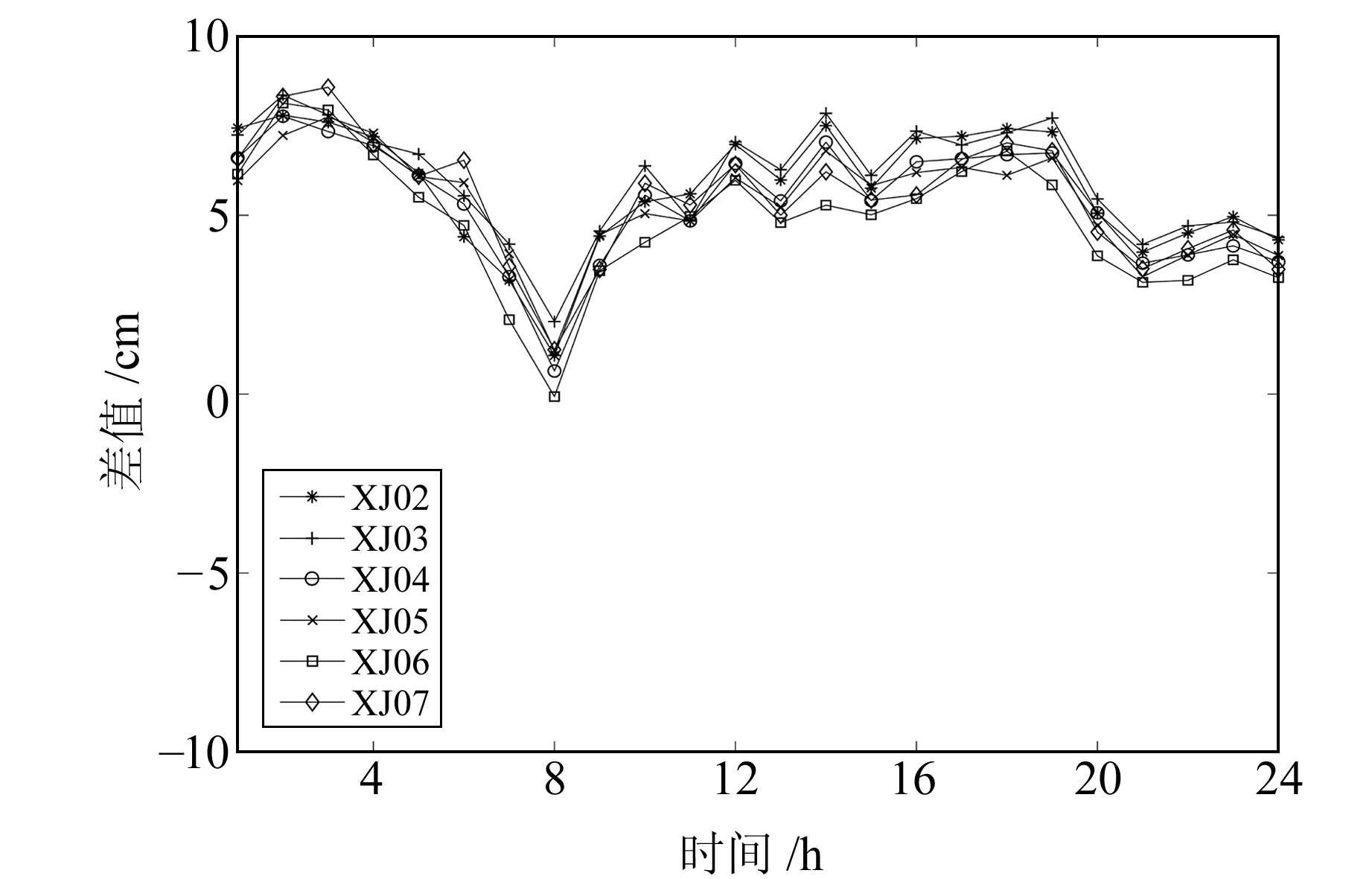
图 1、2分别为2017年年积日1和200的Saastamoinen模型与Bernese软件最终固定的对流层之间的差值。由图可知,Saastamoinen模型的精度可以达到0.1 m。为提高算法的适用性,假设监测站点的初始坐标精度为0.05 m,对流层延迟模型精度为0.2 m。
|
图 1 对流层模型精度评估(年积日为1) Fig. 1 Evaluation of tropospheric model accuracy(doy=1) |
|
图 2 对流层模型精度评估(年积日为200) Fig. 2 Evaluation of tropospheric model accuracy(doy =200) |
根据误差传播定律:
| $ \begin{array}{*{20}{l}} {{\varepsilon _{\nabla \Delta \rho }} = 2{\varepsilon _p} = 0.10{\rm{m}}}\\ {{\varepsilon _{\nabla {\Delta _{{\rm{tro}}{{\rm{p}}_1}}}}} = {\varepsilon _{\nabla \Delta {\delta _{{\rm{tro}}{{\rm{p}}_2}}}}} = 0.2{\rm{m}}}\\ {{\varepsilon _b} = 1.1547} \end{array} $ | (3) |
令
| $ \left|\nabla \Delta N_{1}-\frac{\lambda_{1}}{\lambda_{2}} \nabla \Delta N_{2}-b\right| \leqslant 1.1547 $ | (4) |
由式(4)可知,模糊度线性组合构成了一个误差带,在利用消电离层组合求出模糊度后可以在这个区间搜索固定模糊度,这样就能有效解决传统方法在单历元求解模糊度遇到的秩亏问题,缩小模糊度搜索空间。
1.3 搜索固定模糊度当模糊度固定之后,还有3个坐标参数、2个对流层延迟残差参数未知,因此,至少需要6颗卫星进行双差处理方可实现参数求解。为了增加冗余观测,本文选择7颗卫星进行解算。首先,通过截止高度角筛选出符合要求的卫星; 然后,利用PDOP值最小的原则挑选出7颗卫星,并选取高度角最大的卫星作为参考卫星来组成双差方程。
通过分析式(2)不难发现,双频模糊度之间有一定的周期,也就是
单历元变形解算主要流程为:
1) 读取数据,利用Saastamoinen模型改正对流层延迟;
2) 组成无电离层组合,利用直接取整法获得模糊度的初始值;
3) 利用单历元算法搜索固定模糊度;
4) 利用Ratio值检验模糊度固定的可靠性,当Ratio小于3时,跳过该历元; 当Ratio大于3时,更新监测站点坐标及对流层延迟,继续下一个历元。
2 实验结果与分析 2.1 实验数据GPS观测数据来源于山西大同的变形监测站点,分别选择3.2 km、15.4 km及35.2 km等3条不同长度的基线2017-02-01的观测数据,接收机为安科双频监测型接收机,采样间隔为30 s。
2.2 实验结果利用本文方法对3.2 km基线进行解算,结果见图 3,并统计最终计算出的L1波段双差模糊度的固定解与浮点解之间的差值,结果见图 4。

|
图 3 3.2 km基线解算结果 Fig. 3 Results of 3.2 km baseline |
|
图 4 模糊度整数值与浮点值之差 Fig. 4 Difference between fixed value and float value |
从图 3可以看出,在基线较短的情况下,利用单历元算法可以很好地实现高精度的解算。同时,通过图 4可以发现,最终固定的双差模糊度与直接计算出的浮点值之间差值大多都在0.5周以内。也就是说,在基线较短的情况下,通过双差可以很好地消除电离层延迟、对流层延迟及其他相关误差,因此,可以直接利用取整的方法实现模糊度的固定。
对15.4 km基线的坐标进行解算并计算出L1波段双差模糊度的固定解与浮点解之间的差值,得到图 5、6。
|
图 5 15.4 km基线解算结果 Fig. 5 Results of 15.4 km baseline |
|
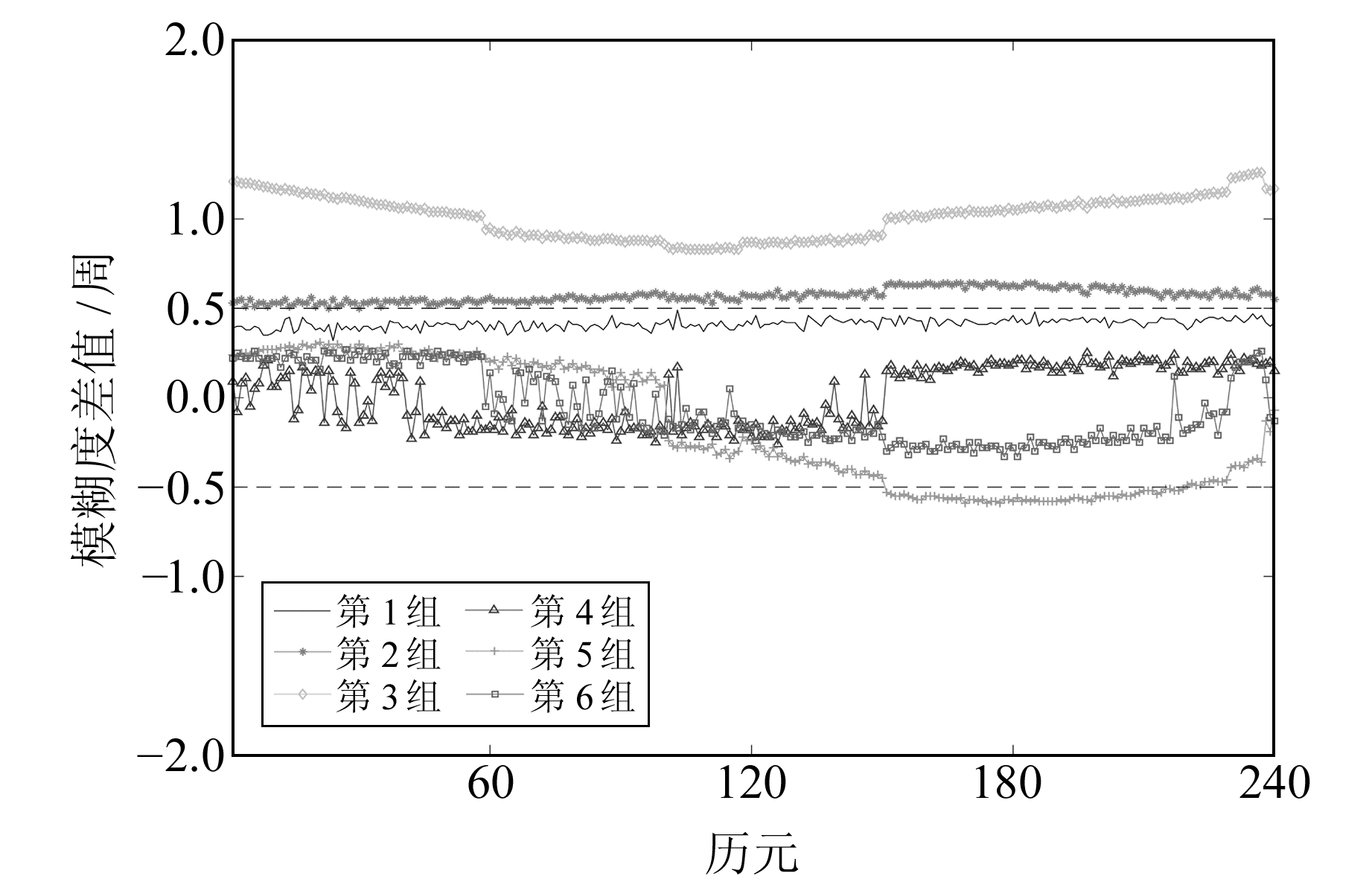
图 6 模糊度整数值与浮点值之差 Fig. 6 Difference between fixed value and float value |
由图 5可知,当基线较长时,利用本文的单历元算法也可以实现解算。由图 6可知,最后固定的双差模糊度与直接求解出的浮点值有一定的差距,有一部分大于0.5周,甚至有些会大于1.5周。表明当基线变长时,仅通过双差不能将对流层延迟残差缩小到可以忽略的程度。因此,当基线变长时,传统的单历元算法由于没有考虑电离层及对流层延迟而不再适用,本文算法在搜索固定模糊度中利用了双频观测信息,并顾及了对流层残差的影响,在解算中利用2个参数来估计对流层延迟残差,可以较好地估计出对流层延迟,从而实现模糊度的固定。
为充分验证本文方法的适用性,将基线长度延长到35.2 km,同样统计解算结果及模糊度固定后的数值与浮点值之间的差值,得到图 7、8和表 1。
|
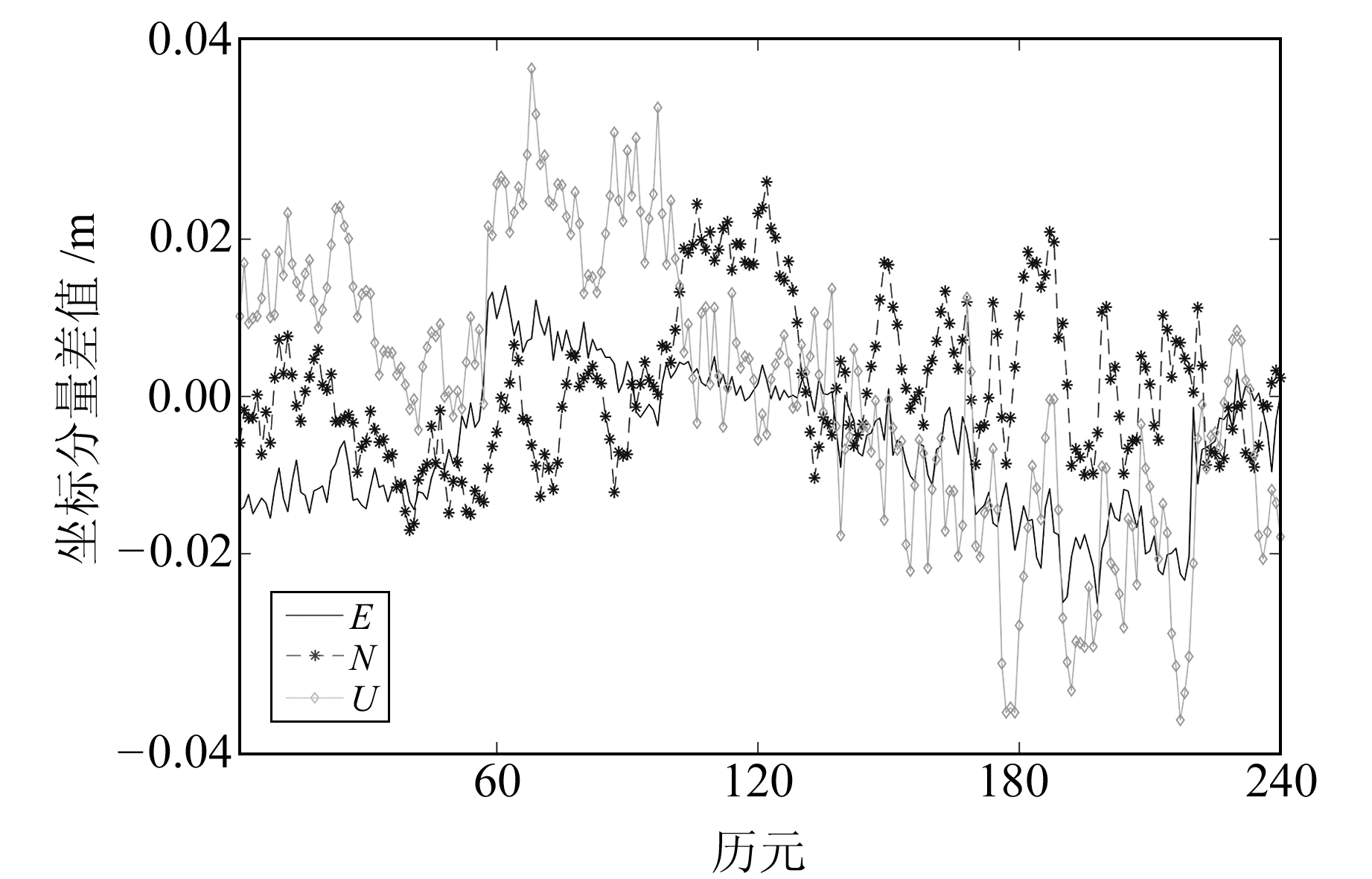
图 7 35.2 km基线解算结果 Fig. 7 Results of 35.2 km baseline |
|
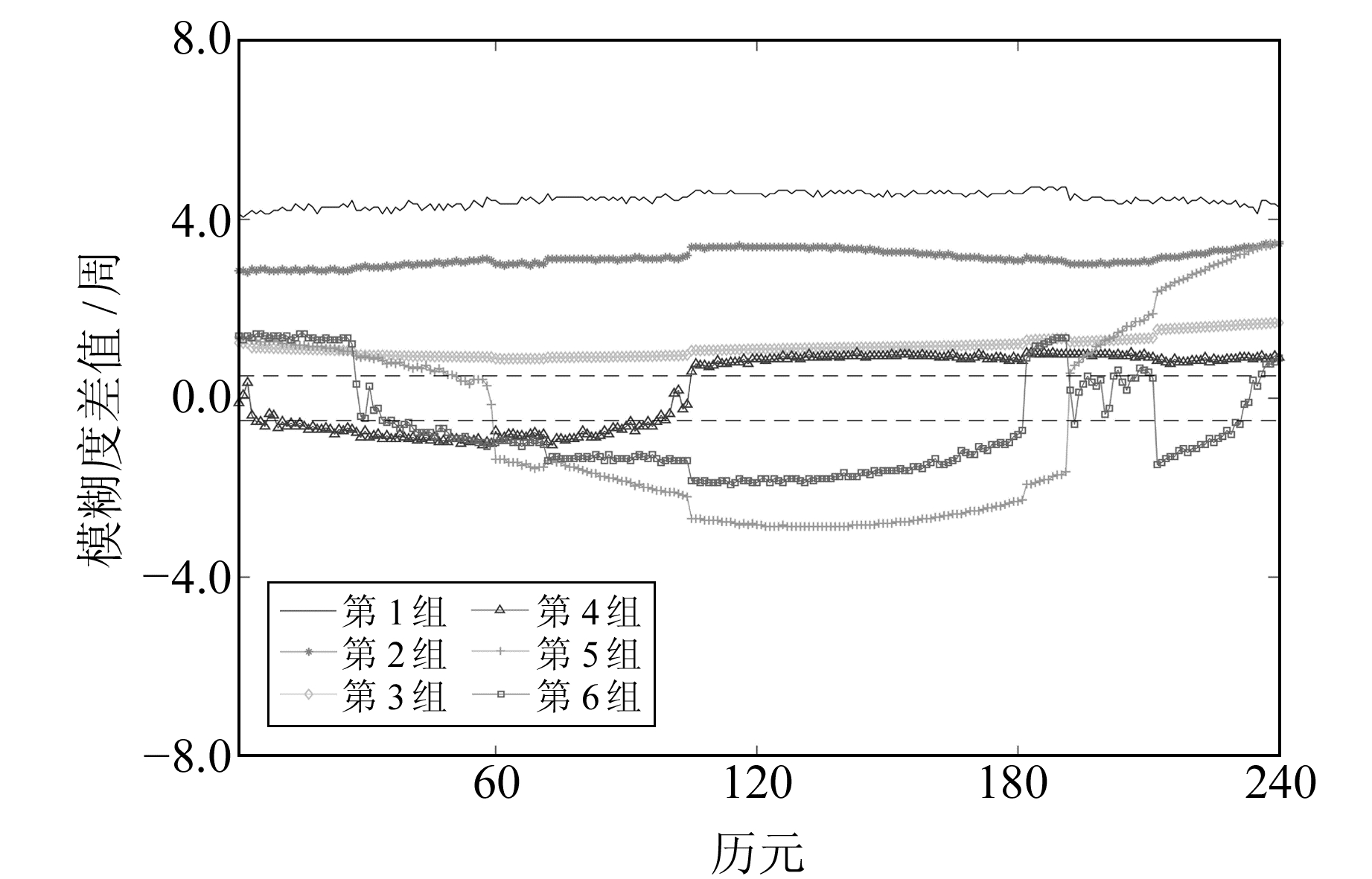
图 8 模糊度整数值与浮点值之差 Fig. 8 Difference between fixed value and float value |
|
|
表 1 解算结果统计 Tab. 1 Statistics of the solution results |
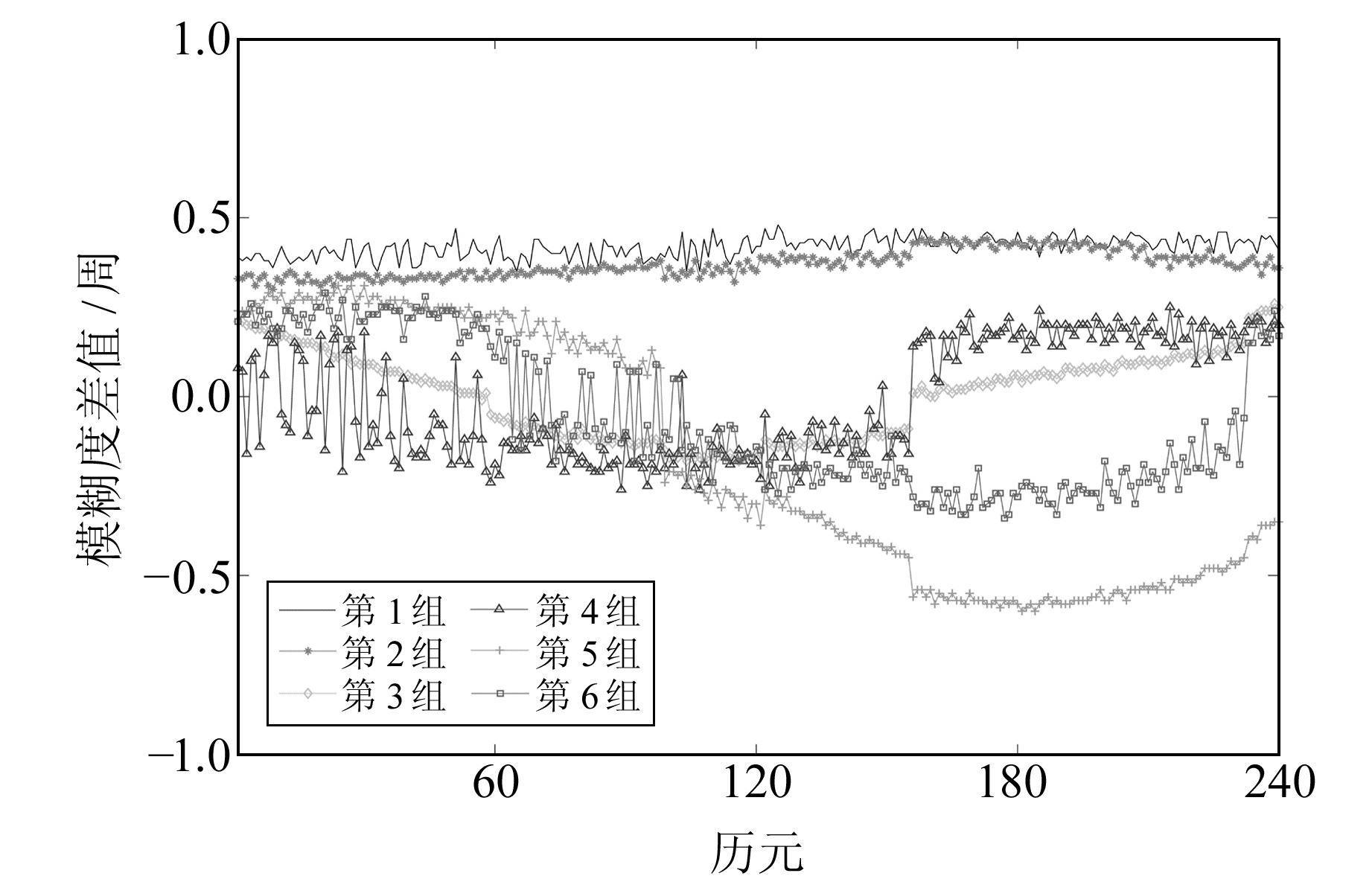
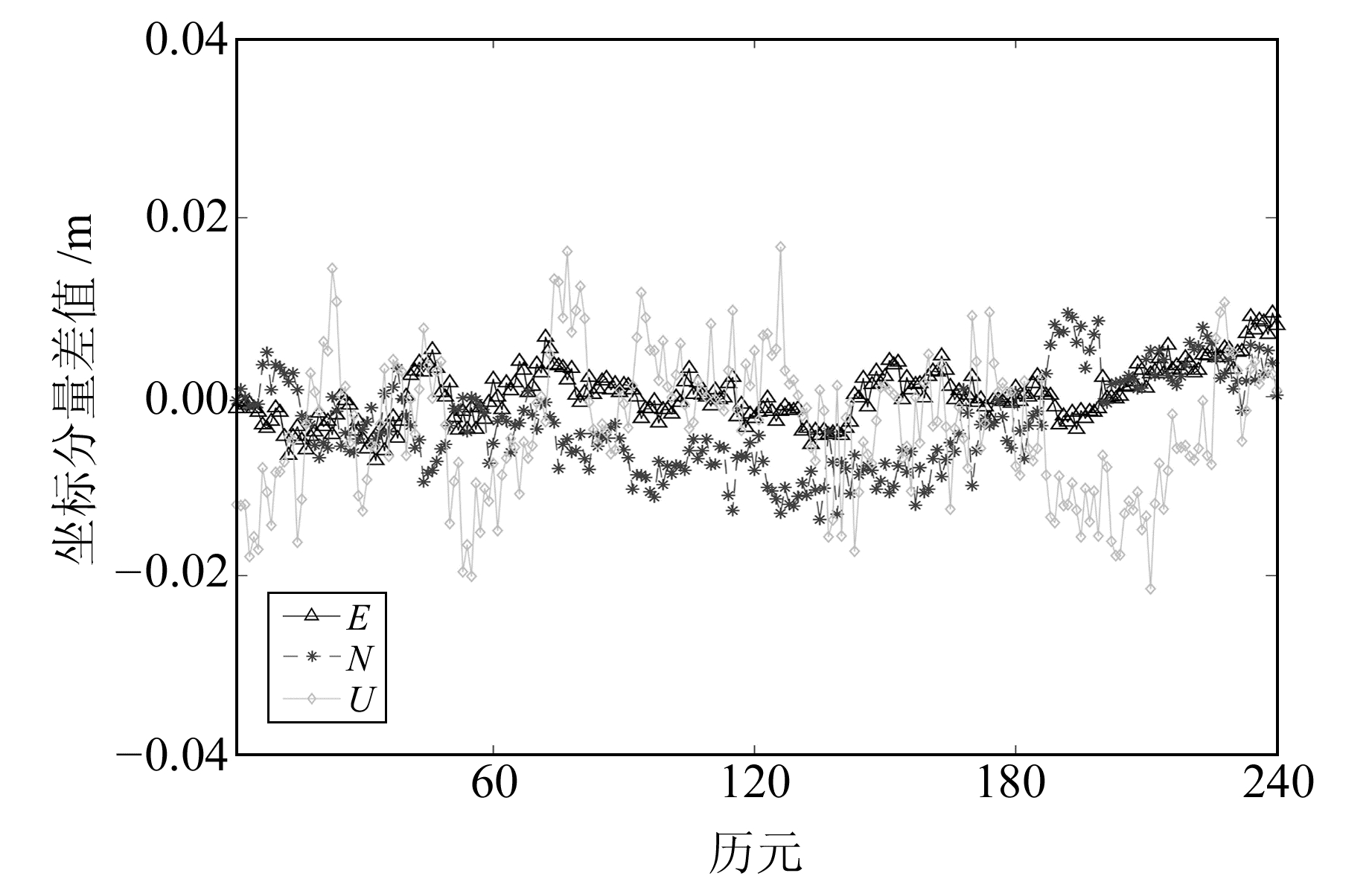
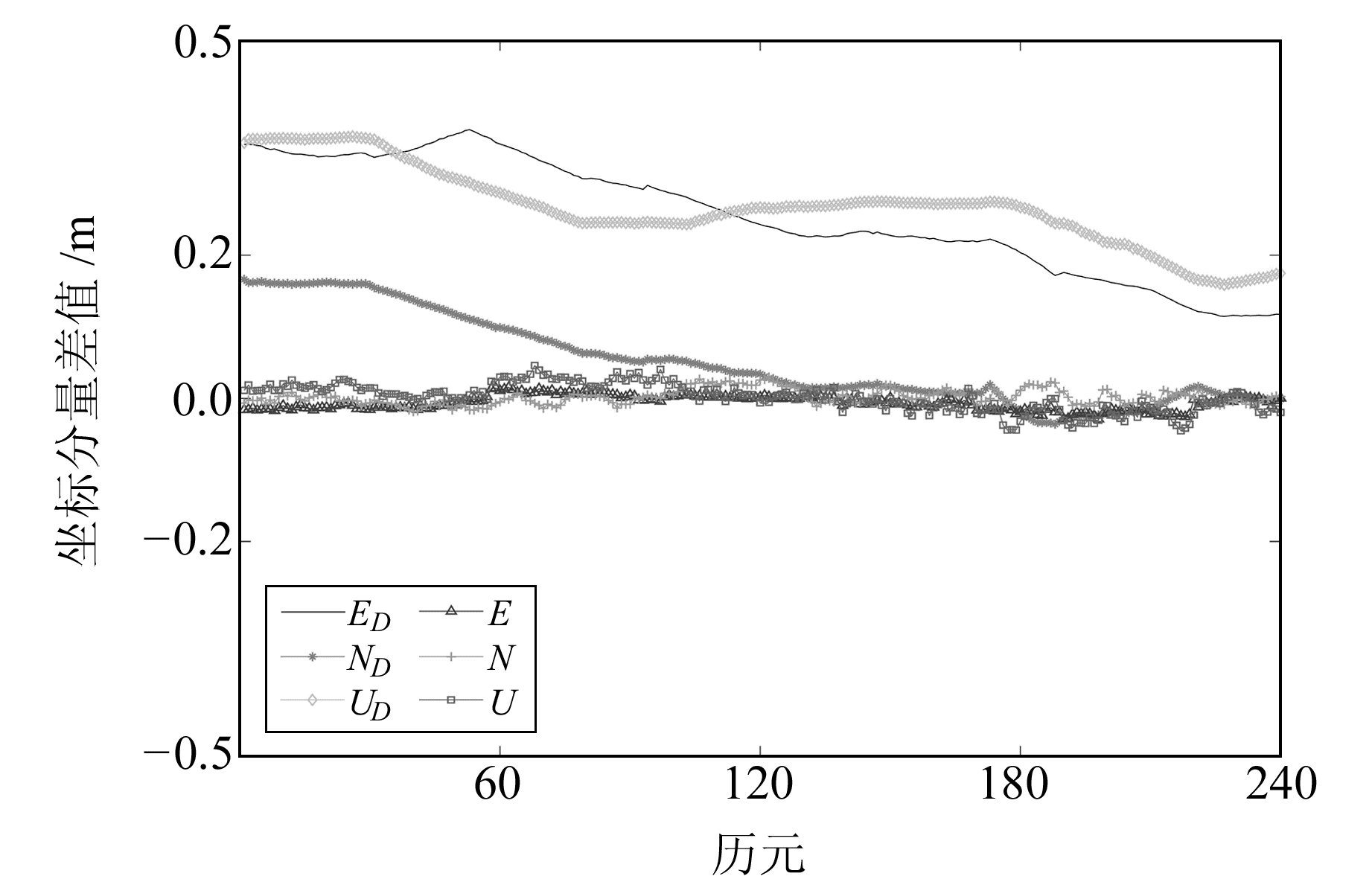
由图 8可知,当基线较长时,双差后的对流层延迟仍存在较大误差,对模糊度的固定产生较大影响。此时,不能简单地认为双差后的大气误差可以基本消除,对模糊度直接取整已经不能实现模糊度的正确固定。而本文提出的单历元算法可以较好地实现模糊度的固定,在240个历元中成功固定了236个。为分析对流层延迟对模糊度固定的影响,将直接取整的解算结果与本文解算结果进行对比,结果见图 9。图中,ED、ND、UD为直接取整的单历元方法的解算结果,E、N、U为本文方法的解算结果。
|
图 9 35.2 km基线2方法对比 Fig. 9 Comparison of the two methods of 35.2 km |
由图 9可知,当基线变长时,对直接去双差后的模糊度进行取整不能正确固定模糊度,也就不能实现模糊度的固定。考虑大气误差后,用本文方法加以改正或避免,可得到较好的解算结果。
2.3 结果分析当基线较短时,直接利用双差处理残余的大气延迟对模糊度固定的影响较小,可以利用直接取整的方法来固定。但当基线慢慢变长时,只通过双差很难消除大气延迟的影响,双差后获得的模糊度中掺杂着大气延迟误差,不能简单地通过取整来固定模糊度。从图 4、6中可以看出,最后固定的双差模糊度与直接双差得到的模糊度之间的差值不一定都小于0.5,有的甚至相差几个模糊度。用本文方法与直接取整的单历元算法对35.2 km的长基线进行解算。可以看出,当基线变长后,传统的单历元算法不能很好地实现模糊度的固定; 而当充分考虑大气误差后,给定模糊度搜索空间,并利用参数估计对流层延迟时,可以实现在中长基线下的单历元数据解算。
3 结语GPS技术具有操作简单、数据可靠、自动化程度高、精度高等优势,在变形监测中得到广泛应用,但在进行数据解算时,存在计算量大且容易受周跳影响等问题。对此,可利用单历元算法解决。传统的单历元算法由于没有考虑到双差后的大气延迟等问题,并不适用基线较长的情况。因此,本文利用GPS双频观测值及变形监测的特性,考虑电离层延迟,分析双频模糊度之间的约束关系,提出一种新的单历元模糊度固定方法。具体为:1)利用双频电离层延迟之间的相关性,得到2个波段双差模糊度之间的约束关系,并利用监测站点的近似坐标及参考站坐标确定模糊度的初始值; 2)根据监测站点的近似坐标精度和大气延迟误差确定模糊度搜索空间; 3)利用无电离层组合进行模糊度搜索与固定,并通过实验验证该算法的可用性。实验结果表明,当基线较短时,解算精度一般优于1 cm; 当基线长度达到35 km时,在240个历元中可以成功固定236个模糊度,解算精度保持在3 cm左右,这可能是由于受观测噪声等因素的影响,可以尝试通过滤波或长时间观测取均值等方法来消除。同时,在未能成功固定的4个历元中,有2个获得了正确的模糊度组合却未能通过Ratio值检验,在今后的实验中还需改进对模糊度可靠性的检验方法。
| [1] |
Jonge D P, Tiberius C. The LAMBDA Method for Integer Ambiguity Estimation: Implementation Aspects[M]. Delft: Delft University of Technology, 1996
(  0) 0) |
| [2] |
Frei E. Rapid Static Positioning Based on the Fast Ambiguity Resolution Approach FARA: Theory and First Results[J]. Manuscripta Geodaetica, 1990, 15(6): 325-356
(  0) 0) |
| [3] |
陈永奇, Lutes J. 单历元GPS变形监测数据处理方法的研究[J]. 武汉测绘科技大学学报, 1998, 23(4): 324-328 (Chen Yongqi, Lutes J. Development of the Nethadology for Single Epoch GPS Deformation Monitoring[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1998, 23(4): 324-328)
(  0) 0) |
| [4] |
戴吾蛟, 朱建军, 丁晓利, 等. GPS建筑物振动变形监测中的单历元算法研究[J]. 武汉大学学报:信息科学版, 2007, 32(3): 234-237 (Dai Wujiao, Zhu Jianjun, Ding Xiaoli, et al. Single Epoch Ambiguity Resolution in Structure Monitoring Using GPS[J]. Geomatics and Information Science of Wuhan University, 2007, 32(3): 234-237)
(  0) 0) |
| [5] |
戴吾蛟. GPS精密动态变形监测的数据处理理论与方法研究[D].长沙: 中南大学, 2007 (Dai Wujiao.The Data Processing Theory and Method of GPS Precision Dynamic Deformation Monitoring[D]. Changsha: Central South University, 2007) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1190458
(  0) 0) |
| [6] |
唐卫明, 刘经南, 施闯, 等. 三步法确定网络RTK基准站双差模糊度[J]. 武汉大学学报:信息科学版, 2007, 32(4): 305-308 (Tang Weiming, Liu Jingnan, Shi Chuang, et al. Three Steps to Determine Double Difference Ambiguities Resolution of Network RTK Reference Station[J]. Geomatics and Information Science of Wuhan University, 2007, 32(4): 305-308)
(  0) 0) |
| [7] |
温亚鑫, 戴吾蛟.一种中长基线变形监测网的单历元模糊度解算算法[C].第9届中国卫星导航学术年会, 哈尔滨, 2018 (Wen Yaxin, Dai Wujiao. A Single Epoch Ambiguity Resolution Algorithm for Medium and Long Baseline Deformation Monitoring Netword[C].The 9th China Satellite Navigation Conference, Harbin, 2018)
(  0) 0) |
| [8] |
王新洲, 花向红, 邱蕾. GPS变形监测中整周模糊度解算的新方法[J]. 武汉大学学报:信息科学版, 2007, 32(1): 24-26 (Wang Xinzhou, Hua Xianghong, Qiu Lei. A New Method for Integer Ambiguity Resolution in GPS Deformation Monitoring[J]. Geomatics and Information Science of Wuhan University, 2007, 32(1): 24-26)
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39

