2. 安徽理工大学测绘学院,安徽省淮南市舜耕中路168号,232001;
3. 东南大学仪器科学与工程学院,南京市四牌楼2号,210096;
4. 金寨县国土资源局,安徽省六安市金寨县,237300
在GPS/BDS短基线解算时,测站间的大气空间相关性较强,相关误差可通过双差削弱,整周模糊度也较易实现快速的固定[1]。而在GPS/BDS中长基线解算时,大气延迟将成为主要的误差源,对模糊度固定的影响较为明显。相关学者对此问题进行了大量研究。李博峰等[2]先用2个固定的宽巷模糊度计算电离层延迟,再用电离层延迟辅助解算双差宽巷模糊度,实现中长基线的解算; 祝会忠等[3]由观测方程方差矩阵对宽巷模糊度进行分组,并结合双差宽巷模糊度与载波相位观测值准确解算出L1/L2双差整周模糊度; 黄令勇等[4]对比分析TCAR算法改进后的电离层改正法与无几何无电离层组合法解算北斗三频长基线模糊度的效果。
本文先进行数据预处理,在宽巷模糊度得到固定后,构建出无电离层组合双差观测值,由Kalman滤波算法实现L1、B1基频模糊度浮点解的解算,使用LAMBDA算法实现模糊度的固定。以在安徽理工大学三维移动变形平台采集的实测数据为例,对GPS、BDS、GPS/BDS模式下的46.6 km、20.8 km、63.4 km三维移动变形中长基线进行解算,对比分析固定率、正确率、RMS值、中误差等指标,得出部分有益结论。
1 GPS、BDS系统时空基准的统一GPST与BDT的转换关系可表示为:
| $ \left\{ {\begin{array}{*{20}{c}} {{\rm{BD}}{{\rm{T}}_{周数}} = {\rm{GPS}}{{\rm{T}}_{周数}} + {\rm{1356}}}\\ {{\rm{BD}}{{\rm{T}}_{周内秒数}} = {\rm{GPS}}{{\rm{T}}_{周内秒数}} + {\rm{14}}\;\;\;} \end{array}} \right. $ | (1) |
GPS系统采用的是WGS-84坐标系统,BDS系统采用的是2000中国大地坐标系统(CGCS2000),WGS84与CGCS2000的坐标系统间虽然存在一定的差异,但是两者间的坐标原点一致,长半轴、引力常数、扁率、自转角速度等参数较为接近。对于相对定位而言,可选择各系统的参考卫星来削弱相对偏差的影响,不进行坐标系统间的转换,直接将其视为统一坐标系统使用即可[5-6]。
2 GPS/BDS组合中长基线解算策略高精度的中长基线解算时,一般采用无电离层组合观测值模型。由于无电离层组合观测值的组合系数为实数,使得整周模糊度失去整数特性,无法实现直接固定,进而影响定位精度[7-8]。因此,在整周模糊度固定时,先由多个历元平滑来实现宽巷模糊度的固定,并将固定的宽巷模糊度代入无电离层组合观测值中,由Kalman滤波算法计算出基频模糊度的浮点解,使用LAMBDA算法实现基频模糊度的固定[9-10]。
2.1 GPS/BDS组合宽巷模糊度的固定若测站m、n同时观测到卫星j、k,以k为参考卫星,站间星间双差宽巷方程为:
| $ \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {\lambda _{\rm{w}}}\varphi _{mn, {\rm{w}}}^{jk} = \rho _{mn}^{jk} + T_{mn}^{jk} + \frac{{f_1^j}}{{f_2^j}}I_{mn, 1}^{jk} + \\ \;\;\;\;\lambda _{\rm{w}}^jN_{mn, {\rm{w}}}^{jk} + \left( {\lambda _{\rm{w}}^j - \lambda _{\rm{w}}^k} \right)N_{mn, {\rm{w}}}^k + \varepsilon _{mn, {\rm{w}}}^{jk} \end{array}\\ {P_{mn, {\rm{w}}}^{jk} = \rho _{mn}^{jk} + T_{mn}^{jk} + \frac{{f_1^j}}{{f_2^j}}I_{mn, 1}^{jk} + r_{mn, {\rm{w}}}^{jk}\;\;\;\;} \end{array}} \right. $ | (2) |
式中,λw为宽巷波长,φ为载波相位观测值,P为伪距观测值,ρ为接收机与卫星间的距离,T为对流层延迟,fi为观测值频率,I为电离层延迟,Nw为宽巷模糊度,ε为载波观测值噪声,r为伪距观测值噪声。由式(2)消除几何相关项、电离层延迟、对流层延迟项,得:
| $ N_{mn, {\rm{w}}}^{jk} = \left( {{\lambda _{\rm{w}}}\varphi _{mn, {\rm{w}}}^{jk} - P_{mn, {\rm{w}}}^{jk}} \right)/\lambda _{\rm{w}}^j $ | (3) |
由于宽巷模糊度的波长较长,可对宽巷模糊度进行滤波处理:
| $ \begin{array}{l} N'\left( i \right) = \\ N'\left( {i - 1} \right) + \frac{1}{i}\left( {N\left( i \right) - N'\left( {i - 1} \right)} \right) \end{array} $ | (4) |
式中,N(i)为第i个历元的宽巷模糊度,N′(i)为第i个历元滤波后的宽巷模糊度。
2.2 GPS/BDS组合基频模糊度的固定在确定双差模糊度的值后,将固定后的宽巷模糊度代入无电离层组合观测值中:
| $ \begin{array}{l} \Delta \nabla {\varphi _{{\rm{IF}}}} = {f_1}/\left( {{f_1} + {f_2}} \right)\Delta \nabla {\varphi _1} - {f_1}/\left( {{f_1} + {f_2}} \right) \cdot \\ \Delta \nabla {\varphi _2} = 1/{\lambda _{\rm{w}}}(\Delta \nabla \rho + \Delta \nabla T) + {f_1}/\left( {{f_1} + {f_2}} \right) \cdot \\ \Delta \nabla {N_1} - {f_1}/\left( {{f_1} + {f_2}} \right)\Delta \nabla {N_2} \end{array} $ | (5) |
式中,Δ
| $ \begin{array}{l} \Delta \nabla {N_1}{\rm{ = }}\frac{1}{{{\lambda _n}}}\left( {{\lambda _n}\Delta \nabla {\varphi _{\rm{I}}}_{\rm{F}} - \Delta \nabla \rho - \Delta \nabla T} \right) - \\ \;\;\;\;\;\;\;\;\;\;{f_2}/\left( {{f_1} - {f_2}} \right)\Delta \nabla {N_{\rm{w}}} \end{array} $ | (6) |
式中,Δ
由于基站的卫地距可计算得到,轨道和多路径的影响可有效削弱,此时Δ
| $ \begin{array}{l} \Delta \nabla T_{mn}^{jk}{\rm{ = }}{\left( {\Delta \nabla T_{mn}^{jk}} \right)_{{\rm{sasstamoinen}}}} + {\rm{ZW}}{{\rm{D}}_m}\left( {{\rm{MF}}\left( {e_m^k} \right) - } \right.\\ \left. {{\rm{MF}}\left( {e_m^j} \right)} \right) - {\rm{ZW}}{{\rm{D}}_n}\left( {{\rm{MF}}\left( {e_n^k} \right) - {\rm{MF}}\left( {e_n^j} \right)} \right) \end{array} $ | (7) |
由于基线的长度相对于卫星到接收机的距离较短,MF、ZWD基本相同,用相对天顶对流层延迟RZWD代替基线两端测站的天顶湿分量,近似认为emj≈enj、emk≈enk,则:
| $ \Delta \nabla T_{mn}^{jk}{\rm{ = }}{\left( {\Delta \nabla T_{mn}^{jk}} \right)_{_{{\rm{sasstamoinen}}}}} + {\rm{RZW}}{{\rm{D}}_{mn}}\left( {{\rm{MF}}\left( {e_{mn}^k} \right) - {\rm{MF}}\left( {e_{mn}^j} \right)} \right) $ | (8) |
综合相位观测值与伪距观测值,组成的双差观测方程可表示为:
| $ \left( \begin{matrix} \underset{n\times 1}{\mathop{{\mathit{\boldsymbol{L}}_{L}}\left( t \right)}}\, \\ \underset{n\times 1}{\mathop{{\mathit{\boldsymbol{L}}_{p}}\left( t \right)}}\, \\ \end{matrix} \right)=\left( \begin{matrix} \underset{n\times 1}{\mathop{\mathit{\boldsymbol{A}}\left( t \right)}}\, & \underset{n\times n}{\mathop{\mathrm{B}\left( t \right)}}\, \\ \underset{n\times 1}{\mathop{\mathit{\boldsymbol{A}}\left( t \right)}}\, & \underset{n\times n}{\mathop{\mathit{\boldsymbol{O}}}}\, \\ \end{matrix} \right)\underset{\left( n+1 \right)\times 1}{\mathop{\mathit{\boldsymbol{X}}}}\, +\mathit{\boldsymbol{\xi}} $ | (9) |
其中,
| $ {\mathit{\boldsymbol{L}}_L}\left( t \right) = \left( {\begin{array}{*{20}{c}} {{\lambda _{\rm{w}}}\Delta \nabla \left( {{\varphi _{{\rm{IF}}}}} \right)_{pq}^{1k} - \Delta \nabla \rho _{pq}^{1k} - {{\left( {\Delta \nabla T_{pq}^{1k}} \right)}_0} - \frac{{{f_2}}}{{{f_1} - {f_2}}} \cdot \frac{{17C}}{{77{f_1} - 60{f_2}}} \cdot \Delta \nabla \left( {{N_{\rm{w}}}} \right)_{pq}^{1k}}\\ \vdots \\ {{\lambda _{\rm{w}}}\Delta \nabla \left( {{\varphi _{{\rm{IF}}}}} \right)_{pq}^{nk} - \Delta \nabla \rho _{pq}^{nk} - {{\left( {\Delta \nabla T_{pq}^{nk}} \right)}_0} - \frac{{{f_2}}}{{{f_1} - {f_2}}} \cdot \frac{{17C}}{{77{f_1} - 60{f_2}}} \cdot \Delta \nabla \left( {{N_w}} \right)_{pq}^{nk}} \end{array}} \right), $ |
| $ {\mathit{\boldsymbol{L}}_p}\left( t \right) = \left( {\begin{array}{*{20}{c}} {{\lambda _{\rm{w}}}\Delta \nabla \left( {{\varphi _{{\rm{IF}}}}} \right)_{pq}^{1k} - \Delta \nabla \rho _{pq}^{1k} - {{\left( {\Delta \nabla T_{pq}^{1k}} \right)}_0}}\\ \vdots \\ {{\lambda _{\rm{w}}}\Delta \nabla \left( {{\varphi _{{\rm{IF}}}}} \right)_{pq}^{nk} - \Delta \nabla \rho _{pq}^{nk} - {{\left( {\Delta \nabla T_{pq}^{nk}} \right)}_0}} \end{array}} \right), $ |
| $ \underset{n\times 1}{\mathop{\mathit{\boldsymbol{A}}\left( t \right)}}\, =\left( \begin{matrix} \text{MF}\left( e_{_{pq}}^{1} \right)-\text{MF}\left( e_{_{pq}}^{k} \right) \\ \vdots \\ \text{MF}\left( e_{_{pq}}^{n} \right)-\text{MF}\left( e_{_{pq}}^{k} \right) \\ \end{matrix} \right), \underset{n\times n}{\mathop{\mathit{\boldsymbol{B}}\left( t \right)}}\, =\left( \begin{matrix} \frac{17C}{77{{f}_{1}}-60{{f}_{2}}} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & \frac{17C}{77{{f}_{1}}-60{{f}_{2}}} \\ \end{matrix} \right),\\ \mathit{\boldsymbol{X}}=\left( \begin{matrix} \text{RZWD} \\ \lambda \Delta \nabla \left( {{N}_{1}} \right)_{pq}^{1k} \\ \vdots \\ \lambda \Delta \nabla \left( {{N}_{1}} \right)_{pq}^{nk} \\ \end{matrix} \right) $ |
可将式(9)简记为Ln= Bn Xn+ Vn, Vn~N(0, Rn)。此外,正常大气状态下的天顶方向湿延迟随时间的变化幅度较小,故可将相对湿延迟看作随机游走的过程,通过卡尔曼滤波进行估计:
| $ {\rm{RZWD}}\left( {t + \tau } \right) = {\rm{RZWD}}\left( t \right) + \omega \left( t \right) $ | (10) |
式中,ω(t)为相对天顶湿延迟在t时刻的零均值白噪声,可取0.000 1~0.000 9 m2/h。双差对流层延迟的值一般较小,可将RZWD的初值设为0.0 m,对应的状态转移矩阵与动态噪声可表示为:
| $ \begin{array}{l} \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {t + \tau , t} \right) = \left[ {\begin{array}{*{20}{c}} 1&0& \cdots &0\\ 0&1& \cdots &0\\ \vdots & \vdots & \ddots & \vdots \\ 0&0& \cdots &1 \end{array}} \right], \\ \mathit{\boldsymbol{Q}} = \left[ {\begin{array}{*{20}{c}} {\delta _w^2}&0& \cdots &0\\ 0&{{e^{ - 16}}}& \cdots &0\\ \vdots & \vdots & \ddots & \vdots \\ 0&0& \cdots &{{e^{ - 16}}} \end{array}} \right] \end{array} $ | (11) |
周跳探测与修复后,可将整周模糊度看作不变的常数,初值可通过初始历元最小二乘来确定,状态转移噪声为0,并以此建立状态噪声方差阵,可得到离散系统的卡尔曼滤波方法为:
| $ \left\{ \begin{matrix} {\mathit{\boldsymbol{X}}_{n}}={\mathit{\boldsymbol{X}}_{n-1}}+{\mathit{\boldsymbol{W}}_{n}},{\mathit{\boldsymbol{W}}_{n}}\text{ }\!\!\tilde{\ }\!\!\text{ }~N\left( 0,{\mathit{\boldsymbol{Q}}_{n}} \right) \\ {\mathit{\boldsymbol{L}}_{n}}={\mathit{\boldsymbol{B}}_{n}}{\mathit{\boldsymbol{X}}_{n}}+{\mathit{\boldsymbol{V}}_{n}},{\mathit{\boldsymbol{V}}_{n}}\text{ }\!\!\tilde{\ }\!\!\text{ }~N\left( 0,{\mathit{\boldsymbol{R}}_{n}} \right) \\ \end{matrix} \right. $ | (12) |
式中,Qn为状态噪声方差阵,Rn为观测误差方差阵。在进行卡尔曼滤波时,由卫星高度角等建立的随机模型可确定Qn的先验值,得到卡尔曼滤波方差的解为:
| $ \left\{\begin{array}{l}{\boldsymbol{P}_{n, n-1}=\boldsymbol{P}_{n-1, n-1}+\boldsymbol{Q}_{n}} \\ {\boldsymbol{J}_{n}=\boldsymbol{P}_{n, n-1} \boldsymbol{B}_{n}^{\mathrm{T}}\left(\boldsymbol{B}_{n} \boldsymbol{P}_{n, n-1} \boldsymbol{B}_{n}^{\mathrm{T}}+\boldsymbol{R}_{n-1}\right)^{-1}} \\ {\boldsymbol{P}_{n, n}=\left(\boldsymbol{E}-\boldsymbol{J}_{n} \boldsymbol{B}_{n}\right) \boldsymbol{P}_{n, n-1}} \\ {\boldsymbol{X}_{n}=\boldsymbol{X}_{n-1}+\boldsymbol{J}_{n}\left(\boldsymbol{L}_{n}-\boldsymbol{B}_{n} \boldsymbol{X}_{n-1}\right)}\end{array}\right. $ | (13) |
式中,E为单位阵,Jn为增益矩阵,Pn, n为Xn的方差,Pn, n-1为Xn的预测方差。随着卫星的起落,Xn的维数也随之发生变化,故为了保持滤波的连续性,需要对Pn, n、Qn、Rn进行动态更新。由式(13)就可解算出基频的整周模糊度与对流层天顶延迟的浮点解,再利用LAMBDA算法即可实现基频整周模糊度的固定。将固定的L1、B1模糊度代入无电离层组合双差观测方程中,对流层延迟干分量用模型进行改正,湿分量通过基频模糊度固定Kalman滤波得到,就可解算出流动站的坐标。
3 三维移动变形平台实例分析 3.1 实验数据来源选用2018-01-31海星达H32系列接收机采集的实验数据,将接收机分别放置于淮南市寿县正阳关镇(JZ50P)、合肥市长丰县(JZ20P)、安徽理工大学北门的三维移动变形平台上(KLABB),形成3条中长基线。实验前通过调整平台位置使其3条导轨方向分别与地平坐标系的东、北、垂直方向基本一致,设置采样间隔为1 s(表 1)。第1时段,各参考站、三维移动变形平台(KLABB)初始位置静态观测1 h; 第2时段,在时段1的基础上,三维移动变形平台(KLABB)沿导轨方向运动到最大值(X轴1 000.0 mm,Y轴800.0 mm,Z轴500.0 mm),静态观测1 h。设置卫星高度角为15°,系统内采用高度角定权,系统间采用等权方式。
|
|
表 1 三维移动变形平台基线信息 Tab. 1 3D mobile deformation platform baseline information |
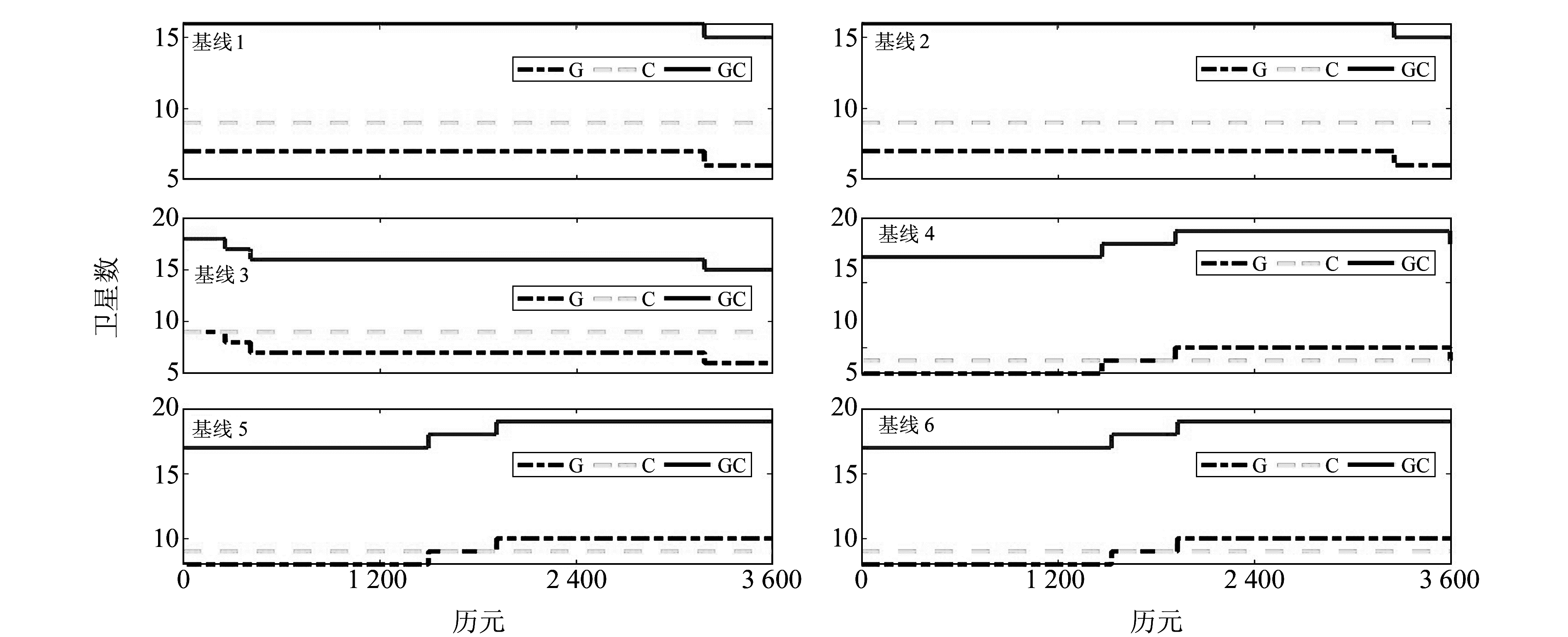
由图 1可知,GPS/BDS的可见卫星数可达17~18颗,较单系统增加约1倍; 基线1~3中,BDS的可见卫星数稳定在9颗,而GPS的可见卫星数处于6~9颗之间,且波动幅度较大; 基线4~6中,BDS卫星数稳定在9颗,而GPS的卫星数变化较大,部分历元GPS的卫星数超过了BDS。
|
图 1 各条基线可见卫星数的分布情况 Fig. 1 Distribution of visible satellites of each baseline |
由图 2可知,BDS的PDOP值普遍大于GPS,BDS的PDOP值基本处于2.5左右,波动幅度小,而GPS的PDOP值波动较大。这是由于BDS的GEO卫星与IGSO卫星可实现对区域的连续覆盖,卫星的升降较少,GPS卫星的升降较多; GPS/BDS的PDOP值比GPS、BDS的都小,说明双系统组合卫星的空间几何构型得到明显改善,系统稳定性也得到相应提高。

|
图 2 各条基线PDOP值分布情况 Fig. 2 Distribution of PDOP values of each baseline |
本文用模糊度固定率、正确率对基线解算的有效性进行检验,以ratio≥2的历元与有效历元数的比值作为模糊度的固定率,并将各个历元的固定解与GNSS网平差结果进行比较,相同则认为是正确的,以正确固定的历元数与有效历元数的比值作为模糊度的正确率(表 2,单位%)。
|
|
表 2 各条基线模糊度固定情况 Tab. 2 Fixed ambiguity of each baseline |
总体而言,GPS/BDS的固定率、正确率比GPS、BDS有部分提升,GPS/BDS较GPS各基线正确率分别提升2.9%、-0.08%、1.41%、-0.47%、0.33%、1.81%,较BDS各基线正确率分别提升-0.54%、-0.08%、1.47%、-0.73%、0.32%、0.54%;基线1与基线4中,BDS的模糊度固定率、正确率均高于GPS,GPS/BDS组合系统的固定率与正确率介于两者之间,其固定率均高于90.0%,正确率均高于80.0%;基线2与基线5的固定率、正确率最高,GPS、BDS及其组合系统的模糊度固定率均接近100%,正确率接近90%;基线3与基线6的固定率、正确率最低,基线3的整周模糊度固定率、正确率优于80.0%,基线6的固定率、正确率优于85.0%。
从图 3、4(采样率1 s)可知,各基线解算结果X、Y、Z方向的坐标偏差大部分都集中在1.0~2.0 cm,其中X、Y方向相比Z方向偏差更为集中,各条基线在Z方向的波动都比X、Y方向的大,基线3、基线6的三维坐标偏差相对于基线1~4的变化要大。

|
图 3 基线1~3三维方向坐标偏量 Fig. 3 3D direction coordinate offset of baseline 1-3 |

|
图 4 基线4~6三维方向坐标偏量 Fig. 4 3D direction coordinate offset of baseline 4-6 |
由表 3(单位mm)可见,各基线在X、Y、Z方向的精度优于3.0 cm,3D精度优于3.5 cm,Z方向精度较X、Y方向稍差。总体而言,GPS与BDS的定位精度基本一致,GPS/BDS较GPS、BDS系统的精度有一定提高,GPS/BDS较GPS各基线3D精度分别提升6.0 mm、-0.7 mm、0.2 mm、2.7 mm、0.3 mm、-0.2 mm,较BDS各基线3D精度分别提升-0.5 mm、-0.7 mm、0.8 mm、0.7 mm、0.2 mm、-0.5 mm。为了能计算出点位的移动变形量,将时段1的基线1、基线2与时段2的基线4、基线5解算出的坐标与平差解算的初始坐标作差,得到N、E、U方向的变形量(图 5,采样率1 s)。
|
|
表 3 各条基线向量的内符合精度(RMS) Tab. 3 Internal coincidence accuracy (RMS) of each baseline vector deviation |
|
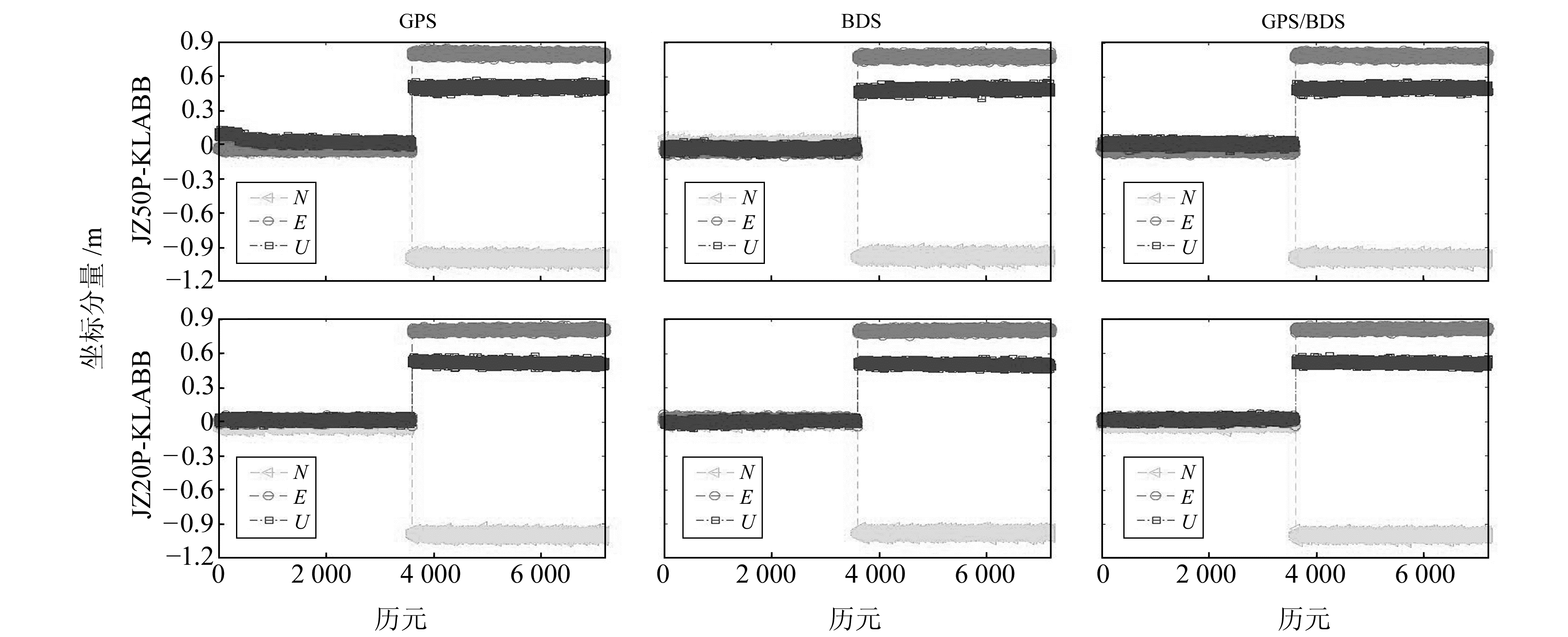
图 5 三维移动变形平台(KLABB)移动变形变化量 Fig. 5 Three-dimensional moving deformation platform (KLABB) movement deformation change |
由图 5可知,JZ50P-KLABB、JZ20P-KLABB基线解算的移动变化值趋于一致,时段1前3 600历元KLABB点N、E、U方向均在0.0 m附近,时段2后3 600历元KLABB点N方向趋于1.0 m、E方向趋于0.8 m、U方向趋于0.5 m,与实验设计的N、E、U方向分别变化0.996 m、0.782 m、0.486 m保持一致。为了给出KLABB点在N、E、U方向的偏差,将解算出的N、E、U方向变化量与参考值作差,相应的各方向偏差绝对值分布如图 6、7所示。
|
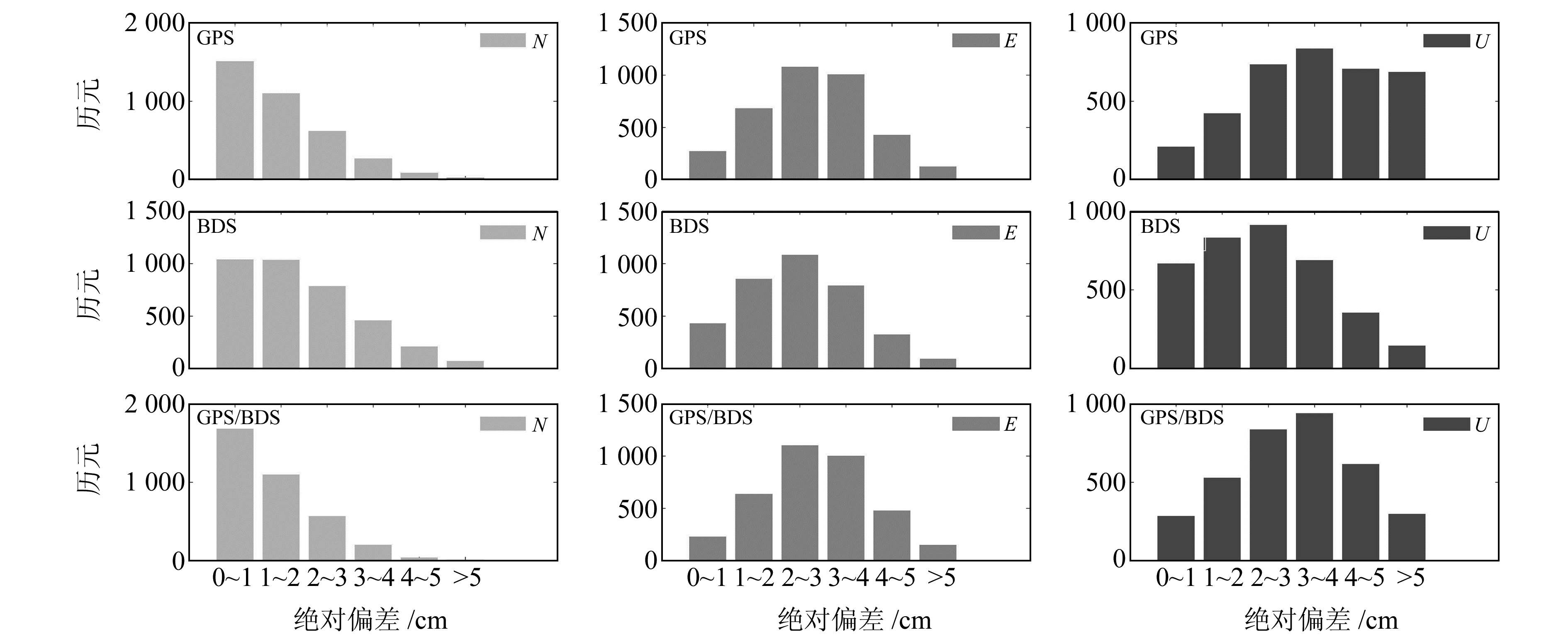
图 6 JZ50P-KLABB基线N、E、U方向移动变形绝对偏差分布 Fig. 6 Absolute deviation distribution of JZ20P-KLABB moving deformation in N, E and U directions |
|
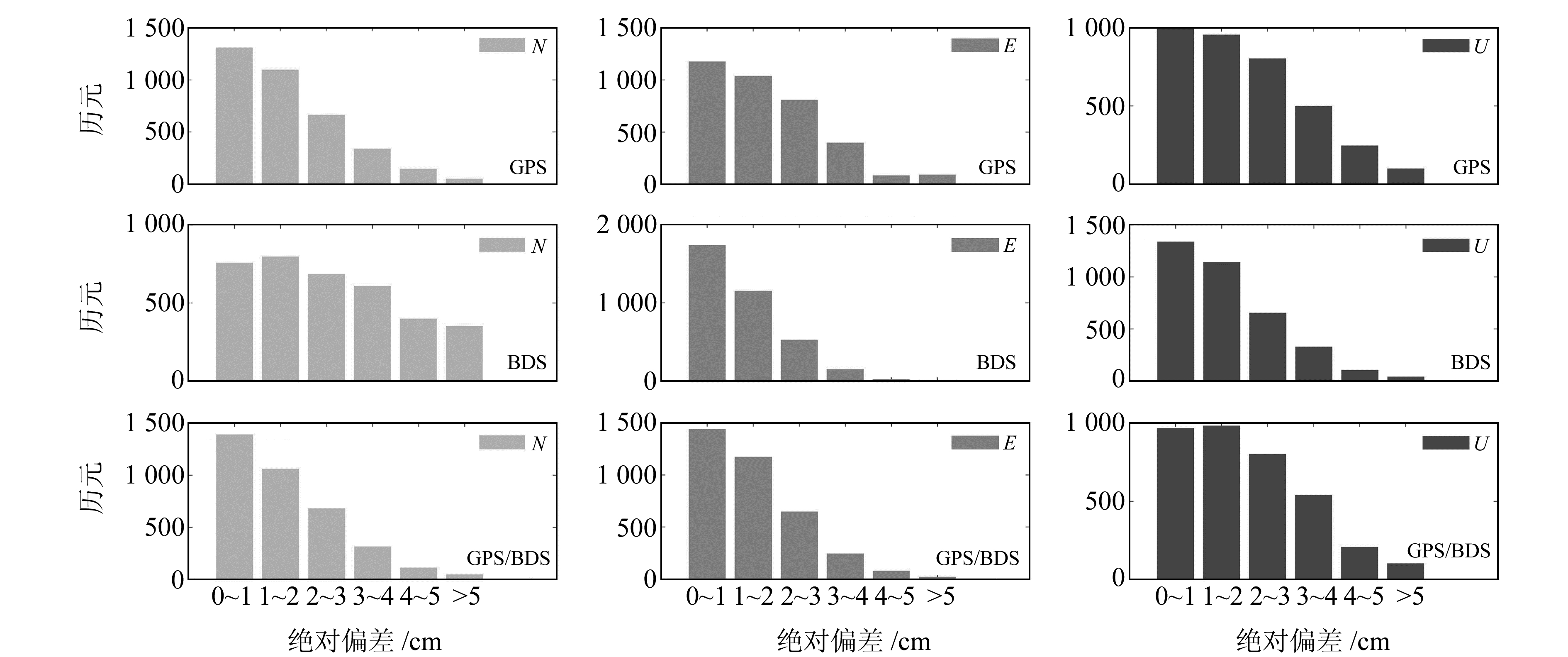
图 7 JZ20P-KLABB基线N、E、U方向移动变形绝对偏差分布 Fig. 7 Absolute deviation distribution of JZ20P-KLABB moving deformation in N, E and U directions |
由图 6、7可知,GPS/BDS比GPS、BDS解算的变形量精度稍高,JZ50P-KLABB基线解算的变形量在N、E、U方向偏差集中在0~3.0 cm、2.0~4.0 cm、2.0~4.0 cm;GPS在U方向精度较差,JZ20P-KLABB基线解算的变形量在N、E、U方向偏差集中在0~2.0 cm、0~3.0 cm、0~3.0 cm,较JZ50P-KLABB基线解算的结果更佳。由于实验时无法使导轨精确对准N、E、U方向,因此,将解算出的2个时段变化距离与实验参考移动距离作差,得到KLABB点的空间距离变化偏差,如表 4(单位%)所示。
|
|
表 4 移动变形距离误差分布 Tab. 4 Motion deformation distance error distribution |
由表 4可知,各种模式下JZ50P-KLABB、JZ20P-KLABB基线对应移动变形距离偏差都呈现出逐渐递减的趋势,GPS/BDS组合系统移动变形距离偏差在4.0 cm之内的比例可达94.12%、99.89%;JZ50P-KLABB基线GPS、BDS、GPS/BDS基线解算出的KLABB点移动变形距离偏差在0~2 cm之间的比例为42.39%、54.95%、43.02%,在0~3 cm之间的比例为61.19%、75.91%、61.95%,BDS的解算结果优于GPS,GPS/BDS较GPS的解算精度有所提升; JZ20P-KLABB基线GPS、BDS、GPS/BDS解算出的KLABB点移动变形距离偏差在0~0.02 m之间的比例为67.45%、70.03%、70.21%,在0~0.03 m之间的比例为86.35%、87.78%、88.13%,BDS与GPS的精度基本相同,GPS/BDS精度优于单系统; 由于时段1的JZ50P-KLABB数据质量较差,且大气延迟随着距离的增加而增加,基线解算精度亦下降,因此J20P-KLABB基线较JZ50P-KLABB基线解算的KLABB点移动变形距离偏差都更小更集中,且分布更均匀。
由表 5可知,GPS与BDS的中误差相当,GPS/BDS中误差最小,各模式下的移动变形距离中误差优于25.0 mm,相对中误差优于1/55.0。JZ50P-KLABB中,GPS/BDS相对GPS、BDS的中误差分别减小6.25%、7.41%,相对中误差分别减小5.82%、7.15%;JZ20P-KLABB中,GPS/BDS移动变形距离中误差最小为18.8 mm,相对中误差达1/69.4,相对GPS、BDS的中误差分别减小3.09%、3.59%,相对中误差分别减小2.64%、3.48%。
|
|
表 5 移动变形距离精度指标分布 Tab. 5 Mobile deformation distance accuracy index distribution |
本文在固定宽巷模糊度的基础上构建出无电离层组合观测值,由Kalman滤波算法实现L1、B1基频模糊度浮点解的解算,使用LAMBDA算法实现模糊度的固定。并对GPS、BDS、GPS/BDS模式下46.6 km、20.8 km、63.4 km三维移动变形中长基线进行解算,对比固定率、正确率、RMS值、中误差等基线解算指标,得出以下结论:
1) 总体而言,GPS/BDS组合相对GPS、BDS增加了共视卫星的数目,增强了卫星在空间的几何结构,定位精度有所提升,GPS/BDS各基线模糊度固定率、正确率优于82.08%、81.53%,X、Y、Z、3D方向的精度可达15.4 mm、15.9 mm、20.1 mm、30.0 mm。
2) 移动变形量解算中,GPS/BDS精度提升最为明显,46.6 km基线中较GPS、BDS中误差分别减小6.25%、7.41%,相对中误差分别减小5.82%、7.15%;20.8 km基线中双系统解算中误差最小为18.8 mm,相对中误差为1/69.4,较GPS、BDS中误差分别减小3.09%、3.59%,相对中误差分别减小2.64%、3.48%。
| [1] |
高猛, 徐爱功, 祝会忠, 等. GPS长距离参考站间低高度角模糊度快速解算方法[J]. 中国矿业大学学报, 2017, 46(3): 664-671 (Gao Meng, Xu Aigong, Zhu Huizhong, et al. Rapid Algorithm of Ambiguity Resolution for Low Elevation Angle Satellite between Long-Range GPS Reference Stations[J]. Journal of China University of Mining & Technology, 2017, 46(3): 664-671)
(  0) 0) |
| [2] |
李博峰, 沈云中, 周泽波. 中长基线三频GNSS模糊度的快速算法[J]. 测绘学报, 2009, 38(4): 296-301 (Li Bofeng, Shen Yunzhong, Zhou Zebo. A New Method for Medium and Long Range Three Frequency GNSS Rapid Ambiguity Resolution[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 296-301 DOI:10.3321/j.issn:1001-1595.2009.04.003)
(  0) 0) |
| [3] |
祝会忠, 高星伟, 秘金钟, 等. 一种GPS整周模糊度单历元解算方法[J]. 测绘科学, 2011, 36(4): 9-11 (Zhu Huizhong, Gao Xingwei, Bei Jinzhong, et al. An Algorithm of GPS Ambiguity Resolution on Single-Epoch[J]. Science of Surveying and Mapping, 2011, 36(4): 9-11)
(  0) 0) |
| [4] |
黄令勇, 宁德阳, 吕志平, 等. 两种长基线模糊度解算方法在北斗三频应用中的比较[J]. 大地测量与地球动力学, 2014, 34(5): 101-105 (Huang Lingyong, Ning Deyang, Lü Zhiping, et al. Comparative Study on Two Long-Baseline Ambiguity Reesolution Methods in Application of Beidou/Compass Triple-Frequency[J]. Journal of Geodesy and Geodynamics, 2014, 34(5): 101-105)
(  0) 0) |
| [5] |
徐龙威, 刘晖, 张明, 等. 不同截止高度角多模GNSS组合单点定位性能分析[J]. 大地测量与地球动力学, 2015, 35(6): 987-991 (Xu Longwei, Liu Hui, Zhang Ming, et al. Performance Assessment of Multi-GNSS Single Point Positioning with Different Cut-off Elevation Angles[J]. Journal of Geodesy and Geodynamics, 2015, 35(6): 987-991)
(  0) 0) |
| [6] |
安向东. GPS与北斗伪距单点定位性能对比分析[J]. 全球定位系统, 2014(3): 8-14 (An Xiangdong. The Comparative Analysis of Performance about GPS and BDS in Single Point Positioning[J]. GNSS Word of China, 2014(3): 8-14)
(  0) 0) |
| [7] |
唐卫明, 刘经南, 施闯, 等. 三步法确定网络RTK基准站双差模糊度[J]. 武汉大学学报:信息科学版, 2007, 32(4): 305-308 (Tang Weiming, Liu Jingnan, Shi Chuang, et al. Three Steps Method to Determine Double Difference Ambiguities Resolution of Network RTK Reference Station[J]. Geomatics and Information Science of Wuhan University, 2007, 32(4): 305-308)
(  0) 0) |
| [8] |
邓建, 潘树国, 王胜利. 基于最优组合的长基线网络RTK三频载波模糊度快速解算[J]. 中国惯性学报, 2012, 20(5): 587-592 (Deng Jian, Pan Shuguo, Wang Shengli. Fast Resolution for Three-Frequency Carrier Ambiguity of Long-Range Network RTK Based on Optimal Combination[J]. Journal of Chinese Inertial Technology, 2012, 20(5): 587-592)
(  0) 0) |
| [9] |
祝会忠, 刘经南, 唐卫明, 等. 长距离网络RTK基准站间整周模糊度单历元确定方法[J]. 测绘学报, 2012, 41(3): 359-365 (Zhu Huizhong, Liu Jingnan, Tang Weiming, et al. The Algorithm of Single-Epoch Integer Ambiguity Resolution between Long-Range Network RTK Base Stations[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 359-365)
(  0) 0) |
| [10] |
吕伟才, 高井祥, 张书毕, 等. 宽巷约束的网络RTK基准站间模糊度固定方法[J]. 中国矿业大学学报, 2014, 43(5): 933-937 (Lü Weicai, Gao Jingxiang, Zhang Shubi, et al. A Method of Fixing Integer Ambiguity between Base Stations in Network RTK with Wide-Lane Ambiguity Restriction[J]. Journal of China University of Mining & Technology, 2014, 43(5): 933-937)
(  0) 0) |
| [11] |
黄丁发, 周乐韬, 刘经南, 等. 基于Internet的VRS/RTK定位算法模型及实验研究[J]. 武汉大学学报:信息科学版, 2007, 32(3): 220-224 (Huang Dingfa, Zhou Letao, Liu Jingnan, et al. Intenet Based VRS/RTK Positioning Algorithm and Experiment[J]. Geomatics and Information Science of Wuhan University, 2007, 32(3): 220-224)
(  0) 0) |
| [12] |
周乐韬, 黄丁发, 袁林果, 等. 网络RTK参考站间模糊度动态解算的卡尔曼滤波算法研究[J]. 测绘学报, 2007, 36(2): 37-42 (Zhou Letao, Huang Dingfa, Yuan Linguo, et al. A Kalman Filtering Algorithm for Online Integer Ambiguity Resolution in Reference Station Network[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 37-42)
(  0) 0) |
2. School of Geodesy and Geomatics, Anhui University of Science and Technology, 168 Mid-Shungeng Road, Huainan 232001, China;
3. College of Instrument Science and Engineering, Southeast University, 2 Sipailou, Nanjing 210096, China;
4. Land and Resources Bureau of Jinzhai County, Jinzhai County, Lu'an 237300, China
 2019, Vol. 39
2019, Vol. 39

