2. 信息工程大学导航与空天目标学院,郑州市科学大道62号,450001
随着北斗系统的完善和发展,相关导航定位技术也需要同步推进。周跳探测和修复技术作为北斗系统数据预处理的重要组成部分,对高精度定位导航应用起到至关重要的作用。
现有的周跳探测方法主要有多项式拟合法[1]、电离层残差法[2]、Turboedit法[3]、卡尔曼滤波[4]等方法,但这些方法都存在一定的局限性。其中Turboedit法中,MW(Melbourne-Wübbena)组合观测值受伪距精度影响较大[5]。甘雨等[6]和范丽红等[7]对MW观测值进行改进,对伪距噪声进行滤波处理。刘柳等[8]采用MW组合和无几何相位组合对不敏感周跳进行实验,结果表明,MW组合和2个无几何相位组合能有效减少不敏感周跳数目。
本文主要针对MW组合中伪距噪声较大的问题,提出采用B2和B3频点观测值组成优选的MW组合观测值,并联合2个弱电离层的无几何相位组合进行北斗三频数据的周跳探测和修复实验。该方法能有效降低电离层误差和噪声误差的影响,提高组合观测量的探测精度,实时有效地探测和修复发生的大小周跳。
1 基本原理 1.1 伪距和载波相位观测值| $ \begin{align} & {{P}_{{{f}_{i}}}}=\rho +c \delta {{t}_\text{r}}-c \delta {{t}^{\text{s}}}+ \\ & \ \ \ I+\text{Trop}+{{M}_{P}}+{{\varepsilon }_{P}} \\ \end{align} $ | (1) |
| $ \begin{align} & {{\lambda }_{i}} {{\mathit{\Phi }}_{{{f}_{i}}}}=\rho +c \delta {{t}_{\rm r}}-c \delta {{t}^{\text{s}}}-I+ \\ & \ \ \ \ \text{Trop}+{{\lambda }_{i}} {{N}_{i}}+M\varphi +\varepsilon \varphi \\ \end{align} $ | (2) |
式中,Pfi和Φfi分别为在频率fi(i=1, 2, 3)上的伪距观测值和载波相位观测值,其中f1=1.561 098×109 Hz,f2=1.207 14×109 Hz,f3=1.268 52×109 Hz; ρ为卫星到接收机之间的几何距离; c为光速; δtr和δts分别为接收机钟差和卫星钟差; I为电离层延迟误差; εP和εΦ分别为伪距噪声和载波相位噪声; MP和Mφ分别为伪距观测量和载波相位观测量的多路径误差; Trop为对流层延迟误差; λi(i=1, 2, 3)为对应频点波长,其中λ1=0.192 m,λ2=0.248 3 m,λ3=0.236 3 m; Ni为在频率fi上的整周模糊度。
1.2 MW组合组合观测值表达式为:
| $ \begin{align} & {{\mathit{\Phi }}_{ij}}={{\mathit{\Phi }}_{{{f}_{i}}}}-{{\mathit{\Phi }}_{{{f}_{j}}}}-(\frac{{{f}_{i}}{{P}_{i}}+{{f}_{j}}{{P}_{j}}}{{{f}_{i}}+{{f}_{j}}}\cdot {{\lambda }_{ij}})= \\ & {{N}_{i}}-{{N}_{j}}-{{\eta }_{ij}}I+{{\varepsilon }_{ij}}, i, j=1, 2, 3, i\ne j \\ \end{align} $ | (3) |
| $ {{\lambda }_{ij}}=({{\lambda }_{i}}+{{\lambda }_{j}})/({{\lambda }_{i}}{{\lambda }_{j}}) $ | (4) |
载波相位观测值整周模糊度作差表示为:
| $ {{N}_{ij}}={{N}_{i}}-{{N}_{j}}={{\mathit{\Phi }}_{{{f}_{i}}}}-{{\mathit{\Phi }}_{{{f}_{j}}}}- \\ (\frac{{{f}_{i}}{{P}_{i}}+{{f}_{j}}{{P}_{j}}}{{{f}_{i}}+{{f}_{j}}}\cdot {{\lambda }_{ij}})-\eta \cdot I+{{\varepsilon }_{ij}} $ | (5) |
| $ {{\eta }_{ij}}\text{=}2(\frac{1}{c{{f}_{\text{i}}}}-\frac{1}{c{{f}_{j}}}) $ | (6) |
| $ {{\varepsilon }_{ij}}=\left[ \left( \frac{\varepsilon {{\mathit{\Phi }}_{i}}}{{{\lambda }_{i}}}-\frac{\varepsilon {{\mathit{\Phi }}_{j}}}{{{\lambda }_{j}}} \right)-\left( \frac{{{f}_{i}}-{{f}_{j}}}{{{f}_{i}}+{{f}_{j}}} \right)\left( \frac{\varepsilon {{P}_{i}}}{{{\lambda }_{i}}}+\frac{\varepsilon {{P}_{j}}}{{{\lambda }_{j}}} \right) \right] $ | (7) |
通过历元间差分,可以得到周跳探测量为:
| $ \begin{align} & \Delta {{N}_{ij}}=\Delta {{N}_{i}}-\Delta {{N}_{j}}=\Delta {{\mathit{\Phi }}_{{{f}_{i}}}}-\Delta {{\mathit{\Phi }}_{{{f}_{j}}}}- \\ & (\frac{{{f}_{i}}\Delta {{P}_{i}}+{{f}_{j}}\Delta {{P}_{j}}}{{{f}_{i}}+{{f}_{j}}}\cdot {{\lambda }_{ij}})-\eta \cdot \Delta I+\Delta {{\varepsilon }_{ij}} \\ \end{align} $ | (8) |
由误差传播定律可以得到组合观测值的中误差δij为:
| $ {{\delta }_{ij}}=\sqrt{2\delta _{\varphi }^{2}+{{\lambda }_{ij}}^{2}(\frac{f_{i}^{2}+f_{j}^{2}}{{{({{f}_{i}}+{{f}_{j}})}^{2}}})\delta _{P}^{2}} $ | (9) |
式中,Φij为MW组合观测量; λij为MW组合波长,B2和B3频点组合波长为λ23=4.884 2 m,比λ12(0.847 m)更长; εij为MW组合后的噪声; ηij为MW组合后的电离层系数; Δ为历元间差分的符号; Nij为MW组合后的整周模糊度; ΔNij为MW组合整周模糊度历元间差分得到的观测量。
式(7)组合观测值中不存在卫星位置、接收机位置及时间参数,所以可以用于实时动态的周跳探测。在MW组合的周跳探测量中,周跳探测的主要误差来自于电离层残差和伪距噪声[5]。由式(6)可知,信号的频率越接近,系数ηij就越小,对电离层的影响就越小; 组合观测值的噪声主要是由伪距噪声构成的,假设3个频点产生的噪声误差相同,εP1=εP2=εP3=ε0,载波相位的噪声相对伪距噪声极其微小,因此忽略载波相位噪声的影响。简化式(7)可以得到
| $ {\rm Round}(|{N^{i + 1}} - {N^i}|){\rm{ = }}0 $ | (10) |
满足上述条件,则判定发生周跳。
1.3 无几何相位组合组合观测值表达式[9]为:
| $ \begin{array}{l} {\lambda _{ijk}}{\mathit{\Phi }_{ijk}} = \rho + c\delta {t_{\rm r}} - c\delta {t^{\rm s}} + {\rm{Trop}} - \\ \;\;\;\;\;\;\;\;\;\;{\eta _{ijk}}I + {\lambda _{ijk}}{N_{ijk}} + {\varepsilon _{ijk}} \end{array} $ | (11) |
其中,
| $ {\eta _{ijk}} = {\lambda _{ijk}}(i\frac{1}{{f_1^2}} + j\frac{1}{{f_2^2}} + k\frac{1}{{f_3^2}}) $ | (12) |
| $ {N_{ijk}} = i{N_1} + j{N_2} + k{N_3} $ | (13) |
| $ {\varepsilon _{ijk}} = i{\varepsilon _1} + j{\varepsilon _2} + k{\varepsilon _3} $ | (14) |
| $ {\lambda _{ijk}} = \frac{{{\lambda _1}{\lambda _2}{\lambda _3}}}{{i{\lambda _2}{\lambda _3} + j{\lambda _1}{\lambda _3} + k{\lambda _1}{\lambda _2}}} $ | (15) |
| $ i + j + k = 0 $ | (16) |
通过历元间差分可以得到周跳探测量为:
| $ \Delta {N_{ijk}} = \Delta {\mathit{\Phi }_{ijk}} - {\eta _{ijk}} \cdot \frac{{\Delta I}}{{{\lambda _{ijk}}}} + \frac{{\Delta {\varepsilon _{ijk}}}}{{{\lambda _{ijk}}}} $ | (17) |
式中,i、j、k分别为3个频点上观测值组合的系数; λijk为北斗三频组合观测值的波长; ηijk为北斗三频组合观测值的电离层系数; ΔNijk为北斗三频组合观测值的相邻历元间整周模糊度差值,为确保整周模糊度为整数,观测值系数i、j、k需要限定为整数; Δεijk为北斗三频组合观测值的噪声误差相邻历元间的差值。
1.4 无几何相位组合系数的优选原则为了使组合观测值能够准确地探测到北斗三频周跳,应该尽量减小电离层残差和噪声误差对组合观测值的影响。本文依据式(12)中的组合观测值电离层系数ηijk最小和式(14)中的组合观测值噪声εijk最小的原则选取无几何相位观测值组合系数[10]。通过程序实现,可以得到不同系数组合得到的电离层系数和噪声对组合观测值影响的大小。以[-10, 10]为搜索区间搜索i、j、k,步长为1,得到较优的电离层系数和噪声系数较小的组合,结果见表 1。
|
|
表 1 不同组合系数对应的组合波长、电离层系数、噪声系数 Tab. 1 Combined wavelength, ionospheric coefficient and noise coefficient for different combinations |
北斗三频周跳探测需要采用3组探测量进行探测,载波相位组合只能得到2组线性无关的组合,根据上表得到的电离层系数和噪声系数的数值大小,利用电离层系数最小和噪声系数最小的原则,采取(0, -1, 1)和(1, 0, -1)的组合来进行周跳探测。联合MW组合、(0, -1, 1)和(1, 0, -1)组合对北斗三频周跳进行实时探测,在电离层延迟误差忽略的条件下,根据误差传播定律,可以得到无几何相位周跳探测量估值的标准差为:
| $ {\delta _{ijk}} = {\delta _\varphi }\sqrt 2 \sqrt {{{(i{\lambda _1})}^2} + {{(j{\lambda _2})}^2} + {{(k{\lambda _3})}^2}} $ | (18) |
三频无几何相位组合周跳探测条件为:
| $ {\rm{|}}{N_{ijk}}(i + 1) - {N_{ijk}}(i){\rm{|}} \ge \zeta {\delta _{ijk}} $ | (19) |
式中,δφ为原始载波相位观测值的误差; ζ为常数; ζδijk为进行无几何相位周跳探测的阈值。ζ的大小决定了不敏感周跳的数目,本文取3倍δijk作为周跳探测的阈值,能有效减少不敏感周跳的数目,同时减少漏探的周跳数目。当相邻历元间组合模糊度作差满足式(19)时,判定该历元发生周跳。
1.5 周跳的修复方法北斗三频周跳的修复需要选择3个线性无关的观测值组合对3个频点上产生的周跳进行修复。本文选择弱电离层的MW组合和2个弱电离层、最小噪声的无几何相位组合对北斗三频数据的周跳进行修复。观测值组合系数分别为(i1, j1, k1)、(λ1i2, λ2j2, λ3k2)和(λ1i3, λ2j3, λ3k3),其中,对于MW组合构成第1探测量,i、j、k分别属于整数,整周模糊度也同样是整数。根据文献[11],当δΔN<0.2周时,取整成功率能够达到98.8%,采用B2和B3频点的MW组合观测噪声δΔN=0.190 1周,通过取整来对周跳进行修复,可以保证周跳修复的准确率。第2、3探测量通过最小二乘原则获取的周跳探测值存在不稳定解,本文采用最小二乘搜索法进行周跳的搜索和修复。
采用取整的方法将MW探测量进行取整得到整数周跳n1,无几何相位组合探测量得到的周跳估值分别为n2和n3,那么原始观测值的组合系数、理论周跳值(ΔN1, ΔN2, ΔN3)和周跳估值(n1, n2, n3)之间存在如下关系:
| $ \mathit{\boldsymbol{AX}} = \mathit{\boldsymbol{L}} $ | (20) |
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {{i_1}}&{{j_1}}&{{k_1}}\\ {{\lambda _1} \times {i_2}}&{{\lambda _2} \times {j_2}}&{{\lambda _3} \times {k_2}}\\ {{\lambda _1} \times {i_3}}&{{\lambda _2} \times {j_3}}&{{\lambda _3} \times {k_3}} \end{array}} \right] $ | (21) |
| $ \mathit{\boldsymbol{X}}{\rm{ = }}{\left[ {\begin{array}{*{20}{c}} {\Delta {N_1}}&{\Delta {N_2}}&{\Delta {N_3}} \end{array}} \right]^{\rm{T}}} $ | (22) |
| $ \mathit{\boldsymbol{L = }}{\left[ {{n_1}\;\;{n_2}\;{n_3}} \right]^{\rm{T}}} $ | (23) |
采用最小二乘范数原则[12-13]对无几何相位探测量探测的周跳进行匹配修复,搜索中心为X= A-1L,以搜索步长2为搜索半径进行周跳匹配修复[13]。
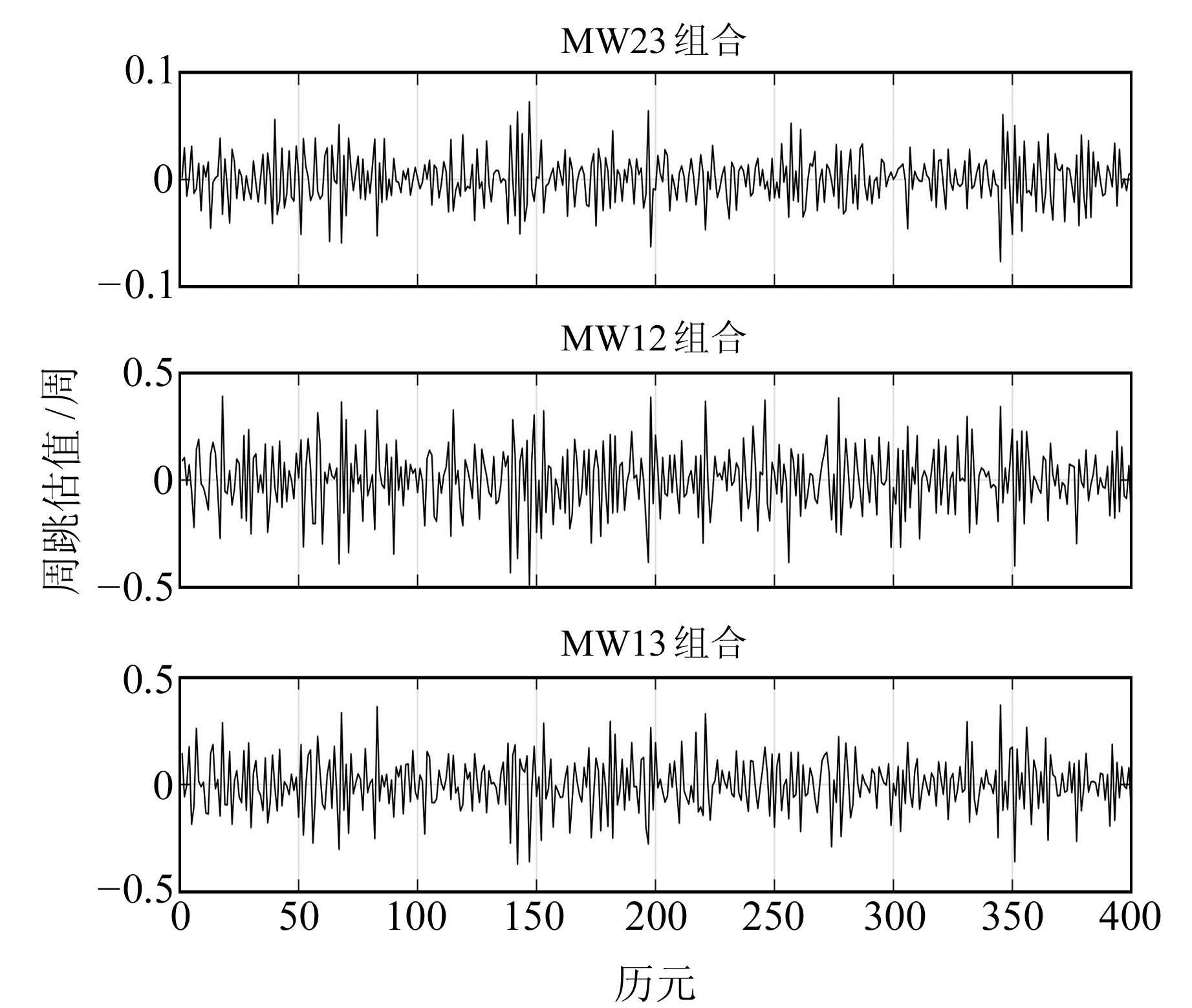
2 实验分析采用2018年年积日20的河南省北斗地基增强系统郑州基站(ZZJZ)的三频数据进行实验。为了探究不同频点组合的MW组合探测精度,采用C14号卫星数据,采样间隔为30 s,得到3组组合观测值的探测估值,结果见图 1。
|
图 1 不同频率MW组合探测量对比 Fig. 1 Comparison of MW combination detections of different frequencies |
图 1是不同频率组合的MW组合周跳估值,MW23、MW12和MW13分别表示B2B3、B1B2和B1B3频率组合的MW组合。由图 1可知,采用MW23组合的周跳探测量的探测精度范围为[-0.1, 0.1]周,采用MW12和MW13组合的周跳探测量精度范围为[-0.5, 0.5]周,采用B2和B3频点组合的MW23组合的周跳探测精度更高,更加有利于周跳的探测和修复。
采用B2和B3频点组合的MW观测值的探测精度优于其他频点观测值的MW组合,将采用B2和B3频点的MW组合、(1, 0, -1)和(0, 1, -1)组合对3种不同轨道的卫星所选观测历元中人为地加入周跳组合,利用自编程序进行周跳探测和修复实验。选用2018年年积日20的河南省北斗地基增强系统郑州基站(ZZJZ)的三频数据进行周跳探测和修复实验,数据采样间隔为30 s,进行探测的卫星为C02、C06和C14(3颗卫星分别属于不同轨道类型)。在所选历元中,随着时间历元的变化,卫星高度角分别呈39.7°~39°,77.2°~64°和67.3°~34.1°的趋势变化。不同轨道卫星的周跳探测结果见图 2。同时统计不同类型轨道卫星周跳探测的理论探测量(MW组合、(1, 0, -1)和(0, 1, -1)组合单位分别为周、m和m)、估计值、周跳修复值,结果见表 2。

|
图 2 MW组合、(1, 0, -1)组合和(0, 1, -1)组合加入小、大周跳条件下的周跳探测图 Fig. 2 Cycle slip detection diagram with MW combination, (1, 0, -1) combination and (0, 1, -1) combination added to small and large cycle conditions |
|
|
表 2 不同类型轨道卫星周跳探测结果 Tab. 2 Detection results of cycle slips of different types of orbiting satellites |
表 2分别对C02、C06和C12等3种不同轨道卫星加入不同大小的周跳并统计探测结果。分别在历元89、149、209、269和309处加入小周跳组合(1, 0, 0)、(0, 1, 0)、(0, 1, 1)、(1, 0, 1)和(1, 1, 1),在历元89和269处加入大周跳组合(2 363, 0, 1 920)和(0, 2 363, 2 483)。其中,加入的大周跳组合满足n1/n3=λ3/λ1和n2/n3=λ3/λ2的比例关系。表 2中的小周跳探测结果表明,对于C02、C06和C12卫星,如果周跳组合满足(n, n1, n2)且n1= n2,则MW探测量对这类周跳组合表现为不敏感; 无几何相位探测量(1, 0, 1)对满足周跳组合(0, n, 0)条件的周跳组合的探测结果为0.012 m,相对于图 1(c)中的探测范围[-0.005 m, 0.005 m],足以将周跳探测出来。只是图 2中无几何相位探测量(1, 0, -1)的探测精度范围在[-0.5 m, 0.5 m],远大于0.012 m,所以在图 2(a)、2(c)和2(e)中的无几何相位探测量(0, 1, -1)中的309历元中没有明显显示出来。同时,无几何相位探测量(1, 0, -1)对于特殊周跳组合n1/n3=λ3/λ1和只发生在B1频点的周跳不敏感; 无几何探测量(1, 0, -1)对于特殊周跳组合(0, n, 0)不敏感。无几何相位探测量(0, 1, -1)对于特殊周跳组合(n, 0, 0)不敏感,当C02、C06和C14卫星分别加入周跳组合(0, 1, 1)和(1, 1, 1)时,(0, 1, -1)的探测结果是0.012 m,相对于图 1中(0, 1, -1)探测精度范围,完全能够探测出来,只是图 2(a)、2(c)和2(e)中(0, 1, -1)的显示范围远远大于0.012 m,图中未能明显显示出来。对于图 2(b)、2(d)和2(f)中大周跳的探测结果,探测量未能探测出的不敏感周跳组合同小周跳的探测结果一致。虽然3组观测量在对北斗三频数据进行周跳探测的过程中,单独进行探测会存在不敏感周跳,但是采用3组观测值同时进行周跳探测的时候,就不存在不敏感周跳。实验结果说明,该方法能够探测出在任何位置出现的任意大小的周跳。
表 2统计了周跳修复的正确率。MW组合作为第1探测量,采用取整的方式进行周跳的修复,B2和B3频点的MW组合观测δΔN=0.190 1周,小于0.2周,取整成功率能够达到98.8%,可以确保MW组合成功修复周跳。对于第2、3探测量通过最小二乘原则得到的周跳探测值存在不稳定解的问题,需要采用最小二乘搜索的方法进行周跳的搜索和修复。结果表明,该方法能够准确修复各种大小的周跳。
3 结语针对现有MW组合存在伪距噪声大的问题,联合改进的MW组合和无几何相位组合对北斗三频周跳进行探测和修复,根据实验结果得到以下结论:
1) 采用B2和B3信号组成的北斗优选MW观测值伪距观测值较优,并且周跳探测精度相对于B1和B2、B1和B3信号组成的MW观测值的探测精度更高,更有利于周跳的探测和修复。
2) 优选的北斗MW观测值能有效地削弱组合观测量的电离层和噪声影响,提高周跳探测精度; 联合无几何相位组合(1, 0, -1)和(0, 1, -1)能够实时准确地探测大、小周跳。虽然MW组合及2个无几何相位组合对于一些特殊周跳组合不敏感,但3个探测量同时进行周跳探测,能有效减少不敏感周跳的数量,还能够准确修复探测到的大小周跳。
| [1] |
李明, 高星伟, 徐爱功. 一种改进的周跳多项式拟合方法[J]. 测绘科学, 2008, 33(4): 82-83 (Li Ming, Gao Xingwei, Xu Aigong. A Modified Polynomial Fitting of Cycle-Slip Processing[J]. Science of Surveying and Mapping, 2008, 33(4): 82-83 DOI:10.3771/j.issn.1009-2307.2008.04.027)
(  0) 0) |
| [2] |
陈品馨, 章传银, 黄昆学. 用相位减伪距法和电离层残差法探测和修复周跳[J]. 大地测量与地球动力学, 2010, 30(2): 120-124 (Chen Pinxin, Zhang Chuanyin, Huang Kunxue. Cycle Slips Detection and Repairing by Use of Phase Reduce Pseudorange Law and Ionized Layer Remnant Method of Difference[J]. Journal of Geodesy and Geodynamics, 2010, 30(2): 120-124)
(  0) 0) |
| [3] |
张小红, 曾琪, 何俊, 等. 构建阈值模型改善TurboEdit实时周跳探测[J]. 武汉大学学报:信息科学版, 2017, 42(3): 285-292 (Zhang Xiaohong, Zeng Qi, He Jun, et al. Improving TurboEdit Real-Time Cycle Slip Detection by the Construction of Threshold Model[J]. Geomatics and Information Science of Wuhan University, 2017, 42(3): 285-292)
(  0) 0) |
| [4] |
刘伟平, 郝金明, 汪平, 等. Kalman滤波在周跳探测与修复中的应用[J]. 大地测量与地球动力学, 2009, 29(6): 101-103 (Liu Weiping, Hao Jinming, Wang Ping, et al. Study on Cycle Slip Detection and Repair by Use of Kalman Filtering[J]. Journal of Geodesy and Geodynamics, 2009, 29(6): 101-103)
(  0) 0) |
| [5] |
Cai C S, Liu Z Z, Xia P F, et al. Cycle Slip Detection and Repair for Undifferenced GPS Observations under High Ionospheric Activity[J]. GPS Solutions, 2013, 17(2): 247-260 DOI:10.1007/s10291-012-0275-7
(  0) 0) |
| [6] |
甘雨, 隋立芬, 戚国宾, 等. 利用EMD阈值消噪改进MW组合周跳探测性能[J]. 大地测量与地球动力学, 2015, 35(4): 666-670 (Gan Yu, Sui Lifen, Qi Guobin, et al. Improving the Performance of MW Combined Observation on Cycle Slip Detection Using EMD Threshold De-Noising[J]. Journal of Geodesy and Geodynamics, 2015, 35(4): 666-670)
(  0) 0) |
| [7] |
范丽红, 王利, 张明, 等. 基于MW与STPIR组合的周跳探测与修复方法研究[J]. 武汉大学学报:信息科学版, 2015, 40(6): 790-794 (Fan Lihong, Wang Li, Zhang Ming, et al. A Combination of MW and Second-Order Time-Difference Phase Ionospheric Residual for Cycle Slip Detection and Repair[J]. Geomatics and Information Science of Wuhan University, 2015, 40(6): 790-794)
(  0) 0) |
| [8] |
刘柳, 吕志伟, 于晓东, 等. GNSS三频周跳探测与修复算法[J]. 测绘学报, 2017, 46(4): 453-459 (Liu Liu, Lü Zhiwei, Yu Xiaodong, et al. Real-Time Cycle-Slip Detection and Repair Algorithm of GNSS Triple-Frequency Observations[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(4): 453-459)
(  0) 0) |
| [9] |
黄令勇, 宋力杰, 王琰, 等. 北斗三频无几何相位组合周跳探测与修复[J]. 测绘学报, 2012, 41(5): 763-768 (Huang Lingyong, Song Lijie, Wang Yan, et al. Beidou Triple-Frequency Geometry-Free Phase Combination for Cycle-Slip Detection and Correction[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 763-768)
(  0) 0) |
| [10] |
张小红, 何锡扬. 北斗三频相位观测值线性组合模型及特性研究[J]. 中国科学:地球科学, 2015, 45(5): 601-610 (Zhang Xiaohong, He Xiyang. BDS Triple-Frequency Carrier-Phase Linear Combination Models and Their Characteristics[J]. Science China: Earth Sciences, 2015, 45(5): 601-610)
(  0) 0) |
| [11] |
李金龙, 杨元喜, 徐君毅, 等. 基于伪距相位组合实时探测与修复GNSS三频非差观测数据周跳[J]. 测绘学报, 2011, 40(6): 717-722 (Li Jinlong, Yang Yuanxi, Xu Junyi, et al. Real-Time Cycle-Slip Detection and Repair Based on Code-Phase Combinations for GNSS Triple-Frequency Un-Diffierenced Observations[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 717-722)
(  0) 0) |
| [12] |
Yao Y F, Gao J X, Wang J, et al. Real-Time Cycle-Slip Detection and Repair for Beidou Triple-Frequency Undifferenced Observations[J]. Survey Review, 2016, 48(350): 367-375 DOI:10.1080/00396265.2015.1133518
(  0) 0) |
| [13] |
姚一飞, 高井祥, 王坚, 等. 北斗三频载波观测值的周跳实时探测与修复[J]. 中国矿业大学学报, 2014, 43(6): 1 140-1 148 (Yao Yifei, Gao Jingxiang, Wang Jian, et al. Real-Time Cycle-Slip Detection and Repair for Compass Triple-Frequency Carrier Phase Observations[J]. Journal of China University of Mining and Technology, 2014, 43(6): 1 140-1 148)
(  0) 0) |
2. School of Navigation and Aerospace Target, Information Engineering University, 62 Kexue Road, Zhengzhou 450001, China
 2019, Vol. 39
2019, Vol. 39

