大地测量反演是大地测量研究的主要方式之一,即利用大地测量技术(如GPS观测、水准测量、重力测量等)测得的地表形变来解释地壳深部断层滑动的动力过程。利用多种数据联合反演能更客观、准确地反映地壳深部断层运动特征,进而对其真实运动规律进行研判和解释,国内外学者在此方面已有一定的研究成果。Lisowski等[1]利用多种大地测量数据对1989年加州洛马普列塔地震同震滑动进行联合反演; 李爽等[2]研究多种数据联合反演模式及算法; 刘琦等[3]利用GPS、水准和强震动观测资料联合反演2013年芦山7.0级地震同震滑动分布; Zhao[4]利用重力和GPS数据对红河断裂带活动进行反演计算。本文将一种新的群智能算法——微粒群优化算法(particle swarm optimization,PSO)引入到大地测量联合反演非线性算法的研究中[5],并基于GPS和水准数据对祁连山北缘断裂三维滑动速率进行反演。
1 带惯性权重微粒群算法的原理及方法微粒群优化算法基本原理来源于人工生命,假设有n+1个微粒,微粒群以特定速率在D维空间中运动,运动速率根据个体微粒运动速率与微粒群运动速率经验进行实时动态调整。
在微粒群进化方程中引入惯性权重因子w以优化微粒群算法,此时微粒i在D维中的位置x与速度v的更新公式为[6]:
| $ \begin{array}{l} {v_{ij}}(k + 1) = w{v_{ij}}(k) + {c_1}{r_{1j}}\left[ {{p_{ij}}(k) - {x_{ij}}(k)} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{c_2}{r_{2j}}(k)\left[ {{g_j}(k) - {x_{ij}}(k)} \right] \end{array} $ | (1) |
| $ {\mathit{x}_{\mathit{ij}}}{\rm{(}}\mathit{k}{\rm{ + 1) = }}{\mathit{x}_{\mathit{ij}}}{\rm{(}}\mathit{k}{\rm{) + }}{\mathit{v}_{\mathit{ij}}}{\rm{(}}\mathit{k}{\rm{ + 1)}} $ | (2) |
式中,w为惯性权重,使微粒保持运动惯性,在算法开始时,赋予w一较大正值,用以保证微粒在算法初始阶段能以较大的速度步长在整个空间内搜索优秀种子,w在搜索过程中逐渐线性减小,保证微粒在后期搜索中更容易得到全局最优解[7]; c1、c2为微粒运动的加速度,用以调整全局最优微粒和个体最优微粒的最大运动步长[8]; r1j、r2j的区间范围为[0, 1];pij=(pi1, pi2, …piD)为个体微粒i的最优位置; gj=(g1, g2, …gD)为微粒群的全局最优位置。Vi=(vi1, vi2, …viD)为微粒i当前飞行的速度; Xi=(xi1, xi2, …xiD)为微粒i当前的位置。
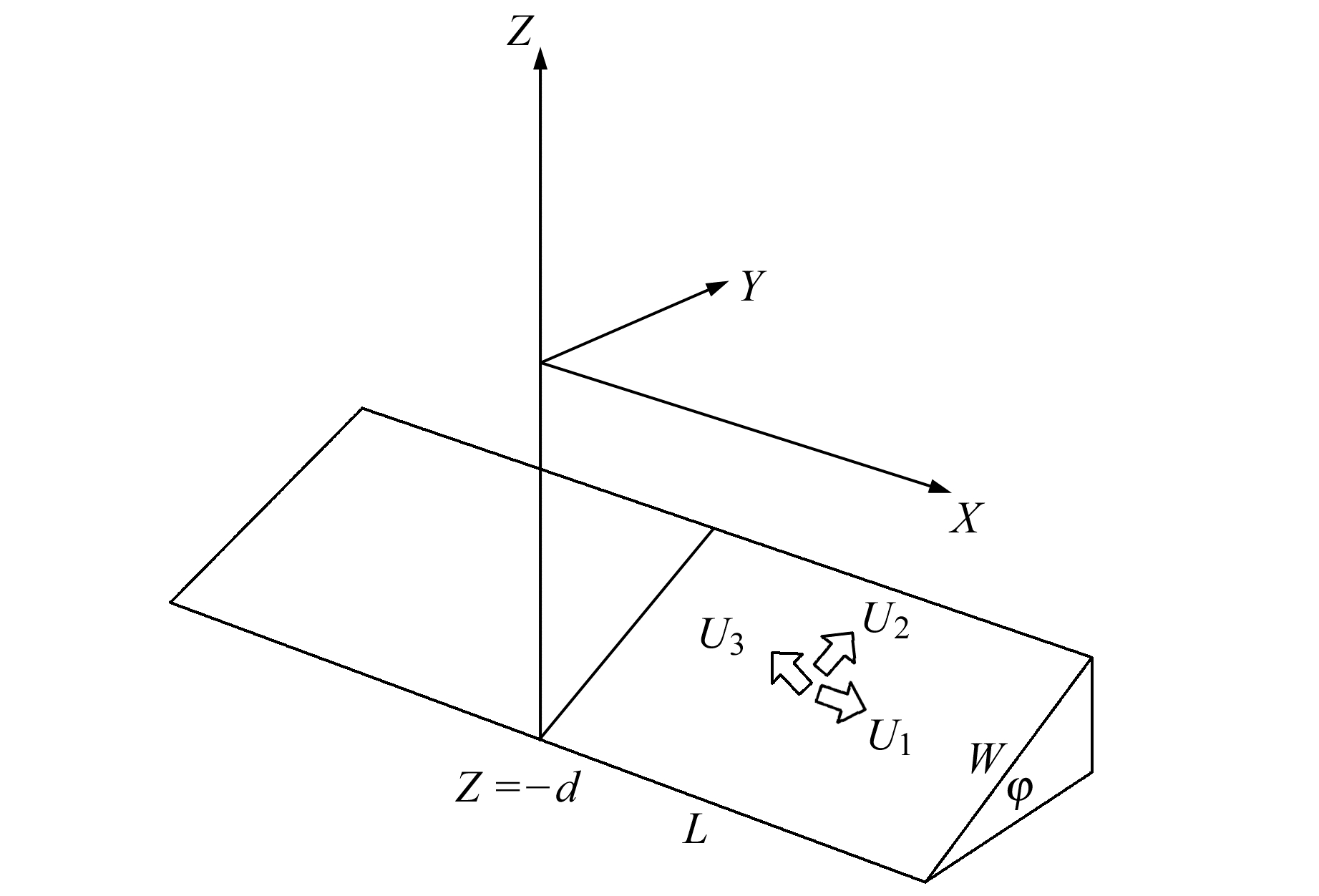
2 矩形位错理论模型断层参数(包括断层倾角φ、断层长度L、断层宽度W、断层深度d,矩形断层上盘相对于下盘分别在走向、倾向和法向的滑动量Ui(i=1, 2, 3)[9])与地面上GPS观测的三维位移速率场之间的关系可通过如下矩形位错理论模型来表示[10-11]。图 1中,X轴指向断层走向,Z轴指向断层的垂线方向,Y轴构成右手坐标系。
|
图 1 矩形位错模型 Fig. 1 Rectangle dislocation model |
GPS观测得到的地面三维位移场速率ui(i= x, y, z)可以写为:
| $ {u_i} = f\left( {\xi , \eta , \zeta , {U_j}, L, W, d, \varphi } \right) $ | (3) |
为了验证微粒群算法在联合反演中的有效性和稳定性,深入理解实际三维形变场与断层深部活动的关系,利用位错模型引起的地表水平位移和高程变化的解析式,结合祁连山北缘断裂的地质背景及青藏高原东北缘2001~2004年GPS数据和2000~2006年水准数据,对断裂的三维滑动速率进行联合反演。建立2种数据联合反演模型的关键步骤之一就是确定2种数据在反演中所占的权重[12]。本文采用2种定权方案:方案1为常规定权法,即根据粗略的先验信息,较主观地取λ∈(0, 1)内的某一数值; 方案2为把λ作为未知数,与断层参数一同反演,确定权重。
联合反演模型(目标函数)为:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;{\lambda _{{\rm{GPS}}}}\sum\limits_{{\rm{GPS}}} {{{\left( {\frac{{{u^{{\rm{obs}}}} - u(m)}}{{{u^{{\rm{obs}}}}}}} \right)}^2}} + \\ \left( {1 - {\lambda _{{\rm{GPS}}}}} \right)\sum\limits_{{\rm{leveling }}} {{{\left( {\frac{{{h^{{\rm{obs}}}} - h(m)}}{{{h^{{\rm{obs}}}}}}} \right)}^2}} = \min \end{array} $ | (4) |
式中,λGPS为GPS观测得到的水平位移在目标函数中所占权重; uobs、hobs分别为GPS和水准测量的实测值; u(m)、h(m)分别为利用位错理论模型计算出的地表水平位移和高程变化值。
为使模型更接近真实断裂带,采用微分思想,将复杂断裂看成是多个小的矩形断层组合[12],根据断裂带的分布排列等几何特征进行断裂形态的几何分段。
方案1中,给定λGPS的值为0.5,利用微粒群算法进行联合反演,反演结果见表 1。
|
|
表 1 方案1反演结果 Tab. 1 Inversion results of plan 1 |
方案2中,将权λGPS限定在[0, 1]区间内作为未知参数与断层三维滑动速率一同反演,即要求微粒群在四维空间(U1, U2, U3, λGPS)中搜索,最终输出反演结果见表 2。
|
|
表 2 方案2反演结果 Tab. 2 Inversion results of plan 2 |
表 3为蚁群算法联合反演断层滑动速率的反演结果。从表 1~3不难发现,祁连山北缘断裂主要滑动特征为右旋走滑和逆冲,且空间分布不均匀。断裂右旋走滑和逆冲2个分量明显大于挤压分量,与前人结论[13-16]基本一致。比较以上反演结果, 并列于表 4。
|
|
表 3 蚁群反演结果 Tab. 3 Inversion results by ant colony algorithm |
|
|
表 4 反演结果比较 Tab. 4 Comparison of inversion results |
由表 4看出,无论是数值还是数据的稳定性和收敛程度,微粒群算法反演结果都优于蚁群算法。而方案2通过灵活调整观测值所占权重,更合理地反映了不同观测值在不同区域的响应大小,其结果优于方案1。
4 结语1) 微粒群算法收敛速度快、稳定性高,结合经典的矩形位错理论模型,是一种可以有效求解断层三维滑动速率反演问题的优化算法。
2) 祁连山北缘断裂滑动空间分布不均匀,其主要运动特征是以右旋走滑和逆冲为主,同时兼有相互挤压。
3) 在多种数据联合反演计算中,不同类别的测量数据所占权重不同。以水准数据和GPS数据为例,若二者分布大致均衡,在联合反演中,GPS数据所占的权重远大于水准数据,也就意味着以走滑和倾滑为主的断层深部运动带来的地面响应以水平运动为主。同时,顾及权比的方法比常规定权的方法得到的结果与地质资料更吻合。
| [1] |
Lisowski M, Prescott W H, Savage J C, et al. Geodetic Estimate of Coseismic Slip during the 1989 Loma Prieta, California, Earthquake[J]. Geophysical Research Letters, 1990, 17(9): 1 437-1 440 DOI:10.1029/GL017i009p01437
(  0) 0) |
| [2] |
李爽, 许才军, 王新洲. 论多种数据联合反演的模式及算法[J]. 大地测量与地球动力学, 2002, 22(3): 78-82 (Li Shuang, Xu Caijun, Wang Xinzhou. Models and Algorithms of Joint Inversion with Verious Kinds of Data[J]. Journal of Geodesy and Geodynamics, 2002, 22(3): 78-82)
(  0) 0) |
| [3] |
刘琦, 闻学泽, 邵志刚. 基于GPS、水准和强震动观测资料联合反演2013年芦山7.0级地震同震滑动分布[J]. 地球物理学报, 2016, 59(6): 2 113-2 125 (Liu Qi, Wen Xueze, Shao Zhigang. Joint Inversion for Coseismic Slip of the 2013 MS7.0 Lushan Earthquake from GPS and the Strong Motion Observation[J]. Chinese Journal of Geophysics, 2016, 59(6): 2 113-2 125)
(  0) 0) |
| [4] |
Zhao S R. Joint Inversion of Observed Gravity and GPS Baseline Changes for the Detection of the Active Fault Segment at the Red River Fault Zone[J]. Geophysical Journal International, 1995, 122(1): 70-88 DOI:10.1111/j.1365-246X.1995.tb03537.x
(  0) 0) |
| [5] |
杨维, 李歧强. 粒子群优化算法综述[J]. 中国工程科学, 2004, 6(5): 87-94 (Yang Wei, Li Qiqiang. Survey on Particle Swarm Optimization Algorithm[J]. Engineering Science, 2004, 6(5): 87-94 DOI:10.3969/j.issn.1009-1742.2004.05.018)
(  0) 0) |
| [6] |
Parsopoulos K E, Plagianakos V P, Magoulas G D, et al.Improving Particle Swarm Optimizer by Function" Stretching" [A]//Hadjisavvas N, Pardalos P.Advances in Convex Analysis and Global Optimization[M].The Netherlands: Kluwer Academic Publishers, 2001
(  0) 0) |
| [7] |
刘杰, 张永志, 王宏宇, 等. 用多种数据及粒子群算法反演河西地区主要断层运动[J]. 大地测量与地球动力学, 2010, 30(5): 28-31 (Liu Jie, Zhang Yongzhi, Wang Hongyu, et al. Activities of Main Faults in Hexi Area Inversed by Using Particle Swarm Optimization Algorithm from Multiple Data[J]. Journal of Geodesy and Geodynamics, 2010, 30(5): 28-31)
(  0) 0) |
| [8] |
Eberhart R C, Shi Y H.Particle Swarm Optimization: Developments, Applications and Resources[C].Proceedings of the IEEE Congress on Evolutionary Computation, Piscataway, 2001
(  0) 0) |
| [9] |
刘杰.粒子群算法反演断层滑动速率[D].西安: 长安大学, 2011 (Liu Jie.Three-Dimension Slip Velocity of Faults Inversed by Particle Swarm Optimization[D].Xi'an: Chang'an University, 2011) http://cdmd.cnki.com.cn/article/cdmd-11941-1011186169.htm
(  0) 0) |
| [10] |
Okada Y. Surface Deformation Due to Shear and Tensile Faults in a Half-Space[J]. Bulletin of the Seismological Society of America, 1985, 75(4): 1 135-1 154
(  0) 0) |
| [11] |
Okada Y. Internal Deformation Due to Shear and Tensile Faults in a Half-Space[J]. Bulletin of the Seismological Society of America, 1992, 82(2): 1 018-1 040
(  0) 0) |
| [12] |
独知行, 欧吉坤, 靳奉祥, 等. 联合反演模型中相对权比的优化反演[J]. 测绘学报, 2003, 32(1): 15-19 (Du Zhixing, Ou Jikun, Jin Fengxiang, et al. Optimizing Inversion of Relative Power in Joint Inversion Model[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(1): 15-19 DOI:10.3321/j.issn:1001-1595.2003.01.004)
(  0) 0) |
| [13] |
业成之. 祁连山北缘断裂带的现代构造运动[J]. 地震地质, 1990, 12(3): 275-281 (Ye Chengzhi. Recent Tectonic Movement along the North-Frontal Qilianshan Fault Zone[J]. Sismology and Geology, 1990, 12(3): 275-281)
(  0) 0) |
| [14] |
张希, 江在森, 王双绪, 等. 青藏块体东北缘GPS与水准资料的三维负位错联合反演[J]. 国际地震动态, 2007(7): 61-66 (Zhang Xi, Jiang Zaiseng, Wang Shuangxu, et al. United Inversion of Three-Dimensional Negative Dislocation by GPS and Leveling Observation in Northeastern Margins of Qinghai-Tibet Block[J]. Recent Developments in World Seismology, 2007(7): 61-66 DOI:10.3969/j.issn.0253-4975.2007.07.009)
(  0) 0) |
| [15] |
国家地震局地质研究所, 国家地震局兰州地震研究所. 祁连山-河西走廊活动断裂系[M]. 北京: 地震出版社, 1993 (Institute of Seismology of State Seismological Bureau, Lanzhou Institute of Seismology of State Seismological Bureau. Active Fault System of Qilian-Hexi[M]. Beijing: Seismological Press, 1993)
(  0) 0) |
| [16] |
丁国瑜, 蔡文伯. 中国岩石圈动力学概论[M]. 北京: 地震出版社, 1991 (Ding Guoyu, Cai Wenbo. Introduction to Lithospheric Dynamics of China[M]. Beijing: Seismological Press, 1991)
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39

