2. 国家自然资源部大地测量数据处理中心,西安市友谊东路334号,710054;
3. 西安长庆科技工程有限责任公司,西安市未央路151号,710018;
4. 山东省国土测绘院,济南市经十路2301号,250102
地壳垂直运动的长期观测可为国家提供地面沉降信息,对环境预测、防灾减灾具有重要意义,也极大地推动了大陆动力学、区域应力场以及地壳运动等方面的研究。大地测量是定量描述地壳垂直运动的重要方法之一,而多期精密水准观测数据是地壳垂直运动研究最可靠的基础数据。国内外学者利用多次开展的全国、区域范围的精密水准测量分析地壳垂直运动规律[1-2]。GNSS技术是地壳运动研究的新方法,已应用于青藏高原等典型地区的地壳运动监测[3-6]。Hao等[7]将GNSS点垂直运动速度作为约束条件,研究GNSS与水准融合的青藏高原地壳垂直运动。国内外学者也利用多项式[2]、多面函数[8-9]等方法建立地壳运动模型。在目前地壳垂直运动的研究中,通常利用稳定的水准点构建地壳垂直运动模型,但实际中可能会出现水准稳定点分布不均匀甚至空白区的情况,无法实现地壳垂直运动的有效建模。而国家、行业、省市CORS系统已正常运营,分布均匀且稳定的CORS能够改善地壳垂直运动建模点的分布状况,有利于提高区域地壳垂直运动模型的精度与可靠性。
基于以上研究,本文提出一种GNSS与水准融合的地壳垂直运动模型建立方法,利用稳定的CORS数据填补水准网站的空白区,解决少量稳定水准点无法建模的问题,提高区域地壳垂直运动的模型精度。
1 GNSS与水准数据处理 1.1 GNSS数据处理利用山东省136个CORS与陆态网络18个CORS 2010~2015年观测数据计算站点三维速度,按照沉降范围将测站分3区进行解算。计算分2步[10]:1)利用GAMIT软件求解基准站单日解,得到H文件。GLOBK将区域子网的单日松弛解H文件与SOPAC提供的全球子网的单日松弛解H文件进行合并,得到包含全球IGS站点和山东CORS坐标的单日松弛解及方差-协方差矩阵。利用GLOBK通过7参数相似变换,将各站点坐标的单日松弛解变换至IGS核心站坐标定义的ITRF2008框架下,得到ITRF2008框架下的坐标单日解。2)扣除坐标序列中大气、土壤水及积雪、非海洋潮汐等负荷影响,获得测站坐标序列及速度。
1.2 多期水准网数据处理采用Kalman滤波方法处理多期精密水准网数据,该方法在动力学模型预报的基础上,利用观测信息进一步修正,提高计算结果的可靠性。
动力学模型预报值
| ${\mathit{\boldsymbol{\bar X}}_k} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k, k - 1}}\mathit{\boldsymbol{\hat X}}{}_{k - 1}$ | (1) |
| ${\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{{{\mathit{\bar X}}_k}}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k, k - 1}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{{{\mathit{\hat X}}_{k - 1}}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k, k - 1}^T + {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{{W_k}}}$ | (2) |
式中,
Kalman滤波解及协方差矩阵为:
| ${\mathit{\boldsymbol{\hat X}}_k} = {\mathit{\boldsymbol{\bar X}}_k} + {\mathit{\boldsymbol{K}}_k}({\mathit{\boldsymbol{L}}_k} - {\mathit{\boldsymbol{A}}_k}{\mathit{\boldsymbol{\bar X}}_k})$ | (3) |
| ${\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{{{\mathit{\hat X}}_k}}} = (\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_k}{\mathit{\boldsymbol{A}}_k}){\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{{{\mathit{\bar X}}_\mathit{k}}}}$ | (4) |
式中,Kk为增益矩阵; Lk为高差观测向量; Ak为系数矩阵; I为单位矩阵。
2 区域垂直运动模型建立方法董鸿闻等[2]结合地质构造理论,将垂直运动分为地表垂直运动与地壳垂直运动,垂直运动模型为:
| $\begin{array}{l} \mathit{\boldsymbol{V}} = {\mathit{\boldsymbol{A}}_0}{\mathit{\boldsymbol{X}}_0} + \mathit{\boldsymbol{B\lambda }} - \mathit{\boldsymbol{L}} = {\mathit{\boldsymbol{A}}_0}{\mathit{\boldsymbol{X}}_0} + \mathit{\boldsymbol{B}}(\mathit{\boldsymbol{\lambda '}} + \mathit{\boldsymbol{\lambda ''}}) - \\ \;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{L}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_0}}&\mathit{\boldsymbol{B}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{X}}_0}}\\ {\mathit{\boldsymbol{\lambda ''}}} \end{array}} \right] + \mathit{\boldsymbol{B\lambda '}} - \mathit{\boldsymbol{L}} \end{array}$ | (5) |
式中,λ′为地壳垂直运动参数向量; λ″为地表垂直运动参数向量; B为垂直运动速度对应系数矩阵; X0为待估点高程未知参数; A0为高程未知参数对应的系数矩阵; V为残差向量。
地壳垂直运动速率λ′i可以采用三次多项式拟合:
| $ \begin{array}{l} \lambda _i^\prime = {a_0} + {a_1}\Delta {B_i} + {a_2}\Delta {L_i} + {a_3}{\left( {\Delta {B_i}} \right)^2} + \\ \;{a_4}\Delta {B_i}\Delta {L_i} + {a_5}{\left( {\Delta {L_i}} \right)^2} + {a_6}{\left( {\Delta {B_i}} \right)^3} + \\ {a_7}{\left( {\Delta {B_i}} \right)^2}\Delta {L_i} + {a_8}\Delta {B_i}{\left( {\Delta {L_i}} \right)^2} + {a_9}{\left( {\Delta {L_i}} \right)^3} \end{array} $ | (6) |
式中,ΔBi、ΔLi为某点相对于参考点的纬度差、经度差。则某点地表垂直运动速率λ″i为:
| ${\mathit{\lambda ''}_i} = {\lambda _i} - {\lambda _i}^\prime $ | (7) |
将多项式系数作为待估参数:
| $ \mathit{\boldsymbol{x}} = {\left[ {\begin{array}{*{20}{c}} {{a_0}}&{{a_1}}&{{a_2}}&{{a_3}}&{{a_4}}&{{a_5}}&{{a_6}}&{{a_7}}&{{a_8}}&{{a_9}} \end{array}} \right]^{\rm{T}}} $ | (8) |
按照水准点、CORS稳定点的地表垂直速率平方和最小原则,引入抗差估计原理,抑制异常误差影响,提高参数估计精度。目标函数为:
| $\min = \mathit{\Omega } = \sum\limits_{i = 1}^n {{p_i}\rho ({{\mathit{\lambda ''}}_i}} )$ | (9) |
参数抗差估计解为[11]:
| $ \mathit{\boldsymbol{\hat X}} = {\left( {\mathit{\boldsymbol{A}}_1^{\rm{T}}{{\mathit{\boldsymbol{\overline P}} }_1}{\mathit{\boldsymbol{A}}_1}} \right)^{ - 1}}\mathit{\boldsymbol{A}}_1^{\rm{T}}{\mathit{\boldsymbol{\overline P}} _1}{\mathit{\boldsymbol{l}}_1} $ | (10) |
式中,l1=λ-A1x0; A1为系数矩阵; x0为参数近似值。
| ${\mathit{\boldsymbol{\bar P}}_i} = \left\{ {\begin{array}{*{20}{c}} {1.0}&{}&{\left| {\frac{{{\mathit{\boldsymbol{V}}_i}}}{{{\sigma _0}}}} \right| \le {k_0}}\\ {\left| {\frac{{{k_0}{\sigma _0}}}{{{\mathit{\boldsymbol{V}}_i}}}} \right|}&{}&{\left| {\frac{{{\mathit{\boldsymbol{V}}_i}}}{{{\sigma _0}}}} \right| > {k_0}} \end{array}} \right.$ | (11) |
式中,初始权矩阵P1根据高差观测值精度确定; Vi为第i个观测值残差; k0取值范围为1.0~1.5;σ0为残差中位数。
3 算例分析算例采用山东省及周边地区CORS的GNSS观测数据和多期精密水准数据,GNSS观测时间为2010~2015年,水准点为一等水准点,共4期,观测时间分别为1960年左右、1980年左右、1988年左右以及2012年左右。为了保持水准点与CORS速度的同期性,尽量选取1998年与2012年观测的水准点; 对于点稀疏区,根据具体情况选取稳定点。对于CORS,尽可能选取基岩点; 对于稀疏区,也可以选取稳定点。利用山东省80多个CORS、山东省及周边多期500多个水准点成果建立地壳垂直运动模型。
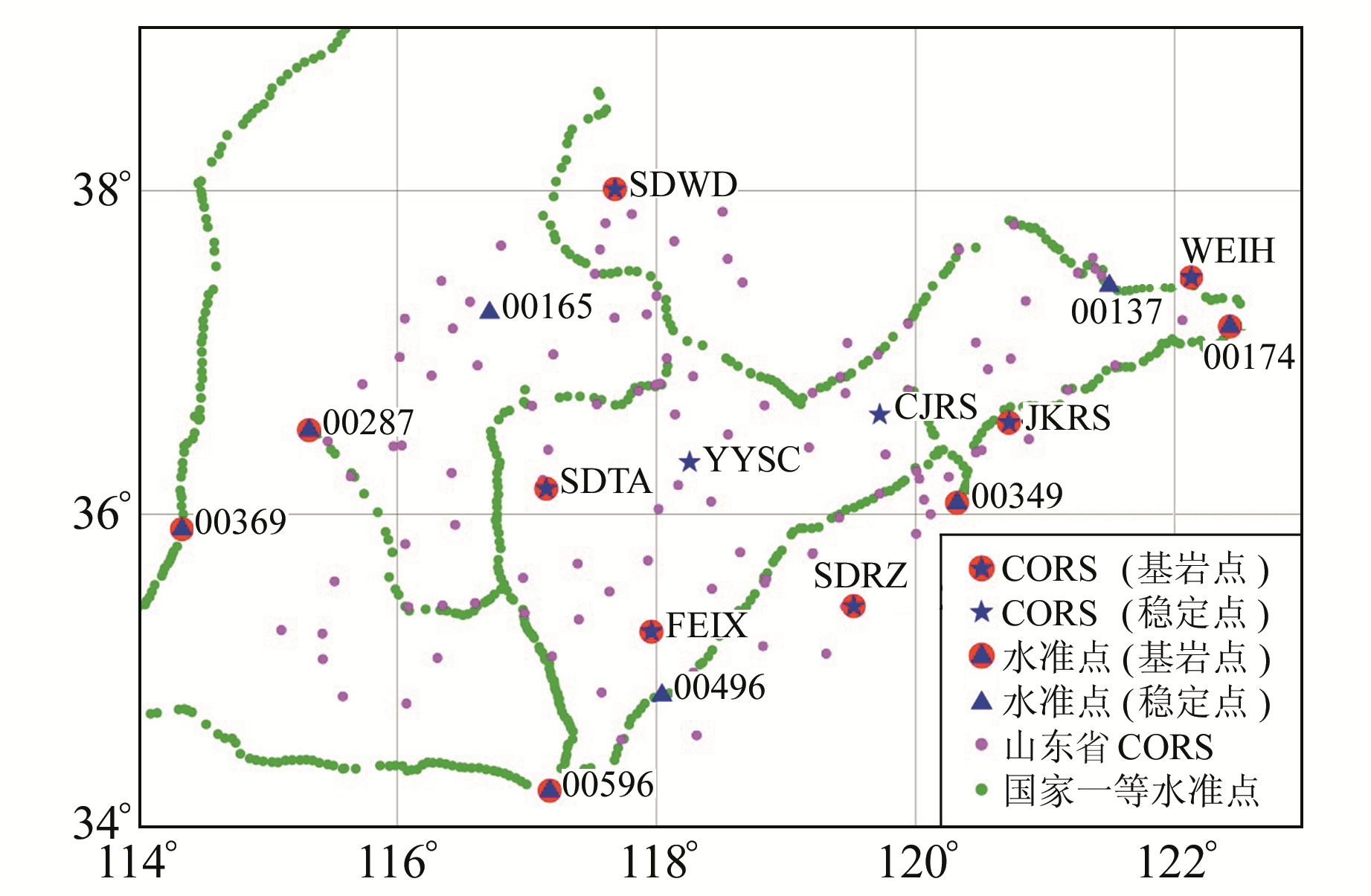
考虑点位分布的均匀性、稳定性,最终选取6个基岩点、2个稳定点CORS以及8个水准稳定点作为拟合点,详细信息见表 1,分布见图 1。
|
|
表 1 GNSS、水准点信息 Tab. 1 The information of GNSS points and level points |
|
图 1 地壳垂直运动建模所用的GNSS、水准点分布 Fig. 1 The distribution of GNSS and level points for vertical crustal movement model |
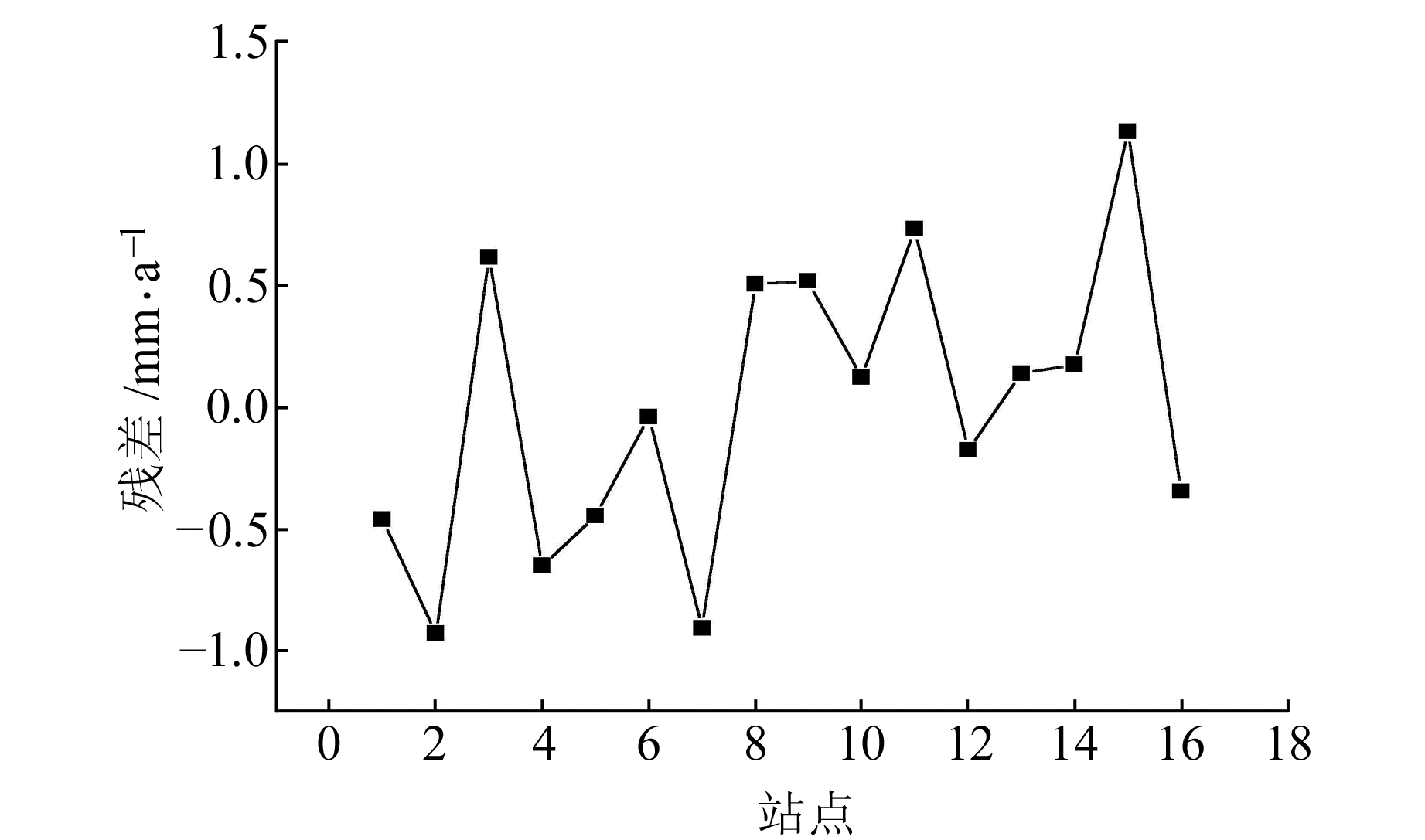
采用多项式拟合地壳垂直运动模型,水准点、CORS的权根据其垂直运动速度精度确定,利用IGGⅡ等价权函数抑制异常数据影响,拟合精度为0.6 mm,拟合点残差见图 2,山东区域地壳垂直运动等值线见图 3。
|
图 2 地壳垂直运动拟合点残差 Fig. 2 The residual graph of fitting points for vertical crustal movement model |

|
图 3 地壳垂直运动等值线 Fig. 3 The contours of vertical crustal movement |
由以上计算结果可以看出:
1) 利用稳定的CORS与水准点数据获取了高精度的区域垂直运动速度λ; 利用地表垂直运动速率平方和最小原则,采用三次多项式拟合方法,通过IGGⅡ等价权函数抑制异常数据影响,获得了内符合精度0.6 mm的高精度区域地壳垂直运动速度λ′,提高了区域地壳垂直模型的精度。
2) 采用稳定的CORS与水准点建立高精度区域地壳垂直运动模型,充分发挥了高精度水准数据的可靠性; 利用稳定的CORS填补了水准点空白区,提高了地壳垂直运动建模控制点的密度。根据垂直方向精度确定权值,在一定程度上实现了GNSS与水准数据的有效融合,该方法克服了因水准点数量少而无法建立模型的问题,改善了区域地壳垂直模型的可靠性。
3) 该地壳垂直运动模型与利用GNSS数据获取的垂直运动模型存在一定的差异。在地壳垂直运动建模过程中,首先选取了稳定的水准点和CORS,即使在沉降区域,也是选取垂直运动速度较小的控制点,尽量降低地面沉降造成的垂直运动影响。该模型基本上能够反映山东区域地壳垂直运动整体趋势,更加接近于采用稳定水准基准点所建立的地壳垂直运动模型。
4) 山东区域地壳垂直运动呈现北降南升、西北降东南升的总体趋势。与江苏交界处最大上升速率约为5 mm/a,山东半岛也呈5 mm/a上升趋势; 德州区域最大下降速率为5 mm/a,菏泽地区下降速率也达到4 mm/a。该地壳垂直运动结果与董鸿闻等[2]的研究结果基本一致。
4 结语GNSS与水准数据融合是区域地壳垂直运动研究的发展趋势,这有利于发挥GNSS高时间分辨率和水准的高精度优势,同时也能克服因水准点少而无法建模的弊端。随着国家、行业、省市CORS系统的逐步完善,连续或多期GNSS数据将成为地壳垂直运动研究的重要基础数据,大大提升地壳垂直运动模型建立的控制点密度与模型精度。现代大地基准一期工程项目已经获得新一期全国一等水准观测数据,这些数据也蕴含着丰富的大陆地壳垂直运动信息。因此,利用多期GNSS和水准资料研究全国地壳垂直运动长期变化与近期变化是当前大地测量与地球动力学工作者的重要任务。
致谢: 感谢山东省国土测绘院与陆态网络中心提供的观测数据。
| [1] |
Kowalczyk K, Rapinski J. Adjustment of Vertical Crustal Movement Network on the Basis of Last Three Leveling Campaigns in Poland[J]. Reports on Geodesy and Geoinformatics, 2012, 92(1): 123-134
(  0) 0) |
| [2] |
董鸿闻, 顾旦生, 李国智, 等. 中国大陆现今地壳垂直运动研究[M]. 西安: 西安地图出版社, 2002 (Dong Hongwen, Gu Dansheng, Li Guozhi, et al. Research on Vertical Recent Crustal Movement of the Mainland of China[M]. Xi'an: Xi'an Cartographic Publishing House, 2002)
(  0) 0) |
| [3] |
顾国华. GPS观测得到的中国大陆地壳垂直运动[J]. 地震, 2005, 25(3): 1-8 (Gu Guohua. Vertical Crustal Movement Obtained from GPS Observation in China's Mainland[J]. Earthquake, 2005, 25(3): 1-8)
(  0) 0) |
| [4] |
王双绪, 蒋锋云, 郝明, 等. 青藏高原东缘现今三维地壳运动特征研究[J]. 地球物理学报, 2013, 56(10): 3 334-3 345 (Wang Shuangxu, Jiang Fengyun, Hao Ming, et al. Investigation of Features of Present 3D Crustal Movement in Eastern Edge of Tibet Plateau[J]. Chinese Journal of Geophysics, 2013, 56(10): 3 334-3 345)
(  0) 0) |
| [5] |
梁诗明.基于GPS观测的青藏高原现今三维地壳形运动研究[D].北京: 中国地震局地质研究所, 2014 (Liang Shiming. Three Dimensional Velocity Field of Present-Day Crustal Motion of the Tibetan Plateau Inferred from GPS Measurements[D]. Beijing: Institute of Geology, CEA, 2014)
(  0) 0) |
| [6] |
陈醒, 程鹏飞, 成英燕, 等. 基于河北CORS的地壳垂直运动速度场模型研究[J]. 大地测量与地球动力学, 2013, 33(4): 48-51 (Chen Xing, Cheng Pengfei, Cheng Yingyan, et al. Model of Crustal Vertical Movement Velocity Field Based in Hebei CORS Network[J]. Journal of Geodesy and Geodynamics, 2013, 33(4): 48-51)
(  0) 0) |
| [7] |
Hao M, Wang Q L, Shen Z K, et al. Present Day Crustal Vertical Movement Inferred from Precise Leveling Data in Eastern Margin of Tibetan Plateau[J]. Tectonophysics, 2014, 632: 281-292 DOI:10.1016/j.tecto.2014.06.016
(  0) 0) |
| [8] |
王文利, 陈士银, 董鸿闻, 等. 利用多面函数拟合中国陆地垂直运动速率图[J]. 测绘通报, 2002(8): 6-8 (Wang Wenli, Chen Shiyin, Dong Hongwen, et al. China Vertical Crustal Movement Rate Chart Made by Multiple-Surface Function Fitting[J]. Bulletin of Surveying and Mapping, 2002(8): 6-8 DOI:10.3969/j.issn.0494-0911.2002.08.002)
(  0) 0) |
| [9] |
曾安敏, 秦显平, 刘光明, 等. 中国大陆水平运动速度场的多面函数模型[J]. 武汉大学学报:信息科学版, 2013, 38(4): 394-398 (Zeng Anmin, Qin Xianping, Liu Guangming, et al. Hardy Multi-Quadric Fitting Model Chinese Mainland Horizontal Crustal Movement[J]. Geomatics and Information Science of Wuhan University, 2013, 38(4): 394-398)
(  0) 0) |
| [10] |
姜卫平, 夏传义, 李昭, 等. 环境负载对区域GPS基准站时间序列的影响分析[J]. 测绘学报, 2014, 43(12): 1 217-1 223 (Jiang Weiping, Xia Chuanyi, Li Zhao, et al. Analysis of Environmental Loading Effects on Regional GPS Coordinate Time Series[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(12): 1 217-1 223)
(  0) 0) |
| [11] |
杨元喜. 自适应动态导航定位[M]. 北京: 测绘出版社, 2006 (Yang Yuanxi. Adaptive Navigation and Kinematic Positioning[M]. Beijing: Surveying and Mapping Press, 2006)
(  0) 0) |
2. Geodetic Data Processing Centre of Ministry of Natural Resources, 334 East-Youyi Road, Xi'an 710054, China;
3. Xi'an Changqing Technology Engineering Co Ltd, 151 Weiyang Road, Xi'an 710018, China;
4. Institute of Land Surveying and Mapping of Shandong Province, 2301 Jingshi Road, Ji'nan 250102, China
 2019, Vol. 39
2019, Vol. 39


