2. 国家自然资源部流域生态与地理环境监测重点实验室, 南昌市广兰大道 418 号, 33001;
3. 江西省数字国土重点实验室, 南昌市广兰大道418号, 330013
病态问题在测量数据处理过程中时常碰见,随着总体最小二乘(TLS)理论的拓展,病态同样出现在TLS算法中。为解决这类问题,葛旭明等[1]推导出病态TLS广义正则化法;袁振超等[2]推导了病态TLS正则化法;王乐洋等[3]将处理病态问题的虚拟观测解法应用于TLS算法中。在考虑加权的情况下,王乐洋等[4]推导了病态加权TLS平差的岭估计解法,顾勇为等[5]推导了病态加权TLS靶向病灶的正则化方法。
与林东方等[6]提出的用法矩阵小奇异值对应的特征向量构造正则化矩阵的方法相似,王乐洋等[4]的病态加权TLS靶向病灶的正则化方法根据系数矩阵的列向量是否受扰将系数矩阵分成受扰矩阵和非受扰矩阵,求得正则化矩阵后靶向修正奇异值。现存在的问题是,在TLS迭代中,系数矩阵不断微变,若要靶向修正,正则化矩阵也应随之而变。针对此问题,本文推导了2种病态TLS靶向奇异值修正法,均是先求出新系数矩阵,再求靶向修正的正则化矩阵,最后迭代计算出最佳估值。用算例进行实验,并与多种方法进行对比,结果表明,本文方法有一定优势。
1 病态总体最小二乘正则化法G-M模型是顾及观测向量L的随机误差e,平差模型及最小二乘平差准则为:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{L}} = \mathit{\boldsymbol{AX}} + \mathit{\boldsymbol{e}},\mathit{\boldsymbol{e}} \sim N\left( {0,\sigma _0^2\mathit{\boldsymbol{I}}} \right)\\ f\left( \mathit{\boldsymbol{e}} \right) = {\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{e}} = \min \end{array} \right. $ | (1) |
式中,A为m×n系数矩阵,L为m×1观测向量,X为n×1未知参数向量,σ02是单位权方差,e为n×1随机误差向量。其最小二乘估计及估计的协方差为:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\hat X}} = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{L}}\\ {\mathop{\rm cov}} \left( {\mathit{\boldsymbol{\hat X}}} \right) = \sigma _0^2{\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}} \right)^{ - 1}} \end{array} \right. $ | (2) |
最小二乘估计是无偏估计,方差可由协方差矩阵之迹表示[7]:
| $ D\left( {\mathit{\boldsymbol{\hat X}}} \right) = {\rm{tr}}\left[ {{\mathop{\rm cov}} \left( {\mathit{\boldsymbol{\hat X}}} \right)} \right] = \sigma _0^2\sum\limits_{i = 1}^n {\frac{1}{{\mathit{\Lambda }_i^2}}} $ | (3) |
式中,Λi为系数矩阵A的奇异值。
随着测量数据的复杂多样性,顾及到A存在一定的误差,观测模型变成EIV模型,在EIV模型下的TLS平差较为合理。EIV模型为:
| $ \mathit{\boldsymbol{L}} = \left( {\mathit{\boldsymbol{A}} + {\mathit{\boldsymbol{E}}_A}} \right)\mathit{\boldsymbol{X}} + \mathit{\boldsymbol{e}} $ | (4) |
式(3)可以改写成:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{L}} = \left( {\mathit{\boldsymbol{A}} + {\mathit{\boldsymbol{E}}_A}} \right)\mathit{\boldsymbol{X}} + \mathit{\boldsymbol{e}} = \mathit{\boldsymbol{AX}} + \\ \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{I}}&{{\mathit{\boldsymbol{X}}^{\rm{T}}} \otimes \mathit{\boldsymbol{I}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{e}}\\ {{\mathit{\boldsymbol{e}}_A}} \end{array}} \right],{\mathit{\boldsymbol{e}}_A} = {\rm{vec}}\left( {{\mathit{\boldsymbol{E}}_A}} \right)\\ \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{e}}\\ {{\mathit{\boldsymbol{e}}_A}} \end{array}} \right] \sim N\left( {\left[ {\begin{array}{*{20}{c}} 0\\ 0 \end{array}} \right],\sigma _0^2\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}_n}}&0\\ 0&{{\mathit{\boldsymbol{I}}_n} \otimes {\mathit{\boldsymbol{I}}_n}} \end{array}} \right]} \right) \end{array} \right. $ | (5) |
式中,EA为系数矩阵A的误差阵,vec(·)为拉直变换,⊗为Kronecker积,In为单位阵。平差准则为:
| $ f\left( {{\mathit{\boldsymbol{E}}_A},\mathit{\boldsymbol{e}}} \right) = \mathit{\boldsymbol{e}}_A^{\rm{T}}{\mathit{\boldsymbol{e}}_A} + {\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{e}} = \min $ | (6) |
再构造拉格朗日目标函数:
| $ \begin{array}{*{20}{c}} {F\left( {{\mathit{\boldsymbol{E}}_A},\mathit{\boldsymbol{e}}} \right) = }\\ {\mathit{\boldsymbol{e}}_A^{\rm{T}}{\mathit{\boldsymbol{e}}_A} + {\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{e}} + 2{\mathit{\boldsymbol{\lambda }}^{\rm{T}}}\left[ {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{e}} - \mathit{\boldsymbol{AX}} - {\mathit{\boldsymbol{E}}_A}\mathit{\boldsymbol{X}}} \right]} \end{array} $ | (7) |
整理得到法方程式:
| $ {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A\hat X}} - {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{L}} = \mathit{\boldsymbol{\hat X}}\frac{{{{\left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{A\hat X}}} \right)}^{\rm{T}}}\left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{A\hat X}}} \right)}}{{1 + {{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}}}} $ | (8) |
令
| $ {\mathit{\boldsymbol{\hat X}}^{\left( {k + 1} \right)}} = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}} \right)^{ - 1}}\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{L}} + {{\mathit{\boldsymbol{\hat X}}}^{\left( k \right)}}{{\mathit{\boldsymbol{\hat \mu }}}^{\left( k \right)}}} \right) $ | (9) |
用迭代法求解参数,可以采用最小二乘估计作为迭代初值,当
当系数矩阵病态时,法矩阵ATA求逆会变得极不稳定,以均方误差作为估值参考依据,由式(3)可以看出,当存在Λi接近于0时,方差将会非常大,导致求出的参数估值不可靠[7]。
在EIV平差模型下,正则化法是在TLS平差准则上加入稳定泛函:
| $ \begin{array}{*{20}{c}} {f\left( {{\mathit{\boldsymbol{E}}_A},\mathit{\boldsymbol{e}}} \right) = {\rm{vec}}{{\left( {{\mathit{\boldsymbol{E}}_A}} \right)}^{\rm{T}}}{\rm{vec}}\left( {{\mathit{\boldsymbol{E}}_A}} \right) + }\\ {{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{e}} + \alpha {\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{RX}} = \min } \end{array} $ | (10) |
式中,R为正则化矩阵,α为大于0的正则化参数。则参数估计为:
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat X}}}^{\left( {k + 1} \right)}} = {{\left[ {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}} + \alpha \left( {1 + {{\mathit{\boldsymbol{\hat X}}}^{\left( k \right)T}}{{\mathit{\boldsymbol{\hat X}}}^{\left( k \right)}}} \right)\mathit{\boldsymbol{R}}} \right]}^{ - 1}} \cdot }\\ {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{L}} + {{\mathit{\boldsymbol{\hat X}}}^{\left( k \right)}}{{\hat \mu }^{\left( k \right)}}} \right)} \end{array} $ | (11) |
依式(11)进行迭代计算,当
从式(11)可以看出,法矩阵加入相应的稳定泛函后求逆将变得正常、稳定,使得参数估值可靠。
2 病态总体最小二乘靶向奇异值修正法林东方等[6]基于小奇异值特征向量构造正则化矩阵:
| $ {\mathit{\boldsymbol{R}}_1} = \sum\limits_{i = j}^n {{\mathit{\boldsymbol{G}}_i}\mathit{\boldsymbol{G}}_i^{\rm{T}}} $ | (12) |
式中,Gi为法矩阵ATA小奇异值对应的特征向量。小特征值的判定方法可依据特征值标准差分量之和占标准差比重达到95%以上,即
| $ \sum\limits_{i = j}^n {\frac{1}{{{\mathit{\Lambda }_i}}}} \ge 95\% \sum\limits_{i = 1}^n {\frac{1}{{{\mathit{\Lambda }_i}}}} $ | (13) |
矩阵R1只修正小奇异值,可以将其叫作靶向矩阵,参数则与岭参数相同,在降低方差的同时避免不必要的偏差,使估值更为合理。
顾勇为等[5]介绍了病态加权TLS靶向病灶的正则化方法,挑选出系数矩阵A中的涉干扰列向量,并靶向修正,顾及A的误差并考虑权重求得参数估值。但其研究中的靶向矩阵是固定矩阵,且只修正法矩阵ATA,而病态TLS估计顾及了误差矩阵EA的影响。针对该问题,本文提出2种病态TLS靶向奇异值修正法。
2.1 方法1根据EIV模型L=(A+EA)X+e和病态TLS平差准则f(EA, e)=vec(EA)Tvec(EA)+eTe+αXTRX=min,构建拉格朗日目标函数[8]:
| $ \begin{array}{*{20}{c}} {F\left( {{\mathit{\boldsymbol{E}}_A},\mathit{\boldsymbol{e}}} \right) = \mathit{\boldsymbol{e}}_A^{\rm{T}}{\mathit{\boldsymbol{e}}_A} + {\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{e}} + \alpha {\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{RX}} + }\\ {2{\mathit{\boldsymbol{\lambda }}^{\rm{T}}}\left[ {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{e}} - \mathit{\boldsymbol{AX}} - {\mathit{\boldsymbol{E}}_A}\mathit{\boldsymbol{X}}} \right]} \end{array} $ | (14) |
求一阶偏导得:
| $ \left\{ \begin{array}{l} \frac{{\partial F}}{{\partial \mathit{\boldsymbol{e}}}} = 2{\mathit{\boldsymbol{e}}^{\rm{T}}} - 2{\mathit{\boldsymbol{\lambda }}^{\rm{T}}} = 0\\ \frac{{\partial F}}{{\partial {\mathit{\boldsymbol{e}}_A}}} = 2\mathit{\boldsymbol{e}}_A^{\rm{T}} + 2{\mathit{\boldsymbol{\lambda }}^{\rm{T}}}\left( {{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}} \otimes {\mathit{\boldsymbol{I}}_n}} \right) = 0\\ \frac{{\partial F}}{{\partial \mathit{\boldsymbol{\hat X}}}} = 2\alpha {\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{R}} - 2{\mathit{\boldsymbol{\lambda }}^{\rm{T}}}\left( {\mathit{\boldsymbol{A}} + {\mathit{\boldsymbol{E}}_A}} \right) = 0 \end{array} \right. $ | (15) |
由式(15)可得e=λ、EA=λXT,并将其代入式(4):
| $ \mathit{\boldsymbol{L}} - \mathit{\boldsymbol{A\hat X}} = {\mathit{\boldsymbol{E}}_A}\mathit{\boldsymbol{\hat X}} + \mathit{\boldsymbol{e}} = \lambda \left( {{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}} + 1} \right) $ | (16) |
根据式(16)求得:
| $ \mathit{\boldsymbol{e}} = \mathit{\boldsymbol{\lambda }} = \left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{A\hat X}}} \right){\left( {{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}} + 1} \right)^{ - 1}} $ | (17) |
可得到:
| $ {\mathit{\boldsymbol{\hat E}}_A} = \mathit{\boldsymbol{\lambda }}{\mathit{\boldsymbol{\hat X}}^{\rm{T}}} = \left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{A\hat X}}} \right){\left( {{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}} + 1} \right)^{ - 1}}{\mathit{\boldsymbol{\hat X}}^{\rm{T}}} $ | (18) |
进而由EA重新构造出系数矩阵
| $ \mathit{\boldsymbol{\hat A}} = \mathit{\boldsymbol{A}} + {\mathit{\boldsymbol{E}}_A} $ | (19) |
然后用正则化法求解参数
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat X = }}{{\left[ {{{\left( {\mathit{\boldsymbol{A}} + {\mathit{\boldsymbol{E}}_A}} \right)}^{\rm{T}}}\left( {\mathit{\boldsymbol{A}} + {\mathit{\boldsymbol{E}}_A}} \right) + \alpha \mathit{\boldsymbol{R}}} \right]}^{ - 1}}{{\left( {\mathit{\boldsymbol{A}} + {\mathit{\boldsymbol{E}}_A}} \right)}^{\rm{T}}}\mathit{\boldsymbol{L}}}\\ { = {{\left( {{{\mathit{\boldsymbol{\hat A}}}^{\rm{T}}}\mathit{\boldsymbol{\hat A}} + \alpha \mathit{\boldsymbol{R}}} \right)}^{ - 1}}{{\mathit{\boldsymbol{\hat A}}}^{\rm{T}}}\mathit{\boldsymbol{L}}} \end{array} $ | (20) |
根据式(18)~式(20)进行迭代计算,迭代式为:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\hat E}}_A^{\left( k \right)} = \left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{\hat X}}}^{\left( k \right)}}} \right){\left( {{{\mathit{\boldsymbol{\hat X}}}^{\left( k \right){\rm{T}}}}{{\mathit{\boldsymbol{\hat X}}}^{\left( k \right)}} + 1} \right)^{ - 1}}{{\mathit{\boldsymbol{\hat X}}}^{\left( k \right){\rm{T}}}}\\ {{\mathit{\boldsymbol{\hat X}}}^{\left( {k + 1} \right)}} = {\left( {{{\mathit{\boldsymbol{\hat A}}}^{\left( k \right){\rm{T}}}}{{\mathit{\boldsymbol{\hat A}}}^{\left( k \right)}} + \alpha \mathit{\boldsymbol{R}}} \right)^{ - 1}}{{\mathit{\boldsymbol{\hat A}}}^{\left( k \right){\rm{T}}}}\mathit{\boldsymbol{L}} \end{array} \right. $ | (21) |
当
根据EIV模型L=(A+EA)X+e,令
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{L}} = \mathit{\boldsymbol{\tilde AX}} + \mathit{\boldsymbol{e}}\\ \mathit{\boldsymbol{A}} = \mathit{\boldsymbol{A}} - {\mathit{\boldsymbol{E}}_A} \end{array} \right. $ | (22) |
将上式转置可以得到:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{L}}^{\rm{T}}} = {\mathit{\boldsymbol{X}}^{\rm{T}}}{{\mathit{\boldsymbol{\tilde A}}}^{\rm{T}}} + {\mathit{\boldsymbol{e}}^{\rm{T}}}\\ {\mathit{\boldsymbol{A}}^{\rm{T}}} = {{\mathit{\boldsymbol{\tilde A}}}^{\rm{T}}} - \mathit{\boldsymbol{E}}_A^{\rm{T}} \end{array} \right. $ | (23) |
根据文献[10-11],可以将此模型称作多元联合平差模型。与P-EIV模型[12]解算方法相类似,将
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{L}}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{A}}^{\rm{T}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{X}}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{I}}_n}} \end{array}} \right]{\mathit{\boldsymbol{\tilde A}}^{\rm{T}}} + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{e}}^{\rm{T}}}}\\ { - \mathit{\boldsymbol{E}}_A^{\rm{T}}} \end{array}} \right] $ | (24) |
平差准则为:
| $ f\left( {\mathit{\boldsymbol{e}},{\mathit{\boldsymbol{E}}_A}} \right) = {\left\| {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{e}}^{\rm{T}}}}\\ { - \mathit{\boldsymbol{E}}_A^{\rm{T}}} \end{array}} \right]} \right\|_F} = \min $ | (25) |
式中,‖·‖F为F-范数。或将
| $ {\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{I}}_n}} \end{array}} \right]^{\rm{T}}}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{L}}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{A}}^{\rm{T}}}} \end{array}} \right] = {\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{I}}_n}} \end{array}} \right]^{\rm{T}}}\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{I}}_n}} \end{array}} \right]{\mathit{\boldsymbol{\hat A}}^{\rm{T}}} $ | (26) |
从而得到:
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat A}}}^{\rm{T}}} = {{\left[ {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat X}}}&{{\mathit{\boldsymbol{I}}_n}} \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{I}}_n}} \end{array}} \right]} \right]}^{ - 1}} \cdot \left[ {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat X}}}&{{\mathit{\boldsymbol{I}}_n}} \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{L}}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{A}}^{\rm{T}}}} \end{array}} \right]} \right]}\\ { = {{\left[ {\mathit{\boldsymbol{\hat X}}{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}} + {\mathit{\boldsymbol{I}}_n}} \right]}^{ - 1}} \cdot \left[ {\mathit{\boldsymbol{\hat X}}{\mathit{\boldsymbol{L}}^{\rm{T}}} + {\mathit{\boldsymbol{A}}^{\rm{T}}}} \right]} \end{array} $ | (27) |
再将式(27)转置,得:
| $ \mathit{\boldsymbol{\hat A}} = \left[ {\mathit{\boldsymbol{L}}{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}} + \mathit{\boldsymbol{A}}} \right] \cdot {\left[ {\mathit{\boldsymbol{\hat X}}{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}} + {\mathit{\boldsymbol{I}}_n}} \right]^{ - 1}} $ | (28) |
根据求得的
| $ \mathit{\boldsymbol{\hat X}} = {\left( {{{\mathit{\boldsymbol{\hat A}}}^{\rm{T}}}\mathit{\boldsymbol{\hat A}} + \alpha \mathit{\boldsymbol{R}}} \right)^{ - 1}} \cdot {\mathit{\boldsymbol{\hat A}}^{\rm{T}}}\mathit{\boldsymbol{L}} $ | (29) |
根据式(28)和式(29)进行迭代计算,迭代式为:
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\hat A}}}^{\left( k \right)}} = \left[ {\mathit{\boldsymbol{L}}{{\mathit{\boldsymbol{\hat X}}}^{\left( k \right){\rm{T}}}} + \mathit{\boldsymbol{A}}} \right] \cdot {\left[ {{{\mathit{\boldsymbol{\hat X}}}^{\left( k \right)}}{{\mathit{\boldsymbol{\hat X}}}^{\left( k \right){\rm{T}}}} + {\mathit{\boldsymbol{I}}_n}} \right]^{ - 1}}\\ {{\mathit{\boldsymbol{\hat X}}}^{\left( {k + 1} \right)}} = {\left( {{{\mathit{\boldsymbol{\hat A}}}^{\left( k \right){\rm{T}}}}{{\mathit{\boldsymbol{\hat A}}}^{\left( k \right)}} + \alpha \mathit{\boldsymbol{R}}} \right)^{ - 1}} \cdot {{\mathit{\boldsymbol{\hat A}}}^{\left( k \right){\rm{T}}}}\mathit{\boldsymbol{L}} \end{array} \right. $ | (30) |
当
上述2种病态TLS靶向奇异值修正法都是先求出改正的系数矩阵
从式(21)和式(30)看出,2种方法的迭代式相似,不同之处在于系数矩阵
方法1的求取公式为:
| $ {\mathit{\boldsymbol{\hat A}}_1} = \mathit{\boldsymbol{A}} + \left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{A\hat X}}} \right){\left( {{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}} + 1} \right)^{ - 1}}{\mathit{\boldsymbol{\hat X}}^{\rm{T}}} $ | (31) |
展开得到:
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat A}}}_1} = \mathit{\boldsymbol{A}} + \mathit{\boldsymbol{L}}{{\left( {{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}} + 1} \right)}^{ - 1}}{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}} - }\\ {\mathit{\boldsymbol{A\hat X}}{{\left( {{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}} + 1} \right)}^{ - 1}}{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}} \end{array} $ | (32) |
方法2的求取公式为:
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat A}}}_2} = \mathit{\boldsymbol{L}}{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}} \cdot }\\ {{{\left[ {\mathit{\boldsymbol{\hat X}}{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}} + {\mathit{\boldsymbol{I}}_n}} \right]}^{ - 1}} + \mathit{\boldsymbol{A}}{{\left[ {\mathit{\boldsymbol{\hat X}}{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}} + {\mathit{\boldsymbol{I}}_n}} \right]}^{ - 1}}} \end{array} $ | (33) |
将两式相减可得:
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat A}}}_1} - {{\mathit{\boldsymbol{\hat A}}}_2} = \mathit{\boldsymbol{A}} + \left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{A\hat X}}} \right){{\left( {{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}} + 1} \right)}^{ - 1}}{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}} - }\\ {\mathit{\boldsymbol{L}}{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}} \cdot {{\left[ {\mathit{\boldsymbol{\hat X}}{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}} + {\mathit{\boldsymbol{I}}_n}} \right]}^{ - 1}} - \mathit{\boldsymbol{A}}{{\left[ {\mathit{\boldsymbol{\hat X}}{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}} + {\mathit{\boldsymbol{I}}_n}} \right]}^{ - 1}}} \end{array} $ | (34) |
合并同类项:
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat A}}}_1} - {{\mathit{\boldsymbol{\hat A}}}_2} = \mathit{\boldsymbol{A}}\left\{ {{\mathit{\boldsymbol{I}}_n} - {{\left( {{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}} + 1} \right)}^{ - 1}}\mathit{\boldsymbol{\hat X}}{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}} - \left[ {\mathit{\boldsymbol{\hat X}}{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}} + } \right.} \right.}\\ {\left. {\left. {{{\left. {{\mathit{\boldsymbol{I}}_n}} \right]}^{ - 1}}} \right\} + \mathit{\boldsymbol{L}}{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}{{\left[ {{{\left( {{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}} + 1} \right)}^{ - 1}}{\mathit{\boldsymbol{I}}_n} - \left\{ {\mathit{\boldsymbol{\hat X}}{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}} + {\mathit{\boldsymbol{I}}_n}} \right.} \right]}^{ - 1}}} \right\}} \end{array} $ | (35) |
因为参数
式(35)中
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{M}}{\mathit{\boldsymbol{M}}^{\rm{T}}} - \sum\limits_{i = 1}^n {{\mathit{\boldsymbol{M}}_i}\frac{{{\rho _i}}}{{1 + \sum\limits_{i = 1}^n {{\rho _i}} }}} \mathit{\boldsymbol{M}}_i^{\rm{T}} - \sum\limits_{i = 1}^n {{\mathit{\boldsymbol{M}}_i}\frac{1}{{1 + {\rho _i}}}} \mathit{\boldsymbol{M}}_i^{\rm{T}} = }\\ {\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{M}}_i}\left( {1 - \frac{{{\rho _i}}}{{1 + \sum\limits_{i = 1}^n {{\rho _i}} }} - \frac{1}{{1 + {\rho _i}}}} \right)} \mathit{\boldsymbol{M}}_i^{\rm{T}} = }\\ {\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{M}}_i}\left( {\frac{{{\rho _i} \cdot \sum\limits_{i = 1}^n {{\rho _i}} - \rho _i^2}}{{\left( {1 + \sum\limits_{i = 1}^n {{\rho _i}} } \right) \cdot \left( {1 + {\rho _i}} \right)}}} \right)} \mathit{\boldsymbol{M}}_i^{\rm{T}}} \end{array} $ | (36) |
式中,ρ为矩阵
式(35)中
| $ \begin{array}{*{20}{c}} {\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{M}}_i}\left( {\frac{1}{{1 + \sum\limits_{i = 1}^n {{\rho _i}} }} - \frac{1}{{1 + {\rho _i}}}} \right)} \mathit{\boldsymbol{M}}_i^{\rm{T}} = }\\ {\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{M}}_i}\left( {\frac{{{\rho _i} - \sum\limits_{i = 1}^n {{\rho _i}} }}{{\left( {1 + \sum\limits_{i = 1}^n {{\rho _i}} } \right) \cdot \left( {1 + {\rho _i}} \right)}}} \right)} \mathit{\boldsymbol{M}}_i^{\rm{T}}} \end{array} $ | (37) |
则式(35)可表示为:
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat A}}}_1} - {{\mathit{\boldsymbol{\hat A}}}_2} = }\\ {\mathit{\boldsymbol{A}}\left\{ {\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{M}}_i}\left( {\frac{{{\rho _i} \cdot \sum\limits_{i = 1}^n {{\rho _i}} - \rho _i^2}}{{\left( {1 + \sum\limits_{i = 1}^n {{\rho _i}} } \right) \cdot \left( {1 + {\rho _i}} \right)}}} \right)\mathit{\boldsymbol{M}}_i^{\rm{T}}} } \right\} + }\\ {\mathit{\boldsymbol{L}}{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\left[ {\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{M}}_i}\left( {\frac{{{\rho _i} - \sum\limits_{i = 1}^n {{\rho _i}} }}{{\left( {1 + \sum\limits_{i = 1}^n {{\rho _i}} } \right) \cdot \left( {1 + {\rho _i}} \right)}}} \right)\mathit{\boldsymbol{M}}_i^{\rm{T}}} } \right]} \end{array} $ | (38) |
综上所述,式(36)、式(37)不等于0,故而式(38)也不等于0,即
采用文献[13]中的模拟病态问题算例,其中,
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {2.000\;0}&{ - 5.000\;0}&{1.000\;0}&{1.000\;0}&{ - 9.500\;0}\\ { - 2.000\;0}&{4.000\;0}&{1.000\;0}&{ - 1.050\;0}&{8.500\;0}\\ { - 2.000\;0}&{1.000\;0}&{1.000\;0}&{ - 1.000\;0}&{2.400\;0}\\ { - 1.000\;0}&{2.500\;0}&{4.000\;0}&{ - 0.500\;0}&{7.000\;0}\\ { - 1.000\;0}&{3.200\;0}&{4.000\;0}&{ - 0.500\;0}&{8.400\;0}\\ {1.000\;0}&{1.000\;0}&{ - 3.000\;0}&{0.400\;0}&{0.490\;0}\\ {3.000\;0}&{7.000\;0}&{ - 3.000\;0}&{1.500\;0}&{12.700\;0}\\ {5.000\;0}&{ - 1.000\;0}&{ - 2.000\;0}&{{\rm{2}}{\rm{.500}}\;{\rm{0}}}&{ - 3.000\;0}\\ {4.000\;0}&{2.000\;0}&{ - 2.000\;0}&{{\rm{2}}.0{\rm{1}}0\;0}&{3.000\;0}\\ {4.000\;0}&{3.000\;0}&{ - 2.000\;0}&{{\rm{2}}.000\;0}&{{\rm{5}}.000\;0} \end{array}} \right],\mathit{\boldsymbol{L}} = \left[ {\begin{array}{*{20}{c}} { - 10.500\;0}\\ {10.450\;0}\\ {1.400\;0}\\ {12.000\;0}\\ {14.100\;0}\\ { - 0.110\;0}\\ {21.200\;0}\\ {1.500\;0}\\ {9.010\;0}\\ {12.000\;0} \end{array}} \right] $ |
未知参数有5个,即X=[x1 x2 x3 x4 x5]T,真值为X=[1 1 1 1 1]T,现对A和L加入随机噪声,eL~N(0, σ02In),evec(A)~N(0, σ02In⊗Im),σ0=0.1。随机噪声由MATLAB生成,得到的系数矩阵和观测向量为:
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {1.881\;2}&{ - 5.118\;6}&{1.012\;9}&{1.080\;6}&{ - 9.533\;1}\\ { - 2.220\;2}&{3.894\;4}&{1.0656}&{ - 1.026\;8}&{8.415\;6}\\ { - 1.901\;4}&{1.147\;2}&{0.883\;2}&{ - 1.099\;0}&{2.449\;8}\\ { - 1.051\;9}&{2.505\;6}&{3.953\;9}&{ - 0.366\;0}&{7.148\;8}\\ { - 0.967\;3}&{3.078\;3}&{3.973\;8}&{ - 0.471\;0}&{8.345\;4}\\ {1.023\;4}&{0.995\;9}&{ - 3.121\;3}&{0.547\;9}&{0.405\;3}\\ {3.002\;1}&{6.887\;2}&{ - 3.131\;9}&{1.613\;8}&{12.6750}\\ {4.899\;6}&{ - 1.134\;9}&{ - 1.906\;9}&{2.431\;6}&{ - 2.933\;7}\\ {3.905\;3}&{1.973\;9}&{ - 1.998\;9}&{1.880\;8}&{2.914\;6}\\ {3.962\;6}&{3.095\;3}&{ - 2.064\;5}&{1.992\;7}&{4.879\;9} \end{array}} \right],\mathit{\boldsymbol{L}} = \left[ {\begin{array}{*{20}{c}} { - 10.512\;0}\\ {10.443\;0}\\ {1.448\;5}\\ {11.940\;0}\\ {14.085\;0}\\ { - 0.153\;5}\\ {21.192\;0}\\ {1.653\;5}\\ {8.949\;4}\\ {11.865\;0} \end{array}} \right] $ |
可知法矩阵条件数为2.083 8×104,严重病态。为比较新方法与其他方法解算结果的优劣,分别用最小二乘(LS)、总体最小二乘(TLS)、总体最小二乘正则化法(R-TLS)、总体最小二乘靶向病灶的正则化法(TR-TLS)、本文方法1和方法2进行平差解算,并比较参数估值与真值的差值范数
|
|
表 1 不同方法参数估计结果 Tab. 1 Results of different estimations |
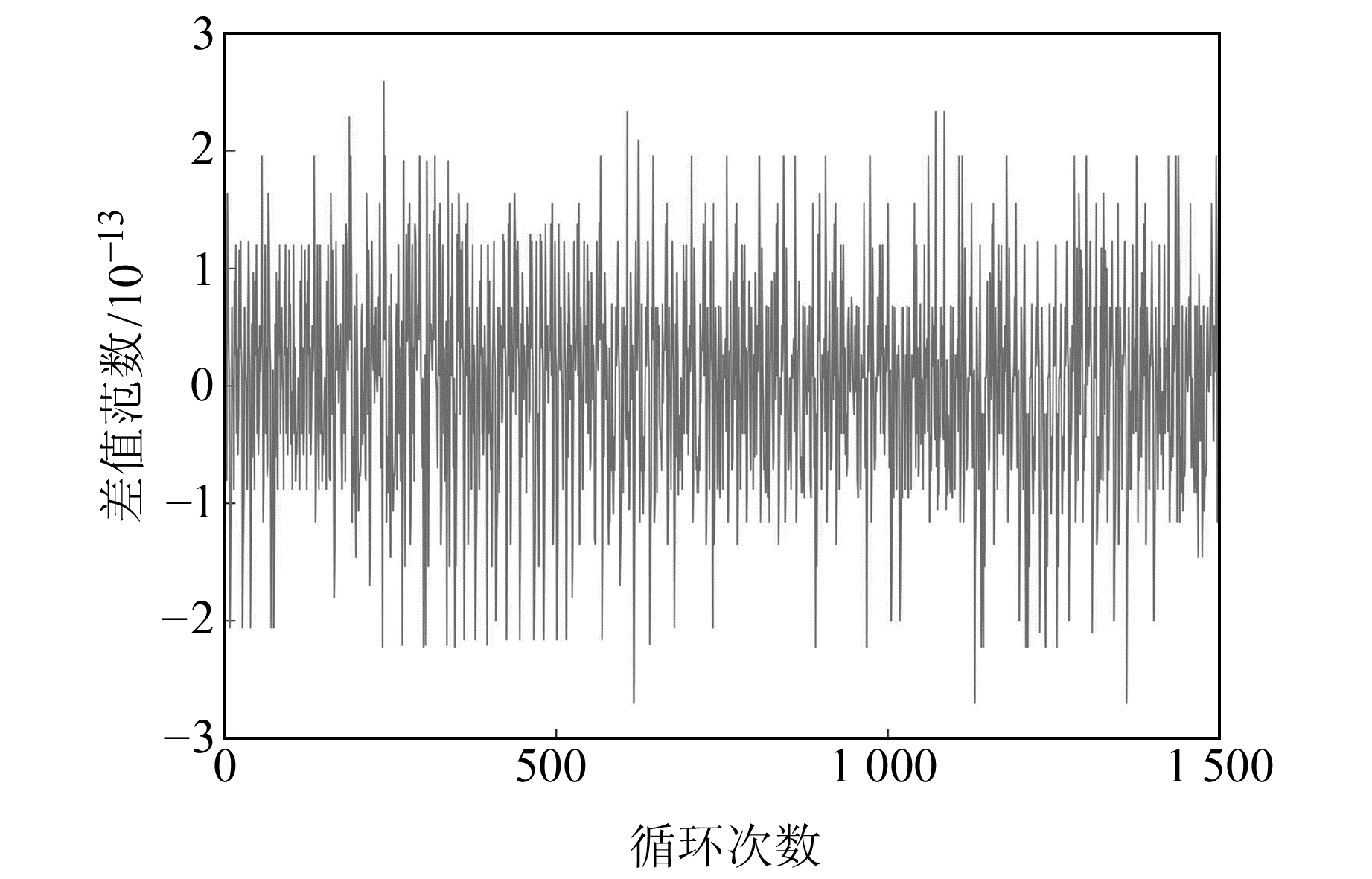
由于2种新方法结果非常接近,为进一步比较2种方法,在给定数据中加入相同均值和方差的随机噪声,用MATLAB循环计算1 500次,对比两者的迭代次数和差值范数,并计算其差值范数之差,结果见图 1~3。

|
图 1 新方法迭代次数 Fig. 1 New method iterations |

|
图 2 新方法差值范数 Fig. 2 New method difference norm |
|
图 3 2种方法差值范数之差 Fig. 3 The difference between the difference norms of the two methods |
采用文献[14]中的空间测边网算例,P1、P2、…、P9为9个已知点坐标,已知点到2个未知点P10、P11(模拟真值分别为(0 m,0 m,0 m)和(7 m,10 m,-5 m))的观测距离也已知。2个未知点之间的观测距离为d10, 11=13.107 85 m,各距离为等精度观测,中误差为±0.001 m。根据19个等精度观测距离确定2个未知点坐标,具体数据见表 2,点位见图 4。
|
|
表 2 各点坐标和距离 Tab. 2 Points coordinates and distance |
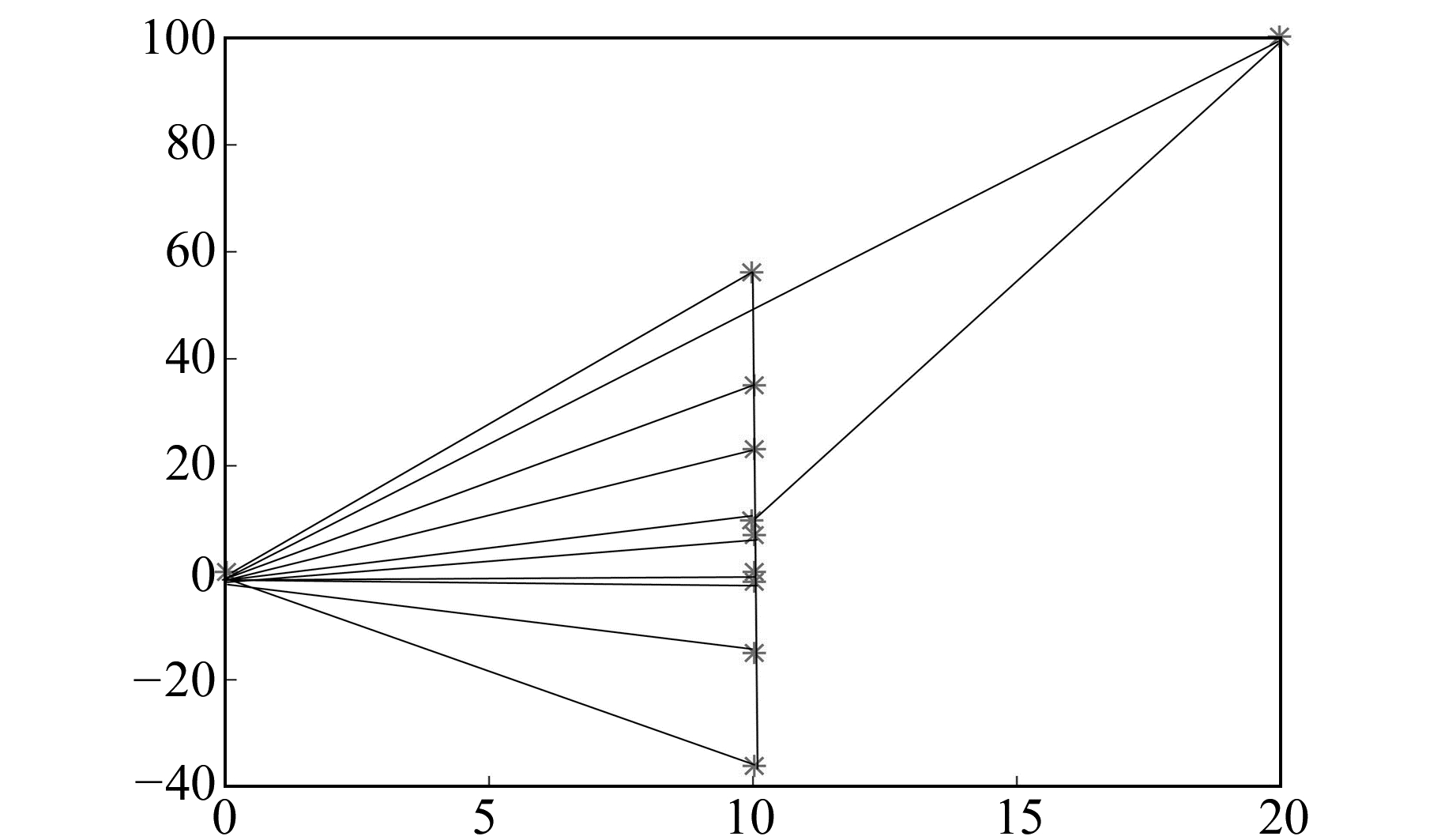
|
图 4 控制点点位 Fig. 4 Control points bitmap |
在该算例中,法矩阵条件数为4.601 6×103,属于病态问题。分别用LS、TLS、R-TLS、TR-TLS、本文方法1和方法2进行平差解算,并比较参数估值与真值的差值范数
|
|
表 3 不同方法参数估计结果 Tab. 3 Results of different estimations |
从2个算例可以看出,病态性对结果有巨大影响。2个算例的TLS差值范数分别为6.735 0和33.126 2,比LS的差值范数1.308 8和10.353 3大,说明TLS估计比LS估计更容易受病态影响。而R-TLS和TR-TLS所得结果均相差不大,差值范数均远小于TLS结果,说明正则化法可以有效地提高解的可靠性及稳定性,克服病态带来的影响。
本文2种新方法的结果比其他方法优,说明该方法比R-TLS和TR-TLS适用性好,也说明病态TLS靶向奇异值修正法在处理病态问题上具有一定优势。2种新方法求得的结果非常接近,针对此情况,本文在算例1给定的A和L中加入随机噪声并模拟计算1 500次,作出2种方法的迭代次数(图 1)及差值范数(图 2),并计算差值范数之差(图 3)。从图 1~2中看出,两者迭代次数和差值范数几乎相等,而图 3表明,2种方法结果仍存在较小差异。由此可知,本文2种方法在一定精度上结果相等,而理论上不相等。
4 结语本文提出2种病态TLS靶向奇异值修正法,方法1是在EIV模型下构建TLS平差准则和拉格朗日目标函数,求出EA并得到新的系数矩阵,再采用新的靶向矩阵作为正则化矩阵的正则化法,迭代求出参数估值;方法2是模仿联合平差模型和P-EIV模型,建立相应的平差准则,再求出新的系数矩阵
将2种新方法代入算例计算,得到的结果优于R-TLS和TR-TLS方法,说明2种新方法比R-TLS和TR-TLS在处理病态问题时适用性好。同时,证明2种方法理论上不相等,而在一定精度上结果相等。
| [1] |
葛旭明, 伍吉仓. 病态总体最小二乘问题的广义正则化[J]. 测绘学报, 2012, 41(3): 372-377 (Ge Xuming, Wu Jicang. Generalized Regularization to Ill-posed Total Least Squares Problem[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 372-377)
(  0) 0) |
| [2] |
袁振超, 沈云中, 周泽波. 病态总体最小二乘模型的正则化算法[J]. 大地测量与地球动力学, 2009, 29(2): 131-134 (Yuan Zhenchao, Shen Yunzhong, Zhou Zebo. Regularized Total Least Squares Solution to Ill-Posed Error-in-Variable Model[J]. Journal of Geodesy and Geodynamics, 2009, 29(2): 131-134)
(  0) 0) |
| [3] |
王乐洋, 于冬冬. 病态总体最小二乘问题的虚拟观测解法[J]. 测绘学报, 2014, 43(6): 575-581 (Wang Leyang, Yu Dongdong. Virtual Observation Method to Ill-Posed Total Least Squares Problem[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(6): 575-581)
(  0) 0) |
| [4] |
王乐洋, 许才军, 鲁铁定. 病态加权总体最小二乘平差的岭估计解法[J]. 武汉大学学报:信息科学版, 2010, 35(11): 1 346-1 350 (Wang Leyang, Xu Caijun, Lu Tieding. Ridge Estimation Method in Ill-Posed Weighted Total Least Squares Adjustment[J]. Geomatics and Information Science of Wuhan University, 2010, 35(11): 1 346-1 350)
(  0) 0) |
| [5] |
顾勇为, 归庆明, 赵俊. 病态加权总体最小二乘靶向病灶的正则化方法[J]. 大地测量与地球动力学, 2016, 36(3): 253-256 (Gu Yongwei, Gui Qingming, Zhao Jun. Target Focus Regularization as Compared with Ill-Posed Weighted Total Least Squares[J]. Journal of Geodesy and Geodynamics, 2016, 36(3): 253-256)
(  0) 0) |
| [6] |
林东方, 朱建军, 宋迎春, 等. 正则化的奇异值分解参数构造法[J]. 测绘学报, 2016, 45(8): 883-889 (Lin Dongfang, Zhu Jianjun, Song Yingchun, et al. Construction Method of Regularization by Singular Value Decomposition of Design Matrix[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(8): 883-889)
(  0) 0) |
| [7] |
崔希璋, 於宗俦, 陶本藻, 等. 广义测量平差[M]. 武汉: 武汉大学出版社, 2009 (Cui Xizhang, Yu Zongchou, Tao Benzao, et al. Generalized Surveying Adjustment[M]. Wuhan: Wuhan University Press, 2009)
(  0) 0) |
| [8] |
Tikhonov A N, Arsenin V Y. Solutions of Ill-posed Problems[J]. Mathematics of Computation, 1977, 32(144): 491-491
(  0) 0) |
| [9] |
顾勇为, 归庆明, 张璇, 等. 大地测量与地球物理中病态性问题的正则化迭代解法[J]. 测绘学报, 2014, 43(4): 331-336 (Gu Yongwei, Gui Qingming, Zhang Xuan, et al. Iterative Solution of Regularization to Ill-Conditioned Problems in Geodesy and Geophysics[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(4): 331-336)
(  0) 0) |
| [10] |
王乐洋, 余航. 总体最小二乘联合平差[J]. 武汉大学学报:信息科学版, 2016, 41(12): 1 683-1 689 (Wang Leyang, Yu Hang. Total Least Squares Joint Adjustment[J]. Geomatics and Information Science of Wuhan University, 2016, 41(12): 1 683-1 689)
(  0) 0) |
| [11] |
王乐洋, 赵英文, 陈晓勇, 等. 多元总体最小二乘问题的牛顿解法[J]. 测绘学报, 2016, 45(4): 411-417 (Wang Leyang, Zhao Yingwen, Chen Xiaoyong, et al. A Newton Algorithm for Multivariate Total Least Squares Problems[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(4): 411-417)
(  0) 0) |
| [12] |
Xu P L, Liu J N, Shi C. Total Least Squares Adjustment in Partial Errors-in-Variables Models: Algorithm and Statistical Analysis[J]. Journal of Geodesy, 2012, 86(8): 661-675 DOI:10.1007/s00190-012-0552-9
(  0) 0) |
| [13] |
鲁铁定.总体最小二乘平差理论及其在测绘数据处理中的应用[D].武汉: 武汉大学, 2010 (Lu Tieding. Research on the Total Least Squares and Its Applications in Surveying Data Processing [D].Wuhan: Wuhan University, 2010) http://www.cnki.com.cn/Article/CJFDTotal-CHXB201304028.htm
(  0) 0) |
| [14] |
郭建锋.测量平差系统病态性的诊断与处理[D].郑州: 信息工程大学, 2002 (Guo Jianfeng.The Diagnosis and Process of Ill-conditioned Adjustment System[D].Zhengzhou: Information Engineering University, 2002) http://cdmd.cnki.com.cn/Article/CDMD-90008-2002124626.htm
(  0) 0) |
2. Key Laboratory of Watershed Ecology and Geographical Environment Monitoring, MNR, 418 Guanglan Road, Nanchang 330013, China;
3. Jiangxi Province Key Lab for Digital Land, 418 Guanglan Road, Nanchang 330013, China
 2019, Vol. 39
2019, Vol. 39


