2. 南京工业大学测绘科学与技术学院,南京市浦珠南路30号,211800;
3. 东南大学交通学院,南京市进香河路35号,210096
在对地面目标进行三维激光扫描时,为获得扫描对象完整的轮廓点云数据,需要通过多个测站进行扫描测量。由于在不同位置扫描时,坐标系统为各站的站心坐标系,为得到目标完整的点云信息,需将不同测站获取的点云数据转换到同一坐标系进行统一拼接[1]。数据在拼接配准时需要布设若干用于归一坐标系的标靶,而球形标靶因其各方向球心点固定且唯一,在配准时被普遍采用[2],但在标靶周围有干扰源或扫描的标靶点云本身含有密集噪声时,会对配准精度和最终的点云质量造成较大影响。
目前,对点云数据配准算法的研究较多,但对于球形标靶扫描含有粗差的情况有所忽视[3-5]。有学者提出用总体最小二乘法和整体拟合法来提高球心坐标精度以实现精密配准[6-7],但其忽略了球心是由球面数据拟合的实际情况,未分辨错误点对球心拟合的影响;李嘉等[8]对复杂点云场景中的球形目标识别进行研究发现,依据微分几何属性和曲率差异能够快速找到球状物,但并不能提高球心拟合精度。对于散乱点云,也有学者尝试用拉普拉斯(Laplace)滤波法、领域滤波法、小波去噪等方法对点云图像或散乱点云进行滤波、压缩处理[9-10],但其研究并未充分顾及到标靶本身点云含有粗差或噪声的情况。
基于小波阈值去噪对离散数据有良好的去噪效果,本文采用此法对球面外围离散噪声进行滤波处理,依去噪后的点云数据拟合出球心坐标,对比去噪前后球心拟合的精度差异,并以此作为配准关联点进行点云拼接,对比检查点的位移偏差和整体点云配准精度。实验证明,小波阈值去噪方法用于球形标靶点云去噪可行有效,去噪后数据可准确拟合球心位置,从而提高被扫描物体的整体配准精度。
1 球形标靶特性与球心拟合 1.1 球形标靶的特征球形标靶的球心位置唯一,各方向观测点云均匀,在高精度的点云拼接和仪器精度指标检定中被普遍采用。相对于平面标靶,球形标靶不受激光束的位置束缚,可识别的距离更远[11]。
1.2 球形标靶配准基本原理球形标靶配准是点云数据配准中常用且精度较高的配准方法,实施中首先在相邻测站的重叠区域放置3个或更多的球形标靶,相邻测站的标靶ID号须相同。标靶布设应避免共面,尽量与多个测站点通视。在对目标进行扫描时,也对公共区域的标靶进行精准扫描,经数据处理提取标靶的中心位置坐标,最终根据标靶的中心坐标完成数据配准[3-4]。
目前,基于球形标靶的主要配准算法包括四元素法、七参数法、迭代最近点法(ICP算法)或其相关改进及融合方法[12]。由于ICP算法时常会出现迭代终止情况,本文使用七参数配准方法。设2个站点为A和B,2站均可观测到点M,扫描M点得到坐标M1(x1, y1, z1)和M2(x2, y2, z2)。第一站扫描的坐标M1通过旋转和平移得到第二站扫描得到的坐标M2,基本原理如下:
| $ \left[ {\begin{array}{*{20}{c}} {x_m^2}\\ {y_m^2}\\ {z_m^2} \end{array}} \right] = \lambda \left[ {\begin{array}{*{20}{c}} {{r_{00}}}&{{r_{01}}}&{{r_{02}}}\\ {{r_{10}}}&{{r_{11}}}&{{r_{12}}}\\ {{r_{20}}}&{{r_{21}}}&{{r_{22}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {x_m^1}\\ {y_m^1}\\ {z_m^1} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{t_x}}\\ {{t_y}}\\ {{t_z}} \end{array}} \right] $ | (1) |
对于二维数据,可通过直线拟合、曲线拟合、对数拟合等方法掌握其规律;对于三维球面,至少需采集球面上4个点的扫描数据方可计算出球心坐标。设拟合的球心坐标为(x0, y0, z0),半径为r,每个球面点拟合后估值与实际值的差值为:
| $ \begin{array}{*{20}{c}} {{e_i}\left( {{x_0},{y_0},{z_0},r} \right) = {{\left( {{x_i} - {x_0}} \right)}^2} + }\\ {{{\left( {{y_i} - {y_0}} \right)}^2} + {{\left( {{z_i} - {z_0}} \right)}^2} - {r^2}} \end{array} $ | (2) |
差值平方和为:
| $ E\left( {{x_0},{y_0},{z_0},r} \right) = \sum\limits_{i = 1}^N {{e_i}{{\left( {{x_0},{y_0},{z_0},r} \right)}^2}} $ | (3) |
E为x0、y0、z0、r的函数。令E分别对x0、y0、z0、r求偏导数,令其值为0,即可求出x0、y0、z0、r:
| $ \begin{array}{l} \left\{ \begin{array}{l} \frac{{\partial E}}{{\partial {x_0}}} = 0\\ \frac{{\partial E}}{{\partial {y_0}}} = 0\\ \frac{{\partial E}}{{\partial {z_0}}} = 0\\ \frac{{\partial E}}{{\partial r}} = 0 \end{array} \right. \to \left\{ \begin{array}{l} \sum\limits_{i = 1}^N {{e_i}\frac{{\partial {e_i}}}{{\partial {x_0}}}} = 0\\ \sum\limits_{i = 1}^N {{e_i}\frac{{\partial {e_i}}}{{\partial {y_0}}}} = 0\\ \sum\limits_{i = 1}^N {{e_i}\frac{{\partial {e_i}}}{{\partial {z_0}}}} = 0\\ \sum\limits_{i = 1}^N {{e_i}\frac{{\partial {e_i}}}{{\partial r}}} = 0 \end{array} \right. \to \\ \left\{ \begin{array}{l} \sum\limits_{i = 1}^N {{e_i}\left( {{x_i} - {x_0}} \right)} = 0\\ \sum\limits_{i = 1}^N {{e_i}\left( {{y_i} - {y_0}} \right)} = 0\\ \sum\limits_{i = 1}^N {{e_i}\left( {{z_i} - {z_0}} \right)} = 0\\ \sum\limits_{i = 1}^N {{e_i}r} = 0 \end{array} \right. \to \left\{ \begin{array}{l} \sum\limits_{i = 1}^N {{e_i}{x_i}} = 0\\ \sum\limits_{i = 1}^N {{e_i}{y_i}} = 0\\ \sum\limits_{i = 1}^N {{e_i}{z_i}} = 0\\ \sum\limits_{i = 1}^N {{e_i}} = 0 \end{array} \right. \end{array} $ | (4) |
令
| $ \left\{ \begin{array}{l} \bar x = \frac{1}{N}\sum\limits_{i = 1}^N {{x_i}} ,\bar y = \frac{1}{N}\sum\limits_{i = 1}^N {{y_i}} ,\bar z = \frac{1}{N}\sum\limits_{i = 1}^N {{z_i}} \\ \overline {xy} = \frac{1}{N}\sum\limits_{i = 1}^N {{x_i}{y_i}} ,\overline {xz} = \frac{1}{N}\sum\limits_{i = 1}^N {{x_i}{z_i}} ,\\ \;\;\;\;\overline {yz} = \frac{1}{N}\sum\limits_{i = 1}^N {{y_i}{z_i}} \\ \overline {{x^2}} = \frac{1}{N}\sum\limits_{i = 1}^N {x_i^2} ,\overline {{y^2}} = \frac{1}{N}\sum\limits_{i = 1}^N {y_i^2} ,\\ \;\;\;\;\overline {{z^2}} = \frac{1}{N}\sum\limits_{i = 1}^N {z_i^2} \\ \overline {{x^2}y} = \frac{1}{N}\sum\limits_{i = 1}^N {x_i^2{y_i}} ,\overline {{x^2}z} = \frac{1}{N}\sum\limits_{i = 1}^N {x_i^2{z_i}} ,\\ \;\;\;\;\overline {x{y^2}} = \frac{1}{N}\sum\limits_{i = 1}^N {{x_i}y_i^2} \\ \overline {{y^2}z} = \frac{1}{N}\sum\limits_{i = 1}^N {y_i^2{z_i}} ,\overline {x{z^2}} = \frac{1}{N}\sum\limits_{i = 1}^N {{x_i}z_i^2} ,\\ \;\;\;\;\overline {y{z^2}} = \frac{1}{N}\sum\limits_{i = 1}^N {{y_i}z_i^2} \\ \overline {{x^3}} = \frac{1}{N}\sum\limits_{i = 1}^N {x_i^3} ,\overline {{y^3}} = \frac{1}{N}\sum\limits_{i = 1}^N {y_i^3} ,\overline {{z^3}} = \frac{1}{N}\sum\limits_{i = 1}^N {z_i^3} \end{array} \right. $ | (5) |
得:
| $ \left\{ \begin{array}{l} \frac{{\overline {{x^3}} }}{{\bar x}} - 2{x_0}\frac{{\overline {{x^2}} }}{{\bar x}} + x_0^2 + \frac{{\overline {x{y^2}} }}{{\bar x}} + 2{y_0}\frac{{\overline {xy} }}{{\bar x}} + \\ \;\;\;\;y_0^2 + \frac{{\overline {x{z^2}} }}{{\bar x}} - 2{z_0}\frac{{\overline {xz} }}{{\bar x}} + z_0^2 = {r^2}\\ \frac{{\overline {{x^2}y} }}{{\bar y}} - 2{x_0}\frac{{\overline {xy} }}{{\bar y}} + x_0^2 + \frac{{\overline {{y^3}} }}{{\bar y}} - 2{y_0}\frac{{\overline {{y^2}} }}{{\bar y}} + \\ \;\;\;\;y_0^2 + \frac{{\overline {{z^2}y} }}{{\bar y}} - 2{z_0}\frac{{\overline {zy} }}{{\bar y}} + z_0^2 = {r^2}\\ \frac{{\overline {{x^2}z} }}{{\bar z}} - 2{x_0}\frac{{\overline {xz} }}{{\bar z}} + x_0^2 + \frac{{\overline {{y^2}z} }}{{\bar z}} - 2{y_0}\frac{{\overline {yz} }}{{\bar z}} + \\ \;\;\;\;y_0^2 + \frac{{\overline {{z^3}} }}{{\bar z}} - 2{z_0}\frac{{\overline {yz} }}{{\bar z}} + z_0^2 = {r^2}\\ \overline {{x^2}} - 2{x_0}\bar x + x_0^2 + \overline {{y^2}} - 2{y_0}\bar y + y_0^2 + \\ \;\;\;\;\overline {{z^2}} - 2{z_0}\bar z + z_0^2 = {r^2} \end{array} \right. $ | (6) |
以矩阵形式写出:
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {\overline {{x^2}} - {{\bar x}^2}}&{\overline {xy} - \bar x\bar y}&{\overline {xz} - \bar x\bar z}\\ {\overline {xy} - \bar x\bar y}&{\overline {{y^2}} - {{\bar y}^2}}&{\overline {yz} - \bar y\bar z}\\ {\overline {xz} - \bar x\bar z}&{\overline {yz} - \bar y\bar z}&{\overline {{z^2}} - {{\bar z}^2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_0}}\\ {{y_0}}\\ {{z_0}} \end{array}} \right] = \frac{1}{2} \cdot \\ \left[ \begin{array}{l} \left( {\overline {{x^3}} - \bar x\overline {{x^2}} } \right) + \left( {\overline {x{y^2}} - \bar x\overline {{y^2}} } \right) + \left( {\overline {x{z^2}} - \bar x\overline {{z^2}} } \right)\\ \left( {\overline {{x^2}y} - \bar y\overline {{x^2}} } \right) + \left( {\overline {{y^3}} - \bar y\overline {{y^2}} } \right) + \left( {\overline {y{z^2}} - \bar y\overline {{z^2}} } \right)\\ \left( {\overline {{x^2}z} - \bar z\overline {{x^2}} } \right) + \left( {\overline {z{y^2}} - \bar z\overline {{y^2}} } \right) + \left( {\overline {{z^3}} - \bar z\overline {{z^2}} } \right) \end{array} \right] \end{array} $ | (7) |
求解该矩阵得到x0、y0、z0值,代入式(1)~(6),得到r值。
2 离散小波阈值去噪基本原理小波阈值去噪在非平稳信号处理、工程监测和图像处理中被广泛应用,其去噪的基本步骤为:1)选定小波基函数和分解层数,对信号进行分解;2)确定阈值的与及高频次系数门限阈值,并量化处理;3)信号重构。本文根据点云噪声的特点,根据非线性离散小波原理进行分解和重构,以达到去噪的目的[13]。
据Fourier变换原理,把信号函数f(x)中的尺度因子a和平移因子b离散化,离散过程中对a和b进行采样,a=a0j,b=kb0a0j,得到离散小波函数(DWT):
| $ \begin{array}{*{20}{c}} {{D_f}\left( {j,k} \right) = \left\langle {f,{\psi _{j,k}}} \right\rangle = }\\ {{{\left| a \right|}^{ - \frac{j}{2}}}\int {\psi \left( {a_0^{ - j} - k{b_0}} \right)f\left( x \right){\rm{d}}x} } \end{array} $ | (8) |
将信号f(x)按不同频率进行分解:
| $ f\left( x \right) = {A_{j - 1}}f\left( x \right) = {A_j}f\left( x \right) + {D_j}f\left( x \right) $ | (9) |
其中,Ajf(x)为信号f(x)中频率小于2-j的部分,Djf(x)为频率介于2-j~2-j+1之间的部分。
将小波分解式写成矩阵形式:
| $ {\mathit{\boldsymbol{C}}_{j + 1}} = \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{C}}_j},j = 1,2, \cdots ,J $ | (10) |
| $ {\mathit{\boldsymbol{D}}_{j + 1}} = \mathit{\boldsymbol{G}}{\mathit{\boldsymbol{C}}_j},j = 1,2, \cdots ,J $ | (11) |
式中,尺度函数对应的低通滤波器用H表示,H =(hk-2n);小波函数对应的带通滤波器用G表示,G =(gk-2n);在2j分辨率下的离散逼近用Cj来表示;在2j分辨率下的离散细节用Dj来表示,J为最大尺度。Mallat重构算法为:
| $ {\mathit{\boldsymbol{\tilde C}}_j} = \mathit{\boldsymbol{\bar H}}{\mathit{\boldsymbol{\tilde C}}_{j + 1}} + \mathit{\boldsymbol{\bar G}}{\mathit{\boldsymbol{\tilde D}}_{j + 1}},j = J,J - 1, \cdots ,1 $ | (12) |
式中,H和G分别为H和G的共轭矩阵。
将含有噪声的信号分解在不同频带内,重构时把噪声相应的高频细节信号Dj置零,得到去噪后信号:
| $ \hat f\left( x \right) = {A_J}\hat f\left( x \right) = \sum\limits_{k \in Z} {{{\mathit{\boldsymbol{\tilde C}}}_{J,k}}{\varphi _{J,k}}\left( x \right)} $ | (13) |
球形标靶点云本质是一些包含三维坐标信息的散点集合。从原理上看,标靶点云噪声与标靶球形表面采样点的信息无相关性,而标靶球表面的采集信息才是其有效的特征信息,也反映了球形标靶的本质属性。在实际工作中难以完全准确剔除扫描物体特征外的噪声,球形标靶的扫描点云应是一组到固定球心点等距的点集,可认为是有序点云的大量集合,有一定的规律性;而噪声可认为是散乱点云的少量集合,表现出不规律的上下浮动离散特性。基于小波去噪不仅幅度、频率和系数可调,且具有平滑和保留特征较好的特性。因此,本文尝试用离散小波阈值方法对球形标靶的扫描点云进行去噪处理。
3 实例分析点云噪声通常可分为2种:一种与被扫描目标的点云数据交织在一起,不易分辨;另一种距离被扫描物体实际点云数据集甚远,有明显的不完整、不匹配特性,可通过在处理软件中设定一定的阈值半径、格网间隔予以区分[14]。球形标靶一般体积不大,表面纹理反射介质差别不大,其点云扫描噪声基本以第一种为主。
本文采用小波阈值去噪方法对球形标靶的点云进行处理,依据去噪后的数据拟合球心坐标,从而为高精度的点云配准提供条件。
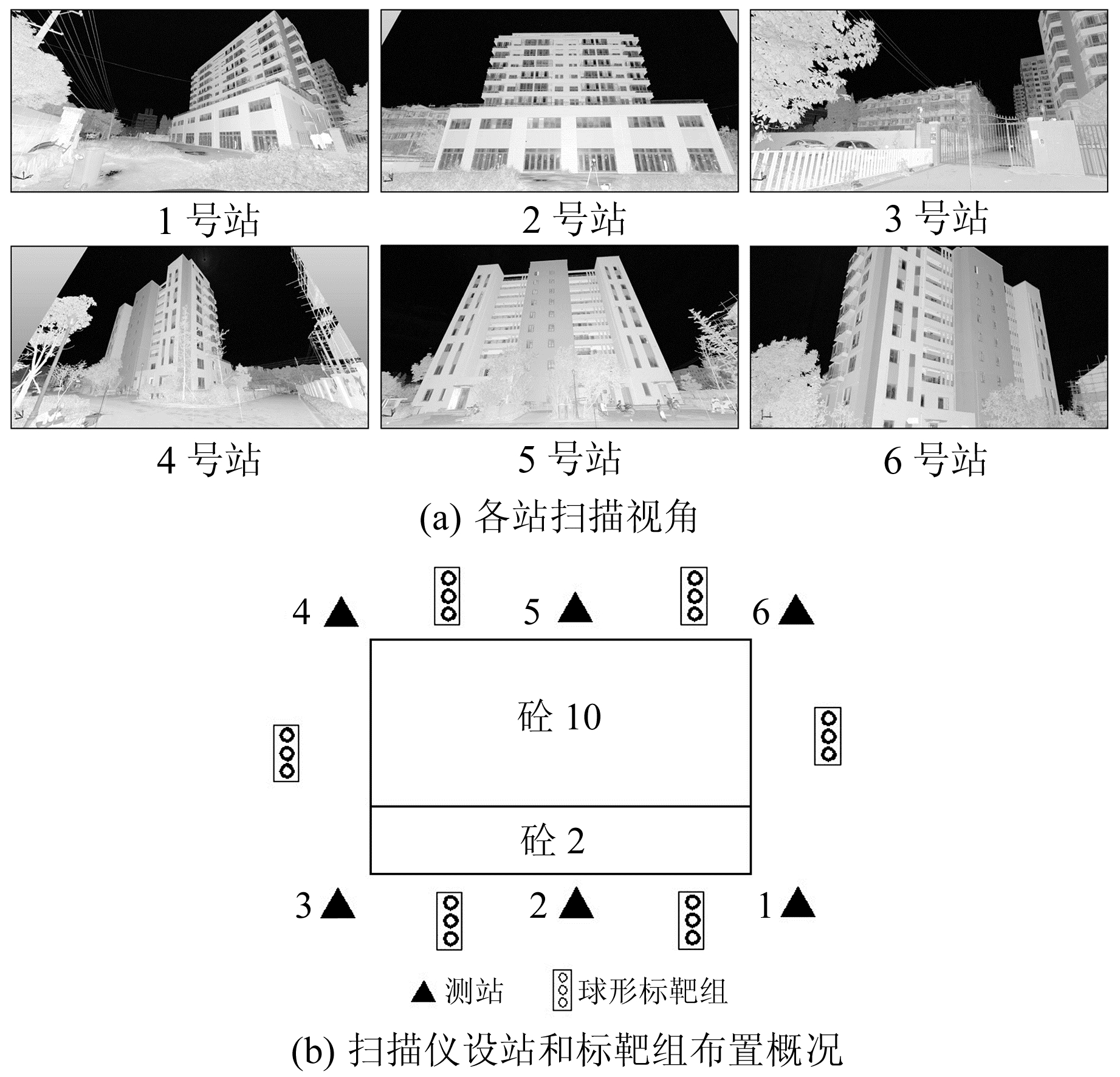
3.1 实验概况实验选用徕卡Scanstation C10型脉冲式三维激光扫描仪,视角范围为水平方位360°×垂直方位270°,扫描速度可达50 000点/s,扫描测程约300 m。内业处理采用Terrasolid软件,主要运用其中的TerraMatch、TerraScan模块。选取一栋10层楼房作为扫描研究对象,其楼房外轮廓点云及扫描架站、标靶组布置见图 1。
|
图 1 三维激光扫描布置与实景图 Fig. 1 3D laser scanning resettlement and real view |
按拟定的观测计划得到各站扫描点云,在明确具体的某一处点云集和球形标靶的对应关系后,设置一定的门限,将球形标靶外大于等于2倍半径的点云滤除,再经过抽稀处理,选取“only every 100th point”,将滤除后的点云进行小波去噪。本文选取1、2号测站之间的球形标靶进行研究,单个标靶球的直径为150 mm。
点云最终配准误差除与球心精度有关外,也与扫描仪连续多站的对中、定向误差积累和仪器本身测量精度有关。采用徕卡TPS1202型全站仪测量并计算得到各测站坐标,6个测站构成一个闭合导线,实测角度闭合差为11″,坐标增量闭合差均在3 mm左右,高程闭合差为1.2 mm。依角度等精度反向配赋及坐标按边长比例反向配赋原则,对观测值进行改正得改正后坐标,根据误差传播定律,测站的点位中误差小于1.5mm。基于测站坐标精度较高的情况,本文暂不考虑连续测站误差累积对点云配准精度的影响。
3.2 小波阈值法去噪过程 3.2.1 适用于点云去噪的小波基与分解层数的确定不同的小波基函数有不同的数学特点,一般指正交性、消失矩阶数、紧支性、正则性和对称性几个方面,也带来不同的去噪效果,小波基函数的选取一般从信号本身特点和小波基属性两方面考虑。鉴于标靶球点云数据量大且非连续,本文采用DWT处理。从数学特性上来说,紧支性、对称性、正则性几方面不能同时满足,选取小波基时应综合考虑[15]。常用的去噪小波基函数特性见表 1。
|
|
表 1 常用去噪小波基函数特性 Tab. 1 Characteristics of some commonly used wavelet functions for de-noising |
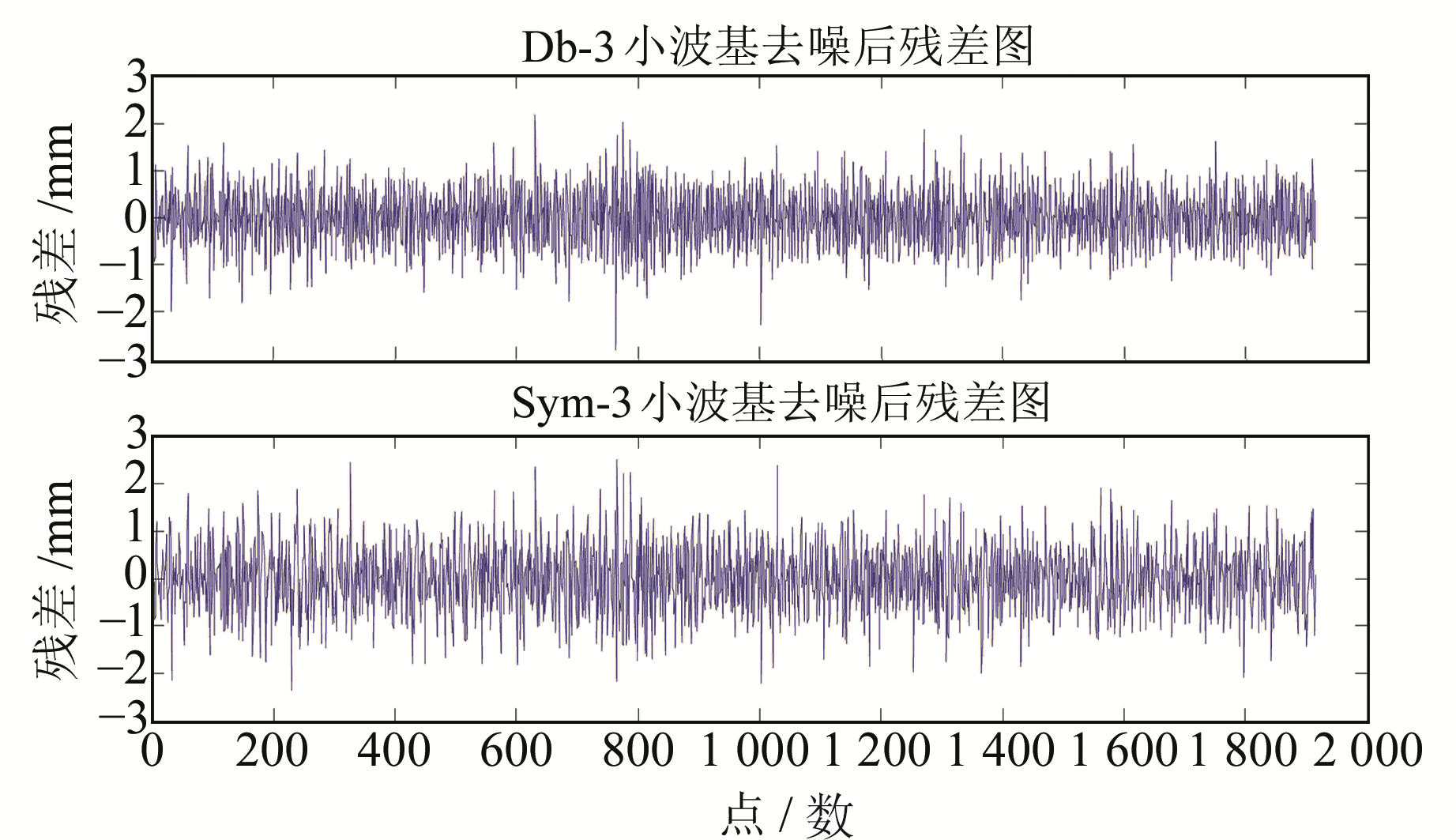
为避免在多层次分解和重构中边缘部分出现过大畸变,采用具对称性或近似对称性的双正交小波基;紧支撑性好的小波基可以更好地提取信号局部特性;良好正则性和较小消失距的小波基可避免信号突变。因此,结合点云特点和小波基特点,选取db-N、sym-N系作为本文的实验小波基。通过对白噪声的初步检定分析,采用3层分解对同一信号进行分解重构去噪。经比较,db-3小波基相较于sym-3小波基去噪后残差密度更集中,较大残差值(≥2 mm)更少,信号曲线更光滑。由此认为,针对标靶球点云数据的数量和均值、峰值等特点,选择db-3小波基去噪是合理的。2种小波基去噪后的残差见图 2。
|
图 2 不同小波基函数去噪效果对比图 Fig. 2 Contrast diagram of denoising effect of different small wave base functions |
在对同一标靶球的数据进行拼接后,可得大概的球心坐标,但此坐标没有经过噪点分离。以此球心为暂定球心,坐标定为(x0, y0, z0),75 mm的标靶球半径为求差的过滤门限,并以固定值r表示,得到各扫描点超出标靶球表面的距离差值为Δdi=

|
图 3 T2标靶球点云去噪过程 Fig. 3 T2 target ball point cloud de-noising process map |
|
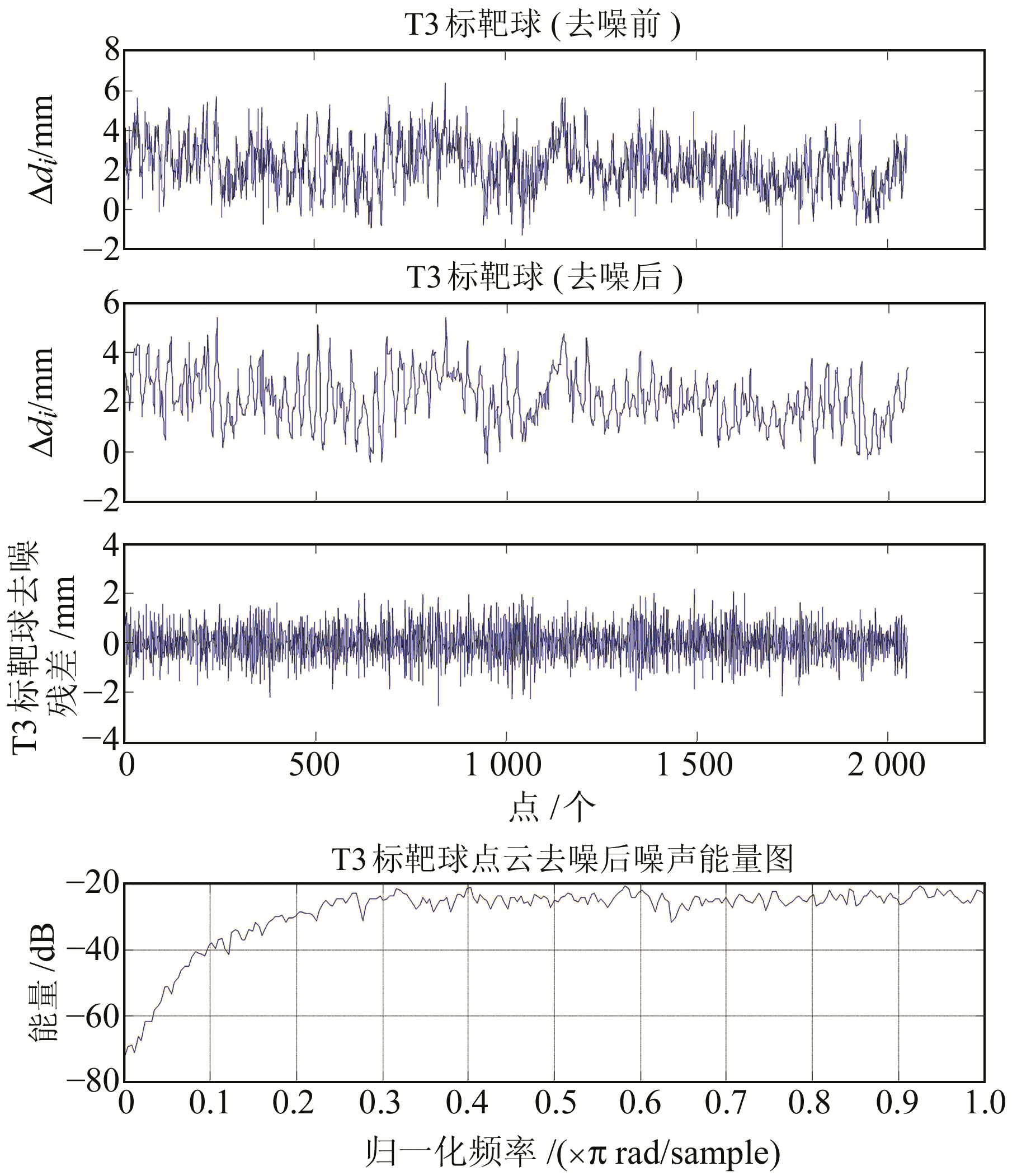
图 4 T3标靶球点云去噪过程 Fig. 4 T3 target ball point cloud de-noising process map |
经定量分析,去噪后的点云信息数据均达到一定程度的滤除噪声效果,残差分布均匀,高频噪声得到弱化,扫描点到暂定球心距离与半径差值的最大值和平均值均有所减小(表 2、3)。
|
|
表 2 去噪前后Δdi最大值对比 Tab. 2 The maximum value comparison table of Δdi value before and after de-noising |
|
|
表 3 去噪前后Δdi均值对比 Tab. 3 The mean value comparison table of Δdi value before and after de-noising |
依据计算结果可知,球心拟合精度提高了约0.8 mm。同理,每相邻测站的拼接需至少3个同名球形标靶,对此,两站间的T4标靶球和其余5个测站的标靶球也作了类似的去噪处理。Terrasolid软件需人工识别标靶并设立同名关系后才能完成粗配准,最终得到6站球形标靶去噪后的点云数据,基于此数据可精确拟合出每个球形标靶的球心点坐标。
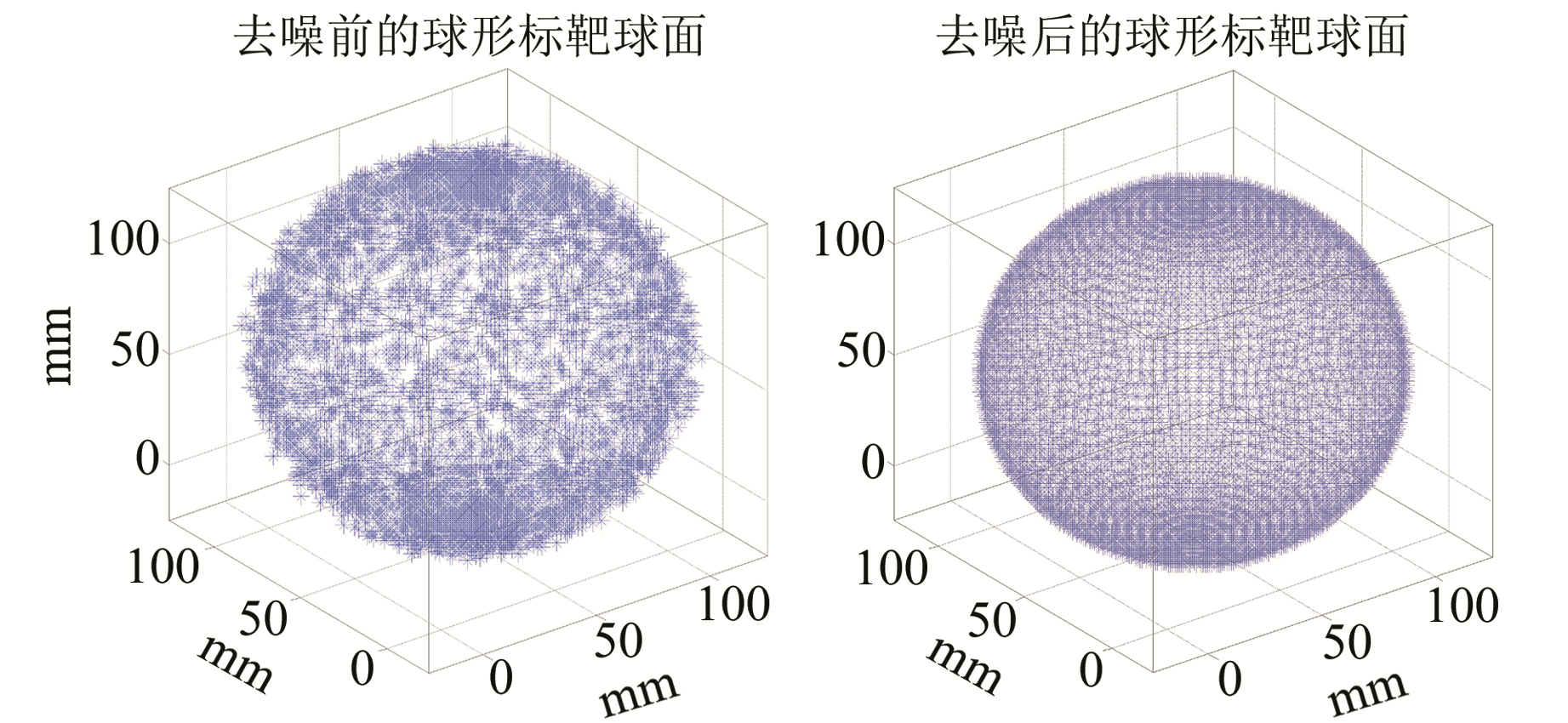
3.3 去噪后数据的球心拟合对球形标靶的点云去噪,可过滤掉一些距离球心过远的噪声点,这些噪声点可能是扫描的大误差点或环境造成的激光遮蔽点。以T2标靶球为例,去噪后的球面相对去噪前光滑程度有明显提高,见图 5。
|
图 5 去噪前后球形标靶球面对比 Fig. 5 Contrast diagram of spherical target spherical surface before and after de-noising |
对去噪后的数据进行拟合计算,得到每个球形标靶的精确球心坐标,精密的点云配准也是以准确的球心坐标为前提的。球面拟合和球心坐标计算本质上都属于离散点曲面拟合[16],本文采用MATLAB的lsqcurvefit函数来拟合定位出球心坐标。对1、2号测站之间3个球形标靶的点云进行去噪,并基于去噪后的数据进行球心拟合,得到精确的球心坐标。球形标靶球心的坐标系与地面架站点的坐标系相同,平面坐标为城市独立坐标系,高程为1985国家高程基准,取值精确到mm级(表 4)。
|
|
表 4 标靶球精密球心坐标统计 Tab. 4 Center coordinates statistics table for each spherical target |
对6站共18个参与转换参数解算的标靶球进行去噪,去噪后球心的拟合精度可提高0.8 mm,依据去噪后拟合的各球形标靶的球心坐标进行精密配准,得到扫描物体的整体点云。选取扫描目标的4个铝合金窗户窗角(识别误差低于1 mm)作为检查点进行点位坐标符合精度的比对,发现依去噪后球形标靶的点云进行配准,配准精度有所提高。因配准拼接的误差来源是多方面的,在其余因素不变的情况下,只比较标靶球去噪前后检查点坐标拼接误差,可体现球形标靶去噪对点云拼接的影响程度(表 5,单位mm)。
|
|
表 5 检查点坐标内符合精度残差 Tab. 5 Intra-accuracy residual table of checkpoint coordinates |
由表 5可知,同一检查点精密配准后坐标差值减小约5 mm。由于单个球心拟合精度的提高使球心误差的传递和积累有所减小,扫描物体的整体点云配准精度也有所提高。
为了更直观地观察球形标靶去噪对点云拼接后影像的总体影响,将球形标靶去噪前后的拼接误差放大10倍,即5 mm放大至50 mm,将扫描物体的点云拼接影像进行展示(图 6)。

|
图 6 球形标靶去噪前后配准点云对比 Fig. 6 Contrast map of registration point cloud before and after de-noising of spherical target |
从图 6可看出,经标靶去噪后的拼接点云影像错位重叠情况有所改善,点云拼接误差减小,扫描物体点云清晰度总体得到提高。
4 结语以某栋高层建筑为扫描对象,采用6站拼接的全景地面三维激光扫描,进行粗配准、球形标靶点云小波去噪、精密球心拟合和标靶去噪后的精密配准研究,得出以下结论:
1) 针对标靶点云的特性,分析不同小波基的数学特点,对比不同小波基去噪效果后认为,db-3小波基更适合此类数据的去噪。在用小波阈值去噪方法对球形标靶点云进行去噪处理后发现,去噪后的球形标靶点云曲面光滑,噪声能量减弱,对于实验标靶球的大小而言,扫描点至球心距离与球半径差值Δdi的最大值减少约1.7 mm,均值减少约0.8 mm。
2) 基于去噪后的球形标靶点云拟合出精确的球心坐标,以此坐标作为精密配准的关联点,配准后的点云影像较未经标靶去噪配准的点云影像更为清晰,重叠度减弱。将楼房中的清晰窗角点作为检查点进行检核,以高精度全站仪采集得到的坐标作为真值,并与拼接后的楼房点云检查点坐标进行比较可发现,对于同一点的拼接距离平均缩短5 mm左右。基于ASIFT算法对影像重叠度进行判别和评估后认为,扫描物体整体点云配准精度提升20%左右。
3) 必须重视用于坐标转换的地面三维激光扫描标靶研究,其扫描质量和数据纠偏质量直接影响最终拼接的点云精度。用小波阈值去噪方法对球形标靶点云去噪是有效的,去噪后的数据可以更精确地拟合出同名特征点的中心坐标,是提高点云配准精度的有效手段。
| [1] |
盛业华, 张卡, 张凯, 等. 地面三维激光扫描点云的多站数据无缝拼接[J]. 中国矿业大学学报, 2010, 39(2): 233-237 (Sheng Yehua, Zhang Ka, Zhang Kai, et al. Seamless Multi Station Merging of Terrestrial Laser Scanned 3D Point Clouds[J]. Journal of China University of Minim and Technology, 2010, 39(2): 233-237)
(  0) 0) |
| [2] |
姚吉利, 马宁, 贾象阳, 等. 球形标靶的固定式扫描大点云自动定向方法[J]. 测绘学报, 2015, 44(4): 431-437 (Yao Jili, Ma Ning, Jia Xiangyang, et al. An Approach for Automatic Orientation of Big Point Clouds from the Stationary Scanners Based on the Spherical Targets[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(4): 431-437)
(  0) 0) |
| [3] |
程效军, 施贵刚, 王峰, 等. 点云配准误差传播规律的研究[J]. 同济大学学报:自然科学版, 2009, 37(12): 1 668-1 672 (Cheng Xiaojun, Shi Guigang, Wang Feng, et al. Research on Point Cloud Registration Error Propagation[J]. Journal of Tongji University:Natural Science, 2009, 37(12): 1 668-1 672)
(  0) 0) |
| [4] |
郑德华, 岳东杰, 岳建平. 基于几何特征约束的建筑物点云配准算法[J]. 测绘学报, 2008, 37(4): 465-468 (Zheng Dehua, Yue Dongjie, Yue Jianping. Geometric Feature Constraint Based Algorithm for Building Scanning Point Cloud Registration[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(4): 465-468)
(  0) 0) |
| [5] |
杨帆, 常俊飞. 基于一致性球的点云配准算法研究[J]. 大地测量与地球动力学, 2018, 38(1): 87-91 (Yang Fan, Chang Junfei. Point Cloud Registration Algorithm Based on the Consistency of the Ball[J]. Journal of Geodesy and Geodynamics, 2018, 38(1): 87-91)
(  0) 0) |
| [6] |
Rsehetyuk Y, Horemuz M, Sjoberg L E. Determination of the Optimal Diameter for Spherical Targets Used in 3D Laser Scanning[J]. Survey Review, 2005, 38(297): 243-253 DOI:10.1179/sre.2005.38.297.243
(  0) 0) |
| [7] |
Franaszek M, Cheok G S, Witzgall C. Fast Automatic Registration of Range Images from 3D Imaging Systems Using Sphere Targets[J]. Automation in Construction, 2009, 18(3): 265-274
(  0) 0) |
| [8] |
李嘉, 阿依古丽·阿曼, 郑德华. 复杂场景三维点云中未知球形目标的自动识别方法[J]. 计算机辅助设计与图形学学报, 2013, 25(10): 1 489-1 496 (Li Jia, Ayiguli Aman, Zheng Dehua. Automatically Identifying Uncertain Spherical Targets in 3D Point Clouds of Complex Scenario[J]. Journal of Computer-Aided Design and Computer Graphics, 2013, 25(10): 1 489-1 496)
(  0) 0) |
| [9] |
郝泳涛, 肖文生, 胡雅俊. 离散点云数据的小波变换处理算法[J]. 同济大学学报:自然科学版, 2009, 37(5): 674-679 (Hao Yongtao, Xiao Wensheng, Hu Yajun. Method of Data Processing for Discrete Cloud Based on Wavelet Tansform[J]. Journal of Tongji University:Natural Science, 2009, 37(5): 674-679)
(  0) 0) |
| [10] |
徐工, 程效军. 基于小波技术的散乱点云自适应压缩算法[J]. 同济大学学报:自然科学版, 2013, 41(11): 1 738-1 743 (Xu Gong, Cheng Xiaojun. Adaptive Reduction Algorithm of Scattered Point Clouds Based on Wavelet Technology[J]. Journal of Tongji University:Natural Science, 2013, 41(11): 1 738-1 743)
(  0) 0) |
| [11] |
徐辛超, 徐爱功, 于丹. 地面三维激光扫描点云拼接影响因素分析[J]. 测绘通报, 2017(2): 14-18 (Xu Xinchao, Xu Aigong, Yu Dan. Study on Influence Factors of Scanning Point Cloud Registration of 3D Laser[J]. Bulletin of Surveying and Mapping, 2017(2): 14-18)
(  0) 0) |
| [12] |
张步, 姚顽强, 陈鹏. 基于几何特征的建筑物点云配准方法[J]. 大地测量与地球动力学, 2015, 35(3): 416-420 (Zhang Bu, Yao Wanqiang, Chen Peng. Research on Building Scanning Point Cloud Registration Based on Geometric Feature Constraint[J]. Journal of Geodesy and Geodynamics, 2015, 35(3): 416-420)
(  0) 0) |
| [13] |
李明峰, 欧江霞, 王永明, 等. 基于改进小波阈值去噪法的变形预测研究[J]. 大地测量与地球动力学, 2014, 34(3): 68-71 (Li Mingfeng, Ou Jiangxia, Wang Yongming, et al. Study on Deformation Prediction Based on Improved Wavelet Threshold De-Noising Method[J]. Journal of Geodesy and Geodynamics, 2014, 34(3): 68-71)
(  0) 0) |
| [14] |
谢宏全, 谷风云, 李勇, 等. 基于激光点云数据的三维建模应用实践[M]. 武汉: 武汉大学出版社, 2014 (Xie Hongquan, Gu Fengyun, Li Yong, et al. Application of 3D Modeling Based on Laser Point Cloud Data[M]. Wuhan: Wuhan University Press, 2014)
(  0) 0) |
| [15] |
余腾, 胡伍生, 孙小荣, 等. 基于运营期地铁轨行区监测数据的去噪小波基函数选取[J]. 铁道标准设计, 2017, 10(2): 213-217 (Yu Teng, Hu Wusheng, Sun Xiaorong, et al. Selection of Denoising Wavelet Basis Function Based on Monitoring Data of Subway Line Area during Operation[J]. Railway Standard Design, 2017, 10(2): 213-217)
(  0) 0) |
| [16] |
张毅, 闫利, 杨红, 等. 地面激光扫描球形标靶的球心误差研究[J]. 武汉大学学报:信息科学版, 2012, 37(5): 598-601 (Zhang Yi, Yan Li, Yang Hong, et al. Spherical Center Error of Sphere Target in TLS[J]. Geomatics and Information Science of Wuhan University, 2012, 37(5): 598-601)
(  0) 0) |
2. School of Geomatics Science and Technology, Nanjing Technology University, 30 South-Puzhu Road, Nanjing 211800, China;
3. School of Transportation, Southeast University, 35 Jinxianghe Road, Nanjing 210096, China
 2019, Vol. 39
2019, Vol. 39

