垂线偏差的测定是大地测量中一个十分重要的工作,常用的测定方法有天文大地测量法、重力测量法、地球重力场模型法、GNSS水准法和数字天顶摄影仪法等[1]。天文大地测量法是利用天文测量与大地测量获得同一点不同基准的坐标,通过简单计算确定测站点的垂线偏差,工作量大,且在城市实施的难度较大[2];重力测量法是借助重力异常数据,按斯托克斯法确定垂线偏差,主要受重力异常数据精度及分辨率等因素的影响[3-4];地球重力场模型法是直接利用重力位系数确定垂线偏差[5-6],受重力场模型精度和地形起伏的影响较大;GNSS水准方法是利用若干条基线求出测站点的一组垂线偏差分量(ξ,η),效率较低,且受基线间夹角和地形起伏的影响较大[7];数字天顶摄影仪法是基于天文大地测量理论,利用CCD成像、GNSS定位等技术,经过一定的数据处理来确定测站点的垂线偏差,其精度可达±0.05″[8-9],美国GSVS项目各测站点的垂线偏差即通过该方法测得[10-11]。随着cm级甚至亚cm级(相对)精度大地水准面模型的广泛建立,利用大地水准面模型获取较高精度的垂线偏差成为可能。
本文对计算垂线偏差的GNSS水准法进行梳理,设计2种垂线偏差计算方案,在此基础上简化利用大地水准面模型计算垂线偏差的公式,并进行有关实验计算与精度分析。
1 原理与方法 1.1 由大地水准面模型计算垂线偏差的简便数学模型| $ u = - \frac{{{\rm{d}}N}}{{{\rm{d}}s}} $ | (1) |
式中,s为大地水准面沿任意方向上铅垂面与参考椭球面交线的长度(简称距离)。可将垂线偏差u分解为南北分量ξ和东西分量η,则:
| $ u = \xi {\rm{cos}}\alpha + \eta {\rm{sin}}\alpha $ | (2) |
式中,α为投影方向的大地方位角。联合式(1)和式(2)可得:
| $ - \frac{{{\rm{d}}N}}{{{\rm{d}}s}} = \xi {\rm{cos}}\alpha + \eta {\rm{sin}}\alpha $ | (3) |
假设地球表面有距离很近的A、B 2点,用差分值代替式(3)中的微分值,可以得出:
| $ - \frac{{\Delta {N_{AB}}}}{{\Delta {s_{AB}}}} \approx \xi {\rm{cos}}{\alpha _{AB}} + \eta {\rm{sin}}{\alpha _{AB}} = u $ | (4) |
式中,ΔNAB、ΔsAB、αAB分别为A和B之间的大地水准面差距之差(计算时以高程异常差代替)、距离和大地方位角。如果采用GNSS水准测量法确定垂线偏差,由式(4)可进一步得:
| $ - \frac{{\Delta {h_{AB}} - \Delta {H_{AB}}}}{{\Delta {s_{AB}}}} \approx \xi {\rm{cos}}{\alpha _{AB}} + \eta {\rm{sin}}{\alpha _{AB}} $ | (5) |
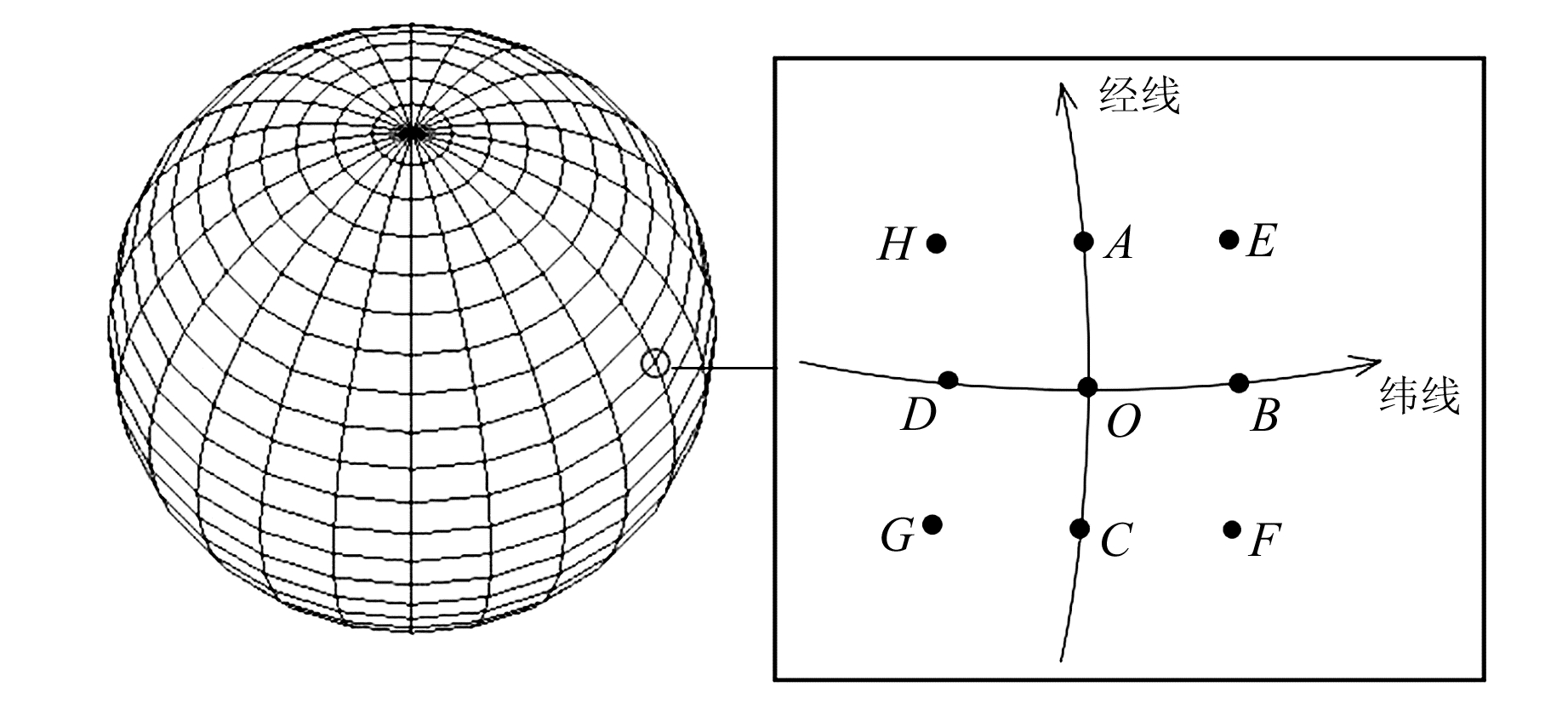
式中,ΔhAB为通过GNSS测量获取的大地高差,ΔHAB为通过水准测量获取的正常高差。此外,还可利用大地水准面模型计算垂线偏差。大地水准面模型法较GNSS水准法简便,如果计算方案设计合理,可省去矩阵求逆的步骤,更容易实现。下面以求取测站点O的垂线偏差为例详细介绍该方法。如图 1所示,已知测站点O的大地经纬度,假设取点间距为1′,设计2种方案。
|
图 1 利用大地水准面模型计算垂线偏差原理 Fig. 1 The principle of calculating deflection of the vertical by geoid model |
方案1:仅考虑南北东西4个方向,即利用A、B、C、D 4个已知点计算O点的垂线偏差分量。计算步骤如下:1)在O点的南北(经线)和东西(纬线)方向分别取A、B、C、D 4个已知点,并确定4点的大地坐标(O点纬度和经度分别增加或减小1′可得4点坐标);2)通过大地水准面模型分别计算O点和4个已知点之间的高程异常差ΔNOA、ΔNOB、ΔNOC和ΔNOD;3)利用Vincenty公式分别计算O点和4个已知点之间的距离ΔsOA、ΔsOB、ΔsOC和ΔsOD;4)由于αOA、αOB、αOC、αOD近似为0°、90°、180°和270°,将计算所得的高程异常差和距离分别代入式(4),得:
| $ \left\{ \begin{array}{l} {\xi _1} = - \frac{{\Delta {N_{OA}}}}{{\Delta {s_{OA}}}}\\ {\eta _1} = - \frac{{\Delta {N_{OB}}}}{{\Delta {s_{OB}}}}\\ {\xi _2} = \frac{{\Delta {N_{OC}}}}{{\Delta {s_{OC}}}}\\ {\eta _2} = \frac{{\Delta {N_{OD}}}}{{\Delta {s_{OD}}}} \end{array} \right. $ | (6) |
计算O点垂线偏差南北分量和东西分量的简便公式为:
| $ \left\{ \begin{array}{l} {\xi _{O1}} = \frac{{{\xi _1} + ( - {\xi _2})}}{2}\\ {\eta _{O1}} = \frac{{{\eta _1} + ( - {\eta _2})}}{2} \end{array} \right. $ | (7) |
方案2:在方案1的基础上增加近似东北、东南、西南、西北方向的4个已知点,由A、B、C、D、E、F、G、H 8个点计算O点的垂线偏差分量。其中,E、F、G、H的坐标同样可通过O点纬度和经度分别增加或减少1′得到。根据式(4),先利用OE和OF2个方向求出一组垂线偏差分量(ξ3, η3),再利用OH和OG 2个方向求出另一组分量(ξ4, η4),具体公式为[12]:
| $ \left\{ \begin{array}{l} {\xi _3} = \frac{{{u_{OE}}\sin{\alpha _{OF}} - {u_{OF}}\sin{\alpha _{OE}}}}{{\sin\left( {{\alpha _{OF}} - {\alpha _{OE}}} \right)}}\\ {\eta _3} = \frac{{{u_{OE}}\cos{\alpha _{OF}} - {u_{OF}}\cos{\alpha _{OE}}}}{{\sin({\alpha _{OE}} - {\alpha _{OF}})}}\\ {\xi _4} = \frac{{{u_{OG}}\sin{\alpha _{OH}} - {u_{OH}}\sin{\alpha _{OG}}}}{{\sin({\alpha _{OH}} - {\alpha _{OG}})}}\\ {\eta _4} = \frac{{{u_{OG}}\cos{\alpha _{OH}} - {u_{OH}}\cos{\alpha _{OG}}}}{{\sin({\alpha _{OG}} - {\alpha _{OH}})}} \end{array} \right. $ | (8) |
式中,uOE为通过ΔNOE和ΔsOE求得的垂线偏差,uOF、uOG和uOH同理。由式(8)可进一步求出通过E、F、G、H点得到的垂线偏差分量(ξO2, ηO2):
| $ \left\{ \begin{array}{l} {\xi _{O2}} = \frac{{{\xi _3} + {\xi _4}}}{2}\\ {\eta _{O2}} = \frac{{{\eta _3} + {\eta _4}}}{2} \end{array} \right. $ | (9) |
将(ξO2, ηO2)与方案1求得的(ξO1, ηO1)对应分量取平均,即可得到O点垂线偏差分量的最终计算结果。
1.2 精度估计可由大地水准面差距之差的精度估计垂线偏差的计算精度。对式(4)应用误差传播定律:
| $ \sigma _u^2 = \frac{1}{{\Delta s_{AB}^2}}(\sigma _{\Delta {N_{AB}}}^2) + {\left( {\frac{{\Delta {N_{AB}}}}{{\Delta s_{AB}^2}}} \right)^2}\sigma _{\Delta {s_{AB}}}^2 $ | (10) |
其中,等式右侧第二项中的ΔsAB为一个4次项,其影响可忽略不计。将式(10)简化为:
| $ \sigma _u^2 = \frac{1}{{\Delta s_{AB}^2}}(\sigma _{\Delta {N_{AB}}}^2) $ | (11) |
由式(11)可知,垂线偏差的计算精度σu与高程异常差的精度σΔNAB及距离ΔsAB有关。考虑到当前大地水准面模型的实际分辨率、GNSS水准法的外业工作量及取值近似对计算结果的影响等因素,本文仅对取点间距不大于2′的情况展开讨论。当σΔNAB=±5 mm,ΔsAB=1 km时,垂线偏差的中误差σu≈±1.0″。表 1(单位(″))列出了不同ΔsAB、σΔNAB对应的σu值。
|
|
表 1 垂线偏差的计算精度 Tab. 1 The accuracy of the calculating deflection of the vertical |
通过模拟方法探讨由大地水准面模型计算垂线偏差时,大地水准面不同精度、不同取点间距和已知点选取及个数对计算结果的影响,基本流程见图 2。选取一个垂线偏差较大的点(本文选取美国GSVS2014项目中的GSVS091号点),已知其大地经纬度,先采用重力场模型EIGEN-6C4(2 190阶)计算GSVS091点的垂线偏差分量ξ0和η0,并以此作为真值,再由EIGEN-6C4求出GSVS091点与各已知点间的高程异常差ΔN,通过ΔN求出一组垂线偏差ξ1和η1。理论上,由地球重力场模型直接计算出的ξ0、η0和由本文方法求得的ξ1、η1是等价的。为了分析不同情况下ξ1、η1的计算精度,采用上述2种计算方案,且在ΔN中分别加入±5 mm、±10 mm、±15 mm和±20 mm正态分布的随机误差,模拟计算1 000次,将所得的垂线偏差值ξ1、η1与真值比较,并统计其计算精度。

|
图 2 模拟计算流程 Fig. 2 Simulation flow chart |
方案1和方案2均按3种取点间距(30″、1′和2′)进行模拟计算,计算结果及精度统计分别见表 2和3。结果表明:1)采用方案1和方案2计算垂线偏差分量时,若要计算精度优于±1″,取点间距为30″、1′和2′时所对应的大地水准面的相对精度应分别优于±5 mm、±10 mm和±20 mm;2)利用大地水准面模型计算得到的垂线偏差,其精度受已知点数量和取点间距的联合影响,当取点间距一定时,大地水准面的相对精度越高,垂线偏差的计算精度越高;当大地水准面相对精度一定时,适当增加取点间距,对提高垂线偏差分量的计算精度有利;3)随着取点间距的增加,2种方案计算所得的残差平均值(系统差)会变大,因为式(1)为微分关系式,其计算结果会受近似取值的影响,实际计算时不建议取点间距大于2′。
|
|
表 2 方案1计算结果 Tab. 2 Calculation results of scheme one |
|
|
表 3 方案2计算结果 Tab. 3 Calculation results of scheme two |
利用美国GSVS2011和GSVS2014项目的数据验证本文方法的计算精度。GSVS2011项目是一条从Austin到Corpus Christi的线形测量项目,全长约300 km,布设有218个测站点,整体呈南北走向;GSVS2014是GSVS2011的后续项目,是一条从Denison到Cedar Rapids的线形测量项目,全长约325 km,共204个测站点,整体呈东西走向。这2个项目均包括GPS测量、垂线偏差测量和精密水准测量等内容,其中垂线偏差数据是通过数字天顶摄影仪法(CODIAC camera)获取的,精度达到±0.05″[10-11]。
利用2个项目中各测站点的大地经纬度数据和GEOID12B大地水准面模型(分辨率为1′),计算测站点和已知点之间的高程异常差ΔN和距离(其中GEOID12B模型的大地水准高差精度在GSVS2011和GSVS2014项目区域分别为±9 mm和±5 mm)。按照本文方法,以3种取点间距(30″、1′和2′)计算各测站点的垂线偏差,并与GSVS项目垂线偏差的实测值进行比较,精度统计结果见表 4。
|
|
表 4 GSVS项目垂线偏差计算精度统计结果 Tab. 4 Calculation accuracy statistics of deflection of the vertical of GSVS project |
由表 4可知:1)当取点间距相同时,方案1与方案2的计算精度基本相当,总体精度优于±0.4″,说明本算例中已知点的个数和取点间距对垂线偏差计算精度的影响较小。2)当已知点个数相同时,取点间距增加,由大地水准面模型计算得到的GSVS2011项目的垂线偏差精度稍有提高,而GSVS2014项目的垂线偏差精度几乎没有变化(特别是东西方向分量)。实际上,随着距离的增加,2点间大地水准面相对精度可能也会降低,但取不同间距时,垂线偏差精度的差异小于0.05″,就本文方法的精度而言,这种差异完全可以忽略。3)实际计算时,建议取点间距为大地水准面模型分辨率,并采用方案1计算。
3.2 算例2选取美国西部一块5°×5°的区域(40°~45°N,100°~105°W,分辨率为1′),该区域垂线偏差较大,利用GEOID12B大地水准面模型,采用本文方法计算该区域的垂线偏差(取相邻4个格网点,计算分辨率为1′),并将计算值与DEFLEC12B模型值比较。其中,垂线偏差模型DEFLEC12B是GEOID12B的伴生产品,ξ和η的变化范围约为-54″~58″。通过GSVS2011和GSVS2014项目的实测垂线偏差来评估DEFLEC12B模型,精度统计结果见表 5。
|
|
表 5 DEFLEC12B的精度评估 Tab. 5 Accuracy estimation |
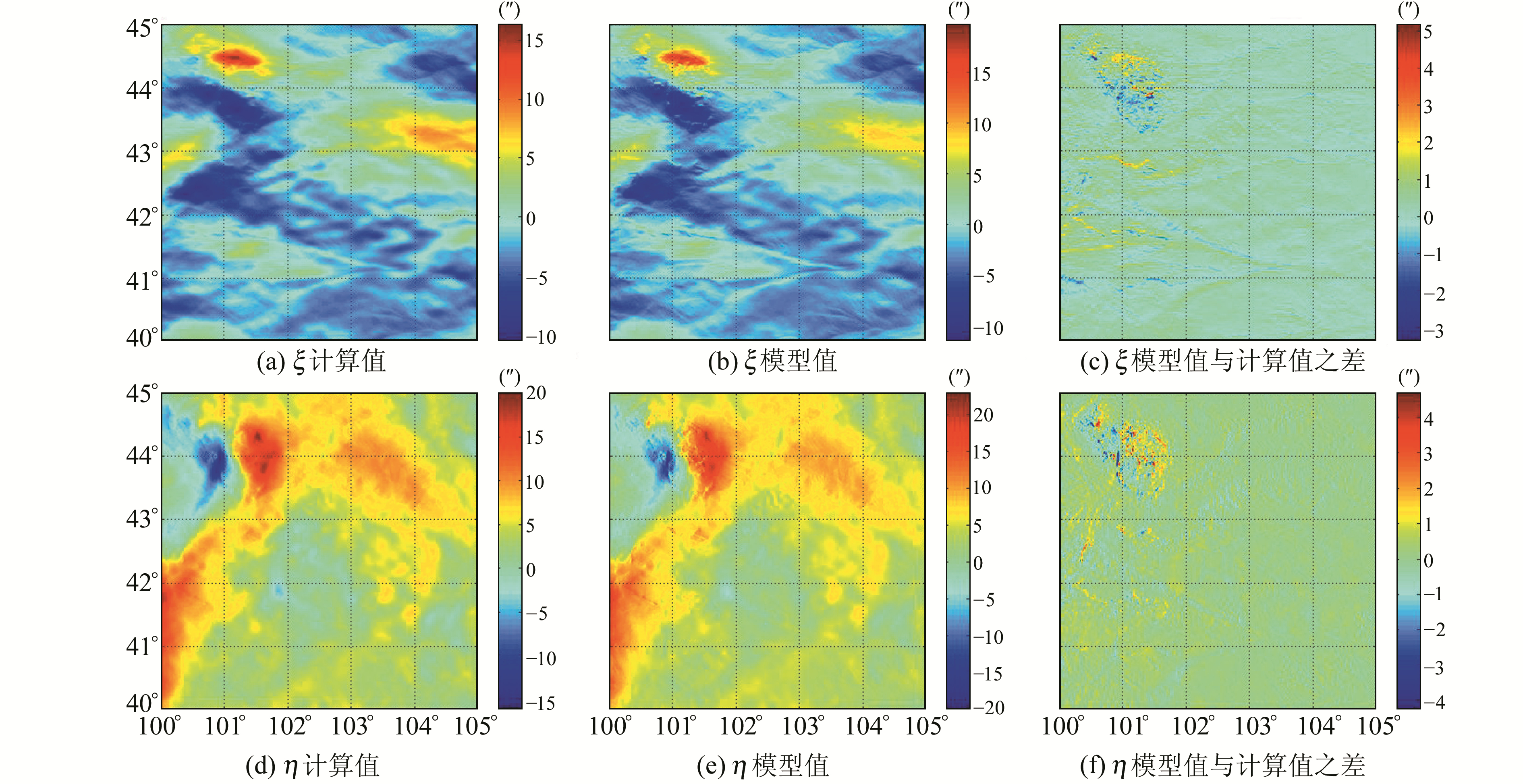
由表 5可知,DEFLEC12B模型垂线偏差的精度优于±0.5″。算例2的计算结果见图 3,其中,图 3(a)和3(d)分别为利用GEOID12B模型计算得到的ξ和η值,图 3(b)和3(e)为DEFLEC12B的ξ和η模型值,图 3(c)和3(f)为计算值与相应模型值的差,精度统计结果见表 6。
|
图 3 垂线偏差计算值与模型值比较 Fig. 3 Comparison of the deflection of vertical between calculated values and the true values |
|
|
表 6 计算结果统计 Tab. 6 Calculation results statistics |
由图 3和表 6可以看出,本文方法计算结果与DEFLEC12B模型符合较好,差异较大的值出现在地形起伏较大的地区,计算精度优于±0.5″。
4 结语本文设计了2种采用GNSS水准法计算垂线偏差的方案,在此基础上给出由大地水准面模型计算垂线偏差的简便方法,并通过模拟及实测数据进行验证,结论如下:
1) 模拟计算结果表明,若想获取优于±1 ″精度的垂线偏差,建议采取方案1,且取点间距为1′,大地水准面模型的相对精度为±10 mm。
2) 基于GEOID12B大地水准面模型,利用方案1计算GSVS2011和GSVS2014两个项目测站点垂线偏差,并与实测结果进行比较。结果表明,2个算例中垂线偏差的精度均优于±0.5″,说明利用相对精度为cm甚至亚cm级的大地水准面模型可获取较高精度的垂线偏差。在实际计算中,取点间距可与大地水准面模型的分辨率一致。
3) 本文模拟计算与实测数据处理结果稍有差异,主要原因可能是模拟计算点的垂线偏差较大,且估计的是单个点的垂线偏差精度;而实测数据处理中测区垂线偏差较小,且评估的是所有测站点垂线偏差的整体精度。
致谢: 感谢ICGEM提供重力场模型数据,NGS提供GSVS项目及GEOID12B等数据。
| [1] |
张永毅, 张兴福. 垂线偏差的确定方法及精度分析[J]. 大地测量与地球动力学, 2016, 36(5): 395-399 (Zhang Yongyi, Zhang Xingfu. Determination and Accuracy Analysis of Vertical Deflection[J]. Journal of Geodesy and Geodynamics, 2016, 36(5): 395-399)
(  0) 0) |
| [2] |
孔祥元, 郭际明, 刘宗泉. 大地测量学基础[M]. 武汉: 武汉大学出版社, 2010 (Kong Xiangyuan, Guo Jiming, Liu Zongquan. Foundation of Geodesy[M]. Wuhan: Wuhan University Press, 2010)
(  0) 0) |
| [3] |
宁津生, 郭春喜, 王斌, 等. 我国陆地垂线偏差精化计算[J]. 武汉大学学报:信息科学版, 2006, 31(12): 1 035-1 038 (Ning Jinsheng, Guo Chunxi, Wang Bin, et al. Refined Determination of Vertical Deflection in China Mainland Area[J]. Geomatics and Information Science of Wuhan University, 2006, 31(12): 1 035-1 038)
(  0) 0) |
| [4] |
李月锋, 丁行斌. 垂线偏差时变的研究进展[J]. 地球物理学进展, 2008, 23(6): 1 736-1 745 (Li Yuefeng, Ding Xingbin. Progress in Studying Plumb Line Variations[J]. Progress in Geophysics, 2008, 23(6): 1 736-1 745)
(  0) 0) |
| [5] |
Hirt C. Prediction of Vertical Deflections from High-Degree Spherical Harmonic Synthesis and Residual Terrain Model Data[J]. Journal of Geodesy, 2010, 84(3): 179-190 DOI:10.1007/s00190-009-0354-x
(  0) 0) |
| [6] |
邢志斌, 李姗姗, 曲政豪, 等. 局部区域模型垂线偏差快速算法[J]. 测绘科学, 2015, 40(12): 38-43 (Xing Zhibin, Li Shanshan, Qu Zhenghao, et al. A Fast Calculation Approach for Model Vertical Deflection in Local Area[J]. Science of Surveying and Mapping, 2015, 40(12): 38-43)
(  0) 0) |
| [7] |
Tse C M, Bki Iz H. Deflection of the Vertical Components from GPS and Precise Leveling Measurements in Hong Kong[J]. Journal of Surveying Engineering, 2006, 132(3): 97-100 DOI:10.1061/(ASCE)0733-9453(2006)132:3(97)
(  0) 0) |
| [8] |
Hirt C, Seeber G. Accuracy Analysis of Vertical Deflection Data Observed with the Hannover Digital Zenith Camera System TZK2-D[J]. Journal of Geodesy, 2008, 82(6): 347-356 DOI:10.1007/s00190-007-0184-7
(  0) 0) |
| [9] |
郭金运, 宋来勇, 常晓涛, 等. 数字天顶摄影仪确定垂线偏差及其精度分析[J]. 武汉大学学报:信息科学版, 2011, 36(9): 1 085-1 088 (Guo Jinyun, Song Laiyong, Chang Xiaotao, et al. Vertical Deflection Measure with Digital Zenith Camera and Accuracy Analysis[J]. Geomatics and Information Science of Wuhan University, 2011, 36(9): 1 085-1 088)
(  0) 0) |
| [10] |
Smith D A, Holmes S A, Li X P, et al. Confirming Regional 1 cm Differential Geoid Accuracy from Airborne Gravimetry: The Geoid Slope Validation Survey of 2011[J]. Journal of Geodesy, 2013, 87(10-12): 885-907 DOI:10.1007/s00190-013-0653-0
(  0) 0) |
| [11] |
Wang Y M, Becker C, Breidenbach S, et al. Preliminary Results of the Geoid Slope Validation Survey 2014 in Iowa[C].AGU Fall Meeting, San Francisco, 2014
(  0) 0) |
| [12] |
李建忠. 用GPS测定垂线偏差[J]. 测绘工程, 1999(2): 34-37 (Li Jianzhong. Determining Component of Vertical Deflection Using GPS[J]. Engineering of Surveying and Mapping, 1999(2): 34-37 DOI:10.3969/j.issn.1006-7949.1999.02.007)
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39


