2. 中国电子科技集团第38研究所,合肥市香樟大道199号,230031
大面积地下煤炭开采活动容易引起地面沉降,破坏地表结构,诱发滑坡、塌陷、地裂缝等地质灾害,严重威胁区域的可持续发展[1]。中国作为世界第一大产煤国,煤炭开采引起的地面沉降、塌陷和积水等矿区地质灾害问题一直是矿业企业和当地政府亟待解决的问题。为保证采矿工作的顺利实施,需要对矿区地表形变进行长期有效的监测和预测,掌握由采动而引发的形变特征及规律,从而避免灾害的发生。
近年来,相比于测站稀疏且耗时耗力的传统水准、GPS测量技术[2],连续覆盖、高精度和高度自动化的差分合成孔径雷达技术(D-InSAR)成为获取地表形变信息的有效手段[3]。全球诸多学者对D-InSAR地表形变监测进行了大量研究,并实现了其mm级的观测精度[4],但由于易受时间、空间失相干与大气延迟的影响,D-InSAR不能获得时间上连续的沉降监测结果。针对这一缺点,基于小基线集和奇异值分解的时序InSAR小基线集SBAS技术被提出[5]。目前,SBAS技术被广泛应用于地震[6]、火山[7]、冰川[8]、地下水开采及煤矿开采引发的地表形变监测和分析中。目前,对SBAS技术的研究主要集中于大范围[9]和长时间跨度[10]的形变监测和分析,针对小区域和小时间跨度的连续动态监测分析及结合其进行形变预测的研究相对较少。
本文利用欧空局重访周期12 d、连续13景的哨兵卫星Sentinel-1雷达影像数据,采用SBAS-InSAR技术对淮南潘集矿区内的居民区杨聚庄进行形变监测和分析,并根据矿区开采沉陷的实际形变特征,提出一种基于灰色模型和优化支持向量机回归的组合预测模型。利用灰色模型的线性预测优势,结合支持向量机模型对非线性数据优良的泛化能力和学习能力,对矿区沉降进行高效能的预测。
1 SBAS技术基本原理和预测模型建立 1.1 SBAS基本原理时序InSAR技术是在传统InSAR技术基础上发展起来的,通过对多时序SAR数据的相位统计特征进行参数估计,可以有效减小由干涉相位中大气延迟、低相干等因素引入的误差。作为时序InSAR技术分支之一的SBAS,其基本原理是将常规D-InSAR的监测形变结果作为单一观测值,然后根据最小二乘准则得到高精度的形变序列。详细的SBAS原理、技术可参考文献[11]。
假设获取了N+1景SAR影像,且影像获取时间t按时间顺序(t0,…,tn)排列,依据时空干涉基线阈值条件自由组合,可生成M幅干涉图,且M满足:
| $ \frac{{N + 1}}{2} \le M \le N\left( {\frac{{N + 1}}{2}} \right) $ | (1) |
假设干涉图j是由tA、tB时间获取的影像干涉图生成(tB > tA),在去除平地效应与地形相位影响后,干涉图j中任意一个像素的干涉相位可表示为:
| $ \begin{array}{l} \delta {\varphi _j} = \varphi \left( {{t_B}} \right) - \varphi \left( {{t_A}} \right) = {\varphi _{{\rm{def}}, j}} + {\varphi _{{\rm{topo}}, j}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\varphi _{{\rm{atm}}, j}} + {\varphi _{{\rm{noise}}, j}} \end{array} $ | (2) |
式中,φ(tB)和φ(tA)分别为tB和tA时刻SAR影像的相位值,φdef, j为此时间段内卫星视线向的形变相位,φtopo, j为参考DEM不精确引入的残余地形相位误差,φatm, j为大气相位误差,φnoise, j为噪声相位。SBAS-InSAR 的具体处理流程见图 1。

|
图 1 结合SBAS-InSAR技术和灰色支持向量机模型进行矿区形变监测和预测的处理流程 Fig. 1 Processing flowchart of mine deformation monitoring and prediction in mining area based on SBAS-InSAR technology and GM-SVR model |
通常意义上,信息不完全的系统被称为灰色系统。在建立等时距灰色预测模型前,需将所有原始时间序列视为具有灰色特征的灰色量,再对数据进行预处理,将杂乱无章的数据转换为有序数据,弱化其随机性,然后建立微分方程,进而预测未来发展趋势。该模型的优势在于,对数据样本小或含不确切信息的系统适用性很强,可以挖掘内部连续变化过程中有序的数学规律,详细原理可参考文献[12]。
支持向量机是数据挖掘中的新方法,是建立在专门研究小样本情况下机器学习规律的统计学理论基础上的通用学习方法。该方法将低维的非线性问题映射至高维空间,通过高维空间中的决策函数解决低维空间的非线性问题,且具备相应的惩罚机制,防止过拟合现象的发生。其基本思路是假设样本集{xi,yi}的最优回归函数为f(x, y), 为了使
| $ R\left[ f \right] = \smallint cf\left( {x, y} \right){\rm{d}}\mathit{P}\left( {x, y} \right) $ | (3) |
极小[13],回归方程的最优化问题转化为:
| $\frac{1}{2}\left\| \omega \right\| {^2} + c\frac{1}{k}\sum\limits_{i = 1}^k {{L_\varepsilon }({y_i}, f({x_i}))} $ | (4) |
通过引入非负松弛变量ξ和ξ*来度量ε不敏感带外训练样本点的偏离程度,再引入拉格朗日乘子α,根据KKT(Karush-Kuhn-Tucker)约束条件,将样本映射到高维Hilbert空间,在高维空间中对转换后的结果进行线性回归处理,最后得到非线性回归函数。
本文建立组合预测模型,通过等时距GM(1,1)模型建立初始预测模型,对样本进行初次拟合以掌握样本的原始内在发展趋势,然后将灰色模型预测值与原始样本进行比较,得到残差值序列。由于矿区地表沉降的复杂性,监测获取的数据波动较大,灰色模型预测得到的残差序列的非线性特征通常很高。因此,采用网格搜索惩罚参数c和核函数中方差G的优化支持向量机回归模型,利用其转换到高维空间的非线性回归优势对残差序列的内在规律进行挖掘,建立残差改正模型。通过对样本在模型中的训练,输入需要预测的时间序列,得到灰色模型的预测值及SVR模型的残差改正,将预测值与残差改正值求和,即得到组合模型的预测值。结合SBAS-InSAR时序分析的形变预测技术流程如图 1所示。
2 实例计算和结果分析 2.1 研究区概况和数据集淮南矿区地处我国东部,位于安徽省淮南市中部,北邻淮河,面积约3 000 km2(116°21′21″~117°11′59″E,32°32′45″~33°0′24″N),是我国东南地区最大的煤炭基地。整个矿区地势较为平坦,平均海拔在30~40 m。由于矿区煤炭资源开发程度不断提高,采空区面积也不断增加,留下了极大的安全隐患,引起相关部门的重视。
哨兵卫星是欧洲航天局“哥白尼计划”中的对地观测卫星,是继ERS和ENVISAT后又一颗具有重要意义的C波段遥感卫星。与传统的条带观测模式和扫描观测模式不同,哨兵数据采用了新的逐行扫描地形观测(TOPSAR)宽幅模式。本文以淮南潘集矿区内杨聚庄为研究区,收集2016-12-27~2017-05-20共13景C波段Sentinel-1A IW影像(极化方式为VV,且全为升轨数据),同时收集了相应的哨兵卫星精密轨道文件。
2.2 SBAS监测结果及分析采用SBAS-InSAR方法对影像数据进行处理:1)由于原始的影像数据覆盖范围较大,本文对数据进行裁剪,裁剪后的范围如图 2所示;2)为了获取可靠的地表形变监测结果,选取时间基线阈值为60 d和空间基线阈值为150 m生成干涉连接图;3)根据连接图的连接关系生成差分干涉图集,采用精密轨道数据去除平地效应,同时利用SRTM3 DEM数据消除地形相位;4)采用最小费用流法对小基线干涉图进行相位解缠;5)根据振幅与相位的稳定性选择研究区内的稳定点,利用3阶多项式模型进行轨道精炼,消除轨道误差引起的趋势相位;6)进行变形速率反演和地理编码,并根据大气相位的时空特性对相干点的大气延迟相位进行分离,最后根据入射角的余弦对视线向形变进行分割,得到地面垂直位移。

|
图 2 研究区形变序列图 Fig. 2 Deformation sequence of the study area |
图 2为研究区2016-12-27~2017-05-20部分时间形变序列图,所有图像均显示以2016-12-27为参考时间的形变累计量,每幅图的右上角表示的是此幅影像的获取时间。图 3为研究区的形变速率。由图 2和3可知,研究区在监测时间段内由采矿引起的最大累积地面垂直沉降为48 mm,平均累积沉降为17.8 mm,最大形变速率达到-90 mm/a,沉降量由北向南逐渐增大,沉降速率显著加快,形成明显的沉降漏斗。

|
图 3 研究区的形变速率和GPS观测站位置 Fig. 3 Cumulative deformation rate of the study area and location of GPS station |
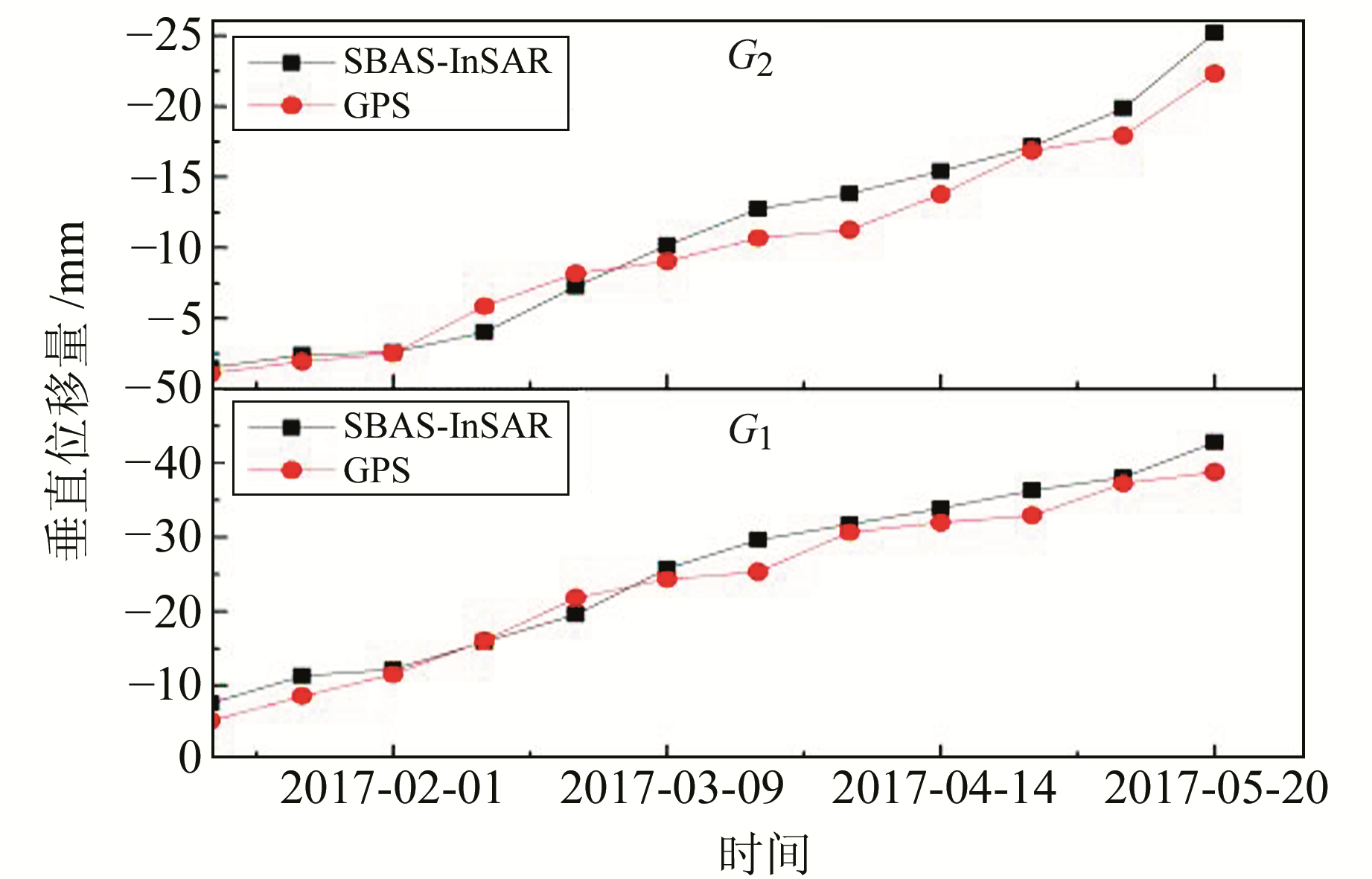
为检验SBAS技术在监测由采矿引起的沉降方面的准确性,采用北斗/GPS组合系统(以下简称GPS)的双差静态定位测量结果进行验证。GPS系统1 h解的高程方向精度优于4 mm,满足本次研究区变形监测精度的需求。测站点分布如图 3所示(图 3左边2幅图为GPS观测站实地图)。图 4为SBAS-InSAR技术和GPS技术在观测点的形变序列观测结果对比。由图可知,G1点的SBAS-InSAR和GPS测量结果之间,垂直位移最大绝对误差、相对误差和平均绝对误差分别为4.33 mm、2.38 mm和2.01 mm; G2点分别为2.87 mm、1.61 mm和1.34 mm,2组结果十分相近,符合矿山测量中形变监测的要求[14]。
|
图 4 SBAS-InSAR和GPS获取的2个观测点形变时间序列对比 Fig. 4 Comparison of vertical deformation time series of two observation points obtained by SBAS-InSAR and GPS |
对SBAS-InSAR技术获取的观测点(图 3)时间序列数据进行拟合预测,同时,为验证本文提出的灰色优化支持向量机模型在矿区沉降预测中的性能,建立另外2种方案进行比较分析:1)方案1,利用单一的灰色GM(1,1)模型进行预测;2)方案2,利用单一的支持向量机SVR模型进行预测。方案均采用2016-12-27~2017-04-02前8期(每期时间间隔为12 d)的沉降数据作为建模的训练样本,2017-04-02~2017-05-20后4期的数据作为预测的测试样本,具体数据和结果见表 1~4和图 5。
|
|
表 1 G1点各模型拟合结果对比 Tab. 1 The contrast of each model calculation results of G1 |
|
|
表 2 G1点各模型预测结果对比 Tab. 2 Comparison of predicted results of each model in point G1 |
|
|
表 3 G2点各模型拟合结果对比 Tab. 3 The contrast of each model calculation results of G2 |
|
|
表 4 G2点各模型预测结果对比 Tab. 4 Comparison of predicted results of each model in point G2 |
|
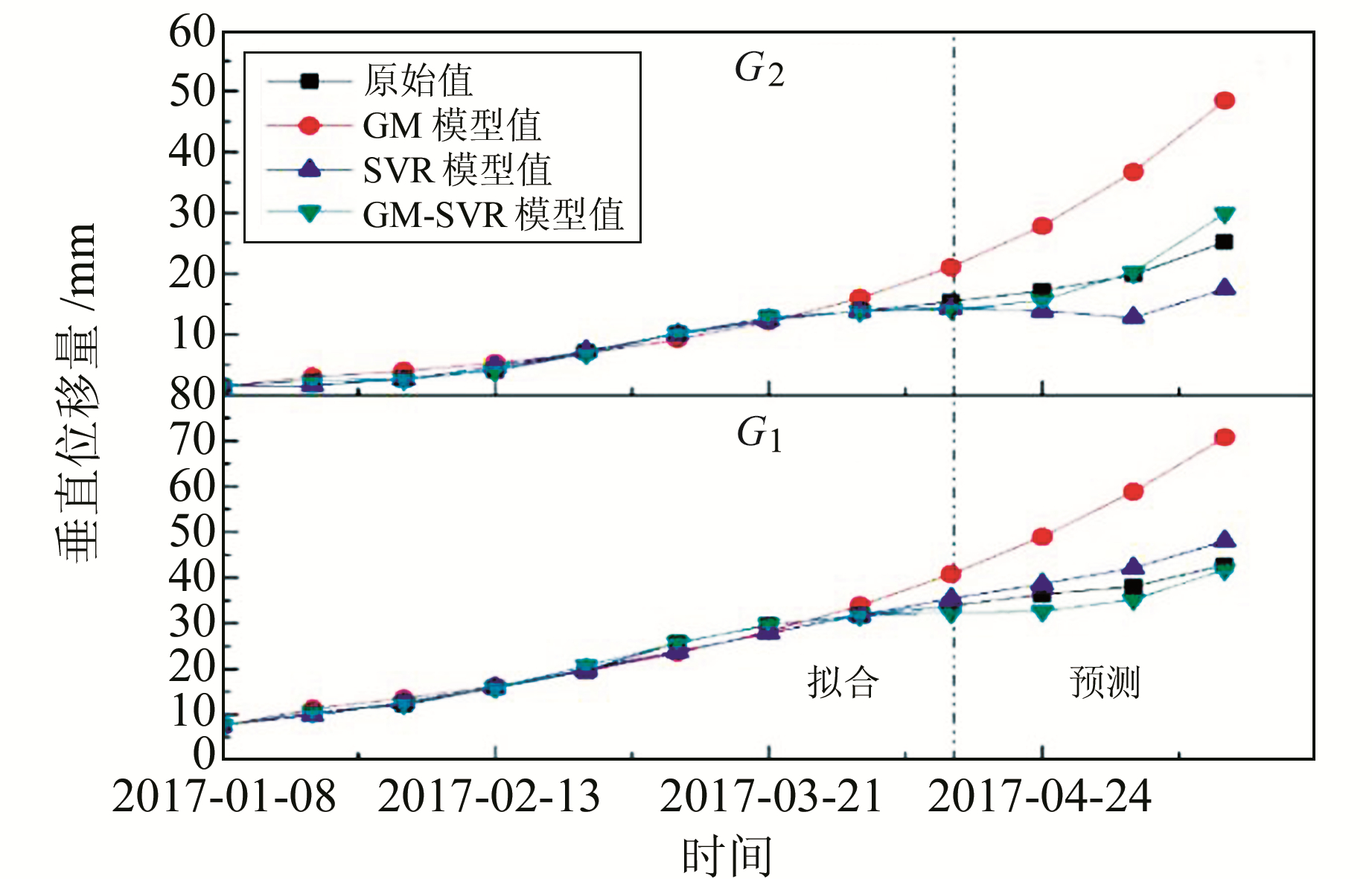
图 5 观测点原始值和3种模型拟合、预测结果对比 Fig. 5 Comparison of the original values of the observation points and the results of the three mode |
由图 5可知,2个观测点在观测期内形变序列相似,总体呈增长趋势,其中1~7期沉降量逐渐加大,7~11期沉降趋于平缓。通过图 5中比较可以看出,灰色模型、支持向量机模型和本文提出的灰色优化支持向量机组合模型在2个观测点的拟合效果都比较理想,但在预测效果的比较中,灰色模型的预测结果不理想,偏差较大,要明显低于支持向量机模型和本文组合模型效果。
从表 1可看出,在G1点观测期内灰色模型、支持向量机模型和本文组合模型的拟合效果较好,且结果较为稳定,其中组合模型的拟合效果最好,相对误差普遍控制在2%以下。表 2为3种模型在G1点基于训练样本的预测结果,可以看出,灰色模型的预测结果不理想,预测值与实测值偏差较大;支持向量机模型和本文组合模型预测效果相对较好,预测结果较稳定,总体精度较高。表 3为3种模型在G2点的拟合结果,可以看出,与在G1点的结果不同,灰色模型和支持向量机模型的拟合效果变差,精度和稳定性都有所下降,其中灰色模型和支持向量机模型拟合的最大相对误差达到52.8%和32.78%;而本文组合模型依然保持较高的精度和稳定性。表 4为3种模型在G2点的沉降预测结果,灰色模型预测结果与在G1点的结果相近,精度依然不高。不同于在G1点较好的预测结果,支持向量机模型在G2点的预测效果也不够理想,最大相对误差达到35.5%。本文组合模型与在G1点的预测结果相似,依然保持很高的精度和稳定性,相对误差普遍控制在10%以下。由此可知,对于研究区沉降形变序列,灰色模型预测结果十分不理想,已基本偏离实测值,而单一的支持向量机模型预测结果也不够稳定,只有本文组合模型表现出较高的精度和稳定性。
对于模型精度的检验,一般有残差大小、关联度和后验方差3种检验方法。为了更加全面直观地评定本文组合模型的性能,拟采用均方根误差(RMSE)和平均绝对误差(MAE)2项指标进行评定(表 5,单位mm)。
|
|
表 5 各模型精度对比 Tab. 5 Accuracy comparison of each model |
由表 5可知,灰色模型的精度较低,2点的均方根误差都接近10 mm;支持向量机模型相比于灰色模型显示出了较好的精度,但在稳定性方面有所欠缺;只有本文的组合模型保持了很好的全局预测能力,各项指标均优于其他2种模型。
3 结语本文利用时序InSAR技术对矿区开采导致的居民区沉降进行监测和分析,并结合矿区开采沉陷的实际形变特征,综合灰色模型强大的线性处理能力和支持向量机优良的学习能力、泛化能力及高维空间非线性处理能力等优势,建立了可靠的形变预测组合模型。
监测结果表明,研究区杨聚庄自2016-12监测开始,一直受地下采煤活动的影响。截至2017-05-20,最大累积垂直沉降量为48 mm,最大形变速率为-90 mm /a,整个地区由北向南沉降量逐渐加大,形成明显的沉降漏斗。针对矿区开采引起的复杂形变,通过与传统预测模型相比较,凸显了本文组合预测模型的优良性能,模型预测结果的均方根误差小于2 mm,平均绝对误差小于1 mm。这一结果表明,GM-SVR组合模型和SBAS-InSAR相结合,可以实现沉降地区的快速动态监测和灾害预警,对预防相应灾害的发生有一定的参考价值。
| [1] |
Yue H Y, Liu G, Guo H, et al. Coal Mining Induced Land Subsidence Monitoring Using Multiband Spaceborne Differential Interferometric Synthetic Aperture Radar Data[J]. Journal of Applied Remote Sensing, 2011, 5(14)
(  0) 0) |
| [2] |
Szczerbowski Z, Jura J. Mining Induced Seismic Events and Surface Deformations Monitored by GPS Permanent Stations[J]. Acta Geodynamicaet Geomaterialia, 2015, 12(3): 237-248
(  0) 0) |
| [3] |
杨亚夫, 朱建军, 王永哲, 等. 利用Sentinel-1A数据、D-InSAR和沿轨干涉技术获取2016年高雄MS6.7地震三维形变场[J]. 大地测量与地球动力学, 2017, 37(4): 339-343 (Yang Yafu, Zhu Jianjun, Wang Yongzhe, et al. 3D Displacement Field of 2016 Kaohsiung MS6.7 Earthquake from D-InSAR and Along-Track Interferometry with Ascending and Descending Sentinel-1A Images[J]. Journal of Geodesy and Geodynamics, 2017, 37(4): 339-343)
(  0) 0) |
| [4] |
Zebker H A, Goldstein R M. Topographic Mapping from Interferometric Synthetic Aperture Radar Observations[J]. Journal of Geophysical Research: Solid Earth, 1986, 91(B5): 4 993-4 999 DOI:10.1029/JB091iB05p04993
(  0) 0) |
| [5] |
Berardino P, Fornaro G, Lanari R, et al. A New Algorithm for Surface Deformation Monitoring Based on Small Baseline Differential SAR Interferograms[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 40(11): 2 375-2 383
(  0) 0) |
| [6] |
Huang J, Khan S D, Ghulam A, et al. Study of Subsidence and Earthquake Swarms in the Western Pakistan[J]. Remote Sensing, 2016, 8(11): 1-17
(  0) 0) |
| [7] |
Samsonov S, Beavan J, González P J, et al. Ground Deformation in the Taupo Volcanic Zone, New Zealand, Observed by ALOS PALSAR Interferometry[J]. Geophysical Journal International, 2011, 187(1): 147-160 DOI:10.1111/j.1365-246X.2011.05129.x
(  0) 0) |
| [8] |
Euillades L D, Euillades P A, Riveros N C, et al. Detection of Glaciers Displacement Time-Series Using SAR[J]. Remote Sensing of Environment, 2016, 184: 188-198 DOI:10.1016/j.rse.2016.07.003
(  0) 0) |
| [9] |
Zhou L, Guo J M, Hu J Y, et al. Wuhan Surface Subsidence Analysis in 2015-2016 Based on Sentinel-1A Data by SBAS-InSAR[J]. Remote Sensing, 2017, 9(10)
(  0) 0) |
| [10] |
余鹏飞, 贾治革, 熊维, 等. 西藏亚东-谷露裂谷带运动特征的InSAR研究[J]. 大地测量与地球动力学, 2017, 37(6): 594-598 (Yu Pengfei, Jia Zhige, Xiong Wei, et al. Study on the Deformation Characters of Yadong-Gulu Rift by InSAR[J]. Journal of Geodesy and Geodynamics, 2017, 37(6): 594-598)
(  0) 0) |
| [11] |
Lanari R, Mora O, Manunta M, et al. A Small-Baseline Approach for Investigating Deformations on Full-Resolution Differential SAR Interferograms[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(7): 1 377-1 386 DOI:10.1109/TGRS.2004.828196
(  0) 0) |
| [12] |
李克昭, 李志伟, 丁安民, 等. 灰线性加权非等距GM(1, 1)形变预测模型[J]. 大地测量与地球动力学, 2016, 36(6): 513-516 (Li Kezhao, Li Zhiwei, Ding Anmin, et al. Deformation Prediction Model of Gray Line Weighted Non-Equidistance GM(1, 1)[J]. Journal of Geodesy and Geodynamics, 2016, 36(6): 513-516)
(  0) 0) |
| [13] |
Tong H Z, Chen D R, Peng L Z. Analysis of Support Vector Machines Regression[J]. Foundations of Computational Mathematics, 2009, 9(2): 243-257 DOI:10.1007/s10208-008-9026-0
(  0) 0) |
| [14] |
Diao X P, Wu K, Zhou D W, et al. Integrating the Probability Integral Method for Subsidence Prediction and Differential Synthetic Aperture Radar Interferometry for Monitoring Mining Subsidence in Fengfeng, China[J]. Journal of Applied Remote Sensing, 2016, 10(1): 16-28
(  0) 0) |
2. The 38th Research Institute of China Electronics Technology Group Corporation, 199 Xiangzhang Road, Hefei 230031, China
 2019, Vol. 39
2019, Vol. 39


