2. 山东科技大学测绘科学与工程学院,青岛市前湾港路579号,266590;
3. 中国地质大学(武汉)信息工程学院,武汉市鲁磨路388号,43007;
4. 青岛市勘察测绘研究院,青岛市山东路189号,266032;
5. 云南大学国际河流与生态安全研究院,昆明市云学路,650500
CORS大地高时序中通常混有噪声误差,除了包含环境负荷及非负荷垂向形变外,还包含仪器误差造成的影响,抑制了形变信息的精度与可靠性,因此分离基准站的垂向形变信号与噪声,确定其可靠变化趋势尤为重要。消除时间序列中仪器噪声常用的方法有最小均方滤波和最小二乘滤波[1]。最小均方滤波要求输入的序列具有平稳性,而最小二乘滤波则适用于非平稳序列,并已知序列中噪声的先验统计信息。另外,噪声误差中的高频部分亦可采用低通滤波方式消除,但该方法难以适用于全频段误差的改正。构建时间序列自协方差矩阵,根据其特征值变化反映有用信号与噪声的分布,可采用奇异谱分析方法实现CORS时序的降噪处理。
奇异谱分析(SSA)源自Karhumen-Loeve分解理论,是一种用于分析一维时间序列的主成分分析方法[2]。SSA方法具有明显优势,即不受限于正弦波假定、无需先验信息、可稳定识别与强化周期信号等[3-4],能通过有限时间长度序列的动力重构,并结合经验正交函数从含有噪声的时序中尽可能多地提取有用信息。目前,国内外已开展大量研究工作,但多数侧重SSA方法的实现[5-7],对于方法本身的可靠性验证相对较少。
本文针对CORS大地高时序信噪混叠问题,结合仿真与实验,通过SSA方法分解与重构大地高变化时序主成分,实现形变信号的提取。在仿真中充分考虑了主成分分量个数截取原则,采用关中地区17座CORS大地高时序对SSA方法的结果进行统计分析,验证SSA方法的提取效果。
1 SSA方法原理SSA是一种主成分分析的时序处理方法,针对中心化后的一维时间序列,按给定的嵌入空间维数构造时滞矩阵,并截断一定个数的主分量,重构趋势与周期项信号[2]。
对于混有噪声且已中心化的日值时间序列{x1, x2, …, xN},给定嵌入维度M,构建M×(N-M+1)维时间滞后矩阵,即为空间坐标矩阵X:
| $ \begin{array}{l} \mathit{\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} {{x_1}}&{{x_2}}& \cdots &{{x_{i + 1}}}& \cdots &{{x_{N - M + 1}}}\\ {{x_2}}&{{x_3}}& \cdots &{{x_{i + 2}}}& \cdots &{{x_{N - M + 2}}}\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {{x_M}}&{{x_{1 + M}}}& \cdots &{{x_{i + M}}}& \cdots &{{x_N}} \end{array}} \right] = \\ \;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {{X_1}}&{{X_2}}& \cdots &{{X_{i + 1}}}& \cdots &{{X_{N - M + 1}}} \end{array}} \right] \end{array} $ | (1) |
1) 计算空间坐标矩阵X的M×N维自协方差矩阵Tx及其特征值λk与特征向量Ek:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{T}}_x} = }\\ {\left[ {\begin{array}{*{20}{c}} {c\left( 0 \right)}&{c\left( 1 \right)}& \cdots & \cdots & \cdots & \cdots &{c\left( {M - 1} \right)}\\ {c\left( 1 \right)}&{c\left( 0 \right)}&{c\left( 1 \right)}& \cdots & \cdots & \cdots & \cdots \\ \cdots &{c\left( 1 \right)}& \cdots & \cdots & \cdots & \cdots & \cdots \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots &{c\left( 1 \right)}\\ {c\left( {M - 1} \right)}& \cdots & \cdots & \cdots & \cdots &{c\left( 1 \right)}&{c\left( 0 \right)} \end{array}} \right]} \end{array} $ | (2) |
其中,矩阵Tx为Toeplitz矩阵。c(j)为延时为j时xi的协方差,c(j)与xi的关系式为:
| $ c\left( j \right) = \frac{1}{{N - j}}\sum\limits_{t = 1}^{N - j} {{x_t}{x_{t + j}}} , 0 \le j \le M - 1 $ | (3) |
对矩阵Tx分解特征值,得到M个特征值λk(k=1, 2, …, M),将其由大至小排序:λ1 > λ2 > … > λM≥0,同时求解对应的特征向量Ek。
2) 计算向量Xi在Ek上的投影。时序的k个主成分(PC)aik可表示为第i个状态向量Xi在Ek上的投影,即
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\mathit{\boldsymbol{a}}_i^k = {\mathit{\boldsymbol{X}}_i}{\mathit{\boldsymbol{E}}^k} = \\ \sum\limits_{j = 1}^M {{x_{i + j}}\mathit{\boldsymbol{E}}_j^k} {\rm{ }}, {\rm{ }}0 \le i \le M - 1 \end{array} $ | (4) |
3) 重建成分序列。根据投影aik与特征向量Ek可得到各个主成分重构序列(RC):
| $ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathit{\boldsymbol{x}}_i^k=\\ \left\{ \begin{array}{l} \frac{1}{i}\sum\limits_{j = 1}^M {\mathit{\boldsymbol{a}}_{i - j}^k\mathit{\boldsymbol{E}}_j^k, 1 \le i \le M - 1} \\ \frac{1}{M}\sum\limits_{j = 1}^M {\mathit{\boldsymbol{a}}_{i - j}^k\mathit{\boldsymbol{E}}_j^k, \mathit{M} \le i \le N - M + 1} \\ \frac{1}{{N - i + 1}}\sum\limits_{j = i - N + M}^M {\mathit{\boldsymbol{a}}_{i - j}^k\mathit{\boldsymbol{E}}_j^k, N - M + 2 \le i \le N} \end{array} \right. $ | (5) |
4) 重构时间序列。PC能够反映时间序列的变化特征,可根据能量相对关系分离时序形变信号与噪声,截断合适个数的主成分分量有利于形变的提取。为提高信噪比,本文截取顺序排列中贡献大的PC进行时序重构,降低噪声影响:
| $ \mathit{\boldsymbol{\hat x}}{_i} = \sum\limits_{k = 1}^p {\mathit{\boldsymbol{x}}_i^k} , i = 1, 2, \cdots , N $ | (6) |
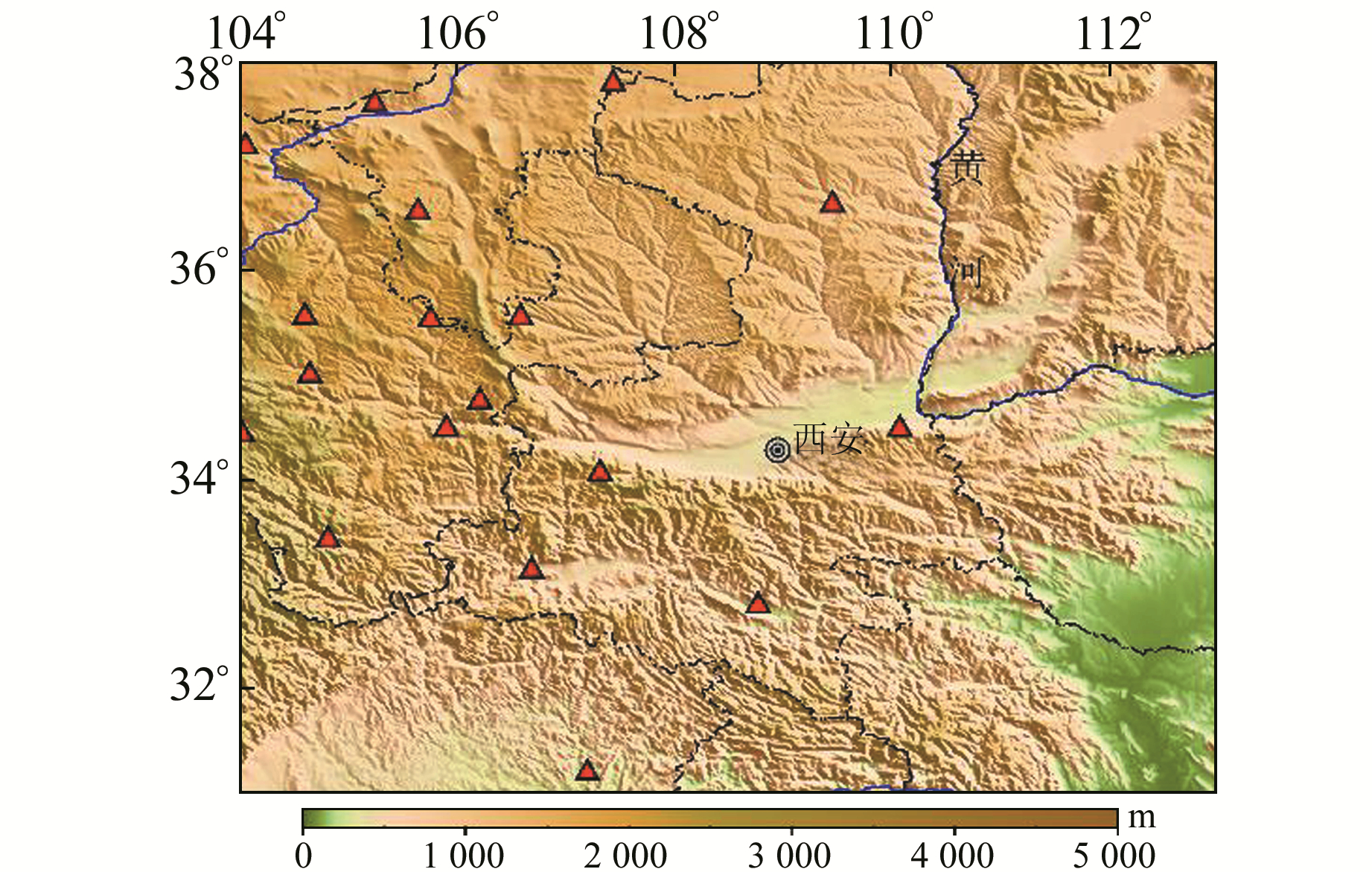
选取陕西、甘肃等地17座CORS最近6 a的连续GNSS观测数据,采用美国航空航天局喷气推进实验室(JPL)的GIPSY/OASIS软件和精密单点定位(PPP)模式进行处理,求取单日松弛约束解。再利用JPL的联合平差软件QOCA对其按严密平差方法进行解算,获得ITRF2008框架下各监测站大地高变化时间序列。CORS解算时的地球动力学改正采用国际地球自转和参考系服务(IERS)2010协议,其中的固体潮、海潮、1 d和0.5 d大气潮负荷影响已被移除[8]。CORS位置分布见图 1。
|
图 1 CORS位置分布 Fig. 1 The map of CORS position |
CORS实测数据中混入粗差会影响空间坐标矩阵的自协方差矩阵构建,并且根据误差传播定律可知,还会导致自协方差矩阵特征值与特征向量求解产生偏差,影响主成分分量重构与噪声分离的精度。因此,准确定位并剔除时间序列中的粗差是序列分析的基础。对于时间序列粗差剔除的方法有多种,包括拉依达准则和IQR(四分位距)准则,由于时序本身粗差对中位数和IQR影响较小,相比拉依达准则,IQR准则更具稳健性。除了粗差影响之外,数据还存在由测量仪器等导致的缺数情况,也存在由于受地震、接收机或天线变动等影响导致的数据阶跃。当数据存在明显的阶跃时,应首先对其进行阶跃项改正,然后进行缺失数据补偿。
1) 阶跃项改正。采用最小二乘线性拟合方法消除阶跃项,利用阶跃发生前后时间段内时间序列拟合直线在阶跃点处的截距差值,分析和修复线性趋势改变对时间序列的影响。图 2为GSTS站点U分量阶跃项经最小二乘拟合修复后的结果。

|
图 2 粗差剔除及阶跃项改正后的GSTS站大地高变化时序 Fig. 2 Geodetic height change time series from GSTS station after gross error elimination and step correction |
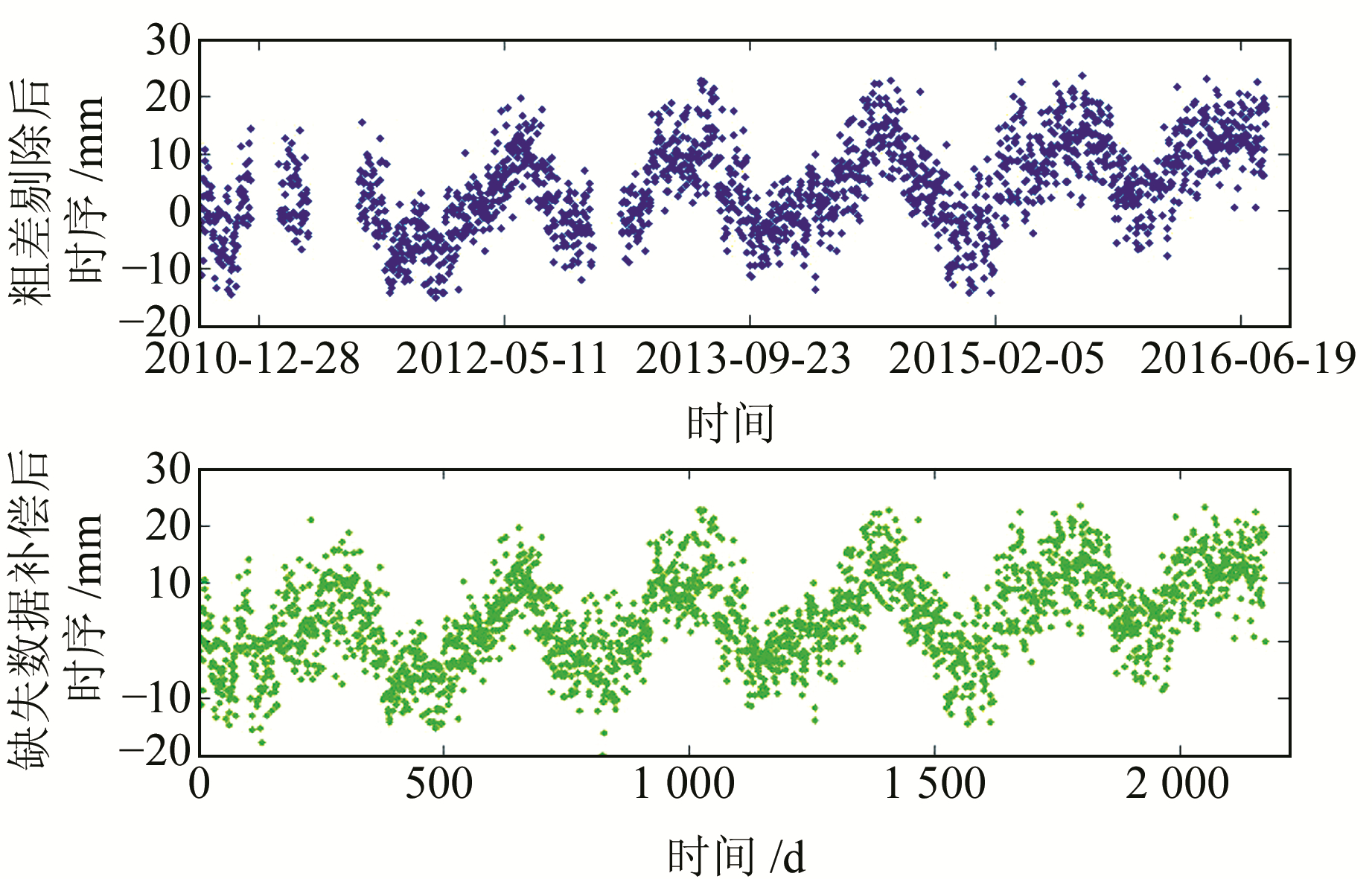
2) 缺失数据补偿。对序列基于最小二乘原理拟合其常数项、线性项、1 a项及0.5 a项,对缺失时段补偿拟合时序,并添加相应的噪声,添加的噪声序列默认为理想白噪声。图 3为SNYA站点U分量观测数据经缺失补偿后的结果。
|
图 3 粗差剔除及缺失数据补偿后的SNYA站大地高变化时序 Fig. 3 Geodetic height change time series from SNYA station after gross error elimination and missing data compensation |
对CORS日值观测数据进行预处理后,采用SSA方法进行时序分解与重构。在应用SSA方法之前,需确定嵌入维数与截断主分量个数,嵌入维数的选取会影响时序中各主成分的分离度。CORS监测时序中通常包含仪器噪声,若嵌入维数选取较小,形变信号与噪声误差混叠严重,难以分离,将导致监测结果的可靠性变差。Hassani等[9]证明了嵌入维数M最大只能取
根据CORS的时序特征,假设大地高时序受大气负荷等环境因素的影响主要表现为季节性变化,可用如下公式定量描述:
| $ H\left( t \right) = {H_0}\left( t \right) + n\left( t \right) $ | (7) |
| $ {H_0}\left( t \right) = 10{\rm{sin}}(\frac{{2\pi }}{{365}}t) $ | (8) |
式中,H0(t)为理想大地高变化,n(t)为仪器噪声,t为时间。仪器噪声采用均值为0 mm、方差为4 mm2的高斯白噪声模拟,序列长度为N=2 000。模拟的测站大地高变化序列见图 4。

|
图 4 模拟的CORS大地高变化实际时序与高斯白噪声 Fig. 4 Simulated actual time series of geodetic height change from CORS and Gaussian white noise |
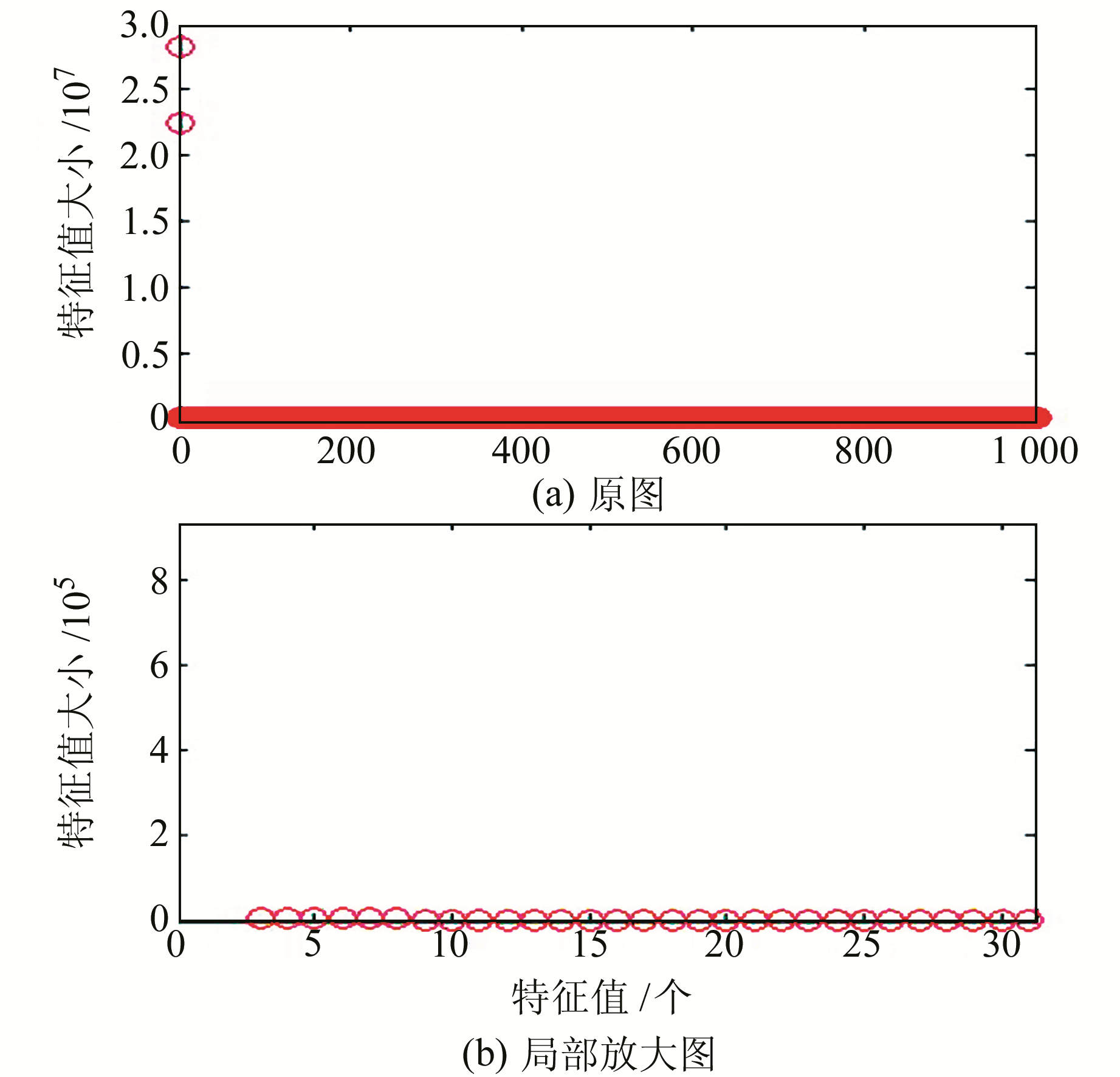
选择嵌入维数M=1 000,对大地高时序进行SSA时序分解与重构。根据SSA方法,求取模拟时序自协方差矩阵的特征值(图 5(a)),每个特征值大小见图 5(b),可以发现,3阶以后的特征值变化率趋于零。根据模拟实际时序标准差7.13 mm,本文计算了前8阶各RC标准差所占百分比(图 6)。
|
图 5 模拟的CORS大地高变化时序特征值变化曲线 Fig. 5 Simulated eigenvalue change curve based on geodetic height change time series from CORS |
|
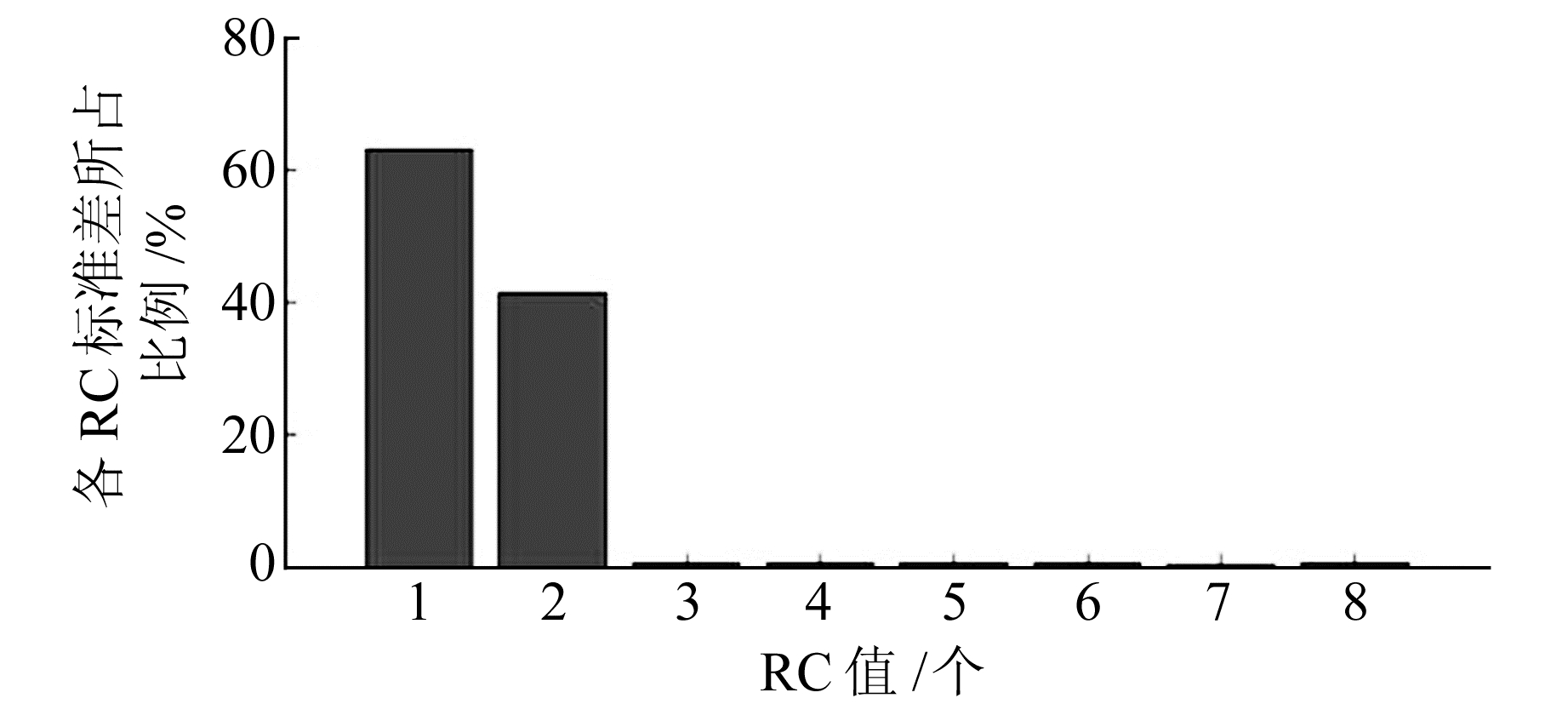
图 6 前8阶各RC标准差占原始时序标准差的百分比 Fig. 6 The first 8 stages of each RC standard deviation as a percentage of the original time standard deviation |
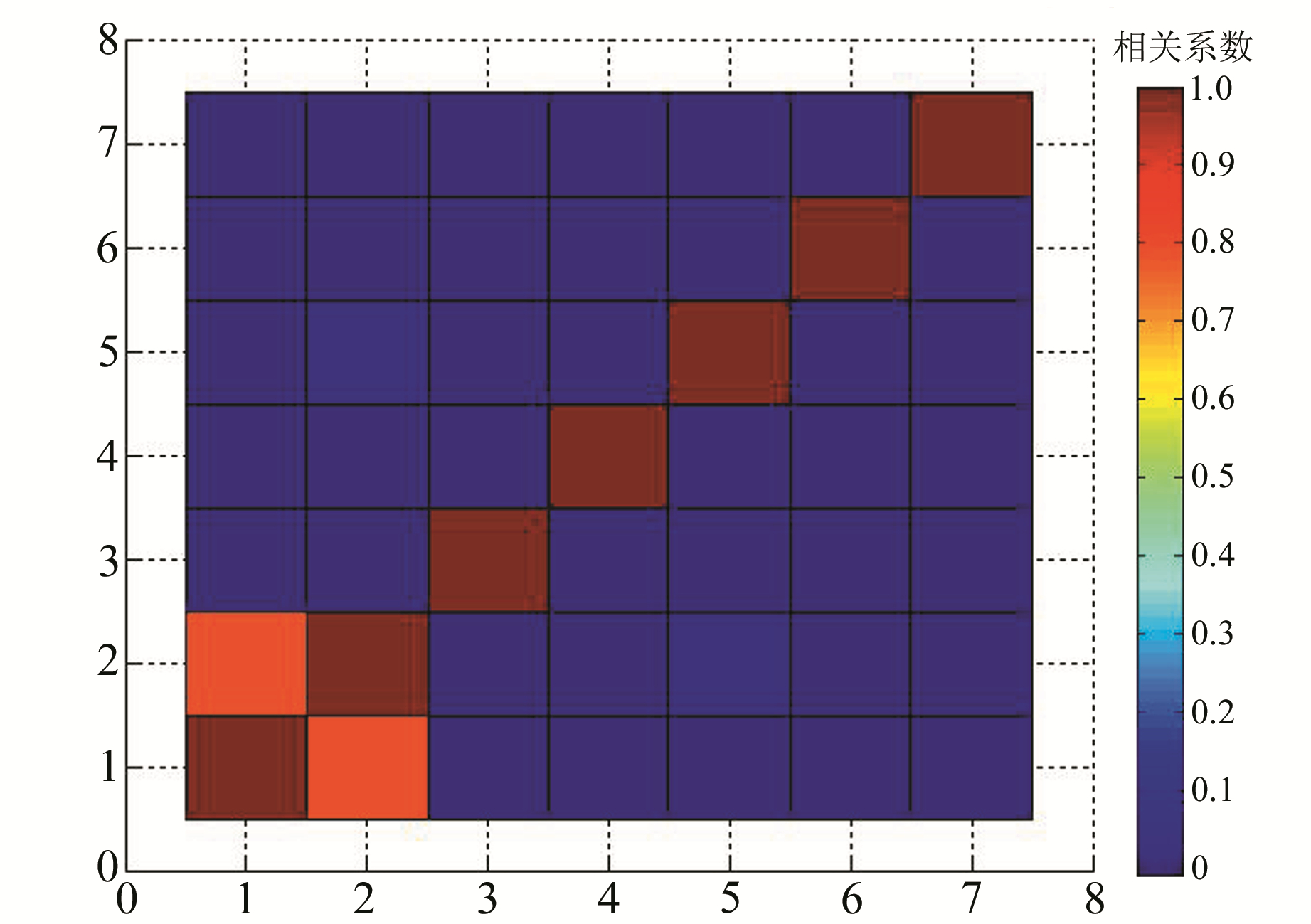
从图 6可以看出,RC1和RC2的主成分标准差占原始时序标准差比例较高,分别为63.1%和41.4%,RC3之后的RC贡献率较低。为了增加选取截断个数的可靠性,进一步采用重构时间序列W-correlation方法[10]对RC进行周期对分析(图 7)。
|
图 7 前8阶重构部分的W-correlation Fig. 7 W-correlation of the first 8th-order reconstruction |
若2个RC相关系数大于0.75,则认为二者具有相同的周期性。从图 5可以发现,RC1与RC2属于同一周期成分,当i > 2时,各重构时序之间相互独立,周期特征较弱。综合图 5~7,选择截断长度L=2,利用嵌入维数与截断长度进行时序分解与重构,得到降噪后的大地高变化(图 8)。

|
图 8 CORS大地高变化模拟时序与重构时序及残差序列 Fig. 8 Simulated and reconstructed and residual time series from CORS geodetic height change |
由图 8可知,重构时序与原始时序曲线基本重合,重构残差时序基本在零值上下波动。本文对理想时序(不含噪声)、模拟噪声、重构时序和残差时序分别进行统计(表 1),可以发现,重构后的大地高变化时序均值和标准差与理想时序很接近。为了查看剩余噪声分布情况,针对观测时序的离散性,采用离散傅里叶变换实现噪声时序在时间域和频率域的转换(图 9)。

|
图 9 噪声序列的频谱分布与幅度分布直方图 Fig. 9 Spectrum distribution and amplitude distribution histogram of the noise sequence |
|
|
表 1 CORS大地高变化模拟时序及重构时序的均值与标准差 Tab. 1 Mean and standard deviation of simulation and reconstruction timing of geodetic height change of CORS |
从图 9可以看出,重构残差时序能量幅值在各频段上分布均匀,符合白噪声的频谱分布特性,残差序列幅值服从高斯正态分布。分离的噪声序列标准差为1 mm,均值为0.03 mm,与添加的噪声统计特性符合程度较高。仿真结果表明,SSA方法可有效分离形变信号与噪声误差,实现降噪。
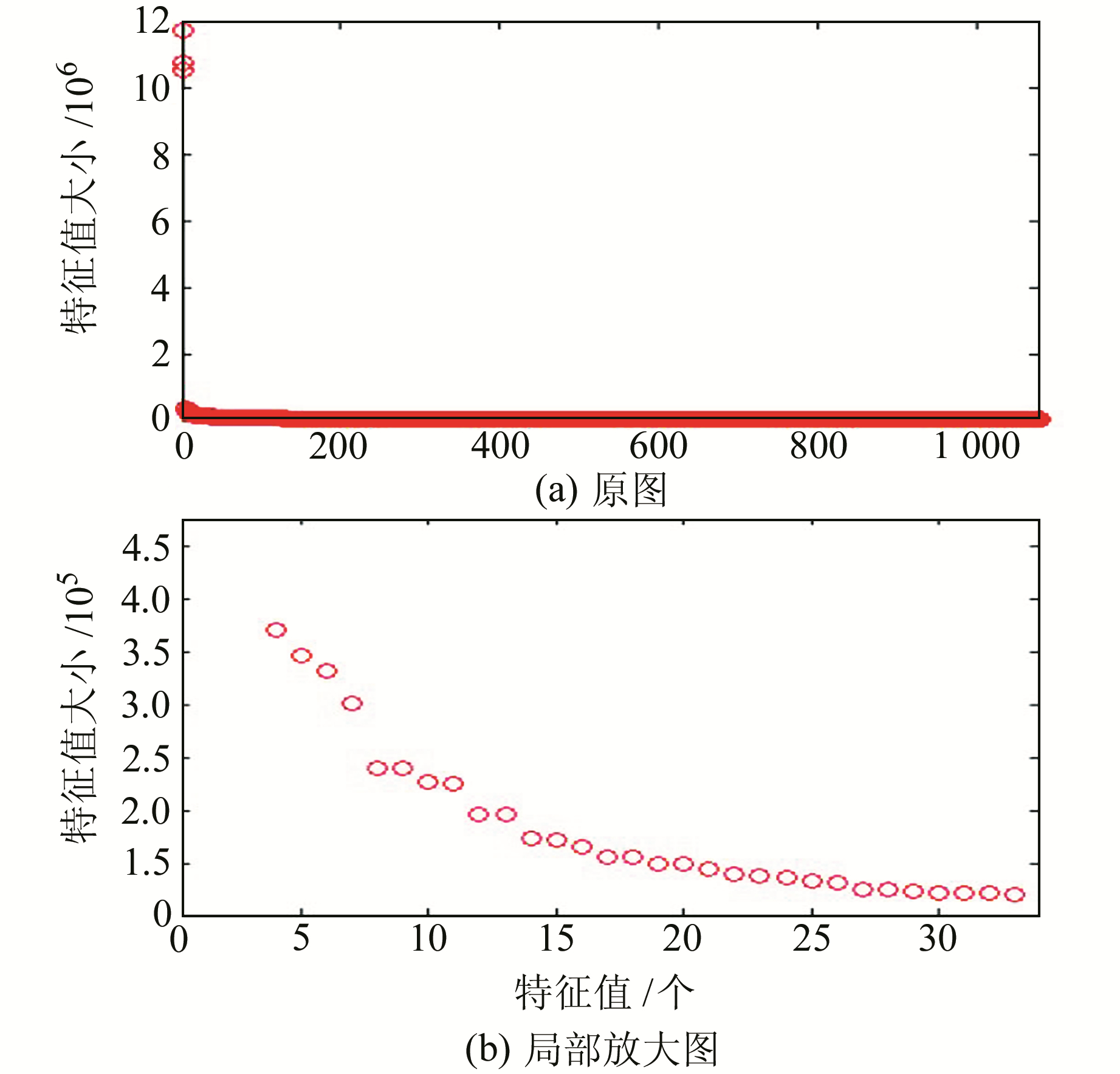
2.2 CORS大地高时序形变信息提取基于SSA方法的仿真效果,将该方法应用在17座基准站大地高时序分析中,用于提取形变信号。本文以GSLX站点为例,给出相关结果。根据GSLX站点大地高时序长度2 152,选择嵌入维数为1 076,并构建时序的自协方差矩阵,求解其对应的特征值(图 10)。
|
图 10 CORS大地高变化实际时序的特征值变化曲线 Fig. 10 Curve of eigenvalues of the actual time series of geodetic height change from CORS |
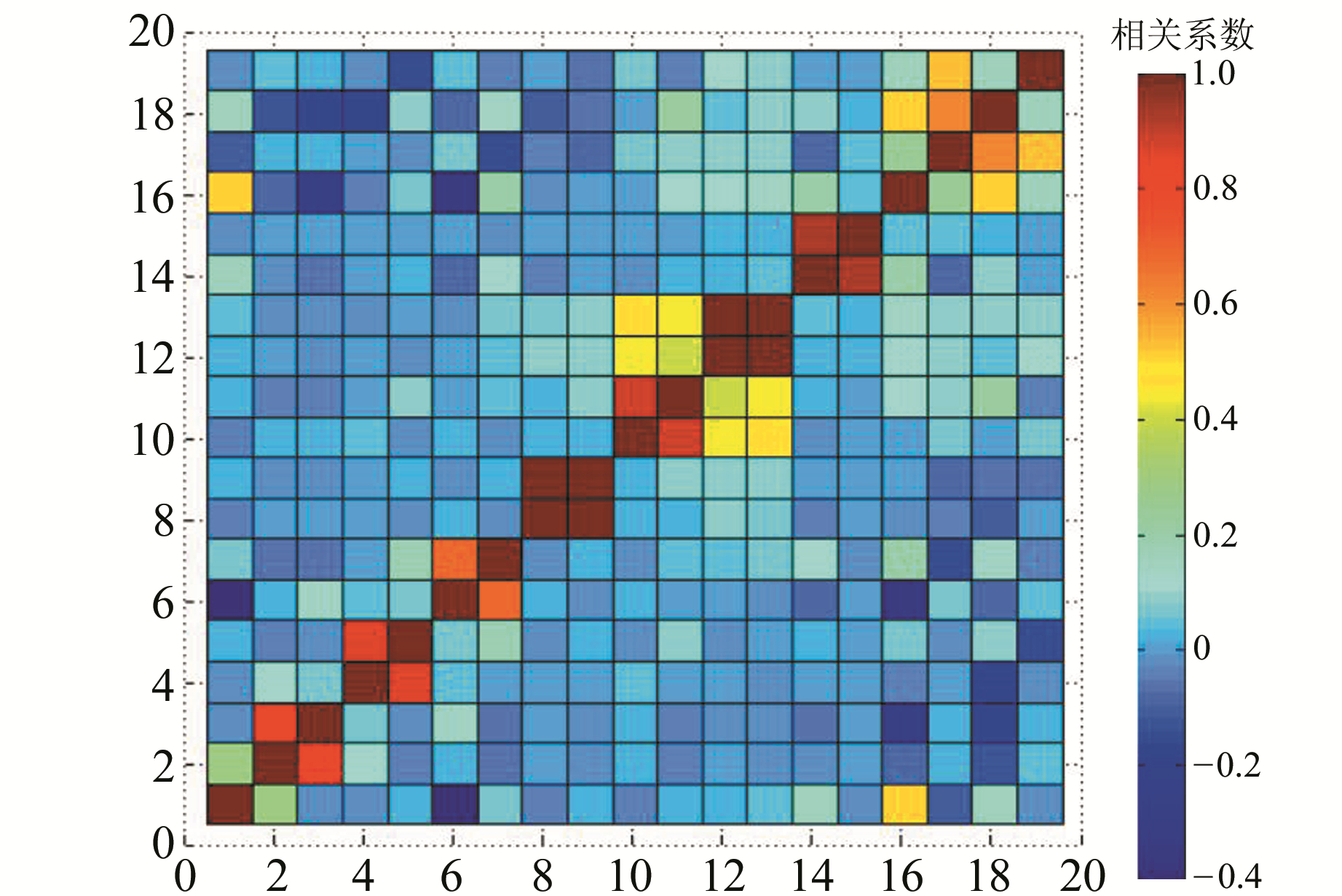
从图 10可以看出,第15个以后的特征值变化率逐渐趋于零。此外,仍采用W-correlation方法对测站重构的RC进行周期对分析(图 11),若2个RC相关系数大于0.75,则同样认为二者具有相同的周期性。时序重构成分RC1为趋势项,RC2-RC3、RC4-RC5、RC6-RC7、RC8-RC9、RC10-RC11、RC12-RC13、RC14-RC15分别属于同一周期成分。当i > 15时,各时序成分周期性较弱,可认为噪声占主要部分。将前15阶主要信息成分合并,并进行FFT频谱分析(图 12)。
|
图 11 前20阶重构部分的W-correlation Fig. 11 W-correlation of the first 20th-order reconstruction |
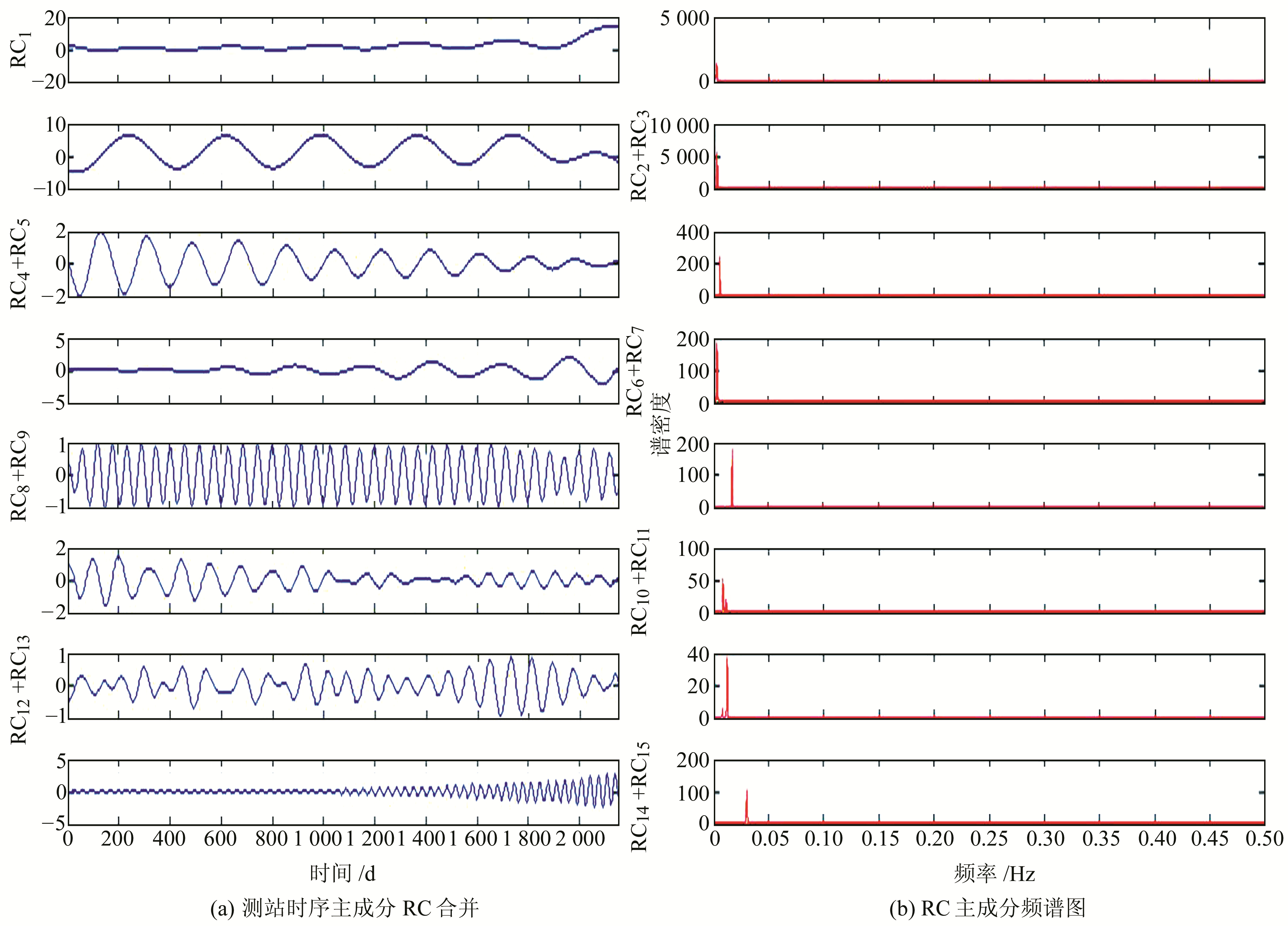
|
图 12 CORS大地高时序各RC成分及对应的频谱分布 Fig. 12 RC components from geodetic height time series of CORS and corresponding spectral distribution |
由图 12可以发现,测站大地高时序中合并的周期成分表现为不同的周期特征。第1主成分为趋势项,第2主成分表现为370 d年周期变化,第3主成分表现为185 d半年周期变化,第4、5主成分为270 d、57 d的周期变化,第6、7主成分为118 d、80 d的周期变化,第8主成分为33 d的月变化。从图 10(b)还可以发现,大地高时序以1 a和0.5 a变化为主导,季节性特征明显。由SSA得到的GSLX站点周期统计见表 2。
|
|
表 2 SSA方法得到的GSLX站周期统计 Tab. 2 Cycle statistics from GSLX station obtained by SSA method |
将RC1~RC15主成分进行合并与重构大地高形变时序,即选择截断长度为15,前15阶主成分合并后呈现的时序特征如图 13所示。
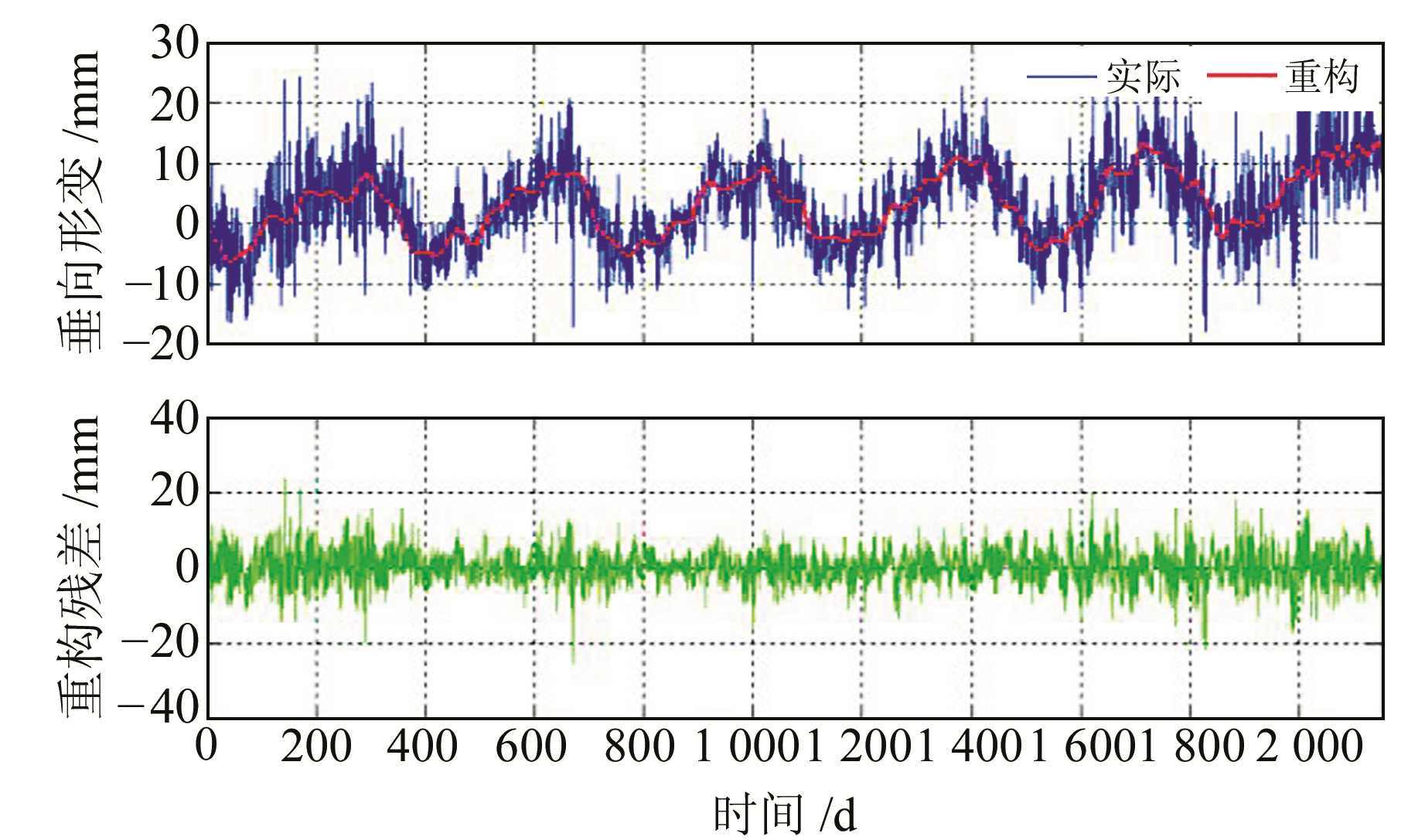
|
图 13 GSLX站大地高变化实际时序与重构时序及残差序列 Fig. 13 Actual and reconstructed and residual time series from GSLX station geodetic height change |
由图 13可以发现,分离噪声以后的重构曲线相对平滑,重构后的大地高时序季节性变化特征更为明显。为有效说明SSA方法对CORS垂向形变时序的降噪效果,本文计算了17座CORS的重构时序及剩余噪声的相关信息(表 3)。
|
|
表 3 CORS大地高时序形变信息提取结果相关统计 Tab. 3 Statistics on extraction results of deformation information on geodetic height timing from CORS |
由表 3可知,采用SSA方法后,多数测站大地高时序重构标准差明显减小,误差减小约在15.0%~32.7%。残差序列标准差大部分在3.76~5.39 mm范围内浮动,数学期望接近零。重构时序的残差部分主要表现为随机噪声特性,这可能与测站仪器误差混叠有关。对于原始大地高时序标准差偏大的个别测站,经SSA方法重构后垂向形变信号标准差也明显减小,减小幅度为16.7%。综上所述,CORS大地高时序形变信息可利用SSA方法有效提取,重构后时序的信噪比明显增强,可用于地壳垂向形变信息的表达。
3 结语本文依托CORS垂向形变时序特征,针对SSA方法原理进行了仿真实验,并将SSA方法应用到实际测站大地高变化时序分析中,取得了可靠的效果。仿真结果表明,SSA方法可以较好地识别和提取时序形变信息,重构后时序的噪声影响大幅减小,说明该方法可起到降噪平滑的作用。对于实际测站大地高变化,重构时序在精度上有一定改善,信噪比得到提升,季节性变化特征更为显著。本文对GNSS测站缺失数据进行补偿时,理想地认为CORS坐标序列中的噪声为单一白噪声,在后续研究中将增加对有色噪声、闪烁噪声、随机游走噪声等的考虑。基于SSA方法对测站垂直分量有用信号的提取效果,可尝试将SSA方法应用到后续测站水平分量信息提取中,以分析CORS水平运动线性与周期性特征,获取更多的水平形变信息。
| [1] |
张勇, 吕达仁. 一种基于海面背景的WindSat极化通道替代定标方法研究[J]. 遥感技术与应用, 2014, 29(5): 727-734 (Zhang Yong, Lü Daren. Vicarious Calibration of WindSat Polarimetric Channels Based Sea Surface Background[J]. Remote Sensing Technology and Application, 2014, 29(5): 727-734)
(  0) 0) |
| [2] |
Vautard R, Yiou P, Ghil M. Singular-Spectrum Analysis: A Toolkit for Short, Noisy Chaotic Signals[J]. Physica D:Nonlinear Phenomena, 1992, 58(1-4): 95-126 DOI:10.1016/0167-2789(92)90103-T
(  0) 0) |
| [3] |
Shen Y, Guo J Y, Liu X, et al. Long-Term Prediction of Polar Motion Using a Combined SSA and ARMA Model[J]. Journal of Geodesy, 2018, 92(3): 333-343 DOI:10.1007/s00190-017-1065-3
(  0) 0) |
| [4] |
王解先, 连丽珍, 沈云中. 奇异谱分析在GPS站坐标监测序列分析中的应用[J]. 同济大学学报:自然科学版, 2013, 41(2): 282-288 (Wang Jiexian, Lian Lizhen, Shen Yunzhong. Application of Singular Spectral Analysis to GPS Station Coordinate Monitoring Series[J]. Journal of Tongji University:Natural Science, 2013, 41(2): 282-288)
(  0) 0) |
| [5] |
Nikolaidis R. Observation of Geodetic and Seismic Deformation with the Gobal Positioning System[D]. San Diego: University of California, 2002 http://www.mendeley.com/catalog/observation-geodetic-seismic-deformation-global-positioning-system/
(  0) 0) |
| [6] |
李敬唐. 奇异谱分析滤波法及其在GPS多路径去噪中的应用[J]. 测绘地理信息, 2017, 42(3): 10-13 (Li Jingtang. Singular Spectrum Analysis and Its Application in GPS Multipath Filtering[J]. Journal of Geomatics, 2017, 42(3): 10-13)
(  0) 0) |
| [7] |
毛鹏宇, 陈义, 孟鑫. 基于奇异谱分析的地基GPS反演可降水量可行性分析[J]. 大地测量与地球动力学, 2017, 37(9): 933-936 (Mao Pengyu, Chen Yi, Meng Xin. Feasibility Analysis of Precipitable Water Vapor Retrieval with Ground-Based GPS Based on Singular Spectrum Analysis[J]. Journal of Geodesy and Geodynamics, 2017, 37(9): 933-936)
(  0) 0) |
| [8] |
Petit G, Luzum B. IERS Conventions 2010[Z].2010
(  0) 0) |
| [9] |
Hassani H, Mahmoudvand R, Zokaei M. Separability and Window Length in Singular Spectrum Analysis[J]. Comptes Rendus Mathematique, 2011, 349(17-18): 987-990 DOI:10.1016/j.crma.2011.07.012
(  0) 0) |
| [10] |
Hsieh W W. Nonlinear Multivariate and Time Series Analysis by Neural Network Methods[J]. Reviews of Geophysics, 2004, 42(1): 1 003-1 027
(  0) 0) |
2. College of Geomatics, Shandong University of Science and Technology, 579 Qianwangang Road, Qingdao 266590, China;
3. Faculty of Information Engineering, China University of Geosciences, 388 Lumo Road, Wuhan 430074, China;
4. Qingdao Geotechnical Investigation and Surveying Research Institute, 189 Shandong Road, Qingdao 266032, China;
5. Institute of International Rivers and Eco-Security, Yunnan University, Yunxue Road, Kunming 650500, China
 2019, Vol. 39
2019, Vol. 39


