2. 中国科学院国家授时中心,西安市书院东路3号,710600
目前,对于Galileo精密单点定位(precise point positioning,PPP)的研究已有一些初步成果,静态和动态PPP的精度分别可以达到cm和dm级[1-2]。相对于GPS动态PPP,GPS/Galileo组合动态PPP可以提高大约30%的定位精度,并有效减少收敛时间[3]。为满足实时定位的需求,国际GNSS服务机构2007年开始实施实时计划项目GNSS-RTPP,并于2013年提供实时精密产品[4-5]。最初的实时产品只能提供GPS和GLONASS双系统改正数[6],随着多系统的发展,多系统实时产品的需求也随之增加。由法国国家空间研究中心(CNES)提供的实时精密产品CLK93已经包含4大导航系统[7]。张锡越等[8]对系统的实时产品进行了评估,发现GPS轨道和钟差精度分别优于8 cm和0.3 ns,Galileo轨道和钟差的精度分别达到4.42 cm和0.18 ns。尽管已有诸多学者对实时PPP作过研究,但最新的Galileo实时产品对GPS/Galileo组合PPP的贡献并未有详细的分析。本文在多系统实时产品的基础上,重点分析GPS/Galileo组合单双频和实时静动态PPP的定位精度,剖析Galileo对组合PPP的贡献。
1 精密单点定位模型在利用GNSS进行PPP时常采用的基本观测方程可表示为:
| $ \begin{array}{c} P_{{\rm{r}}, j}^{\rm{s}} = \rho _{\rm{r}}^{\rm{s}} + c\cdot {\rm{d}}{t_{\rm{r}}} - c\cdot {\rm{d}}{t^{\rm{s}}} + {\rm{M}}{{\rm{F}}_{\rm{d}}}\left( e \right)\cdot {Z_{\rm{d}}} + \\ {\rm{M}}{{\rm{F}}_{\rm{w}}}\left( e \right)\cdot {Z_{\rm{w}}} + \gamma _j^{\rm{s}}\cdot I_{r, 1}^{\rm{s}} + ({\rm{d}}_{{\rm{r}}, j}^{\rm{s}} - {\rm{d}}_j^{\rm{s}}) + \varepsilon _{{\rm{r}}, j}^{\rm{s}}\left( P \right) \end{array} $ | (1) |
| $ \begin{array}{l} \varPhi _{{\rm{r}}, j}^{\rm{s}} = \rho _r^{\rm{s}} + c\cdot {\rm{d}}{t_{\rm{r}}} - c\cdot {\rm{d}}{t^{\rm{s}}} + {\rm{M}}{{\rm{F}}_{\rm{d}}}\left( e \right)\cdot \\ {Z_{\rm{d}}} + {\rm{M}}{{\rm{F}}_{\rm{w}}}\left( e \right)\cdot {Z_{\rm{w}}} - \gamma _j^{\rm{s}}\cdot I_{r, 1}^{\rm{s}} + \lambda _j^{\rm{s}}\cdot \\ (N_{{\rm{r}}, j}^{\rm{s}} + b_{{\rm{r}}, j}^{\rm{s}} - b_j^{\rm{s}}) + \varepsilon _{{\rm{r}}, j}^{\rm{s}}\left( \varPhi \right) \end{array} $ | (2) |
式中,r和s分别为接收机和卫星,Pr, js和Φr, js分别为伪距和载波观测值,λjs为频率j上的波长,ρrs为卫星和接收机之间的几何距离,c为光速,dtr和dts分别为接收机和卫星钟差,e为卫星的高度角,MFd(e)和MFw(e)分别为对流层干、湿迟延映射函数[9],Zd、Zw分别为天顶对流层干、湿延迟,Ir, 1s为频率f1s对应的电离层,γjs为频率的相关系数,且γjs=(f1s/fjs)2,dr, js和djs分别为接收机和卫星端与频率相关的码偏差,Nr, js为模糊度,br, js和bjs分别为与频率相关的接收机和卫星端的相位偏差,εr, js(P)和εr, js(Φ)分别为伪距和载波的测量噪声及多路径误差等未被模型化的误差。
对于双频PPP,采用消电离层组合来消除一阶电离层的影响,具体表达式为[10-11]:
| $ \begin{array}{c} {P_{{\rm{IF}}}} = {\rm{ }}\frac{{f_1^2\cdot {P_1} - f_2^2\cdot {P_2}}}{{f_1^2 - f_2^2}} = \rho _{\rm{r}}^{\rm{s}} + c\cdot {\rm{d}}{t_{\rm{r}}} - \\ c\cdot {\rm{d}}{t^{\rm{s}}} + {\rm{M}}{{\rm{F}}_{\rm{d}}}\left( e \right)\cdot {Z_{\rm{d}}} + {\rm{M}}{{\rm{F}}_{\rm{w}}}\left( e \right)\cdot {Z_{\rm{w}}} + \\ (d_{{\rm{r, IF}}}^{\rm{s}} - d_{{\rm{IF}}}^{\rm{s}}) + \varepsilon _{\rm{r}}^{\rm{s}}({P_{{\rm{IF}}}}) \end{array} $ | (3) |
| $ \begin{array}{l} {\varPhi _{{\rm{IF}}}} = {\rm{ }}\frac{{f_1^2\cdot {\varPhi _1} - f_2^2\cdot {\varPhi _2}}}{{f_1^2 - f_2^2}} = \rho _{\rm{r}}^{\rm{s}} + c\cdot {\rm{d}}{t_{\rm{r}}} - \\ c\cdot {\rm{d}}{t^{\rm{s}}} + {\rm{M}}{{\rm{F}}_{\rm{d}}}\left( e \right)\cdot {Z_{\rm{d}}} + {\rm{M}}{{\rm{F}}_{\rm{w}}}\left( e \right)\cdot {Z_{\rm{w}}} + \lambda _{{\rm{IF}}}^{\rm{s}}\cdot \\ (N_{{\rm{IF}}}^{\rm{s}} + b_{{\rm{r, IF}}}^{\rm{s}} - b_{{\rm{IF}}}^{\rm{s}}) + \varepsilon _{\rm{r}}^{\rm{s}}({\varPhi _{{\rm{IF}}}}) \end{array} $ | (4) |
式中,PIF和ΦIF分别为消电离层组合后的伪距和载波观测值,dr, IFs和dIFs分别为消电离层组合后的接收机和卫星端与频率相关的码偏差,NIFs为载波相位消电离层组合观测值的模糊度,br, IFs和bIFs分别为消电离层组合后的接收机和卫星端的相位偏差,εrs(PIF)和εrs(ΦIF)分别为伪距和载波消电离层组合的测量噪声及多路径误差等未被模型化的误差,其余参数同式(1)和式(2)。
在GPS/Galileo组合PPP模型中,本文以GPS时间系统为参考,增加系统间偏差(ISB)参数[2, 12]。需要注意的是,单频PPP需要对码偏差(DCB)进行修正[13-14]。另外,在构建单频PPP模型时容易出现秩亏的现象,但CNES提供的实时产品中不仅包含轨道和钟差改正信息,还包含相应的码偏差、相位偏差和电离层信息,因此,可利用CNES产品中的电离层作为约束条件,避免秩亏现象对定位结果的影响。考虑到实时电离层改正信息的精度较低,将其权重设为和伪距观测相同的值。表 1为实时PPP解算中采用的观测模型及参数估计策略。
|
|
表 1 PPP数据处理策略 Tab. 1 PPP data processing strategy |
为了详细分析GPS/Galileo组合实时PPP的精度,分别对GPS和GPS/Galileo组合单双频静动态PPP进行实验分析,选取10个MGEX站点(WUH2、JFNG、MIZU、GMSD、DJIG、KAT1、NNOR、CUT0、PARK、HARB)2018年年积日182~191共10 d的观测数据,采样率为30 s,实时轨道和钟差改正信息采用以SSR(state space representation)形式发布的CLK93实时数据流(由CNES提供),更新频率为5 s。数据处理时,以1 d的观测数据为一个弧段,对每个弧段进行实时静态与动态PPP解算,并将结果与已知坐标对比,获得E、N、U 3个方向的坐标偏差,用来分析不同定位模式下PPP的定位精度。
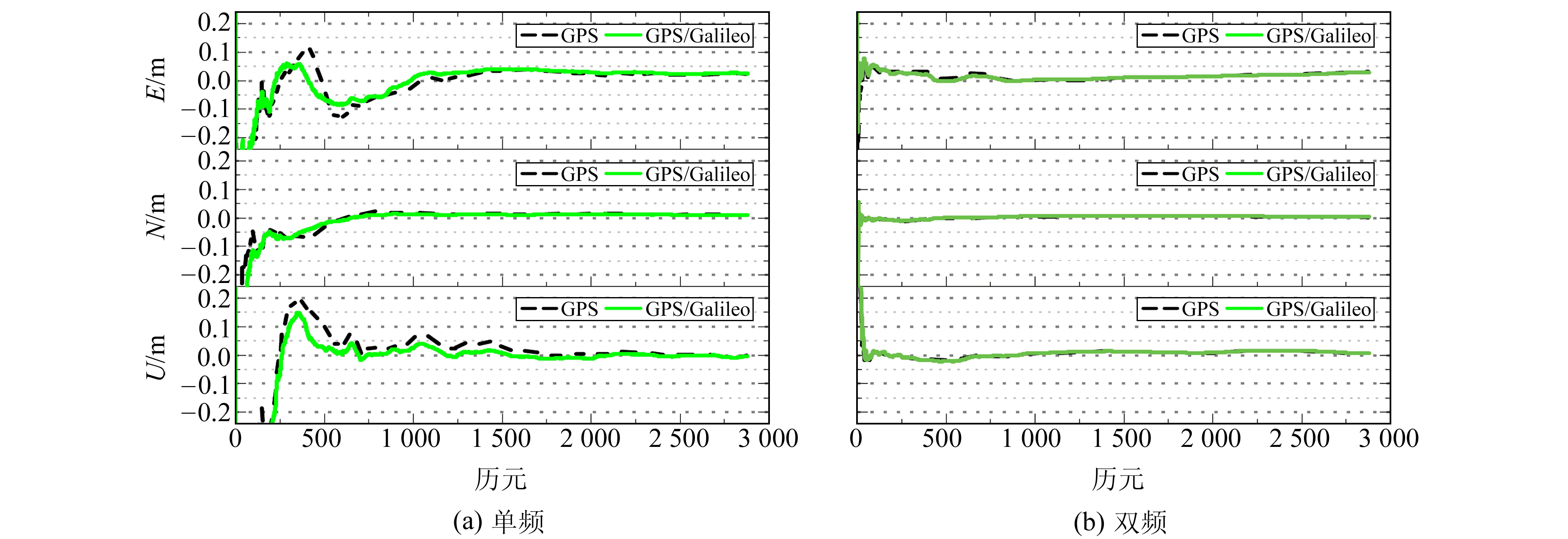
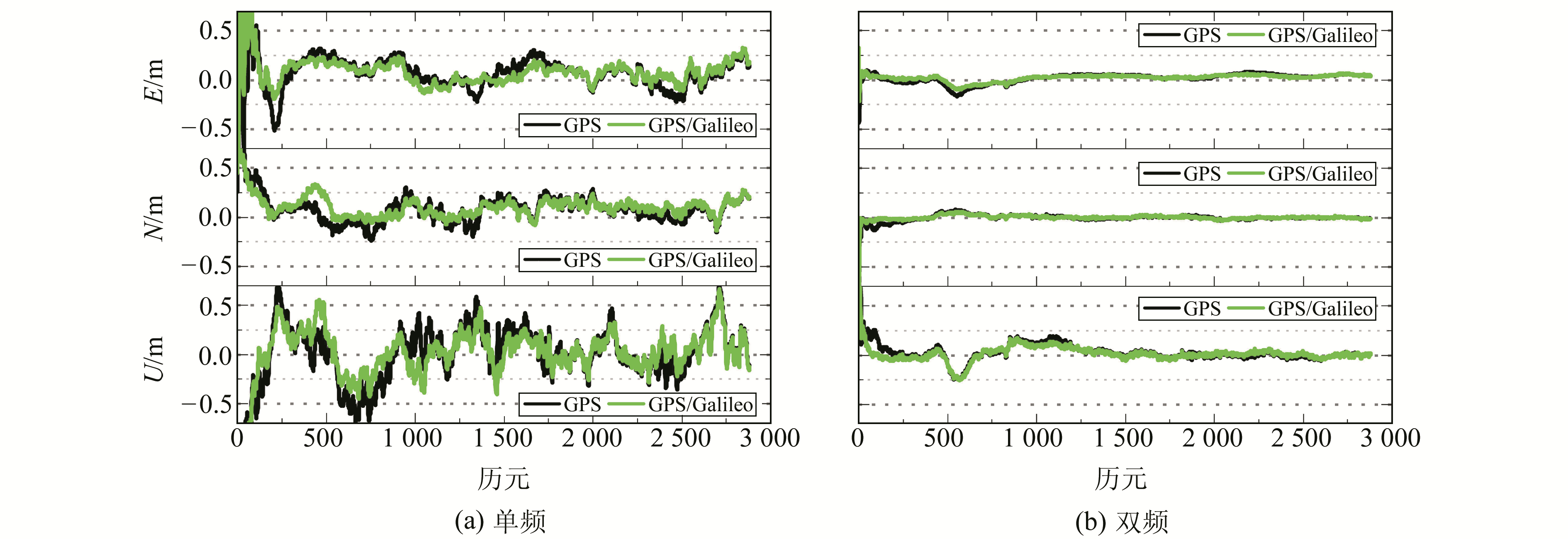
2.2 结果分析为对比2种模式下PPP的定位精度,图 1、2分别给出JFNG站点年积日182的实时静态和动态定位偏差序列,图 3~6为不同定位模式下10个站点10 d共计100组数据的精度统计结果。从图 1可以看出,2种模式的实时静态单频PPP都具有较长的收敛时间,主要是因为单频PPP模型中将电离层延迟作为参数估计,无法通过频率组合方式削弱电离层的影响。但相对于GPS,GPS/Galileo组合增加了有效观测数据,改善了空间几何结构,有助于PPP快速收敛,特别是单频PPP的收敛性能有较为明显的改善。从图 2可以看出,对于实时动态PPP,单频的定位精度较差,尤其是U方向,较双频存在明显波动,这主要是由于U方向和电离层延迟相关性较大所致。另外,加入Galileo后收敛性能和定位精度均较单纯的GPS有一定程度的提高。因此,无论单双频还是动静态模式,Galileo的加入能有效改善空间几何结构,对组合PPP的解算性能有一定的贡献。
|
图 1 GPS和GPS/Galileo实时静态定位结果 Fig. 1 The positioning results of the real-time static GPS and GPS/Galileo PPP |
|
图 2 GPS和GPS/Galileo实时动态定位结果 Fig. 2 The positioning results of the real-time kinematic GPS and GPS/Galileo PPP |
|
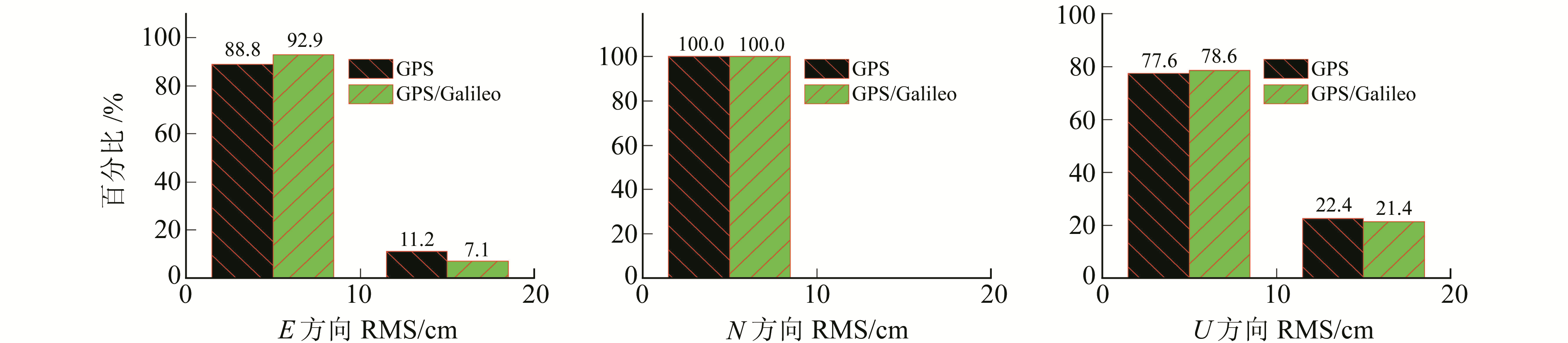
图 3 单频实时静态PPP的RMS Fig. 3 RMS of the single-frequency real-time static PPP |
|
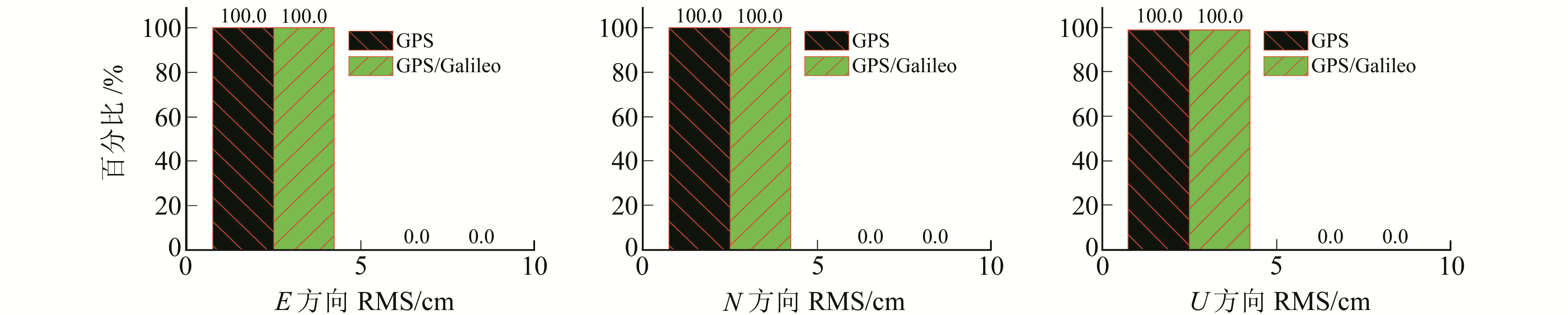
图 4 双频实时静态PPP的RMS Fig. 4 RMS of the dual -frequency real-time static PPP |
|
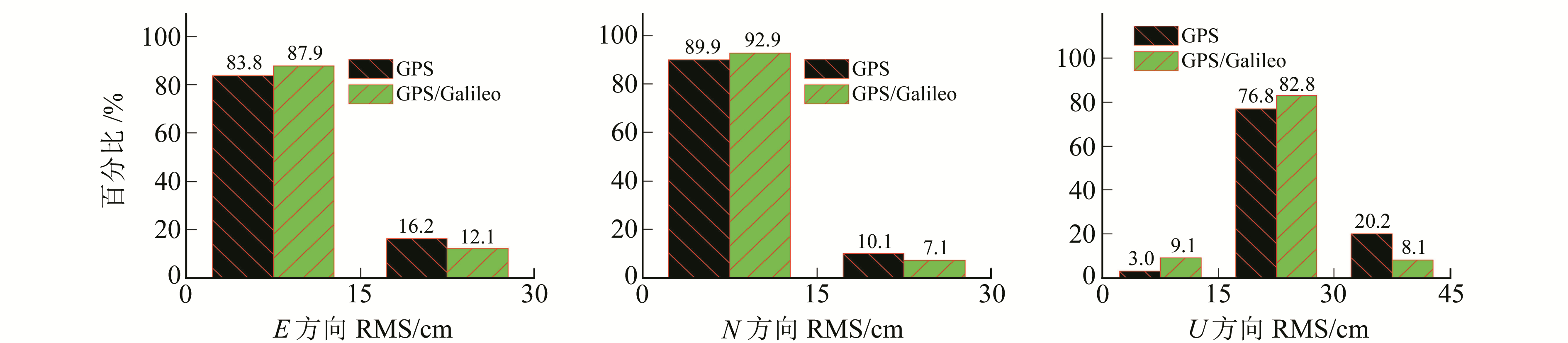
图 5 单频实时动态PPP的RMS Fig. 5 RMS of the single-frequency real-time kinematic PPP |
|
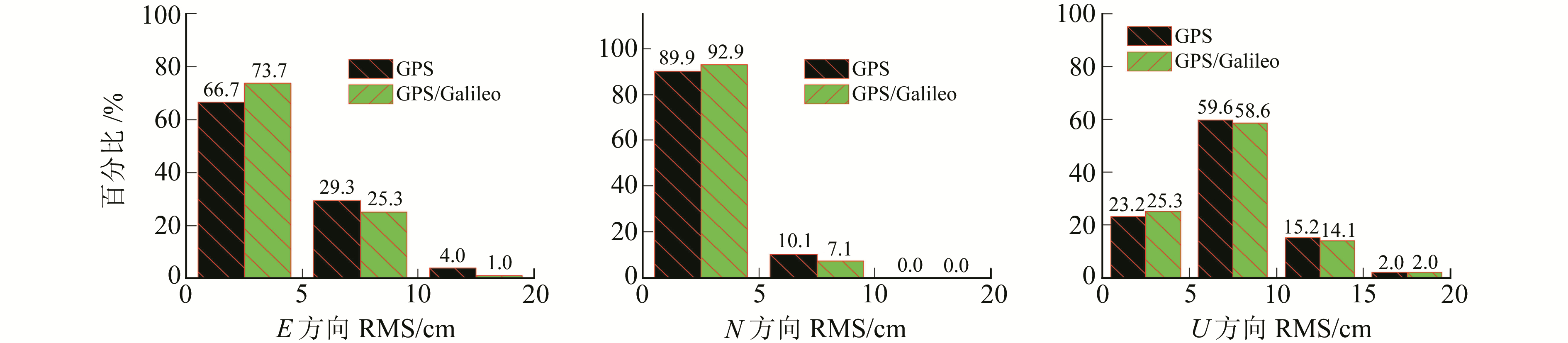
图 6 双频实时动态PPP的RMS Fig. 6 RMS of the dual-frequency real-time kinematic PPP |
为进一步分析滤波收敛后GPS/Galileo组合PPP的定位精度和稳定性,对1 d数据进行实时解算,并从均方根(RMS)误差角度与GPS进行对比。图 3和4为GPS和GPS/Galileo组合单双频实时静态PPP的RMS统计结果。由图 3可知,GPS单频实时静态PPP在E方向的定位精度有88.8%优于10 cm,而GPS/Galileo组合为92.9%,略优于GPS;而对于N和U方向,2种模式的定位精度相当,在N方向完全优于10 cm,U方向定位精度较差,分别有77.6%和78.6%优于10 cm。结合图 1(a)可知,Galileo的加入对PPP定位精度改善不明显的主要原因是,其加入后定位精度的提高主要体现在收敛初期,一旦达到稳定状态,对精度的改善作用将逐渐降低。对于双频实时静态PPP,其定位精度明显优于单频PPP,且2种模式精度相当,在E、N、U 3个方向的定位精度均优于5 cm(图 4)。因此,尽管在单双频实时静态处理中GPS/Galileo组合PPP取得了较好的定位效果,但Galileo对组合定位精度的贡献并不明显。
图 5、6为单双频实时动态PPP的RMS统计信息。从图 5可以看出,GPS单频实时动态PPP在E和N方向定位精度分别有83.8%和89.9%优于15 cm,而GPS/Galileo组合为87.9%和92.9%,分别提高了4.9%和3.3%;U方向的定位精度较差,GPS有79.8%优于30 cm,GPS/Galileo组合为91.9%,较GPS提高了15.2%,改善效果较为明显。从图 6可以看出,对于双频实时动态PPP,3个方向均取得较好的定位效果。整体上,GPS和GPS/Galileo组合模式在E和N方向均有超过96.0%优于10 cm,U方向有98.0%优于15 cm,其中,GPS双频实时动态PPP在E和N方向的定位精度分别有66.7%和89.9%优于5 cm,而GPS/Galileo组合为73.7%和92.9%,较GPS提高了10.5%和3.3%。相对于静态PPP而言,动态PPP参数估计采用白噪声方式,其定位结果与前一个历元的先验信息相关性较小,受卫星空间结构的影响较大,Galileo的加入对定位精度有较明显的改善。
为从整体上分析Galileo对GPS/Galileo组合PPP定位精度的贡献,表 2、3分别给出单双频实时静动态定位结果的平均RMS。由表 2可知,对于双频实时静态PPP,GPS和GPS/Galileo组合模式均取得较好的定位效果,但单频PPP效果较差,二者定位精度相当,在E和N方向偏差约4 cm,U方向约7 cm。在实时动态PPP(表 3)中,相对于单纯的GPS,GPS/Galileo组合单频PPP的定位精度在E、N、U 3个方向上分别提高了5.4%、4.9%、10.4%,双频PPP的定位精度分别提高了6.5%、6.5%、5.4%。结合图 6可知,Galileo对GPS/Galileo组合实时动态PPP定位精度的提高有较大贡献。
|
|
表 2 实时静态PPP的平均RMS Tab. 2 The average RMS for the real-time static PPP |
|
|
表 3 实时动态PPP的平均RMS Tab. 3 The average RMS for the real-time kinematic PPP |
本文采用CNES提供的多系统实时轨道和钟差信息,实现GPS/Galileo组合单双频实时静动态PPP,并对定位精度进行分析。结果表明,因电离层延迟处理策略的不同,双频PPP收敛性能明显优于单频。相较于GPS双频动态PPP,GPS/Galileo组合能够一定程度上缩短收敛时间,但改善效果没有单频明显。对于定位精度,在实时静态定位中,GPS/Galileo组合单频PPP定位效果较好,在E、N、U方向分别有92.9%、100.0%、78.6%优于10 cm,但较GPS的定位精度改善并不明显;同时,两者的实时双频静态定位精度相当,均优于5 cm。在实时动态定位中,Galileo对GPS/Galileo组合的贡献较大,单频PPP在E和N方向平均精度约为10 cm,U方向约为22 cm;双频PPP精度较高,E和N方向平均精度约为4 cm,U方向约为7 cm。由此可知,不管单双频还是动静态模式,Galileo的加入能有效改善空间几何结构,对GPS/Galileo组合PPP的解算性能有一定的贡献。
| [1] |
Kouba J, Héroux P. Precise Point Positioning Using IGS Orbit and Clock Products[J]. GPS Solutions, 2001, 5(2): 12-28 DOI:10.1007/PL00012883
(  0) 0) |
| [2] |
Li X X, Zhang X H, Ren X D, et al. Precise Positioning with Current Multi-Constellation Global Navigation Satellite Systems:GPS, GLONASS, Galileo and Beidou[J]. Scientific Reports, 2015(5): 8 328
(  0) 0) |
| [3] |
Xia F Y, Ye S R, Xia P F, et al. Assessing the Latest Performance of Galileo-only PPP and the Contribution of Galileo to Multi-GNSS PPP[J]. Advances in Space Research, 2019, 63(9): 2 784-2 795 DOI:10.1016/j.asr.2018.06.008
(  0) 0) |
| [4] |
Elsobeiey M, Al-Harbi S. Performance of Real-Time Precise Point Positioning Using IGS Real-Time Service[J]. GPS Solutions, 2015, 20(3): 565-571
(  0) 0) |
| [5] |
Shi J B, Yuan X X, Cai Y, et al. GPS Real-Time Precise Point Positioning for Aerial Triangulation[J]. GPS Solutions, 2016, 21(2): 405-414
(  0) 0) |
| [6] |
Kazmierski K, Hadas T, SoŠnica K. Weighting of Multi-GNSS Observations in Real-Time Precise Point Positioning[J]. Remote Sensing, 2018, 10(1): 84
(  0) 0) |
| [7] |
佘忠伦, 高雅萍, 阿苦建英. 数据时效性对多系统实时PPP的影响分析[J]. 测绘科学, 2019, 44(2): 150-157 (She Zhonglun, Gao Yaping, Aku Jianying. The Influence Analysis of Multi-GNSS Real-Time PPP on Data Timeliness[J]. Science of Surveying and Mapping, 2019, 44(2): 150-157)
(  0) 0) |
| [8] |
张锡越, 赵春梅, 王权, 等. 多系统融合单频精密单点定位[J]. 测绘科学, 2018, 43(3): 29-34 (Zhang Xiyue, Zhao Chunmei, Wang Quan, et al. Precise Point Positioning with Multi-System Fusion for Single Frequency[J]. Science of Surveying and Mapping, 2018, 43(3): 29-34)
(  0) 0) |
| [9] |
Böhm J, Niell A, Tregoning P, et al. Global Mapping Function (GMF):A New Empirical Mapping Function Based on Numerical Weather Model Data[J]. Geophysical Research Letters, 2006, 33(7)
(  0) 0) |
| [10] |
Kouba J. A Guide to Using the IGS Products[Z]. Canada, 2015 https://kb.igs.org/hc/en-us/articles/201271873-A-Guide-to-Using-the-IGS-Products
(  0) 0) |
| [11] |
Zhao X W, Wang S L, Liu C, et al. Assessing the Performance of Multi-GNSS Precise Point Positioning in Asia-Pacific Region[J]. Survey Review, 2017, 49(354): 186-196 DOI:10.1080/00396265.2016.1151576
(  0) 0) |
| [12] |
Cai C S, Gao Y, Pan L, et al. Precise Point Positioning with Quad-Constellations:GPS, Beidou, GLONASS and Galileo[J]. Advances in Space Research, 2015, 56(1): 133-143 DOI:10.1016/j.asr.2015.04.001
(  0) 0) |
| [13] |
Guo F, Zhang X H, Wang J L. Timing Group Delay and Differential Code Bias Corrections for Beidou Positioning[J]. Journal of Geodesy, 2015, 89(5): 427-445 DOI:10.1007/s00190-015-0788-2
(  0) 0) |
| [14] |
Ge Y L, Zhou F, Sun B Q, et al. The Impact of Satellite Time Group Delay and Inter-Frequency Differential Code Bias Corrections on Multi-GNSS Combined Positioning[J]. Sensors, 2017, 17(3): 602 DOI:10.3390/s17030602
(  0) 0) |
2. National Time Service Center, CAS, 3 East-Shuyuan Road, Xi'an 710600, China
 2019, Vol. 39
2019, Vol. 39

