大地电磁测深法利用地球天然电磁场进行地电结构探测，无需人工场源，具有很大的探测深度，在地球物理勘探中运用广泛^[1-2]。在大地电磁测深中，对所得数据进行反演是极为重要的一步。大地电磁反演方法大多是基于水平层状均匀介质模型提出的，如Bostick反演法等^[3-4]。Bostick反演法运算简单，反演速度快，无需初始模型，能直接反映地电结构, 但该方法只是一种近似反演算法，实际应用中多用来为精确反演提供初始模型^[3]。徐世浙等^[5]提出一种曲线对比法，不需要初始模型，并且精度比Bostick方法高，但需要进行迭代运算。

Bostick反演法的近似性主要体现在2个方面^[4]：1)用渐近线交点处的视电阻率近似代替该频点所对应深度以上的视电阻率，误差受该方法固有原理限制；2)采用希尔伯特变换把导数项dlogρ_A/dlogω用相位来代替，误差是由运算过程中对一些项的忽略造成，是可以减小的。Boehl等^[6]定性地指出，希尔伯特变换近似造成的误差在一定条件下可以忽略。陈乐寿等^[7]采用级数方法对Bostick方法进行推导，也作了近似，得到和文献[6]相同的结果。但以往研究并未定量给出误差在各种情况下的大小，所以具体造成的误差大小并不可知，在一些情况下可能导致Bostick反演结果与实际情况出入较大。针对此问题，本文给出希尔伯特变换所造成误差的计算方法，并给出修正后的Bostick反演公式，最后通过对2个2层模型进行反演验证修正的有效性。

1 Bostick反演法原理

Bostick反演法是根据视电阻率-频率曲线的渐近特性推导得到的，即当频率大于渐近线交点所对应的频率时，视电阻率值受频率的影响很小，并且趋近于交点处对应的视电阻率值^[4]。Bostick反演法的基本反演公式为：

$ \sigma \left( z \right) = {\rm{ }}\frac{1}{{{\rho _A}}} {\rm{ }}\frac{1 +{\frac{{{\rm{dlog}}{\rho _A}}}{{{\rm{dlog}}\omega }}}}{{1 - \frac{{{\rm{dlog}}{\rho _A}}}{{{\rm{dlog}}\omega }}}} $

(1)

$ D = {\rm{ }}\sqrt {\frac{{{\rho _A}}}{{\omega \mu }}} $

(2)

式中，ρ_A为视电阻率，D为介质厚度。

通过测量计算得到视电阻率-频率曲线，可根据曲线获得视电阻率值、频率值及导数dlogρ_A/dlogω，即可反演得到电导率随深度变化的曲线。但在实际情况中，考虑到测量误差，实际测得的曲线大多不平滑，求导会造成较大误差^[4]，因此，在使用Bostick反演算法时应该设法避免对实测曲线求导数。考虑到一维介质中大地电磁阻抗是最小相位函数^{[1, 6]}，振幅与相位之间的关系可以由希尔伯特变换公式^[4]给出：

$ \varphi ({\omega _0}) = - {\rm{ }}\frac{1}{{\rm{ \mathsf{ π} }} }\int\limits_{ - \infty }^{ + \infty } {\frac{{{\rm{ log}}\left| {Z\left( \omega \right)} \right|}}{{{\omega _0} - \omega }}{\rm{d}}\omega } {\rm{ }} $

(3)

对式(3)进行推导^[6]得：

$ \begin{array}{l} s({y_0}) = {\rm{ }}\frac{2}{\pi }{\rm{ }}\varphi ({\omega _0}) + \\ \frac{{2}}{{\rm{ \mathsf{ π} }} ^2}\int\limits_{ - \infty }^\infty {[s({y_0}) - s\left( y \right)]f({y_0} - y){\rm{d}}y} {\rm{ }} \end{array} $

(4)

式中，$s\left( y \right) = \frac{{{\rm{d}}({\rm{ln}}|Z\left( \omega \right)|)}}{{{\rm{dln}}\omega }}{\rm{ }}, f({y_0} - y) = $${\rm{lncoth}}({\rm{ }}\frac{{{\rm{ }}|y - {y_0}|}}{2}{\rm{ }}), y = {\rm{ln}}\omega ,{y_0} = {\rm{ln}}{\omega _0}$。

得到式(4)后，进一步推导^[6]可以得到电阻率的反演公式：

$ \rho \left( D \right) \approx {\rho _A}\left( \omega \right)\left( {\frac{\pi }{{2\varphi \left( \omega \right)}}{\rm{ }} - 1} \right) $

(5)

式中，φ(ω)可以从相位曲线上读出来，式(2)和式(5)即为Bostick反演公式。

2 希尔伯特变换近似所造成的误差

在Bostick反演法中，利用希尔伯特变换避免了由于实测曲线不平滑造成的误差，但在采用希尔伯特变换求解dlogρ_A/dlogω与相位φ(ω)之间的关系时，忽略了式(4)的第2项，从而造成误差。

本节给出求解希尔伯特变换所造成误差的方法，即分别求解得到式(4)中的第1项与第2项。

令

$ {Z_1}({y_0}) = \int\limits_{ - \infty }^\infty {{\rm{ }}s\left( y \right)f({y_0} - y){\rm{d}}y} $

(6)

$ {Z_2}({y_0}) = \int\limits_{ - \infty }^\infty {[s({y_0}) - s\left( y \right)]f({y_0} - y){\rm{d}}y} {\rm{ }} $

(7)

式中，f(y₀－y)已有显式表达式，但s(y)没有，所以要先求s(y)表达式，再求Z₁(y₀)与Z₂(y₀)的大小。

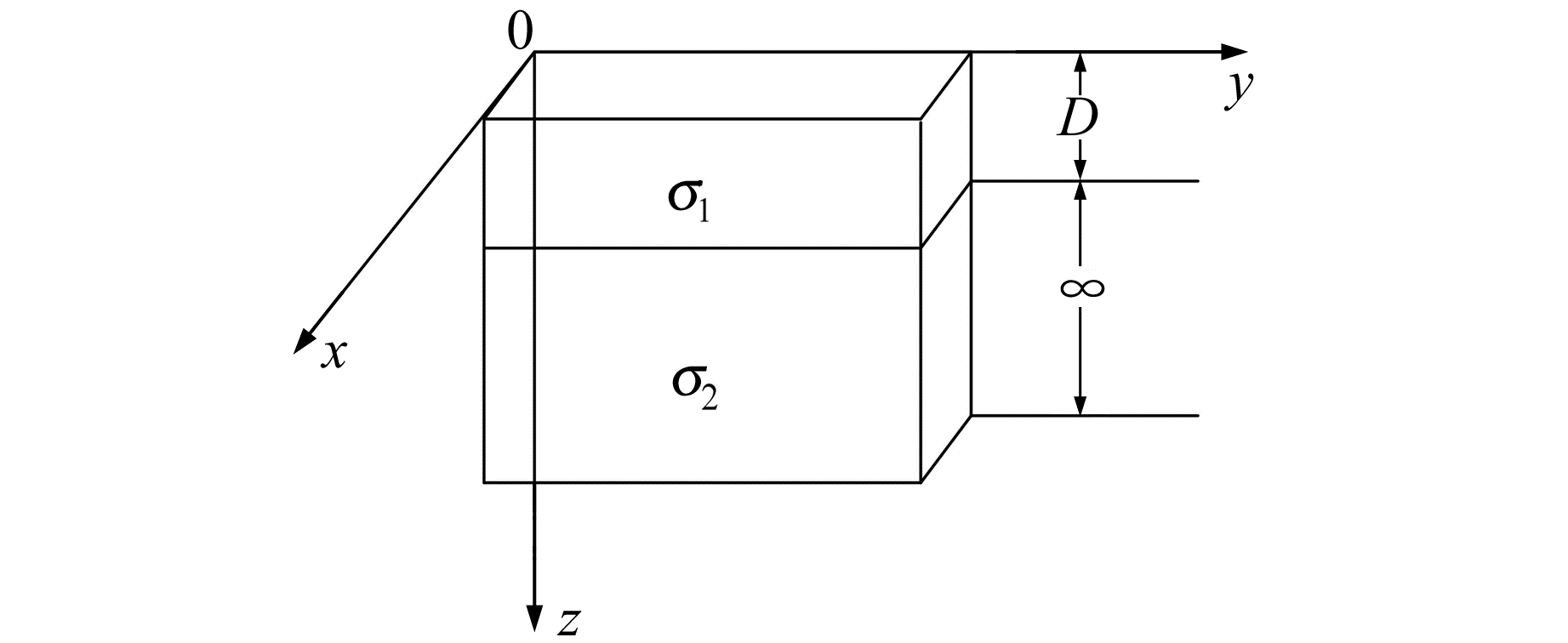
2.1 求s(y)显式表达式

对于图 1所示的均匀水平2层介质模型，设场源位于高空，场源的电场方向为x方向，磁场方向为y方向，波沿z轴正方向传播，即E =E_xe_x，H =H_ye_y，且E_x、H_y对x、y的导数皆为0。

在此模型下，推导得到水平2层介质模型表面的阻抗表达式^{[1, 8-9]}为：

$ Z\left( \omega \right) = {\rm{ }}\frac{{\omega \mu }}{{{k_1}}}{\rm{ }}\frac{{1 + {K_{12}}{{\rm{e}}^{2{\rm{i}}{k_1}D}}}}{{1 - {K_{12}}{{\rm{e}}^{2{\rm{i}}{k_1}D}}}} $

(8)

式中，${k_1} = \sqrt {{\rm{i}}\omega \mu {\sigma _1}} , {k_2} = \sqrt {{\rm{i}}\omega \mu {\sigma _2}} , {K_{12}} = {\rm{ }}\frac{{{k_1} - {k_2}}}{{{k_1} + {k_2}}}$。

将式(8)代入s(y)表达式中：

$ \begin{array}{c} s\left( y \right) = \frac{{{\rm{d}}({\rm{ln}}\left| {Z\left( \omega \right)} \right|)}}{{{\rm{d}}({\rm{ln}}\omega )}}{\rm{ }} = {\rm{ln}}\sqrt {\frac{{\omega \mu }}{{{\rm{i}}{\sigma _1}}}} + \\ \frac{{{\rm{d}}({\rm{ln}}|1 + {K_{12}}{{\rm{e}}^{2{\rm{i}}{k_1}D}}|)}}{{{\rm{d}}({\rm{ln}}\omega )}}{\rm{ }} - \frac{{{\rm{d}}({\rm{ln}}|1 - {K_{12}}{{\rm{e}}^{2{\rm{i}}{k_1}D}}|)}}{{{\rm{d}}({\rm{ln}}\omega )}} \end{array} $

(9)

对式(9)进行化简，得：

$ s\left( y \right) = {\rm{ }}\frac{1}{2}{\rm{ }} - {K_{12}}A{{\rm{e}}^{u - A{{\rm{e}}^u}}}\frac{{K_{12}^2{{\rm{e}}^{ - 2A{{\rm{e}}^u}}}[{\rm{sin}}(A{{\rm{e}}^u}) - {\rm{cos}}(A{{\rm{e}}^u})\left] + \right[{\rm{sin}}(A{{\rm{e}}^u}) + {\rm{cos}}(A{{\rm{e}}^u})]}}{{1 - 2K_{12}^2{{\rm{e}}^{ - 2A{{\rm{e}}^u}}}{\rm{cos}}(2A{{\rm{e}}^u}) + K_{12}^4{{\rm{e}}^{ - 4A{{\rm{e}}^u}}}}} $

(10)

式中，$A = {\rm{ }}\sqrt {2\mu {\sigma _1}} D, u = {\rm{ }}\frac{1}{2}{\rm{ln}}\omega $。

2.2 求取Z₁(y₀)与Z₂(y₀)之间的关系

得到s(y)的显式表达式后，采用数值方法分别计算Z₁(y₀)、Z₂(y₀)的大小。若要进行数值运算，需要确定参数K₁₂、A，即需要确定均匀2层介质模型的电阻率ρ₁、ρ₂及第1层深度D。当已知各参数量时，即可采用MATLAB通过编程计算Z₁(y₀)、Z₂(y₀)的大小。

3 修正方法

由式(4)、式(6)、式(7)及相位函数表达式可知，式(4)可写为：

$ s({y_0}) = {\rm{ }}\frac{2}{{\rm{ \mathsf{ π} }} }(1 + {\rm{ }}\frac{{{Z_2}}}{{{Z_1}}})\varphi ({\omega _0}) $

(11)

将y₀变为y，则式(11)可写为：

$ s\left( y \right) = {\rm{ }}\frac{2}{\pi }\left( {1 + {\rm{ }}\frac{{{Z_2}}}{{{Z_1}}}} \right)\varphi \left( \omega \right) $

(12)

对卡尼亚视电阻率公式${\rho _A} = {\rm{ }}\frac{{{{\left| Z \right|}^2}}}{{\omega \mu }}$两边求对数可得:

$ {\rm{ln}}{\rho _A} = 2{\rm{ln}}\left| Z \right| - {\rm{ln}}\omega - {\rm{ln}}\mu $

(13)

式(13)两边对lnω求导数可得：

$ \frac{{{\rm{d}}({\rm{ln}}{\rho _A})}}{{{\rm{d}}({\rm{ln}}\omega )}}{\rm{ }} = 2{\rm{}}\frac{{{\rm{d}}({\rm{ln}}\left| Z \right|)}}{{{\rm{d}}({\rm{ln}}\omega ){\rm{ }}}}{\rm{}} - 1 $

(14)

又由$s\left( y \right) = \frac{{{\rm{d}}({\rm{ln}}\left| {Z\left( \omega \right)} \right|)}}{{{\rm{d}}({\rm{ln}}\omega )}}$及式(12)、式(14)可得：

$ \frac{{{\rm{d}}({\rm{ln}}{\rho _A})}}{{{\rm{d}}({\rm{ln}}\omega )}}{\rm{ }} = {\rm{ }}\frac{4}{{\rm{ \mathsf{ π} }} }(1 + {\rm{ }}\frac{{{Z_2}}}{{{Z_1}}})\varphi \left( \omega \right) - 1 $

(15)

将式(15)代入Bostick反演公式(1)，即可得修正后的Bostick反演公式为：

$ \rho \left( D \right) = {\rho _A}\left( \omega \right)\left( {\frac{{\rm{ \mathsf{ π} }} }{{2{\rm{ }}\left( {1 + {\rm{ }}\frac{{{Z_2}({y_0})}}{{{Z_1}({y_0}){\rm{ }}}}} \right)\varphi \left( \omega \right){\rm{ }}}} - 1} \right) $

(16)

其中，$ D = \sqrt {{\rm{ }}\frac{{{\rho _A}\left( \omega \right)}}{{\omega \mu }}} $为反演深度，ρ_A(ω)为视电阻率，φ(ω)为相位，Z₂(y₀)/Z₁(y₀)可由程序计算得到。

4 模型检验及讨论

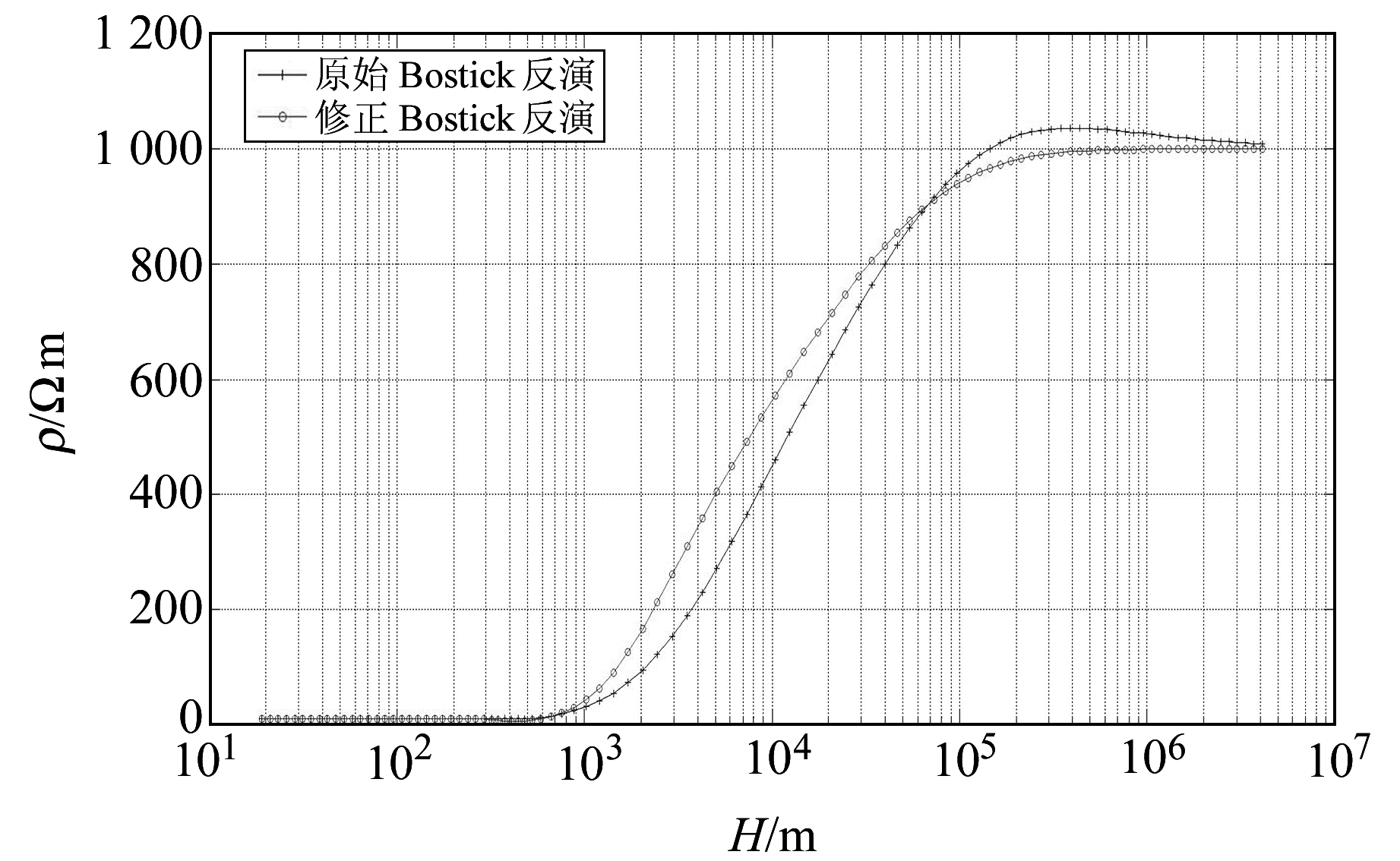
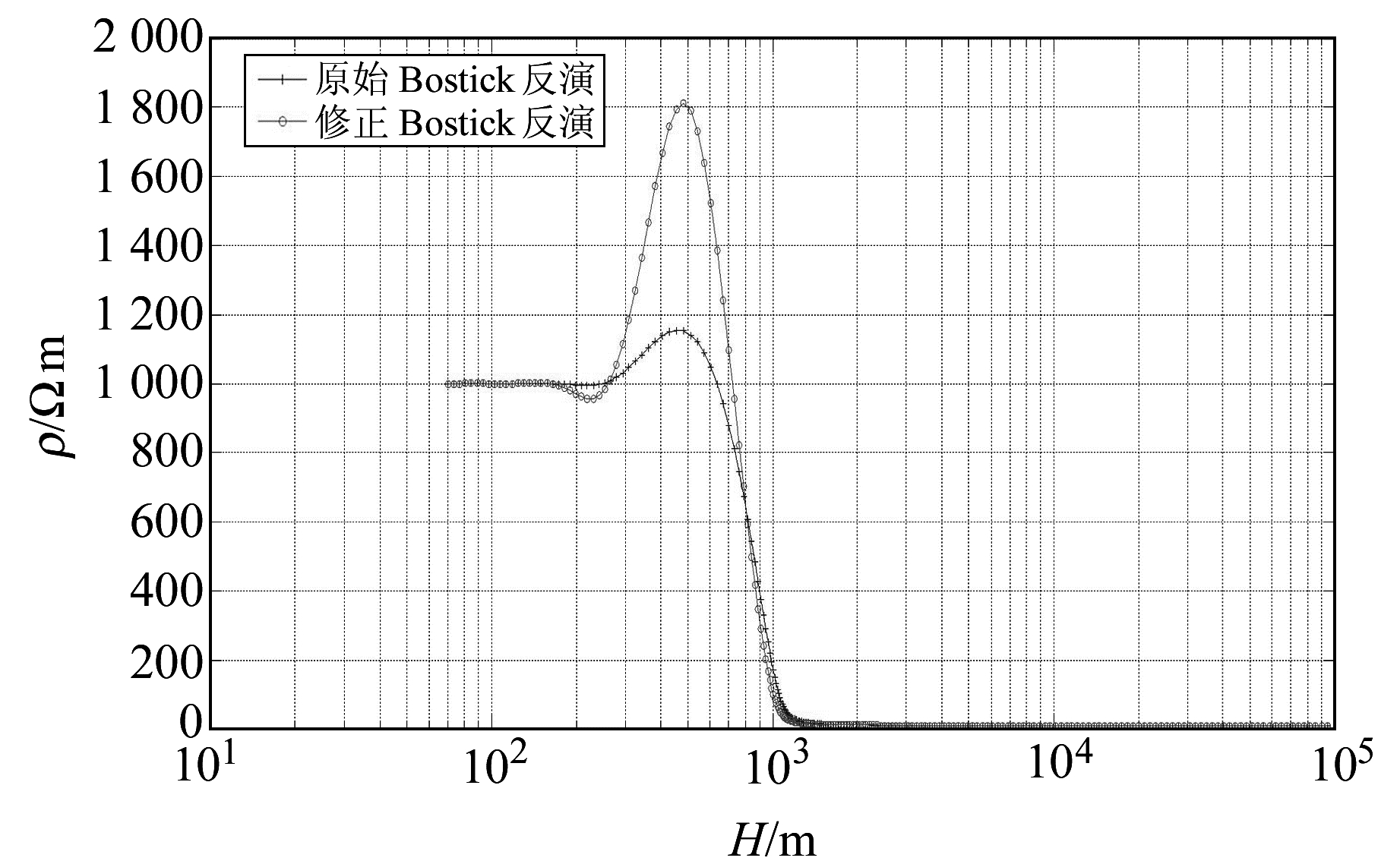
为了验证修正效果，设计2个2层理论模型，模型示意图如图 1所示，各个模型参数见表 1，其中ρ₁为第1层介质电阻率，ρ₂为第2层介质电阻率，D为第1层介质厚度。通过计算得到各个模型的原始Bostick反演结果及修正后的Bostick反演结果，如图 2、3所示。

由图 2、3可知：

1) 在深度较浅时，修正后的Bostick反演结果与原始的Bostick反演结果都接近真值。

2) 在深度趋近第1层厚度时，修正后的Bostick反演结果与原始的Bostick反演结果均有“超调”，但修正后的Bostick反演结果超调比原始的Bostick反演结果超调大，尤其是当第1层电阻率大于第2层电阻率时。

3) 当深度继续增加，反演电阻率结果均趋近于第2层真实电阻率，而修正后的Bostick反演结果趋近速度更快，并且更加准确、没有超调。

5 结语

综上所述，对于水平2层均匀介质模型，原始的Bostick反演方法和修正后的Bostick方法所得结果总体差别不大。在低阻模式下，修正后的Bostick方法反演结果较优，可以更好地反映分界面及第2层介质的电阻率；但在高阻模式下，当深度趋近于第1层介质厚度时，修正后的Bostick反演方法超调较大。造成此现象的原因是视电阻率频率曲线在深度趋近于第1层介质厚度时有一个小的超调，并且此时Z₂(y₀)/Z₁(y₀)为负数，所以修正后的Bostick反演方法相比原始的Bostick方法超调更大。

本文给出了希尔伯特变换所造成误差的计算方法，并对原始Bostick方法进行修正，修正后的Bostick方法消除了原始Bostick方法的一些误差，在一定程度上提高了反演的准确性。

致谢: 雷银照教授提出了本文的研究选题，并在研究思路及文章写作过程中给予建议及帮助，在此表示衷心感谢！