2. 中国地震局第一监测中心,天津市耐火路7号,300180
重力手段在地震预报等研究工作中发挥了重要作用[1-4]。以重力剖面为基础的研究手段应用较为广泛,但剖面测量点有限,往往需要通过内插甚至外推,才能获取更为连续的重力异常整体趋势信息。其中,最小曲率方法是重力数据内插和外推运算中较为成熟的方法之一[5-7]。但传统的最小曲率方法在进行重力剖面内插和外推时,需要专门考虑待解算结点与约束点之间的4种关系,即待解算结点右侧存在约束点、左侧存在约束点、两侧均存在约束点和两侧均没有约束点[6-7]。当约束点位于待解算结点的两侧时,需要通过泰勒展开进行推导才能得到相应表达式,推导过程复杂,且会造成一定的精度损失。
本文在前人研究基础上,对最小曲率解算方法进行部分改进。首先利用余弦变换计算待解算结点的初值[6],其次在进行最小曲率迭代解算时,将约束点也考虑为待解算结点统一解算。由此,参与计算的所有点均成为同类型的“待解算结点”,可以直接利用无约束点的最小曲率迭代公式[8]进行解算。改进后的最小曲率解算方法避免了分别考虑待解算结点与约束点之间的4种关系,也不需要泰勒展开,从而提高了解算精度。
1 算法原理最小曲率微分方程的差分表达形式为[9]:
| $ \begin{array}{c} \mu \left( i \right) = - {\rm{ }}\frac{1}{6}{\rm{ }}\{ \mu \left( {i + 2} \right) + \mu \left( {i - 2} \right) - 4[\mu \left( {i + 1} \right) + \\ \mu \left( {i - 1} \right)]\} , i = 1, 2, \ldots , n \end{array} $ | (1) |
式中,边界条件μ(-1)、μ(0)、μ(n+1)、μ(n+2)的具体定义见文献[6]。
在进行最小曲率内插和外推前,需要先对待解算结点赋初值。本文首先结合约束点信息,利用余弦变换方法进行初值赋值[6, 9],约束点仍为已知值;其次将约束点也作为待解算结点,使用基于无约束点迭代方法(式(2))进行统一迭代解算。为了使解算结果更为平滑,不强制使约束点值等于原始真值,当迭代次数超出预先设定的最大迭代次数,或前后2次迭代误差小于预先设定的最大相对误差时,迭代终止。迭代表达式为:
| $ \begin{array}{c} {\mu ^{(k)}}\left( i \right) = - {\rm{ }}\frac{1}{6}{\rm{ }}\{ {\mu ^{(k - 1)}}\left( {i + 2} \right) + {\mu ^{(k)}}\left( {i - 2} \right) - \\ 4[{\mu ^{(k - 1)}}\left( {i + 1} \right) + {\mu ^{(k)}}\left( {i - 1} \right)]\} , i = 1, 2, \ldots , n \end{array} $ | (2) |
模型数据为2个高斯分布函数的加和形式,单位mGal,表达式为:
| $ f\left( x \right) = {\rm{ }}\frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }} {\delta _1}} }}{\rm{e}}^{{\frac{{ - \left( {x - \mu } \right)2}}{{2{\delta_1 ^2}}}}} + {\rm{ }}\frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }} {\delta _2}} }}{{\rm{e}}^{\frac{{ - {{(x + \mu )}^2}}}{{2\delta _2^2}}}} $ | (3) |
其中,μ=3, δ1=2, δ2=1.5。
图 1为原函数、选取的已知点及余弦函数赋予初值的分布情况,1号点和2号点代表最外侧的2个约束点,3号点和4号点代表外推的2个边界点,由1号点和2号点求平均获得。由此可知,1号点到3号点、2号点到4号点之间的待解算结点为外推点,1号点和2号点之间的点为内插点。在本例中,等间距地选取13个点作为约束点,并设定内插100个点(均匀内插),均匀地向两侧各外推20个点。
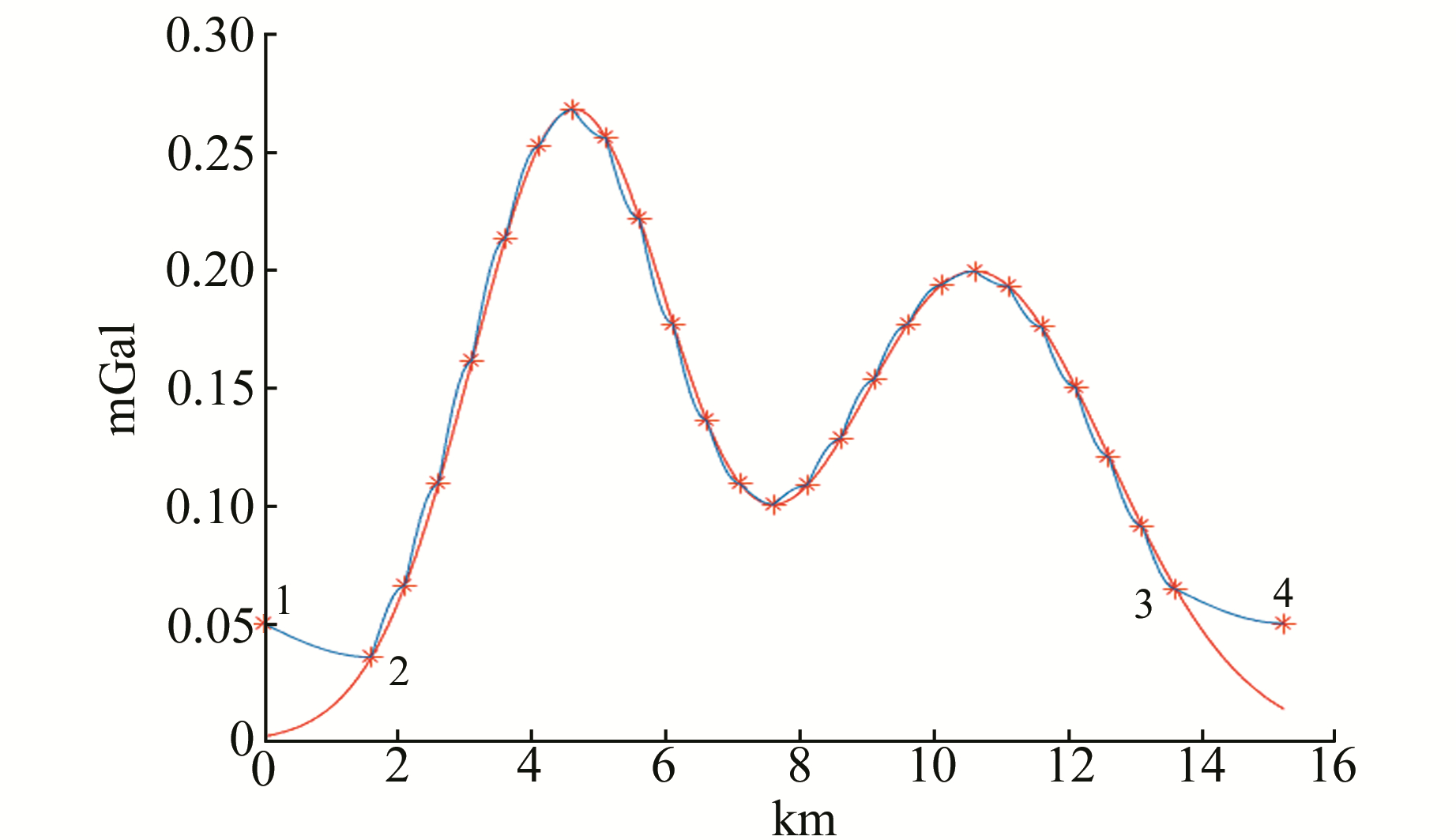
|
红线:原函数曲线;蓝线:余弦变换;红色*:约束点,2个端点为外推的端点值 图 1 原函数曲线与余弦变换结果 Fig. 1 Comparison of real value and calculation results with cosin transformation |
分别利用传统的最小曲率法和改进的最小曲率法解算,设定迭代次数为10次,解算结果见图 2。从图 2(a)可以看出,虽然改进前后2种方法的迭代结果相差不大,但从图 2(b)(图 2(a)局部放大)可以看出,在蓝色圆圈部位即约束点附近,黑色实线(改进后的最小曲率方法)更加贴近红色实线(原函数曲线)。

|
红线:原函数曲线;红色*:约束点,2个端点为外推的端点值(由约束点外侧2个点求平均获得);黑线:改进的最小曲率计算结果;青线:传统的最小曲率计算结果 图 2 改进前后最小曲率迭代方法解算对比结果 Fig. 2 Comparison of the minimum curvature calculation before and after modification |
为对比解算结果,根据以下判定准则来量化评价计算精度:
| $ v = {\rm{ }}\sqrt {\frac{{{{\left( {{f^\prime } - f} \right)}^2}}}{N}} $ | (4) |
式中,f′为最小曲率迭代计算结果, f为真值, N为计算结点个数。
由2种方法的计算精度(表 1)可知,改进的最小曲率迭代方法要略优于传统的最小曲率迭代方法。
|
|
表 1 改进前后的差异性统计计算精度 Tab. 1 Statistical calculation accuracy of difference before and after improvement |
重力剖面数据左上角起始点坐标为115.79°E、41.08°N,右下角终止点坐标为117.84°E、38.08°N。剖面线从河北省张家口市开始,途经北京、天津,终止于河北省沧州市。共选取287个约束点进行最小曲率迭代计算,设定内插点数为150个(均匀内插),两侧均匀外推点数各20个(外推后的2个端点值为外侧2个约束点的平均值)。如图 3所示,改进后的最小曲率迭代结果(黑色曲线)很好地拟合了约束点(红色*号)的变化趋势,基本沿约束点“穿越”而过;而传统的最小曲率迭代方法不能很好地拟合约束点变化趋势。尤其在振荡较为突出的区域,改进的最小曲率迭代方法拟合效果更好。设定前后2次迭代的相对误差≤10-5 mGal时停止,最终,改进的最小曲率迭代法迭代106次,传统的最小曲率迭代方法迭代482次。

|
红色*:约束点; 黑线:改进的最小曲率计算结果;青线:传统的最小曲率计算结果 图 3 改进方法与传统方法插值和外推结果 Fig. 3 Comparison of the minimum curvature calculation before and after improvement |
改进后的最小曲率迭代方法不需要考虑待解算结点与约束点之间4种关系的问题,更为简洁。从精度上看,改进后的最小曲率迭代方法避免了因使用泰勒展开造成的精度损失,解算结果表明,其精度略优于传统的最小曲率方法,在约束点附近差异最为明显。这也与实际情况相符,因为将约束点作为待解算结点进行考虑,相当于对插值点进行了加密,且加密点为理论真值,等于对迭代计算增加了约束条件,而这个约束条件是有利于解算结果趋向理论值的。
但当剖面数据的峰值信息缺失时,利用最小曲率迭代方法进行插值和外推,会产生较为严重的畸变。原因在于,利用余弦变换为待插结点赋予初值时,其算法认为两侧的约束点即为剖面数据峰值。如果在重力异常峰值已知的前提下,通过在峰值附近选取约束点的方式可以弥补这一不足。在实际中往往很难获知出现峰值的位置,因此针对峰值缺失的问题,需要作进一步研究。
| [1] |
申重阳, 杨光亮, 谈洪波, 等. 维西-贵阳剖面重力异常与地壳密度结构特征[J]. 地球物理学报, 2015, 58(11): 3 952-3 964 (Shen Chongyang, Yang Guangliang, Tan Hongbo, et al. Gravity Anomalies and Crustal Density Stucture Characteristics of Profile[J]. Chinese Journal of Geophysics, 2015, 58(11): 3 952-3 964)
(  0) 0) |
| [2] |
徐东卓, 朱传宝, 孟宪纲, 等. 山西中北部地区地壳垂直形变时空演化特征及与强震的关系[J]. 地震研究, 2018, 41(3): 446-450 (Xu Dongzhuo, Zhu Chuanbao, Meng Xiangang, et al. Temporal and Spatial Evolution Characteristics of Crust Vertical Deformation and Its Relationship with Strong Earthquakes in Central and Northern Shanxi[J]. Journal of Seismological Research, 2018, 41(3): 446-450 DOI:10.3969/j.issn.1000-0666.2018.03.014)
(  0) 0) |
| [3] |
王同庆, 陈石, 梁伟锋, 等. 2016年门源MS6.4地震前的区域重力场变化与定量参数分析[J]. 地震地质, 2018, 40(2): 349-360 (Wang Tongqing, Chen Shi, Liang Weifeng, et al. The Variation of Regional Gravity Field and Quantitative Parameter Analysis before 2016 Menyuan MS6.4 Earthquake[J]. Seismology and Geology, 2018, 40(2): 349-360 DOI:10.3969/j.issn.0253-4967.2018.02.005)
(  0) 0) |
| [4] |
孟庆筱, 党学会. GPS约束下九寨沟地区断裂带现今运动速率的非连续接触模拟研究[J]. 地震研究, 2018, 41(3): 390-397 (Meng Qingxiao, Dang Xuehui. Research on Crustal Deformation in the Jiuzhaigou Area under the Constraints of GPS Results by Discontinuous Contact Model[J]. Journal of Seismological Research, 2018, 41(3): 390-397 DOI:10.3969/j.issn.1000-0666.2018.03.007)
(  0) 0) |
| [5] |
骆遥, 吴美平. 位场向下延拓的最小曲率方法[J]. 地球物理学报, 2016, 59(1): 240-251 (Luo Yao, Wu Meiping. Minimum Curvature Method for Downward Continuation of Potential Field Data[J]. Chinese Journal of Geophysics, 2016, 59(1): 240-251)
(  0) 0) |
| [6] |
王万银, 邱之云, 刘金兰, 等. 位场数据处理中的最小曲率扩边和补空方法研究[J]. 地球物理学进展, 2009, 24(4): 1 327-1 338 (Wang Wanyin, Qiu Zhiyun, Liu Jinlan, et al. The Research to the Extending Edge and Interpolation on the Minimum Curvature Method in Potential Field Data Processing[J]. Progress in Geophysics, 2009, 24(4): 1 327-1 338)
(  0) 0) |
| [7] |
王万银, 邱之云. 一种稳定的位场数据最小曲率网格化方法研究[J]. 地球物理学进展, 2011, 26(6): 2 003-2 010 (Wang Wanyin, Qiu Zhiyun. The Research to a Stable Minimum Curvature Gridding Method in Potential Data Processing[J]. Progress in Geophysics, 2011, 26(6): 2 003-2 010)
(  0) 0) |
| [8] |
王万银. 位场数据处理中的最小曲率方法及Fortran语言程序设计[M]. 北京: 地质出版社, 2010 (Wang Wanyin. The Minimum Curvature Method in Geophysical Data Processing and Fortran Programme Design[M]. Beijing: Geological Publishing House, 2010)
(  0) 0) |
| [9] |
Love A E H. The Mathematical Theory of Elasticity[M]. Cambridge: Cambridge University Press, 1926
(  0) 0) |
2. The First Curst Monitoring and Application Center, CEA, 7 Naihuo Road, Tianjin 300180, China
 2019, Vol. 39
2019, Vol. 39

