2. 中国地震局地壳应力研究所武汉创新基地,武汉市洪山侧路40号,430071
传统的应变研究由于受采样周期的限制,主要应用于潮汐信号、板块形变等长周期变化的分析。随着观测技术的成熟,应变仪器的采样率也进入了秒采样甚至更高频,以期上连测震、下接GPS频段。2003年美国主导的板块边界观测计划(PBO)开始实施,使用秒采样的Gladwin四元件张量应变仪为观测手段,连同地震计、倾斜仪、GPS进行同址观测,以期获得北美-太平洋板块边界形变场的四维特征[1]。其后我国的高频应变观测也进入快速发展期,2008年池顺良等[2]利用YRY-4型四元件钻孔应变仪在姑咱台进行100 Hz采样实验,恰好记录了康定的3次地震,可以清晰地分辨出P波和S波;刘琦等[3]选取10 Hz采样的应变资料,通过对2012年苏门答腊北部海域8.6级地震进行同震频谱分析发现,其与宽频地震计具有较好的一致性,说明YRY-4钻孔应变仪高频端的监测是可靠的。Barbour和Agnew[4]通过对PBO应变数据和地震仪数据对比分析认为,PBO钻孔应变仪记录的短周期地震信号的信噪比不亚于宽频地震计。本文以PBO综合钻孔同址记录的2017-09-08墨西哥8.1级地震波信号为例进行同震分析,并与同址地震计进行比较,分析其记录的可靠性,为后期开展PBO综合钻孔数据同震研究提供先行条件。
1 观测数据2017-09-08墨西哥发生8.1级地震,USGS公布的发震时刻为UTC 04:49:19,震中为(15.022°N,93.899°W),震源深度47.4 km。以PBO观测站记录的地震波数据为研究对象,选取钻孔应变仪与地震仪同址观测的14个站点(表 1)记录的地震波数据,对地震发生后1 h的连续观测数据进行分析。
|
|
表 1 站点信息 Tab. 1 Site information |
PBO钻孔应变仪(BSM)采集的原始数据是仪器四元件记录的电容值时间序列,需要对原始电容值g进行变换[5],转换为便于研究的线性拉伸应变e:
| $ e=R \frac{g / C}{1-g / C} $ | (1) |
式中,e为线性应变,R为固定电容板间隙与仪器直径的间隙比率,C因子考虑了模数转换的动态范围。
仪器的记录由非潮汐和潮汐等信号成分组成,为了提取有效的目标地震信号,需对原始数据进行预处理,剔除突跳、尖峰等已知干扰,对缺值进行有效的插值等,然后滤除线性应变时间序列的低频潮汐成分。PBO BSM信号采样率为1 sps,而PBO的同址地震仪为100 sps,因此需要对地震计记录的地震波数据降采样到1 sps,并根据仪器响应文件提供的灵敏度,将其单位统一在同一个数量级。
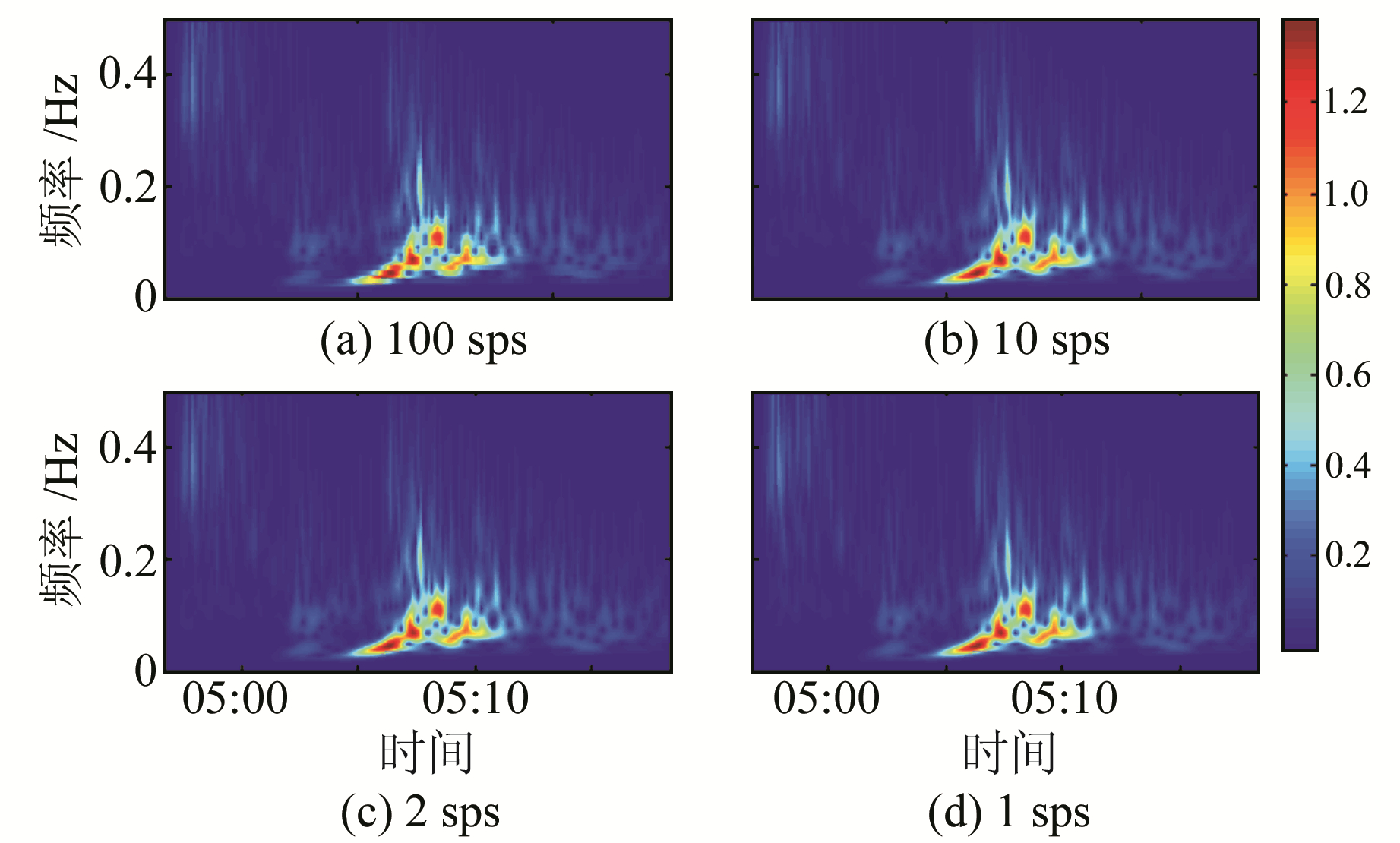
1.2 降采样对预处理后的地震仪记录进行降采样处理,起始采样频率为100 sps,目标采样率为1 sps。图 1为100 sps、10 sps、2 sps和1 sps频段S变换谱,以S变换分别对P波段、S波段、面波波段以及尾波的降采样动态过程进行分析发现,该过程保留了主要震相信息。S变换集合傅里叶变换和小波变换的优点,高频段有较高的时间分辨率,低频段有较高的频率分辨率。其原理如下[6-8]:
|
图 1 地震计记录地震波降采样过程全波段S变换谱 Fig. 1 Seismometer recording drop sampling process S-transformation |
| $ \left\{ {\begin{array}{*{20}{l}} {S[\tau , f] = \sum\limits_{t = 0}^{N - 1} s [t]\exp \left[ { - \frac{{{{(\tau - t)}^2}{f^2}}}{2}} \right]{{\rm{e}}^{\frac{{ - 2{\rm{ \mathsf{ π} }}ift}}{N}}}}\\ {s[t] = \frac{1}{N}\sum\limits_{f = - \frac{N}{2}}^{\frac{N}{2} - 1} {\sum\limits_{f = 0}^{N - 1} S } [\tau , f]{{\rm{e}}^{\frac{{ - 2\pi ift}}{N}}}} \end{array}} \right. $ | (2) |
式中,N为采样点数,t表示时间,f为频率,τ为高斯窗函数的平滑因子。
分析发现,这样逐步降采样不仅使地震波形一致性较好,降采样过程中各主要震相也基本一致。个别震相的谱可能会有细微差别,但在逐步降采样过程中总体上保持了地震波的原有特征。
1.3 PBO钻孔应变仪的自检PBO钻孔应变仪与国内的YRY-4应变仪都由4个元件按次序排列组成。YRY-4应变仪的元件在水平面按间隔45°分布,各元件观测记录为si,因此YRY-4自检[9]符合以下关系:
| $ S_{i}=k s_{i} $ | (3) |
| $ S_{1}+S_{3}=S_{2}+S_{4} $ | (4) |
PBO钻孔应变仪k个元件在水平面排列顺序为60°、60°、30°。将PBO钻孔应变仪看作由元件组合成的两个子模块:CH0、CH1和CH2元件间隔60°,跨越角120°;CH1和CH3间隔90°。假设元件各分量相对权重是正确的,且仪器与围岩耦合良好,两个子模块提供了两种不同的元件组合模块,且两种子模块组合都占有分量元件CH1,则此两种不同的元件组合子模块彼此相等于面应变[10-11]:
| $ \frac{\left(g_{0} e_{0}+\mathrm{g}_{1} e_{1}+g_{2} e_{2}\right)}{3}=C \varepsilon_{a} $ | (5) |
| $ \frac{\left(g_{1} e_{1}+g_{3} e_{3}\right)}{2}=C \varepsilon_{a} $ | (6) |
式中,gi为分量权值,ei为分量应变,C为元件系数,εa为面应变。自检相关系数见表 2。
|
|
表 2 自检相关系数 Tab. 2 Correlation coefficient |
USGS公布的墨西哥8.1级大地震的震源深度为47.4 km。表 3记录的是在该震源深度下震中距从26°~ 43°的理论P波射线参数[12](模型为IASP91,表 3中“射线参数1”),在该震源深度下,其相应的震中距对应的射线路径参数(表 3中“射线参数2”)为12.3~13.8 km/s。
|
|
表 3 震中距射线路径参数 Tab. 3 Epicentral distance and ray path parameters |
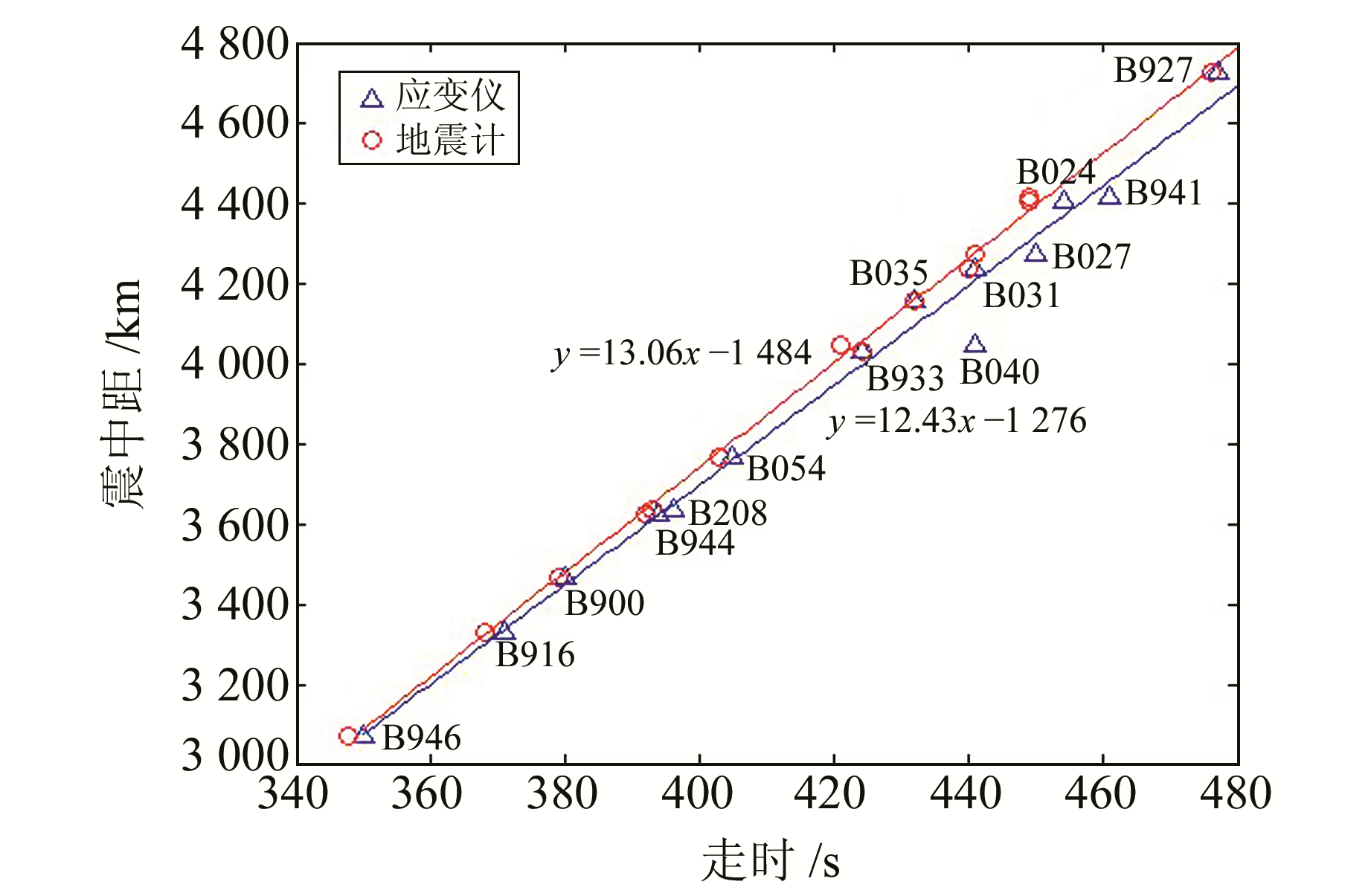
经过上述预处理后,得到校正后的应变地震波信号,根据震中距、走时得到震中距-走时拟合图(图 2)。由图可知,应变仪和地震计两者的拟合均呈一次线性关系,且P波走时随着震中距的增大也相应增加,拟合变化率为12.43 km/s和13.06 km/s(此变化率应为射线路径参数)。图中站点的震中距-走时基本呈线性关系,应变仪B040偏离较大,从其记录的波形中可以发现,该站点应变P波起始振幅响应偏小,因此可能是响应振幅太小、湮没在背景中,影响了对到时的准确拾取。从表 1可知,PBO台站主要分布在墨西哥8.1级大地震震中距27.6°~42.5°范围内,而应变仪与地震仪的射线拟合参数处在表 3记录的参数理论值范围之内。
|
图 2 仪器P波走时与震中距拟合曲线 Fig. 2 Fitting curves of P wave travel time and epicentral distance |
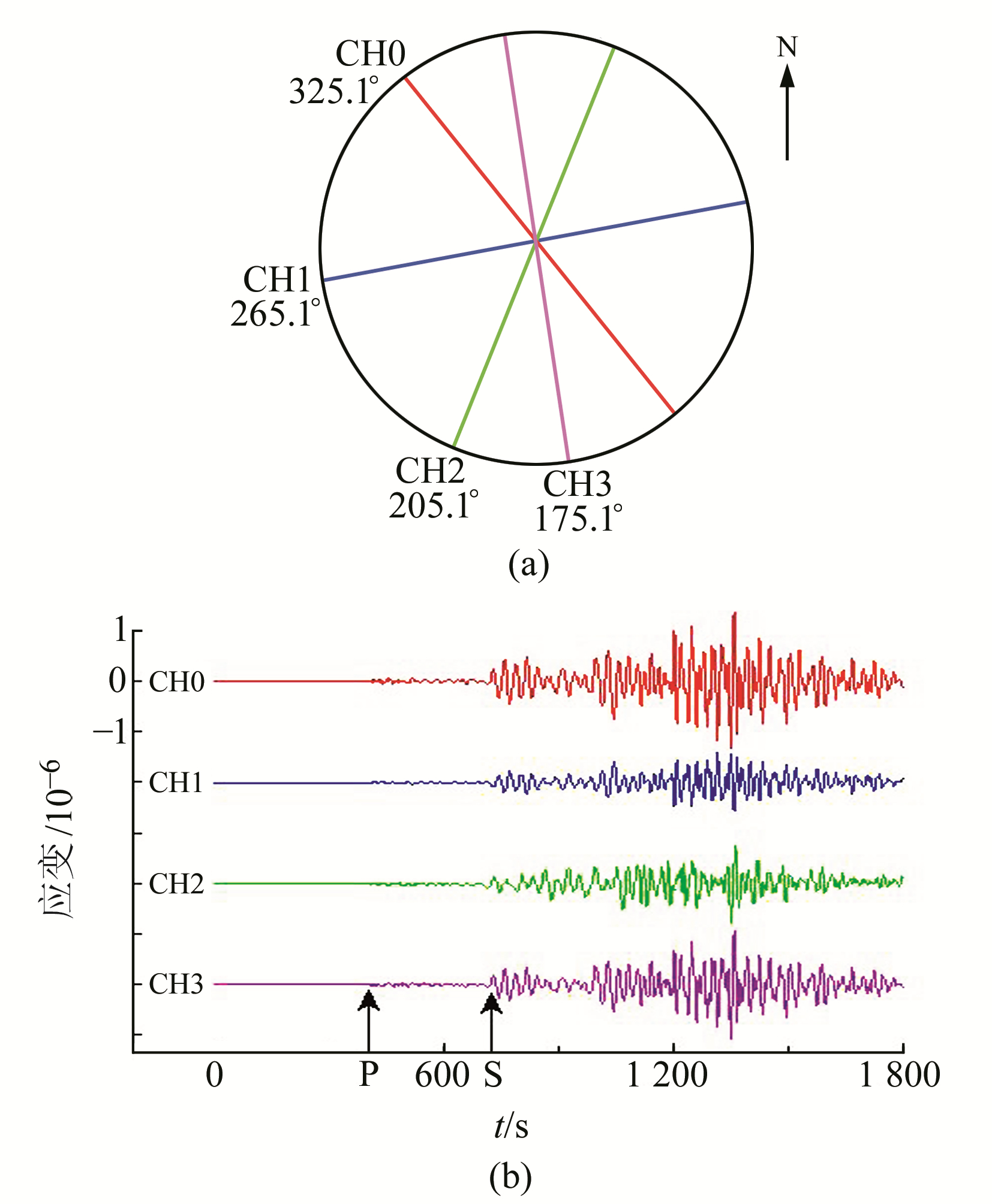
远震情况下体波能量减弱、面波相对发育,如图 3所示,S波段的响应清晰。分别对体波段以及面波段进行该震例下的地震波同址同震分析。受篇幅限制,仅以3个站点为展示对象:B946震中距为3 072 km,B944(44.3897°N,110.679°W)震中距3 623 km(记录远震波形,如图 3),B941震中距4 413 km。结合S变换,分析PBO钻孔应变仪对主震动的记录情况。
|
图 3 PBO钻孔应变网B944站点应变时间序列(各元件颜色与观测记录对应) Fig. 3 Time series of strain from B944 in PBO borehole strain network(the color of each component corresponds to the observation record) |
综合台站包含有应变仪、地震仪等钻孔仪器,取震后40 min连续记录为窗口,分析震后应变仪对主震动的记录情况。图 3为B944台站应变仪记录的地震波形,图 3(a)为应变仪(非标准)水平截面分布示意图,其各元件通过水泥与周围岩石固结,简图表示了各分量元件的方位角;图 3(b)为钻孔应变仪各分量应变(microstrain)记录,在远震时面波发育,仪器为1 sps采样。应变仪S波与P波裸眼可辨振幅变化明显,1 sps钻孔应变仪记录的地震波形的P波响应明显,且之后的震相清晰。对应变仪4个分量进行S变换(图 4)发现,该远震中P波起始响应容易湮没在背景噪声中,PP等能量大的震相到达台站时才可以从背景中辨别;而S波及面波在S变换谱中到时明显区别于其他震相,各分量尾波携带的信号也记录一致,应变仪各分量记录的信号具有一致性。应变仪主要集中在0.02~0.2 Hz,面波组分呈明显的频散特性且明显强于体波,由低频面波过渡到高频面波,尾波逐渐收窄在一定频带范围内。地震仪频谱显示,随着震中距的增加,高频信号逐步减弱,低频信号逐步增强。由于面波能量远超其他波段,全波段S变换中难以对各波段的细节进行分析,故将体波和面波段分开讨论。

|
图 4 站点应变仪地震波记录S变换 Fig. 4 The S-transform of strainmeter earthquake records for B946, B944 and B941 |
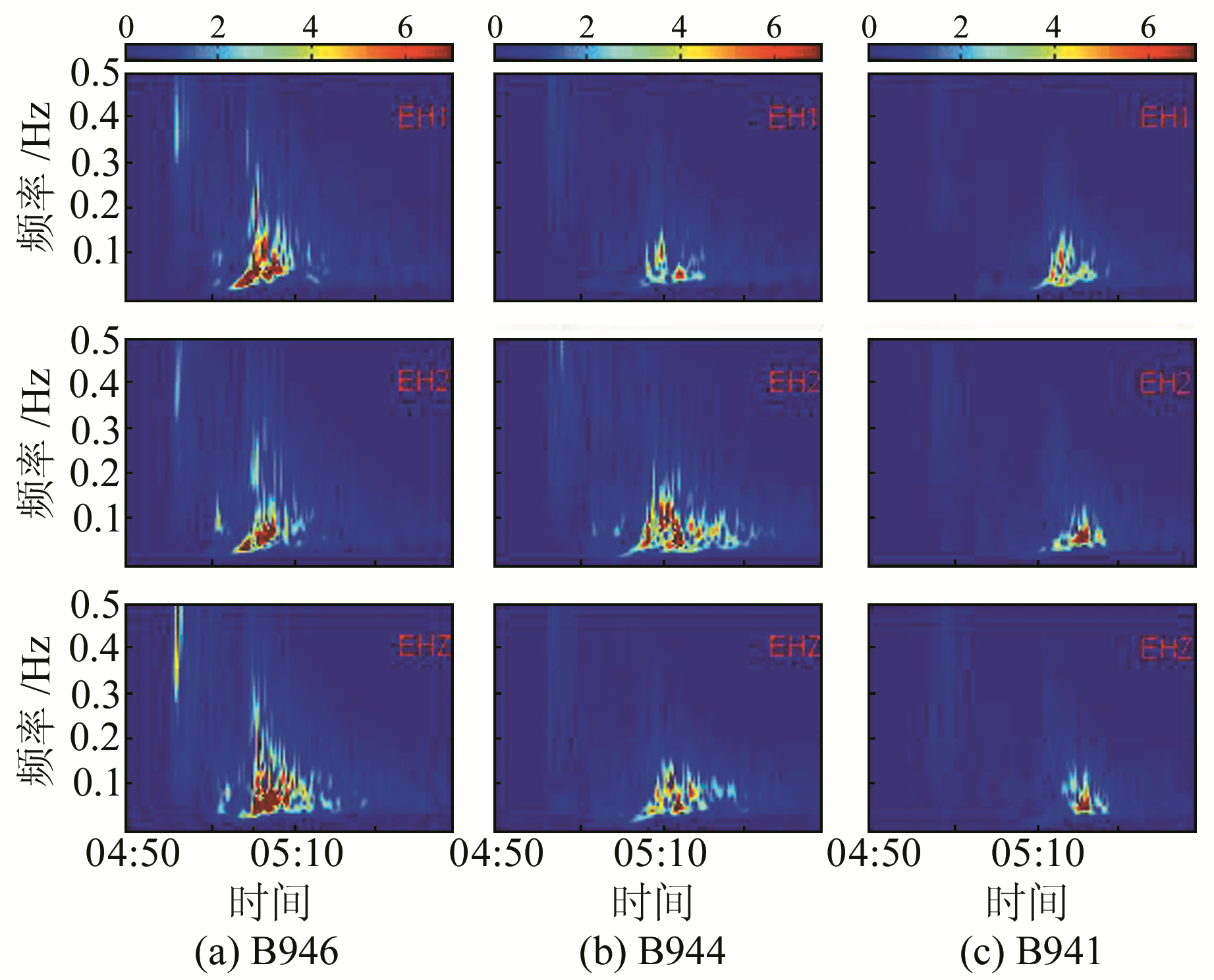
图 4中B946和B941站点应变仪的面波段频散由低频向高频过渡趋势明显,而B944站点的频散收敛不显著。分析认为,这是由于B944钻孔处于黄石公园,其火山发育的地质条件导致地层岩性复杂,射线路径多且杂,从而携带有周围地质特征的波形特性。这可以从同址的地震仪记录信号(图 5)中得到验证,两种仪器的频谱在时间-频率上有很好的一致性。
|
图 5 站点地震仪地震波记录S变换,B946、B944、B941震中距依次增大(EH1和EH2为水平分量,EHZ为垂向分量) Fig. 5 Seismograph record's S transform: B946, B944, B941, which epicenter distance increases in turn (EH1 and EH2 are horizontal components, EHZ is vertical component) |
应变仪与地震仪在波段振幅上存在差异,PBO钻孔应变仪的P/S振幅比多处于0.5以下,而地震仪的P/S则多为1上下。应变仪P波段中,4个元件起跳带有方向性,波形响应一致性较好,主要频段在0.25 Hz以内;S波段中,分量波形趋势仍然保持极高的一致性,且频谱明显强于P波段。而地震仪信号在P波段高频优势明显,到达S波段时仪器记录都偏向中低频。分别对3个测站的同址应变仪与地震仪的变换频谱进行比较得出,地震仪的记录跨越了整个频带,而应变仪记录的波形主要在0.25 Hz以下。
S变换谱的P波段分析表明,钻孔应变仪记录的地震波优势频段为0.2 Hz,分量元件方位越接近震中连线,其记录的面波能量明显越强于其他分量。两种仪器记录的波形发育过程一致性较好。S波段的应变记录主要频段为0.1 Hz,与P波段相比其频率组分更偏向低频;地震仪的S波段频谱也偏向中低频,且连续性较好。
PBO钻孔应变仪记录的面波随着时间呈现由低频向高频转化的过程。这是由于低频信号能传播到较深的地层,传播介质速率较快从而先行到达;而高频面波的传播深度相对较浅,介质速率小而晚到达。随着时间的推移,应变仪面波主频率由0.02 Hz延伸到0.1 Hz,地震仪面波主频率由0.02 Hz延伸到0.12 Hz。地震仪在面波段的频谱与PBO应变仪响应较为一致地记录了面波的发育过程。
3 同震应变主方向四分量观测记录换算为平面应变变化,其相应的主方向、主应力以及最大剪应变等经由观测记录换算而来的量具有更显著的物理意义。因此在前文分析的基础上,进一步探讨PBO钻孔四分量应变仪记录的地震形变场。钻孔应变观测的基本公式为:
| $ S_{\theta_{i}}=A\left(\varepsilon_{1}+\varepsilon_{2}\right)+B\left(\varepsilon_{1}-\varepsilon_{2}\right) \cos 2\left(\theta_{i}-\varphi\right) $ | (7) |
式中,θi为Sθi的方位角,A和B是耦合系数,ε1、ε2分别为最大和最小主应变,φ为应变主方向角。
PBO的Gladwin四分量钻孔应变仪各元件角度差为60°、60°和30°,根据式(7)得:
| $ \left\{\begin{aligned} S_{3}=& A\left(\varepsilon_{1}+\varepsilon_{2}\right)+B\left(\varepsilon_{1}-\varepsilon_{2}\right) \cos 2\left(\theta_{3}-\varphi\right) \\ S_{2}=& A\left(\varepsilon_{1}+\varepsilon_{2}\right)+\frac{1}{2} B\left(\varepsilon_{1}-\varepsilon_{2}\right) \cos 2\left(\theta_{3}-\varphi\right)-\\ & \frac{\sqrt{3}}{2} B\left(\varepsilon_{1}-\varepsilon_{2}\right) \sin 2\left(\theta_{3}-\varphi\right) \\ S_{1}=& A\left(\varepsilon_{1}+\varepsilon_{2}\right)-B\left(\varepsilon_{1}-\varepsilon_{2}\right) \cos 2\left(\theta_{3}-\varphi\right) \\ S_{0}=& A\left(\varepsilon_{1}+\varepsilon_{2}\right)+\frac{1}{2} B\left(\varepsilon_{1}-\varepsilon_{2}\right) \cos 2\left(\theta_{3}-\varphi\right)+\\ & \frac{\sqrt{3}}{2} B\left(\varepsilon_{1}-\varepsilon_{2}\right) \sin 2\left(\theta_{3}-\varphi\right) \end{aligned}\right. $ | (8) |
令
| $ \left\{\begin{array}{l}{S_{02}=S_{0}-S_{2}} \\ {S_{13}=S_{1}-S_{3}}\end{array}\right. $ | (9) |
结合式(8)~(9)整理化简得:
| $ \varphi=\frac{1}{2} \arctan \left(\frac{2}{\sqrt{3}} \frac{S_{02}}{S_{13}}\right)+\theta_{3} $ | (10) |
式中,θ3为PBO四分量钻孔应变仪CH3元件的方位角。综上,可以求得同震应变主方向φ。
以墨西哥8.1级地震为例,基于以上的前期数据处理,数据采样为1 sps,以P波初动和S波初动段代入公式,求得同震应变主方向并取其均值。图 6所示为目标钻孔应变仪记录的地震应变主方向,大部分钻孔应变主方向指向震中方向,少数钻孔应变主方向偏离较大、偏离钻孔,震中连线在10°~15°之间。远震时,地震波经过复杂多变的地壳介质,且仪器易受耦合因子的影响,因此应变主方向不一定完全指向震中。但综合所有研究目标钻孔应变主方向,其主体在同震情况下是指向震中的。

|
图 6 钻孔的同震应变主方向 Fig. 6 Coseismic strain main direction |
综合以上分析,PBO钻孔仪器同震表现良好,应变仪的时间序列与地震记录有较好的一致性。
1) 从震中距-走时拟合曲线可知,应变仪记录的地震波形与地震计记录的波形在信号响应上有较好的一致性。应变仪记录的地震波也能准确记录P、S等主要震相,其记录的波形射线参数符合理论射线参数值,钻孔应变仪记录的地震波是可靠的。
2) PBO钻孔应变仪体波波段的记录能力明显不如对面波的响应,其可能受1 sps采样限制,应变仪最早的设计是针对低频信号的。
3) 应变仪观测在面波段得到较完整的记录,较地震仪在面波段更有优势,可以结合应变仪和地震仪面波资料进行地壳结构研究,或者基于应变面波资料进行进一步研究。
4) 在远震条件下,PBO钻孔应变仪记录的地震信号其同震应变主方向指向震中,表明地震波传播到钻孔时应变仪记录的信号主体是地震波引起的形变。
致谢: 感谢UNAVCO为本文提供PBO钻孔应变数据。
| [1] | |
| [2] |
Qiu Z H, Chi S L, Wang Z M, et al. The Strain Seismograms of P- and S-waves of a Local Event Recorded by Four-Gauge Borehole Strainmeter[J]. Earthquake Science, 2015, 28(3): 209-214 DOI:10.1007/s11589-015-0120-5
(  0) 0) |
| [3] |
刘琦, 张晶, 晏锐, 等. 高采样率四分量钻孔应变同震响应分析[J]. 中国地震, 2013, 28(1): 57-67 (Liu Qi, Zhang Jing, Yan Rui, et al. The Analysis of Coseismic Response of 4-Component Borehole Strainmeters with High Sampling Rate[J]. Earthquake Research in China, 2013, 28(1): 57-67 DOI:10.3969/j.issn.1001-4683.2013.01.006)
(  0) 0) |
| [4] |
Barbour A J, Agnew D C. Detection of Seismic Signals Using Seismometers and Strainmeters[J]. Bulletin of the Seismological Society of America, 2012(6): 2484-2490
(  0) 0) |
| [5] |
Barbour A J, Crowell B W. Dynamic Strains for Earthquake Source Characterization[J]. Seismological Research Letters, 2017(2): 354-370
(  0) 0) |
| [6] |
Stockwell R G, Mansinha L, Lowe R P. Localization of the Complex Spectrum: The S Transform[J]. IEEE Transactions on Signal Processing, 1996(4): 998-1001
(  0) 0) |
| [7] |
刘刚, 聂兆生, 方荣新, 等. 高频GNSS形变波的震相识别:模拟实验与实例分析[J]. 地球物理学报, 2014, 57(9): 2813-2825 (Liu Gang, Nie Zhaosheng, Fang Rongxin, et al. Recognition of Seismic Phases Record by High-Rate GNSS Measurements: Simulation and Case Studies[J]. Chinese J Geophys, 2014, 57(9): 2813-2825)
(  0) 0) |
| [8] |
孟庆筱, 吕健, 李进武, 等. 基于S变换的唐山四分量钻孔应力时频特征分析[J]. 大地测量与地球动力学, 2018, 38(11): 1202-1206 (Meng Qingxiao, Lü Jian, Li Jinwu, et al. Analysis of Time-Frequency Characteristics of Four-Components Borehole Stress at Tangshan Station Based on S-Transform[J]. Journal of Geodesy and Geodynamics, 2018, 38(11): 1202-1206)
(  0) 0) |
| [9] |
邱泽华, 石耀霖, 欧阳祖熙. 四分量钻孔应变观测的实地相对标定[J]. 大地测量与地球动力学, 2005(1): 118-122 (Qiu Zehua, Shi Yaolin, Ouyang Zuxi. Relative in-Situ Calibration of 4-Component Borehole Strain Observation[J]. Journal of Geodesy and Geodynamics, 2005(1): 118-122)
(  0) 0) |
| [10] |
Evelyn R. Tidal Calibration of Plate Boundary Observatory Borehole Strainmeters: Roles of Vertical and Shear Coupling[J]. Journal of Geophysical Research, 2010, B6
(  0) 0) |
| [11] |
BarbourA J, Agnew D C, Wyatt F K. Coseismic Strains on Plate Boundary Observatory Borehole Strainmeters in Southern California[J]. Bulletin of the Seismological Society of America, 2015(1): 431-444
(  0) 0) |
| [12] |
Kennett B L N, Engdahl E R. Travel Times for Global Earthquake Location and Phase Identification[J]. Geophysical Journal of the Royal Astronomical, 1991(2): 429-465
(  0) 0) |
2. Wuhan Base of Institute of Crustal Dynamics, CEA, 40 Hongshance Road, Wuhan 430071, China
 2019, Vol. 39
2019, Vol. 39


