Burris型相对重力仪因其较小的零漂率、便捷的操作性,在勘探、地震、测绘等行业中获得广泛应用[1-3]。Burris型重力仪与LaCoaste重力仪内部弹簧同为金属材质,但由于其增加了蓝牙设备和自动读数系统(核心为电子反馈feedback系统),提高了观测的便利性。Burris型重力仪的自动读数系统使得仪器在大数盘值±25 mGal重力变化范围内无需调节测程即可完成观测,减小了人为操作引起的误差,提高了观测精度,也使得Burris型重力仪在一定程度上能够充当连续重力仪进行连续观测以获得潮汐变化。
多年的使用经验使我们对Burris型相对重力仪积累了一定的认识[4-5]。但近期的野外观测发现,使用Burris型重力仪进行相对重力观测时,当feedback系统中的FBK值超过一定值时,易出现连续2个测段中两端测点上的重力值变化不大、中间重力测点上的重力值变化超过0.1 mGal的现象(单点重力异常)。在多次出现该现象后初步判断,可能由于仪器中的feedback scale参数设置不当造成,在稍后的观测中验证了该判断,即FBK改正值和单点重力异常的出现相关。为认清Burris型重力仪中feedback系统对观测数据的影响,对3台Burris型重力仪feedback scale参数施加不同比例的变化,观察仪器读数与该参数的关系。并利用19层居民楼上不同高度处测点间的重力值差,详细分析研究Burris型重力仪的feedback scale参数对相对重力观测成果的影响。
1 Burris型重力仪反馈系统简介及稳定性检验Burris型重力仪的反馈系统与LaCoste & Romberg-ET型重力仪中的反馈系统原理相同[6-8]。不同的是,Burris型重力仪使用反馈系统后,不仅可以测量几十mGal的重力变化,还可以调节到大的测程,使其量程达到7 000 mGal。在使用中,首先要将Burris型重力仪大数盘调整到与测点处重力值最接近的50的倍数上,此后与该大数盘重力值相差±25 mGal测点上的重力值均可由反馈系统产生不同大小的反馈力测得,而无需再调节大数盘。Burris型重力仪反馈系统中feedback scale因子由人为校准设定,该参数值为系统参数,设定后恒定不变。测量过程中,每个测点上的FBK改正值则代表了反馈力,其大小依赖于该测点上的重力值与大数盘值的差。
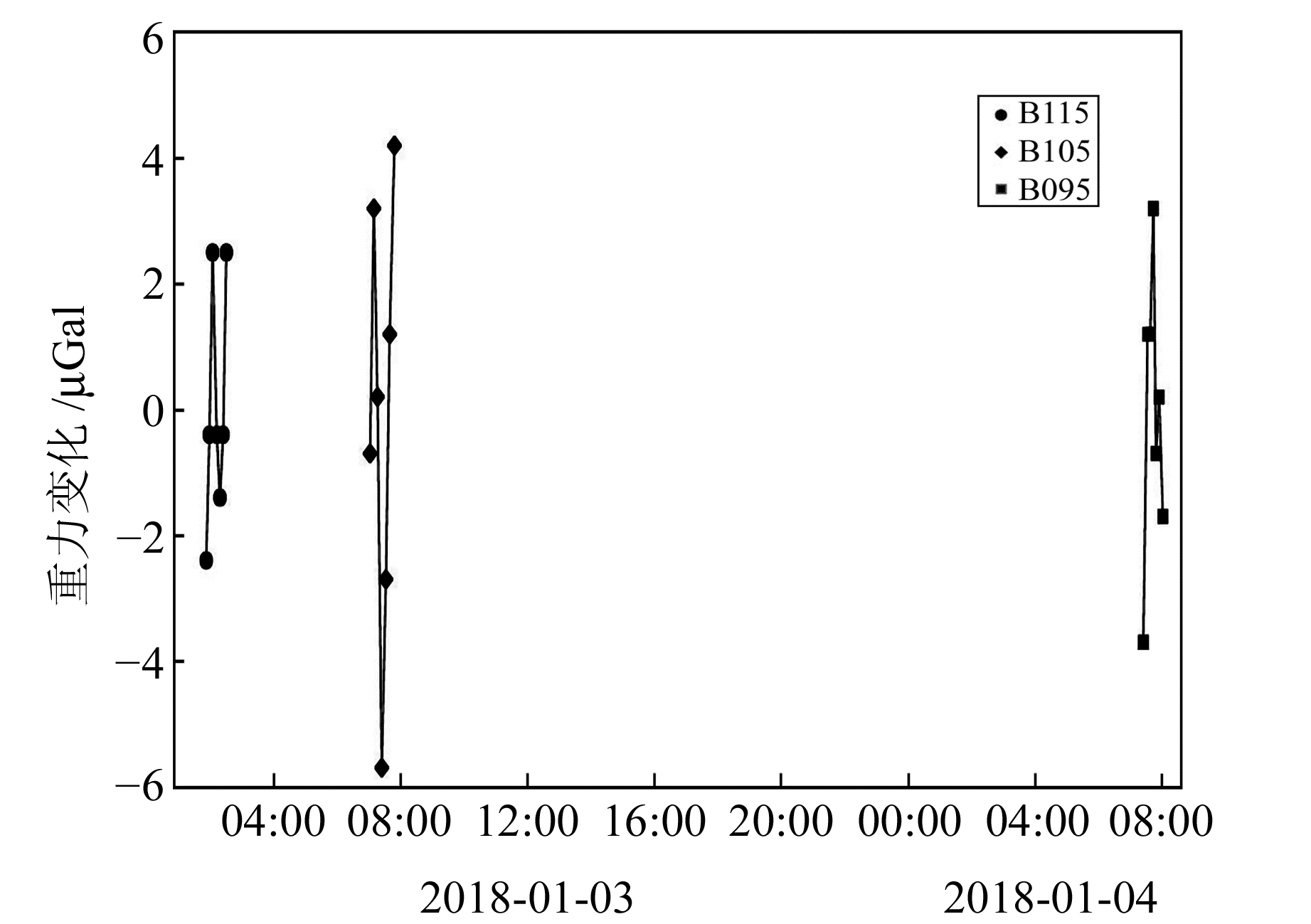
2 仪器稳定性检验本次实验均采用手提仪器进行短距离运输的方式。为了确保仪器测量数据的稳定性,首先在室内测点上对3台仪器进行多次下-上-下的往返重复测量。去除固体潮后,单个测点上的全部测量结果如图 1所示。可以看出,仪器读数变化不明显,在±6 μGal以内。表明在短距离短时间手提仪器情况下,仪器非常稳定,使用此方法一次下-上-下的往返测量即可得到可靠的结果。
|
图 1 3台Burris仪器的重复稳定性 Fig. 1 Repeatability and stability of 3 Burris gravimeters |
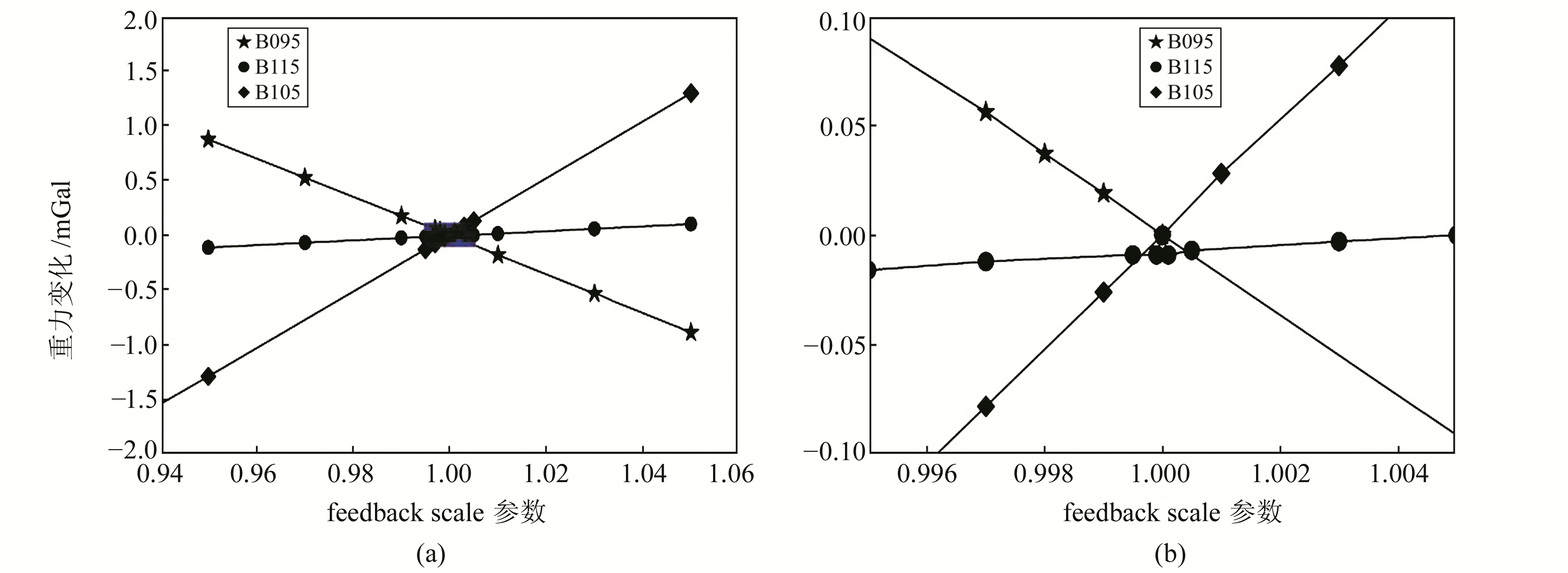
由于内部参数和弹簧状态不同,不同的Burris型相对重力仪在相同测点上反馈校正不同。2018-01-08三台Burris型重力仪B115、B105、B095反馈系统参数及在西安某测点(下称为西安测点)上的FBK改正值如表 1所示。可以看出,3台仪器的FBK改正值基本均匀分布在反馈调节范围±25 mGal内。以表 1显示的feedback scale为标准(1.00),对3台仪器的feedback scale因子给予不同比例的变化,短时间内在同一测点上的仪器读数随feedback scale因子的变化如图 2(图 2(b)为(a)局部放大图)所示。图 2表明,feedback scale因子值与Burris型重力仪读数线性相关,且斜率与FBK改正值有关。feedback scale变化比例相同时,FBK改正值越大,仪器读数的变化也越大。由此可以推断,feedback scale会明显影响相对重力测量成果,即重力段差的大小。3台仪器中,B105的FBK改正值接近±25 mGal,处于能使用的边界上,feedback scale因子变化0.1%时,仪器读数变化0.030 mGal。由此表明,在检调仪器参数时,feedback scale的改正系数小于1.001才能保证该参数的准确性。
|
|
表 1 3台Burris型重力仪在西安测点的反馈参数 Tab. 1 Feedback parameters of 3 Burris gravimeters at Xi'an site |
|
图 2 Feedback scale参数与仪器读数 Fig. 2 Parameter of feedback scale and gravimeter readings |
实验地点位于西安测点附近的19层(包含负一层)居民楼,距离西安测点小于100 m,使用上述3台Burris型相对重力仪乘坐电梯在顶、底楼层往返测量,得到重力段差。重力段差几乎全部由该地的重力垂直梯度引起,而该楼仅有19层,因此段差较小。在不同测点上的测量情况如表 2所示。由表 2可以看出,不同的feedback scale因子得到的段差差别最大可达0.140 mGal,远大于其他参数(如仪器一次项系数)产生的影响[9],更大于相对重力仪的标称测量精度。在本文的段差计算中,使用的仪器一次项系数均为1.000 000。即使一次项系数误差为0.001,因一次项系数不准确引起的误差也在0.017 mGal以内,在分析因feedback scale参数引起的巨大测量误差时可以忽略。
|
|
表 2 不同仪器在不同feedback scale参数下的段差成果 Tab. 2 Gravity difference of 3 Burris gravimeters on different parameters of feedback scale |
表 2表明,3台仪器的feedback scale参数的变化量基本相同(B095增加0.47%,相比于B115增加0.5%),段差变化却相差较大(B095变化0.140 mGal,相比于B115变化0.075 mGal),其原因应与FBK值有关。图 2表明,在feedback scale参数变化时,FBK改正值决定仪器读数变化的方向:FBK改正值为正,随着feedback scale参数变大,仪器读数也相应变大;而FBK改正值为负,随着feedback scale参数变大,仪器读数减小。而B095和B115的FBK改正值符号相反,从而导致上述情况。由此可以推断,若仪器在2个点上的FBK改正值绝对值均接近25、符号相反,则此时即使较小的feedback scale参数变化也会引起2个测点间的重力段差值的巨大变化。
值得注意的是,B105使用1.000 0的feedback scale因子在较低测点(位于居民楼负一层)测量时,FBK值处于能使用的反馈力边界上。使用不同的测程进行读数时,2个测程的读数结果相差0.100 mGal。而使用检调后的feedback scale因子进行测量时,2个测程的读数结果仅相差0.030 mGal。由此表明,当FBK改正值处于能使用的反馈力边界上时,使用准确的feedback scale因子在同一个测点2个测程上进行测量,得到的仪器读数应该基本相等。
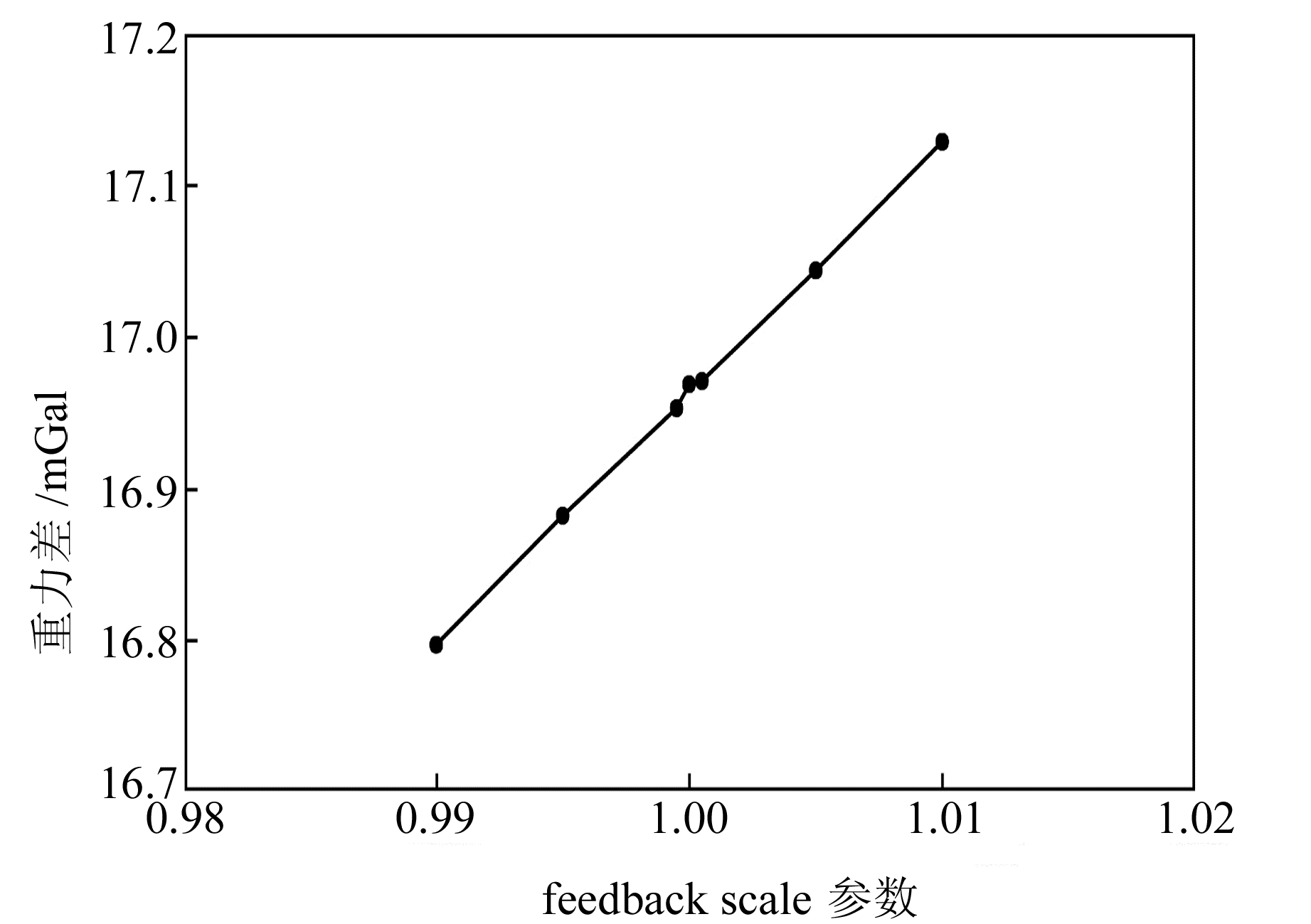
因目前多台仪器正在野外观测中,使用B115仪器测试正在变化中的feedback scale因子下得到的重力段差,以更加清晰地显示出不同的feedback scale因子对测量段差成果的影响,结果如图 3所示。图 3表明,在2个测点上,虽然FBK改正值还远未达到测程调节范围的临界(即FBK值并不接近±25 mGal),但是当feedback scale变化2%时,测量所得段差变化却超过0.300 mGal,与feedback scale因子仅在FBK值接近±25 mGal时对仪器读数影响才较为明显的经验认识有显著不同。
|
图 3 不同feedback scale参数下B115测量得到的段差 Fig. 3 Gravity difference between 2 sites with Burris B115 on different parameters of feedback scale |
本文实验表明,在仪器内部其他参数相同时,Burris型相对重力仪的仪器读数与feedback scale因子线性相关,斜率由FBK改正值决定。而同样的feedback scale变化量,FBK改正值越大,仪器读数的变化量越大。同时,等量的feedback scale变化下,FBK改正值差别越大,重力段差的变化量也越大。因此在不同feedback scale参数下,Burris型相对重力仪的仪器读数和重力段差不同,且差别明显,表明feedback scale参数严重影响相对重力测量成果。因此,在相对重力测量前,对feedback scale参数的检调尤其重要。
在形成连续2个测段的3个测点上,若Burris型重力仪在中间测点上读数,FBK改正值的绝对值较大或接近25 mGal; 而在两端测点上读数时, 2个测点上的FBK改正值基本相等。在上述3个测点上观测时,若feedback scale因子不准确,根据本文实验结果,在中间测点上得到的仪器读数偏差较大,从而出现中间测点上的重力值与往年该点上的重力值变化巨大、两端测点上的重力值变化却不大的单点重力异常现象。因此,在使用Burris型相对重力仪进行测量时,若单点重力值出现较大变化、而紧邻测点上的重力值变化却不明显时,需要注意feedback scale因子的影响,此时需要检调feedback scale是否正确。
根据本文实验,在同一个测点上,当FBK改正值接近±25 mGal时,使用准确的feedback scale参数,变更仪器大盘值,仪器在不同的大盘值上通过调整FBK得到的读数应该相等或相近。因此,在同一个测点使用不同大盘值得到的读数是否相等或相近,可以作为检测该参数是否准确的一种方法。
| [1] |
王西文. 用重力、地震资料联合反演直接预测油气藏的方法[J]. 石油地球物理勘探, 1997, 32(2): 221-228 (Wang Xiwen. Direct Hydocarbon Prediction Using Joint Inversion of Gravimetric and Seismic Data[J]. Oil Geophysics Prospecting, 1997, 32(2): 221-228)
(  0) 0) |
| [2] |
Zhu Y Q, Zhan F B, Zhou J C, et al. Gravity Measurements and Their Variations before the 2008 Wenchuan Earthquake[J]. Bull Seis Soc Am, 2010, 100(5B): 2815-2824 DOI:10.1785/0120100081
(  0) 0) |
| [3] |
周江存, 徐建桥, 孙和平.中国大陆精密重力潮汐改正模型[C].中国测绘学会第9次全国会员代表大会暨学会成立50周年纪念大会, 北京, 2009 (Zhou Jiangcun, Xu Jianqiao, Sun Heping. Accurate Correction Models for Tidal Gravity in Chinese Continent[C]. The 9th National Congress of the Surveying and Mapping Society of China and the 50th Anniversary of the Founding of the Society, Beijing, 2009) http://www.cnki.com.cn/Article/CJFDTotal-DQWX200906009.htm
(  0) 0) |
| [4] |
赵云峰, 祝意青, 梁伟锋, 等. Burris型重力仪性能分析[J]. 地震地磁观测与研究, 2018, 39(2): 178-185 (Zhao Yunfeng, Zhu Yiqing, Liang Weifeng, et al. Study on the Characteristics of Burris Gravimeter[J]. Seismological and Geomagnetic Observation and Research, 2018, 39(2): 178-185 DOI:10.3969/j.issn.1003-3246.2018.02.026)
(  0) 0) |
| [5] |
赵云峰, 隗寿春, 梁伟锋, 等. Burris型重力仪温度特性研究[J]. 大地测量与地球动力学, 2018, 38(8): 877-880 (Zhao Yunfeng, Wei Shouchun, Liang Weifeng, et al. Temperature Characteristics of Burris Relative Gravimeter[J]. Journey of Geodesy and Geodynamics, 2018, 38(8): 877-880)
(  0) 0) |
| [6] |
Valliant H D, Gagnon C, Halfpenny J F. An Inherently Linear Electrostatic Feedback Method for Gravity Meters[J]. J Geophys Res, 1986, 91(B10): 10463-10469 DOI:10.1029/JB091iB10p10463
(  0) 0) |
| [7] |
Jentzsch G, Schulz R, Weis A. Automated Burris Gravity Meter for Single and Continuous Observation[J]. Geodesy and Geodynamics, 2018, 9(3): 204-209 DOI:10.1016/j.geog.2017.09.007
(  0) 0) |
| [8] |
Hugill A L, Valliant H D. Limitations to the Application of Electrostatic Feedback in Gravity Meters[J]. Journal of Geophysical Research: Solid Earth, 1986, 91(B8): 8387-8392 DOI:10.1029/JB091iB08p08387
(  0) 0) |
| [9] |
梁伟锋, 刘芳, 祝意青, 等. 重力仪一次项系数对重力场动态变化的影响研究[J]. 大地测量与地球动力学, 2015, 35(5): 882-88 (Liang Weifeng, Liu Fang, Zhu Yiqing, et al. Research on the Effect of One Degree Term of Chromatic Polynomial of Gravimeter on Gravity Dynamic Change[J]. Journal of Geodesy and Geodynamics, 2015, 35(5): 882-88)
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39

