地基GPS技术是反演大气可降水量的一种常用的、有效的技术手段,可全天候、近实时地提供高时空分辨率的水汽信息,且监测成本低。利用地基GPS技术获取的高精度可降水量(PWV)对预报天气具有重要意义。Braun等[1]利用GPS和水汽辐射计进行对比,验证了GPS探测PWV的可行性。张双成等[2]在深入分析影响地基GPS探测水汽精度的因素后,建立了一种实时地基GPS遥感水汽系统。范士杰等[3]基于非差精密单点定位技术,采用GPT2模型来反演大气可降水量,与测站实测的气象数据相比,GPT2模型数据仍可反演得到较为理想的PWV结果,其精度(RMS)优于±1.5 mm。由可降水量反演原理知,可降水量的精度不仅取决于天顶对流层湿延迟,还取决于加权平均温度。Bevis经验公式法是计算加权平均温度的常用方法,简单方便,但存在区域性差异且依赖于测站实测的地表温度。GPT2w模型是目前精度最高的气象模型,提供了全球加权平均温度的经验值[4]。鉴于Bevis经验公式的不足,本文基于GPT2w模型化加权平均温度反演大气可降水量,并分析模型化加权平均温度的系统偏差对大气可降水量的影响。
1 数据来源目前,GPS在GNSS家族当中应用最广,定位精度最高。为得到良好的实验效果,本文选用数据完整性较好的GPS数据进行实验。选取位于中国境内的5个IGS站(CHAN、BJFS、SHAO、WUHN、KUNM)2013-01和2013-08的观测数据。由于获取的观测数据是多系统混合数据,使用前需对其进行预处理,即过滤掉非GPS观测数据。相应地,选择距离IGS站最近的探空站,以便于获取与IGS站相近的气象资料,并以探空站探测的PWV为参考值,对基于IGS站反演的PWV进行精度检验。无线电探空站具体信息见表 1。美国怀俄明州立大学官网提供了无线电探空资料,下载地址为http://weather.uwyo.edu/upperair/sounding.html。探空站向用户提供每天00:00和12:00(UTC)的探空资料,数据较为丰富。GGOS Atmosphere以2°×2.5°的分辨率提供全球IGS站每天00:00、06:00、12:00和18:00(UTC)的各气象元素的格网数据(http://ggosatm.hg.tuwien.ac.at/DELAY/SITE/),这些格网数据是基于ECMWF的ERA-40再分析资料计算得到的,数据可靠且具有完备性,其提供的温度格网数据可用于计算加权平均温度。
|
|
表 1 参与PWV精度检验的无线电探空站信息 Tab. 1 Information list of radiosonde stations for PWV test |
利用GPS技术探测水汽时,首先选用合适的GPS数据处理软件对GPS数据进行解算,获取对流层天顶总延迟;然后再利用对流层延迟模型(如Saastamoinen模型[5])计算出天顶静力学延迟(即干延迟),将其从天顶总延迟中减去,从而得到与水汽相关的天顶湿延迟;最后利用天顶湿延迟与大气可降水量之间的转换关系(式(1))计算得到大气可降水量:
| $ \mathrm{PWV}=\mathit{\Pi} \cdot \mathrm{ZWD} $ | (1) |
| $ \mathit{\Pi}=\frac{10^{6}}{\rho_{w} R_{v}\left[\left(k_{3} / T_{m}\right)+k_{2}^{\prime}\right]} $ | (2) |
式中,PWV为大气可降水量;ZWD为天顶湿延迟;Π为PWV转换系数,是一个无量纲比例因子;ρw为液态水密度;Rv=461.495 J/(kg ·K)为水汽特定的气体常数;k3=3.739×105 K2/hPa为大气折射常数;Tm为加权平均温度;k′2=k2-(Mw/Md)k1,其中k1=77.689 0 K/hPa、k2=71.295 2 K/hPa均为大气折射常数,Mw=18.015 2 g/mol为湿大气的摩尔质量,Md=28.964 4 g/mol为干大气的摩尔质量。
2.2 加权平均温度的计算通常采用基于统计方法构建的Bevis经验公式(Tm=70.2+0.72 Ts)计算加权平均温度。该经验公式是Bevis等[6]采用美国13个探空站2 a的探空数据建立的,实现了由探空气象资料到地面气象资料的转变,利用起来简单方便。然而Bevis经验公式是一个更适用于中纬度地区的公式,存在区域性差异,由此转换得到的PWV也必定存在区域性差异。
GPT2w模型是GPT系列中的最新模型,且精度最高,其模型表达式见式(3)。对于GPT2w模型,只需要提供测站大地坐标(B, L, H)和年积日(doy)即可输出加权平均温度:
| $ \begin{array}{c}{a=a_{0}+A_{1} \cos \left(\frac{\operatorname{doy}}{365.25} 2 \pi\right)+B_{1} \cos \left(\frac{\operatorname{doy}}{365.25} 2 \pi\right)+} \\ {A_{2} \cos \left(\frac{\operatorname{doy}}{365.25} 4 \pi\right)+B_{2} \cos \left(\frac{\operatorname{doy}}{365.25} 4 \pi\right)}\end{array} $ | (3) |
式中,a为格网点的气压、温度等参数值,a0为均值,A1、B1为年周期振幅,A2、B2为半年周期振幅,这些参数需结合外部格网文件gpt2_1w.grd和测站大地坐标,采用双线性内插法得到。
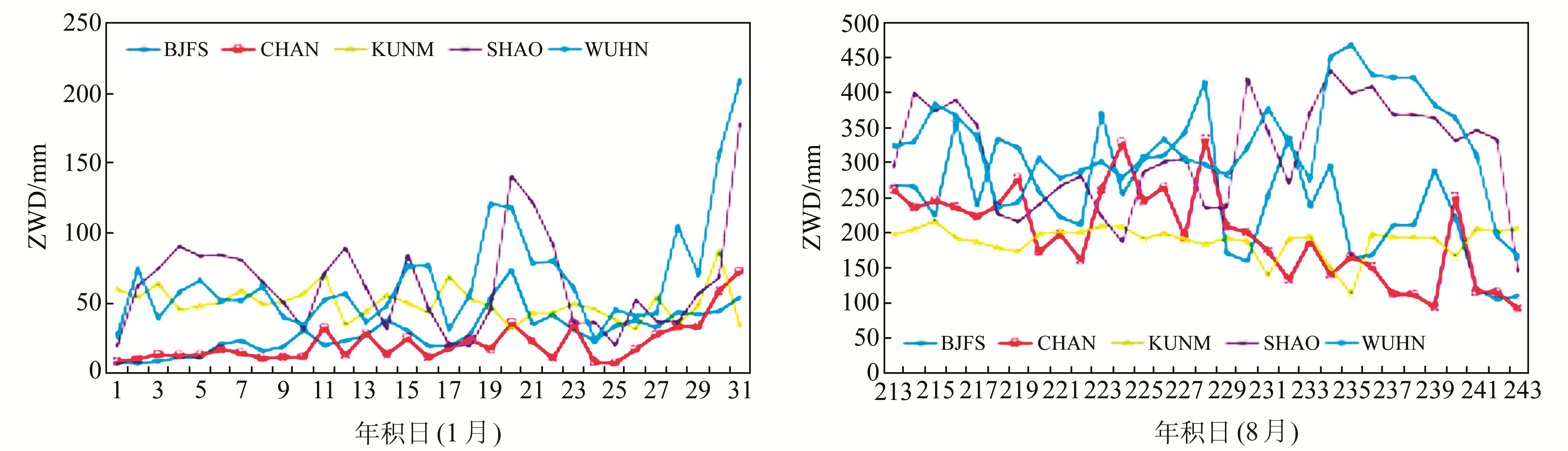
3 实验分析 3.1 基于GPT2w模型化加权平均温度反演可降水量利用GNSSer数据处理软件[7]分别对5个IGS站2013-01和2013-08的数据进行处理。与常用软件不同的是,GNSSer软件采用模型法计算ZHD,采用参数估计法对ZWD逐历元估计,ZWD的估计结果如图 1所示。在1月份,我国正值冬季,空气相对干燥,水汽活跃度不够高,故ZWD的值整体较小,基本上在100 mm以下;在8月份,我国正值夏季,降水量大,水汽活跃度较高,故ZWD值整体较大,均在100 mm以上,最大值接近500 mm。
|
图 1 各个IGS站的ZWD Fig. 1 ZWD at different IGS stations |
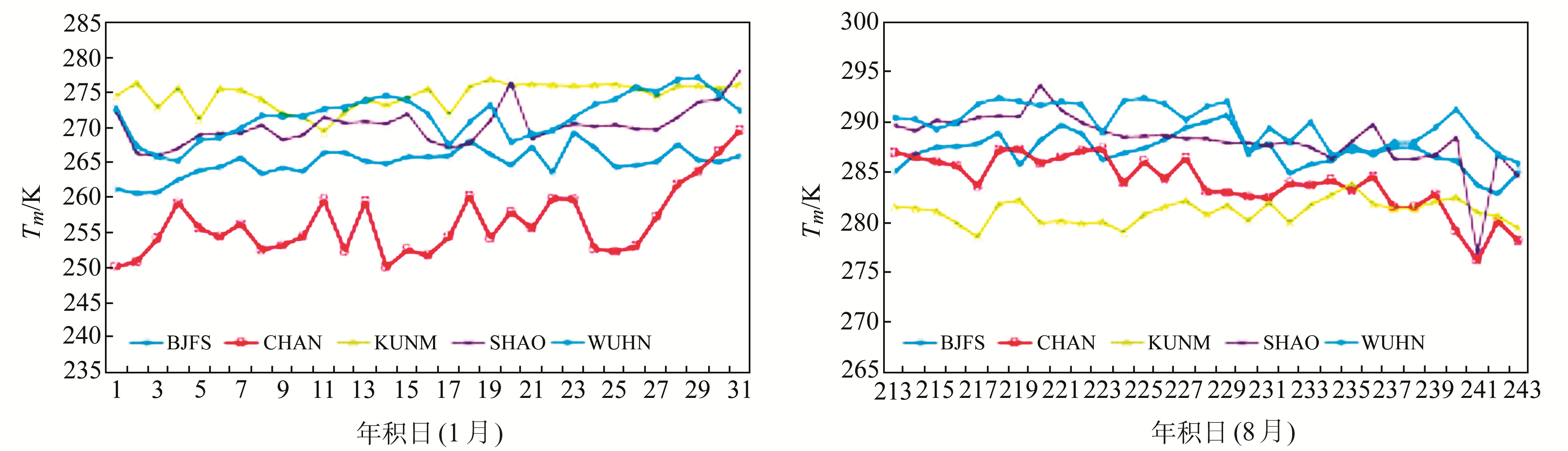
利用GPT2w模型获取5个IGS站的模型化加权平均温度(记作GPT2w_Tm),结果如图 2所示。同时,利用Bevis公式计算5个IGS站的加权平均温度(记作Bevis_Tm),由于无法获取实测的地表温度,故采用GGOS Atmosphere提供的温度格网数据来替代,结果如图 3所示。由图 2可知,在1月份,各个IGS站的GPT2w_Tm变化很小,一个月内的值呈一条直线,而且随着IGS站纬度的递减,GPT2w_Tm的值依次递增。其中,位于同一纬度线附近的WUHN站和SHAO站的GPT2w_Tm值非常接近。在8月份,BJFS站和CHAN站的GPT2w_Tm值发生明显变化,即随着年积日的递增,GPT2w_Tm值递减。其他站的GPT2w_Tm值随着年积日的递增没有发生明显变化,而且与IGS站纬度的关系也不复存在。由图 3可知,各个站的Bevis_Tm在一个月内的变化非常显著,这是由于GGOS Atmosphere提供的温度格网数据接近测站实际温度,可以反映出测站温度较为真实的月变化情况,但整体上来看,Bevis_Tm在1月和8月均和GPT2w_Tm有着相似的特征和变化趋势。

|
图 2 GPT2w模型化加权平均温度 Fig. 2 Weighted mean temperature derived from GPT2w at different IGS stations |
|
图 3 Bevis公式计算的加权平均温度 Fig. 3 Weighted mean temperature calculated by Bevis formula at different IGS stations |
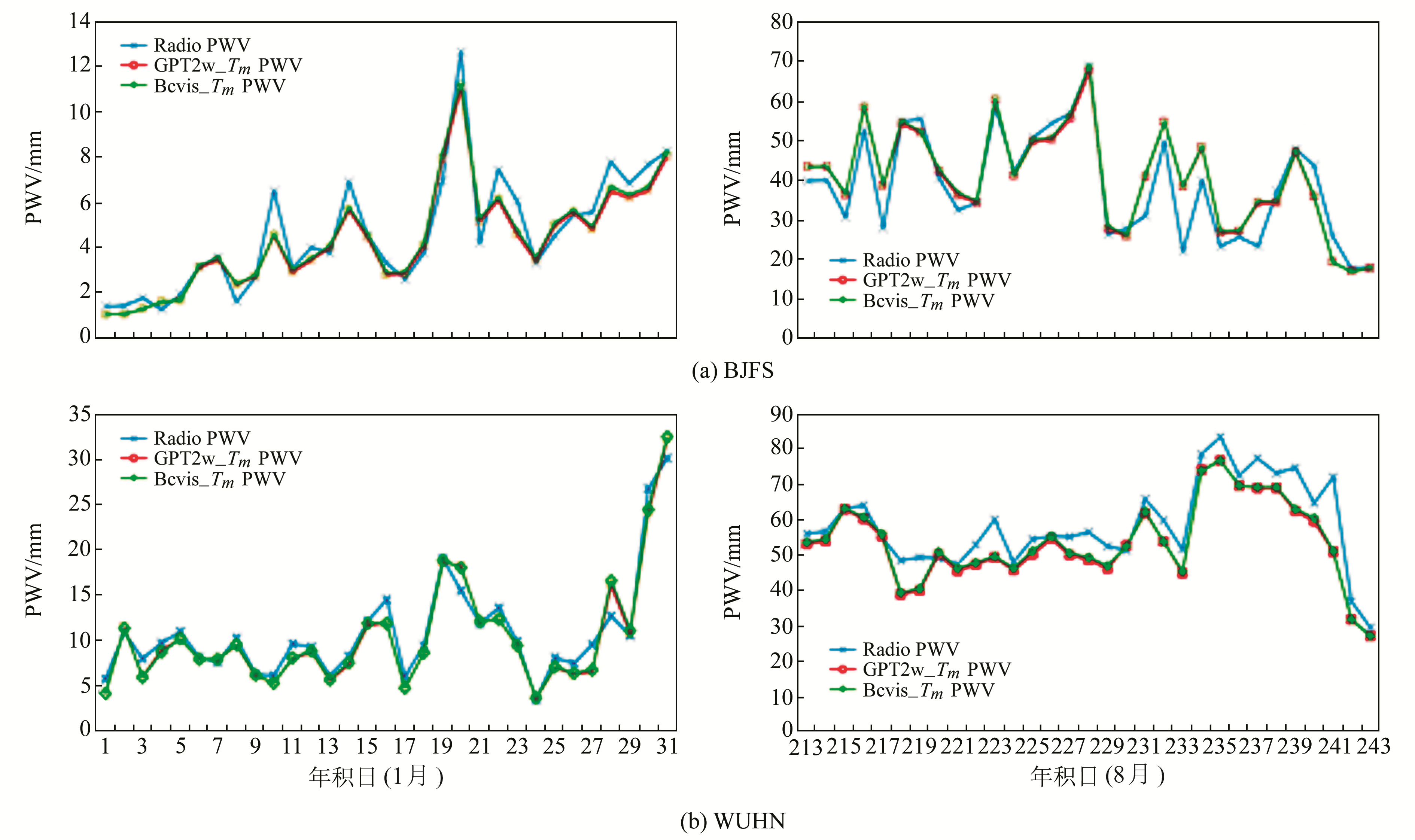
分别采用GPT2w_Tm和Bevis_Tm计算出相应的PWV转换系数,结合经参数估计得到的ZWD反演出PWV,同探空资料提供的PWV进行比对。以BJFS站和WUHN站为例,结果见图 4。图中,Radio/PWV表示由探空资料提供的PWV,GPT2w_Tm/PWV和Bevis_Tm/PWV分别表示基于GPT2w_Tm和Bevis_Tm计算的PWV。由图可见,基于GPT2w_Tm和Bevis_Tm计算的PWV与探空资料提供的PWV具有很高的吻合性,尤其是在1月空气水汽含量较少的情况下,PWV偏差不足1 mm。还可以看出,基于GPT2w_Tm和Bevis_Tm反演的PWV曲线几乎重叠,可见二者偏差极小。表 2(单位mm)和表 3(单位mm)分别给出1月和8月各站PWV的bias和RMS。从表中可以看出,不论是1月还是8月,基于GPT2w_Tm和Bevis_Tm计算的PWV bias和RMS均比较接近。在1月,两者的PWV bias绝对值均不超过1 mm,PWV RMS最大值出现在KUNM站,但不超过2 mm;在8月,两者的PWV bias绝对值较1月偏大,最大值超过5 mm。同样,PWV RMS也较1月偏大,最大值出现在WUHN站,超过6 mm。由此可见,冬季PWV的精度高于夏季,但基于GPT2w_Tm和Bevis_Tm计算的PWV的精度相似性受季节影响不大。
|
图 4 BJFS站和WUHN站可降水量 Fig. 4 PWV at BJFS and WUHN stations |
|
|
表 2 1月各站PWV的bias和RMS Tab. 2 Bias and RMS of PWV in January |
|
|
表 3 8月各站PWV的bias和RMS Tab. 3 Bias and RMS of PWV in August |
综合上述分析发现,地基GPS与探空资料提供的PWV具有很高的吻合性。由于GPS站与探空站不是并址站,而且探空气球在释放后的偏移距离会随着高度升高而逐渐加大,因此,地基GPS反演的PWV与探空资料提供的PWV会存在一定的偏差。Bevis公式依赖于测站实测的地表温度,在附近没有配备气象观测设备的测站处其应用将受到限制,因此Bevis公式不具有普遍适用性。由表 2和表 3可知,GPT2w_Tm/PWV与Bevis_Tm/PWV精度相当,这也间接表明GPT2w_Tm和Bevis_Tm精度相当。而对于GPT2w模型,只需提供测站大地坐标(B, L, H)和年积日(doy)即可获取加权平均温度。故在无法获取测站实测的地表温度时,可采用GPT2w_Tm替代Bevis_Tm。
3.2 附加改正的模型化加权平均温度对可降水量的影响分析滑中豪等[8]检验GPT2w模型化加权平均温度的精度发现,其存在-2.56 K的系统偏差,而这一系统偏差对反演PWV的影响尚不清楚。为此,下文对模型化的加权平均温度进行系统偏差改正,分析这一系统偏差对反演PWV的影响。
利用GPT2w_Tm计算PWV转换系数时,在GPT2w_Tm值上加上系统偏差改正值2.56 K。将新的PWV计算结果与探空资料提供的PWV进行比对,然后对不加改正和附加改正情况下的PWV偏差进行统计分析,结果如表 4(单位mm)和表 5(单位mm)所示。由表 4可见,对于BJFS站、CHAN站和WUHN站,附加改正后PWV的bias和RMS较不加改正的结果均有所改善,但改善效果并不显著,bias提高不到0.1 mm,RMS提高0.01 mm;对于KUNM站和SHAO站,RMS变化很小,bias反而较改正前偏大。由表 5可见,8月份附加改正后PWV的bias和RMS改善程度较1月份略好,其中WUHN站bias和RMS均得到最大改善,分别改善0.5 mm和0.35 mm。
|
|
表 4 1月各站PWV的bias和RMS Tab. 4 Bias and RMS of PWV in January |
|
|
表 5 8月各站PWV的bias和RMS Tab. 5 Bias and RMS of PWV in August |
为了进一步说明附加改正后加权平均温度的精度变化对PWV的影响,分别计算附加改正后1月和8月各站PWV的改善率,如表 6所示。由表可见,1月和8月各站PWV的改善率均不超过1%,而且各站在8月的改善率均低于1月,这可能与夏季空气中水汽含量和活跃度有关。
|
|
表 6 各站附加改正后PWV的改善率 Tab. 6 Improvement rate of PWV with systematic correction |
综合上述分析得出,对加权平均温度进行系统偏差改正后,PWV的精度有一定的改善,在8月份的改善程度略好于1月份;就PWV改善率而言,8月份的改善率不如1月份。整体而言,加权平均温度的系统偏差对反演PWV的影响甚微,可以忽略不计。
4 结语本文对PWV的反演原理和加权平均温度的计算方法作了简单介绍,提出一种基于GPT2w模型化加权平均温度反演PWV的方法,得出以下结论:
1) 在中国地区,基于GPT2w模型化加权平均温度反演的PWV精度与基于Bevis经验公式计算的加权平均温度反演的PWV精度相当,在无法获取测站实测地表温度的情况下,可以利用GPT2w模型化加权平均温度来反演PWV。
2) 对GPT2w模型化加权平均温度进行系统偏差改正后,反演的PWV精度有一定改善,但改善率不到1%,可以忽略。
| [1] |
Braun J J, Rocken C. Water Vapor Tomography within the Planetary Boundary Layer Using GPS[C]. International Workshop on GPS Meteorology, Tsukyba, 2003
(  0) 0) |
| [2] |
张双成, 刘经南, 叶世榕, 等. 顾及双差残差反演GPS信号方向的斜路径水汽含量[J]. 武汉大学学报:信息科学版, 2009, 34(1): 100-104 (Zhang Shuangcheng, Liu Jingnan, Ye Shirong, et al. Retrieval of Water Vapor along the GPS Slant Path Based on Double-Differenced Residuals[J]. Geomatics and Information Science of Wuhan University, 2009, 34(1): 100-104)
(  0) 0) |
| [3] |
范士杰, 臧建飞, 刘焱雄, 等. GPT/2模型用于GPS大气可降水量反演的精度分析[J]. 测绘工程, 2016, 25(3): 1-5 (Fan Shijie, Zang Jianfei, Liu Yanxiong, et al. Accuracy Analysis on GPS Precipitable Water Vapor Inversion Using GPT/2 Models[J]. Engineering of Surveying and Mapping, 2016, 25(3): 1-5 DOI:10.3969/j.issn.1006-7949.2016.03.001)
(  0) 0) |
| [4] |
Böhm J, Möller G, Schindelegger M, et al. Development of an Improved Empirical Model for Slant Delays in the Troposphere(GPT2w)[J]. GPS Solutions, 2015, 19(3): 433-441 DOI:10.1007/s10291-014-0403-7
(  0) 0) |
| [5] |
Saastamoinen J. Contribution to the Theory of Atmospheric Refraction PartⅡ, Refraction Corrections in Satellite Geodesy[J]. Bulletin Geodesique, 1972, 107: 13-34
(  0) 0) |
| [6] |
Bevis M, Businger S, Herring T A, et al. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System[J]. Journal of Geophysical Research, 1992, 97(D14): 15 787-15 801 DOI:10.1029/92JD01517
(  0) 0) |
| [7] |
陈正生.大规模GNSS测量数据分布式计算关键技术研究[D].郑州: 信息工程大学, 2014 (Chen Zhengsheng. Research on the Key Techniques of Distributed Processing on Large Scale GNSS Observation Data[D]. Zhengzhou: Information Engineering University, 2014)
(  0) 0) |
| [8] |
滑中豪, 柳林涛, 梁星辉. GPT2w模型检验以及对流层模型的参数互融[J]. 武汉大学学报:信息科学版, 2017, 42(10): 1 468-1 473 (Hua Zhonghao, Liu Lintao, Liang Xinghui. An Assessment of GPT2w Model and Fusion of a Troposphere Model with in Situ Data[J]. Geomatics and Information Science of Wuhan University, 2017, 42(10): 1 468-1 473)
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39

