利用地基GPS接收机获得的原始观测值可以探测大气水汽含量[1],该方法提出后,出现了大量关于GPS在气象学领域应用的研究[2]。大量研究表明,不管是事后处理还是实时处理模式,利用GPS观测值估计得到的大气水汽含量值和气象传感器观测结果精度相当。如今,用GPS观测值估计得到的天顶对流层延迟(zenith troposphere delay, ZTD)和可降水量(precipitable water vapor, PWV)是气象学应用中重要的组成部分,数以千计的GPS测站实时不间断地解算对流层结果并提供给数值天气预测(numerical weather prediction, NWP)模型。
对流层延迟大多数由大气中的干燥气体引起,称为干分量;其余较少部分是由水汽引起的,称为湿分量。干分量延迟比较稳定,一般可以通过改正模型精确获得,而湿分量延迟改正精度不高,一般通过参数估计方式获得。一旦湿分量延迟精确获得,便可进一步确定可降水量[3],具体公式可参照文献[2, 4]。GNSS对流层延迟估计策略主要有精密单点定位法[5](precise point positioning, PPP)和双差网解法两种。两种方法估计得到的对流层延迟精度相当,但是双差网解法需要长基线(一般大于500 km)来减小空间相关性以获得绝对的对流层延迟量。而精密单点定位法则不需要和其他测站联测,即可获得对流层的绝对延迟量。
随着GLONASS现代化和新兴的Galileo、北斗卫星导航系统(BDS)快速发展,多模GNSS相对于单系统拥有更优良的服务性能和研究价值。文献[6]在分析BDS单系统实时ZTD估计性能后指出,BDS解和GPS解有很高的一致性,且BDS/GPS组合估计得到的ZTD精度要略高于GPS单系统解。之后,他们以同样的方式对GLONASS进行了分析[7]。文献[8]比较GPS、GLONASS、BDS和四系统联合实时ZTD解算发现,四系统联合解算时实时ZTD精度更高,异常值出现的频次大幅度降低。文献[9]也对GPS、GLONASS和Galileo联合实时ZTD解算进行详细分析。由于之前Galileo在轨卫星数较少,以上研究均没有对单独Galileo实时ZTD解算性能进行分析。作为多模GNSS的重要组成部分,近两年来Galileo卫星导航系统快速发展,截止到2018年初,Galileo已有22颗在轨工作卫星,其中包括4颗在轨验证(in-orbit validation, IOV)卫星和18颗完全工作能力(full operate capacity, FOC)卫星,Galileo已经可以实现单独实时ZTD估计,所以Galileo系统实时ZTD估计性能需要进行详细分析。本文采用PPP技术,以GPS作对比,详细分析Galileo实时ZTD估计性能,建立并分析GPS/Galileo组合实时ZTD估计的处理方法。
1 PPP观测方程和处理策略一般情况下,PPP使用双频载波相位和伪距观测值的无电离层组合来消除电离层一阶影响。观测方程可以表示为:
| $ \begin{array}{l}{L=\rho+c\left(\mathrm{d} t_{r}-\mathrm{d} t_{s}\right)+T+B+\varepsilon_{L}} \\ {P=\rho+c\left(\mathrm{d} t_{r}-\mathrm{d} t_{s}\right)+T+\varepsilon_{P}}\end{array} $ | (1) |
式中,L和P分别代表载波相位和伪距观测值的无电离层组合,ρ是卫星到测站的几何距离,c是真空中的光速,dtr和dts分别是接收机和卫星钟差,T表示对流层延迟量,B为模糊度参数,εL和εP分别是载波相位和伪距观测值的测量噪声和多路径影响等。如前文所述,对流层延迟可分为干分量延迟和湿分量延迟,每个分量皆可用天顶方向延迟、梯度和投影函数来表达:
| $ \begin{array}{c}{T=m f_{\mathrm{h}} Z_{\mathrm{h}}+m f_{\mathrm{w}} Z_{\mathrm{w}}+} \\ {m f_{\mathrm{w}} \cot e \cdot\left(G_{\mathrm{N}} \cos a+G_{\mathrm{E}} \sin a\right)}\end{array} $ | (2) |
式中,Zh和Zw表示天顶方向的干分量延迟和湿分量延迟,mfh和mfw代表湿分量延迟和干分量延迟的投影函数,GN和GE为水平面北方向和东方向的梯度,e和a分别为卫星高度角和方位角。当GPS/Galileo组合PPP时,需考虑接收机系统间偏差(internal-system biases, ISB),则式(1)可以表示为:
| $ \left\{\begin{array}{l}{L^{\mathrm{G}}=\rho^{\mathrm{G}}+c\left(\mathrm{d} t_{r}-\mathrm{d} t_{\mathrm{s}}^{\mathrm{G}}\right)+T^{\mathrm{G}}+B^{\mathrm{G}}+\varepsilon_{L}^{\mathrm{G}}} \\ {L^{\mathrm{E}}=\rho^{\mathrm{E}}+c\left(\mathrm{d} t_{r}-\mathrm{d} t_{s}^{\mathrm{E}}\right)+\mathrm{ISB}_{L}^{\mathrm{E}-\mathrm{G}}+T^{\mathrm{E}}+B^{\mathrm{E}}+\varepsilon_{L}^{\mathrm{E}}}\end{array}\right. $ | (3) |
| $ \left\{\begin{array}{l}{P^{\mathrm{G}}=\rho^{\mathrm{G}}+c\left(\mathrm{d} t_{r}-\mathrm{d} t_{s}^{\mathrm{G}}\right)+T^{\mathrm{G}}+\varepsilon_{P}^{\mathrm{G}}} \\ {P^{\mathrm{E}}=\rho^{\mathrm{E}}+c\left(\mathrm{d} t_{r}-\mathrm{d} t_{s}^{\mathrm{E}}\right)+\mathrm{ISB}_{P}^{\mathrm{E}-\mathrm{G}}+T^{\mathrm{E}}+\varepsilon_{P}^{\mathrm{E}}}\end{array}\right. $ | (4) |
式中,上标G和上标E分别代表GPS和Galileo,码系统间偏差ISBPE-G在连续观测弧段内被认为是稳定不变的,当作常数估计;载波相位系统间偏差ISBLE-G可以被模糊度参数吸收,模糊度参数在连续弧段内被当作常数估计。天顶干延迟分量Zh用Saastamoinen模型改正[10],投影函数选择GMF(global mapping functions)投影模型[11]。湿延迟分量Zw每5 min估计一次,北方向和东方向的对流层梯度GN和GE每2 h估计一次,Zw、GN和GE均采用随机游走过程模拟,动态噪声谱密度为2 cm/
|
|
表 1 GPS和Galileo PPP实时ZTD估计策略 Tab. 1 Real-time ZTD estimation strategies of PPP for GPS and Galileo |
本文选择14个MGEX(multi-GNSS experiment)测站(ALIC、BRUN、CUUT、DAE2、DARW、GMSD、HKWS、HOB2、KARR、MCHL、TSK2、WARK、ULAB、XMIS)的观测数据,时间为2017-10-31~12-04,测站均能同时接收GPS和Galileo信号。
PPP性能很大程度上取决于轨道和钟差产品的精度。本文所采用的精密预报轨道产品是利用事后精密轨道,通过轨道动力学积分得到。文献[12]利用42~45 h的观测轨道拟合弧段得到更高性能的预报轨道。本文采用45 h的观测拟合轨道弧长,观测拟合轨道选择武汉大学提供的事后精密轨道(ftp://igs.gnsswhu.cn/);预报轨道采用IGS超快速产品发布的EOP预报值,预报轨道时长为6 h。钟差部分选择武汉大学GNSS中心提供的实时钟差,实时轨道和钟差产品的精度可参照文献[13]。本文基于实时轨道和钟差产品进行事后仿实时解算ZTD。
3 实验结果 3.1 GPS、Galileo、GPS/Galileo解算结果对比为了验证Galileo实时ZTD估计性能,本文分别采用GPS(G)、Galileo(E)和GPS/Galileo(GE)组合3种ZTD实时估计方法计算得到14个MGEX测站的ZTD估值。图 1表示3种实时估计方法得到的2个测站的ZTD的相互差值,由图可见,无论是E-G、G-GE还是E-GE,其ZTD差值都在“0”值附近波动,且均没有出现粗差或异常值;各散点图的振幅情况为:E-G最大,E-GE次之,G-GE最小。这说明,GPS解和GPS/Galileo组合解的符合性最好,GPS在GPS/Galileo组合解算中的贡献优于Galileo,原因可能一是Galileo信号噪声大,以及对于Galileo系统的误差模型还不够完善(特别是PCO和PCV模型);二是Galileo实时轨道和钟差的误差要大于GPS,并且各历元观测到的GPS卫星数更多。尽管如此,Galileo解和GPS解的ZTD差值绝大多数都在-20~20 mm之间波动。另一个值得说明的是,图 1中存在类似周期为1 d的周期项,该周期项的产生是由于GPS和Galileo实时轨道误差所致(预报轨道误差随预报时长的增加而增大,尤其是Galileo卫星预报轨道)。

|
图 1 3种解算方法得到的ZTD差值时间序列 Fig. 1 Time series diagrams of ZTD difference obtained by three solutions |
为具体分析各解算方法结果的符合程度,统计各测站每种实时估计方法得到的ZTD间的相关系数,如表 2所示。除了测站ULAB外,其他测站GPS解和Galileo解间的相关系数均在0.9以上,这显示两系统单独解算的ZTD结果之间具有高度相关性。同时各测站表现出类似的结果:G-GE相关系数最高,其次是E-GE,G-E最低,证明GPS在GPS/Galileo组合估计中贡献的比重大于Galileo,该结果和图 1结论相同。
|
|
表 2 各测站3种实时估计方法得到的ZTD间的相关系数统计 Tab. 2 Correlation coefficient of the ZTD obtained by real-time estimation at each measured station |
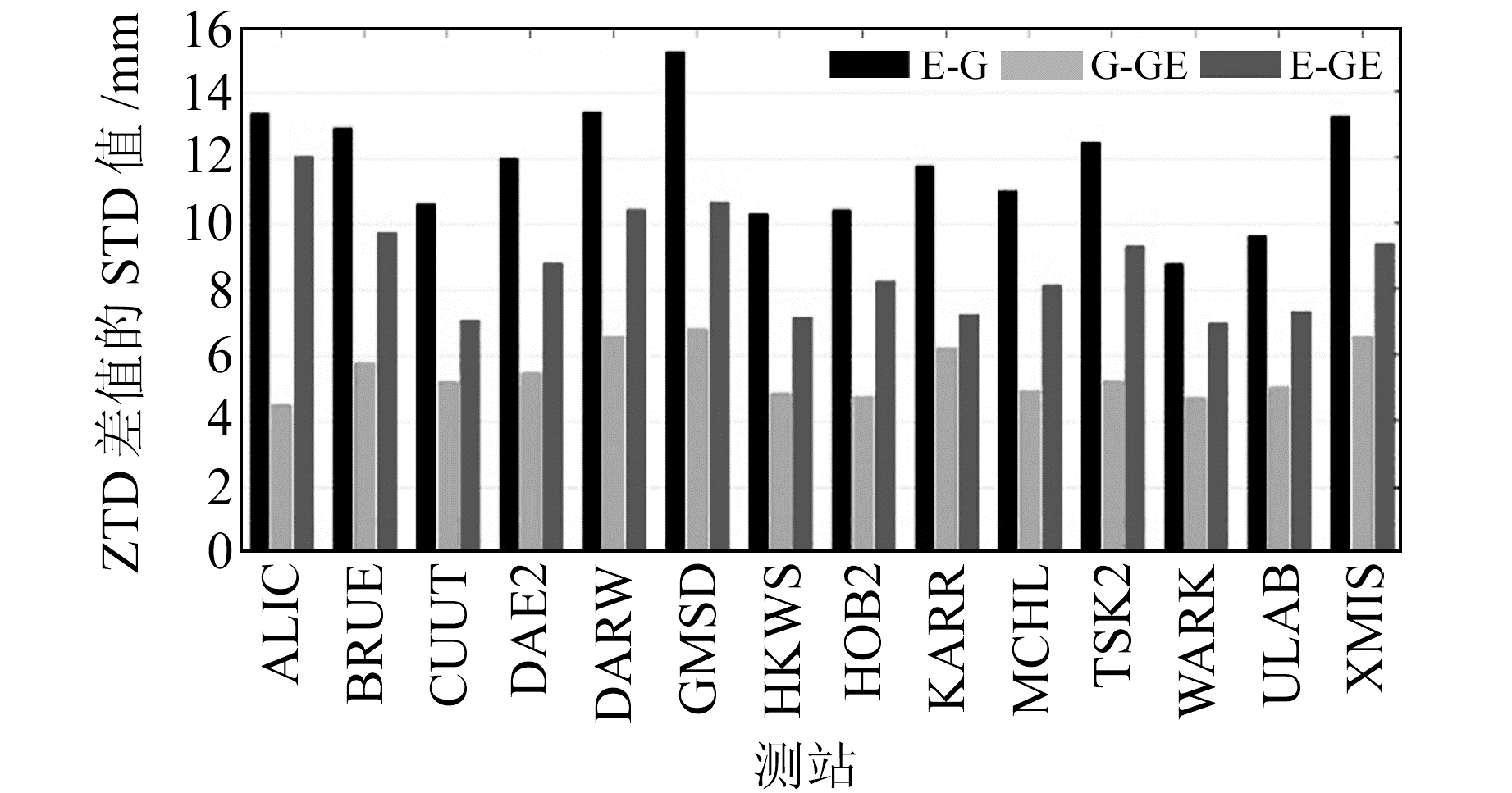
图 2展示的是Galileo解和GPS解得到的ZTD差值的分布,可以明显看出,ZTD差值的分布近似于正态分布,在Galileo解与GPS解的ZTD差值中,没有出现明显的系统偏差。2个测站ZTD差值的均方根值(RMS)分别为10.7 mm和10.0 mm,显示Galileo解和GPS解的一致性处于1 cm的量级。对于2个测站,ZTD差值的均值分别为-0.6 mm和-2.3 mm,标准差(STD)分别为10.7 mm和9.7 mm。图 3展示了14个测站Galileo-GPS、GPS-GPS/Galileo和Galileo-GPS/Galileo ZTD差值的STD值,这些测站Galileo-GPS的STD值在7 ~12 mm(对于PWV相当于1.3~2.3 mm),ZTD差值的均值在几个mm左右(对于PWV小于1 mm)。14个测站ZTD差值的RMS平均值为8.8 mm。Galileo解和GPS解的高度符合证明了Galileo实时ZTD/PWV估计满足精度要求,且该结果完全可以用于气象的预报和监测。

|
图 2 alileo解和GPS解ZTD差值的分布 Fig. 2 ZTD difference distribution of Galileo solution and GPS solution |
|
图 3 Galileo解和GPS解ZTD差值的STD值 Fig. 3 STD values of ZTD difference of Galileo solution and GPS solution |
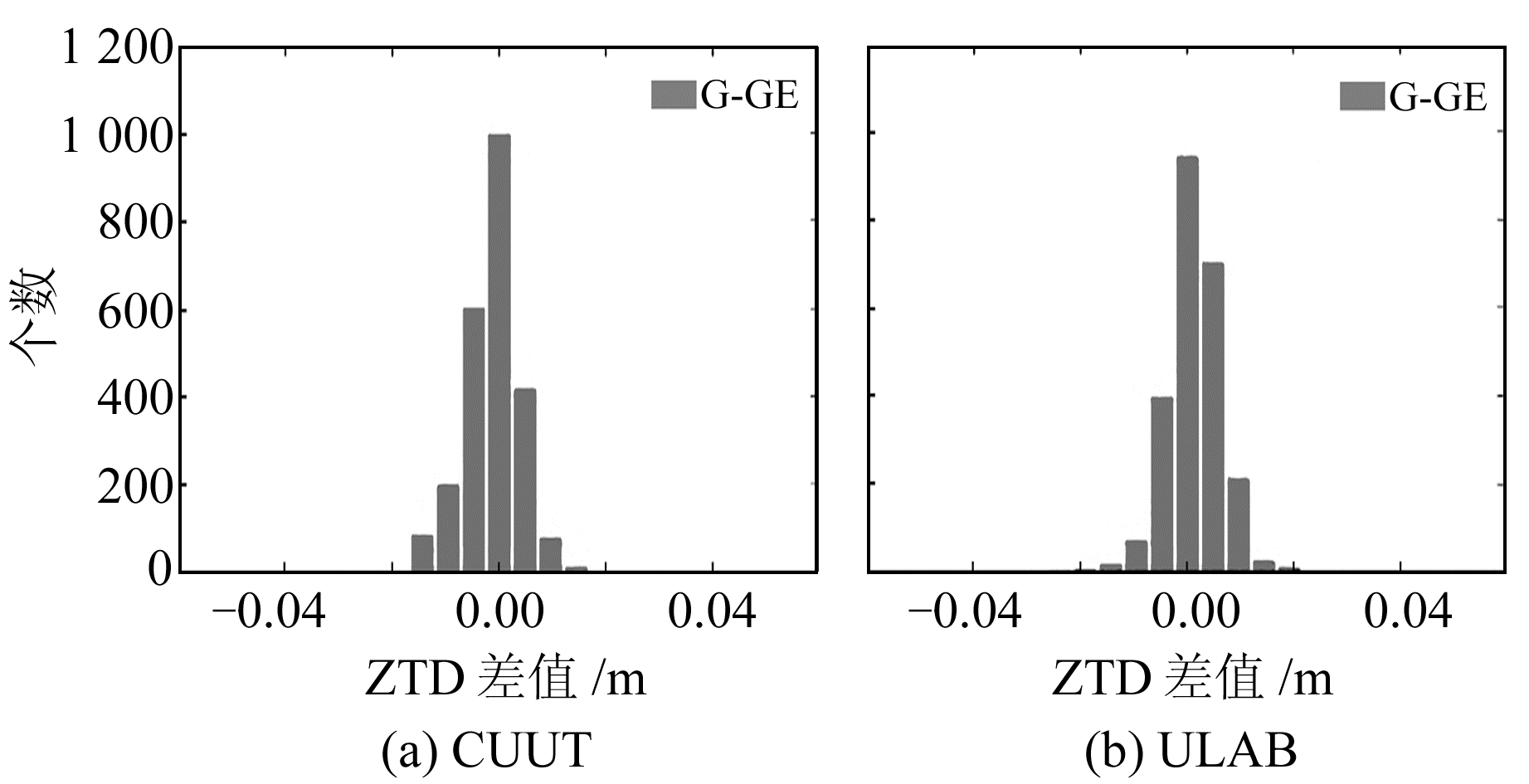
图 4、图 5分别是GPS解和Galileo解相对于GPS/Galileo组合解的ZTD差值的分布。GPS ZTD的差值集中分布在-10~10 mm,而Galileo ZTD差值集中分布在-15~15 mm。2个系统解算的ZTD差值均满足正态分布。很明显,GPS解算的ZTD差值更集中于“0”附近,这显示了GPS解算的噪声和异常值要远少于Galileo。对于测站CUUT,GPS和Galileo ZTD差值的平均值分别为-1.3 mm和-1.9 mm(ULAB:1.2 mm和-1.1mm),GPS和Galileo ZTD差值的STD分别为5.3 mm和7.2 mm(ULAB:5.1 mm和7.4 mm),GPS和Galileo ZTD差值的RMS分别为5.5 mm和7.4 mm(ULAB:5.2 mm和7.5 mm)。该结果显示,GPS解和Galileo解均很好地符合于GPS/Galileo联合解,且GPS解的RMS值优于Galileo结果。
|
图 4 单GPS解和GPS/Galileo组合解ZTD差值的分布 Fig. 4 Distribution of ZTD difference of single GPS solution and GPS/Galileo combination solution |

|
图 5 单Galileo解和GPS/Galileo组合解ZTD差值的分布 Fig. 5 Distribution of ZTD difference of single Galileo solution and GPS/Galileo combination solution |
目前IGS提供了一种新的对流层产品,该产品每5 min给定一个对流层估计值,该估计值是用GIPSY精密单点定位软件处理单个测站的观测数据获得的,精密单点定位计算中采用了IGS最终的轨道和钟差产品,因而具有很高的精度和可靠性。本文使用IGS最终产品来评价3种估计方法实时ZTD值的精度。该最终产品并未提供所有MGEX测站的ZTD估计值,本文评价的测站包括ALIC、DARW、HKWS、KARR、WARK和XMIS。
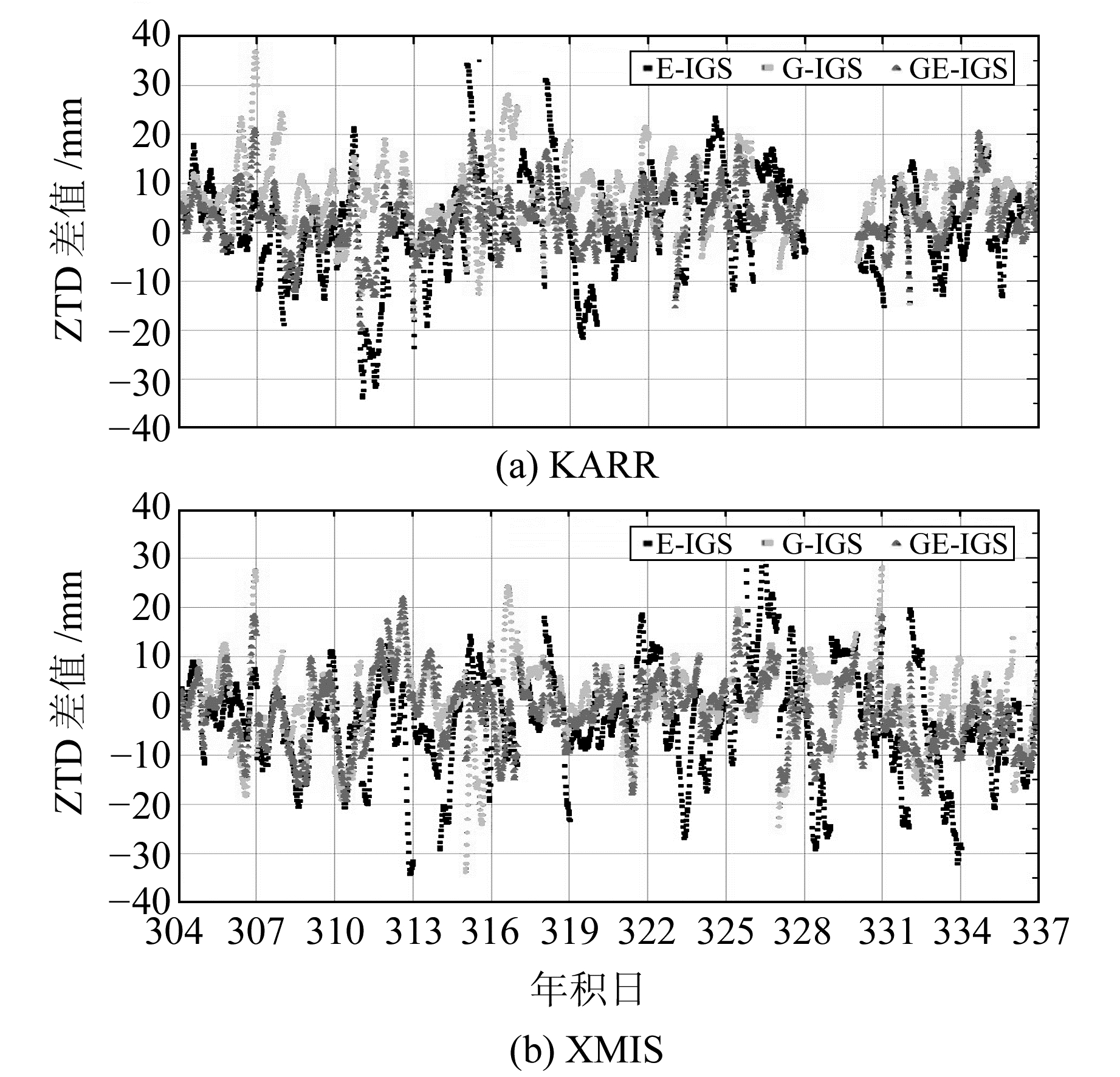
图 6是Galileo、GPS以及GPS/Galileo ZTD实时估计值和IGS最终解的差值,图中测站KARR部分结果缺失是由于观测数据缺失导致。由图可见,Galileo、GPS解的ZTD差值在-35~35 mm,而GPS/Galileo联合解的ZTD差值在-20~20 mm,且绝大多数在-10 ~10 mm。一些GPS或Galileo解的异常值在GPS/Galileo联合解算时消失,可见相对于单一系统解算,联合解算得到的ZTD差值的时间序列更加稳健和平滑。GPS/Galileo联合解算可以提高实时ZTD估计质量,原因在于解算时拥有更多的卫星数以及改进了观测值的几何构型。
|
图 6 3种解算方法和IGS最终解的ZTD差值时间序列 Fig. 6 ZTD difference time series of IGS final solution and three solutions |
图 7给出了Galileo、GPS以及GPS/Galileo ZTD实时估计值和IGS最终解差值的RMS统计。图中GPS/Galileo联合解的精度最高,其次是GPS,最差的是Galileo,这和§3.1中得到的结论一致。即使如此,Galileo解相对于IGS最终解的差值的RMS也处于8.6~14 mm的区间(对于PWV是1.6~2.6 mm),满足气象实时预报和监测的需要。GPS/Galileo联合解算相对于GPS解精度提高了5%~35%,相对于Galileo解精度提高了25%~51%。该结果进一步证明,GPS联合Galileo解算时会大幅提高ZTD/PWV实时估计的性能,同时也验证了Galileo可以应用到实时气象应用中,如数值气象模型、灾害气象监测等。

|
图 7 3种解算方法和IGS最终解ZTD差值的RMS Fig. 7 RMS of ZTD difference of IGS final solutions and three solutions |
本文采用14个MGEX测站的观测数据,利用实时PPP估计方法计算得到Galileo、GPS和GPS/Galileo组合ZTD估值。14个测站的Galileo和GPS ZTD估值的相关系数绝大多数大于0.9,且Galileo-GPS ZTD差值的RMS值在8~16 mm,RMS的平均值为12.3 mm,这证明Galileo解和GPS解的符合性良好,Galileo实时估计的ZTD精度满足要求。同时,IGS最终ZTD产品被用来评价各解算结果的精度,结果显示,GPS/Galileo联合解算时,相对于GPS单系统精度提高了5%~35%,相对于Galileo单系统精度提高了25%~51%。
| [1] |
Bevis M, Businger S, Herring T A, et al. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System[J]. Journal of Geophysical Research Atmospheres, 1992, 97(D14): 15 787-15 801 DOI:10.1029/92JD01517
(  0) 0) |
| [2] |
Rocken C, van Hove T, Ware R. Near Real-Time Sensing of Atmospheric Water Vapor[J]. Geophys Res Lett, 1997, 24: 3 221-3 224 DOI:10.1029/97GL03312
(  0) 0) |
| [3] |
Askne J, Nordius H. Estimation of Tropospheric Delay for Microwaves from Surface Weather Data[J]. Radio Science, 2016, 22(3): 379-386
(  0) 0) |
| [4] |
Davis J L, Herring T A, Shapiro I I, et al. Geodesy by Radio Interferometry: Effects of Atmospheric Modeling Errors on Estimates of Baseline Length[J]. Radio Science, 1985, 20(6): 1 593-1 607 DOI:10.1029/RS020i006p01593
(  0) 0) |
| [5] |
Zumberge J F, Heflin M B, Jefferson D C, et al. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks[J]. Journal of Geophysical Research Solid Earth, 1997, 102(B3): 5 005-5 017 DOI:10.1029/96JB03860
(  0) 0) |
| [6] |
Lu C, Li X, Nilsson T, et al. Real-Time Retrieval of Precipitable Water Vapor from GPS and Beidou Observations[J]. Journal of Geodesy, 2015, 89(9): 843-856 DOI:10.1007/s00190-015-0818-0
(  0) 0) |
| [7] |
Lu C, Li X, Ge M, et al. Estimation and Evaluation of Real-Time Precipitable Water Vapor from GLONASS and GPS[J]. GPS Solutions, 2016, 20(4): 1-11
(  0) 0) |
| [8] |
Li X, Dick G, Lu C, et al. Multi-GNSS Meteorology: Real-Time Retrieving of Atmospheric Water Vapor From Beidou, Galileo, GLONASS, and GPS Observations[J]. IEEE Transactions on Geoscience & Remote Sensing, 2015, 53(12): 6 385-6 393
(  0) 0) |
| [9] |
Ding W, Teferle F N, Kazmierski K, et al. An Evaluation of Real-Time Troposphere Estimation Based on GNSS Precise Point Positioning[J]. Journal of Geophysical Research Atmospheres, 2017, 122
(  0) 0) |
| [10] |
Saastamoinen J. Contributions to the Theory of Atmospheric Refraction. Part Ⅱ. Refraction Corrections in Satellite Geodesy[J]. Bull Geod, 1973, 107(1): 13-34
(  0) 0) |
| [11] |
Boehm J, Niell A, Tregoning P, et al. Global Mapping Function (GMF): A New Empirical Mapping Function Based on Numerical Weather Model Data[J]. Geophysical Research Letters, 2006, 33(7)
(  0) 0) |
| [12] |
Geng T, Zhang P, Wang W, et al. Comparison of Ultra-Rapid Orbit Prediction Strategies for GPS, GLONASS, Galileo and Beidou[J]. Sensors, 2018, 18(2): 477 DOI:10.3390/s18020477
(  0) 0) |
| [13] |
Wang Z, Li Z, Wang L, et al. Assessment of Multiple GNSS Real-Time SSR Products from Different Analysis Centers[J]. ISPRS International Journal of Geo-Information, 2018, 7(3): 85 DOI:10.3390/ijgi7030085
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39


