电离层作为地球大气层的重要组成部分，对无线电导航信号有着显著的影响。随着全球卫星导航系统(global navigation satellite system, GNSS)技术的发展及应用，电离层延迟误差成为GNSS测量、定位、导航的重要误差源之一^[1]。双频GNSS接收机用户利用无电离层组合方法可以较好地消除电离层一阶项的影响，对于单频GNSS接收机用户，可以通过形成半和观测值或采用电离层模型来提高导航定位性能。

目前，国际上利用GNSS数据建立电离层模型已经取得重大进展，国际GNSS服务组织(International GNSS Service, IGS)电离层工作组早已对外发布电离层格网产品，用户可以选取穿刺点附近的有效格网点数据，自行设计模型，内插出经纬度范围内任意一点处的垂直电子含量(vertical total electron content, VTEC)^[2]。虽然目前IGS电离层工作组的工作已经非常成熟，但是由于IGS跟踪站多分布不均匀，高纬度区域跟踪站分布稀疏，导致该地区电离层穿刺点(ionospheric pierce point, IPP)分布较少，能用于电离层拟合建模的数据不足，使利用IGS跟踪站建立电离层拟合模型时高纬度地区的电离层拟合模型精度偏低，一些区域电离层拟合建模结果甚至出现大量与电离层物理特性不相符合的负值、零值^[3]。

当前，不少文献提出基于不等式约束算法来提高GNSS数据处理质量，有效控制GNSS异常值。如文献[4]将不等式约束应用到GPS的数据处理中，利用不等式约束解决GPS定位模糊度初始化的问题。文献[5]将不等式约束条件作为虚拟观测值，研究不等式约束算法在GPS定位中的应用。文献[6]讨论将不等式约束算法应用到GNSS电离层延迟建模当中，分析不等式约束算法对全球电离层模型(global ionosphere model，GIM)格网负值输出点以及硬件延迟的影响。虽然不等式约束算法在GNSS大地测量领域已经有越来越广泛的应用，但是在不等式约束对全球高纬度地区电离层总电子含量影响方面的研究相对较少。基于此，本文研究基于不等式约束算法来改善高纬度地区电离层模型的精度。

为了与欧洲定轨中心电离层产品(center for orbit determination in Europe, CODE)保持一致，本文利用CODE当天参与解算的278个IGS跟踪站2018-01-01~01-09连续9 d的GPS单系统数据，采用不等式约束条件的最小二乘算法(inequality constraint least square，ICLS)进行电离层建模解算，并将建模结果与不采用ICLS算法的建模结果相比较，分析ICLS算法对高纬度地区以及全球电离层模型VTEC精度的改善。

1 基于GPS数据建立全球VTEC模型

对于双频GPS观测数据，信号传播路径的电离层总电子含量TEC与双频P码之差来有如下关系^[6]：

$ \begin{array}{*{20}{c}} {\tilde P_{2j}^i - \tilde P_{1j}^i = 40.28 \times \frac{{{\rm{TEC}}}}{{f_2^2}} - }\\ {40.28 \times \frac{{{\rm{TEC}}}}{{f_1^2}} + {\rm{d}}{q_j} + {\rm{d}}{q^i}} \end{array} $

(1)

式中，f₁、f₂为信号频率；${\rm{d}}{q_j} = {\rm{d}}{q_{2j}} - {\rm{d}}{q_{1j}}、{\rm{d}}{q^i} = {\rm{d}}q_2^i - {\rm{d}}q_1^i $分别为接收机与卫星的硬件延迟；$ \widetilde{P}_{1 j}^{i}$、$\widetilde{P}_{2 j}^{i} $为相位平滑之后的伪距观测值，具体表达式如下：

$ \begin{array}{*{20}{c}} {\tilde P\left( {{t_j}} \right) = \frac{1}{j}{P_4}\left( {{t_j}} \right) + \left( {1 - \frac{1}{j}} \right) \cdot }\\ {\left[ {\tilde P\left( {{t_{j - 1}}} \right) + {L_4}\left( {{t_j}} \right) - {L_4}\left( {{t_{j - 1}}} \right)} \right]} \end{array} $

(2)

式中，P₄(t_j)为平滑之前的同一颗卫星同一个测站不同频率间t_j时刻的码组合观测值，$ \widetilde{P}\left(t_{j-1}\right)$为t_j前一时刻的伪距平滑值，L₄(t_j)、L₄(t_j－1)分别为当前时刻和前一时刻的同一颗卫星同一个测站不同频率间的相位组合观测值。根据式(1)，求得信号传播路径的总电子含量TEC观测方程为^[7]：

$ {\rm{TEC}} = \frac{{f_1^2f_2^2}}{{40.28 \times \left( {f_1^2 - f_2^2} \right)}}\left( {\tilde P_{2j}^i - \tilde P_{1j}^i - {\rm{d}}{q_j} - {\rm{d}}{q^i}} \right) $

(3)

利用根据观测值获取的电离层延迟信息以及电离层单层假设模型，结合球谐函数以及投影函数对电离层总电子含量进行拟合建模，观测方程为^[8]：

$ \begin{array}{*{20}{c}} {{\rm{TEC}} \cdot mf = \sum\limits_{n = 0}^{{n_{\max }}} {\sum\limits_{m = 0}^n {{{\tilde P}_{nm}}\left( {\sin \varphi } \right)} } \cdot }\\ {\left( {{{\tilde A}_{nm}}\cos \left( {m\mu } \right) + {{\tilde B}_{nm}}\sin \left( {m\mu } \right)} \right)} \end{array} $

(4)

式中，$m f=\frac{1}{\cos \left(z^{\prime}\right)} $为投影函数，其中$\sin \left( {{z^\prime }} \right) = \frac{{{R_r}}}{{{R_e} + H}}\sin (z), z $为天顶距，R_r为测站与地心之间的距离，R_e为地球平均半径，H为电离层单层模型高度(取450 km)，将信号传播路径方向上的总电子含量换算到垂直方向的总电子含量；φ为穿刺点的纬度；μ为太阳时角；n_max为球谐函数最大阶数；m为阶数；$ \widetilde{P}_{m n}(\sin \varphi)$为n次m阶归化的拉格朗日函数；$ \widetilde{A}_{n m}$和$ \widetilde{B}_{n m}$为未知的球谐函数系数，在方程中进行参数的统一解算。

2 附不等式约束的最小二乘算法电离层建模

为解决电离层延迟建模中格网点出现零值、负值这一问题，本文采用不等式约束的最小二乘算法，对零值、负值的输出格网点采用非负非零约束，形成约束方程，通过求解附不等式约束的平差问题，优化最小二乘的参数估计解。在解决附不等式约束的最小二乘问题时，先将附不等式约束的最小二乘问题转化为凸二次规划问题，根据库恩-塔克条件将二次规划转化为线性互补问题(linear complementarity problem，LCP)，求解线性互补问题即可得到参数的附加不等式约束的最小二乘最优解^[9]。

在利用球谐函数进行电离层建模时，加入先验约束条件：

$ \begin{array}{*{20}{c}} {\sum\limits_{n = 0}^{{n_{\max }}} {\sum\limits_{m = 0}^n {{{\tilde P}_{nm}}\left( {\sin \varphi } \right)\left( {{{\tilde A}_{nm}}\cos \left( {m\mu } \right) + } \right.} } }\\ {\left. {{{\tilde B}_{nm}}\sin \left( {m\mu } \right)} \right) \ge {W_x}} \end{array} $

(5)

式中，W_x是对VTEC施加的非负值约束，其具体数值跟格网点的经纬度以及太阳时角有关。根据搜索到的格网点，基于格网点的位置以及太阳时角确定W_x的具体数值，加入不等式约束，形成不等式约束方程G，并按照下式计算LCP问题的系数阵E和常数阵c：

$ \left\{ \begin{array}{l} \mathit{\boldsymbol{E}} = \mathit{\boldsymbol{G}}{\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{G}}^{\rm{T}}}\\ \mathit{\boldsymbol{c}} = \mathit{\boldsymbol{G}}{{\mathit{\boldsymbol{\hat X}}}_0} - \mathit{\boldsymbol{W}} \end{array} \right. $

(6)

根据库恩-塔克条件，可以将二次规划问题转化为LCP问题：

$ \left\{ \begin{array}{l} \mathit{\boldsymbol{h}} = \mathit{\boldsymbol{E\mu }} + \mathit{\boldsymbol{c}}\\ {\mathit{\boldsymbol{\mu }}^{\rm{T}}}\mathit{\boldsymbol{h}} = 0,\mu ,h \ge 0 \end{array} \right. $

(7)

根据(7)式可以求得线性互补问题的最优解$\hat{\boldsymbol{\mu}} $。再把求得的最优解$\hat{\boldsymbol{\mu}} $代入最小二乘解进行修正，最终得到附不等式约束的最小二乘解$\hat{\boldsymbol{X}}_{\mathrm{ICLS}} $：

$ {\mathit{\boldsymbol{\hat X}}_{{\rm{ICLS}}}} = {\mathit{\boldsymbol{\hat X}}_{\rm{0}}} + {\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{\hat \mu }} $

(8)

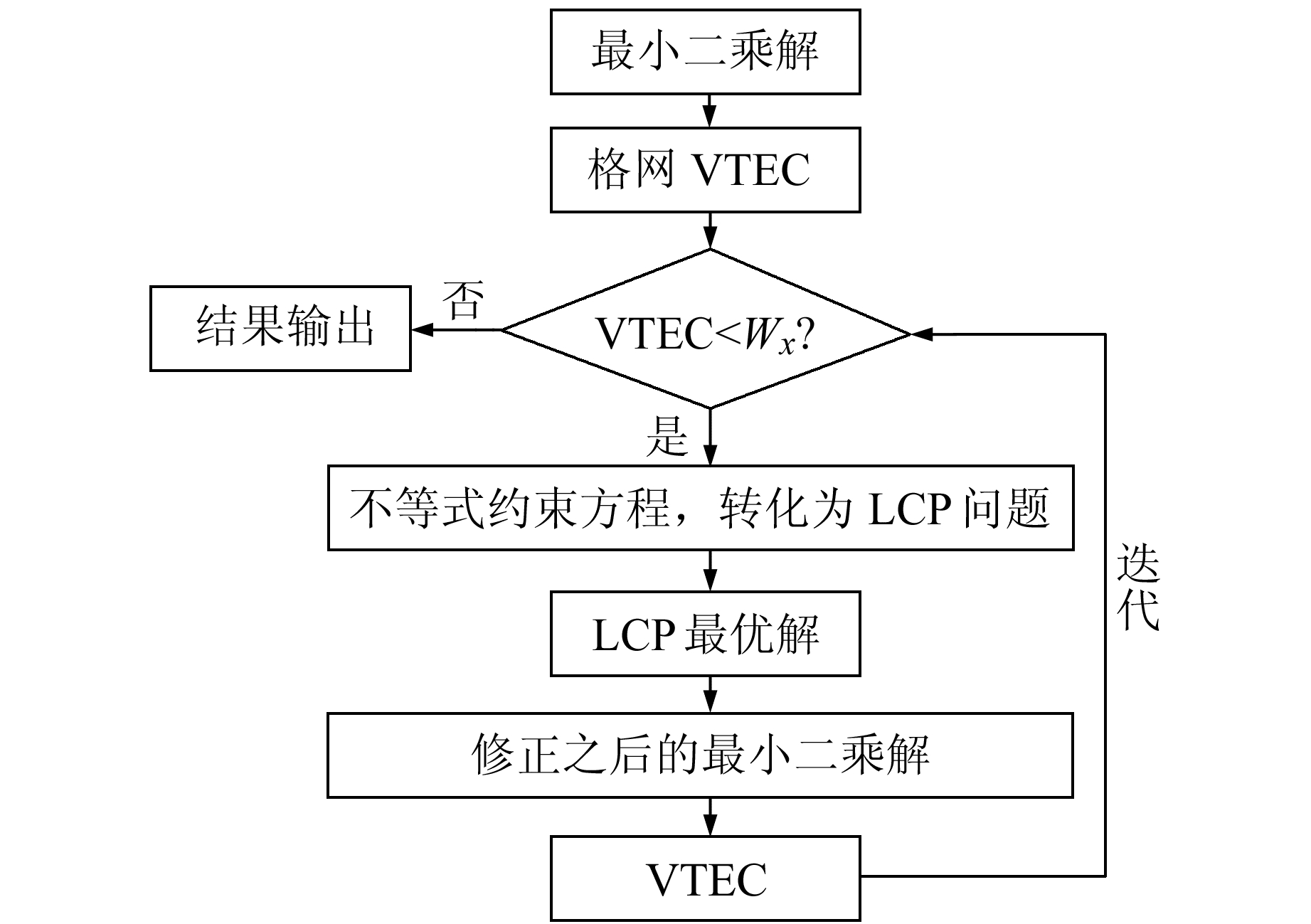
根据附不等式约束算法求得格网VTEC，继续搜索不满足约束条件的格网点，如不满足约束条件则返回式(6)继续计算LCP问题的系数矩阵E以及常数矩阵c。如此迭代，直到满足不等式约束的条件。具体算法流程如图 1所示。

3 实验及结果分析

由于实验结果要与CODE发布的产品(CODG文件)作比较，因此实验采用与CODG电离层解算相同的278个IGS测站2018年年积日第1~9天连续9 d的GPS观测数据，2018年年积日第5天UT11：30~12：00具体穿刺点分布如图 2所示。由图可见，在高纬度地区以及海洋区域没有导航卫星信号穿过电离层，而冬季太阳直射南半球，此时北半球高纬度地区的电离层电子浓度也会相对于中低纬地区低。由此猜测，在该区域格网点VTEC值有可能会出现负值、零值。

采用分段线性化方式对9 d的格网数据按照每天数据分成12个时段进行分段，每个时段2 h，每个时段均采用15阶次的球谐函数进行拟合。将每天12个时段的模型参数按照时间先后顺序排列，将其设置成为一个待估向量，估计时段首尾处的电离层模型系数。按照法方程叠加方式形成法方程，并采用最小二乘参数估计方法解算这些模型参数^[10]。卫星和测站码偏差在1 d之内看作是一个常数，每天只估计一组卫星和测站的码偏差。考虑到若将卫星和测站的硬件延迟分别设置为参数进行最小二乘估计会造成观测方程列向量不满秩，引起法方程秩亏，因此引入卫星DCB“零均值”基准约束^[11]：

$ \sum\limits_{i = 1}^N {{\rm{DC}}{{\rm{B}}^i}} = 0 $

(9)

式中, N为可视卫星数，DCBⁱ为卫星硬件延迟。具体的数据及模型选取策略见表 1。

为评估不等式约束算法对负值、零值格网点的约束影响，本文先计算不加入不等式约束最小二乘法NTSCG(LS)得到的全球电离层电子含量分布(图 3)。

由图 3可见，由于北半球高纬度地区(78°~87.5°N)几乎无测站分布，因此在该区域出现了黑色区域，即该区域出现大量的零值和负值格网点，这有悖于电离层非负的实际物理含义，也会严重影响电离层VTEC拟合模型的精度。在加入附不等式约束的最小二乘NTSCG(ICLS)后，解算得到全球电离层分布图(图 4)。

由图 4可见，在利用加入不等式约束的最小二乘算法后，北半球的高纬度地区格网VTEC出现大量零值、负值的情况有明显改善。

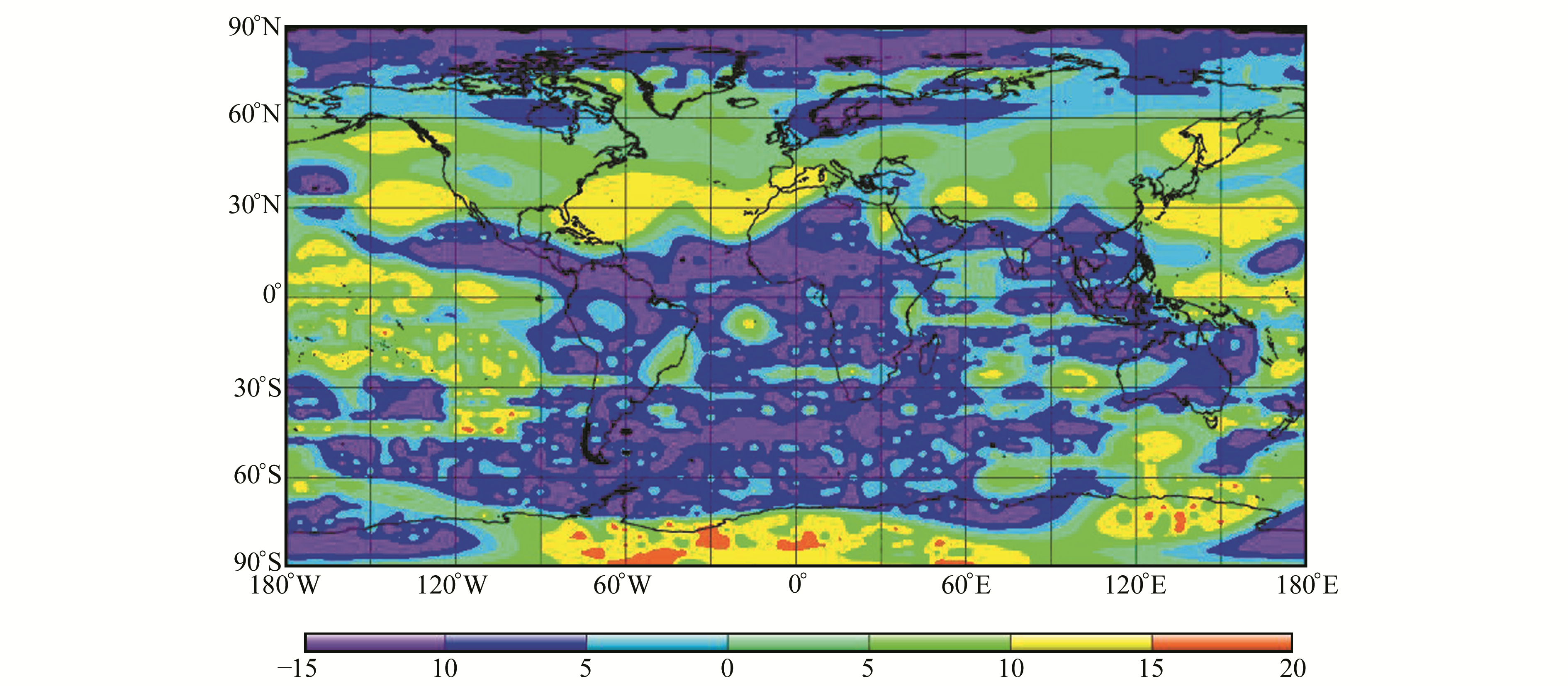
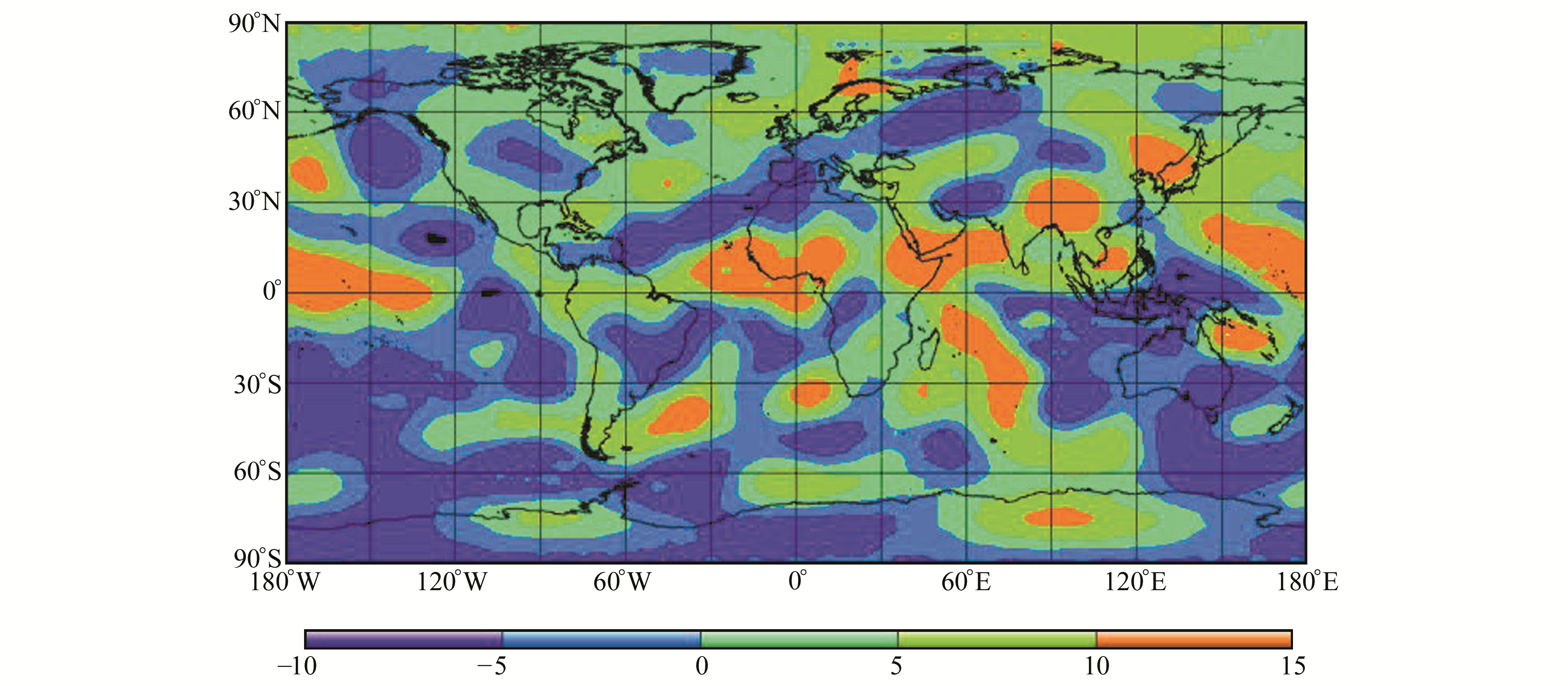
为验证不等式约束算法对全球范围内电离层建模精度的影响，以CODE发布的格网电离层产品作为标准，比较不加入不等式约束最小二乘算法的结果精度与加入不等式约束的最小二乘算法的结果精度，图 5、图 6分别为NTSCG(LS)、NTSCG(ICLS)与CODG之间的全球电离层VTEC分布差异图。

结合图 2可以看出，在北半球高纬以及海洋地区等缺乏观测数据的区域NTSCG(LS)与CODG的VTEC差异非常大，达到-10~15 TECu，部分地区甚至出现了20 TECu的差异。在加入不等式约束后，这些区域NTSCG(ICLS)与CODG的VTEC差异明显减小，在高纬度以及海洋地区绝大部分差异在0~10 TECu。根据式(10)分别统计了NTSCG(LS)和NTSCG(ICLS)与CODG差异的均值mean与均方根RMS：

$ \left\{ \begin{array}{l} {\rm{mean}} = \frac{1}{N}\sum\limits_{i = 1}^N {\left( {{\rm{VTE}}{{\rm{C}}_k} - {\rm{VTE}}{{\rm{C}}_{{\rm{CODE}}}}} \right)} \\ {\rm{RMS}} = \sqrt {\frac{{\sum\limits_{i = 1}^N {{{\left( {{\rm{VTE}}{{\rm{C}}_k} - {\rm{VTE}}{{\rm{C}}_{{\rm{CODE}}}}} \right)}^2}} }}{N}} \end{array} \right. $

(10)

式中，N表示电离层格网点的数目，VTEC_k代表NTSCG(LS)和NTSCG(ICLS)格网点处的VTEC值，VTEC_CODE表示CODE发布的电离层格网文件的格网点VTEC数据。一致性分析统计结果如表 2所示。

由表 2可以看出，在加入不等式约束后，NTSCG与CODG格网点VTEC差异的均值提高0.539 TECu，均方根提高0.768 TECu，说明加入不等式约束条件后使电离层VTEC建模精度有明显提高。

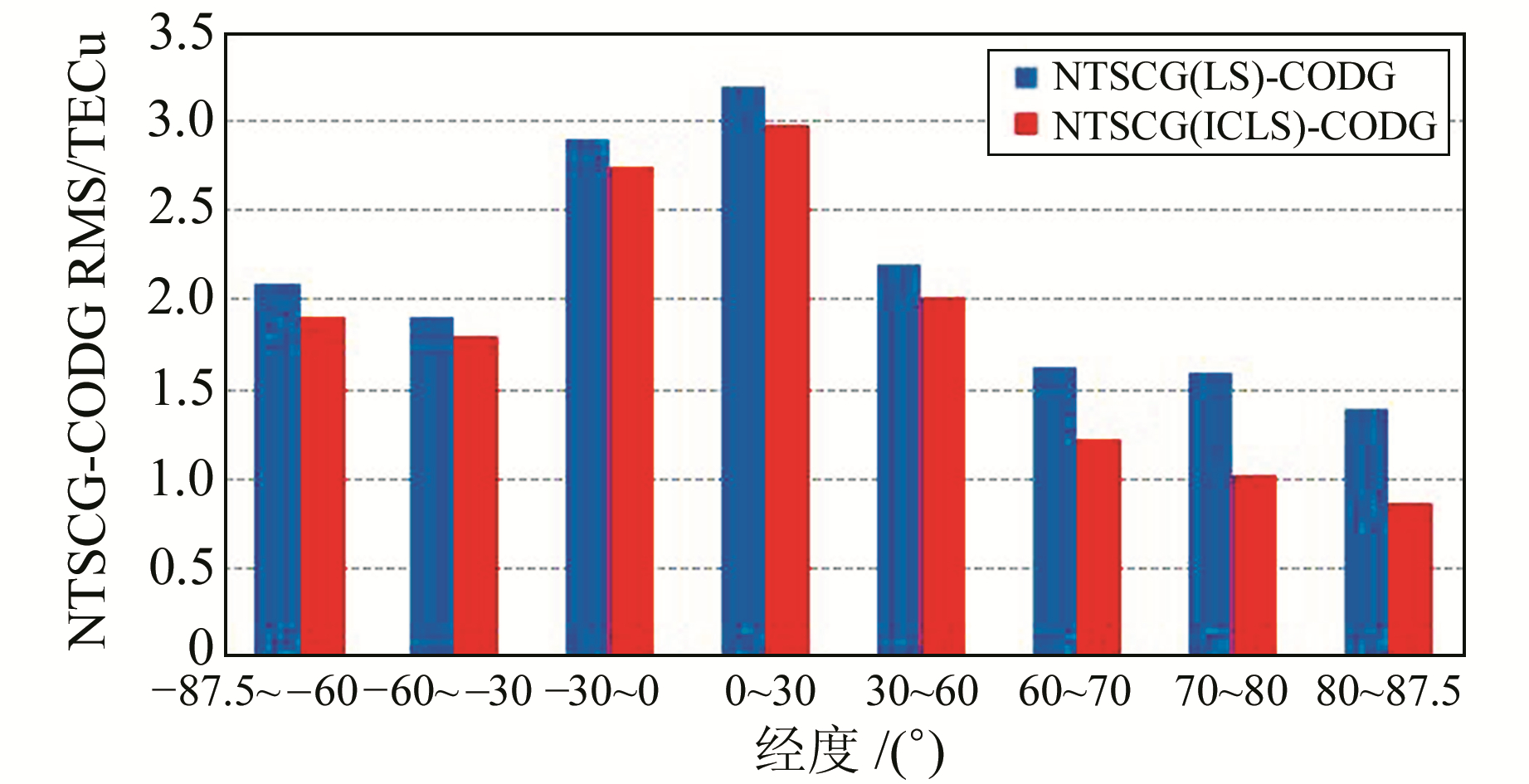
为了进一步说明不等式约束最小二乘算法对高纬度地区建模精度的影响，将全球分为-87.5°~-60°、-60°~-30°、-30°~0°等8个纬度带，分别统计NTSCG(LS)和NTSCG(ICLS)与CODG之间格网差异的RMS(图 7)。

由图 7可见，在北半球NTSCG与CODG的VTEC差异比南半球小，这与南半球有较少的测站观测数据有关。由于低纬度地区TEC变化比较复杂，电离层延迟模型的TEC值与真值差异大，因此NTSCG与CODG格网值差异的RMS也较大。比较NTSCG(LS)-CODG与NTSCG(ICLS)-CODG之间的差异可以看出，北半球高纬度地区差值的差异比中纬、低纬度地区大，由此说明，不等式约束算法使高纬度地区的电离层TEC模型精度有明显提高。

4 结语

因高纬度地区GNSS测站分布稀疏，采用常规的最小二乘算法进行GNSS电离层建模在高纬度地区会存在负值、零值问题。根据电离层VTEC的先验信息，在利用最小二乘算法建模中加入不等式约束条件，将附加不等式约束的最小二乘算法转化为凸二次规划问题，再根据库恩-塔克条件将不等式约束平差问题转化为线性互补问题，然后求线性互补问题的最优解，得到不等式约束的电离层模型最优解。基于GPS实测数据进行验证表明，在加入不等式约束之后，高纬度地区出现大量VTEC零值、负值的现象得到有效改善，同时，在加入不等式约束条件最小二乘算法之后，电离层建模模型精度也得到明显提高。随着多模GNSS数据的增加，在叠加计算求解最优解这一过程中耗时偏长，因此很有必要对算法进一步优化，以提高计算效率。