目前常用的PPP函数模型包括消电离层组合、UofC和基于原始观测值的非组合3种。前2种是基于消电离层组合观测值构建的，差别在于UofC模型引入了半和观测值^[1-2]；非组合PPP基于原始伪距和载波相位观测值构建，保留了GPS信号传输过程中的电离层延迟信息。相较于前两者，非组合模型直接使用原始观测值，避免了观测噪声被放大^[3]，对三频及多频数据的处理更加灵活^[4]，可提供高精度的电离层观测量，有利于高精度电离层建模^[5]。

3种模型对测站坐标、接收机钟差、天顶对流层延迟以及载波相位模糊度等参数的估计策略一致，但非组合模型待估参数还包含受站星仪器偏差影响的电离层斜延迟^[6-7]。对电离层斜延迟参数的随机建模大多基于随机游走模型，但针对全球范围、不同电离层活跃情况下，如何选择合适、通用的随机游走过程的谱密度是一个研究难点^[8]。此外，部分学者研究了对电离层参数采用白噪声估计^[3-4]。目前尚无评估2种建模方式对非组合PPP定位性能影响的研究。

基于以上讨论，本文旨在分析电离层延迟的不同随机建模方式对非组合PPP定位性能的影响。针对传统随机游走过程建模的电离层延迟参数的谱密度不易确定这一难点，本文提出顾及电离层延迟历元间变化的随机游走模型。选取全球均匀分布的170个IGS测站2016-07的观测数据进行评估和分析，从3种电离层延迟随机建模方法对非组合PPP的收敛时间和定位精度指标入手，验证分析3种方法的优缺点。

1 非组合GPS精密单点定位模型 1.1 观测方程

GPS非差非组合双频伪距P和载波L的通用观测方程为:

$ \begin{array}{*{20}{c}} {P_{r,j}^s = \rho _r^s + {\rm{d}}{t_r} - {\rm{d}}{t^s} + T_r^s + }\\ {{\kappa _j}I_{r,1}^s + {d_{r,j}} - d_j^s + \varepsilon _{r,j}^s} \end{array} $

(1)

$ \begin{array}{*{20}{c}} {L_{r,j}^s = \rho _r^s + {\rm{d}}{t_r} - {\rm{d}}{t^s} + T_r^s - {\kappa _j}I_{r,1}^s + }\\ {{\lambda _j}\left( {N_{r,j}^s + {b_{r,j}} - b_j^s} \right) + \xi _{r,j}^s} \end{array} $

(2)

式中，s、r和j(j=1, 2)分别为卫星、接收机和载波频率号；ρ_r^s为卫星到接收机的几何距离；dt_r和dt^s分别为接收机和卫星钟差；T_r^s为视线方向对流层斜延迟；I_{r, 1}^s为第一频率上的电离层斜延迟；κ_j=f₁²/f_j²为电离层频率因子，f为载波频率；λ_j为对应j频率的载波相位波长；N_{r, j}^s为载波相位整周模糊度；d_{r, j}和d_j^s分别为接收机和卫星端伪距硬件延迟；b_{r, j}和b_j^s分别为接收机和卫星端的相位硬件延迟；ε_{r, j}^s和ξ_{r, j}^s分别为伪距和载波相位观测值对应的观测噪声和多路径效应等误差。上述变量中除模糊度和UPD单位为周外，其余各变量的单位均为m。需要注意的是，式(1)和式(2)中不包括卫星和接收机端天线相位中心改正、相对论效应、潮汐负荷形变(固体潮、极潮和海潮)、萨奈克效应(Sagnac effect)、卫星天线相位缠绕(仅对载波观测值)等改正，这些已事先通过模型进行改正^[9]。

为方便起见，定义以下变量：

$ {\alpha _{ij}} = \frac{{f_i^2}}{{f_i^2 - f_j^2}},{\beta _{ij}} = - \frac{{f_j^2}}{{f_i^2 - f_j^2}} $

(3)

$ \begin{array}{l} {\rm{DCB}}_{{P_i}{P_j}}^s = d_i^s - d_j^s,{\rm{DC}}{{\rm{B}}_{r,{P_i}{P_j}}} = {d_{r,i}} - {d_{r,j}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;{d_{r,{\rm{I}}{{\rm{F}}_{ij}}}} = {\alpha _{ij}}{d_{r,i}} + {\beta _{ij}}{d_{r,j}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;d_{{\rm{I}}{{\rm{F}}_{ij}}}^s = {\alpha _{ij}}d_i^s + {\beta _{ij}}d_j^s \end{array} $

(4)

式中，f_i为信号频率(i, j=1, 2;i≠j)，α_ij和β_ij为与信号频率有关的放大因子，DCB_PiPj^s和DCB_{r, PiPj}为卫星和接收机端差分码偏差。

IGS提供的精密卫星钟差一般是基于第一、第二频率双频无电离层组合观测值得到的^[10]。因此，精密卫星钟差包含了双频伪距硬件延迟的线性组合，即

$ {\rm{d}}t_{{\rm{IF}}}^s = {\rm{d}}{t^s} + \left( {{\alpha _{12}}d_1^s + {\beta _{12}}d_2^s} \right) = {\rm{d}}{t^s} + d_{{\rm{I}}{{\rm{F}}_{12}}}^s $

(5)

引入精密卫星轨道和钟差改正，将式(5)代入式(1)和式(2)并线性化得:

$ \left\{ \begin{array}{l} p_{r,1}^s = \mathit{\boldsymbol{u}}_r^s\mathit{\boldsymbol{x}} + {\rm{d}}{{\bar t}_r} + m{f_w}\left( e \right){Z_w} + \\ \;\;\;\bar I_{r,1}^s + \varepsilon _{r,1}^s\\ p_{r,2}^s = \mathit{\boldsymbol{u}}_r^s\mathit{\boldsymbol{x}} + {\rm{d}}{{\bar t}_r} + m{f_w}\left( e \right){Z_w} + \\ \;\;\;{\kappa _2}\bar I_{r,1}^s + \varepsilon _{r,2}^s \end{array} \right. $

(6)

$ \left\{ \begin{array}{l} l_{r,1}^s = \mathit{\boldsymbol{u}}_r^s\mathit{\boldsymbol{x}} + {\rm{d}}{{\bar t}_r} + m{f_w}\left( e \right){Z_w} - \\ \;\;\;\bar I_{r,1}^s + \bar N_{r,1}^s + \xi _{r,1}^s\\ l_{r,2}^s = \mathit{\boldsymbol{u}}_r^s\mathit{\boldsymbol{x}} + {\rm{d}}{{\bar t}_r} + m{f_w}\left( e \right){Z_w} - \\ \;\;\;{\kappa _2}\bar I_{r,1}^s + \bar N_{r,2}^s + \xi _{r,2}^s \end{array} \right. $

(7)

其中，

$ \left\{ \begin{array}{l} {\rm{d}}{{\bar t}_r} = {\rm{d}}{t_r} + {d_{r,{\rm{I}}{{\rm{F}}_{12}}}}\\ \bar I_{r,1}^s = I_{r,1}^s + {\beta _{12}}{\rm{DC}}{{\rm{B}}_{r,{P_1},{P_2}}}\\ \bar N_{r,1}^s = {\lambda _1}\left( {N_{r,1}^s + {b_{r,1}} - b_1^s} \right) + \\ \;\;\;\;\;\left( {d_{{\rm{I}}{{\rm{F}}_{12}}}^s - {d_{r,{\rm{I}}{{\rm{F}}_{12}}}}} \right) + {\beta _{12}}{\rm{DC}}{{\rm{B}}_{r,{P_1},{P_2}}}\\ \bar N_{r,2}^s = {\lambda _2}\left( {N_{r,2}^s + {b_{r,2}} - b_2^s} \right) + \\ \;\;\;\;\;\left( {d_{{\rm{I}}{{\rm{F}}_{12}}}^s - {d_{r,{\rm{I}}{{\rm{F}}_{12}}}}} \right) + {\kappa _2}{\beta _{12}}{\rm{DC}}{{\rm{B}}_{r,{P_1},{P_2}}} \end{array} \right. $

(8)

式中，p_r^s和l_r^s分别为伪距和载波的观测值减去计算值(observed minus computed，OMC)；u_r^s为接收机到卫星的方向余弦向量；x为接收机相对于初始位置的改正量；e为卫星高度角；Z_w为天顶湿延迟；mf_w(e)为湿投影函数，可由全球投影函数(global mapping function，GMF)获取^[11]。从式(6)和式(8)可以看出，本文非组合PPP模型中的电离层斜延迟仅包括接收机DCB，而卫星DCB已事先改正。

通过上述分析，本文的非组合PPP模型的待估参数向量为：

$ \mathit{\boldsymbol{S}} = {\left[ {\mathit{\boldsymbol{x}},{\rm{d}}{{\bar t}_r},{Z_w},{{\mathit{\boldsymbol{\bar I}}}_1},{{\mathit{\boldsymbol{\bar N}}}_1},{{\mathit{\boldsymbol{\bar N}}}_2}} \right]^{\rm{T}}} $

(9)

1.2 电离层延迟的随机模型

本文对电离层延迟的处理分为3个方案：方案1将电离层延迟作为白噪声过程估计；方案2将电离层延迟采用传统的随机游走过程估计；方案3为顾及电离层延迟历元间变化的随机游走过程。

1.2.1 白噪声模型

电离层延迟用白噪声描述可表示为:

$ \bar I_{r,1,0}^s\left( k \right) \sim N\left( {\bar I_{r,1,{P_1}{P_2}}^s\left( k \right),\sigma _{I_{r,1}^s}^2} \right) $

(10)

式中，$ \overline{I}_{r, 1, 0}^{s}(k)$为第k历元的电离层初始值，可通过双频伪距观测值计算得到$\bar I_{r, 1, {P_1}{P_2}}^s(k);\sigma _{\bar I_{r, 1}^s}^2 $为电离层延迟的初始方差。

1.2.2 随机游走模型

电离层延迟$\overline{T}_{r, 1}^{s} $的变化可用随机游走过程来描述：

$ \bar I_{r,1,0}^s\left( k \right) = \hat I_{r,1}^s\left( {k - 1} \right) + {\omega _{\bar I_{r,1}^s}},{\omega _{I_{r,1}^s}} \sim N\left( {0,\sigma _{{\omega _{\bar I_{r,1}^s}}}^2} \right) $

(11)

式中，$\hat I_{r, 1}^s(k - 1) $为k－1历元电离层延迟的估计值；$ \sigma _{{\omega _{\bar I_{r, 1}^s}}}^2 = q_{\bar I_{r, 1}^s}^2\left( {{t_k} - {t_{k - 1}}} \right), {q_{\bar I_{r,1}^s}}$为电离层延迟随机游走过程的谱密度。

式(11)为传统的电离层延迟随机游走模型。再顾及历元间电离层的变化量，本文提出一种新型的电离层延迟随机游走模型：

$ \begin{array}{*{20}{c}} {\bar I_{r,1,0}^s\left( k \right) = \left( {\hat I_{r,1}^s\left( {k - 1} \right) + \Delta \hat I_{r,1}^s\left( k \right)} \right) + }\\ {{\omega _{\bar I_{r - 1}^s}},{\omega _{\bar I_{r - 1}^s}} \sim N\left( {0,\sigma _{{\omega _{\bar I_{r - 1}^s}}}^2} \right)} \end{array} $

(12)

式中，$\Delta_{\overline{I}_{r, 1}^{s}}(k) $为第k和k－1历元的电离层延迟变化量，在卫星s未发生周跳的情况下，可通过双频载波观测值计算，即

$ \begin{array}{*{20}{c}} {{\Delta _{\bar I_{r,1}^s}}\left( k \right) = \frac{{f_2^2}}{{f_1^2 - f_2^2}}\left[ {\left( {L_{r,1}^s\left( k \right) - L_{r,2}^s\left( k \right)} \right) - } \right.}\\ {\left. {\left( {L_{r,1}^s\left( {k - 1} \right) - L_{r,2}^s\left( {k - 1} \right)} \right)} \right]} \end{array} $

(13)

为保证电离层延迟历元间变化量的精度，需要对载波相位观测值作卫星和接收机相位中心改正、相位缠绕改正。

2 实验与结果分析 2.1 数据介绍及处理策略

为验证本文提出模型的可行性，选取全球均匀分布的170个IGS测站2016-07的观测数据(采样间隔为30 s)进行分析。此外，为了评估电离层的活跃度，给出2016-07的3 h间隔的地磁K_p指数(图 1)。K_p指数是地球地磁场扰动指标，可用来表征电离层活跃水平。可以看到，在大部分时间内K_p指数值均小于4.0，而在2016年第189天和第209天电离层明显要活跃得多(K_p均大于6.0)。

实验分别采用静态和仿动态PPP解算模式，将每个测站24 h观测数据分割为8个子时段，每个子时段为3 h观测数据。将各子时段PPP解算结果与参考真值坐标(IGS周解)作差，获得E、N、U方向上的坐标偏差，以分析PPP的收敛时间和定位精度。本文将滤波收敛定义为E、N、U各向定位偏差均优于1 dm。为确保结果的可靠性，同时检查首次收敛时刻后续20个历元的E、N、U方向上的定位偏差，只有当连续20个历元的偏差都在1 dm以内时，才认为滤波结果在该时刻收敛，否则继续向后续历元重复前述方法判定收敛^[12]。本文分析的PPP收敛是基于E、N、U各向收敛，当有至少1个方向在3 h的子时段内没有满足收敛条件时，该子时段将被剔除，不参与收敛和定位精度的统计。

根据卫星高度角和观测值噪声来确定伪距和载波观测值的权，伪距和载波的噪声标准差分别为0.3 m和0.003 m。在参数解算过程中，接收机钟差采用白噪声估计；对流层的干延迟部分采用Saastamoinen模型改正^[13]，而湿延迟部分作为随机游走过程估计^[12]，谱密度取10^－4 m/$\sqrt {\rm{s}} $；载波相位模糊度不固定，保持浮点解状态，在连续弧段内为常数，在发生周跳时重新初始化。对于静态PPP，坐标参数作为常数处理；对于动态PPP，坐标参数当作白噪声过程处理。

2.2 收敛时间

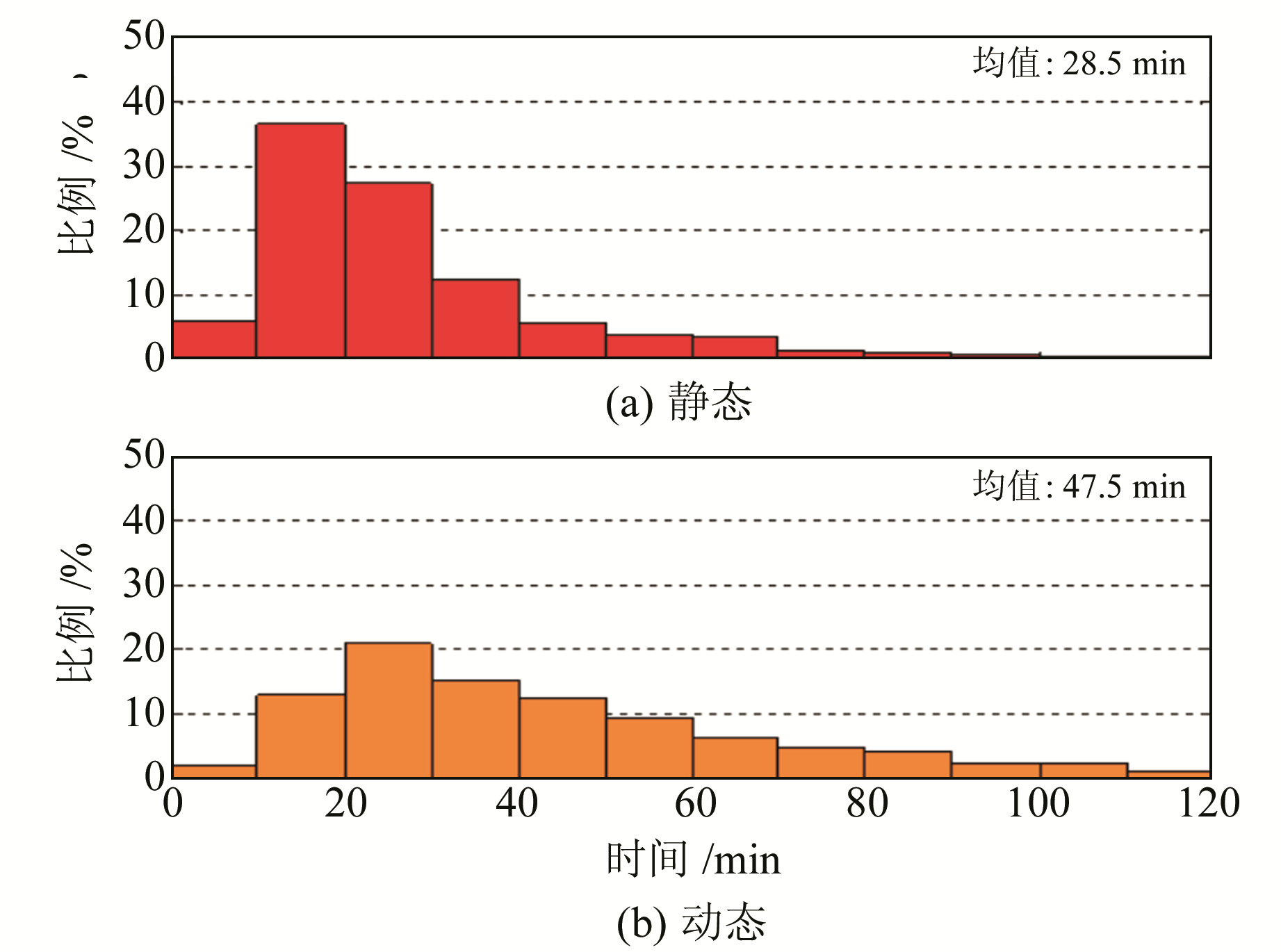
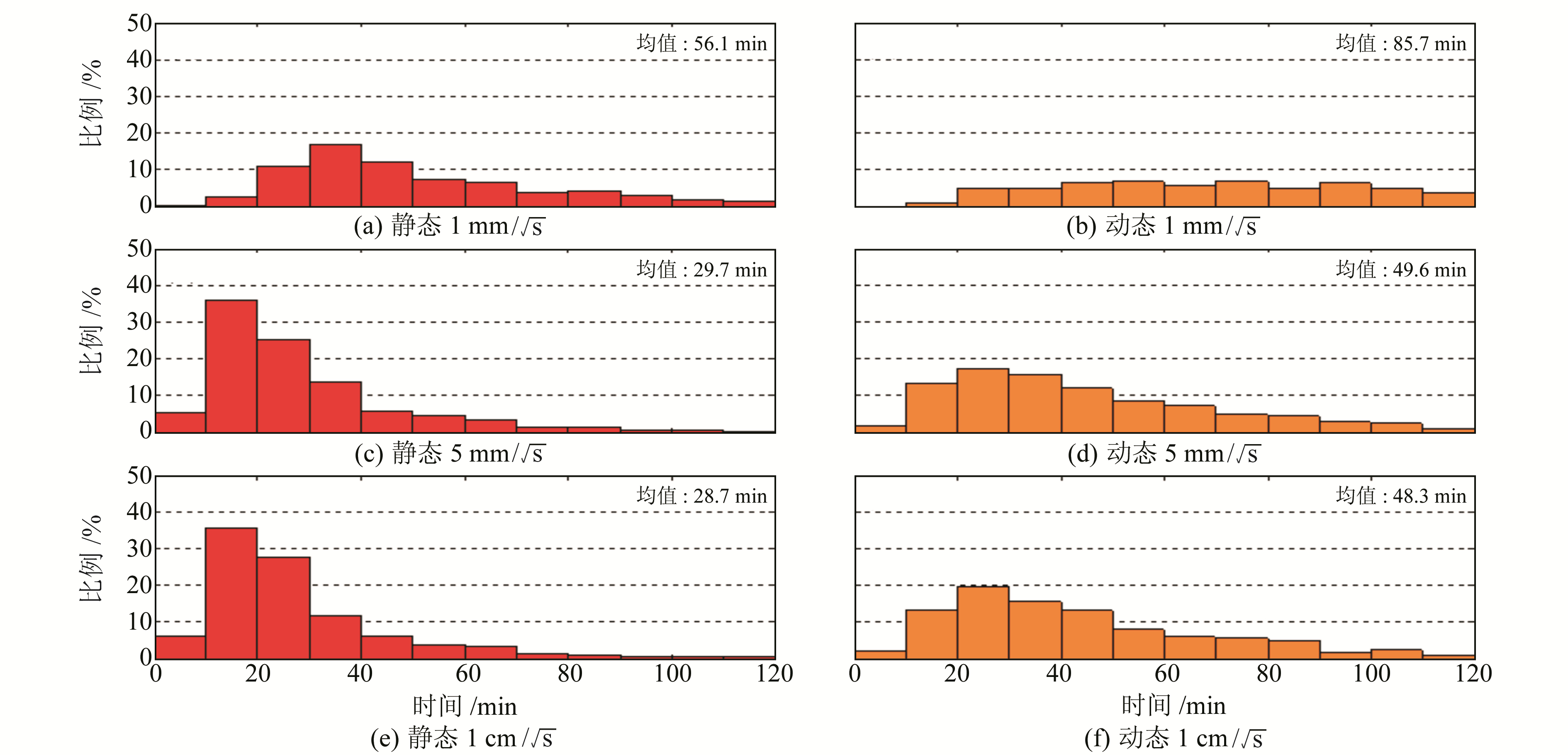
图 2为方案1的静态和动态GPS PPP收敛时间统计结果，平均收敛时间分别为28.5 min和47.5 min。由图可见，静态收敛时间比较集中，大多在10~40 min之内，占76.5%；而动态收敛时间相对比较离散，大多分布于10~90 min，占86.1%。图 3为方案2的静态和动态GPS PPP收敛时间分布图。由图可见，当谱密度$ {q_{\bar I_{r, 1}^s}}$从1 mm/ $\sqrt {\rm{s}} $到5 mm/ $\sqrt {\rm{s}} $时，静态平均收敛时间从56.1 min迅速减至29.7 min，减小了47.1%；动态平均收敛时间从85.7 min骤降至49.6 min，减小了42.1%。当谱密度$ {q_{\bar I_{r, 1}^s}}$从5 mm/$\sqrt {\rm{s}} $到1 cm/$\sqrt {\rm{s}} $时，静态和动态平均收敛时间分别减小1 min左右。对于全球站点来说，当方案2的谱密度$ {q_{\bar I_{r, 1}^s}}$取1 cm/$\sqrt {\rm{s}} $时，静态和动态的平均收敛时间才与方案1的相当。

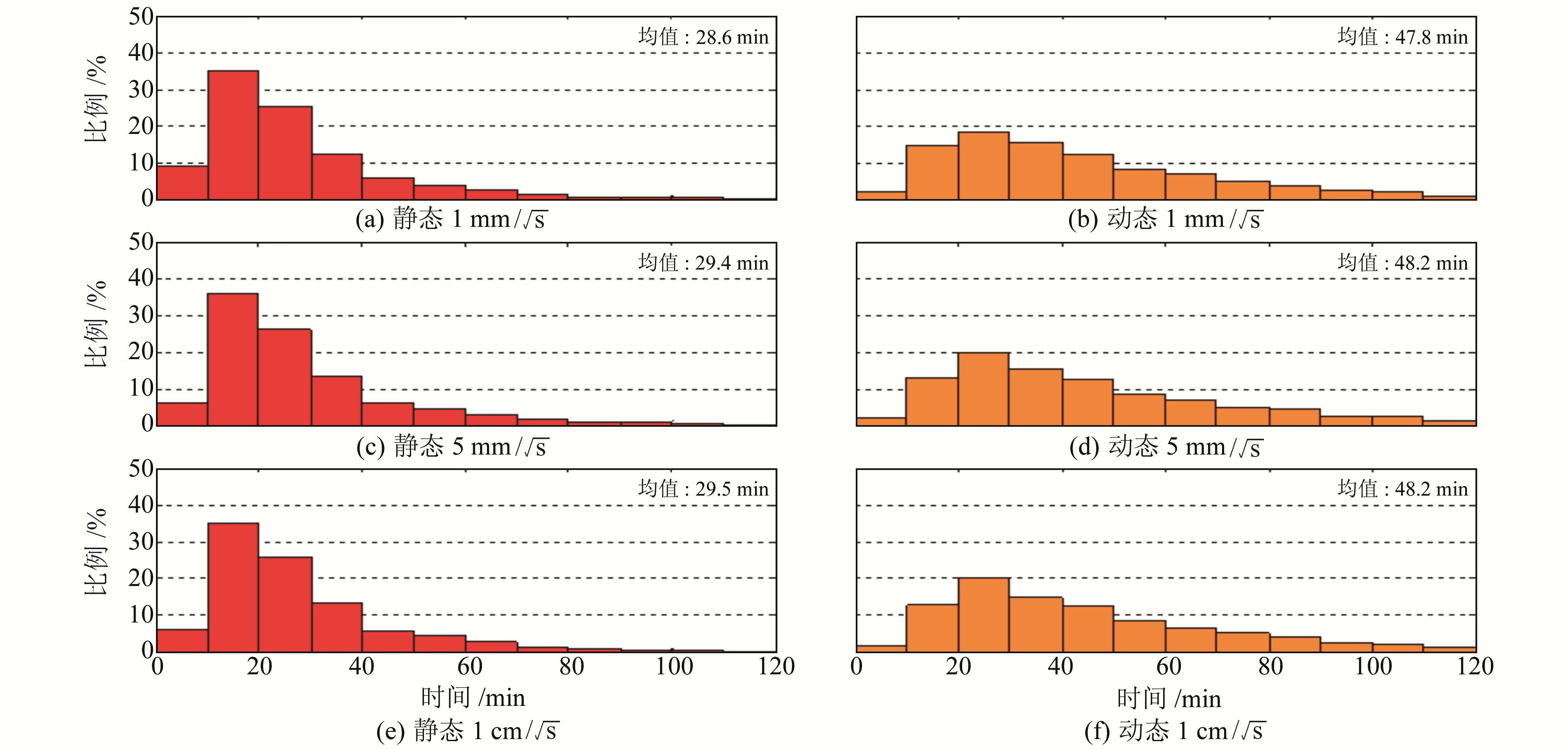
图 4为方案3的静态和动态GPS PPP收敛时间统计结果。由图可见，当谱密度$ {q_{\bar I_{r, 1}^s}}$从1 mm/$\sqrt {\rm{s}} $到5 mm/$\sqrt {\rm{s}} $时，静态和动态平均收敛时间均有小幅增加(静态从28.6 min到29.4 min，动态从47.8 min到48.2 min)。当谱密度$ {q_{\bar I_{r, 1}^s}}$从5 mm/$\sqrt {\rm{s}} $到1 cm/$\sqrt {\rm{s}} $时，静态和动态平均收敛时间基本保持不变。谱密度$ {q_{\bar I_{r, 1}^s}}$的变化对静态和动态平均收敛时间影响不大。在取较小的谱密度(1 mm/ s)时，方案3收敛性能要远优于方案2，静态PPP的收敛时间减少49.0%(从56.1 min减少到28.6 min)，动态PPP的收敛时间减少44.2%(从85.7 min减少到47.8 min)。对于全球站点来说，当方案3的谱密度$ {q_{\bar I_{r, 1}^s}}$取1 mm/$\sqrt {\rm{s}} $时，静态和动态的平均收敛时间与方案1的相当。

2.3 定位精度

图 5为方案1、方案2、方案3的静态和动态GPS PPP三维位置平均RMS统计结果。与平均收敛时间类似，除了方案1在谱密度$ {q_{\bar I_{r, 1}^s}}$为1 mm/$\sqrt {\rm{s}} $的结果较差以外(静态RMS为11.2 cm，动态为17.6 cm)，其他情况下3个方案的RMS相差不大。由图可见，非组合静态GPS PPP三维RMS在5 cm左右，动态在8 cm左右。

3 结语

采用静态和仿动态GPS PPP定位方式，通过收敛时间和定位精度2个指标，系统分析了3种不同方案(白噪声模型、传统随机游走模型和本文提出的顾及电离层延迟历元间变化的随机游走模型)在GPS非组合PPP的定位性能。结果表明，传统随机游走模型易受电离层延迟谱密度的影响，这对于全球不同区域、不同电离层活跃情况下的定位非常不利；本文提出的顾及电离层延迟历元间变化的随机游走模型，PPP收敛时间和定位精度基本不受谱密度的影响，且收敛时间和定位精度与白噪声模型相当。

致谢: 感谢IGS及其分析中心为本文提供实验数据及精密轨道钟差产品服务。