近年来变量误差(errors-in-variables, EIV)^[1]模型得到充分研究^[2-4]。EIV模型考虑经典Gauss-Markov模型所忽略的系数矩阵的误差，能在一定程度上提高参数估值的精度。文献[4]提出Partial EIV模型，提取系数矩阵中存在误差的部分随机元素作为参数迭代求解，减少模型中待改正量的个数，提高计算效率，更适合解决实际问题和进行后续的精度评定工作。

考虑随机模型不准确的问题，文献[5]研究EIV模型的MINQUE(最小范数二次无偏估计)法，分析其可估性、稳定性，并给出由于参数估值偏差引起的方差分量估值的偏差表达式；文献[6]推导相关观测的Partial EIV模型方差分量估计。尽管已有研究证明，方差分量估计能够得到更好的参数估值，然而对于方差分量估计法所获得参数估值的精度却少有研究。目前总体最小二乘非线性精度评定方法主要包括如下几种：基于参数估值的最后一步迭代表达式，由协方差传播律得到参数估值的一阶近似协方差^[7]；求取总体最小二乘参数估值对于观测量的一阶偏导数来计算其协方差阵^[8]；用近似函数法推导参数估值二阶近似的协方差阵和均方误差矩阵^[9]；运用SUT采样法对总体最小二乘算法进行精度评定，并证明能够达到二阶精度^[10-11]；通过蒙特卡罗模拟计算参数估值的近似协方差阵^[12]等。但对于采用方差分量估计方法得到的Partial EIV模型参数估值的精度信息多按照参数估值的最后一步迭代表达式由协方差传播律计算，由于省略了二阶及以上项故只能达到一阶精度。如采用蒙特卡罗模拟法生成大量样本，由于估计中加入方差分量导致计算成本巨大，且存在随机样本点不可估的情况；其次不同模拟次数会对统计结果造成影响。基于二阶导数推导的近似函数虽能获得参数估值的二阶精度信息，但其需要进行Jacobian矩阵计算和复杂的Hessian矩阵推导。本文将SUT法引入Partial EIV模型方差分量估计，通过固定的采样策略生成少量采样点，能够在避免大量计算和复杂公式推导的同时，获得更为精确的参数估值和合理的精度信息。

此外文献[13]等证明，在观测数据量趋于无穷时，EIV模型的参数估值具有渐进无偏性。但现实情况下，由于观测数据总是有限的，模型的非线性会导致TLS解的有偏。同理，SUT法的Partial EIV模型方差分量估计所得的参数估值也会产生偏差，且偏差的大小取决于模型的非线性程度^[4]，所以考虑参数估值的偏差改正是有必要的。

因此，本文将SUT采样法引入到Partial EIV模型方差分量估计中，求解参数估值和精度信息，并给出迭代算法；进一步通过SUT法修正参数初值进行采样，得到偏差改正后的参数估值和二阶精度信息，完善了Partial EIV模型方差分量估计精度评定理论；最后通过算例验证本文方法可行有效。

1 Partial EIV模型解算

Partial EIV的数学模型^[6]表示如下。函数模型为：

$ \left\{ \begin{array}{l} \mathit{\boldsymbol{y}} = \left( {{\mathit{\boldsymbol{\beta }}^{\rm{T}}} \otimes {\mathit{\boldsymbol{I}}_n}} \right)\left( {\mathit{\boldsymbol{h}} + \mathit{\boldsymbol{B\tilde a}}} \right) - {\mathit{\boldsymbol{e}}_y}\\ \mathit{\boldsymbol{a}} = \mathit{\boldsymbol{\tilde a}} - {\mathit{\boldsymbol{e}}_a}\\ {\rm{vec}}\left( {\mathit{\boldsymbol{\tilde a}}} \right) = \mathit{\boldsymbol{h}} + \mathit{\boldsymbol{B\tilde \alpha }} \end{array} \right. $

(1)

随机模型为：

$ \mathit{\boldsymbol{e}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{e}}_y}}\\ {{\mathit{\boldsymbol{e}}_a}} \end{array}} \right] \sim \left( {\left[ {\begin{array}{*{20}{l}} {\bf{0}}\\ {\bf{0}} \end{array}} \right],\sigma _0^2{\mathit{\boldsymbol{Q}}_e} = \sigma _0^2{\mathit{\boldsymbol{P}}^{ - 1}}} \right) $

(2)

式中，y ∈R^n×1为观测向量，e_y∈R^n×1为观测向量误差，${\mathit{\boldsymbol{\tilde a}}} $ ∈R^n×m为系数矩阵的真值，${\mathit{\boldsymbol{\tilde a}}} $ ∈R^t×1为系数矩阵中随机元素组成的真值列向量，e_a∈R^t×1为其误差向量，a ∈R^t×1为系数矩阵中的随机元素组成的列向量，h ∈R^nm×1为系数矩阵中由固定元素组成的列向量，β ∈R^m×1为未知参数向量，B ∈R^nm×t为构造的固定矩阵，$\otimes $表示张量积，vec(·)表示矩阵的拉直运算，$\mathit{\boldsymbol{\tilde A\beta }} = \left( {{\mathit{\boldsymbol{\beta }}^{\rm{T}}} \otimes {\mathit{\boldsymbol{I}}_n}} \right)·{\mathop{\rm vec}\nolimits} (\mathit{\boldsymbol{\tilde A}}), \sigma _0^2 $为单位权方差，矩阵Q_e和P分别表示误差向量e的协因数阵和权阵。

文献[6]将Partial EIV模型线性化：

$ \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{y}}\\ \mathit{\boldsymbol{a}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{e}}_y}}\\ {{\mathit{\boldsymbol{e}}_a}} \end{array}} \right] = f\left( x \right) $

(3)

式中，$f(x) = \left[ {\begin{array}{*{20}{c}} {\left( {{\mathit{\boldsymbol{\beta }}^{\rm{T}}} \otimes {\mathit{\boldsymbol{I}}_n}} \right)(\mathit{\boldsymbol{h}} + \mathit{\boldsymbol{B}}\mathit{\boldsymbol{\widetilde a}})}\\ {\mathit{\boldsymbol{\widetilde a}}} \end{array}} \right], \mathit{\boldsymbol{x}} = \left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{\beta }}\\ {\mathit{\boldsymbol{\widetilde a}}} \end{array}} \right] $。将函数模型于x₀处进行泰勒展开得到：

$ \mathit{\boldsymbol{x}} = {\mathit{\boldsymbol{x}}_0} + \Delta \mathit{\boldsymbol{x}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\beta }}_0}}\\ {{\mathit{\boldsymbol{a}}_0}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {\Delta \mathit{\boldsymbol{\beta }}}\\ {\Delta \mathit{\boldsymbol{a}}} \end{array}} \right] $

(4)

$ \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{y}}\\ \mathit{\boldsymbol{a}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{e}}_y}}\\ {{\mathit{\boldsymbol{e}}_a}} \end{array}} \right] = f\left( {{\mathit{\boldsymbol{x}}_0}} \right) + \mathit{\boldsymbol{\hat J}}\Delta \mathit{\boldsymbol{x}} $

(5)

得到间接平差形式：

$ \mathit{\boldsymbol{\hat L}} + \mathit{\boldsymbol{e}} = \mathit{\boldsymbol{\hat J}}\Delta \mathit{\boldsymbol{\hat x}} $

(6)

式中，$\hat{\boldsymbol{L}}=\left[\begin{array}{l}{\boldsymbol{y}-\boldsymbol{A} \boldsymbol{\beta}_{i}} \\ {\boldsymbol{a}-\boldsymbol{a}_{i}}\end{array}\right], \boldsymbol{e}=\left[\begin{array}{c}{\boldsymbol{e}_{y}} \\ {\boldsymbol{e}_{a}}\end{array}\right], \boldsymbol{Q}=\left[\begin{array}{ll}{\boldsymbol{Q}_{y}} & {\bf{0}} \\ {\bf{0}} & {\boldsymbol{Q}_{a}}\end{array}\right] $,

$ \Delta \mathit{\boldsymbol{\hat x}} = {\left( {{{\mathit{\boldsymbol{\hat J}}}^{\rm{T}}}\mathit{\boldsymbol{Q}}_e^{ - 1}\mathit{\boldsymbol{\hat J}}} \right)^{ - 1}}{\mathit{\boldsymbol{\hat J}}^{\rm{T}}}\mathit{\boldsymbol{Q}}_e^{ - 1}\mathit{\boldsymbol{\hat L}} $

(7)

通过迭代计算得到参数估值为：

$ {\mathit{\boldsymbol{\hat x}}^{i + 1}} = {\mathit{\boldsymbol{\hat x}}^i} + \Delta \mathit{\boldsymbol{\hat x}} $

(8)

$ \mathit{\boldsymbol{\hat e}} = \mathit{\boldsymbol{\hat J}}\Delta \mathit{\boldsymbol{x}} - \mathit{\boldsymbol{\hat L}} $

(9)

2 最小范数二次无偏估计法

文献[6]将Partial EIV模型线性化后推导了其最小范数二次无偏估计(MINQUE法)公式：

$ \left\{ \begin{array}{l} \mathit{\boldsymbol{S}} = {\rm{tr}}\left( {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{Q}}_k}\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{Q}}_l}} \right) = \\ \;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {{\rm{tr}}\left( {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{Q}}_1}\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{Q}}_1}} \right)}&{{\rm{tr}}\left( {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{Q}}_1}\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{Q}}_2}} \right)}\\ {{\rm{tr}}\left( {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{Q}}_2}\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{Q}}_1}} \right)}&{{\rm{tr}}\left( {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{Q}}_2}\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{Q}}_2}} \right)} \end{array}} \right]\\ \mathit{\boldsymbol{W}} = \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat e}}}^{\rm{T}}}\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{Q}}_1}\mathit{\boldsymbol{C\hat e}}}&{{{\mathit{\boldsymbol{\hat e}}}^{\rm{T}}}\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{Q}}_2}\mathit{\boldsymbol{C\hat e}}} \end{array}} \right] \end{array} \right. $

(10)

式中, $ \boldsymbol{C}=\boldsymbol{Q}_{e}^{-1}-\boldsymbol{Q}_{e}^{-1} \hat{\boldsymbol{J}}\left(\hat{\boldsymbol{J}}^{\mathrm{T}} \boldsymbol{Q}_{e}^{-1} \hat{\boldsymbol{J}}\right)^{-1} \hat{\boldsymbol{J}} \boldsymbol{Q}_{e}^{-1}$。

方差分量向量为：

$ \mathit{\boldsymbol{\hat \theta }} = {\mathit{\boldsymbol{S}}^{ - 1}}\mathit{\boldsymbol{W}} $

(11)

3 SUT法

对于非线性函数：

$ \mathit{\boldsymbol{\xi }} = \mathit{\Phi }\left( \mathit{\boldsymbol{X}} \right) $

(12)

SUT法的计算过程^[14]如下：

1) 构造sigma点。根据随机量X的先验统计信息E(X)和D(X)构造2t+1个sigma点χ_i：

$ \left\{ \begin{array}{l} {\mathit{\boldsymbol{\chi }}_0} = E\left( \mathit{\boldsymbol{X}} \right)\\ {\mathit{\boldsymbol{\chi }}_i} = E\left( \mathit{\boldsymbol{X}} \right) + {\left( {\sqrt {t + \lambda } \sqrt {D\left( \mathit{\boldsymbol{X}} \right)} } \right)_i}\\ \;\;\;\;\;\;i = 1,2, \cdots ,t\\ {\mathit{\boldsymbol{\chi }}_i} = E\left( \mathit{\boldsymbol{X}} \right) + {\left( {\sqrt {t + \lambda } \sqrt {D\left( \mathit{\boldsymbol{X}} \right)} } \right)_i}\\ \;\;\;\;\;\;i = t + 1,t + 2, \cdots ,2t \end{array} \right. $

(13)

式中，sigma点共同组成sigma点矩阵$ \mathit{\boldsymbol{\chi }} = \left[ {{\mathit{\boldsymbol{\chi }}_0}, {\mathit{\boldsymbol{\chi }}_1}} \right., \cdots , {\mathit{\boldsymbol{\chi }}_{2t}}];\sqrt {D(\mathit{\boldsymbol{X}})} $为对D(X)进行Cholesky分解生成的下三角矩阵，为矩阵$ (\sqrt{t+\lambda} \sqrt{D(\boldsymbol{X})})$的第i列；$ \lambda=\alpha^{2}(t+\kappa)-t$为比例参数，常数α决定粒子点在E(X)附近的分布范围，取值范围为10^-4≤α≤1，一般推荐值为10^-3(κ为另一个比例参数，通常取值为3-t或0^[14])。

2) 计算sigma点经过非线性变换后的样本点：

$ {\mathit{\boldsymbol{v}}_i} = \mathit{\Phi }\left( {{\mathit{\boldsymbol{\chi }}_i}} \right),i = 0,1, \cdots ,2t $

(14)

3) 确定样本点v_i的权值：

$ \left\{ \begin{array}{l} W_0^m = \lambda /\left( {t + \lambda } \right)\\ W_0^c = \lambda /\left( {t + \lambda } \right) + 1 - {\alpha ^2} + \beta \\ W_i^m = W_i^c = 1/\left( {2\left( {t + \lambda } \right)} \right),i = 1,2, \cdots ,2t \end{array} \right. $

(15)

式中，W_i^m和W_i^c(i=0, 1, 2，…, 2t)分别用于均值和协方差阵计算。对于正态分布，β=2为最优^[14]。

4) 计算非线性函数的均值以及协方差阵：

$ E(\mathit{\boldsymbol{\xi }}) = \sum\limits_{i = 0}^{2t} {W_i^m} {\mathit{\boldsymbol{v}}_i} $

(16)

$ D(\boldsymbol{\xi})=\sum\limits_{i=0}^{2 t} W_{i}^{c}\left(\boldsymbol{v}_{i}-E(\boldsymbol{\xi})\right)\left(\boldsymbol{v}_{i}-E(\boldsymbol{\xi})\right)^{\mathrm{T}} $

(17)

3.1 SUT法精度评定

由式(7)、式(8)可以看出，Partial EIV模型的MINQUE法每一步迭代过程的解向量都是观测向量y和系数矩阵A经过非线性函数

$ g\left(\hat{\boldsymbol{x}}^{i+1}\right)=\hat{\boldsymbol{x}}^{i}+\left(\hat{\boldsymbol{J}}^{\mathrm{T}} \boldsymbol{Q}_{e}^{-1} \hat{\boldsymbol{J}}\right)^{-1} \boldsymbol{J}^{\mathrm{T}} \boldsymbol{Q}_{e}^{-1} \hat{\boldsymbol{L}} $

(18)

计算得到，且参数估值${\mathit{\boldsymbol{\hat \beta }}} $包含于解向量${\mathit{\boldsymbol{\hat x}}} $中。因此，用向量l =[y, a]^T表示观测向量y和随机元素a，参数估值${\mathit{\boldsymbol{\hat \beta }}} $和向量l之间的非线性关系可以表示为：

$ \hat{\boldsymbol{\beta}}^{0}=\varphi(\boldsymbol{l}) $

(19)

式中，φ(·)表示最小二乘估值与观测向量y和随机元素a组成向量l之间的非线性关系。

同理，一步参数迭代估值可以表示为：

$ \hat{\boldsymbol{\beta}}^{1}=g\left(\hat{\boldsymbol{\beta}}^{0}, \boldsymbol{l}\right) $

(20)

因此，最终的参数估值表达式为：

$ \mathit{\boldsymbol{\widehat \beta }} = {\mathit{\boldsymbol{\widehat \beta }}^{i + 1}} = \underbrace {g\left( {g\left( { \cdots g\left( {g\left( {} \right.} \right.} \right.} \right.}_{i + 1}\left. {\left. {\varphi \left( \mathit{\boldsymbol{l}} \right),\mathit{\boldsymbol{l}}} \right),\mathit{\boldsymbol{l}}} \right)\left. { \cdots \left. {,\mathit{\boldsymbol{l}}} \right),\mathit{\boldsymbol{l}}} \right) $

(21)

式(15)表明，总体最小二乘和方差分量估计的迭代过程使得参数估值和观测值之间的非线性关系非常复杂，且逐步的迭代过程使得许多中间变量以及参数和改正数的每一步估值都具有随机性。但已有文献多用参数估值的迭代公式和协方差传播律来获得其精度信息，由于泰勒展开时忽略了高阶项故只能达到一阶精度。若通过近似函数法来进行精度评定，必然需要复杂的求导计算。为了避开复杂的求导运算和公式推导，同时获得更合理的精度信息，本文在Partial EIV模型方差分量估计法中引进SUT采样法^[9]，避免复杂的求导运算，且得到更为精确的参数估值和二阶精度信息。

设计算法1：

1) 通过Partial EIV模型方差分量估计法求得参数估值$ {\mathit{\boldsymbol{\hat \beta }}}$、改正数$ {\mathit{\boldsymbol{\hat V}}}$和方差分量$ \hat{\boldsymbol{\theta}}_{0}^{2}=\left[\hat{\sigma}_{1}^{2}, \hat{\sigma}_{2}^{2}\right]^{\mathrm{T}}$。

2) 根据输入量$l=[\boldsymbol{y}, \boldsymbol{a}]^{\mathrm{T}}、\hat{\boldsymbol{V}}、\boldsymbol{Q}_{{l}} $和方差分量估值$ \hat{\boldsymbol{\theta}}_{0}^{2}$构建观测值向量l的均值和协方差阵$\hat{\boldsymbol{L}} $，$ = \mathit{\boldsymbol{l}} + \hat{\boldsymbol{V}}, {\mathit{\boldsymbol{D}}_l} = \left[ {\begin{array}{*{20}{c}} {\hat \sigma _1^2{\mathit{\boldsymbol{Q}}_y}}&{\bf{0}}\\ {\bf{0}}&{\hat \sigma _2^2{\mathit{\boldsymbol{Q}}_a}} \end{array}} \right] $。

3) 2t+1个sigma点列向量l_i由比例对称采样策略构建：

$ \left\{ \begin{array}{l} {\mathit{\boldsymbol{l}}_0} = \mathit{\boldsymbol{\hat l}}\\ {\mathit{\boldsymbol{l}}_i} = \mathit{\boldsymbol{\hat l}} + {\left( {\sqrt {t + \lambda } \sqrt {{\mathit{\boldsymbol{D}}_l}} } \right)_i}\\ \;\;\;\;\;i = 1,2, \cdots ,t\\ {\mathit{\boldsymbol{l}}_i} = \mathit{\boldsymbol{\hat l}} + {\left( {\sqrt {t + \lambda } \sqrt {{\mathit{\boldsymbol{D}}_l}} } \right)_i}\\ \;\;\;\;\;i = t + 1,t + 2, \cdots 2t \end{array} \right. $

(22)

式中，$\sqrt{\boldsymbol{D}_{l}} $为D_l卡洛斯基分解得到的下三角矩阵，$ \left(\sqrt{t+\lambda} \sqrt{\boldsymbol{D}_{l}}\right)_{i}$为矩阵$ \left(\sqrt{t+\lambda} \sqrt{\boldsymbol{D}_{l}}\right)$的第i列。$\lambda=\alpha^{2}(t+k)-t $为比例参数，常数α的值为0.001；k为另一个比例常数，取0。

4) 计算sigma点列向量经过非线性变换方差分量估计后生成的样本：

$ \boldsymbol{v}_{i}^{\hat{\beta}}=g\left(\boldsymbol{l}_{i}\right), i=0,1,2, \cdots, 2 t $

(23)

5) 确定样本$\boldsymbol{v}_{i}^{\hat{\beta}} $的权值：

$ \left\{\begin{array}{l}{W_{0}^{m}=\lambda /(t+\lambda)} \\ {W_{0}^{c}=\lambda /(t+\lambda)+1-\alpha^{2}+b} \\ {W_{i}^{m}=W_{i}^{c}=1 /(2(t+\lambda)), i=1,2, \cdots, 2 t}\end{array}\right. $

(24)

式中，b=2。

6) 加权计算参数估值的均值$E(\mathit{\boldsymbol{\widehat \beta }}) $、参数估值近似协方差阵${\mathit{\boldsymbol{D}}_{\hat \beta \hat \beta }} $和标准差$ \boldsymbol{\sigma}_{\hat{\beta}_{i}}$：

$ E(\mathit{\boldsymbol{\widehat \beta }}) = \sum\limits_{i = 0}^{2t} {W_i^m} \mathit{\boldsymbol{v}}_i^{\hat \beta } $

(25)

$ \hat{\boldsymbol{\beta}}=E(\hat{\boldsymbol{\beta}}) $

(26)

$ {\mathit{\boldsymbol{D}}_{\hat \beta \hat \beta }} = \sum\limits_{i = 0}^{2t} {W_i^c\left( {\mathit{\boldsymbol{v}}_i^{\hat \beta } - E\left( {\mathit{\boldsymbol{\hat \beta }}} \right)} \right){{\left( {\mathit{\boldsymbol{v}}_i^{\hat \beta } - E\left( {\mathit{\boldsymbol{\hat \beta }}} \right)} \right)}^{\rm{T}}}} $

(27)

$ {\mathit{\boldsymbol{\sigma }}_{\hat \beta }} = \sqrt {{\mathit{\boldsymbol{D}}_{\hat \beta \hat \beta }}} $

(28)

式中，$ E(\mathit{\boldsymbol{\widehat \beta }})$即为SUT法求得的达到二阶精度的参数加权均值，${\mathit{\boldsymbol{\sigma }}_{\hat \beta }} $为其二阶精度信息。本文根据文献[14]方法，以观测值的平差值作为观测值的均值，以观测值的后验协方差阵作为观测值的协方差阵。

3.2 SUT法偏差改正

考虑到模型线性化时省略掉的高次项和复杂的非线性迭代导致的参数估值的有偏性影响，以及初值的变化对方差分量估值的影响较大，因此设计了算法2。在算法1的基础上，对参数估值和改正数进行偏差改正，将偏差改正后的变量进行SUT法采样计算协方差阵和标准差：

$ {\mathit{\boldsymbol{b}}_{\hat \beta }} = E(\mathit{\boldsymbol{\widehat \beta }}) - \mathit{\boldsymbol{\widehat \beta }} $

(29)

$ \mathit{\boldsymbol{\widetilde \beta }} = {\mathit{\boldsymbol{\widehat \beta }}_{{\rm{vee}}}} - {\mathit{\boldsymbol{b}}_{\hat \beta }} $

(30)

$ {\mathit{\boldsymbol{b}}_{{{\mathit{\boldsymbol{\hat e}}}_a}}} = E\left( {{{\mathit{\boldsymbol{\hat e}}}_a}} \right) $

(31)

$ {\mathit{\boldsymbol{\tilde e}}_a} = {\mathit{\boldsymbol{\hat e}}_a} - {\mathit{\boldsymbol{b}}_{{{\hat e}_a}}} $

(32)

进而可以得到偏差改正后的参数估值：

$ \mathit{\boldsymbol{\tilde x}} = \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat \beta }}}_{{\rm{vce}}}} - {\mathit{\boldsymbol{b}}_{{{\hat e}_a}}}}\\ {\mathit{\boldsymbol{a}} - {{\mathit{\boldsymbol{\tilde e}}}_a}} \end{array}} \right] $

(33)

并以此构造新的观测值向量均值$ \mathit{\boldsymbol{\tilde l}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{y}}\\ {\mathit{\boldsymbol{a}} - {{\mathit{\boldsymbol{\tilde e}}}_\mathit{\boldsymbol{a}}}} \end{array}} \right]$，及其协方差阵$ \boldsymbol{D}_{i}=\left[\begin{array}{cc}{\hat{\sigma}_{1}^{2} \boldsymbol{Q}_{y}} & {\bf{0}} \\ {\bf{0}} & {\hat{\sigma}_{2}^{2} \boldsymbol{Q}_{a}}\end{array}\right]$。重复式(23)计算采样点的参数估值：

$ \mathit{\boldsymbol{v}}_i^{\hat \beta } = f\left( {{{\mathit{\boldsymbol{\tilde l}}}_i}} \right),i = 0,1,2, \cdots ,2t $

(34)

得到改正后参数估值的协方差阵和标准差：

$ {\mathit{\boldsymbol{D}}_{\hat \beta \hat \beta }} = \sum\limits_{i = 0}^{2t} {W_i^c\left( {\mathit{\boldsymbol{v}}_i^{\hat \beta } - \mathit{\boldsymbol{\tilde \beta }}} \right){{\left( {\mathit{\boldsymbol{v}}_i^{\hat \beta } - \mathit{\boldsymbol{\hat \beta }}} \right)}^{\rm{T}}}} $

(35)

$ {\mathit{\boldsymbol{\sigma }}_{\hat \beta }} = \sqrt {{\mathit{\boldsymbol{D}}_{\hat \beta \hat \beta }}} $

(36)

4 算例分析 4.1 算例1

为了验证本文思路及方法的有效性，算例1为直线拟合模型，设置参数真值β₁、β₂分别为-1.5和3.2，在0.9~11区间等间距生成真值向量$ {\mathit{\boldsymbol{\tilde x}}}$，并求得${\mathit{\boldsymbol{\tilde y}}} $，分别给$ {\mathit{\boldsymbol{\tilde x}}}$、$ {\mathit{\boldsymbol{\tilde y}}}$加上由matlab函数mvnrnd生成的方差为0.02× Q_x、0.02× Q_y的随机误差，其中观测值y、x和模拟的权值P_y、P_x(Q_x= P_x^－1, Q_y= P_y^－1)见表 1，并用表 2算法进行实验。

直线拟合模型为：

$ \left[ {\begin{array}{*{20}{c}} {{y_1}}\\ {{y_2}}\\ \vdots \\ {{y_{10}}} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {{e_{{y_1}}}}\\ {{e_{{y_2}}}}\\ \vdots \\ {{e_{{y_{10}}}}} \end{array}} \right] = \left( {\left[ {\begin{array}{*{20}{c}} {{x_1}}&1\\ {{x_2}}&1\\ \vdots & \vdots \\ {{x_{10}}}&1 \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {{e_{{x_1}}}}&0\\ {{e_{{x_2}}}}&0\\ \vdots & \vdots \\ {{e_{{x_{10}}}}}&0 \end{array}} \right]} \right)\left[ {\begin{array}{*{20}{c}} {{\beta _1}}\\ {{\beta _2}} \end{array}} \right] $

(37)

其中，[β₁, β₂]^T为待估参数。根据本算例的数据个数，直线拟合模型中固定矩阵B和向量h的形式应为：

$ \mathit{\boldsymbol{h}} = {\left[ {\begin{array}{*{20}{c}} {\underbrace {0\;0 \cdots 0}_{10}}&{\underbrace {1\;1 \cdots 1}_{10}} \end{array}} \right]^{\rm{T}}} $

(38)

$ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} 1\\ 0 \end{array}} \right] \otimes {\mathit{\boldsymbol{I}}_{10}} $

(39)

直线拟合模型不同方案的参数估值见表 3，不同方案的标准差见表 4。$\|\hat{\boldsymbol{\beta}}-\tilde{\boldsymbol{\beta}}\| $为参数估值与真值的差值范数。方案3、方案4、方案5的一阶精度由协方差传播律得到。

由表 3可见，方案4得到的参数估值与其他方案相近，且方案5偏差改正后的参数估值更接近真值，证明SUT法应用于Partial EIV模型方差分量估计的可行性和偏差改正的必要性。同时由表 4可见，方案4得到的精度信息与近似函数法和Partial EIV模型方差分量估计的近似函数法结果相近，表明SUT法在Partial EIV模型方差分量估计精度评定时仍能达到二阶精度。由于考虑了二阶误差，二阶精度信息在数值上都大于一阶精度信息，表明常用方法所得的一阶精度信息可能高估了Partial EIV模型方差分量估计参数估值的精度。为更合理地反映参数估值的精度，有必要研究Partial EIV模型方差分量估计参数估值的高阶精度信息。

4.2 算例2

算例1中直线拟合模型非线性强度弱，观测值误差较小，导致偏差较小。文献[15]指出，系数矩阵的信噪比很大时参数估值的相对偏差很小，LS法与TLS法结果没有必然差别。故将本文方法应用于式(40)更为复杂、非线性更强的四参数坐标转换模型：

$ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{X_1}}\\ {{Y_1}}\\ \vdots \\ {{X_n}}\\ {{Y_n}} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {{e_{{X_1}}}}\\ {{e_{{Y_1}}}}\\ \vdots \\ {{e_{{X_n}}}}\\ {{e_{{Y_n}}}} \end{array}} \right] = \left( {\left[ {\begin{array}{*{20}{c}} {{x_1}}&{ - {y_1}}&1&0\\ {{y_1}}&{{x_1}}&0&1\\ \vdots & \vdots & \vdots & \vdots \\ {{x_n}}&{ - {y_n}}&1&0\\ {{y_n}}&{{x_n}}&0&1 \end{array}} \right] - } \right.}\\ {\left. {\left[ {\begin{array}{*{20}{c}} {{e_{{x_1}}}}&{ - {y_1}}&1&0\\ {{e_{{y_1}}}}&{{x_1}}&0&1\\ \vdots & \vdots & \vdots & \vdots \\ {{e_{{x_n}}}}&{ - {e_{{y_n}}}}&1&0\\ {{e_{{y_n}}}}&{{e_{{x_n}}}}&0&1 \end{array}} \right]} \right)\left[ {\begin{array}{*{20}{c}} {{\beta _1}}\\ {{\beta _2}}\\ {{\beta _3}}\\ {{\beta _4}} \end{array}} \right]} \end{array} $

(40)

模拟5个坐标点，设置转换参数真值$ {\mathit{\boldsymbol{\tilde \beta }}}$ =[0.9 0.6 1 5]^T，给出原坐标点和目标坐标点的权阵P_xy和P_XY，分别给原始坐标和目标坐标加上matlab函数mvnrnd生成的方差为0.025× Q_xy和0.01× Q_XY的随机误差，坐标观测值和协因数阵见表 5。

根据坐标转换模型和坐标点的个数，给出向量h和矩阵B的形式：

$ \mathit{\boldsymbol{h}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{h}}_1}}\\ {{\mathit{\boldsymbol{h}}_2}}\\ {{\mathit{\boldsymbol{h}}_3}} \end{array}} \right],\mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_1}}\\ {{\mathit{\boldsymbol{B}}_2}}\\ {{\mathit{\boldsymbol{B}}_3}}\\ {{\mathit{\boldsymbol{B}}_4}} \end{array}} \right] $

其中，$ {\mathit{\boldsymbol{h}}_1} = {[\underbrace {\begin{array}{*{20}{c}} 0&0& \cdots &0&0 \end{array}}_{20}]^{\rm{T}}}, {\mathit{\boldsymbol{h}}_2} = {[\underbrace {\begin{array}{*{20}{c}} 1&0& \cdots &1&0 \end{array}}_{10}]^{\rm{T}}}, {\mathit{\boldsymbol{h}}_3} = $ $ {[\underbrace {\begin{array}{*{20}{c}} 0&1& \cdots &0&1 \end{array}}_{10}]^{\rm{T}}}, {\mathit{\boldsymbol{B}}_1} = {\mathit{\boldsymbol{E}}_5} \otimes \left[ {\begin{array}{*{20}{c}} 1&0\\ 0&1 \end{array}} \right], {\mathit{\boldsymbol{B}}_2} = {\mathit{\boldsymbol{E}}_5} \otimes $ $ \left[ {\begin{array}{*{20}{c}} 0&{ - 1}\\ 1&0 \end{array}} \right], {\mathit{\boldsymbol{B}}_3} = {\mathit{\boldsymbol{E}}_5} \otimes \left[ {\begin{array}{*{20}{c}} 0&0\\ 0&0 \end{array}} \right], {\mathit{\boldsymbol{B}}_4} = {\mathit{\boldsymbol{E}}_5} \otimes \left[ {\begin{array}{*{20}{l}} 0&0\\ 0&0 \end{array}} \right]$。

由表 6和表 7可以看出，结合SUT法的Partial EIV方差分量估计在坐标转换模型中仍能得到更为合理的参数估值和二阶精度信息。在本算例中，由于模型的非线性，参数估值的最大偏差达到0.036 806，偏差百分比为3.68%，相比于其他方案得到的参数估值，偏差改正后的参数估值最接近真值，证明了偏差改正的必要性。

4.3 算例3

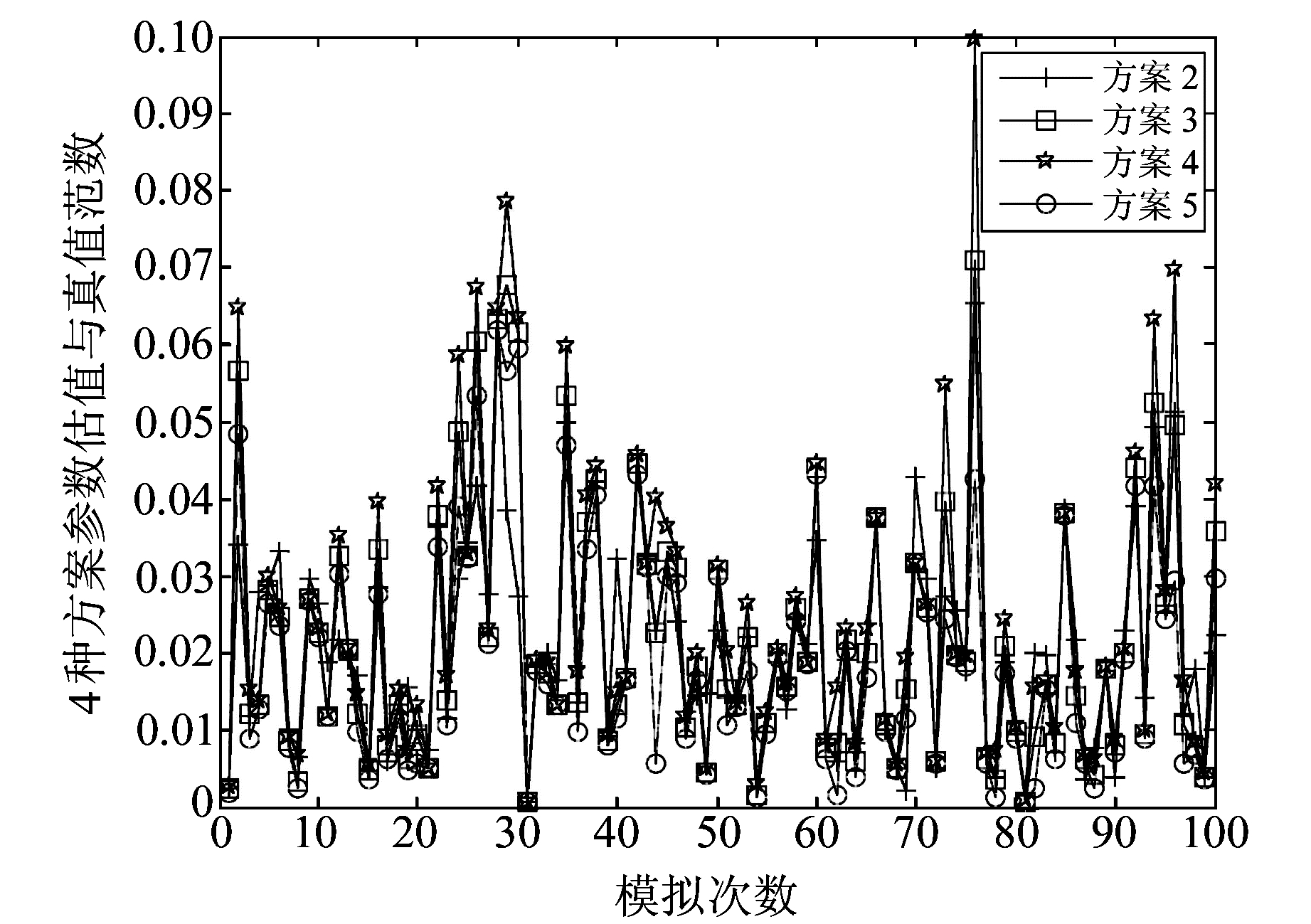
考虑到偶然误差的随机性问题，进行第3个实验。利用matlab函数mvnrnd按照算例1中方差重复进行100次模拟，计算5种方案参数估值与真值的范数，并计算其均值见表 8。由于最小二乘方法的参数估值偏差远大于其他方法的结果，图 1中只绘制了其他4种方法的图像。

如图 1，实验结果表明，在随机模拟100次时，本文通过比较参数估值的方法反映各方案的精度发现，实验结果与算例1的实验结果一致，说明消除误差随机性后本文方案5仍能获得更为精确的参数估值。

5 结语

方差分量估计方法能够有效地纠正随机模型，得到更合理的参数估值，但方差分量估计后的参数估值的精度评定却缺乏相应的重视。本文通过引入SUT采样法对Partial EIV方差分量估计法得到的参数估值进行精度评定，避免复杂的求导运算，得到优于方差分量估计法的参数估值和达到二阶精度的精度信息及其偏差信息。由于非线性迭代存在偏差，且参数初值对后续方差分量估计有较大影响，对SUT法的Partial EIV方差分量估计法得到的参数估值进行偏差改正，通过采样计算，能够得到更为精确的参数估值和合理的二阶精度信息。通过分析算例证明，本文方法是可行而且合理的，是对方差分量估计理论的重要补充。尽管由于SUT法引入了高阶项误差，造成其精度信息与近似函数法获得的精度信息稍有不同，但其避免了近似函数法繁琐的公式推导和偏导计算，且后续可通过研究比例参数α来缩小高阶项误差，并为无法求导的模型的精度评定提供了一种新方法。