2. 武汉大学地球空间环境与大地测量教育部重点实验室, 武汉市珞喻路129 号, 430079
阿留申群岛及其周边区域位于环太平洋地震带(太平洋板块与美洲板块的交界处),地震活动频繁且能量巨大(图 1)。太平洋板块向美洲板块的俯冲是造成阿拉斯加地区地震频发的主要原因。而海底地震或海底滑坡会产生破坏性的海浪,即海啸。目前,美国、澳大利亚、智利、哥伦比亚、厄瓜多尔、印度、泰国等在全球海域共安置了近60个海啸监测系统DART,DART已成为海啸实时监测的重要设备。卫星雷达测高技术可以通过对海面高的观测来提取海啸信息,在2004年苏门答腊海啸[1-3]、2010年智利海啸[4]、2011-03日本海啸[5-6]、2014-04智利海啸[6]的信息提取中得到广泛应用。

|
图 1 阿留申群岛周边区域地震分布 Fig. 1 Earthquake distribution around the Aleutian islands |
2018-01-23 09:31(UTC)科迪亚克岛东南方向大约280 km的阿拉斯加湾发生7.9级地震。地震发生后,太平洋海啸预警中心立即发布海啸预警,表示“可能发生危险性海啸”。随后经过资料分析确认,重新评估灾害的危险程度,取消海啸警报。美国国家气象局在地震发生后也表示,位于地震震中东北部的DART浮标(46410)“记录”到32英尺(约9.75 m)的“水面位移”,然而,最后仅观测到不足1 m高的海浪。本文利用COMCOT海啸传播模型模拟这次海啸,并对结果进行分析。
1 海啸数值模型常用的海啸数值模型有COMCOT(cornell multi-grid coupled tsunami model)[7]、MOST (method of splitting tsunami)[8]、Geoclaw[9]、TUNAMI[10]和我国独立自主研发的CTSU(China tsunami model)[11]等。其中,COMCOT模型利用标准模块化的设计方式,网格设计中采用多重嵌套的方法,其考虑海啸传播的物理过程比较全面。该模型可以对海啸的产生、传播和海啸波登陆阶段进行数值模拟,而且模拟海啸的远洋传播、近海传播和局部地区的淹水等3个过程都非常完善。COMCOT已成功地用于多个海啸事件的数值模拟[12],而且其开源代码便于修改。
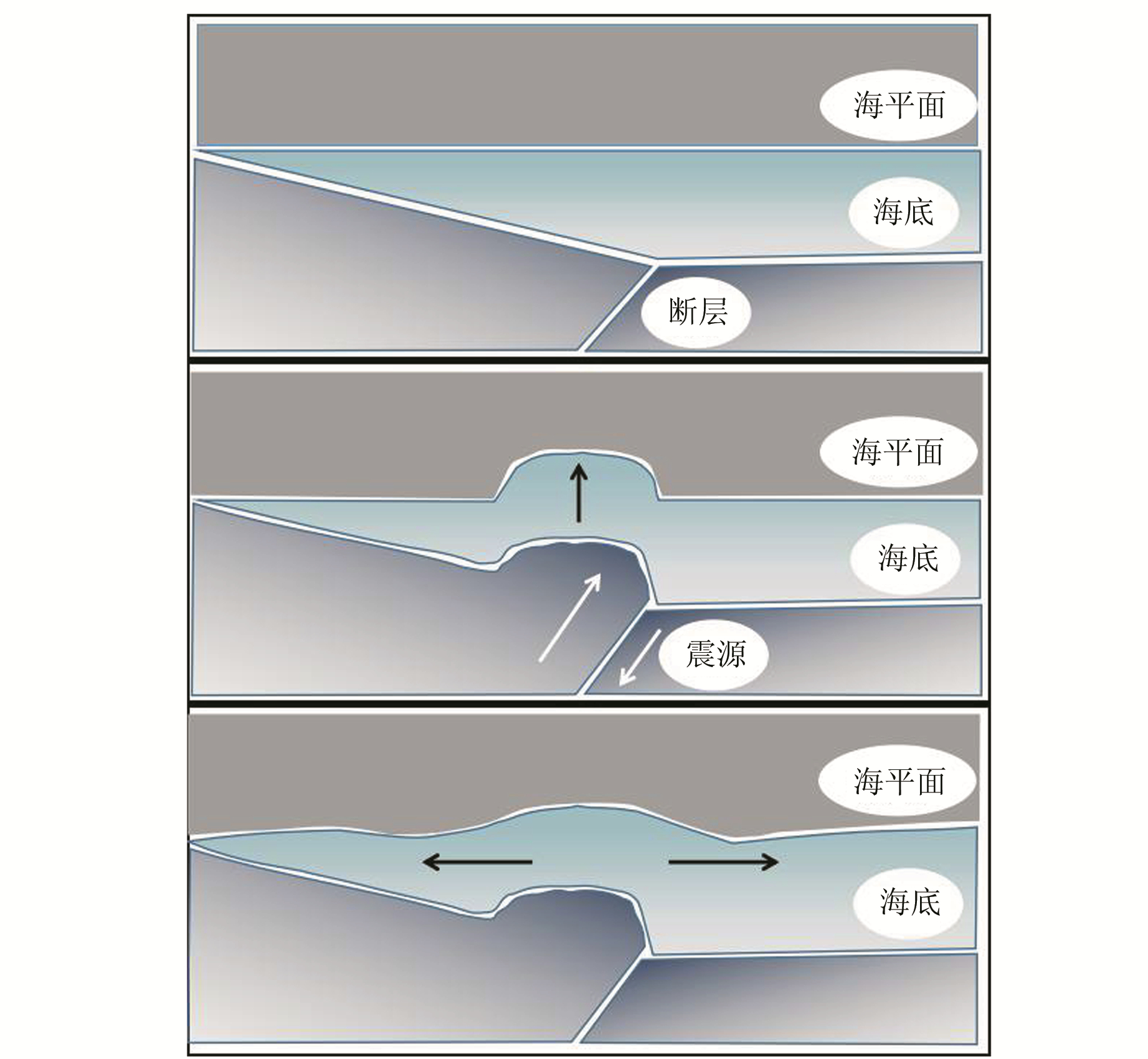
1.1 海啸产生阶段的模拟地震是引发海啸的主要原因。地震引发海啸的过程如图 2所示,2个断层之间相互挤压,当挤压所积蓄的能量到达一定程度,会以地震的形式释放出来,海底会大规模上升或下降,导致上方水体也随之上升或下降,从而引发海啸。
|
图 2 地震引发海啸示意图 Fig. 2 Schematic diagram of earthquake triggered tsunami |
海啸产生阶段的模拟与地震震源机制的联系十分紧密。目前大多数海啸数值模型采取的是瞬时变形-弹性断层模型[13]。地震引起的海床位移可以通过弹性有限断层面理论来计算,该模型将海底断层破裂错位引起的海床变化直接视为水面位移,即海啸产生的初始条件。对于较大的海底地震,海啸波周期远大于地震破裂持续时间和地震引起海底抬升的时间,如果用该模型来模拟,对结果的影响并不大,因此可以采用Okada断层模型来模拟海啸产生的初始阶段。
海啸源的各项参数可以根据均匀位错模型或者震后各机构发布的有限断层模型确定。有限断层模型是利用海啸浮标数据或实时地震数据反演得到详细的地震破裂特征,对于近场海啸的模拟结果更加准确。而均匀位错模型即使没有精细的断层破裂模型,也可以对海啸的传播进行很好的模拟,对于实时海啸灾害的预报具有实际意义[14-15]。
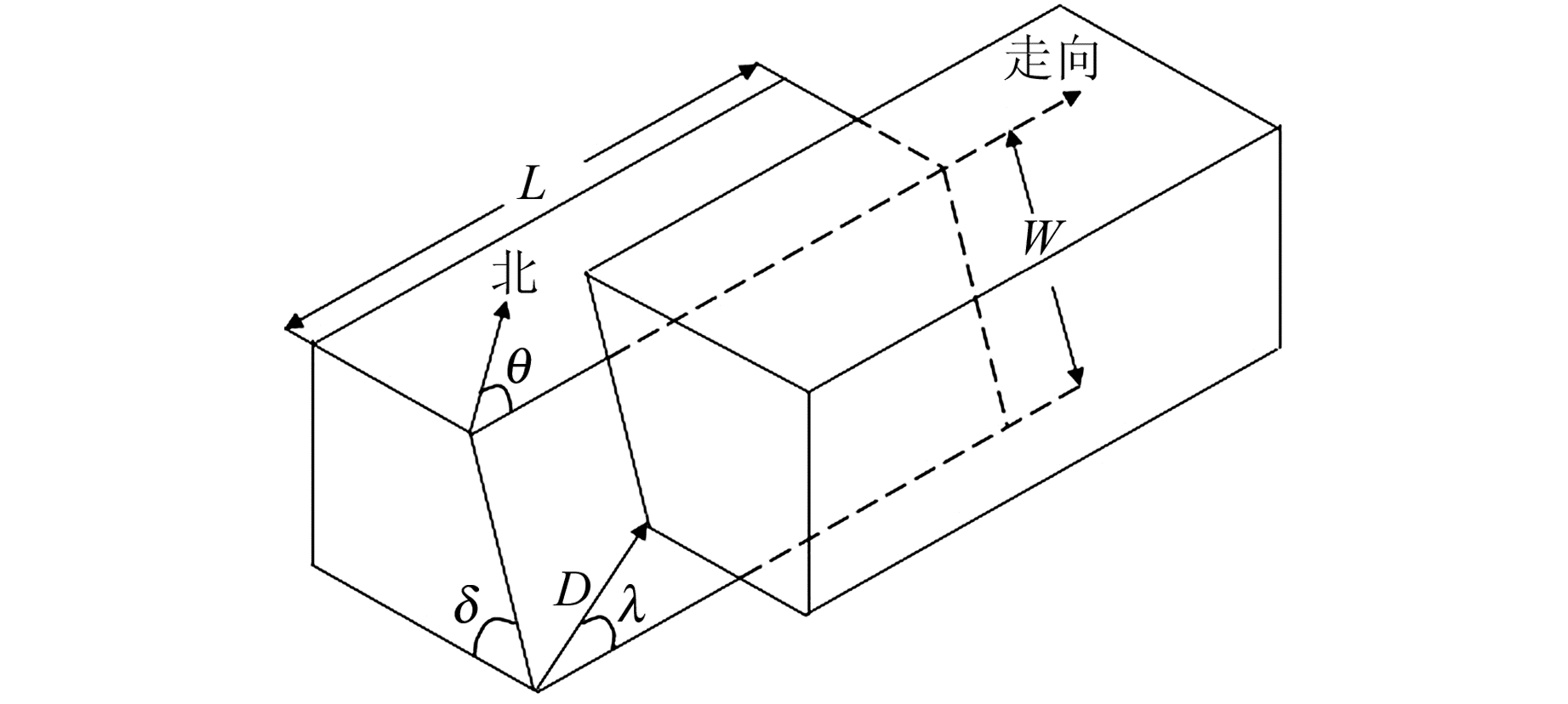
图 3为均匀位错模型描述的海底变化,其中L为断层长度,W为断层宽度,D为滑动距离,λ为滑动角,θ为走向角,δ为倾角。断层参数与地震震级MW的关系根据日本气象厅的经验公式确定,计算公式为:
| $ \left\{\begin{array}{l}{\log L=0.5 M_{W}-1.9} \\ {\log W=0.5 M_{W}-2.2} \\ {\log D=0.5 M_{W}-3.2}\end{array}\right. $ | (1) |
|
图 3 断层模型示意图 Fig. 3 Schematic diagram of fault model |
式中,断层长度L和宽度W的单位为km,断层滑动距离D的单位为m。
1.2 海啸传播数值模型COMCOT海啸传播模型中包括球坐标系和笛卡尔坐标系,根据模拟区域的海底地形可以选择线性或非线性浅水方程。阿拉斯加地震海域的水深较大,此时海啸波的波幅远小于水深,因此可以采用球坐标系的线性浅水方程:
| $ \left\{\begin{array}{l}{\frac{\partial \eta}{\partial t}+\frac{1}{R \cos \varphi}\left\{\frac{\partial P}{\partial \varphi}+\frac{\partial}{\partial \varphi}(\cos \varphi Q)\right\}=-\frac{\partial h}{\partial t}} \\ {\frac{\partial P}{\partial t}+\frac{g h}{R \cos \varphi} \frac{\partial \eta}{\partial \psi}-f Q=0} \\ {\frac{\partial Q}{\partial t}+\frac{g h}{R} \frac{\partial \eta}{\partial \varphi}+f P=0}\end{array}\right. $ | (2) |
式中,η为水面位移,(P, Q)为X方向和Y方向的体积通量,(φ, ψ)为地球纬度和经度,R为地球半径,g为重力加速度,h表示水深,
| $ f=\mathit{\Omega} \sin \varphi $ | (3) |
式中,Ω为地球自转角速度。
COMCOT采用显式交错蛙跳有限差分格式来求解球坐标系下的浅水方程(2),这种数值模式不需要求解涉及非线性和频散的高阶微分,因此用于模拟越洋海啸的效率非常高。
2 海啸数值模拟及结果分析 2.1 震源特征利用Okada模型计算海啸初始水位,所需的断层走向角、倾角、滑动角和震源深度等参数可以由震源机制解得到,而断层长度、宽度和滑动量可以利用式(1)计算得到。
根据震后美国地质调查局(USGS)发布的信息,W-phase矩张量解的走向角为259°、倾角为74°、滑动角为10°,震源坐标为(56.004°N,149.166°W),震源深度为35.5 km。此次地震的断层参数如表 1所示。
|
|
表 1 阿拉斯加地震断层参数 Tab. 1 Fault parameters of Alaska earthquake |
模拟所用的海底地形数据是美国国家海洋和大气管理局(NOAA)网站下载的ETOPO1(http://www.ngdc.noaa.gov/mgg/global/global)。选取网格的空间步长为3′,时间步长的选择需要满足CFL条件,即
| $ \Delta t \leqslant \frac{C \cdot \Delta x}{\sqrt{g h_{\max }}} $ | (4) |
式中,Δx为空间步长,hmax为最大水深,C为大于0小于1的常数,在COMCOT模型中C取0.5,此处取时间步长为1 s,满足CFL条件。
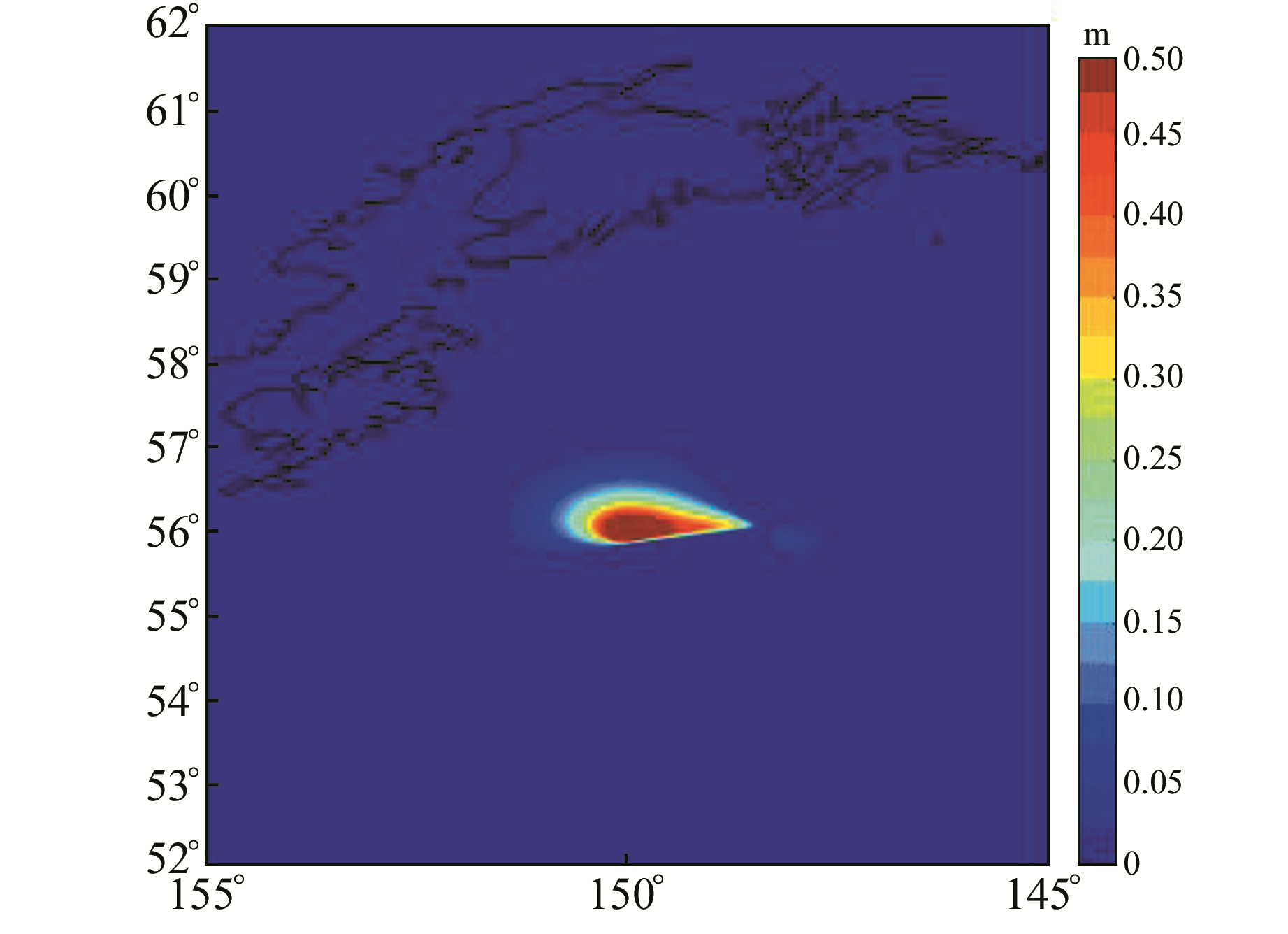
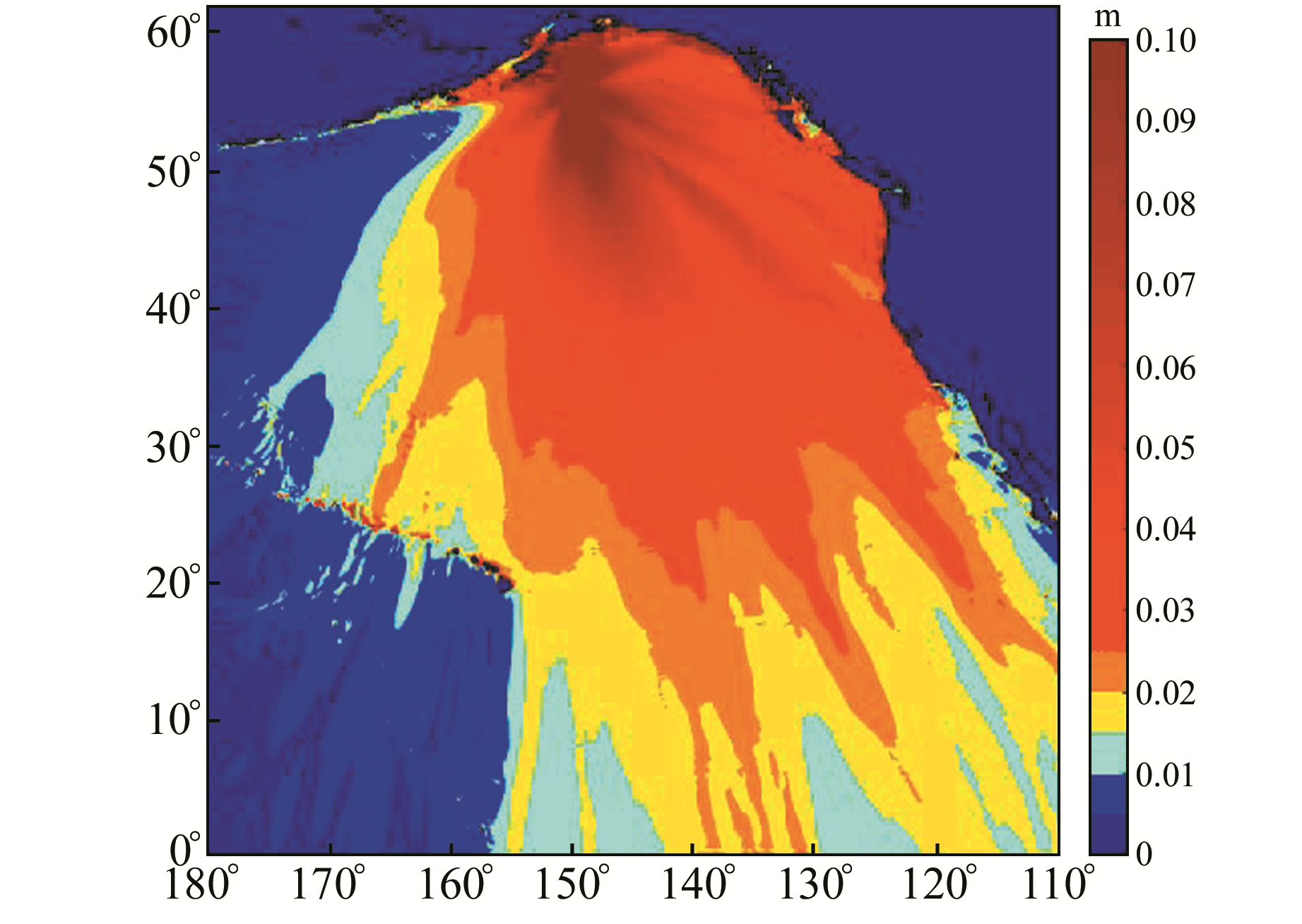
计算区域为180°~250°E、0°~62°N,栅格数量为1 400×1 240,计算结果如图 4~6所示。图 4是海啸初始水面位移图,海啸初始时刻水面的最大高度约0.5 m。图 5是海啸传播过程中的最大水面位移,除了震中附近,水面位移都小于0.1 m。海啸发生1 h后,海啸波的振幅为0.8 m左右(图 6(a))。随着海啸不断向四周传播,其所携带能量的耗散越来越大,振幅越来越小,海啸传播6 h后,海啸波的振幅只有不到3 cm(图 6(f))。
|
图 4 海啸初始水面位移 Fig. 4 Initial surface displacement of tsunami |
|
图 5 最大水面位移分布 Fig. 5 Distribution of maximum surface displacement |
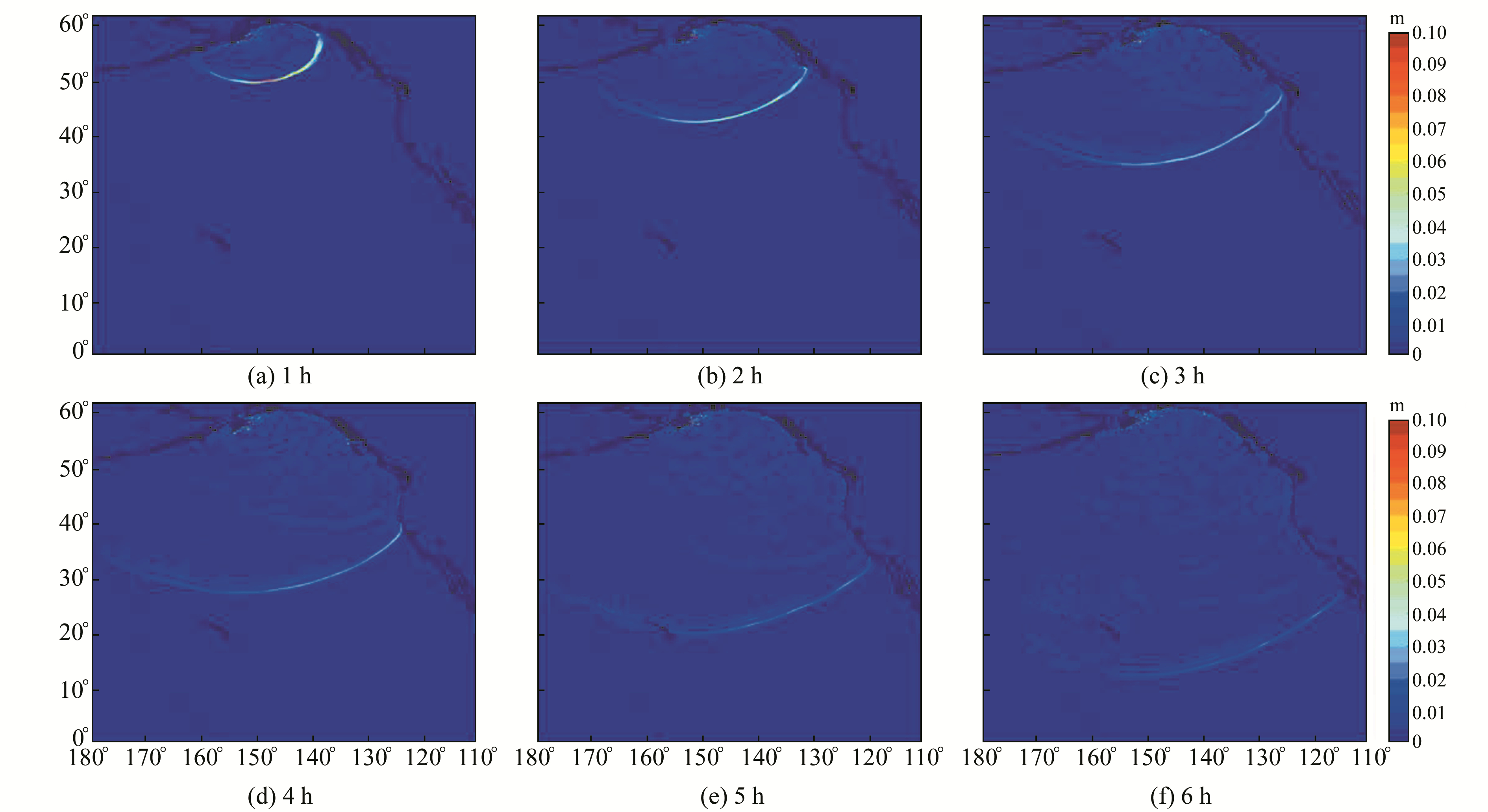
|
图 6 海啸传播过程中的水面位移 Fig. 6 Water surface displacement during the tsunami travelling |
为了验证数值模拟的水位高度,选取5个DART观测站(图 1),将其记录的海啸观测数据与模拟结果进行比较。如图 5所示,在地震发生7 min左右之后,海啸波首先到达距离震中最近的46409观测站(图 7),首波振幅达到13 cm;经过2 h 19 min,海啸波到达距离震中最远的46419观测站(图 7),46402观测站记录到的海啸首波振幅最小,不到1 cm(图 7)。
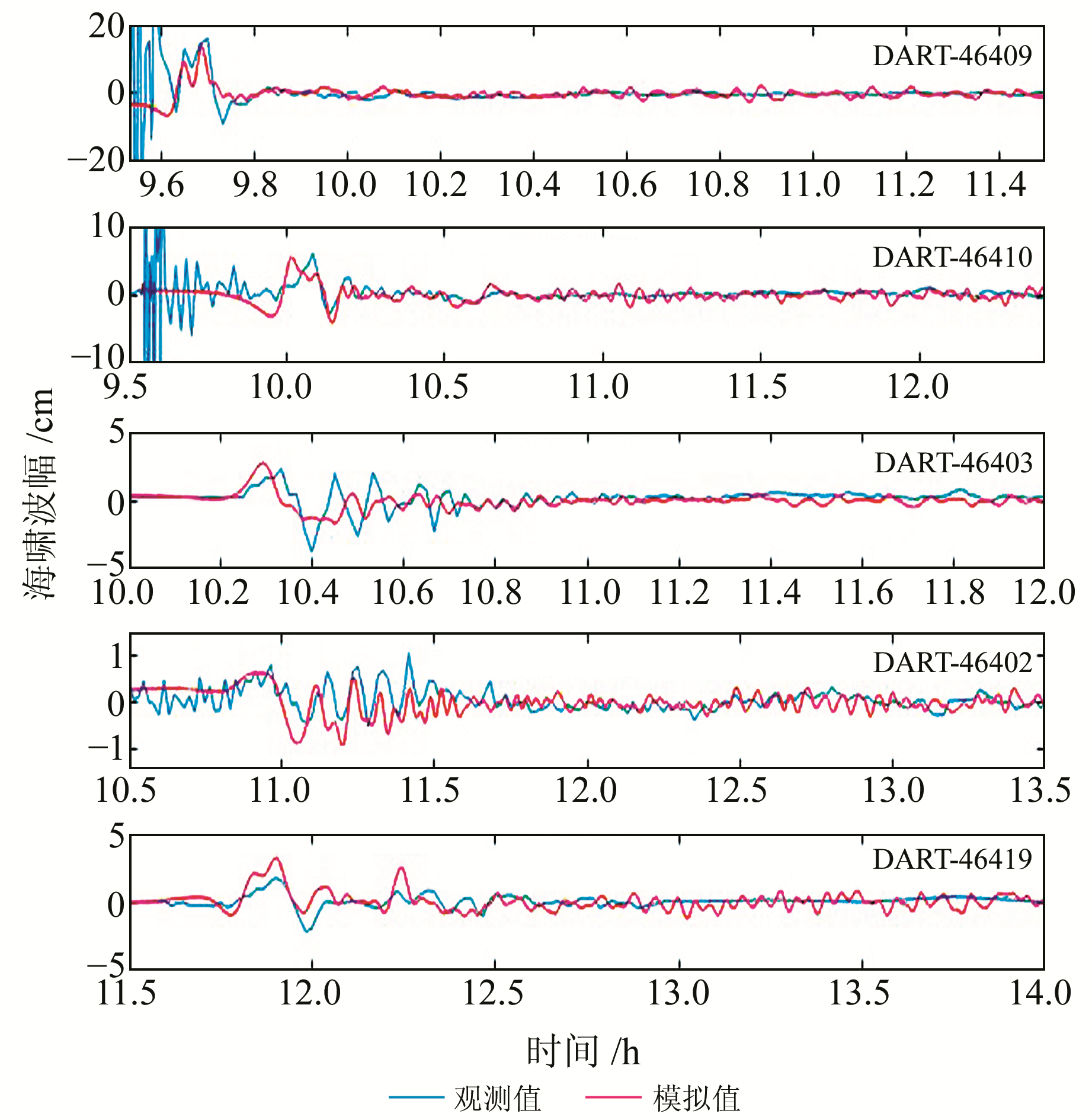
|
图 7 阿拉斯加海啸波幅曲线 Fig. 7 The wave amplitude curve of Alaska tsunami |
从5个观测站记录的海啸观测值曲线与模拟值曲线的对比图来看,利用COMCOT数值模型对海啸波的模拟结果与观测值符合良好,说明海啸初始场参数的选择合理,模拟结果具有非常高的可靠性。特别是对于海啸预警十分重要的首波到达时间与振幅,各观测站的模拟结果与实测数据吻合(图 7)。
表 2给出了DART观测到的海啸首波到达时间、首波振幅与模拟结果之间的比较。从海啸的首波到达时间来看,在所选择的5个观测站点上,时间差异均在4 min以内,而且模拟时间一般比实际观测时间短。这种现象主要是因为实际地震发生过程十分复杂,海底断层的破裂通常不是瞬时完成的,且断层在空间分布上也不均匀,而本文采用的Okada模型比较理想化,因此模拟的海啸发生时的初始水面位移与实际值会有差异。
|
|
表 2 DART观测站记录的首波观测值与模拟值的比较 Tab. 2 Comparison of the first wave measurements and simulations recorded by DART |
对于海啸首波的振幅,距离地震最近的46409观测站振幅最大,实际观测振幅约13 cm,而模拟振幅约9 cm; 随着海啸向远方或开阔海域传播,振幅有逐渐减小的趋势(46403, 46402);在靠近大陆附近,振幅有轻微增加现象(46410, 46419)。这些数值结果基本反映了海啸传播的总体特征。除了距离最近站点(46409)的模拟振幅与实测振幅相差约4 cm之外,其他站点的差异都小于1 cm。对于海啸的首波到达时间,几个站点的观测时间与模拟时间差均在4 min以内。从振幅和时间的比较来看,COMCOT的模拟结果真实地反映了海啸传播过程中不同区域振幅变化与传播时间情况。
3 结语本文利用COMCOT海啸数值模型对2018-01-23阿拉斯加海啸进行数值模拟,重点分析海啸波首波的振幅与时间,并与DART浮标观测资料进行对比分析。其中,振幅差异均在4 cm以内,时间差异在4 min以内。离震源中心较近的DART站点的时间差异最小,但振幅差异最大。总体来看,模拟结果与实际观测资料基本吻合,说明海啸初始场参数的选择合理有效,模拟计算结果真实可靠。
由于使用了震后解算的震源特征参数,因此海啸初始场信息准确,模拟得到的首波振幅与时间精确。如果震源特征参数不够准确,海啸的预测预警需要及时采用大洋盆地中的地震波和监测站探测到的信息,重新解算震源特征参数,再次模拟海啸的传播,评估海啸的危险程度,发布或取消海啸预警。此外,由于海底断层的破裂情况比较复杂,单一理想化的断层模型不能完全替代实际的断层,因此海啸传播过程的模拟结果与实测数据之间会存在一些差异。
| [1] |
Hayashi Y. Extracting the 2004 Indian Ocean Tsunami Signals from Sea Surface Height Data Observed by Satellite Altimetry[J]. Journal of Geophysical Research: Oceans, 2008, 113(C1)
(  0) 0) |
| [2] |
Gower J. The 26 December 2004 Tsunami Measured by Satellite Altimetry[J]. International Journal of Remote Sensing, 2007, 28(13-14): 2 897-2 913 DOI:10.1080/01431160601094484
(  0) 0) |
| [3] |
Sladen A, Hébert H. On the Use of Satellite Altimetry to Infer the Earthquake Rupture Characteristics: Application to the 2004 Sumatra Event[J]. Geophysical Journal International, 2008, 172(2): 707-714 DOI:10.1111/gji.2008.172.issue-2
(  0) 0) |
| [4] |
Hamlington B D, Leben R R, Godin O A, et al. Detection of the 2010 Chilean Tsunami Using Satellite Altimetry[J]. Natural Hazards and Earth System Science, 2011, 11(9): 2 391-2 406 DOI:10.5194/nhess-11-2391-2011
(  0) 0) |
| [5] |
Hamlington B D, Leben R R, Godin O A, et al. Could Satellite Altimetry Have Improved Early Detection and Warning of the 2011 Tohoku Tsunami?[J]. Geophysical Research Letters, 2012, 39(15)
(  0) 0) |
| [6] |
Chu Y C, Li J C. Extraction of Two Tsunamis Signals Generated by Earthquakes around the Pacific Rim[J]. Geodesy and Geodynamics, 2014, 5(2): 38-47
(  0) 0) |
| [7] |
Wang X. User Manual for Comcot Version 1.7(First Draft)[Z]. Cornel University, 2009
(  0) 0) |
| [8] |
Titov V V, Gonzalez F I. Implementation and Testing of the Method of Splitting Tsunami(MOST) Model[R]. NOAA Technical Memorandum ERL PMEL, Pacific Marine Environmental Laboratory, Seattle, 1997
(  0) 0) |
| [9] |
Leveque R J, George D L.High-Resolution Finite Volume Methods for the Shallow Water Equations with Topography and Dry-States[C]//Liu P L F, Yeh H, Synolakis C. Advanced Numerical Models for Simulating Tsunami Waves and Runup[M]. Singapore: World Scientific, 2008
(  0) 0) |
| [10] |
鲍献文, 褚芹芹, 于华明. 海啸数值预报模型研究进展[J]. 中国海洋大学学报:自然科学版, 2013, 43(3): 1-6 (Bao Xianwen, Chu Qinqin, Yu Huaming. The Main Advances of Study on Numerical Forecast Model of Tsunami[J]. Periodical of Ocean University of China, 2013, 43(3): 1-6)
(  0) 0) |
| [11] |
王培涛, 赵联大, 于福江, 等. 海啸灾害数值预报技术研究现状[J]. 海洋预报, 2011, 28(3): 74-79 (Wang Peitao, Zhao Lianda, Yu Fujiang, et al. Review of the Numerical Forecasting Technology on the Tsunami Hazards[J]. Marine Forecasts, 2011, 28(3): 74-79 DOI:10.3969/j.issn.1003-0239.2011.03.012)
(  0) 0) |
| [12] |
Wang X M, Liu P L F. An Analysis of 2004 Sumatra Earthquake Fault Plane Mechanisms and Indian Ocean Tsunami[J]. Journal of Hydraulic Engineering and Research, 2006, 44(2): 147-154 DOI:10.1080/00221686.2006.9521671
(  0) 0) |
| [13] |
Okada Y. Surface Deformation Due to Shear and Tensile Faults in a Halfspace[J]. Bulletin of the Seismological Society of America, 1985, 75(4): 1 135-1 154
(  0) 0) |
| [14] |
景惠敏, 张怀, 吴忠良, 等. 利用海啸数值模拟结果进行海底地震有限断层模型验证[J]. 地震, 2013, 33(4): 207-213 (Jing Huimin, Zhang Huai, Wu Zhongliang, et al. Tsunami Constraints on Finite Fault Models: The March 11, 2011 Tohoku Earthquake[J]. Earthquake, 2013, 33(4): 207-213 DOI:10.3969/j.issn.1000-3274.2013.04.022)
(  0) 0) |
| [15] |
任叶飞.基于数值模拟的我国地震海啸危险性分析研究[D].哈尔滨: 中国地震局工程力学研究所, 2008 (Ren Yefei. Study on China Earthquake Tsunami Hazard Analysis Based on Numerical Simulation[D]. Harbin: Institute of Engineering Mechanics, CEA, 2008) http://cdmd.cnki.com.cn/article/cdmd-85406-2009057353.htm
(  0) 0) |
2. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, 129 Luoyu Road, Wuhan 430079, China
 2019, Vol. 39
2019, Vol. 39

