绝对重力仪一般采用激光干涉测距原理测量重力加速度,即每当落体下落激光半波长的距离时,接收器上便会相应产生一个干涉条纹的变化,由此得到落体的位移信息,结合条纹变化时间得到时间-位移数据,进而重建落体轨迹,解算重力加速度。重建落体轨迹的方法有基于硬件处理法与基于数字信号处理法。硬件方法中,使用电路过零点比较器检测干涉条纹信号中的过零点,在每个过零点处比较器产生一个脉冲信号,每N个零点脉冲信号生成一个脉冲,送入以外部铷原子钟为时间基准的时间间隔分析仪中,由此取得落体的位移-时间数据。数字信号处理法有双采样过零点检测法、复杂外差调制法、加窗二次微分法[1]以及零差干涉条纹正交法[2]。
本文基于Hilbert变换相位平移原理提取各采样点瞬时相位,利用瞬时相位与位移的关系取得各采样点位移,结合采样频率得到位移-时间数据,最后采用最小二乘法拟合落体轨迹,得到位移拟合残差、g值偏差。同时,本文采用数据加窗的方法抑制Hilbert变换过程中产生的吉伯斯现象,使用零相移滤波器与去线性趋势方法去除信号的噪声干扰,降低测量误差。
1 算法原理 1.1 Hilbert变换原理Hilbert变换定义为:
| $ \begin{array}{l} \mathit{\tilde U}{\rm{(}}\mathit{t}{\rm{) =\mathit H}}\left\{ {\mathit{U}{\rm{(}}\mathit{t}{\rm{)}}} \right\} = h{\rm{(}}\mathit{t}{\rm{)}}\mathit{U}{\rm{(}}\mathit{t}{\rm{) = }}\\ \int_{ - \infty }^\infty U (\tau )h(t - \tau ){\rm{d}}\tau = \frac{1}{{\rm{ \mathit{ π} }}}\int_{ - \infty }^\infty {\frac{{U(\tau )}}{{t - \tau }}} {\rm{d}}\tau \end{array} $ | (1) |
式中,
| $ H({\rm{j}}\omega ) = \left\{ \begin{array}{l} {\rm{j}}, \omega < 0\\ 0, \omega = 0\\ - {\rm{j}}, \omega > 0 \end{array} \right. $ | (2) |
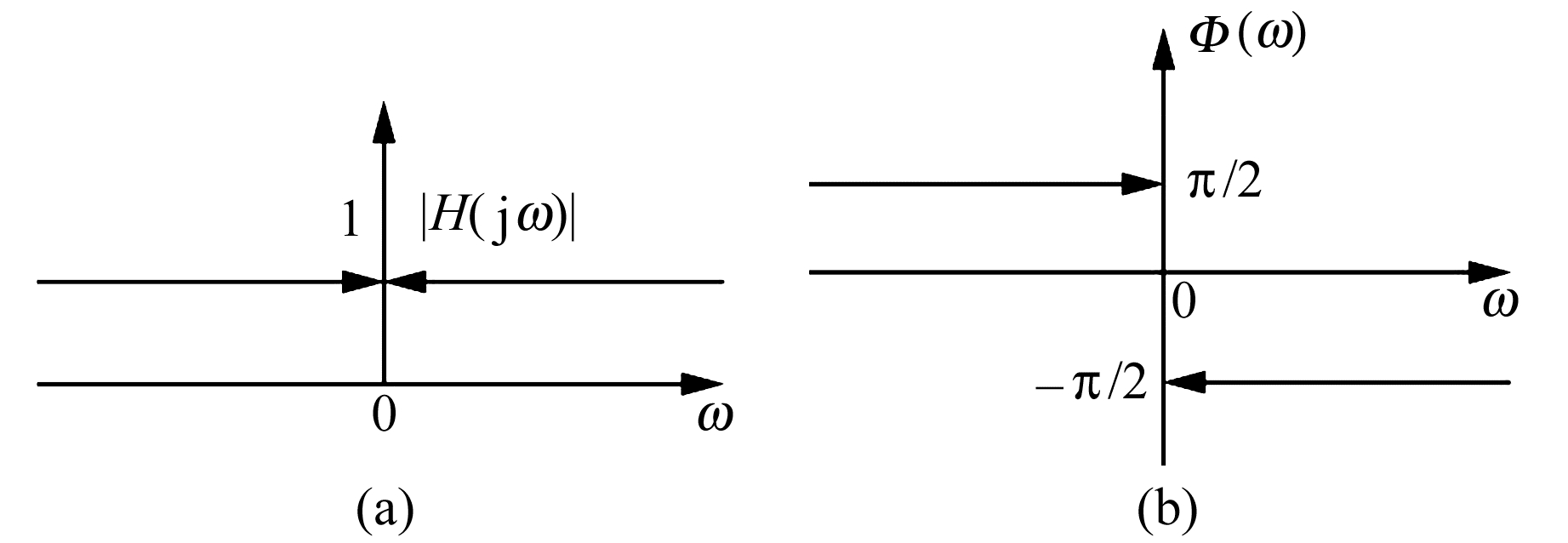
式(2)的频率响应如图 1。可见,Hilbert变换相当于一个全通滤波器,并在正频率与负频率分量中分别产生±π/2的相位移动。
|
图 1 Hilbert变换频率响应 Fig. 1 Frequency response of Hilbert-transform |
此时,U(t)的解析信号为:
| $ \mathit{q}{\rm{(}}\mathit{t}{\rm{) = }}\mathit{U}{\rm{(}}\mathit{t}{\rm{) + i}}\mathit{\tilde U}{\rm{(}}\mathit{t}{\rm{)}} $ | (3) |
由此可得U(t)的瞬时相位:
| $ \mathit{\Phi }(t) = {\tan ^{ - 1}}(H\{ U(t)\} /U(t)) $ | (4) |
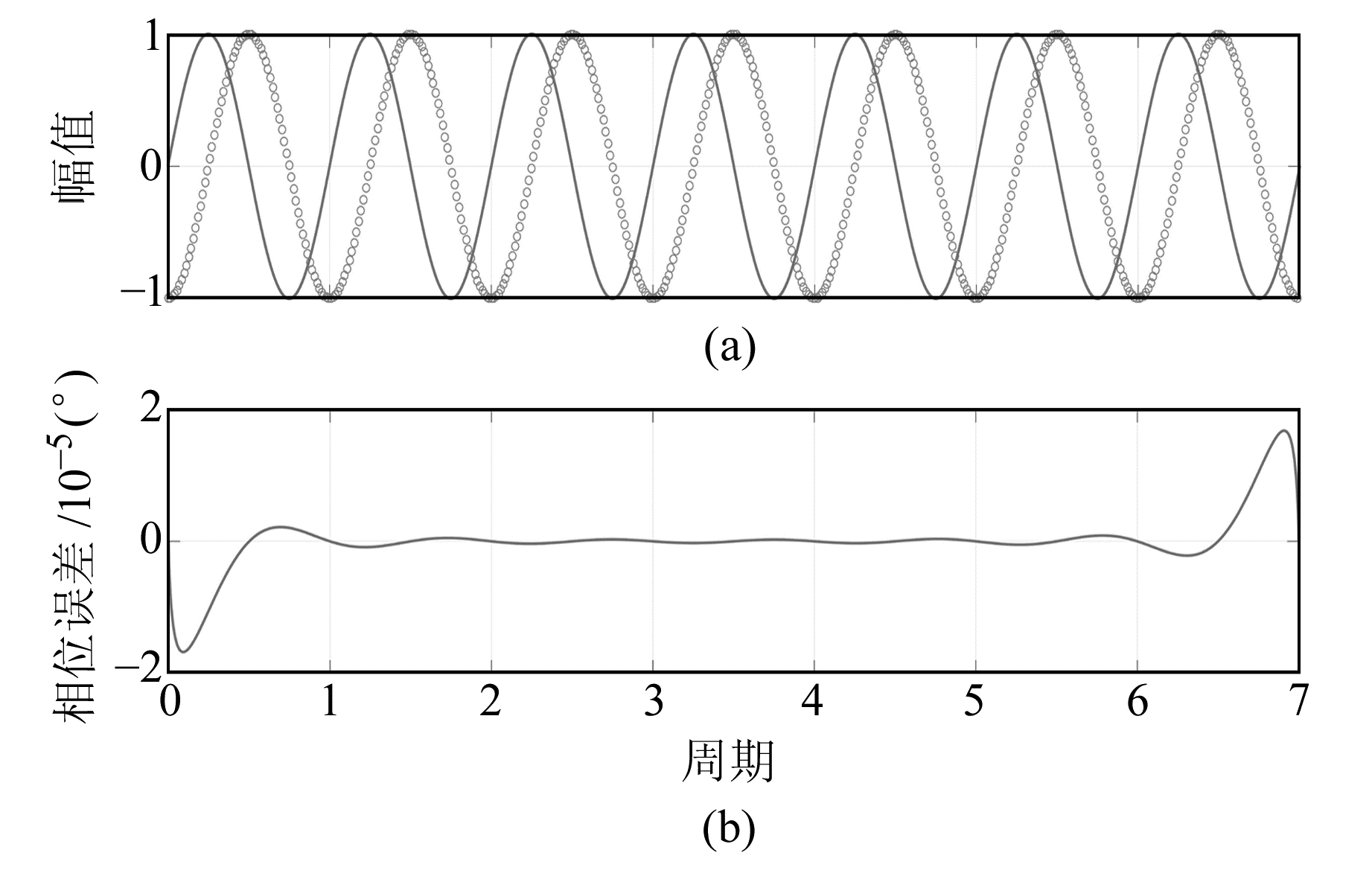
在连续条件下对正弦信号进行Hilbert变换,可得H{sin(x)}=-cos(x)(x>0)。然而离散条件下进行Hilbert变换时(图 2(a)),由于傅里叶变换在非连续区域的吉伯斯现象与离散傅里叶变换误差的影响[3],相位误差两端产生纹波(图 2(b))。由图 2(b)可见,数据中部误差极小,而两端数据误差较大。由于在利用最小二乘法拟合求解g值的过程中,数据段长短不影响经过拟合与修正后最终所得的g0,因此在使用Hilbert变换对干涉条纹进行处理时,为降低误差,在数据拟合前对数据进行加窗选取,去除出现纹波误差的数据段。
|
图 2 正弦信号Hilbert变换的相移及误差 Fig. 2 Phase shift and error of sine signal's Hilbert-transfer |
采用Murata[4]给出的条纹信号模型:
| $ U(t) = {u_0} + \beta t + {A_0}\sin (\mathit{\Phi }(t)) $ | (5) |
式中,u0与β分别为直流偏移与线性漂移成分,A0为条纹信号幅值。根据激光干涉测距原理,当位移S(t)变化为激光半波长λ/2时,对应的相位变化为2π。此时,相位Φ(t)为:
| $ \mathit{\Phi }(t) = 2{\rm{ \mathit{ π} }}\frac{{S(t)}}{{\lambda /2}} = \frac{{4{\rm{ \mathit{ π} }}}}{\lambda }S(t) $ | (6) |
因此,在一个条纹周期内,条纹采样点位移为:
| $ S(t) = \frac{{\lambda \mathit{\Phi }(t)}}{{4{\rm{ \mathit{ π} }}}} $ | (7) |
整个自由落体过程中,位移变化为:
| $ {S^\prime }(t) = \frac{{n\lambda }}{2} + S(t) $ | (8) |
式中,n为条纹周期数,n=0,1,2,…。
在忽略重力梯度的情况下,自由落体规律为:
| $ S(t) = {s_0} + {v_0}t + \frac{1}{2}{g_0}{t^2} $ | (9) |
加入重力梯度影响后,自由落体模型为:
| $ \begin{array}{l} {S^\prime }(t) = {s_0} + {v_0}t + \frac{1}{2}{g_0}{t^2} + \\ \gamma \left( {\frac{1}{2}{s_0}{t^2} + \frac{1}{6}{v_0}{t^3} + \frac{1}{{24}}{g_0}{t^4}} \right) \end{array} $ | (10) |
式中,s0、v0、g0为所选坐标系统原点的初始条件,γ为重力梯度常数。当γ未知时,取γ=0,以二阶落体模型求解g值,并由式(11)修正得到g0:
| $ g = {g_0} + \gamma {h_{{\rm{ef}}}} $ | (11) |
式中,hef为有效测量高度。
在进行重力加速度测量时,当落体在高度H处下落Δx距离时,光束仍需要经历H-Δx距离才能到达接收器,而光的速度是有限的,因此光速的有限性会导致干涉条纹生成时间落后于落体到达该下落位置的时间,最终影响测量结果。因此,需要对时间进行修正[5]:
| $ t_i^\prime = t - \frac{{\Delta x}}{c} = t - \frac{{{s_i} - {s_0}}}{c} $ | (12) |
式中,c为光速,t′i为修正时间,si为第i个观测点的位移。
1.3 零相移滤波原理与去线性趋势处理零相移滤波算法的核心分为滤波、时域翻转信号、再次滤波、再次翻转信号等4步。
首先是翻转信号与原信号的Z变换关系。假设一个有限长序列信号{x(n)},n=1,2,…,n0,将该信号延拓至整个x轴,则信号表达式为:
| $ {x_1} = \left\{ {\begin{array}{*{20}{l}} {x\left( {n\% {n_0}} \right), n\% {n_0} \ne 0}\\ {x\left( {{n_0}} \right), n\% {n_0} = 0} \end{array}} \right. $ | (13) |
其中,%表示取模。同样,假设信号序列{y(n)}为信号{x(n)}时域翻转后的序列,将信号{y(n)}延拓至整个x轴,则延拓信号y1(n)和延拓信号x1(n)关于y轴对称,即y1(n)=x1(-n)。
对以上2个信号进行双边Z变换:
| $ X(z) = \sum\limits_{n = - \infty }^\infty {{x_1}} (n){z^{ - n}} $ | (14) |
| $ \begin{array}{l} Y(z) = \sum\limits_{n = - \infty }^\infty {{y_1}} (n){z^{ - n}} = \sum\limits_{n = - \infty }^\infty {{x_1}} ( - n){z^n} = \\ \;\;\;\;\;\;\;\;\sum\limits_{n = - \infty }^\infty {{x_1}} (n){\left( {{z^{ - 1}}} \right)^n} = X\left( {{z^{ - 1}}} \right) \end{array} $ | (15) |
可知,对信号X(z)进行时域翻转后,该信号Z变换为X(z-1)。假设滤波器的传递函数为H(z),则零相移滤波器的输出Y1(z)为:
| $ {Y_1}(z) = X(z)H(z)H\left( {\frac{1}{z}} \right) $ | (16) |
式中,H(z)为实系数等式,故有H(ejω)=H(e-jω)。令z=ejω,则经过二次滤波和翻转的信号输出为:
| $ \begin{array}{l} {Y_1}\left( {{{\rm{e}}^{{\rm{j}}\omega }}} \right) = X\left( {{{\rm{e}}^{{\rm{j}}\omega }}} \right)H\left( {{{\rm{e}}^{{\rm{j}}\omega }}} \right)H\left( {{{\rm{e}}^{ - {\rm{j}}\omega }}} \right) = \\ \;\;\;\;\;\;\;\;\;\;X\left( {{{\rm{e}}^{{\rm{j}}\omega }}} \right){\left| {H\left( {{{\rm{e}}^{{\rm{j}}\omega }}} \right)} \right|^2} \end{array} $ | (17) |
可知,零相移滤波器的传递函数为|H(ejω)|2,输出信号Y1(ejω)相对于X(ejω)并没有发生相位上的偏移。
由信号模型式(5)可见,条纹信号中包含直流偏移与线性漂移,两者构成信号的线性趋势。采用最小二乘法对信号进行多项式拟合后,信号被分解为各阶数据。从中提取出信号的线性趋势数据,使用原信号减去该数据,便可得到去线性趋势的数据。
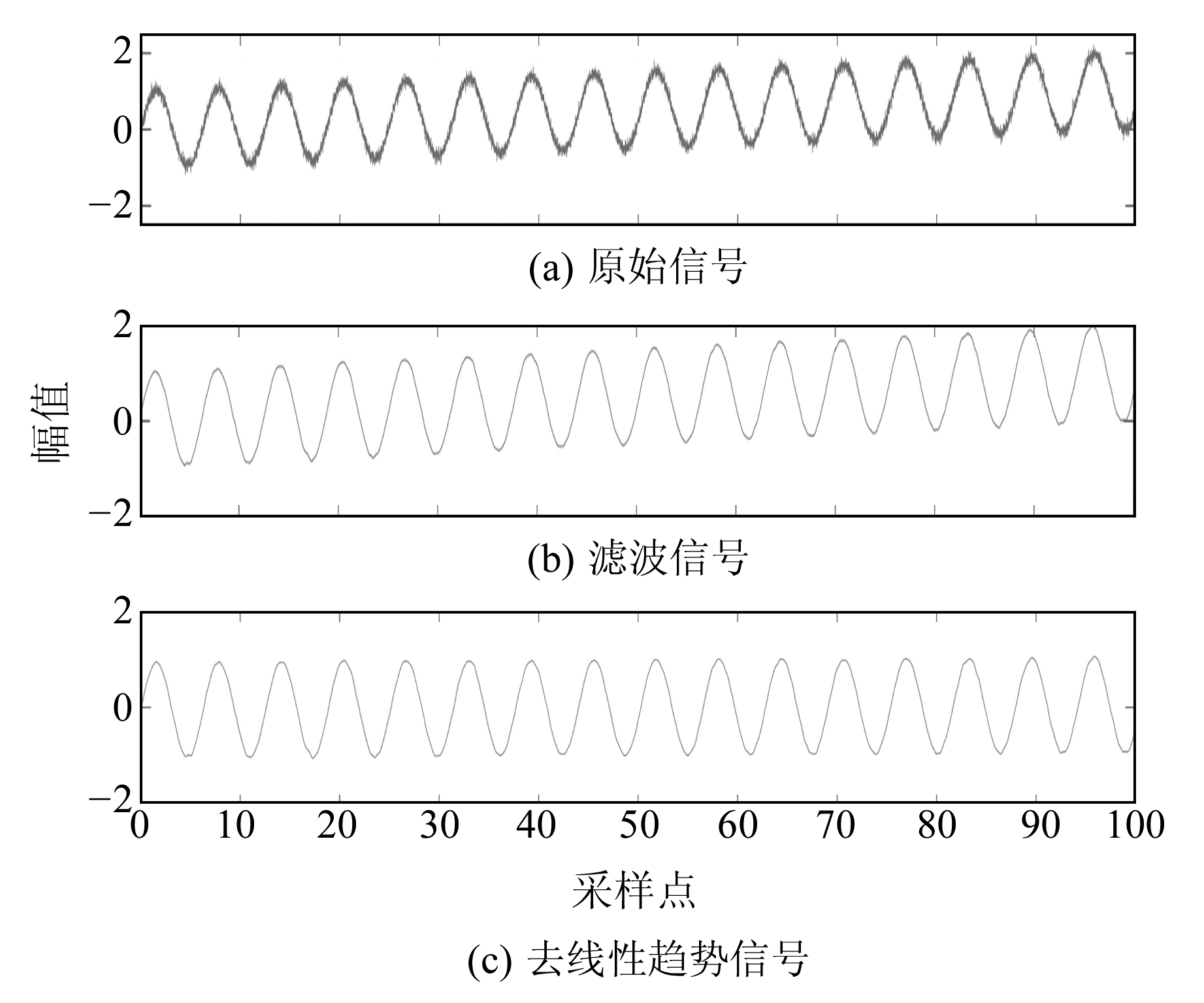
使用式(5),取A0=1,u0=0.01,β=0.01,Φ(t)=t,并引入5%幅值高斯白噪声作为外部噪声,得到信号(图 3(a)); 使用零相移低通滤波器去除信号中的高频噪声信号(图 3(b)); 采用多项式拟合方法分解信号数据,并去除信号的线性趋势(图 3(c))。由图 3可见,信号中的高频噪声与线性趋势被有效去除,且相位不变。
|
图 3 信号高频噪声滤波以及线性噪声去除 Fig. 3 High frequency noise of signal filtering and linear trend removal |
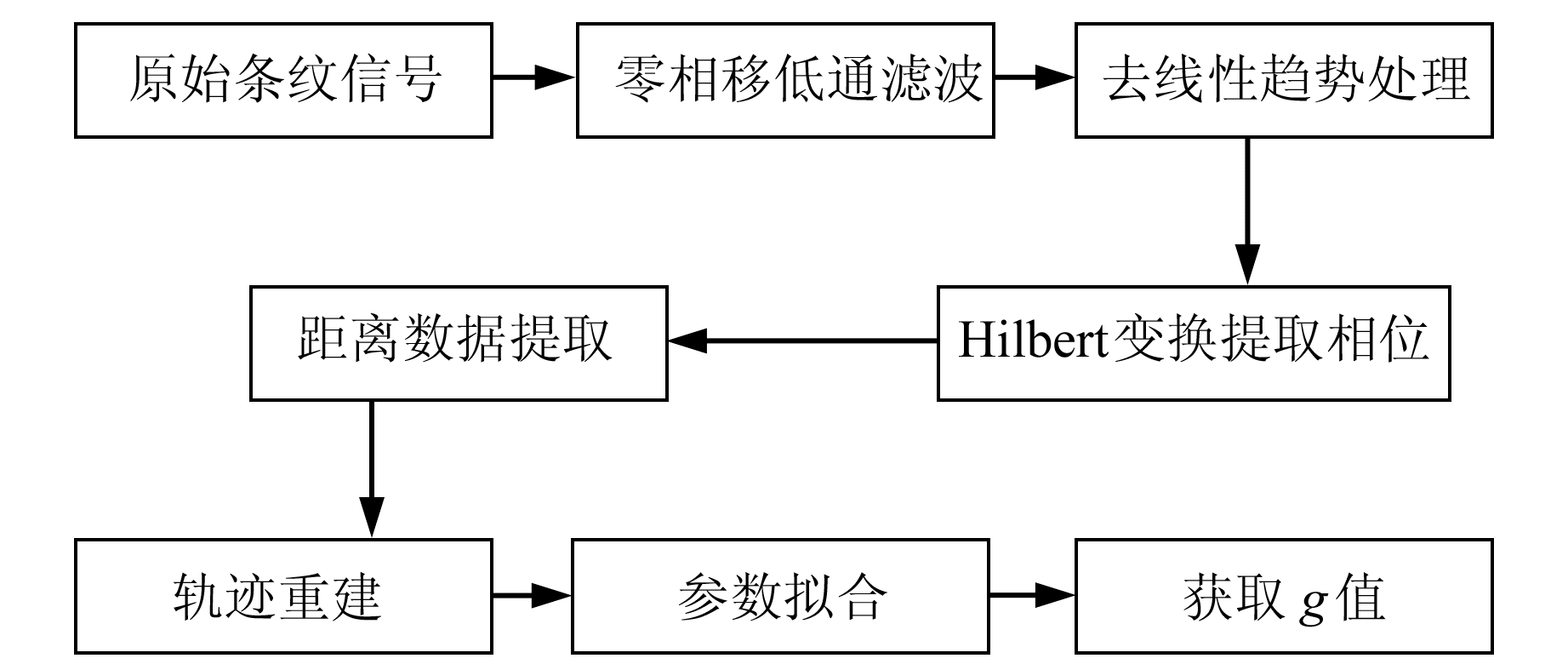
数据处理流程如图 4所示。首先使用零相移低通滤波器去除信号中的高频噪声; 其次对数据进行去线性趋势处理,去除信号中的直流与线性干扰; 然后采用Hilbert变换获取采样点的瞬时相位,由相位信息提取距离信息,结合采样频率获得时间-位移信息; 最后,采用最小二乘法重建落体轨迹,解算出g值。
|
图 4 数据处理流程 Fig. 4 The flow chart of data processing |
使用式(5)、式(9),取g=9.8 m/s2,落体的下落距离为H=25 cm,A0=1,u0=0.01,β=0.01,引入5%幅值高频高斯白噪声作为外部噪声,并使该信号采样频率为200 MHz,建立干涉条纹仿真信号模型。采用本文数据处理流程对数据进行处理,并以频率作为数据窗口依据,分别在去除噪声与保留噪声条件下取得仿真结果(表 1)。
|
|
表 1 g值仿真结果 Tab. 1 Simulation results of g values |
根据标准二阶线性模型最小二乘法[6], g值不确定度为:
| $ {\sigma _g} = \frac{{12\sqrt 5 }}{{{T^2}}} \cdot \frac{{{\sigma _S}}}{{\sqrt N }} $ | (18) |
式中,N为加入计算的数据个数,T为整个数据段的时间,σS为最小二乘位移残差的标准差。
由表 1可见,数据加窗口去除两端数据的方法抑制了吉伯斯现象,降低了σS。但是随着窗口的缩小,去除噪声时,σS的值极小,且随窗口缩小而变小,N与T的减小并不能使σg增大; 未去除噪声时,窗口的缩小并不能进一步改善σS,因此随着N与T的减小,σg不断增大。
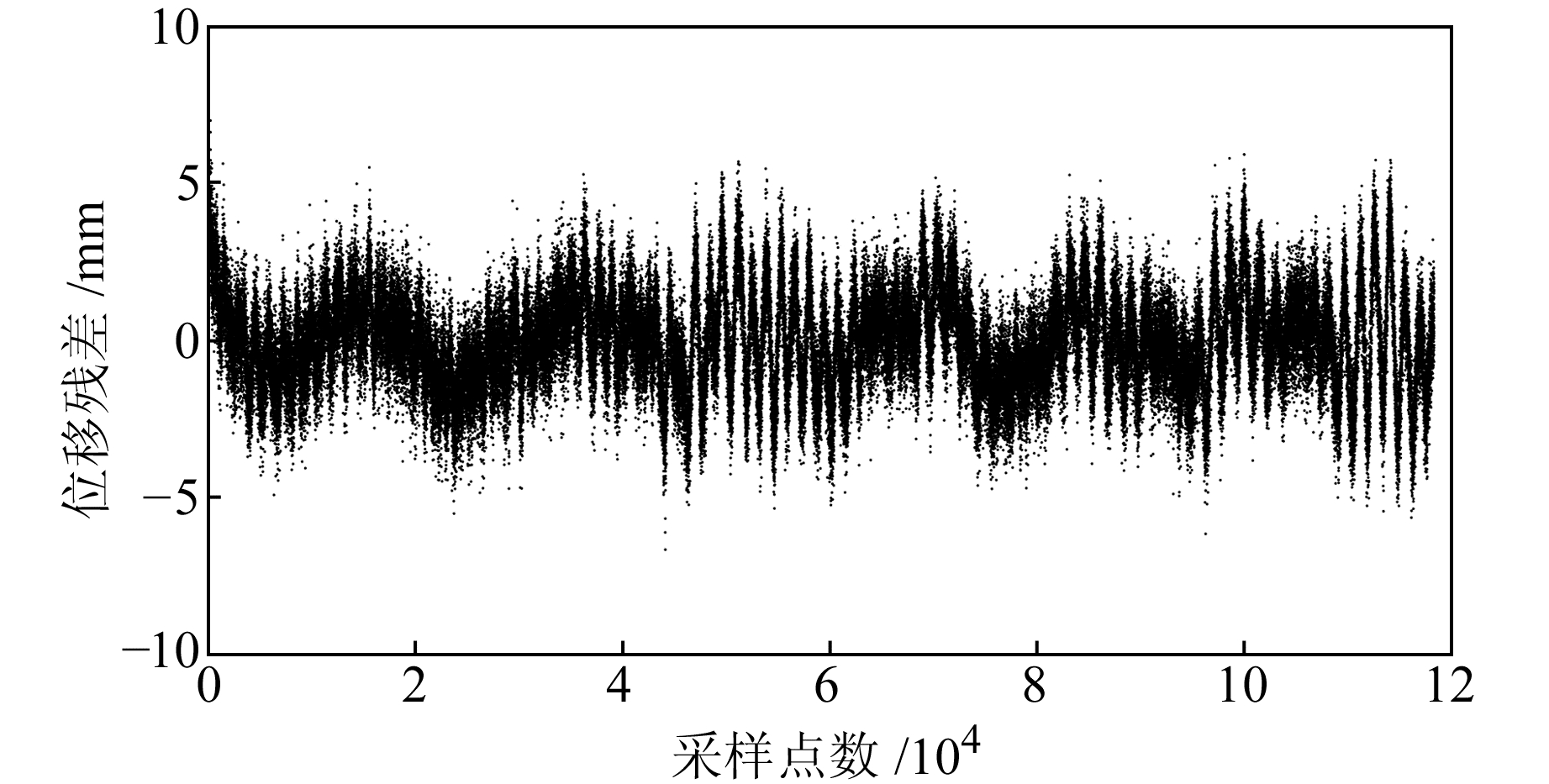
2.2 实验结果与分析在中国地震局地震研究所绝对重力仪上进行9次下落实验,对所得干涉条纹数据进行去噪声后,使用本文方法处理所得数据。数据窗口选取1~6 MHz,其中一次落体实验所得的最小二乘位移拟合残差如图 5所示。
|
图 5 最小二乘拟合位移残差 Fig. 5 Residual of the least squares fitting displacement |
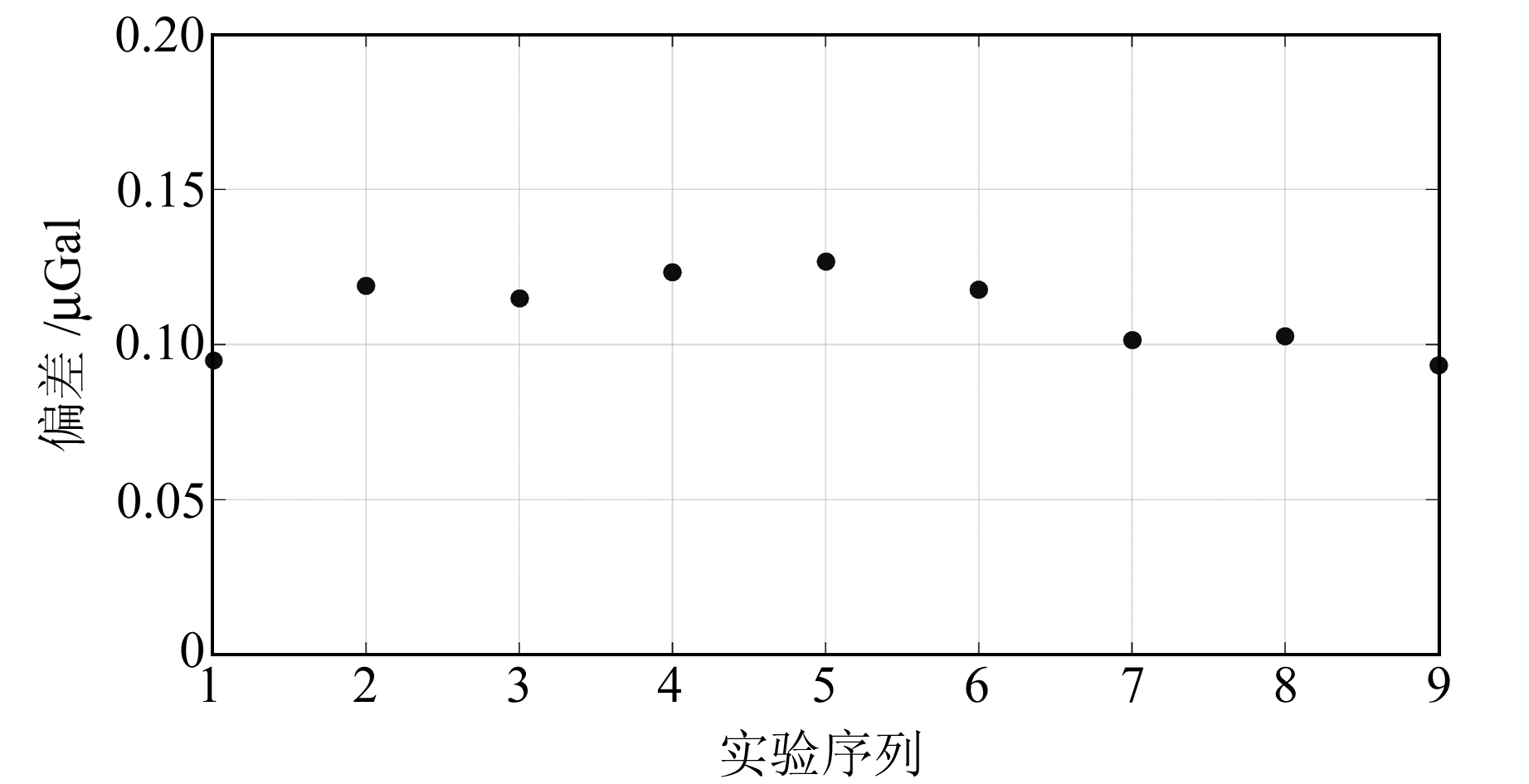
根据该残差可以直接判断数据处理方法的优劣[7]。使用各次实验最小二乘位移残差的标准差作为σS,参与拟合的数据段的时间为T,使用式(18)求解g值不确定度,结果如图 6所示。由图 6可见,g值不确定度在0.2 μGal以内。
|
图 6 实验得到的g值偏差σg Fig. 6 σg of g values obtained from the experiment |
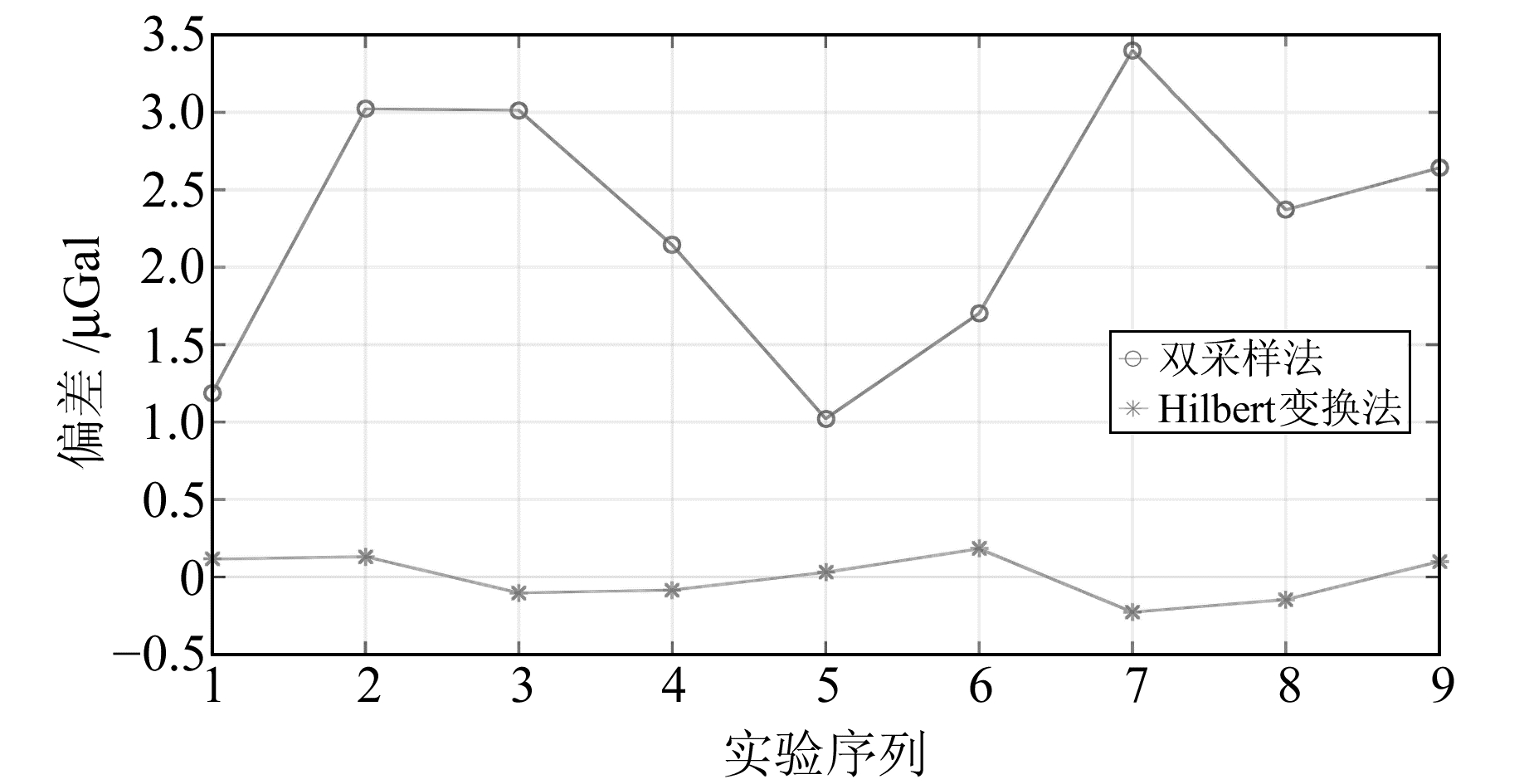
分别使用双采样过零点检测法与本文Hilbert变换法进行数据处理,将结果与仪器真值比较,所得g值误差如图 7所示。由图 7可见,Hilbert变换法所得结果平均误差为0.12 μGal,优于双采样法。
|
图 7 双采样法与Hilbert变换法结果误差 Fig. 7 Errors of two-sample method and Hibert-transfer method |
本文基于Hilbert变换相位平移的原理,结合零相位低通滤波、信号去线性趋势处理,以及拟合数据加窗口选取,实现对重力加速度的精确解算。仿真结果与实验测量所得g值不确定度表明,该方法准确、可靠。实验结果所得平均测量误差为0.12 μGal,相比于双采样法,本文方法具有更高的测量精度。对比仿真结果,g值测量精度仍能通过研究得到进一步提高。
| [1] |
Svitlov S, Masłyk P, Rothleitner C, et al. Comparison of Three Digital Fringe Signal Processing Methods in a Ballistic Free-Fall Absolute Gravimeter[J]. Metrologia, 2011, 47(6): 677
(  0) 0) |
| [2] |
Svitlov S, Araya A. Homodyne Interferometry with Quadrature Fringe Detection for Absolute Gravimeter[J]. Applied Optics, 2014, 53(16): 3 548-3 555 DOI:10.1364/AO.53.003548
(  0) 0) |
| [3] |
Schoukens J, Renneboog J. Modeling the Noise Influence on the Fourier Coefficients after a Discrete Fourier Transform[J]. IEEE Transactions on Instrumentation & Measurement, 1986, 35(3): 278-286
(  0) 0) |
| [4] |
Murata I. A Transportable Apparatus for Absolute Measurement of Gravity[J]. Bulletin of the Earthquake Research Institute University of Tokyo, 1978, 53(1): 49-130
(  0) 0) |
| [5] |
罗志才, 宛家宽. 自由落体式绝对重力仪测量数据处理方法研究[J]. 大地测量与地球动力学, 2016, 36(3): 189-192 (Luo Zhicai, Wan Jiakuan. Research on Free-Fall Absolute Gravimeter Data Processing Method[J]. Journal of Geodesy and Geodynamics, 2016, 36(3): 189-192)
(  0) 0) |
| [6] |
Svitlov S, Rothleitner C, Wang L J. Accuracy Assessment of the Two-Sample Zero-Crossing Detection in a Sinusoidal Signal[J]. Metrologia, 2012, 49(4): 413-424 DOI:10.1088/0026-1394/49/4/413
(  0) 0) |
| [7] |
Svitlov S, Araya A, Tsubokawa T. Digital Fringe Signal Processing Methods in Absolute Gravimetry[C]. IAG Symposium on Terrestrial Gravimetry: Static and Mobile Measurements (TG-SMM 2013), Saint Petersbourg, 2013
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39


