Larson等[1]首先使用GPS多路径信噪比SNRMP幅值监测土壤湿度变化的趋势,得出SNRMP观测值和土壤湿度变化具有一定相关性的初步结论,掀开了利用SNR进行土壤湿度反演的热潮。Chew等[2]将SNRMP的特征参量振幅、相位、有效反射高度分别与土壤湿度进行对比分析,结果表明,SNRMP相位更能反映土壤湿度的变化情况,为本文SNRMP特征参量的选取奠定了基础。敖敏思等[3]采用P041测站2010年PRN12卫星上120 d的SNRMP观测值进行GPS-MR监测土壤湿度变化的实验,验证了SNRMP相位能较好地反映土壤湿度变化趋势,且指数函数能较好地呈现二者的关系。
基于单颗GPS卫星长期的信噪比观测值,SNRMP相位可较好地反映土壤湿度变化的整体趋势,但其时间分辨率较低(往往为1 d),不利于土壤湿度的高动态监测。为此,本文在详细介绍GPS-MR土壤湿度监测理论的基础上,提出一种基于多颗卫星组合的GPS-MR高时间分辨率土壤湿度反演方法,并结合实测土壤湿度进行验证分析。
1 GPS-MR土壤湿度监测方法信噪比观测值SNR主要受天线增益参数、卫星与接收机之间的几何距离、接收机处的仰角、多路径效应等因素的共同影响[4]。当GNSS测站位于近地表土壤时,接收机接收到的信号实际是直射信号和反射信号的合成信号。
SNR具有2个特点:1)SNR与卫星高度角呈正相关关系[5]; 2)SNR降低时多路径效应明显增大[6]。可见,在低卫星高度角情况下,多路径效应成为影响SNR的主导因素,低高度角卫星的SNR观测值承载着测站周围多路径反射物丰富的物理信息。因此,基于GPS-MR的相关研究往往以高度角为5°~30°的卫星SNR观测值为重点关注对象。
SNR观测值默认单位为指数单位dB/Hz,采用GPS-MR进行相关研究前,一般需先按式(1)转换为线性单位V(伏特):
| $ {\rm{SN}}{{\rm{R}}_{{\rm{V}}/{\rm{V}}}} = {10^{\frac{{{\rm{SN}}{{\rm{R}}_{{\rm{dB}}}}_{{\rm{ - Hz}}}}}{{20}}}} $ | (1) |
假设仅存在一次反射,SNR与信号幅度存在如下关系[7]:
| $ {\rm{SN}}{{\rm{R}}^2} = A_C^2 = A_m^2 + A_d^2 + 2{A_m}{A_d}\cos \alpha $ | (2) |
式中,SNR表示接收机接收到的合成信噪比,cosα表示延迟相位的余弦值。鉴于多路径直反射分量数值上的差异,即Am≪Ad,加之SNR随卫星高度角整体呈二次曲线变化趋势[8],构建低阶多项式便可分离直射分量,从而获得近地表土壤水分等多路径因子引起的多路径信噪比SNRMP。图 1为本次实验GPS站点28号卫星(doy:2017-128,UTC:6.92~13.64 h)合成信噪比和去趋势项后的信噪比(即SNRMP)。
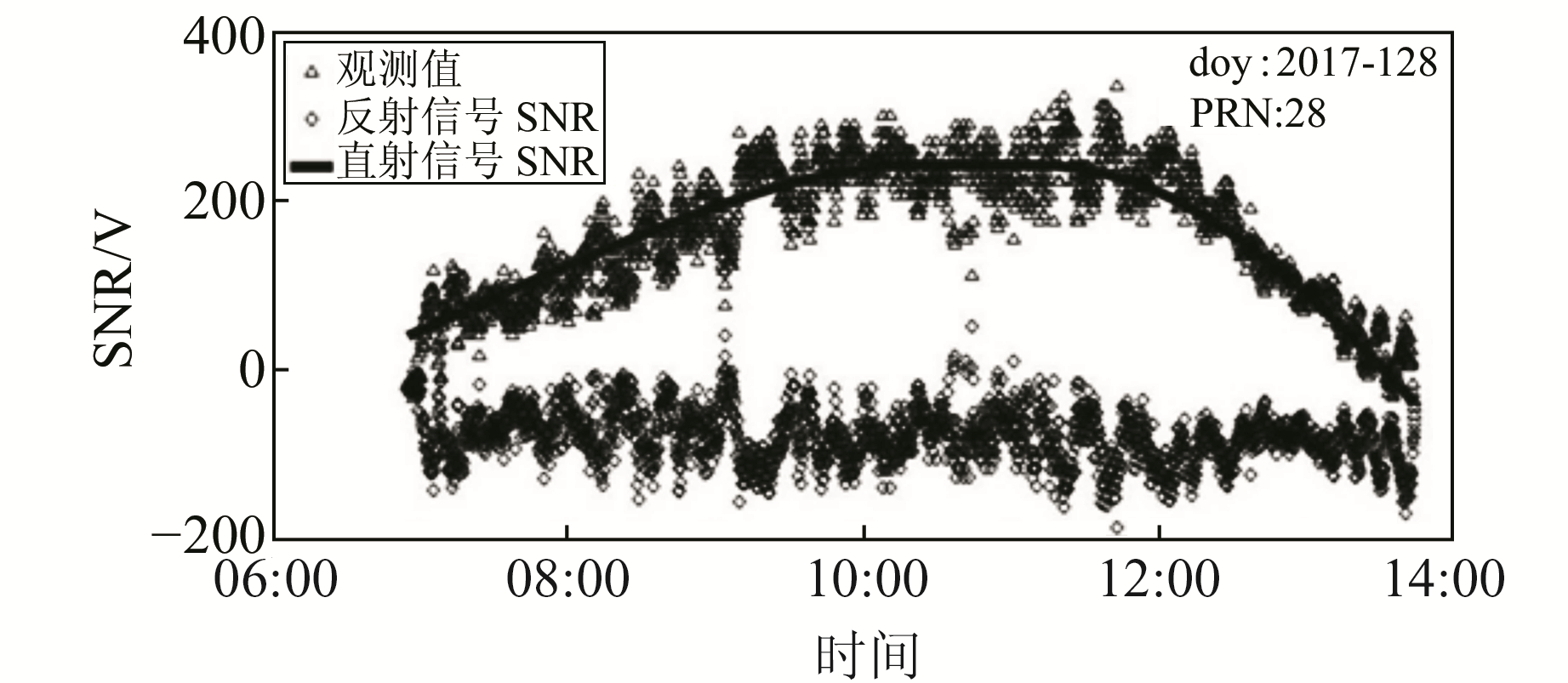
|
图 1 PRN28 SNR变化 Fig. 1 SNR variations of PRN28 |
图 2为去除趋势项后的信噪比残差序列SNRMP重采样图。SNRMP主要表征多路径噪声水平的高低。可以看出,SNRMP呈现明显的周期特性。
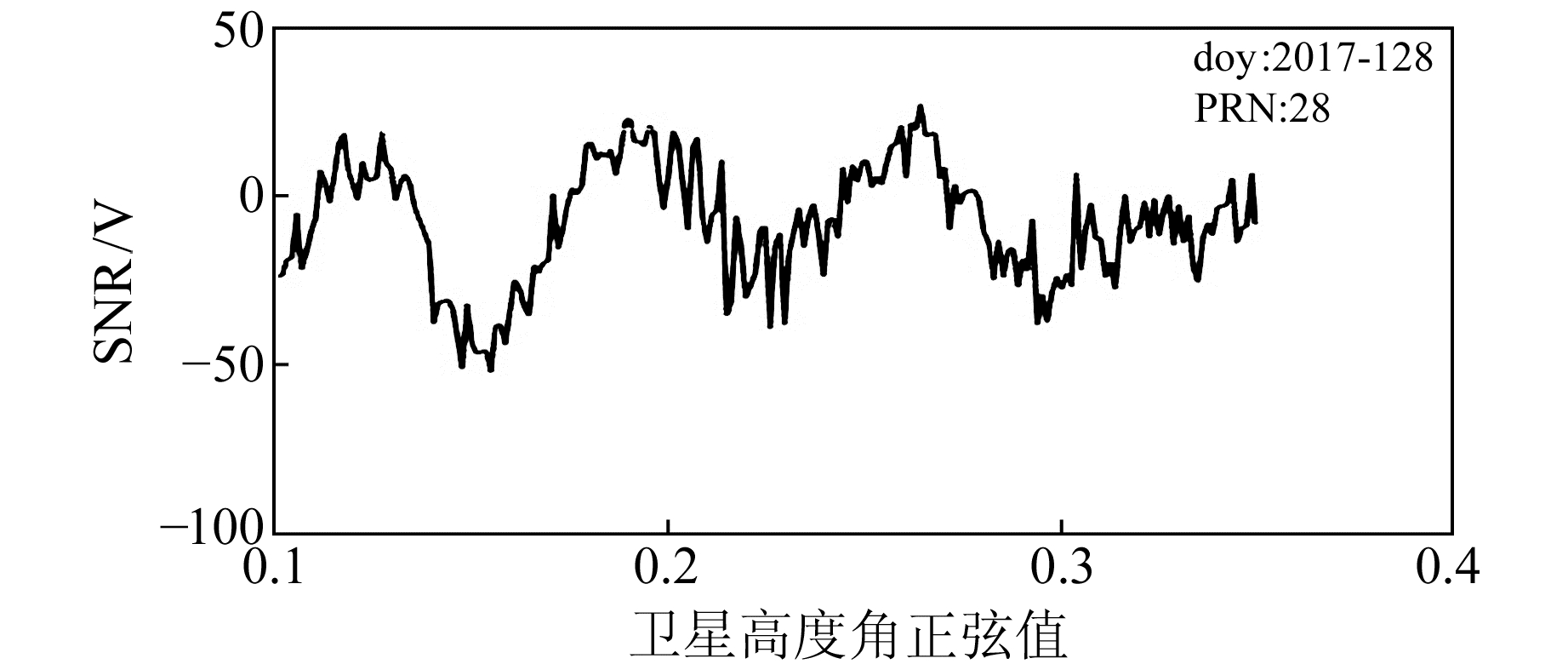
|
图 2 去除趋势项后的SNR残差序列 Fig. 2 SNR variations after detrending |
表征多路径水平的信噪比可表示为:
| $ {\rm{SN}}{{\rm{R}}_{{\rm{MP}}}} = {A_{{\rm{MP}}}}\cos \left( {\frac{{4{\rm{ \mathsf{ π} }}h}}{\lambda }\sin E + {\varphi _{{\rm{MP}}}}} \right) $ | (3) |
式中,λ为载波波长,E为卫星高度角,h为垂直反射距离,AMP和φMP分别为多路径反射分量的相对幅度和相对延迟相位。
记t=sinE, f=2h/λ,则式(3)可简化为标准余弦函数:
| $ {\rm{SN}}{{\rm{R}}_{{\rm{MP}}}} = {A_{{\rm{MP}}}}\cos \left( {2{\rm{ \mathsf{ π} }}ft + {\varphi _{{\rm{MP}}}}} \right) $ | (4) |
由于sinE为非等间距采样,从而导致信噪比残差序列无法保证整周期截断,可通过L-S(Lomb- Scargle)谱分析求得多路径反射信号的频率f,进而借助最小二乘解求幅度和延迟相位[9]。实验证明,延迟相位变化随反射信号渗透深度的变化而变化,而渗透的深度是由土壤介电常数决定的。延迟相位相反数和土壤湿度有较强的相关性[10],故依据延迟相位便可反演土壤湿度。
2 多卫星组合的GPS-MR土壤湿度反演 2.1 有效卫星高度角的选取低仰角卫星信号比高仰角卫星信号发生多路径效应现象的概率更大[11],而卫星高度角是多路径效应的一个重要影响因子。因此,对于既定的反射高度,如何根据卫星仰角挑选出合适的卫星,进而分离出能较好地反映地表反射物信息的信噪比观测值显得至关重要。
对静态接收机而言,接收机天线位置固定不变,由于卫星运动的周期性,GPS卫星相对于接收机天线的位置表现出一定的周期性,进而多路径现象也呈现出周期性的特点。鉴于土壤湿度样本时间间隔为2 h,截取对应土壤湿度样本采样时间段的信噪比为研究对象。经过多次实验发现,对于2 h的时间间隔,当卫星高度角在5.75°~20.48°变化时,SNRMP的周期性最为明显。图 3(a)~(d)为高度角在5.75°~20.48°时不同类型GPS卫星的SNRMP变化情况。
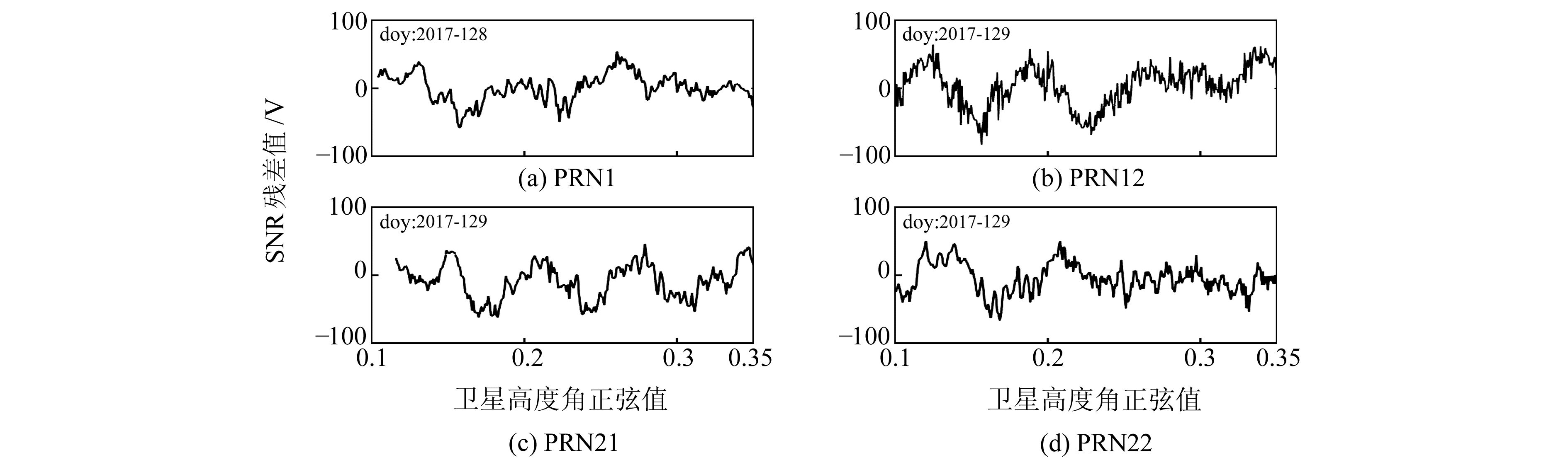
|
图 3 GPS各类卫星SNR残差变化 Fig. 3 GPS SNR residual variation maps of all kinds of satellites |
由图 3可知,无论是Block ⅡR-M(PRN12)、Block ⅡR(PRN21,PRN22),还是新一代Block ⅡF(PRN1)卫星,对于2 h时间间隔,当卫星高度角正弦值在0.1~0.35变化时,即卫星高度角在5.75°~20.48°变化时,实验地点SNRMP的周期特性(余弦特征)最为明显。故卫星高度角在5.75°~20.48°区间的SNRMP可作为本次实验的理想数据源。为论述方便,以下称5.75°~20.48°高度角为有效卫星高度角。
2.2 多GPS卫星组合由于GPS卫星运动的周期性(周期为11 h 58 min),其高度角在1 d中变化较大,使得同一颗卫星能较好地反映地表反射物信息的SNRMP的有效时间非常有限,从而导致采用同一卫星无法实现较高时间分辨率的土壤湿度反演。因此,本文在分析GPS卫星运动特征的基础上,依据土壤样本的采样时间,结合卫星高度角变化特征(即SNRMP的周期特性)进行选星,构建多GPS卫星组合,以改善GPS-MR土壤湿度反演的时间分辨率。
GPS卫星的运动表现为上升阶段和下降阶段。图 4为实验地点GPS卫星的轨迹图,可以看出,每个历元可供选择的卫星较多,但每颗卫星的可见性时间长短不一。1 d中单颗GPS卫星信噪比的持续时间一般在2.5~8 h左右(图 1)。有效卫星高度角对应信噪比持续时间更短,基本维持在0.5~2 h左右(图 5)。
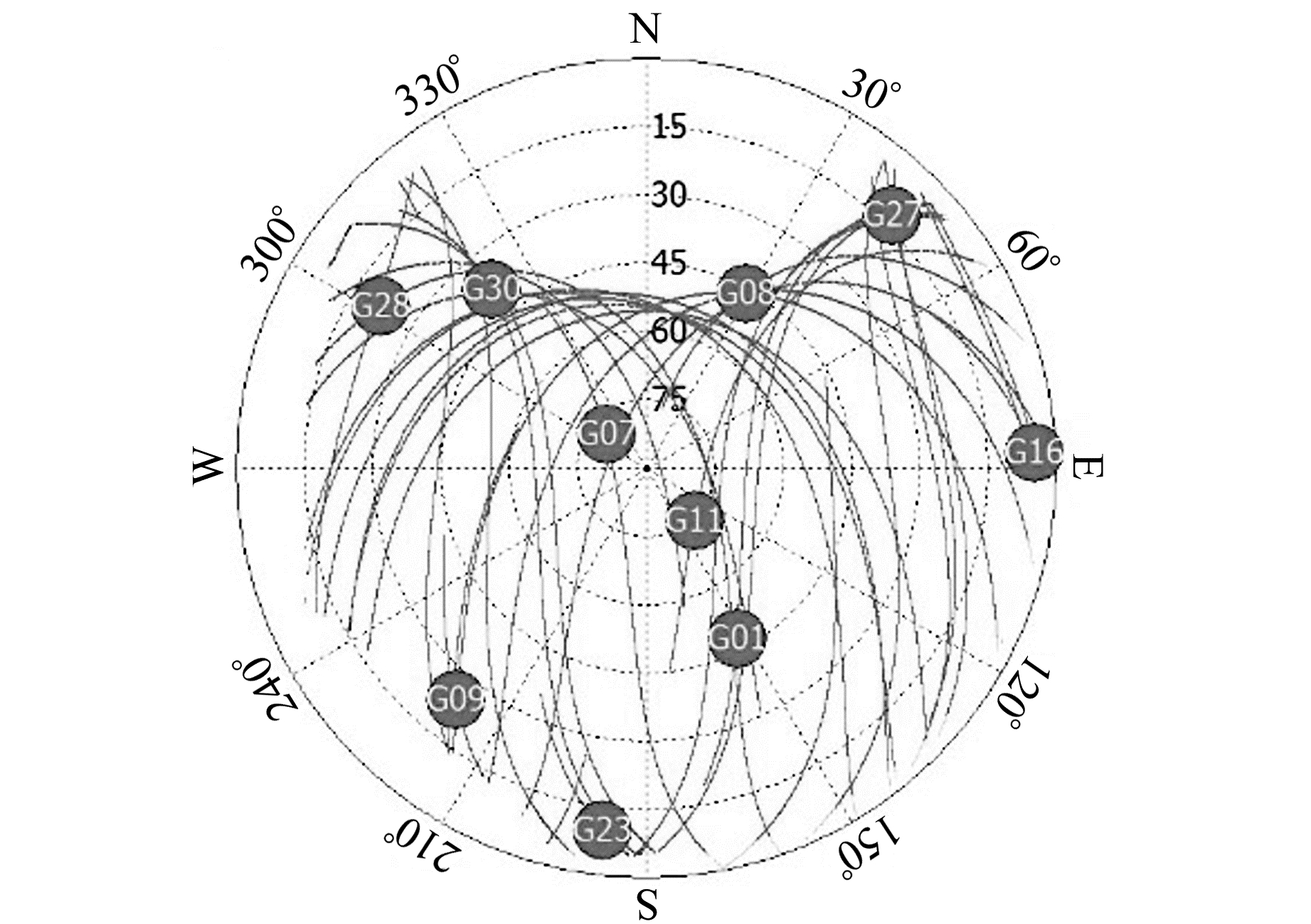
|
图 4 卫星轨迹 Fig. 4 The satellite trajectory |
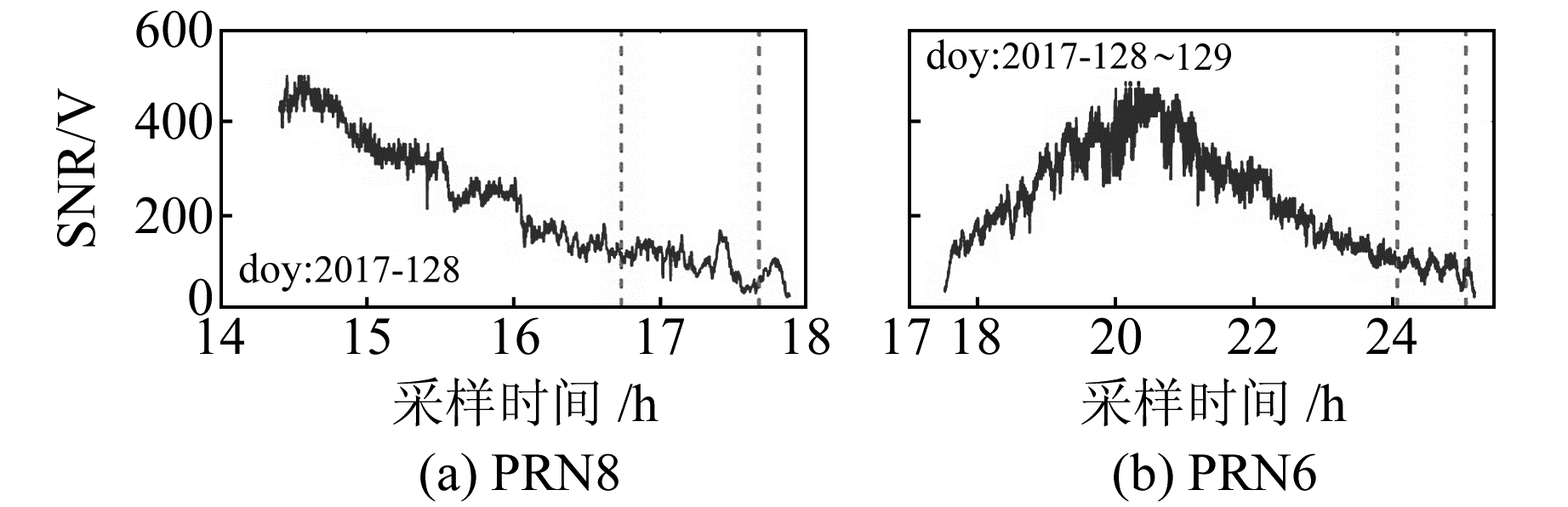
|
图 5 PRN8与PRN6低卫星高度角SNR变化 Fig. 5 SNR variations of PRN8 and PRN6 at low elevation angle |
图 5中2条虚线内为有效卫星高度角持续的时间。可以看出,1 d中PRN8的可见性不足4 h,该时间段内卫星高度角处于下降趋势(即卫星处于下降趋势),有效卫星高度角起止时间为8.7~9.6 h(UTC); PRN6则完成了一个完整的上升和下降过程,卫星可见性近8 h,而其有效卫星高度角持续的时间近1 h。
理论上,在卫星上升和下降过程中,其SNRMP观测值均适用于土壤湿度的监测,从而导致1 d中同一颗卫星可能存在多个有效卫星高度角时间区间,即有效卫星高度角对应的时间不具有单一映射关系。因此,为确保SNRMP观测值与土壤湿度样本时间的一致性,有必要依据土壤湿度采样时间,选择具有有效卫星高度角的卫星构成卫星组合。
3 实验与分析 3.1 数据采集实验GPS站点位于贵州大学新校区(26°26′47.59″ N,106°40′20.73″E),周围地势较为开阔,土壤以单一的黄棕壤为主。测区东西方向61 m、南北方向320 m区域范围内无遮挡物和其他反射源,可以认为是单一裸土,适合开展土壤湿度相关研究。
1) SNRMP观测值的采集。SNRMP观测值采集时间为2017-05-08 14:30~05-09 14:30,天气晴朗,实验前1 d有降雨。使用的GPS接收设备及参数设置见表 1。
|
|
表 1 接收机及参数设置 Tab. 1 Receiver and its parameter settings |
2) 烘焙法测量土壤湿度。土壤湿度采用烘焙法进行测量。土壤采样时间和GPS开始观测的时间一致,每隔2 h采样一次,每次采集5处土壤样本,取样深度为0~5 cm。将采集的土壤样本以密封袋密封保存并带回实验室进行湿度测量。
烘焙法测定土壤湿度的原理为:在105 ℃下,将土壤样品烘烤至恒重,通过烘烤前后质量之差,计算出土壤湿度SWC(soil water content)。公式如下:
| $ {\rm{SWC = }}\frac{{烘烤前质量 - 烘烤后质量}}{{烘烤后质量 - 纸盒重量}} $ | (5) |
式中,SWC为5处土壤样本均值。
3.2 数据处理与分析实验中,采用L1载波上的SNR观测值作为GPS-MR土壤湿度分析的数据源。依据上述对有效卫星高度角的讨论及多卫星组合等方面的介绍,选择PRN8、PRN1、PRN30、PRN28、PRN6、PRN21、PRN12、PRN20、PRN22、PRN23、PRN14、PRN1构成卫星组合。各卫星高度角及SNRMP样本数如表 2。
|
|
表 2 多GPS卫星组合 Tab. 2 The combination of multi-GPS |
在顾及高度角区间大致一致的基础上,采用L-S谱分析及最小二乘方法求取各采样时间节点延迟相位,用以衡量土壤湿度变化的整体趋势,得到反射信号延迟相位和土壤湿度的关系(图 6)。
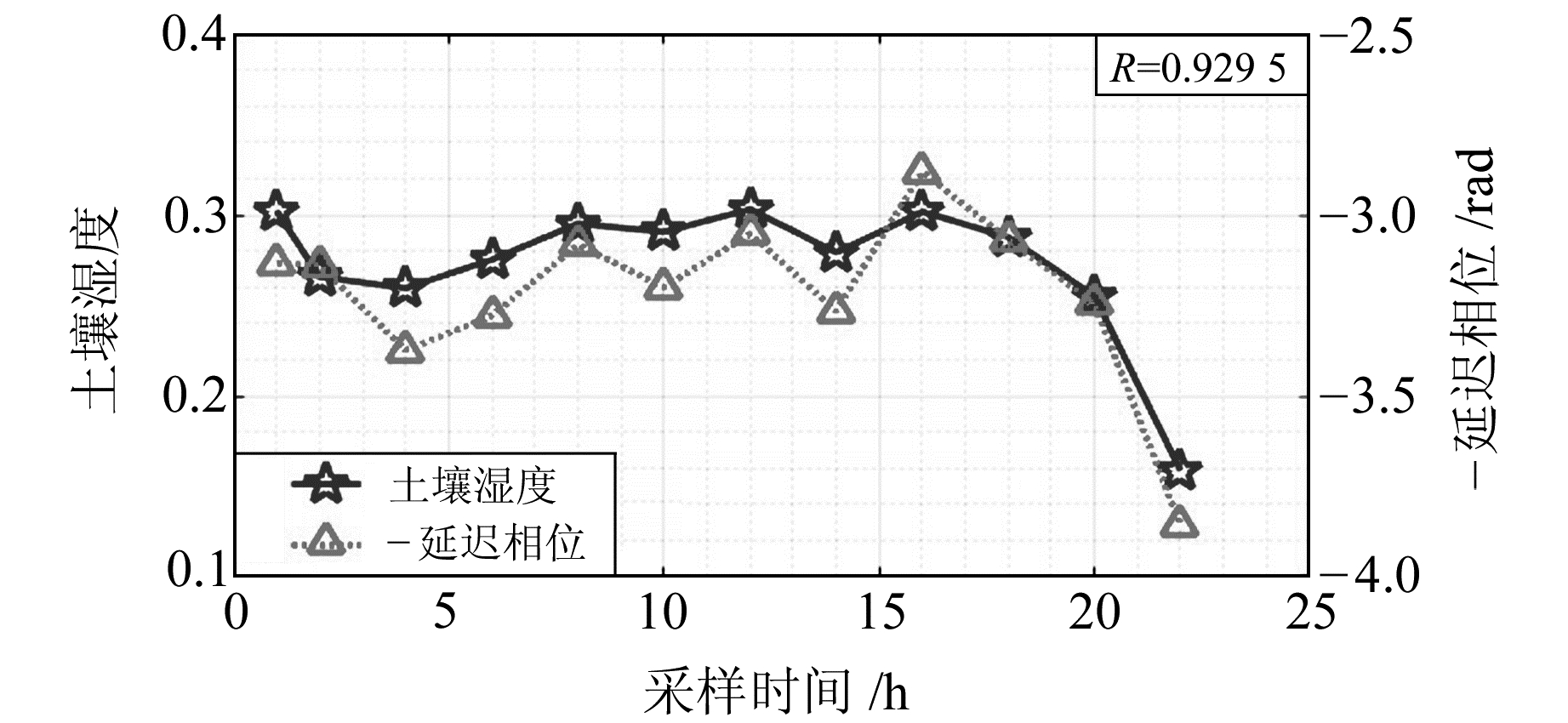
|
图 6 延迟相位与土壤湿度 Fig. 6 Delay phase and soil moisture map |
图 6中实线代表烘焙法所测土壤含水率,虚线代表延迟相位信息,横坐标表示采样时间。由图 6可看出,延迟相位和土壤湿度均存在2个明显的峰值,分别发生在05-08 14:30~16:30和05-08 22:30~24:00+05-09 00:00~06:30,前者可能是由于05-07有降雨事件发生,土壤水分的蒸发过程还在持续,采样前2 h(05-08 14:30~16:30)的土壤湿度值和延迟相位较大; 后者发生在05-09凌晨和清晨,这可能是因为夜间温度较低,近地面的水汽遇冷凝结成露水,导致土壤含水量增加,此后随着太阳照射的增强,地表温度持续上升,土壤湿度迅速下降。总体而言,多卫星延迟相位组合与土壤湿度变化趋势基本一致,延迟相位组合能较好地反映出1 d内2 h时间分辨率土壤湿度的变化趋势,且二者相关系数优于0.92,统计学上表现为显著相关。
为进一步描述土壤湿度和延迟相位的关系,以便依据延迟相位求土壤湿度,基于12对样本数据,采用一元线性回归分析法进行建模,得到图 7所示的回归模型。为检验回归效果,取显著性水平α=0.001,查表得F0.001(1, 10)=21.04,而检验量F=30.978 7。故回归效果显著,土壤湿度和延迟相位存在一定的线性关系。图 8中,横轴代表土壤湿度的样本数,纵轴为土壤湿度实测值与模型值之间的残差及置信区间,残差均方根误差为0.02,说明回归误差较小,可用该模型依据延迟相位求土壤湿度。需要指出,该模型是基于本实验的结果,未必适用于其他研究区域。
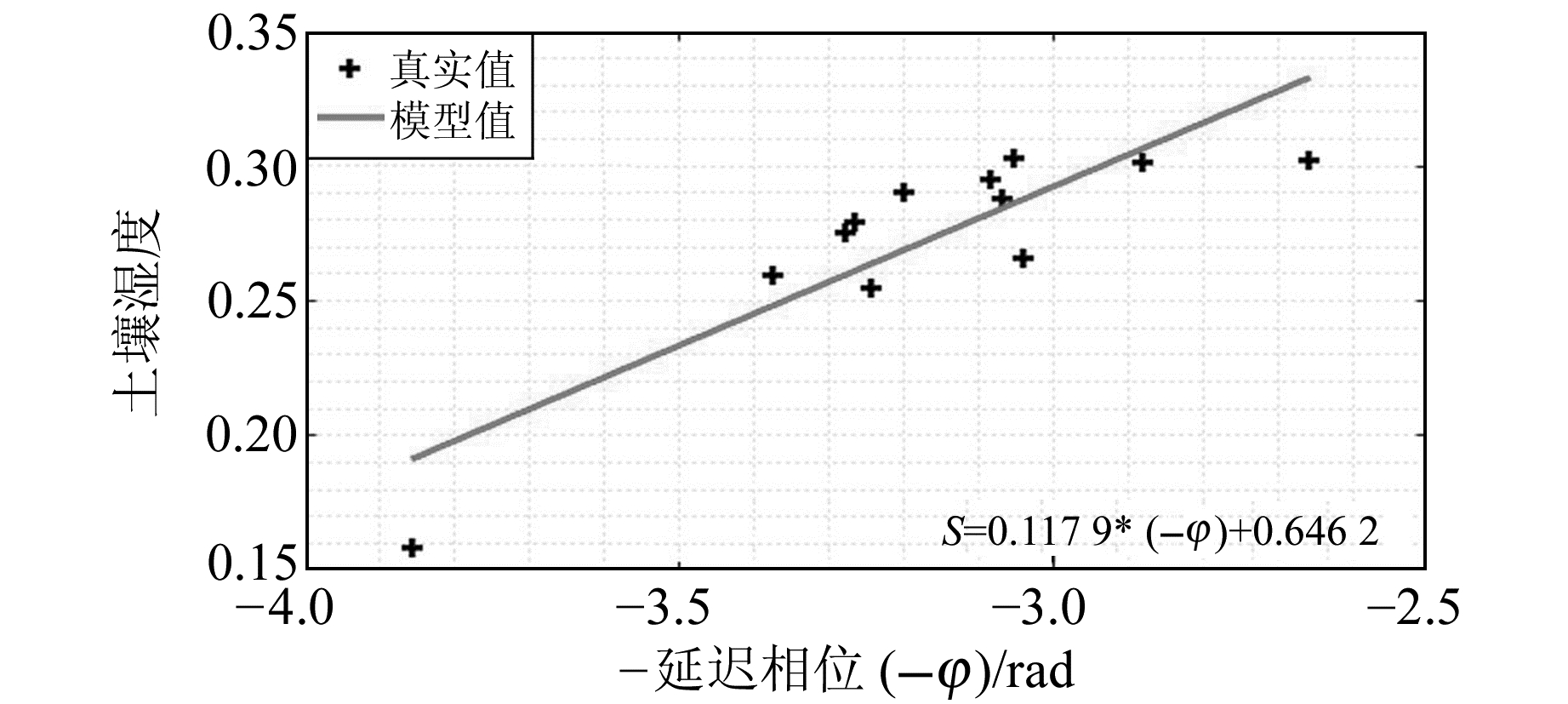
|
图 7 延迟相位与土壤湿度散点分布 Fig. 7 Scatter diagram of relative delay phase and soil moisture |
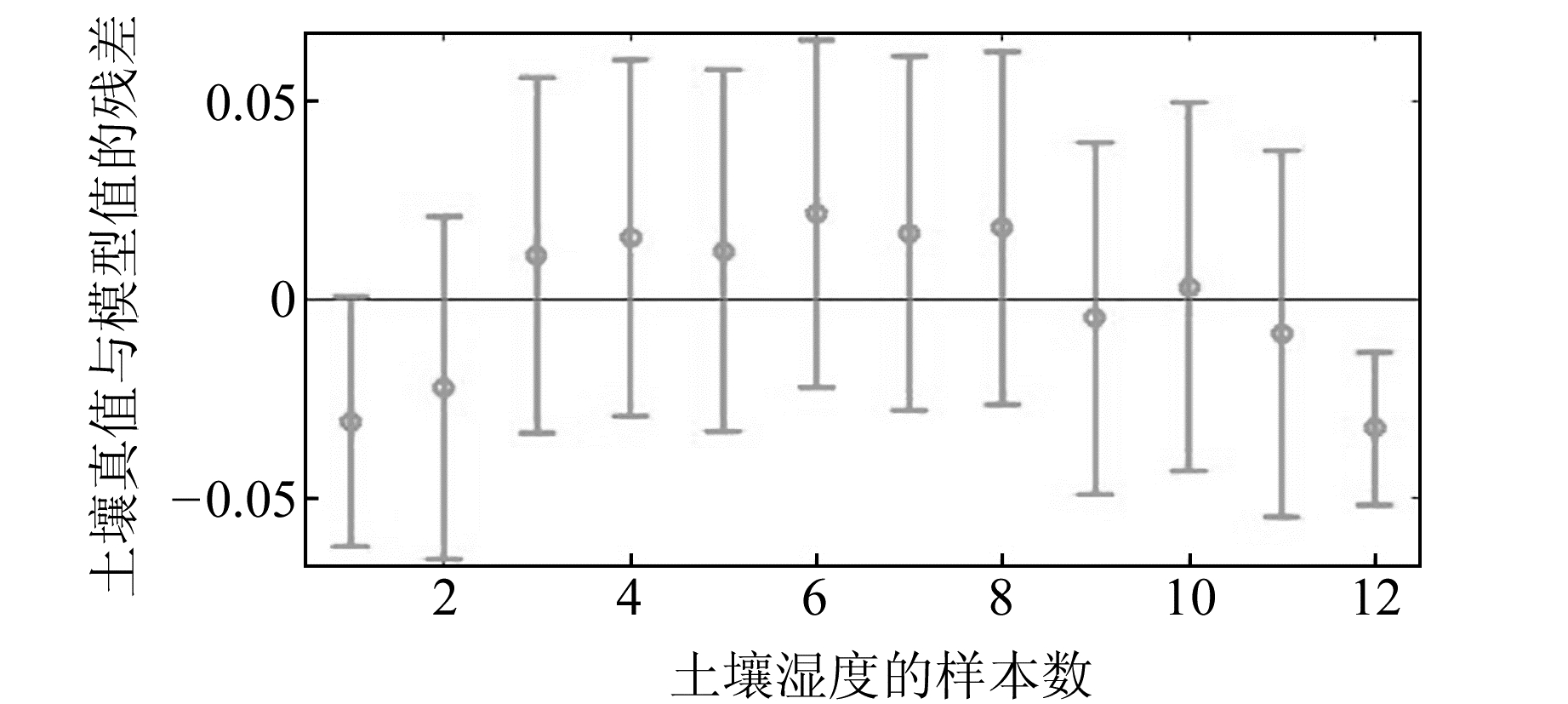
|
图 8 残差及其置信区间 Fig. 8 Residuals and their confidence intervals |
本文在详细给出基于信噪比的GPS-MR技术监测土壤湿度变化趋势基本理论的基础上,鉴于多路径效应和GPS卫星运动的周期特性,以及卫星上升过程和下降过程均可能存在有效卫星高度角,依据土壤湿度样本采样时间,考虑有效高度角的大致区间,实现了采用多卫星组合的GPS-MR技术进行高时间分辨率的土壤湿度反演。为验证该方法的有效性,结合实测信噪比观测值和土壤湿度进行分析。结果表明,多GPS卫星延迟相位组合与土壤湿度整体变化趋势一致,二者相关系数优于0.92,为显著相关; 时间分辨率得到极大改善,由传统的1 d提升为2 h。同时,本文所构建的线性模型能够较好地表征延迟相位和土壤湿度间的关系。分析过程中未顾及温度等其他多路径因子的影响,同时忽略了每个采样区间内反射高度和天线相位中心的变化,这将是后期研究的重点。需要特别指出的是,本文结论是基于实验场地良好的土壤反射环境得出的,其普适性有待进一步验证。
| [1] |
Larson K M, Braun J J, Small E E, et al. Using GPS Multipath to Measure Soil Moisture Fluctuations: Initial Results[J]. GPS Solutions, 2008, 12(3): 173-177 DOI:10.1007/s10291-007-0076-6
(  0) 0) |
| [2] |
Chew C C, Small E E, Larson K M, et al. Effects of Near-Surface Soil Moisture on GPS SNR Data: Development of a Retrieval Algorithm for Soil Moisture[J]. IEEE Transactions on Geoscience & Remote Sensing, 2013, 52(1): 537-543
(  0) 0) |
| [3] |
敖敏思, 朱建军, 胡友健. 利用SNR观测值进行GPS土壤湿度监测[J]. 武汉大学学报:信息科学版, 2015, 40(1): 117-120 (Ao Minsi, Zhu Jianjun, Hu Youjian. Comparative Experiments on with GPS SNR Soil Moisture Monitoring Observations[J]. Geomatics and Information Science of Wuhan University, 2015, 40(1): 117-120)
(  0) 0) |
| [4] |
吴雨航, 陈秀万, 吴才聪. 利用信噪比削弱多路径误差的方法研究[J]. 武汉大学学报:信息科学版, 2008, 33(8): 842-845 (Wu Yuhang, Chen Xiuwan, Wu Caicong. Mitigation of Multi-Path Effect Using SNR Values[J]. Geomatics and Information Science of Wuhan University, 2008, 33(8): 842-845)
(  0) 0) |
| [5] |
尹子明, 孟凡玉, 陈明剑, 等. 卫星导航数据质量分析[J]. 全球定位系统, 2016, 41(1): 54-59 (Yin Ziming, Meng Fanyu, Chen Mingjian, et al. Quality Analysis of Satellite Observation[J]. GNSS World of China, 2016, 41(1): 54-59)
(  0) 0) |
| [6] |
吴丹, 王利, 张勤, 等. GNSS数据质量评估软件的实现及验证分析[J]. 测绘科学技术学报, 2015, 32(4): 344-348 (Wu Dan, Wang Li, Zhang Qin, et al. Implementation and Verification Analysis of the Software of GNSS Data Quality Check[J]. Journal of Geomatic Science and Technology, 2015, 32(4): 344-348 DOI:10.3969/j.issn.1673-6338.2015.04.004)
(  0) 0) |
| [7] |
Strode P R R, Groves P D. GNSS Multipath Detection Using Three-Frequency Signal-to-Noise Measurements[J]. GPS Solutions, 2016, 20(3): 399-412 DOI:10.1007/s10291-015-0449-1
(  0) 0) |
| [8] |
Roussel N, Frappart F, Ramillien G, et al. Detection of Soil Moisture Variations Using GPS and GLONASS SNR Data for Elevation Angles Ranging from 2° to 70°[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2016, 9(10): 4 781-4 794
(  0) 0) |
| [9] |
徐斌, 杨涛, 谭保华, 等. 基于Lomb-Scargle算法的周期信号探测的模拟研究[J]. 核电子学与探测技术, 2011, 31(6): 702-705 (Xu Bin, Yang Tao, Tan Baohua, et al. The Simulate Study of Signal Detection Based on Lomb-Scargle Algorithm[J]. Nuclear Electronics & Detection Technology, 2011, 31(6): 702-705 DOI:10.3969/j.issn.0258-0934.2011.06.026)
(  0) 0) |
| [10] |
叶险峰.基于GNSS信噪比数据的测站环境误差处理方法及其应用研究[D].武汉: 中国地质大学(武汉), 2016 (Ye Xianfeng. Research on Processing Method of GNSS Station Environment Error and Its Application Using SNR Data[D].Wuhan: China University of Geosciences, 2016) http://cdmd.cnki.com.cn/Article/CDMD-10491-1016312031.htm
(  0) 0) |
| [11] |
南阳, 张双成, 张勤, 等. GNSS多径反射探测海平面变化初探[J]. 测绘科学, 2015, 40(12): 125-129 (Nan Yang, Zhang Shuangcheng, Zhang Qin, et al. Preliminary Results of Sea Level Change Monitoring with GNSS MR[J]. Science of Surveying and Mapping, 2015, 40(12): 125-129)
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39


