在对流层中,温度随高度不断变化。Angell等[1]认为,1960~1985年几乎所有气候区域的地表和对流层都变暖,而对流层顶层和平流层底层变冷,即温度梯度在垂直结构上存在变化趋势。李启泰[2]对福安地区温度递减率的变化规律进行分析认为,认识温度递减率的变化规律是了解福安地区农业气象特点的关键。罗贵东等[3]利用温度递减率分析四川省的积温特征,得出四川省积温的平均温度垂直递减率为0.41 ℃/100 m。
除在农业中的应用,大气温度递减率的变化趋势也用于激光雷达对低空大气的长期观测[4]。在GPS气象中,姚宜斌等[5]通过推导地表温度与加权平均温度的非线性关系,建立了温度递减率与加权平均温度之间的关系,但并未分析其对加权平均温度的影响。至今为止,没有学者在拟合加权平均温度的时候将温度递减率作为独立参数进行考虑。本文利用2008~2010年全国84个探空站的数据对温度递减率进行估计,建立温度递减率与地表温度和纬度之间的关系模型,并根据所建立的模型讨论其对加权平均温度的影响。
1 温度递减率模型的建立在估计温度递减率之前要先确定对流层顶,本文采用温度最低点来确定对流层顶[6]。温度递减率在对流层内随高度h近似线性变化:
| $ T = {T_s} + \delta h $ | (1) |
式中,Ts为地表温度,单位K; δ为温度递减率,单位K/km。
将温度递减率作为待拟合参数,采用最小二乘原理对观测时刻的温度垂直廓线进行线性拟合,即可求得对应观测时刻的温度递减率:
| $ \delta = \frac{{\sum\limits_{i = 1}^n {\left( {{T_i} - \bar T} \right)} \left( {{h_i} - \bar h} \right)}}{{\sum\limits_{i = 1}^n {{{\left( {{h_i} - \bar h} \right)}^2}} }} $ | (2) |
首先利用分布在低、中、高纬度区域的4个探空站数据来研究温度递减率随地表温度的实际变化情况。4个探空站信息见表 1,探空站数据一般每天观测2次,时间分辨率不高。由于探空气球在观测中可能出现仪器记录错误等问题,采用3倍中误差对数据进行预处理,以均方根误差RMSE和平均绝对方差MAD对拟合结果进行精度评定。
|
|
表 1 4个探空站的地理信息 Tab. 1 Locations of four radiosonde stations |
分析2008~2010年84个探空站的观测数据发现,温度递减率与地表温度线性相关。假定温度递减率与地表温度有如下关系:
| $ \delta = {a_0} + {a_1}{T_s} $ | (3) |
利用以上4个探空站的数据分别对式(3)进行拟合,采用MATLAB的T检验函数对式(3)的残差进行假设性检验,结果见表 2。
|
|
表 2 4个探空站的假设检验信息 Tab. 2 Hypothesis testing information |
4个探空站的布尔变量都为0,表明残差的均值为0的假设是合理的,95%的置信区间完全包括0均值,且精度很高。从表 3也可以发现,随着纬度的升高,精度有降低的趋势; sig值均为1,远超过0.5。以上检验表明,式(3)的拟合残差属于正态分布,具有合理性。线性拟合结果见表 3。
|
|
表 3 4个探空站的线性拟合结果 Tab. 3 The results of linear fitting |
在以上统计分析的基础上,进一步讨论温度递减率在全国84个探空站的线性拟合情况。图 1反映了a0和a1随纬度的变化。在纬度范围低于35°的区域,除个别异常值外,a0和a1近似线性变化,a0随纬度逐渐降低,a1随纬度逐渐增加; 纬度范围位于35°~40°区域,a0和a1的离散度在增加; 纬度范围在40°以上的区域,a0和a1变化没有规律。徐晓华等[7]利用COSMIC掩星数据分析对流层顶高度变化时指出,对流层顶高度在纬度32°~40°区域内由南向北急剧降低。这种现象在温度递减率的急剧变化上也有体现。
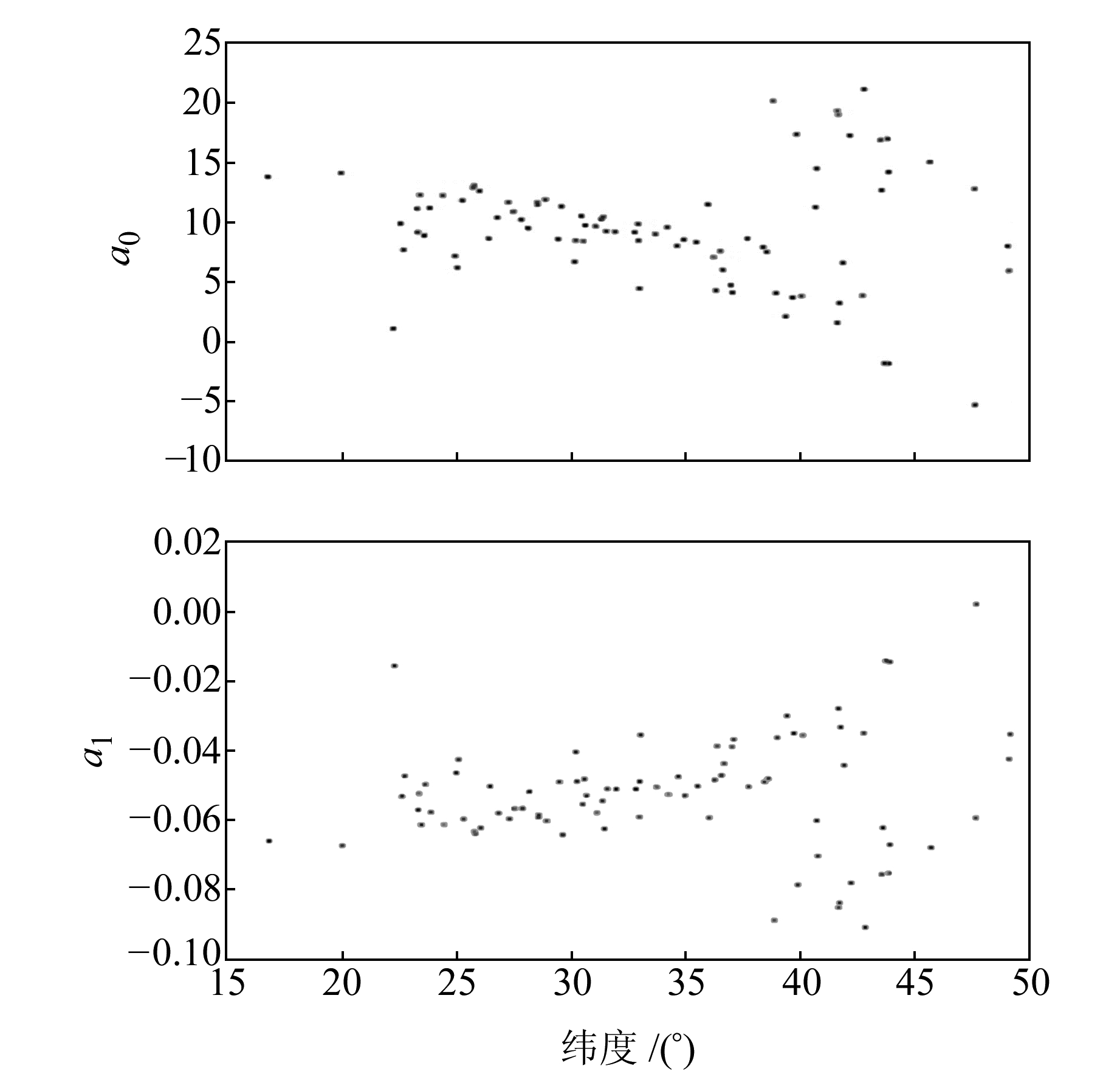
|
图 1 线性拟合系数a0和a1随纬度的变化 Fig. 1 Variation of a0 and a1 with latitudes |
通过以上分析可见,在纬度小于35°范围内,对流层结构稳定,a0和a1的值随纬度呈线性变化。因此,在式(3)的基础上,引入纬度变量φ,将a0、a1分别表示为纬度的线性函数,有:
| $ \delta = {b_0} + {b_1}\varphi + \left( {{b_2} + {b_3}\varphi } \right){T_s} $ | (4) |
式中,bi(i=0, 1, 2, 3)为待拟合系数。
图 2给出了温度递减率拟合模型随时间的变化情况,灰色为拟合值,黑色为真值,所用数据来源于全国分布的84个探空站。受地表温度、测站高度等环境影响,图 3中温度递减率依然存在大量的离散值。拟合得到的各系数项分别为13.66、-17.85、-0.06、0.05,RMSE为0.78 K/km,MAD为0.60 K/km。
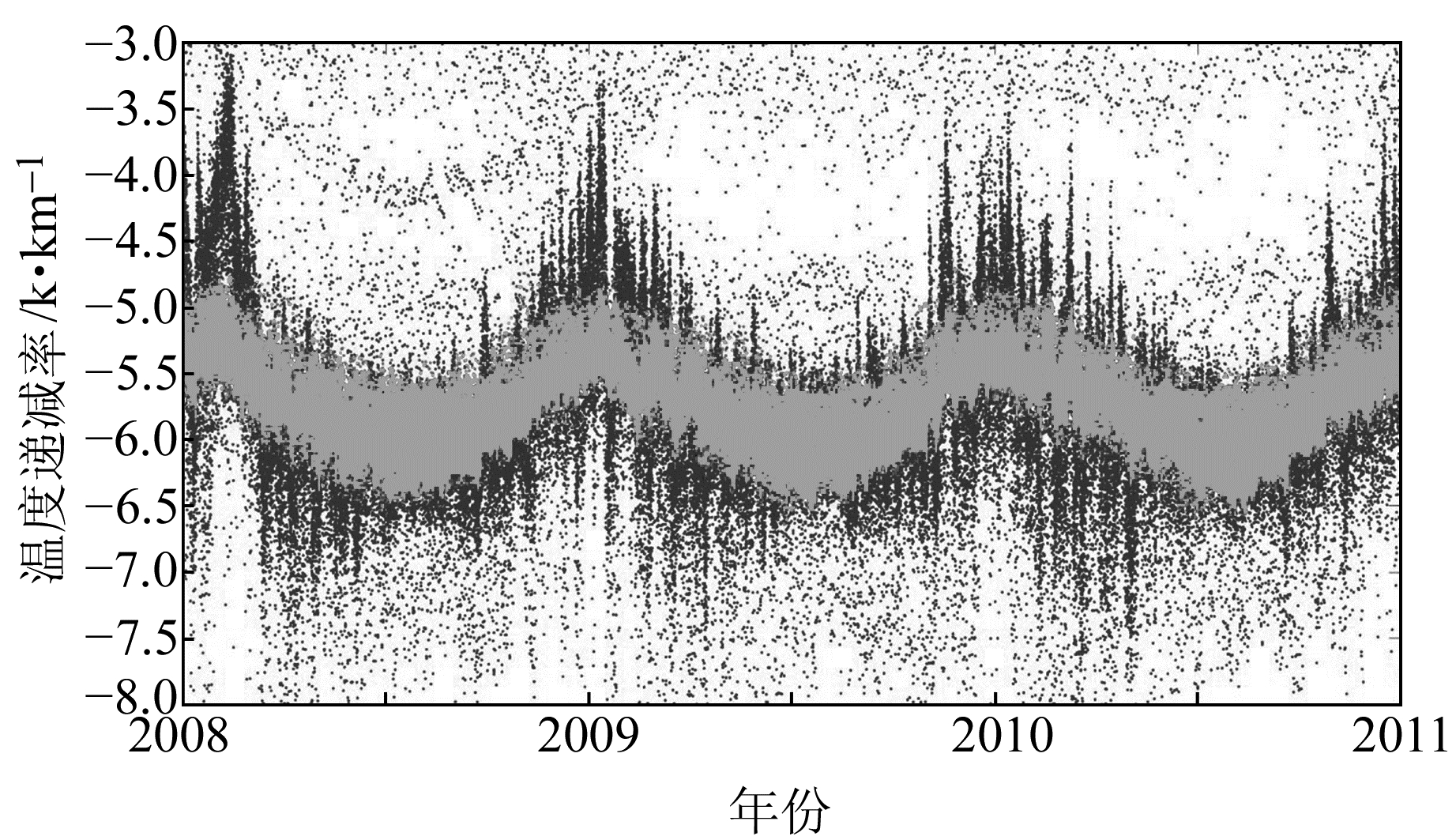
|
图 2 温度递减率的拟合值和真值随时间的变化情况 Fig. 2 The fitting results varying with time |
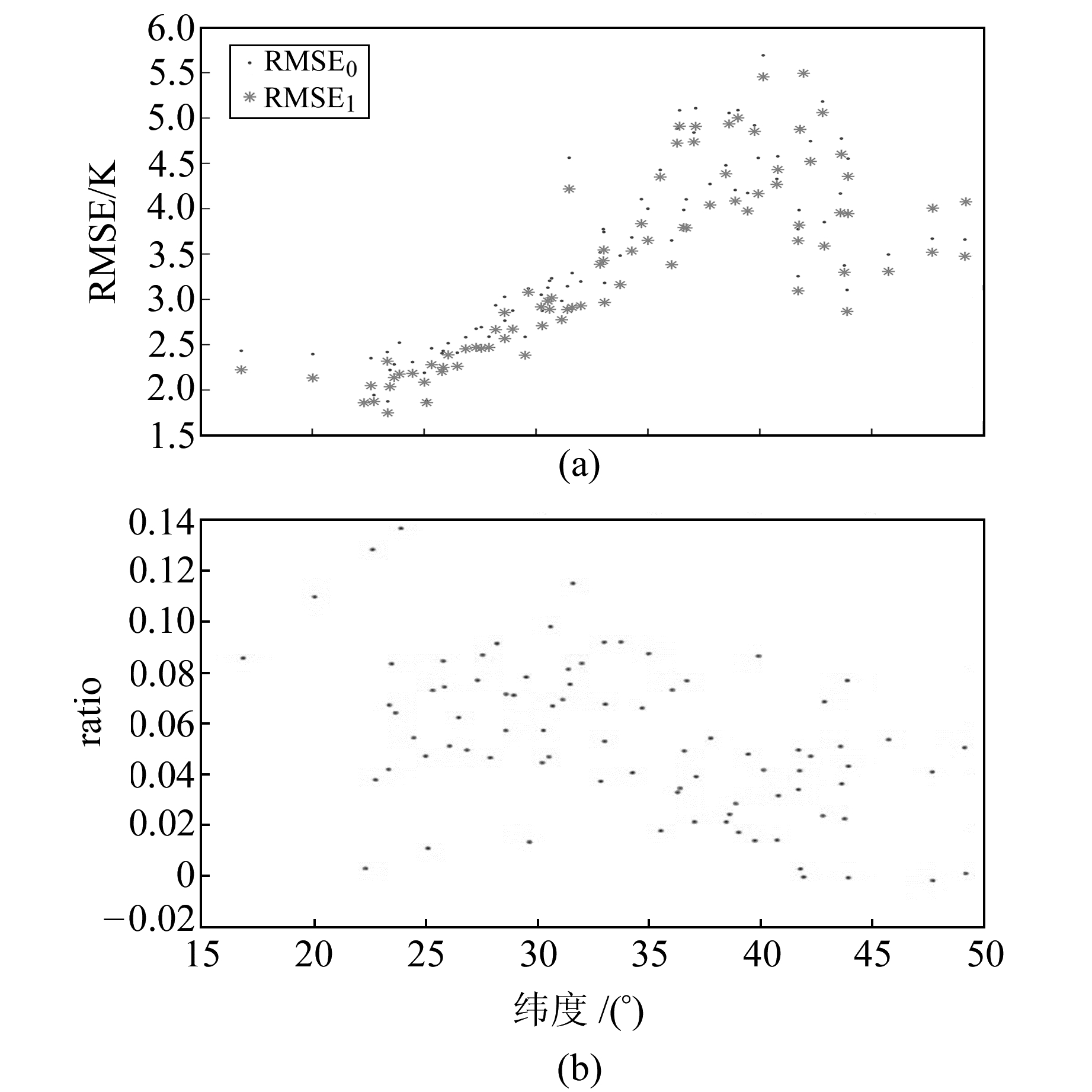
|
图 3 RMSE和ratio随纬度的分布 Fig. 3 The distribution of RMSE and ratio with latitudes |
对于纬度高于35°的地区,温度递减率应采用式(3)的计算方法。
2 温度递减率在加权平均温度中的应用姚宜斌等[5]推导出加权平均温度的非线性表达式,指出不宜将温度递减率作为常数。加权平均温度非线性表达式为:
| $ \begin{array}{l} {T_m} = aT_s^2 + a\delta \left( {{h_s} + {h^\prime }} \right){T_s} + \frac{{b\delta \left( {{h_s} + {h^\prime }} \right)}}{{{T_s}}} + \\ \;\;\frac{{b{{\left( {\delta \sqrt {h_s^2 + {h^{\prime 2}}} } \right)}^2}}}{{3T_s^2}} + \frac{{a{{\left( {\delta \sqrt {h_s^2 + {h^{\prime 2}}} } \right)}^2}}}{3} + b \end{array} $ | (5) |
式中,Ts为地表温度,hs为测站高,h′为对流层顶,a和b为待拟合参数。
利用式(5)的简化形式推得加权平均温度与地表温度的关系,进一步简化为:
| $ {T_m} = {c_1}T_s^2 + {c_2}{T_s} + \frac{{{c_3}}}{{{T_s}}} + \frac{{{c_4}}}{{T_s^2}} + {c_0} $ | (6) |
式中,ci(i=0, 1, 2, 3, 4)为待拟合系数。
基于式(5)来讨论温度递减率对加权平均温度的影响。由于本文不讨论对流层顶和测站高度对加权平均温度的影响,因而将式(5)中的hs和h′作为待拟合系数,整理得:
| $ {T_m} = {d_1}T_s^2 + {d_2}\delta {T_s} + \frac{{{d_3}\delta }}{{{T_s}}} + \frac{{{d_4}{\delta ^2}}}{{T_s^2}} + {d_5}{\delta ^2} + {d_0} $ | (7) |
式中,di(i=0, 1, …, 5)为待拟合系数。
为方便讨论温度递减率对加权平均温度的影响,引入ratio值来评定标准差比值。记式(6)和式(7)的标准差分别为RMSE0和RMSE1,则:
| $ {\rm{ratio}} = \frac{{{\rm{RMS}}{{\rm{E}}_0} - {\rm{RMS}}{{\rm{E}}_1}}}{{{\rm{RMS}}{{\rm{E}}_0}}} $ | (8) |
可以看出,如果RMSE1与RMSE0的差值越大,则说明温度递减率对加权平均温度精度的提高贡献越大。
由图 3(a)可见,RMSE1整体居于RMSE0的下方,表明RMSE1的值整体小于RMSE0,即考虑了温度递减率的加权平均温度模型拥有更高的精度。由图 3(b)可见,ratio值整体随纬度呈现递减的趋势,表明温度递减率对于加权平均温度模型精度提高的贡献是随着纬度的增加而逐渐降低的。
3 结语温度递减率与地表温度有强烈的线性相关性。温度递减率在纬度低于35°区域呈线性递减; 在35°~40°区域内逐渐离散; 在40°以上的区域内变化无规律。温度递减率反映对流层内垂直温度廓线上的变化关系,其四季的变化与对流层顶层的变化表现出相同的趋势。因此,它可以作为判断对流层结构稳定性的参考依据。
温度递减率在纬度35°以内,可以建立区域公式。温度递减率对于加权平均温度有影响,在单个探空站拟合中,它可以有效提高加权平均温度的精度; 在区域拟合中,它可以改善模型拟合值的分布,其精度平均提升0.3 K左右。
| [1] |
Angell J K, 周国华. 1960~1985年对流层和平流层低层全球温度的年、季变化[J]. 气象科技, 1988(1): 52-58 (Angell J K, Zhou Guohua. Annual and Seasonal Variations of Global Temperature in the Troposphere and Lower Stratosphere from 1960 to 1985[J]. Meteorological Science and Technology, 1988(1): 52-58)
(  0) 0) |
| [2] |
李启泰. 对福安地区温度垂直递减率的一些分析[J]. 农业气象, 1980, 1(4): 50-55 (Li Qitai. Some Analysis of Vertical Decline Rate of Temperature in Fu'an Area[J]. Chinese Journal of Agrometeorology, 1980, 1(4): 50-55)
(  0) 0) |
| [3] |
罗贵东, 夏利, 古书鸿. 四川省各温度范围内积温特征分析[J]. 贵州气象, 2016, 40(6): 42-47 (Luo Guidong, Xia li, Gu Shuhong. Analysis of the Characteristics of Accumulated Temperature in Each Degree Celsius in Sichuan[J]. Journal of Guizhou Meteorology, 2016, 40(6): 42-47 DOI:10.3969/j.issn.1003-6598.2016.06.008)
(  0) 0) |
| [4] |
郭劲秋.中低层大气温度和气溶胶廓线的拉曼激光雷达探测研究[D].南京: 南京信息工程大学, 2012 (Guo Jingqiu.The Detection of Temperature and Aerosol Profiles in Middle and Lower Atmosphere Using Raman Lidar[D]. Nanjing : Nanjing University of Information Science & Technology, 2012) http://cdmd.cnki.com.cn/Article/CDMD-10300-1012369307.htm
(  0) 0) |
| [5] |
姚宜斌, 刘劲宏, 张豹, 等. 地表温度与加权平均温度的非线性关系[J]. 武汉大学学报:信息科学版, 2015, 40(1): 112-116 (Yao Yibin, Liu Jinghong, Zhang Bao, et al. Nonlinear Relationship between the Surface Temperature and the Weighted Mean Temperature[J]. Geomatics and Information Science of Wuhan University, 2015, 40(1): 112-116)
(  0) 0) |
| [6] |
高攀, 徐晓华, 张小红, 等. 利用GPS掩星弯曲角确定对流层顶高度[J]. 武汉大学学报:信息科学版, 2012, 37(12): 1 417-1 420 (Gao Pan, Xu Xiaohua, Zhang Xiaohong, et al. Identification of Tropopause Height from GPS Radio Occultation Bending Angle Profile[J]. Geomatics and Information Science of Wuhan University, 2012, 37(12): 1 417-1 420)
(  0) 0) |
| [7] |
徐晓华, 高攀, 张小红. 利用COSMIC掩星弯曲角数据分析中国区域对流层顶结构变化[J]. 地球物理学报, 2013, 56(8): 2 531-2 541 (Xu Xiaohua, Gao Pan, Zhang Xiaohong. Structure and Variation of the Tropopause over China with COSMIC Radio Occultation Bending Angles[J]. Chinese Journal of Geophysics, 2013, 56(8): 2 531-2 541)
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39


