2. 西安测绘研究所,西安市雁塔路中段1号,710054;
3. 地理信息工程国家重点实验室,西安市雁塔路中段1号,710054
对于甚长基线干涉测量(VLBI)、全球导航卫星系统(GNSS)等空间大地测量技术,对流层延迟是一项重要误差源。该延迟与传播路径上的气象因素直接相关,但由于VLBI、GNSS等测站附近的空间气象条件存在非对称性,即使观测高度角相同,来自不同方位的无线电信号在抵达接收天线时也会产生不同的延迟量[1],这种差异在精密空间大地测量中不可忽略。目前计算对流层延迟的方法可分为两类,即利用传播路径上气象数据的直接积分法(也称射线追踪法)和利用空间大地测量观测数据的间接估计法。针对前一种方法,学者们先后利用无线电探空仪[2]、水汽辐射仪[3-4]等设备观测的气象数据及加拿大气象中心(CMC)[5]、美国航空航天局(NASA)[6]、欧洲中尺度气象预报中心(ECMWF)[7]等机构提供的数值天气模型(NWM)计算得到与方位角相关的对流层延迟。虽然该方法可更直接、精确地得到延迟结果,但往往需要已知测站上空各高度层面的准确气象信息,因此实时性较弱。相比之下,VLBI等技术可将对流层延迟作为待估参数与位置、速度等参数一并估计[8],故常作为实时解算的主要方法。在此基础上,本文提出一种对流层延迟水平梯度的精化方法。实验表明,该方法可更精确地反映对流层延迟在各方位角的实际情况,有效提高VLBI数据的解算精度。
1 基本原理 1.1 对流层延迟估计利用VLBI、GNSS等空间大地测量观测数据可实时估计任意方向的斜路径对流层延迟,具体估计公式为[1]:
| $ L = {L_{{\rm{sys}}}} + {L_{{\rm{az}}}} + {g_{{\rm{bend}}}} $ | (1) |
式中,Lsys为对称延迟,即假定延迟与方位角无关时的值; Laz为非对称延迟; gbend为几何弯曲改正[9]。Lsys和Laz可表示为[10]:
| $ {L_{{\rm{sys}}}} = L_{\rm{h}}^z{m_{\rm{h}}}(e) + L_{\rm{w}}^\mathit{z}{m_{\rm{w}}}(e) $ | (2) |
| $ {L_{{\rm{az}}}} = {L_{{\rm{ns}}}}{m_{{\rm{az}}}}(e)\cos \alpha + {L_{{\rm{ew}}}}{m_{{\rm{az}}}}(e)\sin \alpha $ | (3) |
式中,
| $ {m_{{\rm{h}}/{\rm{w}}}}(e) = \frac{{1 + \frac{{{a_{{\rm{h}}/{\rm{w}}}}}}{{1 + \frac{{{b_{{\rm{h}}/{\rm{w}}}}}}{{1 + {c_{{\rm{h}}/{\rm{w}}}}}}}}}}{{\sin e + \frac{{{a_{{\rm{h}}/{\rm{w}}}}}}{{\sin e + \frac{{{b_{{\rm{h}}/{\rm{w}}}}}}{{\sin e + {c_{{\rm{h}}/{\rm{w}}}}}}}}}} $ | (4) |
| $ {m_{{\rm{az}}}}(e) = \frac{1}{{{\rm{ sin}}\mathit{e}{\rm{tan}}\mathit{e}{\rm{ }} + 0.003\;2}} $ | (5) |
式中,ah/w、bh/w、ch/w为干/湿分量的映射函数系数。
将已有的天顶对流层延迟模型作为先验信息,并按照常用的映射函数模型(如NMF、GMF、VMF1等)计算mh(e)、mw(e),即可根据空间大地测量观测值估计出Lhz、Lwz、Lns、Lew,进而得到任意方向的斜路径延迟。
在求取该延迟过程中用到的非对称延迟Laz,其实质是斜路径对流层延迟在方位角域的一阶傅里叶级数展开,并忽略了高阶项,而maz(e)的作用则是剥离延迟与高度角的相关性。可以想象,在气象条件复杂的地区,这种一阶近似产生的截断误差有可能导致数据解算过程中出现不可忽略的影响。后文将针对这一情况进行详细研究。
1.2 射线追踪电磁波在大气中传播时可视为一道“弯曲的”射线。假设测站上空的大气被分为k个层面,si表示射线在层面间的传播路径,近似为直线段,ni表示si路径上的大气平均折射率。于是,该方向的斜路径延迟L为:
| $ \begin{array}{l} L = \sum\limits_{i = 1}^{k - 1} {\left[ {\left( {{n_i} - 1} \right){s_i}} \right]} + {g_{{\rm{bend}}}} = \\ \;\;\;\;\;\;{10^{ - 6}}\sum\limits_{i = 1}^{k - 1} {{N_i}} {s_i} + {g_{{\rm{ bend }}}} \end{array} $ | (6) |
式中,gbend为几何弯曲改正; Ni为大气折射指数,可按下式求取:
| $ \begin{array}{l} {N_i} = \left( {{n_i} - 1} \right) \times {10^6} = {k_1}\frac{{p_i^{\rm{d}}}}{{{T_i}}}{\left( {Z_i^{\rm{d}}} \right)^{ - 1}} + \\ \;\;\;\;\;\;{k_2}\frac{{p_i^{\rm{w}}}}{{{T_i}}}{\left( {Z_i^{\rm{w}}} \right)^{ - 1}} + {k_3}\frac{{p_i^{\rm{w}}}}{{T_i^2}}{\left( {Z_i^{\rm{w}}} \right)^{ - 1}} \end{array} $ | (7) |
式中,k1、k2、k3为常数,取值分别为77.689 K/hPa、71.295 2 K/hPa、375 463 K2/hPa;
本文在后续实验中提及的对流层延迟真实值即为利用ECMWF提供的ERA-interim分层格网气象数据,按照射线追踪原理计算得到的结果。该数据融合了探空气球、气象卫星、地面气象站等多源气象数据,具有较高的权威性,但实时性不足,一般延迟3个月左右。
2 实验与分析 2.1 方位角与斜路径对流层延迟的关系选取武夷山、上海、西安、乌鲁木齐4个地区进行研究(表 1),其年平均降水量分别为2 000 mm以上、1 500~1 600 mm、500~600 mm、200~300 mm,分别代表气候非常湿润、湿润、干燥、非常干燥4种地理环境。
|
|
表 1 待研究地区的大地坐标 Tab. 1 Geodetic of the studied area |
根据射线追踪方法,同时采用ECMWF ERA-interim分层气象数据计算以上4个地区2016年全年6 h分辨率的对流层延迟值,包括360个方位角(0°, 1°, …, 359°)及16个高度角(5°, 6°, …, 10°, 12°, 15°, 20°, 25°, 30°, 40°, …, 80°)方向的斜路径延迟,并将其作为真实值。
利用式(8),统计不同高度角在时域上不同方位角的最大延迟差:
| $ \Delta L_a^e(t) = L_{{a_{\max }}}^e(t) - L_{{a_{\min }}}^e(t) $ | (8) |
式中,t为年积日;
仅选取6个高度角为代表,最大延迟差如图 1所示。高度角域不同方位角的最大延迟差如图 2。
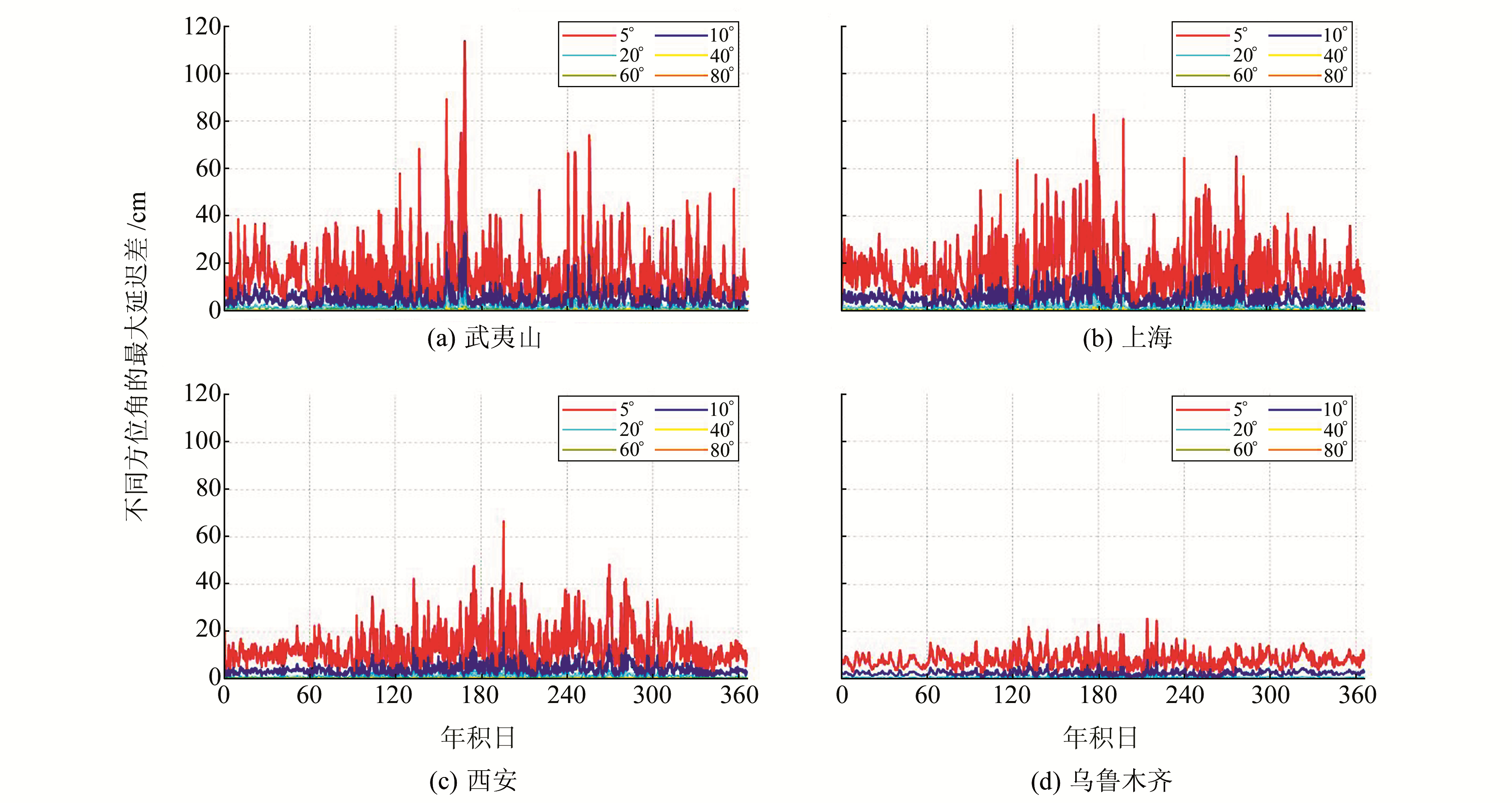
|
图 1 2016年各天对流层延迟在不同高度角、方位角的最大差值 Fig. 1 The maximum differences of tropospheric delay at different elevation and azimuth angles in 2016 |
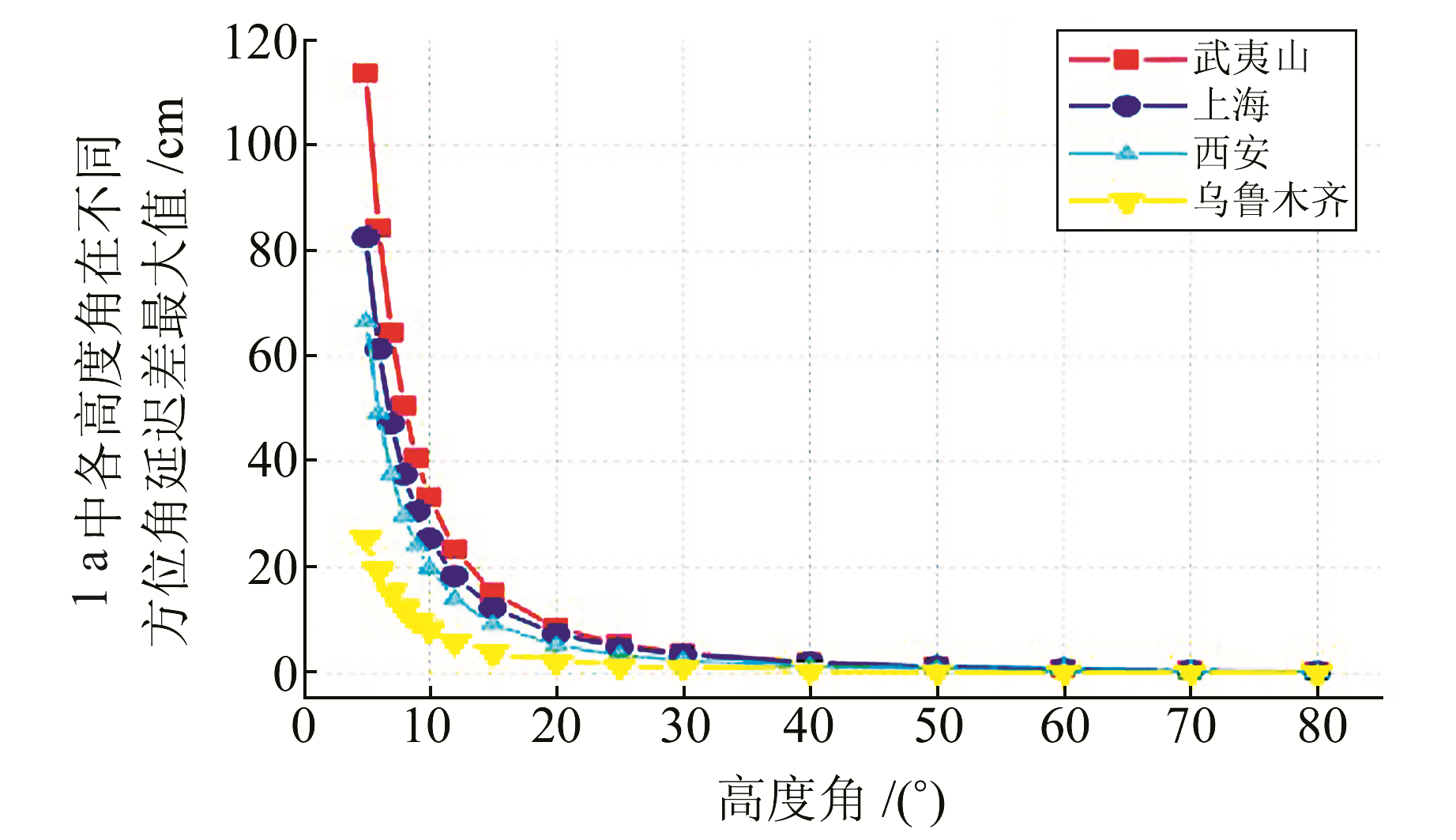
|
图 2 对流层延迟在各高度角、不同方位角的最大差值 Fig. 2 Maximum differences of tropospheric delay at different elevation and azimuth angles |
从图 1、图 2可以看出,方位角与斜路径对流层延迟的关系是:1)在低高度角范围,方位角对斜路径对流层延迟的影响最大可达m级。随着高度角的增大,尤其是5~15°范围,这种影响迅速衰减; 当高度角为20°时,降至cm量级,随后降低趋势减弱。2)随着气候类型从湿润变为干燥,这种影响也随之削弱,如乌鲁木齐在5°高度角时的影响与上海地区10°时的影响相当。之所以出现这种情况,主要是因为对流层延迟与大气中的水汽量密切关联。水汽主要集中在地表 10~12 km以下,随着高度角的增大,被水汽覆盖的信号路径向测站收拢,故受水汽影响的路程逐渐减少。同时由于研究区域半径缩减,不同方位地区的气象条件逐渐与测站趋于一致,进而各方位角延迟的差异逐渐削弱。对于气候湿润地区,其水汽活跃度较高,导致不同方位的水汽含量差别较大,使得延迟影响出现较明显的差异,反之亦然。
考虑到武夷山地区方位角对对流层延迟的影响最大,故后文主要针对该地区进行研究,分析改进对流层延迟水平梯度对结果的影响。
2.2 对流层延迟水平梯度改进根据§1方法,可估计得到对流层延迟水平梯度,进而得到不同方位角的斜路径对流层延迟。利用ERA-interim气象数据,计算并绘出武夷山地区2016年年积日为180、高度角为5°时3个不同时刻对流层延迟在各方位角的情况,如图 3。图中相同颜色的实线、虚线分别表示对应时刻的延迟真实值和利用一阶傅里叶级数的拟合值,可以看出,两者最大差值可达4 cm。
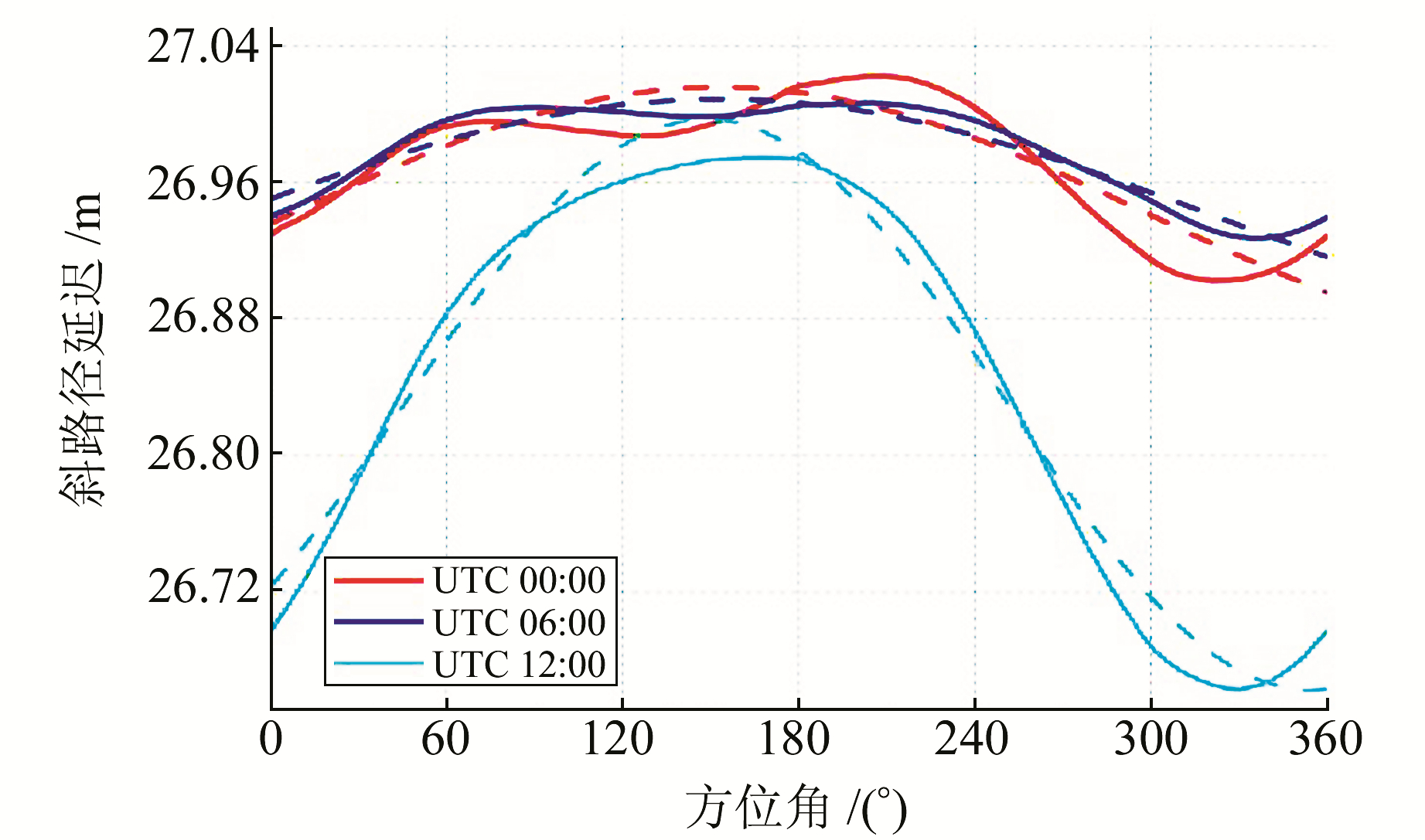
|
图 3 2016年年积日为180、高度角为5°时对流层延迟在各方位角的值 Fig. 3 Values of tropospheric delay in azimuth when doy is 180 and elevation angle is 5° in 2016 |
对武夷山地区方位角域进行频谱分析,并在时域上统计各天的具体振幅,如图 4。从频谱结果可知,周期为360°的分量平均约占总能量的80%,180°周期的分量占13%左右,120°周期的分量约占2%,其余所有分量的总和仅占5%。故后文考虑在原对流层延迟水平梯度的基础上增加二阶、三阶项(分别对应180°和120°周期分量),并研究逼近效果。
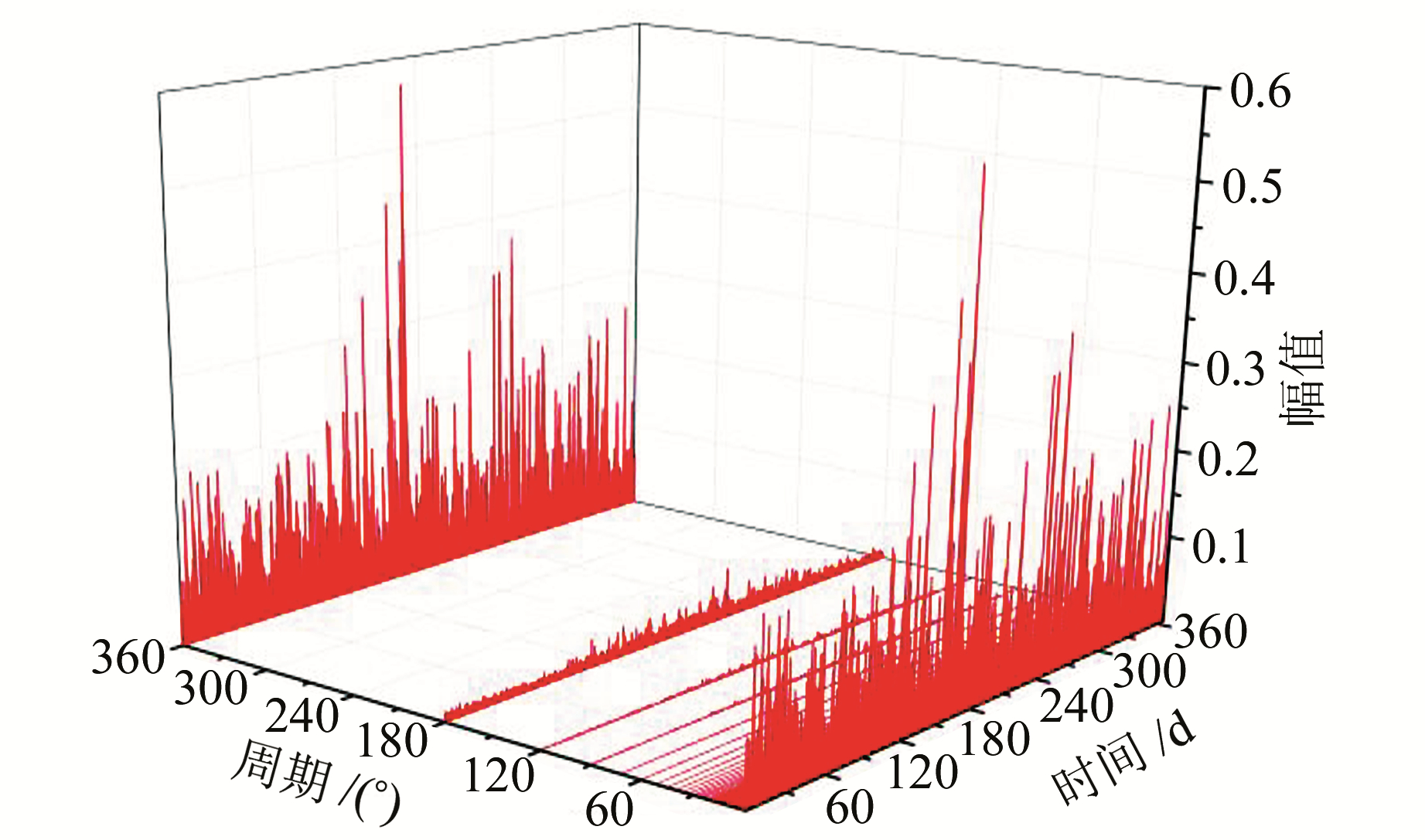
|
图 4 2016年各日对流层延迟在高度角为5°时方位角域的频谱统计 Fig. 4 Spectrum statistics of tropospheric delays in azimuth domain at elevation angle of 5° on each day of 2016 |
分别利用一阶、二阶及三阶傅里叶级数拟合高度角为5°、10°时各方位角的斜路径对流层延迟,并统计各天方位角域的拟合中误差,如图 6。可以看出,二阶级数的拟合效果明显优于一阶,提高约6倍; 随着高度角的增大,这种改进效果并未减小。但由于高度角增大后,方位角对延迟的影响迅速衰减,故可考虑在高度角大于10°时仅用一阶级数拟合即可。另外,相比二阶级数,三阶级数的改进效果大大减弱,因此在低高度角范围建议使用二阶级数,可在保障精度的前提下限制待估参数的个数,控制计算量。
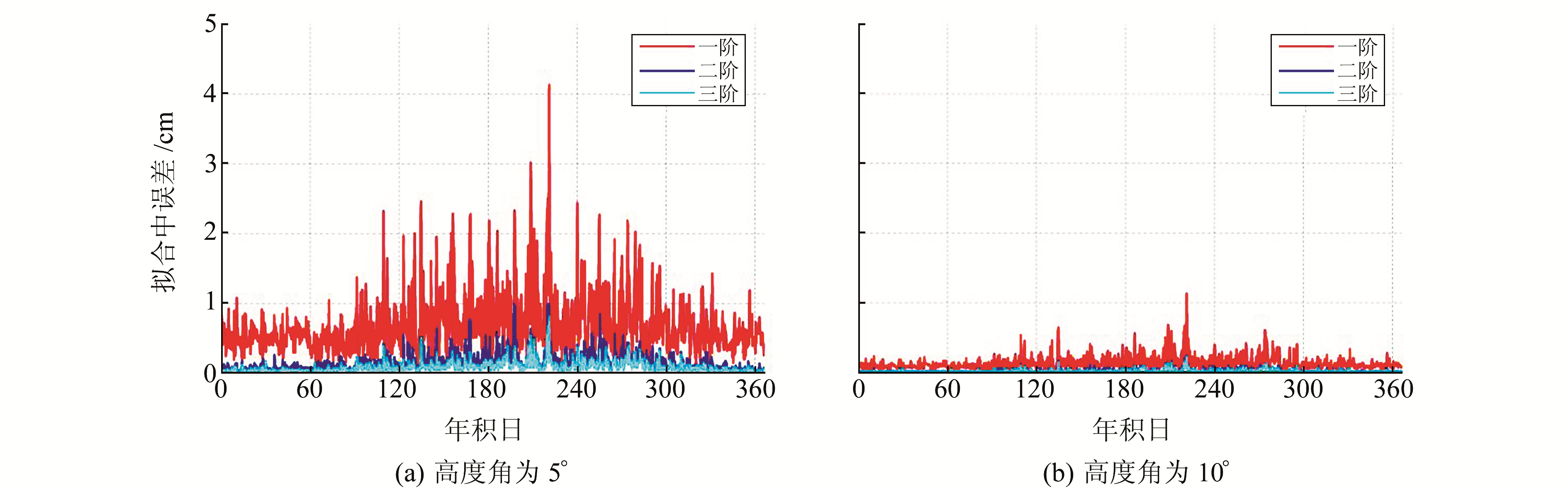
|
图 5 2016年各日利用3种阶数的傅里叶级数拟合不同方位角对流层延迟的中误差统计 Fig. 5 Statistics of fitting results of the formal error of tropospheric delay in different azimuth directions by Fourier series of three orders on each day of 2016 |
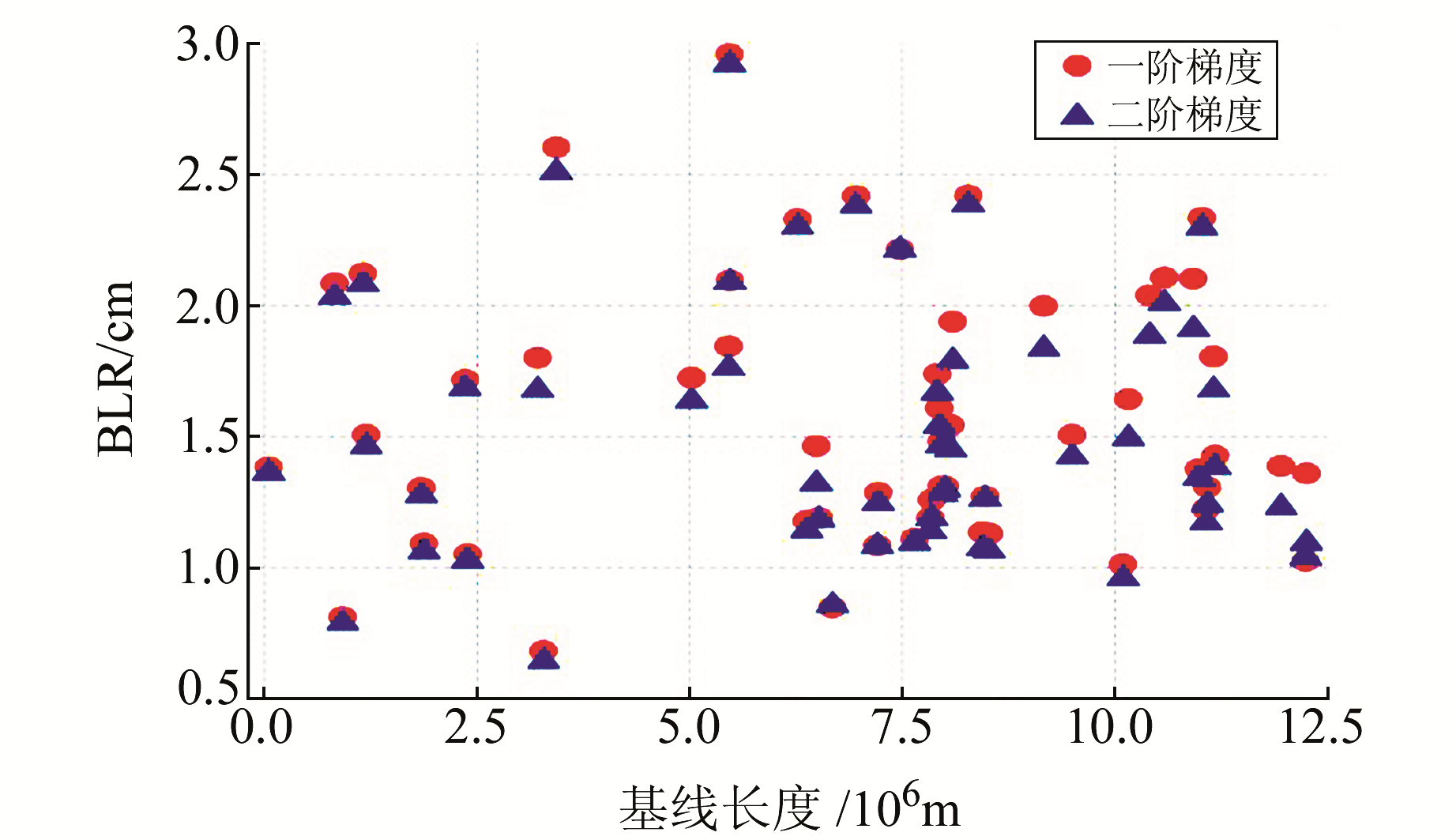
|
图 6 2种梯度估计方法的BLR统计 Fig. 6 BLR statistics of two gradient estimation methods |
为分析一阶、二阶对流层延迟水平梯度对实际测量结果的影响,以下利用国际大地天文VLBI服务(international VLBI service for geodesy and astrometry,IVS)官网上公布的2017-04-18 VLBI实测数据进行研究。该session共有11个测站参与,构成55条基线; 观测射电源75颗,包含7 734个observation、1 131个scan。
利用维也纳技术大学开发的VieVS软件对该session数据进行处理,并按本文提出的方法进行解算,同时与原方法(仅采用一阶梯度)结果对比。各参数估计策略见表 2。
|
|
表 2 参数解算策略 Tab. 2 Parameter resolution strategy |
采用基线可重复度(baseline repeatability,BLR)作为精度指标,统计2种梯度的解算情况如图 6,其中BLR的计算方法见式(9):
| $ {\rm{BLR}} = \sqrt {\frac{{\sum\limits_{i = 1}^n {{w_i}} {{\left( {{b_i} - \bar b} \right)}^2}}}{{\sum\limits_{i = 1}^n {{w_i}} - \left( {\sum\limits_{i = 1}^n {w_i^2} } \right)/\left( {\sum\limits_{i = 1}^n {{w_i}} } \right)}}} $ | (9) |
式中,bi、wi分别为第i条基线的长度及其权重; b为所有基线的加权平均值,一般情况下可设各基线等权。另外,利用射线追踪原理并结合ERA-interim空间分层格网气象数据,计算该日的天顶对流层延迟。将该结果作为真实值,统计2种方法估计的天顶对流层延迟的bias(取绝对值)和STD精度如图 7。

|
图 7 2种梯度估计方法解算的天顶对流层延迟精度统计 Fig. 7 Statistics of zenith tropospheric delay accuracy solved by two gradient estimation methods |
由图 6可见,加入二阶梯度项后,各基线BLR均有不同程度的改善,平均改善幅度约4%。由图 7可见,除个别测站外,二阶梯度项加入后,天顶对流层延迟估计值的bias和STD误差均小于仅用一阶梯度时的情况,分别降低17.2%、13.3%左右。另外,本文所用数据中低高度角观测量较少,平均每测站5°~10°的观测次数仅占总数的7.02%。所以有理由相信,如某次session中低高度角观测比例较大,这种方法的改进效果将更好。
3 结语本文首先对不同气候条件的4个地区进行研究,分析各地在不同高度角时方位角对斜路径对流层延迟的影响。针对一阶对流层延迟水平梯度不能有效反映低高度角范围对流层延迟的非对称性这一情况,提出一种水平梯度的精化方法。根据本文研究,得到以下结论:1)在不同高度角范围,可灵活选取对流层延迟水平梯度的阶数,如可在高度角10°以下时用二阶、大于10°时用一阶。2)不同气象条件的地区可选择不同的对流层延迟估计策略,如武夷山、上海等地在5°~10°高度角时水平梯度需用二阶,而乌鲁木齐等地则只用一阶即可,从而既保证精度,又不至于增加过多的待估参数。但也并非一成不变,如干燥地区在观测期间恰逢阴雨天气,也可考虑用二阶梯度。3)在当前GNSS定位中,因多路径效应等因素的影响,基本会将截止高度角设置为15°,所以本文的研究结果更适用于VLBI观测。
| [1] |
Chen G, Herring T A. Effects of Atmospheric Azimuthal Asymmetry on the Analysis of Space Geodetic Data[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B9): 20 489-20 502 DOI:10.1029/97JB01739
(  0) 0) |
| [2] |
Gardner C S. Correction of Laser Tracking Data for the Effects of Horizontal Refractivity Gradients[J]. Applied Optics, 1977, 16(9): 2 427-2 433 DOI:10.1364/AO.16.002427
(  0) 0) |
| [3] |
Dixon T H, Wolf S K. Some Tests of Wet Tropospheric Calibration for the CASA Uno Global Positioning System Experiment[J]. Geophysical Research Letters, 1990, 17(3): 203-206 DOI:10.1029/GL017i003p00203
(  0) 0) |
| [4] |
Ware R, Alber C, Rochen C, et al. Sensing Integrated Water Vapor along GPS Ray Paths[J]. Geophysical Research Letters, 1997, 24(4): 417-420 DOI:10.1029/97GL00080
(  0) 0) |
| [5] |
Urquhart L, Nievinski F G, Santos M C. Ray-Traced Slant Factors for Mitigating the Tropospheric Delay at the Observation Level[J]. Journal of Geodesy, 2013, 87(10): 981-1 001
(  0) 0) |
| [6] |
Ericsson D, MacMillan D S, Gipson J M. Tropospheric Delay Ray Tracing Applied in VLBI Analysis[J]. Journal of Geophysical Research: Solid Earth, 2014, 119(12): 9 156-9 170 DOI:10.1002/2014JB011552
(  0) 0) |
| [7] |
Hofmeister A, Böhm J. Application of Ray-Traced Tropospheric Slant Delays to Geodetic VLBI Analysis[J]. Journal of Geodesy, 2017, 91(8): 945-964 DOI:10.1007/s00190-017-1000-7
(  0) 0) |
| [8] |
Petit G, Luzum B. Models for Atmospheric Propagation Delays[C]. IERS Conventions 2010, Frankfurt, 2010
(  0) 0) |
| [9] |
Davis J L, Herring T A, Shapiro I I, et al. Geodesy by Radio Interferometry: Effects of Atmospheric Modeling Errors on Estimates of Baseline Length[J]. Radio Science, 1985, 20(6): 1 593-1 607 DOI:10.1029/RS020i006p01593
(  0) 0) |
| [10] |
Niell A E. Global Mapping Functions for the Atmospheric Delay at Radio Wavelengths[J]. Journal of Geophysical Research, 1996, 101(B2): 3 227-3 246 DOI:10.1029/95JB03048
(  0) 0) |
| [11] |
郭际明, 章迪, 史俊波, 等. 利用射线追踪法分析3种典型对流层映射函数在中国区域的精度[J]. 武汉大学学报:信息科学版, 2015, 40(2): 182-187 (Guo Jiming, Zhang Di, Shi Junbo, et al. Using Ray-Tracing to Analyze the Precision of Three Classical Tropospheric Mapping Functions in China[J]. Geomatics and Information Science of Wuhan University, 2015, 40(2): 182-187)
(  0) 0) |
2. Institute of Surveying and Mapping, 1 Mid-Yanta Road, Xi'an 710054, China;
3. State Key Laboratory of Geo-Information Engineering, 1 Mid-Yanta Road, Xi'an 710054, China
 2019, Vol. 39
2019, Vol. 39

